Assessing the Impact of Assimilated Remote Sensing Retrievals of Precipitation on Nowcasting a Rainfall Event in Attica, Greece

Abstract

Accurate short-term rainfall forecasting, an essential component of the broader framework of nowcasting, is crucial for managing extreme weather events. Traditional forecasting approaches, whether radar-based or satellite-based, often struggle with limited spatial coverage or temporal accuracy, reducing their effectiveness. This study tackles these challenges by implementing the Local Analysis and Prediction System (LAPS) enhanced with a forward advection nowcasting module, integrating multiple remote sensing rainfall datasets. Specifically, we combine weather radar data with three different satellite-derived rainfall products (H-SAF, GPM, and TRMM) to assess their impact on nowcasting performance for a rainfall event in Attica, Greece (29–30 September 2018). The results demonstrate that combined high-resolution radar data with the broader coverage and high temporal frequency of satellite retrievals, particularly H-SAF, leads to more accurate predictions with lower uncertainty. The assimilation of H-SAF with radar rainfall retrievals (HX experiment) substantially improved forecast skill, reducing the unbiased Root Mean Square Error by almost 60% compared to the control experiment for the 60 min rainfall nowcast and 55% for the 90 min rainfall nowcast. This work validates the effectiveness of the specific LAPS/advection configuration and underscores the importance of multi-source data assimilation for weather prediction.

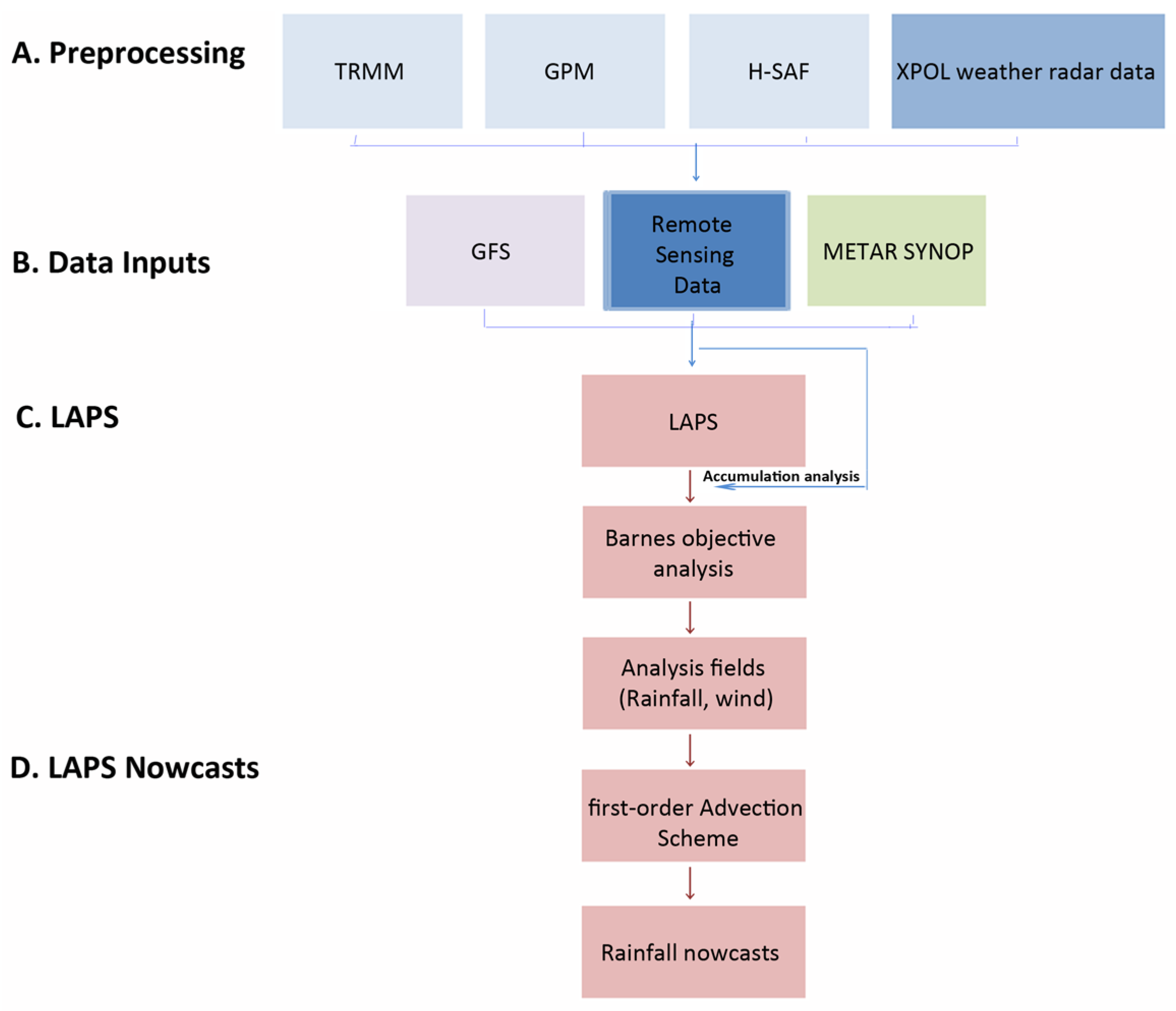
1. Introduction

The rainfall forecast in a short term has been a challenge over the last few decades. Weather forecasts that focus on a short time period of the next few minutes up to six hours ahead and have high temporal and spatial resolution are referred to as the term nowcasting [1,2,3,4]. Nowcasting refers to a detailed analysis and description of current weather conditions and their evolution over very short periods, typically up to six hours ahead, as defined by the World Meteorological Organization [5]. Accurate short-term rainfall forecasting, which is a component of nowcasting, is essential for managing high-impact weather events. Nowcasting is connected with data assimilation in meteorology to improve forecasts for short lead times. The data assimilation cycle entails a number of processes that are repeated, including the collection of observations, the short-range forecast, the comparison of the forecast and observations, and the development of an analysis that combines the forecast and observations. An essential setting that corresponds to the dynamical scales addressed by the observation system and the numerical model is the cycle length in sequential data-assimilating forecasting systems [6]. The cycle’s duration influences how frequently new observations are included into the model. Modern nowcasting often relies on radar and satellite observations, which have complementary strengths: radar offers high-resolution making it possible to monitor rainfall dynamics in detail [7,8], while satellites provide broader coverage [9]. However, both sources have limitations: radar may suffer limited range, and satellite retrievals may have coarser resolution or longer latency. Moreover, numerical models exhibit a “spin-up” problem at small scales, making pure model forecasts unreliable at less than 3 h lead times. To overcome these challenges, blending multiple data sources via data assimilation has become a promising approach.

Previous studies have demonstrated that assimilating radar or satellite data can improve short-term rainfall forecasts [10]. For example, assimilation of radar reflectivity into mesoscale models can improve heavy rainfall prediction [11,12] and radar-derived water vapor retrievals significantly improve rainfall predictions [13,14,15]. Similarly, incorporating satellite-derived rainfall fields into models has shown skill improvements [16,17,18]. Several studies have investigated the assimilation of both radar and satellite rainfall data to improve quantitative rainfall forecasting, demonstrating that combining these observational systems can significantly enhance forecast performance [10,19,20,21,22].

This study aims to build on these findings by investigating the sensitivity of the rainfall nowcasts regarding the assimilation of weather radar data and satellite retrievals. The primary goal is to evaluate how the characteristics of satellite-derived rainfall estimates, such as spatial and temporal resolution, impact the quality of short-term forecasts. The approach involves implementing the Local Analysis and Prediction System (LAPS), configured with a recently developed nowcasting scheme. It is a forward advection scheme which relies on assimilating radar and satellite-derived rainfall retrievals to provide a more complete description of the atmospheric state at a given time. For the purpose of this study the rainfall event affected Athens metropolitan area in Greece on 29 and 30 September 2018, is used. Specifically, it has been assessed how the assimilation of satellite data combined with radar data impacts the accuracy of rainfall nowcasts. The choice of Attica is motivated by its complex topography and coastal influences, which can lead to localized and rapidly evolving rainfall events, making accurate nowcasting particularly challenging and valuable for the region. The availability of high-quality, high-resolution XPOL radar data in this region provides a unique opportunity to assess the impact of integrating such data with different satellite products. Although this study focuses on the Athens metropolitan area as a case study, the methodology and findings are not limited to this location and can be applied to other regions.

While high-resolution radar data alone could support nowcasting through extrapolation techniques such as pySTEPS [23], these approaches are limited in coverage and cannot represent regions outside the radar range. The integration of satellite data ensures broader spatial coverage and enables dynamically consistent initialization of the atmospheric state. By assimilating both data sources within the LAPS, our approach aims to improve the rainfall nowcasting.

The main motivation of this study is to overcome the challenges and limitations of current rainfall nowcasting systems, particularly in achieving accurate and reliable short-term forecasts. Traditional numerical weather prediction (NWP) models suffer from the “spin-up” problem, which occurs during the first few hours of simulations. Additionally, conventional systems often rely on meteorological data from surface weather stations with coarse spatial coverage. These limitations reduce their ability to effectively capture localized and rapidly evolving rainfall events. Thus, the specific contributions of this study are:

• Implementation of a forward-advection nowcasting module within LAPS.
• Evaluation of three assimilation configurations (CTRL, GTX, HX) to assess the impact of radar and satellite retrievals on nowcasting.
• Significant error reduction by the implementation of X-band weather radar estimates blended with H-SAF satellite retrievals.

The method and the description of the data utilized for this study are provided in Section 2. The study area and the synoptic analysis of the event are described in Section 3. Section 4 provides the results, and a thorough discussion and Section 5 summarizes entire outcomes.

2. Methods and Data

Short-term weather forecasting remains a challenge due to the rapid evolution of rainfall events and the limitations of conventional prediction models. This study explores the question: How does integrating high-resolution radar and satellite rainfall retrievals improve nowcasting accuracy compared to conventional methods? To address this, we designed three assimilation experiments:

• CTRL (Baseline): Relies only to the Global Forecast System (GFS) background forecasts combined with METAR and SYNOP in-situ observations.
• GTX Experiment: Incorporates XPOL radar data alongside satellite retrievals from GPM IMERG and TRMM and METAR and SYNOP in-situ observations.
• HX Experiment: Combines XPOL radar data and METAR and SYNOP in-situ observations with H-SAF rainfall retrievals for improved temporal resolution.

Unlike traditional methods that depend solely on radar or satellite data, our approach dynamically integrates multiple sources within LAPS, allowing real-time adjustments in rainfall estimation. The novelty of this approach lies not only in its ability to balance fine-detail radar observations with broad satellite coverage, but also in demonstrating that implementing a forward advection scheme improves forecast accuracy compared to the control experiment, highlighting the benefits of combining satellite and radar data. Although a direct comparison with external nowcasting systems was not conducted, the performance observed in this study is consistent trends reported in other nowcasting studies [24].

The nowcasting method relies on the deployment of a mesoscale 3D-Var data assimilation system, the Local Analysis and Prediction System (LAPS) developed by NOAA. The impact of various remote sensing retrievals on the nowcasting skill of a rainfall event that affected the Athens metropolitan area in Greece on 29 and 30 September 2018 is analyzed. LAPS is a tool for assimilation of mesoscale meteorological data, developed to assimilate data from all available sources, including radar, soundings, satellite, aircraft and meteorological networks and produce a three-dimensional depiction of atmospheric processes that evolves over time and is spatially distributed [25,26]. The Local Analysis and Prediction System (LAPS) was selected for this study due to its ability to provide a simple and effective framework for assimilating a variety of observational data sources, including radar and satellite retrievals, in real-time nowcasting applications. LAPS offers a computationally efficient approach that is particularly suitable for short-term rainfall forecasting, where rapid updates and high temporal resolution are critical [27,28]. While more complex data assimilation systems exist, the results of this study demonstrate that even a simplified system can substantially improve short-term rainfall forecasts.

Before being assimilated into LAPS, the remote sensing data undergoes preprocessing to ensure compatibility. The Radar (XPOL) data is processed using the Self-Consistent Optimal Parameterization-Microphysics Estimation (SCOPE-ME) algorithm [29] and are regridded to the LAPS spatial domain, covering 110 × 110 grid points over Attica, with a spatial resolution of 1 km. Satellite rainfall products from Global Precipitation Measurement (GPM), Tropical Rainfall Measuring Mission (TRMM) and EUMETSAT Satellite Application Facility on Support to Operational Hydrology and Water Management (H-SAF) are processed using the Integrated Multi-satellitE Retrievals for GPM (IMERG) [30], TRMM 3B42 [31], and Blending MW/IR [32] algorithms, respectively. These data are reformatted to LAPS-compatible formats and used as surface rainfall observations (gauge observations).

LAPS employs a three-dimensional variational (3DVAR) assimilation minimizing the difference between observed and model-predicted fields [33], as described by the cost function in Equation (1).

$$J\left(x\right)={\displaystyle \frac{1}{2}}{\left(x-x_b\right)}^T{B}^{-1}\left(x-x^b\right)+{\displaystyle \frac{1}{2}}{\left(H\left(x\right)-y\right)}^T{O}^{-1}\left(H\left(x\right)-y\right)$$

(1)

where B refers to the model error covariance matrix, O denotes the observational error matrix, x corresponds to the control variable, x_b represents the background field, y represents the observation values and H denotes the observation operator. The observation operator H is implemented as a bilinear interpolation operator, which is the link the observation and the model, the background error covariance is derived from multiple iterations of a recursive filter [34] and the observational error is a diagonal matrix.

The assimilation process begins with background first guess fields (forecasts near-to-analysis) derived from the Global Forecast System (GFS) which has a horizontal resolution of 0.25° × 0.25° and is interpolated to the LAPS grid as initial first guess fields. The Global Forecast System (GFS), a widely used numerical weather prediction model, serves as the primary source of background fields in our configuration. Then, multiple data sources, including radar, satellite, and in-situ observations are integrated into LAPS to produce high-resolution analysis fields.

The accumulation analysis for rainfall is based on the Barnes objective analysis, which is designed to blend different data sources effectively. In this study, satellite precipitation products are reformatted and ingested into LAPS as surface observations. Then these satellite-derived observations are blended with the gridded XPOL radar data using the successive correction method of the Barnes multi-pass iteration to perform accumulation analysis for rainfall [27,28]. The process unfolds in two main steps. First, a linear regression is conducted on valid radar–gauge observations pairs to correct biases in the radar estimates across all grid points. Following the bias correction, the successive correction method of the Barnes multi-pass iteration is used to blend and weight the observations with the background fields. This process continues until the consecutive corrections become insignificant. During each iteration, the differences between the observations and the background, along with their corresponding Root Mean Square (RMS) errors are computed. The weights that are assigned to observations are based on representativeness errors and errors of the instruments, while the weight of background points is chosen to accurately reflect the background error [28].

To predict the movement of rainfall, an advection scheme was integrated into LAPS for a 1–3 hours’ time horizon. This scheme models the spatial evolution of rainfall by solving the two-dimensional advection equation, using wind fields derived from LAPS-assimilated data. The process begins with the rainfall fields produced by LAPS, which is then advected in time using the horizontal wind components (u and v) at each grid point. This scheme relied on the advection equation in the x and y directions, which is a first order equation:

$${\displaystyle \frac{𝜕R}{𝜕t}}+u{\displaystyle \frac{𝜕R}{𝜕x}}+v{\displaystyle \frac{𝜕R}{𝜕y}}=0$$

(2)

where, R represents the rainfall rate, t is time, u and v are in the x and y directions, respectively, x and y are the spatial coordinates.

To implement this numerically, the Equation (2) is discretized as follows:

$${\displaystyle \frac{1}{\Delta t}}\left(R_{i,j}^{t+1}-R_{i,j}^t\right)+{\displaystyle \frac{u}{\Delta x}}\left(R_{i,j}^t-R_{i-1,j}^t\right)+{\displaystyle \frac{v}{\Delta y}}\left(R_{i,j}^t-R_{i,j-1}^t\right)=0$$

(3)

Here, Δt represents the time-step, R denotes the rainfall rate, (i,j) refers to the LAPS domain’s grid point, u corresponds to the x direction wind component, Δx refers to the x direction grid increment, v represents the y direction wind component and Δy denotes the y direction grid increment. The rainfall rate at each grid point is updated using wind components at each timestep.

The Courant numbers are calculated in order to see if the time-step that is selected assures the stability of the Equation (3):

$$CU=u{\displaystyle \frac{\Delta t}{\Delta x}}\ge 0$$

(4)

$$\mathrm{C}V=v{\displaystyle \frac{\Delta t}{\Delta y}}\ge 0$$

(5)

where CU represents the x direction Courant number and CV represents the y direction Courant number.

As a stability criterion, it is used the restriction $\mathrm{C}\mathrm{U}+\mathrm{C}\mathrm{V}\mathrm{s}\mathrm{t}$ that is known as the Courant-Friedrichs-Lewy (CFL) condition. With this criterion, it is ensured that the time step used in the simulation is small enough to accurately capture changes in the system and prevent numerical instabilities. The Courant number is calculated at each time step to determine whether the time step used in simulation ensured the stability of the formulation. Additionally, equations (3) through (5) were solved in order to estimate the R variable, which represents the rainfall, at time t+1 [35]. The advection scheme is developed to transfer rainfall over time, solving the transport equation in the assimilation system structure (Figure 1).

Although rainfall is the result of various physical processes, the advection equation has been successfully applied to rainfall nowcasting for short lead times up to 90 min [36,37,38,39]. Nowcasting using the advection-diffusion equation is made possible by studies like Ha and Park [36], which assumed that fluid dynamics governs the motion field of rainfall. Furthermore, the approach avoids numerical instability issues (spin-up effects) common in mesoscale models, making it advantageous for nowcasting. By using a forward advection scheme in a 2D spatial domain with a short lead time (up to 3 h), this model estimates the approximate movement of rainfall fields without incorporating complex physical processes [38]. This approach demonstrates the effectiveness of the advection equation for nowcasting applications [36,37,38,39].

The advection scheme that is embedded in LAPS avoids the “spin up” period, which is a critical issue in the numerical weather prediction mesoscale models, and it is necessary to ensure that the model physics and dynamics become more consistent and reasonable. The scheme’s disadvantage is that it could not be used for forecasting beyond a 3-h time frame because no further physical parameterizations were added. The dynamical processes can no longer be disregarded after the forecast horizon.

Table 1. Characteristics of the proposed LAPS-based approach in the context of other nowcasting methodologies.

Methodology	Data Sources	Forecast Lead Time	Spatial Resolution	Limitations
Traditional NWP	Numerical models	3–6 h	10–50 km	Computationally demanding, limited short-term accuracy
Radar-Based Nowcasting	Weather radar only	Up to 3 h	1–5 km	High accuracy but limited to radar coverage areas
Satellite-Based Nowcasting	Satellite retrievals	1–6 h	10–25 km	Broad coverage but lower resolution
Proposed LAPS-Based Assimilation	Radar with Satellite retrievals	Up to 3 h	1 km	Optimized integration of high-resolution radar with broad satellite data

compares the proposed LAPS-based assimilation approach relative to other general nowcasting methodologies. These represent internal variations of the proposed assimilation scheme rather than comparisons with external nowcasting systems. This comparison highlights the primary advantage of the proposed approach: improved short-term predictability by dynamically fusing radar and satellite data, balancing precision with coverage.

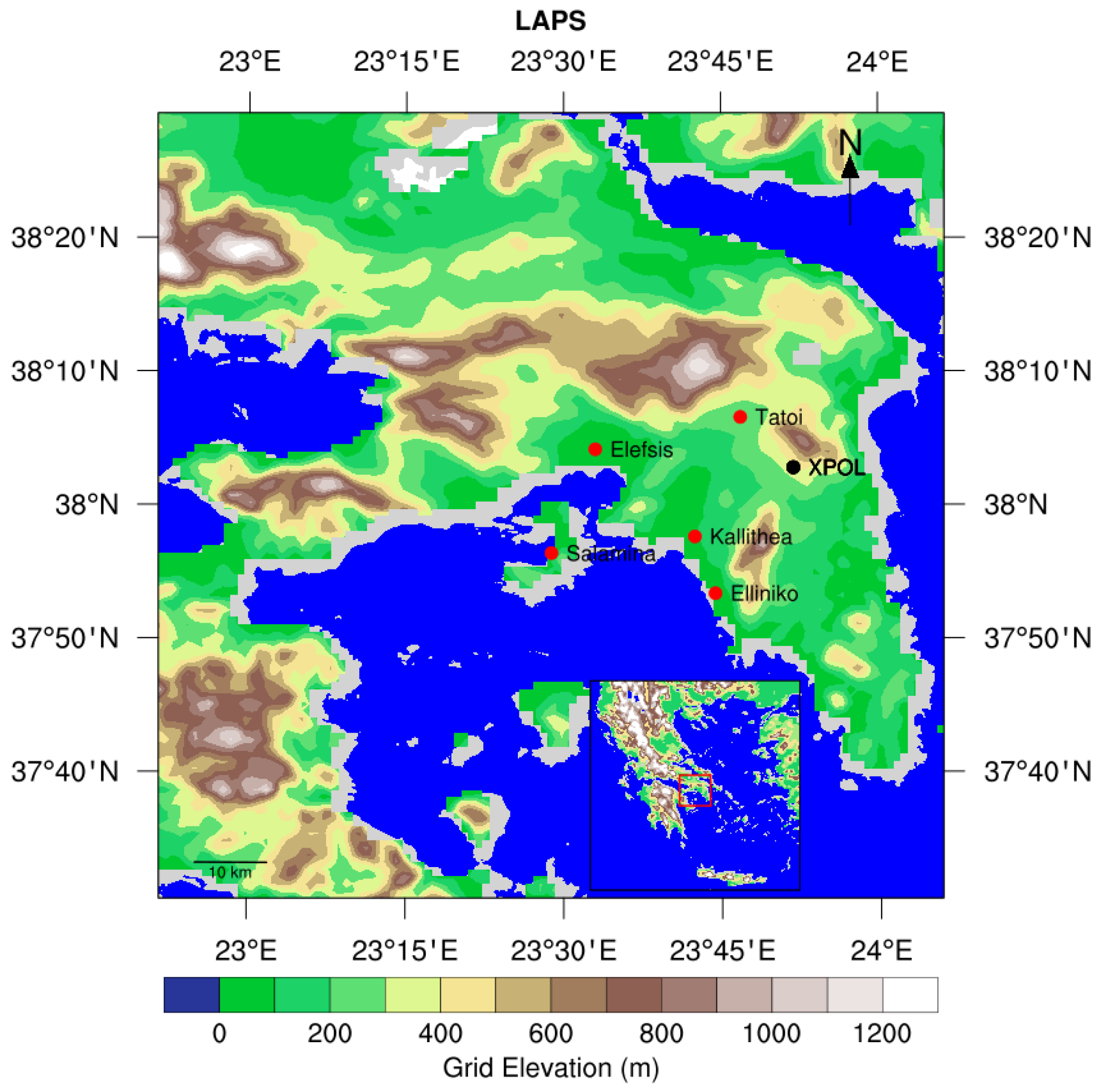
For the needs of this study, LAPS was configured over a domain that covered Attica (Figure 2) and its details are presented in

Table 2. LAPS configuration.

Horizontal grid increment	1 km
Grid points	110 × 110
Vertical levels	41
Background fields	GFS forecasts on 0.25° × 0.25°
Assimilated observations	METAR, SYNOP

. Global Forecast System (GFS) 0.25-degree resolution data from the 29 and 30 September 2018 at 0000 UTC cycle was used to generate 3D background fields.

Three assimilation experiments have been performed, each using GFS near to analysis forecasts as background fields.

The experiments are as follows:

(a)

the control experiment-CTRL, which only the GFS forecasts and METAR and SYNOP in situ observations (GFS + METAR + SYNOP) are used,

(b)

the GTX experiment, which GFS forecasts and METAR and SYNOP in situ observations are combined with XPOL radar data and Global Precipitation Measurement (GPM) and Tropical Rainfall Measuring Mission (TRMM) retrievals (GFS + METAR + SYNOP + GPM + TRMM + XPOL) and

(c)

the HX experiment, which GFS forecasts and METAR and SYNOP in situ observations are combined with XPOL radar data and EUMETSAT Satellite Application Facility on Support to Operational Hydrology and Water Management (H-SAF) retrievals GFS + METAR + SYNOP + H-SAF + XPOL).

The three assimilation experiments were designed to evaluate the impact of different data sources on rainfall nowcasting. The CTRL experiment serves as the baseline, using only Global Forecast System (GFS) forecasts combined with METAR and SYNOP in situ observations. This experiment provides a reference for assessing the improvements brought by the assimilation of additional remote sensing data. The GTX experiment incorporates GFS forecasts, XPOL radar data, and satellite retrievals from the Global Precipitation Measurement (GPM) and Tropical Rainfall Measuring Mission (TRMM). This experiment was designed to evaluate the impact of combining radar data with satellite-derived rainfall estimates from GPM and TRMM, which have different spatial and temporal resolutions (30 min and 3 h, respectively). The HX experiment combines GFS forecasts, XPOL radar data, and satellite retrievals from the EUMETSAT Satellite Application Facility on Support to Operational Hydrology and Water Management (H-SAF). This experiment was included to assess the added value of H-SAF products, which offer higher temporal resolution (15 min). The division of satellite data into two experiments (GTX and HX) allows for a direct comparison of the performance of different satellite products, highlighting the different contributions of each dataset to the nowcasting accuracy.

The assimilated fields and the experiments are listed in

Table 3. LAPS experiments.

Experiment	Assimilated Fields
CTRL	GFS + METAR + SYNOP
GTX	GFS + METAR + SYNOP + GPM + TRMM + XPOL
HX	GFS + METAR + SYNOP + H-SAF + XPOL

. The three assimilation experiments have been performed twice. The first set of experiments was conducted at 29 September 2018. LAPS was run at 15:00 UTC producing analysis fields and advected rainfall fields every 10 min for a total of 90 min. The second set of experiments was conducted at 30 September 2018. LAPS ran at 03:00 UTC producing analysis fields and advected rainfall fields similarly every 10 min for a total of 90 min.

To evaluate nowcasting accuracy, two statistical metrics are analyzed: the BIAS (6) and the unbiased Root Mean Square Error (ubRMSE) (8). These metrics serve distinct purposes: BIAS, reveals consistent systematic over- or underestimation across nowcasts while ubRMSE measures the magnitude of forecast errors by excluding the mean bias component, thus quantifying error independent of systematic bias. Both metrics are calculated by comparing the predicted rainfall values (F_i) with the observed rainfall values (O_i) at each grid point over the LAPS domain for each forecast lead time. Here, N represents the total number of data points, F_i is the predicted value at the ith data point and O_i is the true value at the ith data point. For BIAS and ubRMSE evaluation, the empirical 95% confidence intervals based on the bootstrap technique [40] are computed. Specifically, for each lead time the forecast–observation pairs are resampled with replacement 1000 times to obtain the 95% confidence level. Computing the 97.5th and 2.5th percentiles in the bootstrap distribution, the 95% confidence level is obtained.

$$BIAS={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(F}_i-O_i)$$

(6)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(F_i-O_i\right)}^2}$$

(7)

$$ubRMSE=\sqrt{RMS{E}^2-BIA{S}^2}$$

(8)

Another statistical evaluation is performed using the contingency of

Table 4. Contingency table.

	Observations
Model Forecasts	YES	NO
YES	Hits	False Alarms
NO	Misses	Correct Negatives

that is appropriate for discrete variables, with emphasis on identifying false detections and the accuracy of the experimental outcomes. Two detection metrics (POFD and Accuracy) are estimated for four rainfall thresholds (0.2, 0.5, 1, and 2 mm) using rainfall derived from LAPS nowcasts, validated through XPOL radar data. The evaluation sample size, representing the matched LAPS–XPOL pairs across all thresholds, ranges from 9245 to 9259.

$$POFD={\displaystyle \frac{\mathrm{F}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e} \mathrm{A}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{m}\mathrm{s}}{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{N}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{s}+\mathrm{F}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e} \mathrm{A}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{m}\mathrm{s}}}$$

(9)

$$ACCURACY={\displaystyle \frac{Hits+Correct Negatives}{Total}}$$

(10)

2.1. X-Band Dual-Polarization (XPOL) Weather Radar Data

The X-band dual-polarization (XPOL) Doppler weather radar collects data on both the horizontal and vertical components of the electromagnetic waves that are reflected back to the radar from rainfall particles in the atmosphere and its data allows more detailed insights into the orientation, size, and composition of rainfall particles. The National Observatory of Athens operates the XPOL ground-based radar that is located on Penteli mountain (latitude 38.0491°, longitude 23.8647°) at a height of 500 m above sea level, at the northeast part of Athens Basin, operates the XPOL ground-based radar. Plan position indicator (PPI) mode is used by the radar capturing observations in a 180° wide sector scan (south-west-north) at elevation sweeps of 1°, 2°, and 3° with a 150 m range resolution (maximum range of 120 km) during rainfall events. Antenna rotation rate was 6 degs/s, and less than 2 min was the duration of a full volume scan. To retrieve rainfall values, the Self-Consistent Optimal Parameterization-Microphysics Estimation (SCOPE-ME) X—band dual-polarization algorithm was used [29,41].

2.2. TRMM

The objective of the Tropical Rainfall Measuring Mission (TRMM) was to study the variability and spatial distribution of rainfall [42]. It was a collaborative mission conducted by the Japan Aerospace Exploration Agency (JAXA) and the National Aeronautics and Space Administration (NASA). Five instruments have been installed on TRMM, four of them are used for rainfall: a nine -channel passive Microwave Imager (TMI), a Precipitation Radar (PR), a five channel Visible and Infrared Scanner (VIRS) and a Lightning Imaging Sensor (LSI) [43,44,45]. The purpose of the TMI is to quantify rainfall, water vapor and sea surface temperature. Its swath width is 760 km. The PR radar provides radiance measurements, and its swath width is 215 km [43]. The VIRS provides measurements of rainfall intensity, distribution and type and it has 0.6 to 12 μm wavelength and a 2 km horizontal resolution and a swath width of 720 km. The LSI provides a link between the lighting occurrence and rainfall events [46].

Among the TRMM rainfall products, 3B42 and 3B43 are highly popular. These products have high temporal and spatial resolutions and are widely used in the monitoring and forecasting of extreme events. For the needs of this study TRMM 3B42 products are used that are a high spatial (25 km) and temporal resolution (3 h) rainfall data. The rainfall data have 0.25 degrees a spatial resolution in both latitude and longitude covering the area between 50 S and 50 N. TRMM was in operation from 1997 to 2015. The TRMM Multi-satellite Precipitation Analysis (TMPA) products continued to be produced into the GPM until the end of 2019.

2.3. GPM

The Global Precipitation Measurement (GPM) program succeeded the TRMM [47,48]. The goals of this program are to enhance hydrological modeling, climate modeling and weather forecasts and to improve the knowledge of freshwater availability and water cycle variability [48,49]. Comparing TRMM and GPM, GPM has better resolution than TRMM as the GPM has 10 km spatial and 30 min temporal resolution [50].

The GPM mission comprised of a Core observatory satellite that carries a Dual-frequency Precipitation Radar (DPR) to provide three-dimensional rainfall data and a passive GPM microwave imager (GMI) to estimate rain rate and nine constellation satellites. The DPR includes two radars, a KaPR and a KuPR, with 35.5 GHz and 13.6 GHz frequencies, respectively [30,49,51]. A Ku-band radar had already been used by the TRMM (Tropical Rainfall Measuring Mission) and measures moderate to heavy rain in tropical and mid-latitude regions while a Ka-band measures weak rain in higher latitudes as well [49]. The passive GPM microwave imager (GMI) is a conical scanning, high resolution, multi-channel microwave radiometer. The GMI provides a reference standard to rainfall estimates and has thirteen microwave channels with frequency ranging from 10.65 to 183.31 GHz [49,51].

To estimate rainfall retrievals, the algorithm used is the Integrated Multi-satellitE Retrievals for GPM (IMERG) [52]. Moreover, IMERG Early, IMERG Late and IMERG Final are the three types of IMERG products [53]. The difference among these types is for the data availability as IMERG Early has a 4 h delay (is well-suited for real time applications, such as predicting flash flood), IMERG Late 12 h to 14 h delay (is well-suited for water resource management) and IMERG Final 2.5–3.5 months delay (is well-suited for research). The spatial resolution of the IMERG rainfall data is 0.1° × 0.1°, with a temporal resolution reaching up to 30 min [52,54]. GPM IMERG EARLY half hourly products are chosen for this study.

2.4. H-SAF

EUMETSAT Satellite Application Facility on Support to Operational Hydrology and Water Management (H-SAF) is a program that focuses on parameters related to soil moisture, rainfall and snow. The H-SAF products are derived from measurements collected by microwave and infrared satellite sensors located on geostationary and polar -orbiting satellites [55,56].

The H03B is the H-SAF Operational Products that are used in this study. The spatial resolution of these products ranges from 3 km, near the sub-satellite to 8 km over Europe, with a high temporal resolution of 15 min [56,57]. The algorithm for product H03B is based on the technique blended—satellite “Rapid Update” that was initially created at the Naval Research Laboratory (NRL) [57,58,59,60]. This product measures the ground rainfall rate blending operational geostationary IR imagers and LEO MW sensors [57]. This technique combines the brightness temperatures from the IR geostationary sensors with the rainfall rates from passive microwave (PMW) satellite sensors [61].

3. Synoptic Analysis

Due to its position in the eastern Mediterranean Sea, Greece is vulnerable to Medicanes (Mediterranean hurricanes), which refer to a rare and powerful type of cyclone that forms over the Mediterranean Sea [62,63]. Medicanes are usually storms associated with strong winds and heavy rain and they can display characteristics that are similar to both hurricanes and mid-latitude cyclones. On 27 September 2018 a notable extreme event was formed in Libya around 12:00 UTC [64]. The system developed into three phases [65]. The first phase took place between 27/00 UTC and 28/00 UTC with the formation of an extratropical cyclone [65]. Between 28/06 UTC and 28/12 UTC, the second phase took place when an extratropical cyclone transitioned into Medicane Zorbas. Between 28/18 UTC and 29/18 UTC, the third phase took place with the transformation of Medicane to a strong mid-latitude cyclone. Four days after its formation, Zorbas decayed in the Aegean Sea. The Medicane damaged significantly Southern Greece, including Crete, Peloponnese, Evia, and Athens, with severe winds, torrential rainfall and flooding.

The development of Medicane Zorbas began on 27 September 2018, with the emergence of a low-pressure system at 1007 hPa (Figure 3a) in the central Mediterranean Sea. Concurrently, a warm front and a trough began to take shape over the Mediterranean Sea between Sicily, South Greece and Libya which indicates atmospheric instability that there was a chance for showers. Meanwhile, a weather system associated with a cold anticyclone in central Europe gradually moved eastward towards Greece. This favored the increase of baroclinicity in the lower layers at the coastal areas of eastern Libya. The system was deepening further due to the cold anomaly (Figure 3b) in the Mediterranean Sea. On 29 September 00UTC, the system approached mainland Greece with a low pressure at 997 hPa (Figure 3c) accompanied by a front over Ionion Sea and north Greece. Furthermore, the detached low pressure at the 500 hPa level had moved further northeast affecting the western parts of Greece with geopotential height reaching to 576 gpdam (Figure 3d). On 30 September 2018 at 00UTC, the medicane continued to affect Greece and Turkey. The center of low pressure directed to the northeast had a rise in pressure at 1004 hPa (Figure 3e) and it was accompanied by an occluded front. Eventually, the Medicane moved to north-northeast direction and reached Turkey and gradually dispersed.

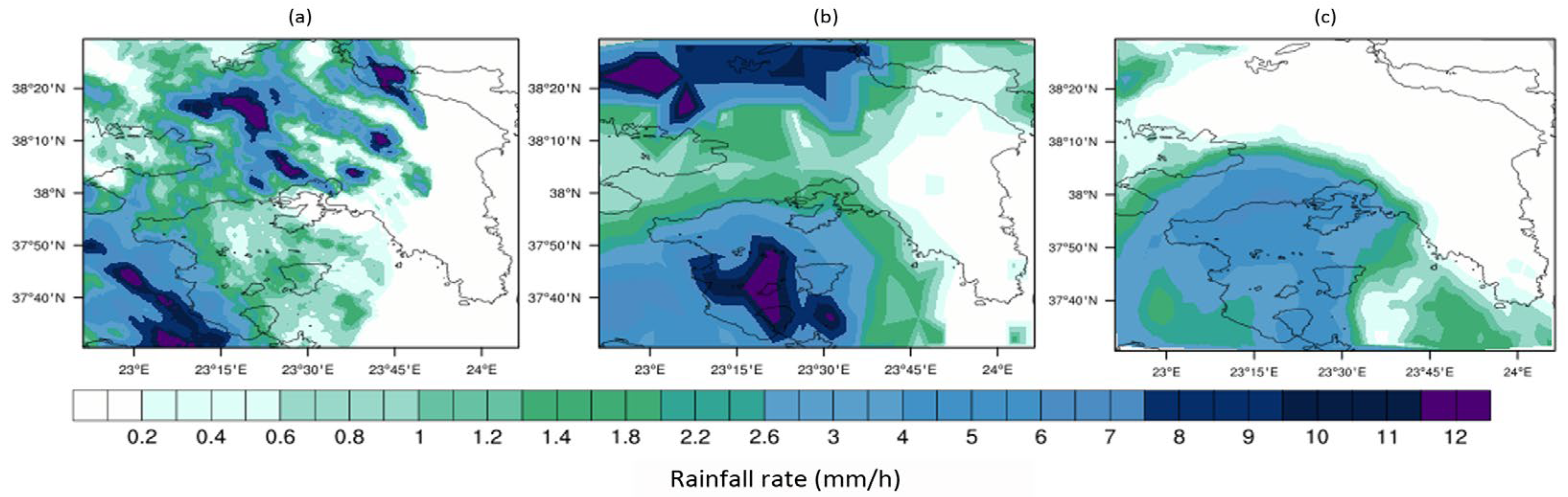
In addition to the analysis maps Figure 4 provides the rainfall characteristics at the analysis time that initiated the first experiment, offering insights into the spatial distribution and intensity of rainfall for 29 September 2018 at 15:00 UTC. Specifically, Figure 4 illustrates (a) radar-derived rainfall rates, (b) GPM + TRMM, rainfall retrievals and (c) H-SAF rainfall retrievals on 29 September 2018 at 15:00 UTC.

4. Results and Discussion

Two sets of experiments were conducted to assess the forward advection scheme’s effectiveness in predicting a rainfall event in the Athens metropolitan area on 29 and 30 September 2018 with different rainfall intensities. The insights into the spatial distribution and variability of rainfall are presented in the panel plots for these experiments. The XPOL radar data processed by the Self-Consistent Optimal Parameterization-Microphysics Estimation (SCOPE-ME) algorithm. This algorithm estimates rainfall rate from polarimetric radar variables and accumulates it over time. This process allows for consistent, independent radar-based rainfall accumulation estimations [29].

4.1. Spatial Pattern Comparison

Figure 5 illustrates the 10-min total rainfall in mm for radar data and the relevant LAPS nowcasts at 15:10, 15:20 and 15:40 UTC on 29 September 2018. Thus, each nowcast corresponds to 10, 20 and 40 min after the LAPS analysis on 29 September at 15:00 UTC. The panel plot (Figure 5) consists of twelve panel figures arranged in a 3 × 4 grid. The leftmost panel is the XPOL radar data at the forecasting times, which are not assimilated into LAPS, and the other three columns are the nowcasts that are produced using three different experiments: the control experiment-CTRL, the GTX experiment and the HX experiment.

Figure 5 provides a comprehensive view of rainfall patterns. In the top panels (15:10 UTC), Figure 5(ai), which is the reference rainfall field from the radar data in its scanning sector, shows moderate rainfall concentrated in the center of the simulation domain, as well as in areas outside the basin, particularly to the southwest and west. The rainfall pattern from HX experiment (Figure 5(di)) is similar to the radar data, but heavier rainfall is presented in areas outside the basin, especially at the south-west part of the domain, while in Athens Basin has more rain cells. In contrast, the control experiment-CTRL (Figure 5(bi)) depicts heavy rain across almost the entire domain, excluding a small northeastern part with no rainfall. The GTX experiment (Figure 5(ci)) indicates intensified rainfall throughout the west area of Athens Basin with limited rain at the southeast, which is an intermediate behavior between the HX and control experiment-CTRL.

In the next lead times, we can see in the radar data that the rain cells at the northwest part of the domain are getting larger and intensified. The GTX and HF experiments show a similar evolution with convergence of the rain cells in this area. The rain at the southwest part shows small movement to the northwest and decrease of its extension in the radar data and all experiments relatively to the first lead time (top row of Figure 5, Figure 5i).

The middle panels present the next 10 min of accumulated rainfall. The radar data (Figure 5(aii)) illustrates intensified rainfall compared to the first lead time (Figure 5(ai)) especially in the northwest part of the domain. Similarly, the HX experiment (Figure 5(dii)) shows an increase in rainfall within Athens Basin and the areas outside to the southwest and west, in comparison to the first lead time (Figure 5(dii)). However, the control experiment-CTRL, (Figure 5(bii)) shows a slightly smaller area of intensified rainfall than the first lead time (Figure 5(bi)). Moreover, the GTX experiment (Figure 5(cii)) shows an increase in heavy rainfall outside the Athens Basin, particularly in the northwest and southwest, compared to the first lead time (Figure 5(ci)).

In the bottom panels (15:40 UTC), the radar data (Figure 5(aiii)) shows increased rainfall compared to the previous left panels. The control experiment-CTRL (Figure 5(biii)) shows a smaller area of intensified rainfall than the previous figures with a larger area in the northeast that has no rainfall. The GTX experiment (Figure 5(ciii)) depicts heavy rainfall, apart from a larger area in the south part of the domain. The HX experiment (Figure 5(diii)) is similar to the radar data (Figure 5(aiii)) but displays different patterns with more scattered rainfall distribution. Throughout all figures, there is a noticeable northwestward movement of rainfall.

The second experiment, with lighter rainfall, has been performed on 30 September 2018 at 03:10, 03:20 and 03:40 UTC, as shown in Figure 6 (each nowcast is for 10, 20 and 40 min after the LAPS analysis on 30 September at 03:00 UTC). On this day, the rainfall is weaker due to a less intense low-pressure system compared to the more intense event of the previous day. Similar to Figure 5, the following panel plot shows the 10-min total rainfall in mm for radar data and the LAPS nowcasts.

In the top panels (03:10 UTC), the radar data (Figure 6(ai)) and the HX experiment (Figure 6(di)) depict dispersed light to moderate rainfall occurrences at the Athens Basin, characterized by varying intensities. The HX experiment produces more rain cells than seen in the radar data, similarly with the result from the previous event shown in Figure 5. Moderate rainfall is observed in areas outside the Athens Basin particularly to the north of Athens Basin. The control experiment-CTRL (Figure 6(bi)) shows a localized concentration of rainfall in the whole area north of the domain but no rain in the southern part. Conversely, the GTX experiment (Figure 6(ci)) illustrates the prevalence of widespread rainfall across the domain with intensified rainfall observed north- northwest of the Athens Basin.

In the next lead times, the radar data show that the rainfall field is moving slowly to the south with small changes. The same movement of the rainfall field can be seen in all the experiments with small change of rain intensity. Thus, intense rain at the edge of the domain in CTRL and GTX experiments is brought to its center, which is not observed in radar data where the rain pattern seems to move more slowly. Thus, the advection of the rainfall field is not exactly the same as the wind field indicates.

In the middle panels (03:20 UTC), the radar data (Figure 6(aii)) shows a slightly broader area of rainfall compared to the first lead time (Figure 6(ai)). Similar to the radar data (Figure 6(aii)) the HX experiment (Figure 6(dii)) shows rainfall that appears to be more widespread than the first lead time (Figure 6(di)). On the other hand, the control experiment-CTRL (Figure 6(bii)) shows increased rainfall suggesting a more intense rainfall event compared to the first lead time (Figure 6(bi)). Additionally, the GTX experiment (Figure 6(cii)) shows increased rainfall intensity in the north–northwest of the Athens Basin compared to the first lead time (Figure 6(ci)).

In the bottom panels (03:40 UTC), the radar data (Figure 6(aiii)) shows more rainfall in the northwest of the Athens Basin. In contrast, the control experiment -CTRL experiment (Figure 6(biii)) exhibits a significant area of rainfall with heavier rainfall event, suggesting a more intense event than observed in previous figures. Moreover, the GTX experiment (Figure 6(ciii)) displays a focused area of heavy rainfall in the northwest of the Athens Basin. Finally, the HX experiment (Figure 6(diii)) shows scattered rainfall similar to the radar data (Figure 6(aiii)) but with distinct patterns. Throughout all figures, rainfall is observed moving in a south direction.

When comparing the two set of experiments, on 29 September with analysis time 15:00 UTC, rainfall is more concentrated, intense and localized in the western and central parts of the domain. In contrast, on 30 September, with analysis time 03:00 UTC, the rainfall patterns show a shift with lighter and more dispersed rainfall, particularly in the northern and central part of the domain.

In the radar data, Figure 5a displays moderate rainfall more concentrated in the southwest and central areas of the domain, while Figure 6a shows rainfall lighter and more dispersed across the domain. In the control experiment-CTRL, Figure 5b shows widespread rainfall across almost the entire domain, excluding the northeastern part. In contrast, Figure 6b shows a weaker system with heavier rainfall in the northern area of the domain, while the southern area remains relatively dry. The GTX experiment in Figure 5c shows intense rainfall in the west and limited rain in the southeast. However, in Figure 6c, the rainfall is still widespread across the domain but is less intense overall, with a heavier concentration in the northern part of the domain. Lastly, in the HX experiment, Figure 5d shows intense rainfall and central parts of the domain while in Figure 6d, the rainfall is more scattered with reduced intensity, especially towards the southern part of the domain.

4.2. Validation Against Ground Stations

Next, the independent rainfall rate observations from two meteorological stations in Attica region (Salamina and Kallithea) operated by Harokopio University are compared to the 10-min rainfall nowcasts for both sets of experiments.

Table 5. Comparison of the ten minutes LAPS rainfall nowcasts (mm) on 29 September 2018 with analysis time 15:00 UTC from 15:10–15:40 UTC and 30 September 2018 with analysis time 03:00 UTC from 3:10–3:40 UTC with implementing control experiment-CTRL, GTX experiment and HX experiment and the recorded rainfall (mm) at Salamina station.

Date	Time (UTC)	Control Experiment-CTRL	GTX Experiment	HX Experiment	Salamina
29 September 2018	15:10	10.9	0.2	0.0	0.0
	15:20	9.8	0.0	0.0	0.0
	15:30	8.8	0.4	0.0	0.0
	15:40	8.0	0.3	0.0	0.0
30 September 2018	03:10	0.0	0.4	0.0	0.0
	03:20	0.0	0.7	0.1	0.0
	03:30	0.3	0.3	0.0	0.0
	03:40	2.9	0.0	0.0	0.0

and

Table 6. As shown in Table 5, this refers to the recorded rainfall data from Kallithea station.

Date	Time (UTC)	Control Experiment-CTRL	GTX Experiment	HX Experiment	Kallithea
29 September 2018	15:10	5.9	0.0	0.0	0.0
	15:20	5.7	0.0	0.3	0.2
	15:30	5.6	0.4	0.3	0.0
	15:40	5.4	0.8	0.0	0.2
30 September 2018	03:10	2.8	0.5	0.0	0.2
	03:20	2.8	0.7	0.2	0.0
	03:30	3.0	0.3	0.2	0.2
	03:40	3.0	0.3	0.3	0.0

present the results from an independent validation of radar-based nowcasts at the locations of ground weather stations. The comparison verifies that the nowcasts perform significantly better in HX experiment when H-SAF satellite products are assimilated with XPOL radar data, as it was already concluded from Figure 5 and Figure 6. It is important to mention that at both meteorological stations, the systematic overprediction of the rainfall in the CTRL experiment was significantly improved in HX experiment (Table 5 and Table 6).

In the GTX experiment there is a systematic overestimation of recorded rainfall. On the other hand, in the HX experiment there is a slight tendency towards overestimating recorded rainfall. Specifically, at Salamina station on 29 September 2018, the HX experiment nowcasts no rainfall in every time slice. However, at the same station on 30 September 2018, there is a slight overestimation at 03:20 UTC with 0.1 mm/10 min. At Kalithea station, the HX experiment generally overestimates rainfall except for two time slices on 29 September 2018 at 15:40 UTC and on 30 September 2018 at 03:10 UTC, where there is an underestimation.

The primary rainfall core, however, was situated away from these two stations. Consequently, an additional comparison is conducted with three other independent meteorological stations within the Hellenic National Meteorological Service’s network. The results between the nowscasts at 12:00 UTC for 29 and 30 September 2018, are presented in

Table 7. Comparison of the LAPS rainfall nowcasts in mm for 12:00 UTC on 29 September 2018, implementing control experiment-CTRL, GTX experiment and HX experiment and the recorded rainfall in mm at Elefsis, Elliniko and Tatoi stations (The stations measurements retrieved from the ECMWF).

Time (UTC)	Station	Control Experiment-CTRL	GTX Experiment	HX Experiment	Past 6 h Rainfall
12:00	Elefsis	0.0	0.1	0.1	7.0
12:00	Elliniko	0.0	0.0	0.0	11.0
12:00	Tatoi	0.0	0.2	0.1	8.0

and

Table 8. As in Table 7, but on 30 September 2018 at 12:00 UTC.

Time (UTC)	Station	Control Experiment-CTRL	GTX Experiment	HX Experiment	Past 6 h Rainfall
12:00	Elefsis	32.3	2.6	2.3	17.0
12:00	Elliniko	31.6	2.4	1.8	0.9
12:00	Tatoi	31.8	13.1	12.3	9.0

. The nowcasts correspond to 6 h ahead of the analysis time at 06:00 UTC.

On 29 September 2018, the control experiment’s nowcasts show no rainfall at any of these stations. There is a significant underestimation from all experiments compared to the observed in-situ data across all stations. At Elliniko station, in particular, the nowcasts of all experiments predict no rainfall despite a recorded value of 11.0 mm/6 h.

On the other hand, on 30 September 2018, the nowcasts of the control experiment have an overestimation of rainfall at all stations. Specifically, rainfall is overestimated in comparison to the in-situ data at the Tatoi and Elliniko stations. Apart from the Elefsis station, where nowcast is 2.3 mm/6 h rather than the recorded value of 17 mm/6 h, the nowcasts of HX experiment are actually closer to the values of the independent stations.

Recognizing the limitation of comparing with two initial raingauge stations (Salamina and Kallithea), additional comparisons are conducted using another three independent meteorological stations (Elliniko, Tatoi, and Elefsis). While these additional stations provided further validation, the overall number of ground weather stations remains insufficient to derive reliable conclusions about the overall performance of the nowcasts.

The surface-based validation presented here relies on a small number of meteorological stations, which limits the spatial representativeness of the results. Some stations also recorded near-zero rainfall, which further complicates interpretation. Therefore, conclusions drawn from these point-based comparisons should be treated in conjunction with the more reliable statistical scores against XPOL radar estimates presented in Section 4.3. However, a denser observation network would be necessary to evaluate system performance more comprehensively.

An important point in the validation results is the underestimation observed in the 6-h nowcasts on 29 September (Table 7), which seems to contradict the general overestimation bias that is identified for shorter lead times in the point-to-point analysis of Section 4.3 (Figure 7a). This discrepancy likely arises from the limitations of the forward advection scheme at longer lead times. As the forecast horizon extends beyond three hours, dynamic processes not represented by the advection model begin to dominate rainfall development. As a result, the model’s ability to track rainfall diminishes, often leading to underestimation.

Given the sparse station density and the presence of near-zero rainfall values these station-based results are best considered a supplement to the more spatially comprehensive grid-to-grid validation against XPOL radar data in the sections that follow.

4.3. Point-Wise Statistics

To quantitatively evaluate forecast accuracy, a point-to-point statistical evaluation is employed between the LAPS-nowcasts and the XPOL radar data (in the forecast time period) that are not assimilated in LAPS. Specifically, XPOL radar data at analysis time T (e.g., 15:00 UTC) is assimilated into LAPS. The nowcasts at T + 10 to T + 90 min are then validated against independent XPOL radar observations at those times. This radar data used for validation is not assimilated into the system, ensuring an independent assessment. The nowcasts applied with lead times of 10 to 90 min and analysis time 15:00 UTC on 29 September 2018 and 03:00 UTC on 30 September 2018. 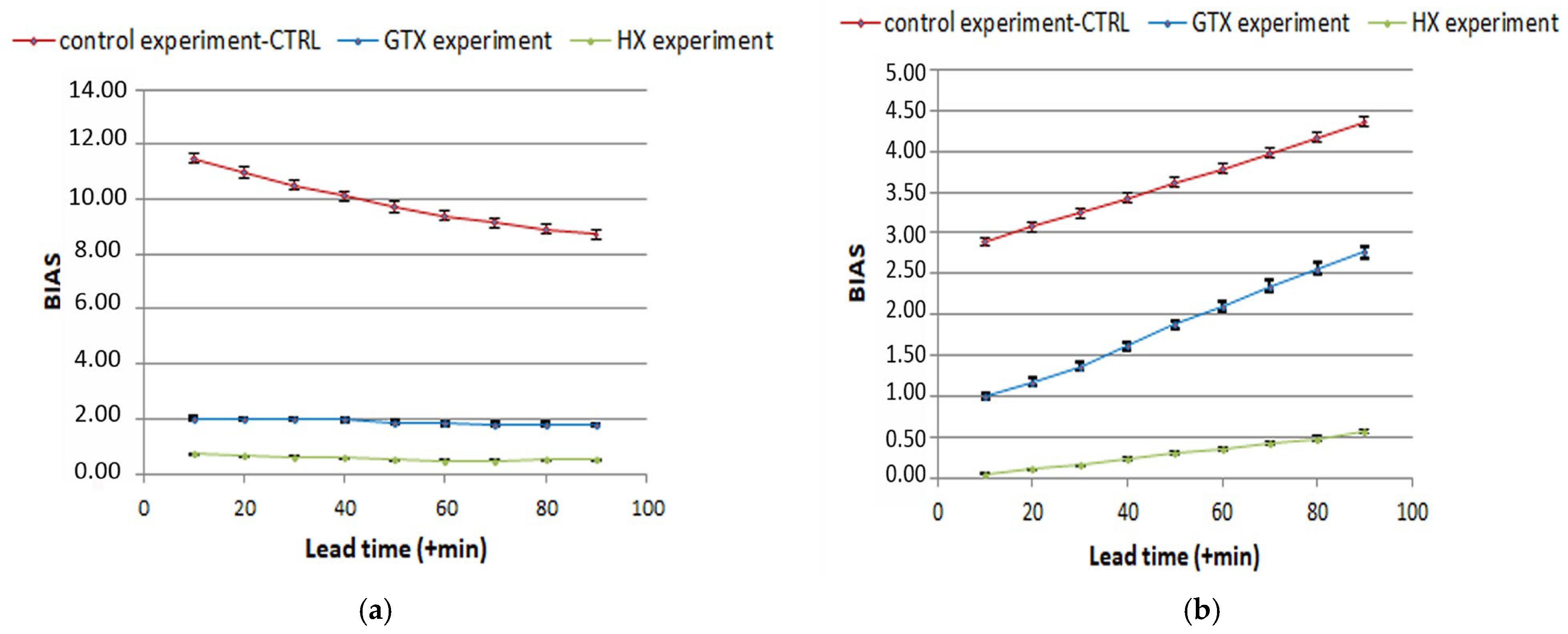It is calculated the BIAS and BIAS scores as presented in Figure 7a,b indicate significant differences among these experiments. More specifically, the HX experiment consistently exhibits the lowest BIAS scores, while the control experiment -CTRL shows the highest. Across all experiments, there is a tendency to overestimate recorded rainfall, as BIAS scores are positive.

On 29 September 2018, with analysis time 15:00 UTC (Figure 7a), there is a trend of decreasing BIAS scores as lead time increases from 10 to 90 min in all experiments. The HX experiment consistently achieves the lowest BIAS scores across all lead times demonstrating superior performance in rainfall prediction accuracy. The BIAS for the HX experiment decreased steadily from 0.71 mm at a 10-min lead time to 0.49 mm at 70 min, with slight variations thereafter. In contrast, the GTX experiment shows significantly higher BIAS scores, ranging from 2.02 mm to 1.77 mm, while the control consistently exhibits the largest biases, starting at 11.48 mm and declining to 8.71 mm. Notably, the confidence intervals for HX remain narrow throughout, underscoring the robustness of its performance.

Although this reduction in BIAS might initially suggest improved forecast skill, it is important to emphasize that this apparent improvement can be misleading. Forecast quality generally degrades with increasing lead time; thus, the declining BIAS likely reflects a statistical artifact rather than a genuine gain in predictive accuracy. Two key mechanisms contribute to this behavior: (1) the advection of intense rainfall cells out of the verification domain, which mechanically reduces the domain-averaged rainfall and hence lowers the positive BIAS; and (2) the positive-negative error cancellation, where overpredicted and underpredicted rainfall regions offset each other, resulting in an artificial reduction of overall bias. This balancing effect of positive and negative errors with the advection of the mostly scattered (rain cells) rainfall field could be misleading to an apparent improvement in nowcasting accuracy. Initially, the nowcasts may show high bias due to intensified rainfall in certain areas, but as the system moves, the differences on average between the observed and forecasted rainfall diminish. For the control experiment-CTRL, the incoming lighter rainfall from the southeast and outgoing higher rainfall from the northwest reduces the significant differences initially observed in the control experiment-CTRL which have very high values and BIAS scores are decreased.

Figure 7. BIAS score (mm) and corresponding 95% confidence intervals derived from bootstrap sampling for rainfall forecasts on (a) 29 September 2018 with analysis time 15:00 UTC, (b) 30 September 2018 with analysis time 03:00 UTC.

Figure 7. BIAS score (mm) and corresponding 95% confidence intervals derived from bootstrap sampling for rainfall forecasts on (a) 29 September 2018 with analysis time 15:00 UTC, (b) 30 September 2018 with analysis time 03:00 UTC.

On 30 September 2018 (analysis time 03:00 UTC), BIAS scores from the HX experiment gradually increase from 0.05 mm to 0.56 mm as lead time extended from 10 to 90 min (Figure 7b). This trend shows a decrease in the accuracy of the predictions over time. At the shortest lead time (+10 min), the HX experiment exhibits the lowest bias of 0.05 mm (95% CI: 0.03–0.07), compared to 1.00 mm (95% CI: 0.96–1.03) for GTX and 2.89 mm (95% CI: 2.84–2.94) for the control experiment-CTRL. As the lead time increases to +90 min, the BIAS for HX is 0.56 mm (95% CI: 0.53–0.59), yet remains substantially lower than GTX (2.76 mm) and the control experiment-CTRL (4.36 mm). The steady, low-bias scores of HX underscores its accuracy in quantitative rainfall nowcasting, significantly outperforming both the baseline and the other experiment. Overall, the HX experiment demonstrates a noteworthy enhancement in nowcast accuracy over time compared to the other two experiments.

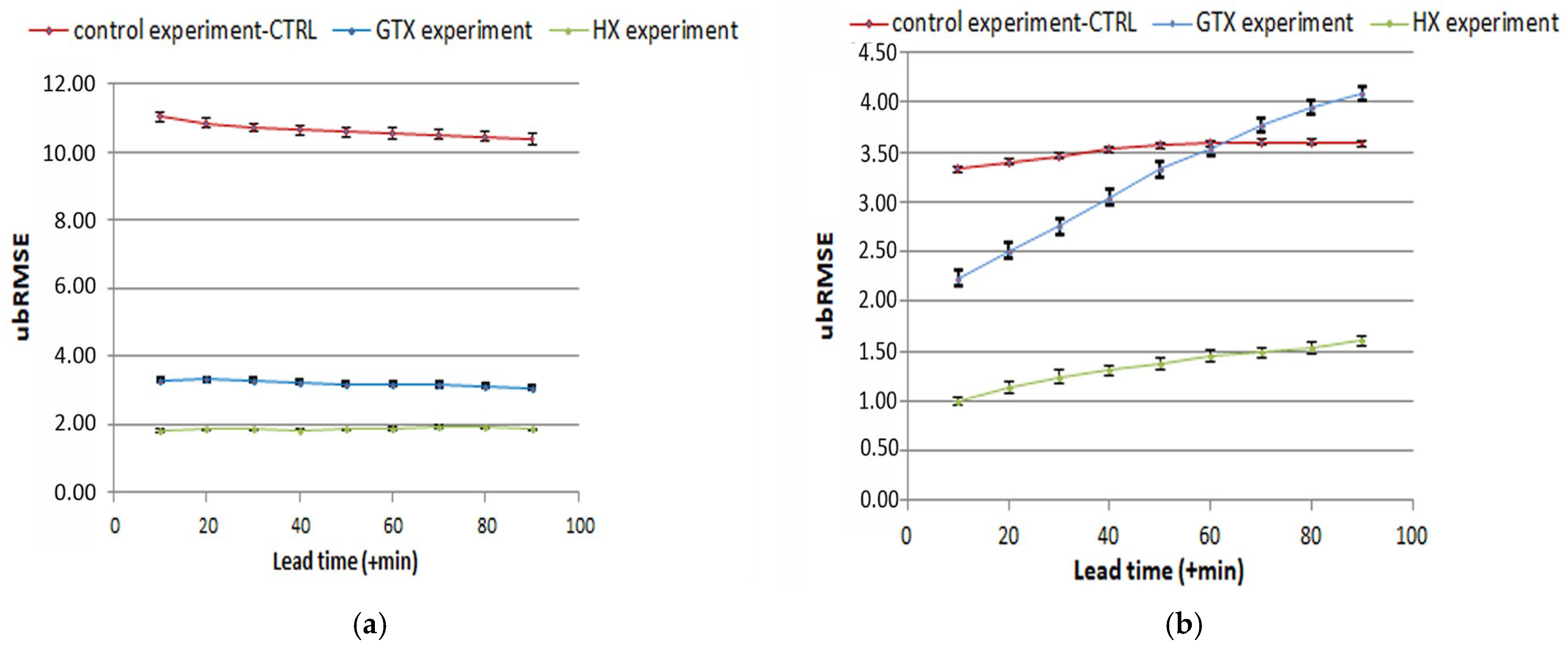
Moreover, the unbiased Root Mean Square Error (ubRMSE) scores that are presented in Figure 8a,b) illustrate the performance differences among the experiments in terms of the random error. On 29 September 2018 (analysis time 15:00 UTC), the HX experiment maintains the lowest ubRMSE across all lead times, although the values vary in a non-monotonic manner (Figure 8a). At 10 min lead time, the HX experiment has the lowest ubRMSE score of 1.83 mm (95% CI: 1.79–1.87 mm), stabilizing near 1.85 mm until 50 min before rising to 1.92 mm at 70 min, indicating a substantial decrease in prediction accuracy. In contrast, the control experiment-CTRL shows a little decreasing ubRMSE scores as lead time increases. The GTX experiment, on the other hand, shows increasing ubRMSE scores for the first 20 min followed by a decrease, but with overall larger values compared to the HX experiment. The GTX experiment shows the lowest ubRMSE score of 3.08 mm at 90 min lead time and the highest score of 3.32 mm at 20 min lead time. As mentioned previously, this may be due to the advection of the rainfall field. Overall, the HX experiment consistently performs better and exhibits lower errors in terms of ubRMSE scores.

For the 30 September event (analysis: 03:00 UTC), the HX experiment exhibits a gradual increase in ubRMSE with lead time, rising from 1.00 mm (10-min forecast, 95% CI: 0.95–1.04 mm) to 1.60 mm (90-min forecast), reflecting diminishing precision as the forecast horizon extends (Figure 8b). Despite this decline, HX maintains superior accuracy compared to CTRL and GTX, both of which show ubRMSE values exceeding 2.0 mm, indicative of systematic overestimation. The GTX experiment, while outperforming CTRL, still demonstrates the ubRMSE score from 2.23 mm (10th minute) to 4.08 mm (90th minute)—with wider confidence intervals than HX. From all above, it is concluded that the HX experiment performs better than the GTX and the CTRL experiments in maintaining prediction accuracy over time. While all experiments show a tendency to overestimate rainfall, the HX experiment demonstrates the most accurate nowcasts, making it the most reliable experiment. However, as the lead time increases, the nowcasting performance decreases.

The analysis of the rainfall event on 29 and 30 September 2018 reveals significant improvements in forecast lead time when assimilating radar and satellite data into the nowcasting system. For the first experiment (29 September), characterized by intense rainfall, the HX experiment provides the most accurate nowcasts. The HX experiment consistently exhibits the lowest BIAS and unbiased RMSE scores, demonstrating a reduction in overestimation and improved spatial accuracy compared to the control experiment-CTRL. For the second experiment (30 September), which featured lighter and more dispersed rainfall, the HX experiment again outperforms the other two experiments, particularly at shorter lead times, where it achieves the highest accuracy and lowest BIAS scores. However, as the lead time increases, the performance of all experiments decreases, with the HX experiment maintaining a relative advantage. These findings indicate that the assimilation of high-resolution satellite data (H-SAF) with radar observations significantly enhances short-term rainfall forecasts. The improvements are more pronounced in intense rainfall events, where the higher temporal and spatial resolution of H-SAF data provides a more accurate representation of rainfall dynamics. This suggests that the integration of advanced remote sensing data can extend the effective forecast lead time for nowcasting systems, particularly in high-impact weather scenarios.

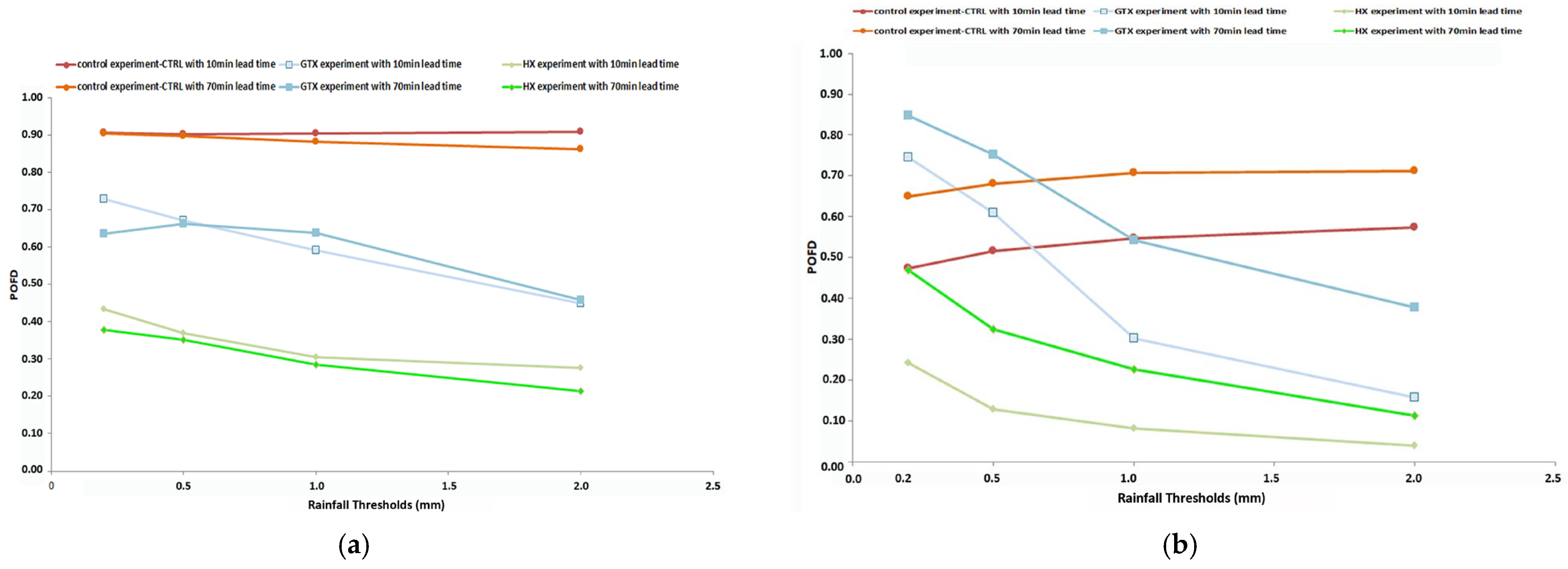
4.4. Detection Skill: Probability of False Detection (POFD) and Accuracy

On 29 September 2018 (analysis time 15:00 UTC), the Probability of False Detection (POFD) varied significantly across experiments and rainfall thresholds (0.2 mm to 2 mm) at both 10 min and 70 min lead times, as shown in Figure 9a. The control experiment-CTRL exhibits a stable POFD score range between 0.86 and 0.91 across all rainfall thresholds, indicating limited skill in distinguishing between true and false rainfall detections. In contrast, the GTX and the HX experiments show reduced POFD scores, especially at higher thresholds highlighting an improved ability to detect false alarms as rainfall intensity increases. The HX experiment stands out with the lowest POFD values, demonstrating superior capability in correctly identifying significant rainfall. While there is a slight increase in POFD score from the 10-min to the 70-min lead time, HX consistently outperformed both GTX and CTRL in minimizing false detections across all thresholds.

On 30 September 2018 (analysis time 03:00 UTC), Figure 9b shows the POFD scores at both 10 min and 70 min lead times. The control experiment -CTRL exhibits a stable range between 0.47 and 0.71 across all rainfall thresholds, indicating consistency. At the 10-min lead time, the control experiment -CTRL exhibits a moderate POFD range (0.47–0.57), demonstrating lack of differentiation in prediction accuracy across thresholds. In contrast, the GTX experiment exhibits a high POFD score of 0.75 at the 0.2 mm threshold but shows a steep decline to 0.16 at 2 mm, suggesting an over-detection tendency for lighter rainfall and improved discrimination for heavier events. The HX experiment, however, demonstrated the most favorable scores—starting at 0.24 and dropping sharply to 0.04 at 2 mm—indicating strong dictation of false alarms. At a 70-min lead time, all experiments showed increased POFD values, signaling a general decline in forecast accuracy over time. The control experiment -CTRL ranges from 0.65 to 0.71, and the GTX experiment ranges from 0.85 at the lowest threshold down to 0.38 at 2 mm. Meanwhile, the HX experiment sustained its advantage with values between 0.47 and 0.11, confirming its ability to maintain lower false alarm rates for higher rainfall thresholds, even as lead time increased. Overall, both figures underscore the superior performance of the HX experiment in minimizing false alarms across all thresholds and lead times. The control experiment-CTRL maintains a stable behavior across rainfall thresholds, while the GTX experiment improves with rainfall intensity.

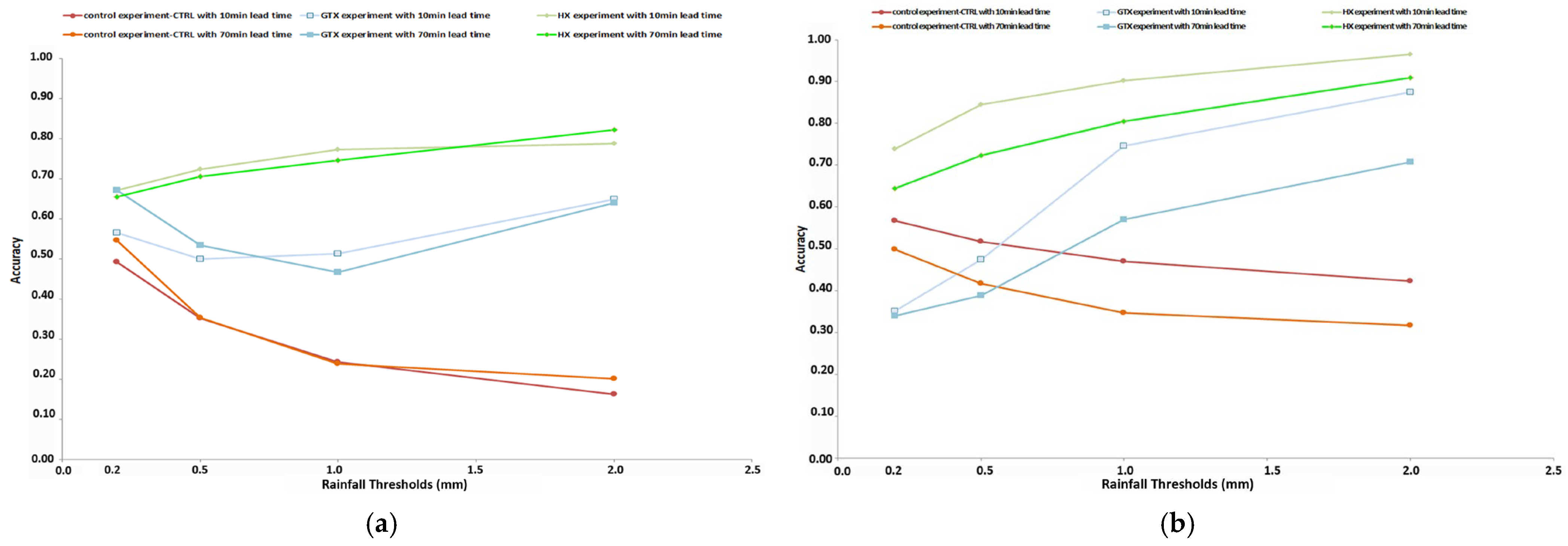
Furthermore, on 29 September 2018 (analysis time 15:00 UTC), Figure 10a shows the accuracy scores at 10 min and 70 min lead times. The HX experiment demonstrates a significant increase in accuracy scores from light to moderate rainfall thresholds ranging between 0.65 and 0.82. The accuracy scores decrease as lead time increases, except for the 2.00 mm threshold where the accuracy score increases a little with lead time. At the 10-min lead time, the HX experiment exhibits the highest accuracy scores, increasing from 0.67 at 0.2 mm to 0.79 at 2 mm, indicating strong capability in detecting heavier rainfall events. In contrast, the GTX experiment exhibits a wider range of accuracy scores varying between 0.57 and 0.65. The control experiment-CTRL shows much lower and decreasing accuracy values, from 0.49 to 0.16, suggesting reduced effectiveness in identifying higher intensity rainfall. At the 70-min lead time, the HX experiment maintains superior performance, with accuracy scores from 0.65 to 0.82, showing a continued increase with rainfall intensity. The CTRL experiment remained relatively weak and unchanged from the 10-min lead time, with values ranging from 0.55 at 0.2 mm to 0.20 at 2 mm. The GTX experiment, while showing some improvement at lower thresholds, is still behind the HX experiment.

Similarly, Figure 10b shows the accuracy scores for 10 min and 70 min lead times on 30 September 2018 with analysis time 03:00 UTC. Both the GTX and the HX experiments show a significant increase in accuracy scores from light to moderate rainfall thresholds. At the 10 min lead time, the GTX and HX experiments show a gradual improvement as the threshold increases, with the HX experiment achieving the highest performance across all threshold levels. In contrast, the control experiment -CTRL shows a gradual decrease in performance as the threshold increases, suggesting reduced effectiveness. At the 70th minute lead time, the GTX and HX experiments continue to improve, although at lower values compared to the 10th minute lead time. Specifically, the HX experiment maintains the highest performance. Meanwhile, the control experiment-CTRL displays a more stable behavior varying between 0.32 and 0.57, across the precipitate thresholds as it was seen in POFD. In conclusion, both figures highlight the HX experiment’s exceptional ability to identify rainfall events at all thresholds and lead times.

In conclusion, the HX experiment demonstrates the most accurate nowcasts regarding both nowcasts and warnings, making it the most reliable experiment. However, as the lead time increases, the nowcasting performance decreases.

4.5. Summary and Interpretation

This study demonstrates that the forward advection scheme implemented in the Local Analysis and Prediction System (LAPS) incorporated with satellite-derived rainfall retrievals and XPOL radar data, significantly improves nowcasting accuracy.

Across all analysis dimensions—spatial structure, ground validation, bias, error metrics, and detection skill—the HX experiment consistently outperformed the other configurations. The lower BIAS in the HX experiment indicates a reduced systematic overestimation of rainfall, a common issue in the control experiment. This improvement suggests that the assimilation of remote sensing data, particularly H-SAF, helps to constrain the model’s tendency towards overprediction. The HX experiment led to a significant improvement in short-term rainfall forecasts, showing a 60% reduction in ubRMSE error at a 60-min and a 55% reduction in ubRMSE error at a 90-min lead time compared to the control experiment-CTRL. The lower ubRMSE signifies a reduction in random errors, pointing to a more spatially accurate and reliable forecast. Moreover, the better POFD and accuracy scores of the HX experiment, especially at higher rainfall thresholds, indicate an enhanced ability to correctly detect significant rainfall events and minimize false alarms, which are crucial for effective early warning systems in flood-prone areas like Attica.

The comparison between the two set of experiments (September 29th and 30th) reveals that the benefits of assimilating high-resolution satellite data are evident for both intense and lighter rainfall events, although the magnitude of improvement may vary. This suggests that the sensitivity to remote sensing data is not limited to specific types of rainfall events but has a broader positive impact on nowcasting accuracy.

While the methodology employed a forward advection scheme within LAPS, the results demonstrate that the choice of assimilated data significantly influences the scheme’s performance. The optimized integration of high-resolution radar with the broad and frequent coverage of H-SAF satellite data proves to be a key factor in enhancing short-term predictability in this region. The methodology developed in this study is adaptable to different geographical regions and data availability, highlighting its potential for widespread application in nowcasting systems.

Although this study does not include a direct benchmark against external nowcasting systems such as pySTEPS or optical flow-based techniques, it provides the relative value of different data assimilation configurations within the LAPS- framework. While focused on a Medicane-type event, the methodology should be tested across a broader range of rainfall patterns, such as frontal systems. Future work will aim to validate the approach under different meteorological scenarios to better assess its operational generalizability.

5. Conclusions

Assimilating remote sensing in NWP models can improve the accuracy of rainfall estimates. In this study, a rainfall event that affected the Athens metropolitan area in Greece on 29 and 30 September 2018 is analyzed through two set of experiments, each focusing on different intensities was used as a case study for the implementation of a forward advection scheme in LAPS as a system of early warnings. In nowcasting mode, several remote sensing measurements are assimilated by LAPS including weather radar data to produce objective analyses. Applying the methodology presented in Section 2, the produced fields were advected and the outputs were presented in Section 4. It was found that assimilating H-SAF with radar rainfall retrievals (HX experiment) substantially improved the short-term predictability of rainfall offering a substantial improvement of almost 60% against the control experiment for the 60 min and 55% for the 90 min unbiased RMSE of the nowcasted rainfall. Indeed, the percentage increases by 10 points at elevations less than or equal to 300 m compared to higher elevations. This is an encouraging outcome as lower elevations are the most flood-prone and vulnerable populated areas. Entire control nowcasts having GFS near to the analysis forecasts as background fields with METAR and SYNOP observations systematically overestimated the rainfall rate (Control experiment-CTRL). Moreover, the assimilation of TRMM and IMERG products with radar data (GTX experiment) also gives nowcasts with a significant systematic overestimation of the rainfall rate.

This study demonstrates that integrating satellite-derived rainfall retrievals with radar data significantly enhances short-term rainfall forecasts, outperforming traditional NWP models and single-source assimilation methods. The LAPS-based forward advection scheme effectively reduces bias and improves accuracy in nowcasting weather events. Among the tested configurations, the HX experiment—incorporating H-SAF satellite data—delivered the most reliable results, highlighting the advantages of higher temporal resolution satellite retrievals. These findings emphasize the importance of multi-source data assimilation for real-time forecasting, particularly in regions with complex rainfall dynamics. Although this case study was conducted in the Attica region, the results underscore the potential applicability of the system to other geographies. LAPS is modular and capable of ingesting various radar and satellite inputs. Beyond this case study, our approach has broader applications in operational weather forecasting and disaster management, providing a scalable framework for improving short-term rainfall predictions.

Assimilating H-SAF rainfall estimates with radar data substantially improved the short-term predictability of rainfall compared to independent measurements. In most of the runs the predictability of the nowcasts decreases with the lead time. Combining radar data with H-SAF and IMERG-TRMM products, rainfall nowcasts were improved due to their higher resolution in both space and time. H-SAF products have 15 min temporal resolution while IMERG and TRMM have a 30-min and 3 h temporal resolution, respectively. Moreover, HSAF products have 8 km spatial resolution over Europe, while IMERG and TRMM have 10 km and 25 km spatial resolution, respectively.

In general, using a forward advection scheme in LAPS which incorporated H-SAF and radar data had benefits such as more precise and timely rainfall forecasts. The scheme’s adaptability, which allowed providing nowcasts using any available data, was an advantage. Radar data, usable in real time, was the most significant source of rainfall information. In case of the absence of the radar data, LAPS with background fields would also provide early warnings. This scheme could predict rainfall’s path and potential impact, allowing the authorities and individuals to take the necessary precautions to protect themselves and minimize the damage. People could be better prepared and make better choices to mitigate potential risks and minimize negative impacts by using nowcasting as a system of early warnings.

It should be noted that the result of this study is based in a case study of a single meteorological event including different rainfall patterns: one with intense, localized rainfall and another with more scattered rainfall. While this provides some variability, future work will expand by testing across more diverse meteorological scenarios. In order to completely assess the system’s capabilities, additional high-impact events have to be tested. Future work will focus on extending this methodology to additional storm events, refining computational efficiency, and integrating machine learning techniques to further enhance forecasting capabilities. Additionally, the advection scheme will be enhanced by incorporating the effects of orography on rainfall distribution.