Using Machine Learning to Develop a Surrogate Model for Simulating Multispecies Contaminant Transport in Groundwater

Abstract

Traditional numerical models have been widely employed to simulate the transport of multispecies reactive contaminants in groundwater systems; however, their high computational cost limits their applicability in real-time or large-scale scenarios. Recent advances in artificial intelligence (AI) offer promising alternatives, particularly data-driven machine learning techniques, for accelerating such simulations. This study presents the development of a surrogate model based on artificial neural networks (ANNs) to simulate the transport and decay of interacting multispecies contaminants in groundwater. High-fidelity training datasets are generated through finite difference-based reactive transport simulations across a wide range of environmental and geochemical conditions. The ANN model is trained to learn the complex nonlinear relationships governing the multispecies transport and transformation processes. Model validation reveals that the ANN surrogate accurately reproduces the spatial–temporal concentration profiles of both original and degradation species, capturing key dynamic behaviors with high precision. Notably, the ANN model achieves up to a 100-fold reduction in computational time compared to traditional analytical or semi-analytical solutions. These results highlight the ANN’s potential as an efficient and accurate surrogate modeling tool for groundwater contamination assessment, offering a valuable advancement for decision-making in environmental risk analysis and remediation planning.

1. Introduction

Groundwater contamination is increasingly causing irreversible harm to human health. Numerous theoretical and experimental studies have been conducted to understand the fate and transport of these contaminants in groundwater systems, with the goal of developing accurate and robust mathematical models for predicting contaminant concentrations. Contaminants may degrade over time, producing a series of degradation byproducts during the process. Therefore, when developing transport models for subsurface environments, it is essential to consider both the original contaminants and those generated through degradation processes [1,2,3,4,5,6,7,8,9,10]. Mathematically, the migration behavior of contaminants and their degradation byproducts is described by a system of coupled advection–dispersion equations (ADEs) [11,12,13,14,15,16,17,18,19]. These coupled ADEs can be solved using either analytical or numerical methods. However, numerical approaches often involve intensive computations and extended processing times, particularly when applied to long-term, large-scale, or complex subsurface systems.

In addition to using analytical approaches that retain fundamental physical principles while incorporating simplified assumptions to reduce the computational burden of multispecies reactive transport simulations in long-term, large-scale, or complex subsurface systems, another effective strategy is the use of surrogate models.

A surrogate model is a computationally efficient approximation that can replace traditional multispecies reactive transport numerical simulations. With the rapid advancement of artificial intelligence and computational power, data-driven machine learning methods have been increasingly applied to construct surrogate models. Data-driven machine learning identifies patterns between inputs and outputs from large datasets to develop predictive models [20,21]. In the context of multispecies reactive transport, machine learning-based surrogate models are trained on input–output data pairs generated by various combinations of simulation conditions. These models learn the relationship between different input parameters and the corresponding simulation outputs, enabling the construction of an efficient surrogate. Unlike physically simplified analytical models that are still grounded in the underlying physical processes, data-driven surrogate models do not incorporate any physical principles. Nevertheless, they offer a significant reduction in computational time for reactive transport simulations. Compared to traditional, physically based numerical models, surrogate models provide improved computational efficiency.

Jatnieks et al. (2016) [22] employed a data-driven surrogate model to replace conventional reactive transport simulations, demonstrating substantial acceleration in computational performance, with several-fold improvements in execution time. However, they noted that numerous unresolved challenges remain, warranting further investigation. De Lucia and Kühn (2021) [23] developed both purely data-driven and physics-informed surrogate models, collectively referred to as Dec Tree v1.0-chemistry, to enhance the computational efficiency of reactive transport simulations. Their study presented and analyzed two distinct approaches to replacing geochemical modeling in reactive transport. The first is purely data-driven and does not incorporate any knowledge of physical mechanisms. The second involves deriving a surrogate model based on solving the actual equations from a full physical representation. Both methods were applied to a simple one-dimensional reactive transport benchmark problem and evaluated accordingly. Li et al. (2022) [24] noted that in reactive transport simulations based on physical processes, the computation of complex chemical reactions typically involves iterative processes, which can be computationally expensive. To address this, they developed a neural network-based surrogate model to serve as a surrogate workflow for reactive transport simulation. Their workflow included: (1) designing the base reactive transport case; (2) developing training experiments; (3) constructing a machine learning-based surrogate model; (4) validating the model; and (5) predicting using the calibrated surrogate model. Results showed that the surrogate model’s predictions closely matched those of the physically based numerical simulations, while significantly reducing computation time. For tasks requiring large-scale computation, such as sensitivity analysis or model calibration, the well-trained surrogate model proved especially useful, offering substantial time savings compared to traditional simulations. Turunen and Lipping (2023) [25] compared a neural network-based metamodel (surrogate model) with a numerical model based on differential equations for simulating the transport of cesium-137 in sandy soil. The surrogate model was developed by training a convolutional neural network (CNN) using outputs from the differential equation model. The size of the training dataset ranged from 5120 to 163,840 samples. They applied both first-order and total-order Sobol methods to evaluate the feasibility of the CNN surrogate model in sensitivity analysis for radioactive nuclide transport. Their results indicated that when the training set reached 40,960 samples or more, the CNN could replicate the outputs of the differential equation model with high accuracy. Furthermore, in the sensitivity analysis, the CNN surrogate produced results comparable to those of the numerical model. These previous studies clearly demonstrate that combining reactive transport modeling with machine learning can substantially reduce computational time.

Although prior studies have explored various machine learning strategies for surrogate modeling in reactive transport, most of these studies have focused on single-species transport or simplified reaction systems. To date, no study has applied a surrogate modeling approach to simulate multispecies reactive transport involving sequential degradation in groundwater systems. This problem is particularly important for environmental scenarios such as the natural attenuation and bioremediation of chlorinated solvent-contaminated groundwater, as well as the safety assessment of radionuclide decay chain transport, where both parent and daughter species coexist over time. In response to this gap, the present study integrates machine learning techniques to develop a fast and accurate surrogate model for simulating the migration of coexisting contaminants and their degradation products in groundwater. This study aims to integrate machine learning methods to develop a rapid predictive model for the migration of contaminants and their degradation products coexisting in aquifers. This research will evaluate the impact of sample size on the accuracy of the surrogate model and its computational efficiency.

2. Machine-Learning-Based Model for Multispecies Transport

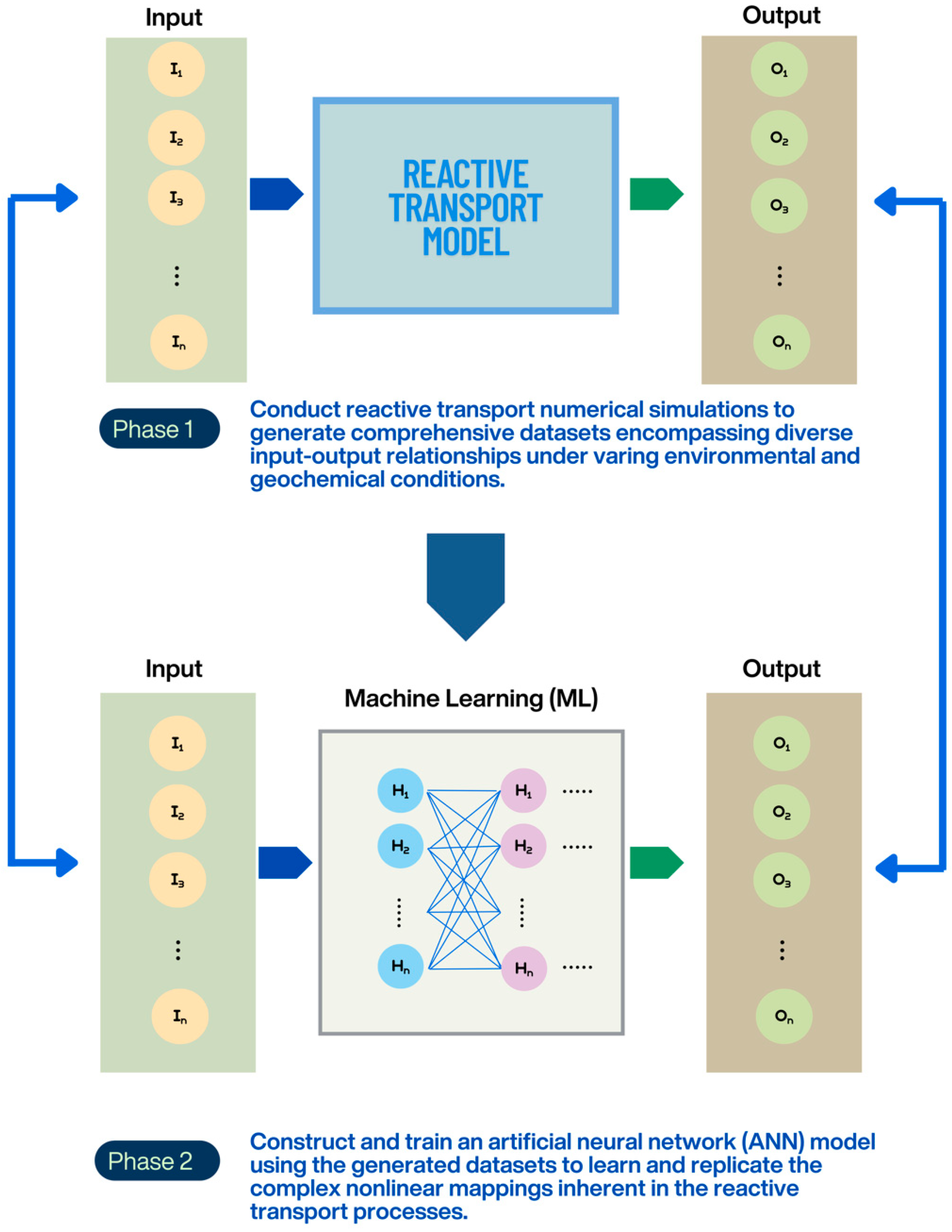
This study develops a rapid prediction model for multispecies contaminant transport by integrating machine learning techniques with reactive transport numerical simulations. The research framework is shown in Figure 1. It consists of two main stages. The first phase involves constructing a model required for reactive transport numerical simulation. The input parameters for the simulation include groundwater seepage velocity, hydrodynamic dispersion coefficient, attenuation factors, and degradation constants for individual contaminants. The output is the concentration of each contaminant. Thus, the first set of input parameters, $I_1$, can be used to perform a reactive transport numerical simulation to generate the first set of output variables, $O_1$, which represent the simulated concentrations of individual contaminants in groundwater. Following the same procedure, a second set of input parameters, $I_2$, can be used to generate a second set of output variables, $O_2$, through simulation. Similarly, a third set of input parameters, $I_3$, yields the third set of output variables, $O_3$, and this process is repeated until the $n$-th set of input parameters, $I_n$, is used to produce the $n$-th set of output variables, $O_n$. The value of $n$ depends on the requirements for training and validating the machine learning model.

Recent studies have explored the use of artificial neural networks (ANNs) in groundwater contaminant transport modeling, particularly for accelerating forward simulations and performing sensitivity analyses [26,27,28,29,30,31]. These works have demonstrated the potential of ANNs to approximate numerical models with substantially reduced computational cost. However, most existing applications focus on single-species transport or simplified reaction systems. In contrast, the present study develops an ANN-based surrogate model tailored for multispecies reactive transport involving sequential degradation, which remains largely unexplored in the current literature.

In the second phase, machine learning is used to develop a surrogate model for multispecies transport. The ANN is used to construct this surrogate model due to its practicality and suitability for this problem. Different sets of input parameters from the reactive transport numerical simulations ($I_1$, $I_2$, $I_3$…$I_n$) serve as the input layer of the ANN model, while the output variables from the simulations ($O_1$, $O_2$, $O_3$…$O_n$) serve as the output layer. The ANN is chosen for its suitability in approximating structured input and output relationships derived from numerical simulations. Compared to more complex architecture, it offers fast training, minimal tuning requirements, and efficient prediction capabilities. In this study, the ANN is trained on simulation data to capture the nonlinear relationships between transport parameters and solute concentrations. To evaluate the predictive performance of the ANN, this study employs cross-validation to ensure the model’s robustness on unseen data.

The research framework is divided into two main phases. In the first phase, a reactive transport numerical model is developed, and various combinations of input parameters ($I_1$, $I_2$, $I_3$…$I_n$) are used to generate the corresponding output results ($O_1$, $O_2$, $O_3$…$O_n$). In the second phase, a surrogate model for reactive transport is constructed using machine learning. Specifically, an ANN is adopted as the machine learning model, where the input parameters from the reactive transport simulations ($I_1$, $I_2$, $I_3$…$I_n$) serve as the inputs to the ANN, and the corresponding output results ($O_1$, $O_2$, $O_3$…$O_n$) are used as the outputs of the ANN model.

This study considers the reactive transport of an original contaminant and its degradation product within a one-dimensional aquifer system. The transport processes incorporated include advection, hydrodynamic dispersion, first-order decay, and linear equilibrium sorption. This study assumes a homogeneous aquifer system and uniform flow. The governing advection–dispersion equation is formulated as follows:

$$R_1{\displaystyle \frac{\partial C_1(x,t)}{\partial t}}=D{\displaystyle \frac{{\partial }^2{C}_1(x,t)}{\partial x^2}}-v{\displaystyle \frac{{\partial }^2{C}_1(x,t)}{\partial x^2}}-{\lambda }_1{R}_1{C}_1(x,t)$$

(1)

$$R_2{\displaystyle \frac{\partial C_2(x,t)}{\partial t}}=D{\displaystyle \frac{{\partial }^2{C}_2(x,t)}{\partial x^2}}-v{\displaystyle \frac{{\partial }^2{C}_2(x,t)}{\partial x^2}}-f_{1\to 2}{\lambda }_2{R}_2{C}_2(x,t)+{\lambda }_1{R}_1{C}_1(x,t)$$

(2)

Equation (1) describes the transport and degradation of the original contaminant, while Equation (2) accounts for the transport of the degradation product, which is formed because of the decay of Species 1 and is also subject to its own decay and transport processes. In these equations, C₁(x,t) and C₂(x,t) are the aqueous concentrations of the original contaminant and degradation product, respectively; t is time; x is the spatial coordinate; v is the seepage velocity; D is the dispersion coefficient; R₁ and R₂ are the retardation factors for the original contaminant and degradation product, respectively; λ₁ and λ₂ are their respective first-order degradation rates; and f_1→2 is the yield coefficient (original contaminant/degradation contaminant).

Assuming the aquifer is initially uncontaminated, the initial condition can be mathematically formulated as follows:

$$C_1(x,t=0)=0$$

(3)

$$C_2(x,t=0)=0$$

(4)

At the inlet boundary, a constant concentration is prescribed for the original contaminant, whereas no source term is imposed for its degradation products. The boundary condition is mathematically defined as

$$C_1(x=0,t)=C_0$$

(5)

$$C_2(x=0,t)=0$$

(6)

where $C_0$ is the constant concentration prescribed for the original contaminant at the inlet boundary.

At the outlet boundary, a zero concentration is prescribed, which can be mathematically expressed as

$$C_1(x=L,t)=0$$

(7)

$$C_2(x=L,t)=0$$

(8)

To facilitate mathematical analysis and the development of a generalized machine learning model, Equations (1)–(8) are nondimensionalized and reformulated as follows:

$$R_1{\displaystyle \frac{\partial C_1(X,T)}{\partial T}}={\displaystyle \frac{1}{Pe}}{\displaystyle \frac{{\partial }^2{C}_1(X,T)}{\partial X^2}}-{\displaystyle \frac{{\partial }^2{C}_1(X,T)}{\partial X^2}}-{\mathsf{\Lambda }}_1{R}_1{C}_1(X,T)$$

(9)

$$R_2{\displaystyle \frac{\partial C_2(X,T)}{\partial T}}={\displaystyle \frac{1}{Pe}}{\displaystyle \frac{{\partial }^2{C}_2(X,T)}{\partial X^2}}-{\displaystyle \frac{{\partial }^2{C}_2(X,T)}{\partial X^2}}-{\mathsf{\Lambda }}_2{R}_2{C}_2(X,T)+f{\mathsf{\Lambda }}_1{R}_1{C}_1(X,T)$$

(10)

$$C_1(X,T=0)=0$$

(11)

$$C_2(X,T=0)=0$$

(12)

$$C_1(X=0,T)=C_0$$

(13)

$$C_2(X=0,T)=0$$

(14)

$$C_1(X=1,T)=0$$

(15)

$$C_2(X=1,T)=0$$

(16)

where $Pe={\displaystyle \frac{vL}{D}}$, ${\mathsf{\Lambda }}_1={\displaystyle \frac{{\lambda }_{1}L}{v}}$ and ${\mathsf{\Lambda }}_2={\displaystyle \frac{{\lambda }_{2}L}{v}}$

The finite difference method is employed to solve the above initial boundary value problem due to its superior computational efficiency, high numerical accuracy, and straightforward implementation. A numerical solution based on the finite difference method, along with its corresponding computational code, has been developed. The code enables the simulation of concentration distributions for the original contaminant and its degradation product under various combinations of input parameters.

Subsequently, an artificial neural network is employed to develop a surrogate model for the transport of multispecies contaminants. By systematically varying combinations of input parameters, the finite difference-based computational model generates a comprehensive dataset that effectively characterizes the transport dynamics of multispecies contaminants. This dataset serves as a crucial foundation for training the artificial neural network surrogate model. Considering the input parameter ranges specified in

Table 1. Ranges of input parameters employed in the finite difference simulations, which were used to generate the training datasets for the artificial neural network (ANN) surrogate model of multispecies contaminant transport.

Parameters	Ranges of Parameters
X	0 to 1
T	0 to 5
Pe	1 to 10
ʌ1	0 to 5
ʌ2	0 to 5
R1	1 to 5
R2	1 to 5

, a large dataset is generated where each input sample (In) consists of 7 features: spatial position (X), time (T), Peclet number (Pe), degradation rates (λ₁, λ₂), and retardation factors (R₁, R₂). Correspondingly, the output contains 2 predicted values: the aqueous concentrations of the original contaminant (C₁) and its degradation product (C₂). To ensure representative coverage while maintaining computational efficiency, a subset of simulations is randomly selected from a uniform parameter grid using a Monte Carlo approach. This sampling strategy avoids reliance on predefined statistical distributions yet preserves diversity across the input data. Once trained, the network can effectively capture the complex transport dynamics of contaminants and their degradation products under a wide range of environmental conditions.

The development of the artificial neural network involves six key steps to ensure that the model operates effectively and accurately. The first step is problem definition and data preparation, during which the problem must be clearly defined and the input and output data collected. Next is dataset splitting, where the dataset is typically divided into training and test sets. Then comes ANN model design, which involves determining the number of hidden layers, the number of neurons in each layer, and selecting appropriate activation functions. This is followed by model training, where the model’s weights are optimized to minimize prediction error. In the model evaluation stage, the test set is used to assess the model’s accuracy and mean squared error (MSE), ensuring that the model is not overfitting. Finally, model optimization is performed to further enhance the predictive accuracy of the artificial neural network in simulating the transport of multispecies contaminants.

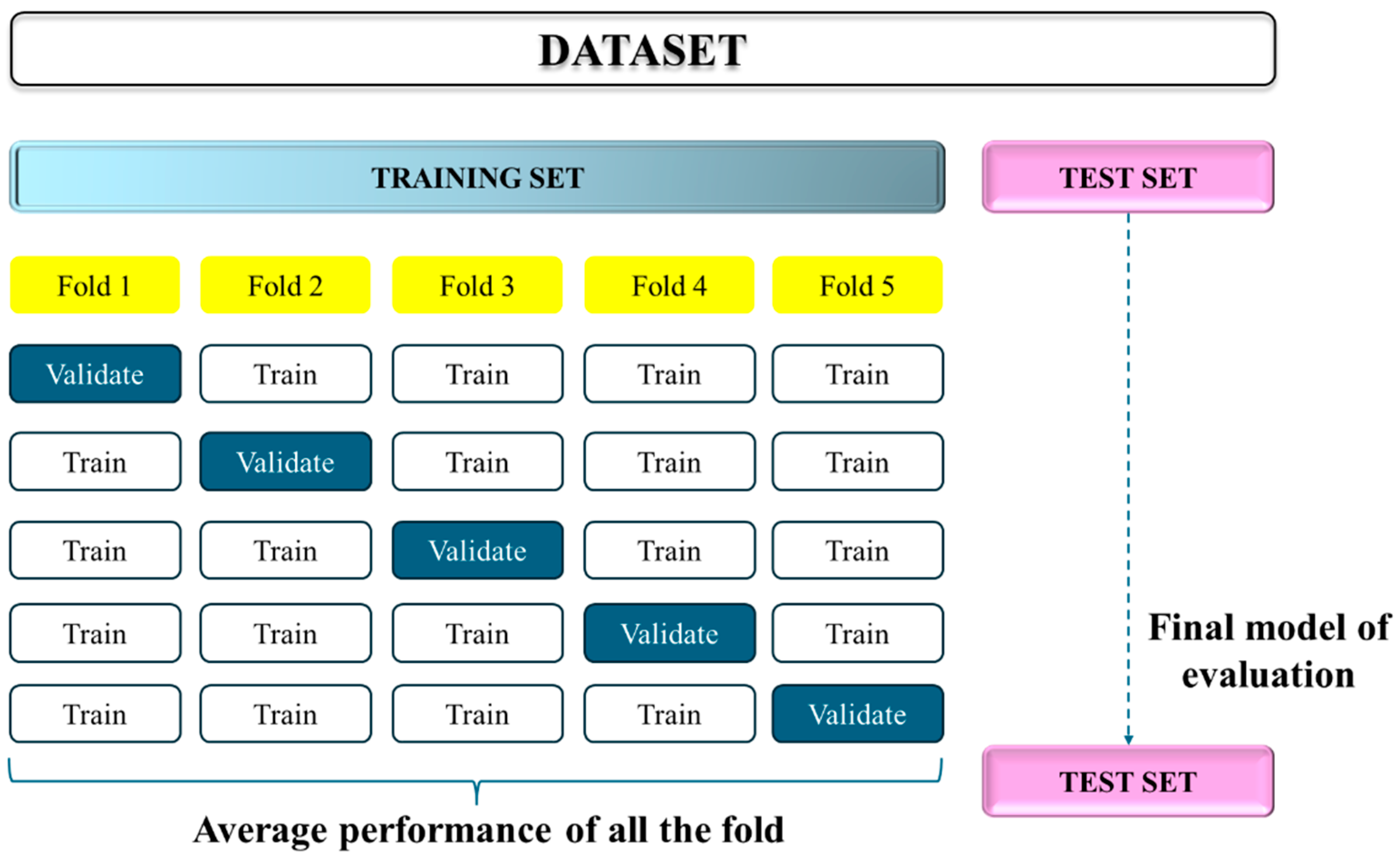
As previously mentioned, the artificial neural network will be trained on input–output datasets derived from finite difference numerical simulations, allowing it to learn and approximate the complex relationships between input parameters and contaminant concentration responses. However, because the finite difference simulations are conducted over densely discretized spatial and temporal grids, using the entire dataset for training would substantially increase the computational cost and training time of the artificial neural network. To reduce the size of the dataset while retaining the key governing patterns required for effective ANN training, this study employs Monte Carlo sampling to extract a representative subset from the full dataset. This approach offers the flexibility to adjust the size of the input–output dataset, enabling efficient model training without compromising the integrity of the underlying transport dynamics. In this study, datasets of varying sizes will be used to evaluate their impact on the performance of artificial neural network (ANN) training. The dataset is partitioned such that 80% is used for training and 20% is used for testing. For the training portion, the k-fold cross-validation method is adopted. This approach divides the training data evenly into k subsets. In each iteration, the model is trained on k-1 subsets and validated on the remaining one. This process is repeated k times, with a different subset used for validation in each iteration (as illustrated in Figure 2). K-fold cross-validation maximizes data utilization and ensures that the model is evaluated across multiple subsets, thereby enhancing both model accuracy and generalization capability. The final model performance is computed as the average of the k-fold validation results, providing a more comprehensive and reliable assessment.

3. Results

Based on the nondimensionalized ADEs described in Equations (9) and (10), the input parameters used to predict the concentration of the original contaminant (C₁) include $X$, $T$, $Pe$, $R_1$, and ${\mathsf{\Lambda }}_1$. In contrast, the input parameters for predicting the concentration of the decay product (C₂) include $X$, $T$, $Pe$, $R_1$, $R_2$, ${\mathsf{\Lambda }}_1$, ${\mathsf{\Lambda }}_2$, and $C_1$. To ensure predictive accuracy, this study develops and trains distinct ANN architectures for each contaminant, as the type and number of input features vary depending on the characteristics of each species. For the original contaminant, the ANN surrogate model is designed with a deep architecture comprising four hidden layers containing 64, 64, 32, and 16 neurons, respectively. In contrast, to capture the increased complexity associated with the transformation and interaction processes of degradation products, a deeper network configuration is employed. Specifically, the ANN model for degradation products consists of six hidden layers, with 64, 64, 64, 32, 32, and 16 neurons, respectively. All hidden layers utilize the Rectified Linear Unit (ReLU) activation function to enhance nonlinearity and mitigate vanishing gradient issues. Model training and weight optimization are conducted using the Adam optimizer, which provides efficient stochastic gradient-based learning and adaptive learning rates, thereby enhancing convergence performance.

To evaluate the impact of training data volume on the performance and predictive accuracy of the ANN models, this study employs datasets of three different sizes: 0.5 million, 1 million, and 2 million samples. Model performance for both the original contaminant and its degradation product is assessed using three error metrics: mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE). The detailed evaluation outcomes are summarized in

Table 2. Performance metrics (MAE, MSE, and RMSE) of the ANN model for predicting the original contaminant and degradation product based on different training dataset sizes.

Contaminant	Model	Sample
		500,000	1,000,000	2,000,000
Original Contaminant	MAE	0.0274	0.0212	0.0179
	MSE	0.0020	0.0011	0.0008
	RMSE	0.0443	0.0339	0.0291
Degradation Product	MAE	0.0138	0.0129	0.0100
	MSE	0.0005	0.0004	0.0002
	RMSE	0.0212	0.0201	0.0152

, based on the results obtained from the independent test datasets. The results indicate that, with increasing training sample size, all three error metrics—MAE, MSE, and RMSE—consistently decrease, demonstrating a notable improvement in model performance as the dataset size increases.

When the training dataset was relatively small (500,000 samples), the impact of ANN architecture on model performance was further investigated. By systematically varying the number of hidden nodes in each layer, this study assessed how network structure influences predictive accuracy. As summarized in

Table 3. The effect of ANN architecture, defined by the configuration of neurons in the hidden layers, on the predictive performance (MAE, MSE, and RMSE) for the original contaminant and degradation product, using 500,000 training samples.

Contaminant	Model	Sample
		64, 32, 16, 16	64, 64, 32, 32	128, 128, 64, 64
Original Contaminant	MAE	0.0274	0.0242	0.0164
	MSE	0.0020	0.0017	0.0009
	RMSE	0.0443	0.0412	0.0306
Degradation Product	MAE	0.0138	0.0114	0.0092
	MSE	0.0005	0.0003	0.0002
	RMSE	0.0212	0.0178	0.0151

, increasing the number of neurons in the hidden layers notably enhanced model accuracy for both the original contaminant and its degradation product. These findings underscore the critical importance of carefully designing the ANN architecture, particularly under data-scarce conditions. Nevertheless, while expanding the network depth or width can improve predictive performance, it inevitably increases model complexity and computational cost. Therefore, optimizing both the training data volume and ANN configuration is essential to achieve an effective balance between predictive accuracy and computational efficiency.

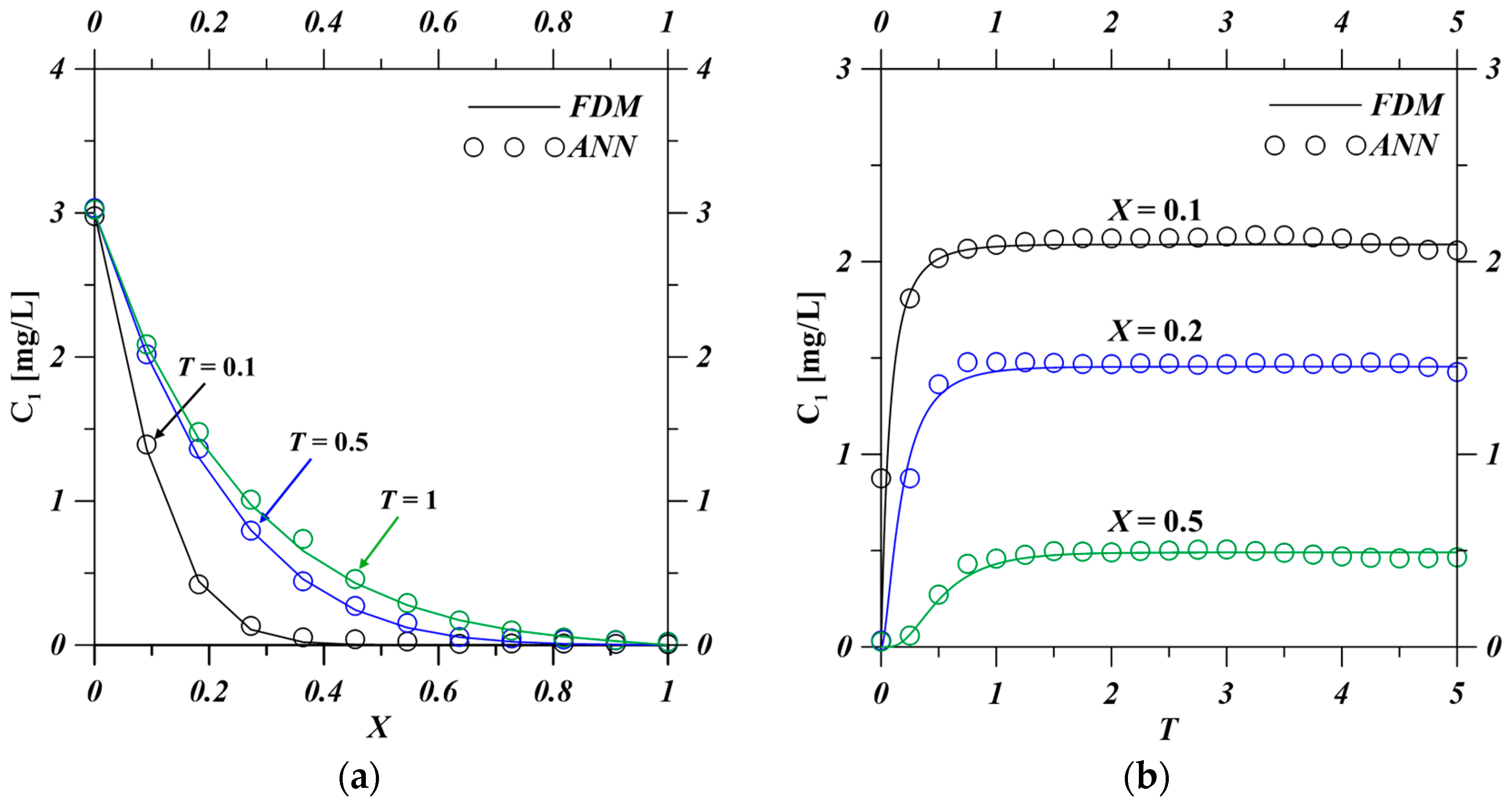
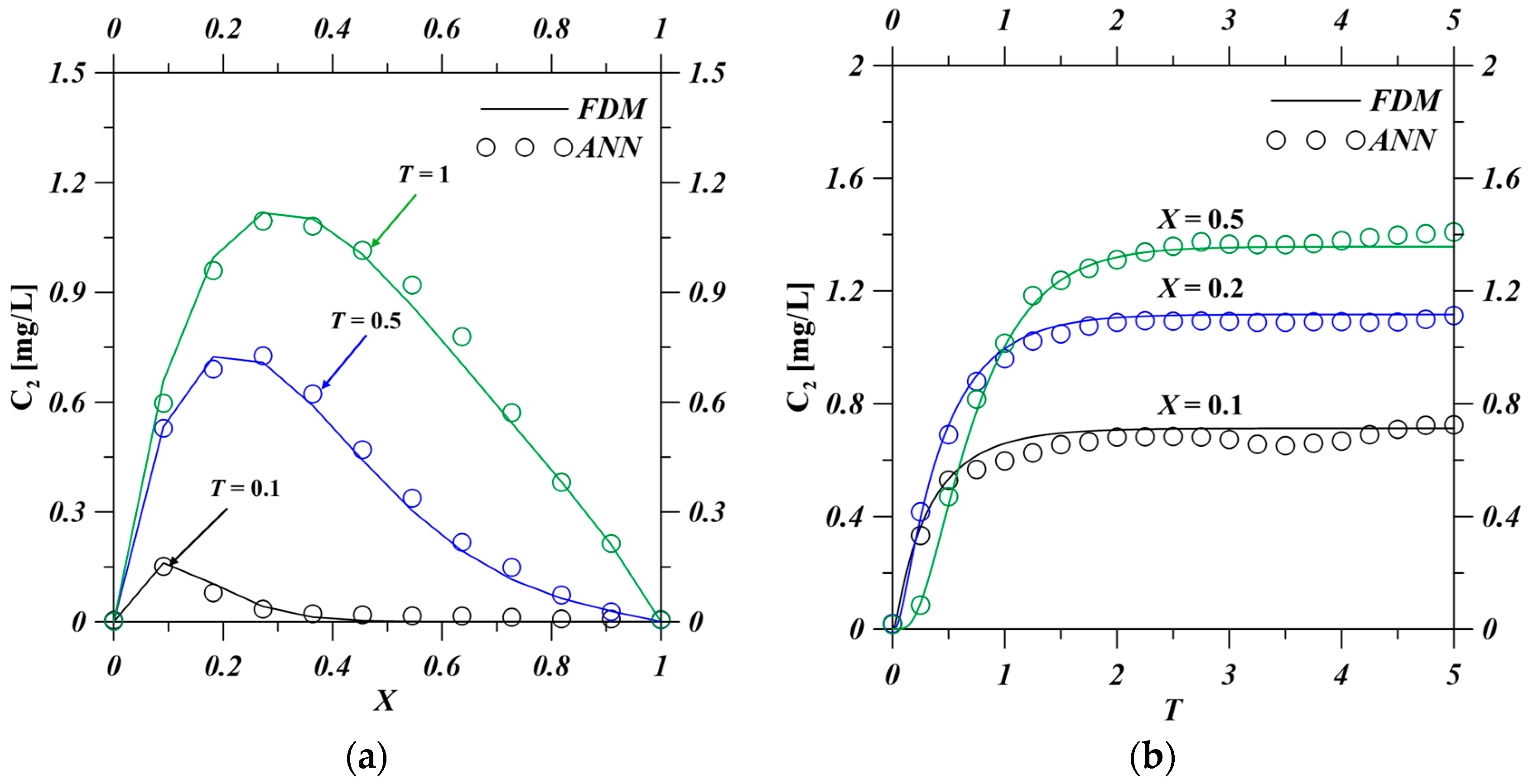
In this study, the predictive performance of the ANN model was comprehensively evaluated by comparing its outputs with those obtained from conventional finite difference method (FDM) simulations. The comparison results, presented in Figure 3 and Figure 4, correspond to both the original contaminant and its degradation product under the following parameter settings: $Pe$ = 5.0, $R_1$ = 4.0, $R_2$ = 2.0, ${\mathsf{\Lambda }}_1$ = 2.0, ${\mathsf{\Lambda }}_2$ = 1.0, and $C_0$ = 3.0 mg/L. As shown in

Table 4. Quantitative evaluation of ANN model performance in predicting the concentrations of the original contaminant and its degradation product. Error metrics include mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), and coefficient of determination (R²) assessed across selected spatial (X) and temporal (T) domains.

Domain Point	Original Contaminant
	Temporal			Spatial
	T = 0.1	T = 0.5	T = 1	X = 0.1	X = 0.2	X = 0.5
MAE	0.0362	0.0142	0.0131	0.029	0.0161	0.0235
MSE	0.0031	0.0003	0.0003	0.0019	0.0004	0.0007
RMSE	0.0555	0.0181	0.0165	0.0432	0.0193	0.0264
R2	0.9736	0.9860	0.9866	0.9875	0.9886	0.9881
Domain Point	Degradation Product
	Temporal			Spatial
	T = 0.1	T = 0.5	T = 1	X = 0.1	X = 0.2	X = 0.5
MAE	0.0047	0.0068	0.0112	0.0216	0.0108	0.0086
MSE	0.0001	0.0001	0.0002	0.0005	0.0002	0.0001
RMSE	0.0086	0.009	0.0138	0.0233	0.0125	0.0099
R2	0.9956	0.9948	0.9914	0.9799	0.9810	0.9894

, the ANN model exhibits high predictive accuracy across both spatial and temporal domains. For the original contaminant, relatively higher errors are observed at early time points (e.g., MAE = 0.0362, T = 0.1) in Table 4, likely due to the steep initial concentration gradients. However, the prediction accuracy improves significantly at later times and central spatial locations, with the lowest RMSE of 0.0165 and the highest R² of 0.9866 recorded at $T$ = 1 in Table 4. In contrast, the ANN model demonstrates notably lower prediction errors for the degradation product, attributed to its smoother and more stable transport behavior. As shown in Table 4, the MAE values remain below 0.0112 across all evaluated time points, with a minimum of 0.0086 in the spatial profiles. RMSE values consistently stay under 0.0138, and R² remains above 0.99 at all temporal points.

These findings confirm that the ANN model effectively captures the spatiotemporal evolution of both parent and daughter species. Specifically, the ANN accurately reproduces the decay behavior of the original contaminant and the rise–decay patterns of the degradation product across space and time. Despite minor discrepancies in transient regions (e.g., at low values of $X$ or $T$), the model consistently achieves low prediction errors, highlighting its strong generalization capability. These performance outcomes provide indirect but strong evidence that the input sampling strategy was adequate in capturing the key transport behaviors represented by the ranges in Table 1. Overall, the ANN-based surrogate offers a computationally efficient and accurate alternative to conventional numerical solvers for modeling multispecies contaminant transport in reactive systems.

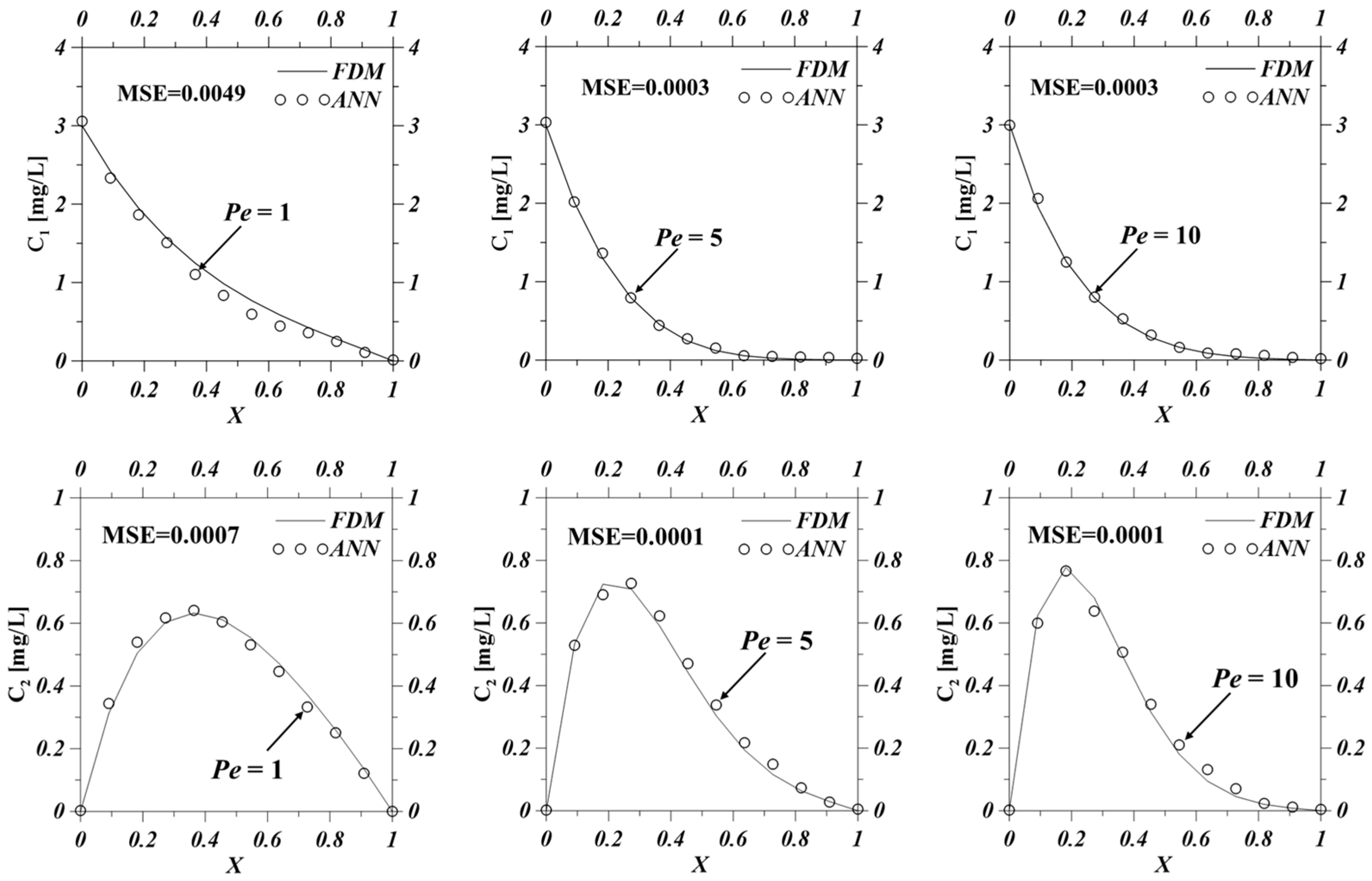
This study also evaluates the performance of the ANN model in simulating multispecies contaminant transport under varying Peclet number ($Pe$) conditions. The Peclet number characterizes the relative importance of advection versus dispersion, with higher $Pe$ values indicating advection-dominated transport regimes. In such scenarios, concentration profiles typically exhibit steep spatial and temporal gradients. Conventional numerical methods often require refined computational grids to accurately resolve these gradients and minimize artificial numerical dispersion. Figure 5 compares the predicted multispecies contaminant concentrations obtained from the ANN and the FDM solution at Peclet numbers of 1, 5, and 10. The results demonstrate that the ANN achieves high accuracy in predicting both original contaminant ($C_1$) and degradation product ($C_2$) concentrations. However, under $Pe$ = 1, which corresponds to a dispersion-dominated regime, the ANN tends to overestimate concentrations, particularly near the source zone. This suggests a limitation in the ANN’s ability to capture dispersion-driven transport behavior. Notably, as the Peclet number increases, the mean squared error (MSE) of the ANN predictions decreases significantly, with the lowest error observed at $Pe$ = 10, indicating enhanced performance under advection-dominated conditions. These findings demonstrate the ANN’s robustness and potential applicability across a wide range of hydrodynamic regimes, particularly in systems where advection is the primary transport mechanism.

One of the notable advantages of ANNs lies in their capacity to substantially reduce computation time, especially for complex, multi-parameter systems. This study directly compares the CPU running times of the ANN and the conventional finite difference method (FDM) under identical computing conditions. All simulations and training were conducted on a system equipped with a 13th Gen Intel^® Core™ i5-1335U CPU and 16 GB of RAM, using Python 3.12.4 without a GPU.

Table 5. Comparison of computation time between ANN and FDM for original contaminant and degradation product with Peclet numbers of 1, 5, and 10, respectively.

Contaminant	Model	Peclet Number
		Pe = 1	Pe = 5	Pe = 10
Original Contaminant	ANN	0.0119 s	0.0110 s	0.0074 s
	FDM	1.8817 s	1.8575 s	1.9228 s
Degradation Product	ANN	0.0454 s	0.0409 s	0.0270 s
	FDM	2.2814 s	2.4709 s	2.8880 s

compares the computation times between the ANN and FDM for different Peclet numbers, using both the original contaminant and its degradation product. The results reveal that the ANN model achieves approximately 158-fold, 168-fold, and 259-fold speed improvements over the FDM in predicting the concentration of the original contaminant (C₁) with Peclet numbers (Pe) of 1, 5, and 10, respectively. For the degradation product concentration (C₂), the performance is also significantly improved, with the ANN model operating 50 times with Pe = 1, 60 times with Pe = 5, and 107 times faster with Pe = 10 than the FDM. Moreover, as the Peclet number increases, the FDM exhibits a rise in computation time, whereas the ANN model maintains consistently fast performance, with a tendency to decrease. This indicates that ANN models are largely unaffected by increases in system complexity. These findings underscore the superior computational efficiency of ANN-based surrogate models, making them especially advantageous in scenarios involving multiple parameters and large numbers of simulation runs.

4. Conclusions

This study presents an artificial intelligence-based surrogate model for simulating the transport of multispecies contaminants, employing artificial neural networks (ANNs) to predict the migration behavior of these contaminants. The training datasets, comprising input–output pairs, were generated using finite difference numerical solutions. The developed ANN model successfully captures complex transport and decay dynamics, demonstrating strong potential as a computationally efficient alternative to conventional numerical approaches. Notably, the ANN model achieved a 50- to 259-fold reduction in computation time compared to the finite difference method. This advantage becomes particularly significant under high Peclet number (Pe) conditions, where conventional numerical methods often face considerable computational demands. Consequently, the ANN-based surrogate model offers a promising solution for real-time prediction and large-scale spatiotemporal simulations of multispecies contaminant transport. Future work will extend the surrogate modeling framework to multidimensional and field-scale applications. Such efforts will further enhance the model’s robustness, scalability, and practical utility for real-world assessments of groundwater contamination.

While the ANN surrogate model achieves high predictive accuracy and significantly reduces computational time, it still has certain limitations. The current implementation is limited to one-dimensional, synthetic scenarios, and its generalizability to higher-dimensional or real-world groundwater systems has not yet been evaluated. Moreover, as a data-driven approach, its accuracy may decline if applied outside the range of sampled input parameters. These aspects should be considered when interpreting the results, and future work will aim to extend the ANN-based framework to more complex transport conditions and practical applications.