Half-Century Review and Advances in Closed-Form Functions for Estimating Soil Water Retention Curves
Abstract
1. Introduction
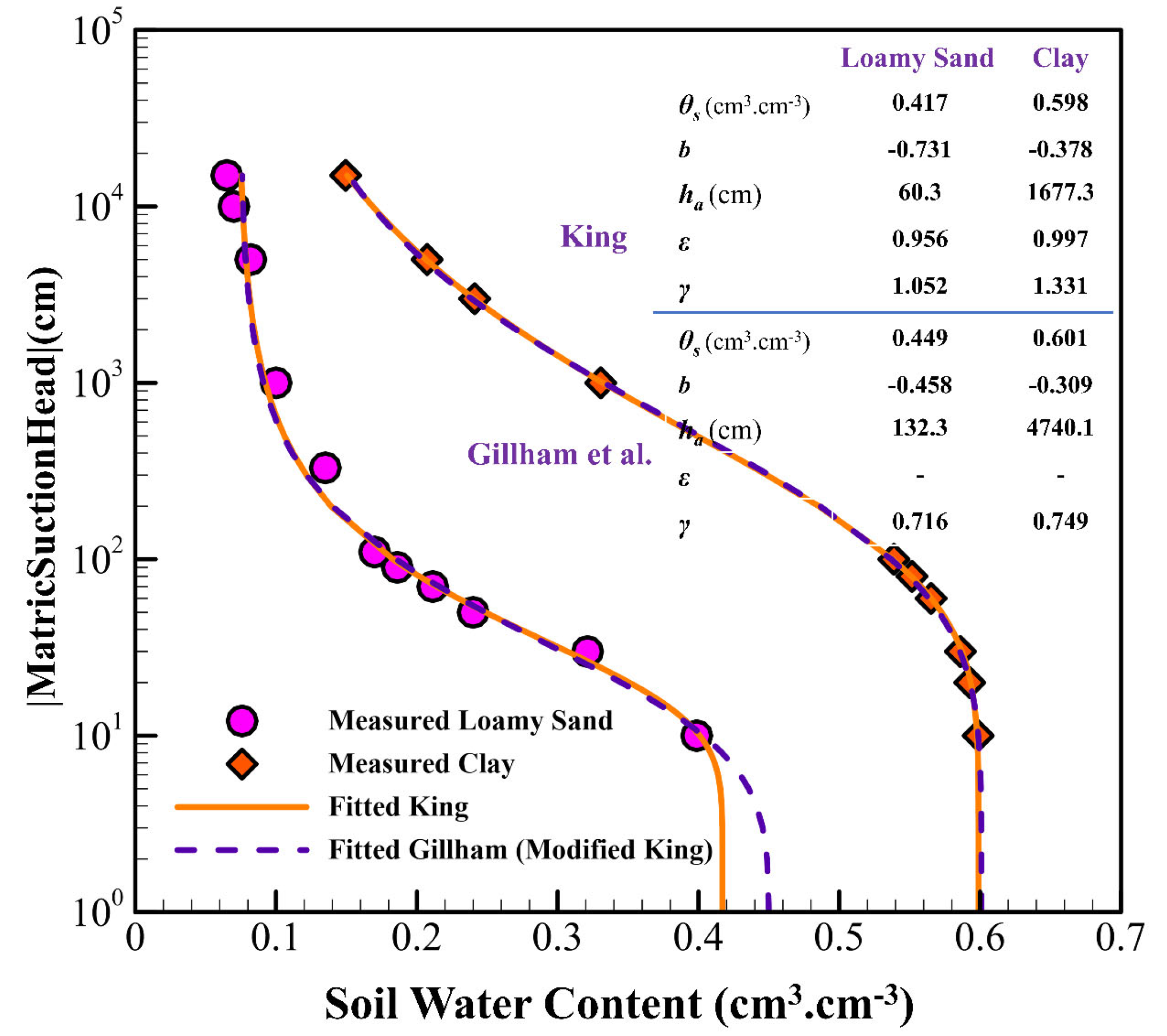
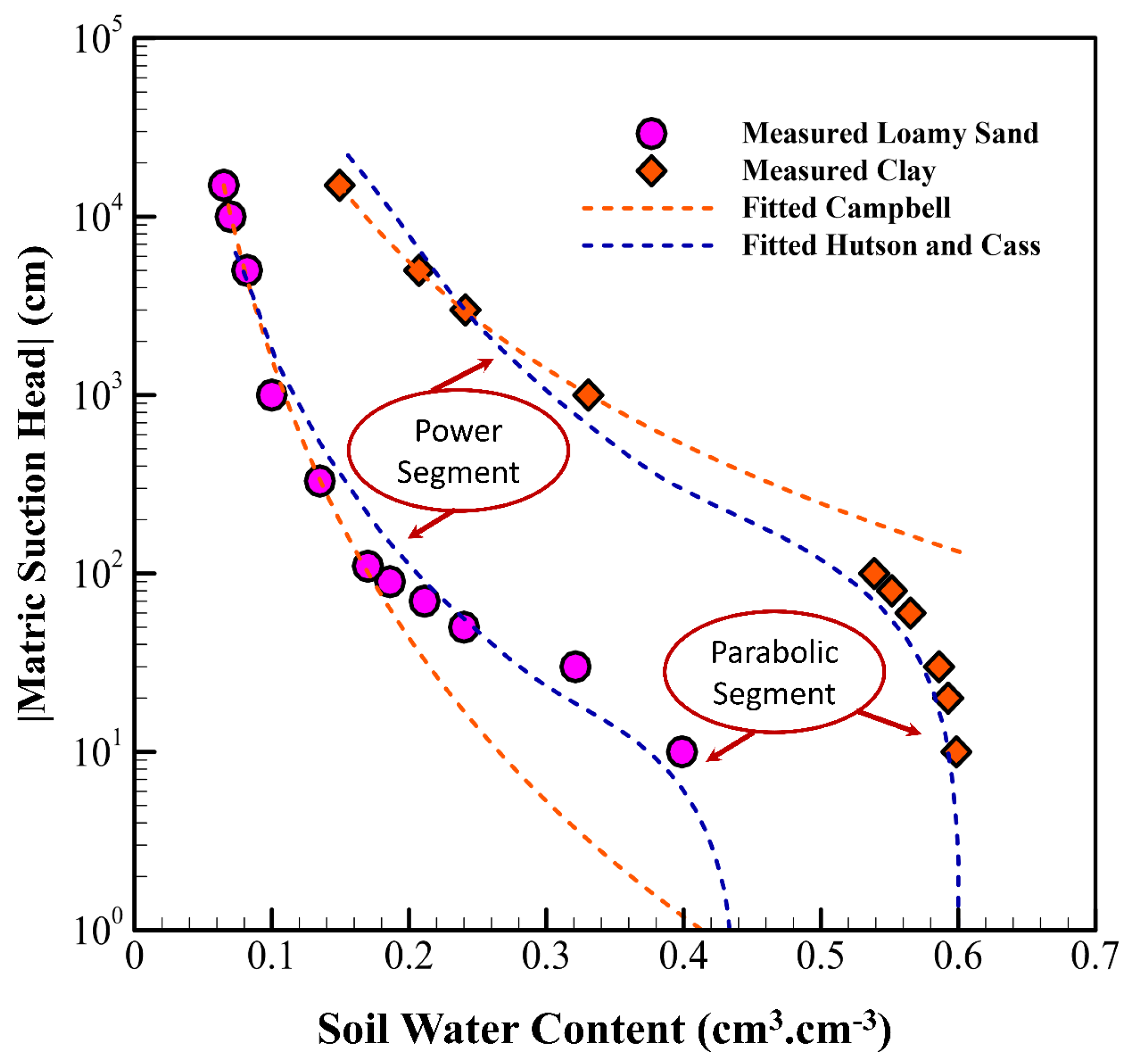
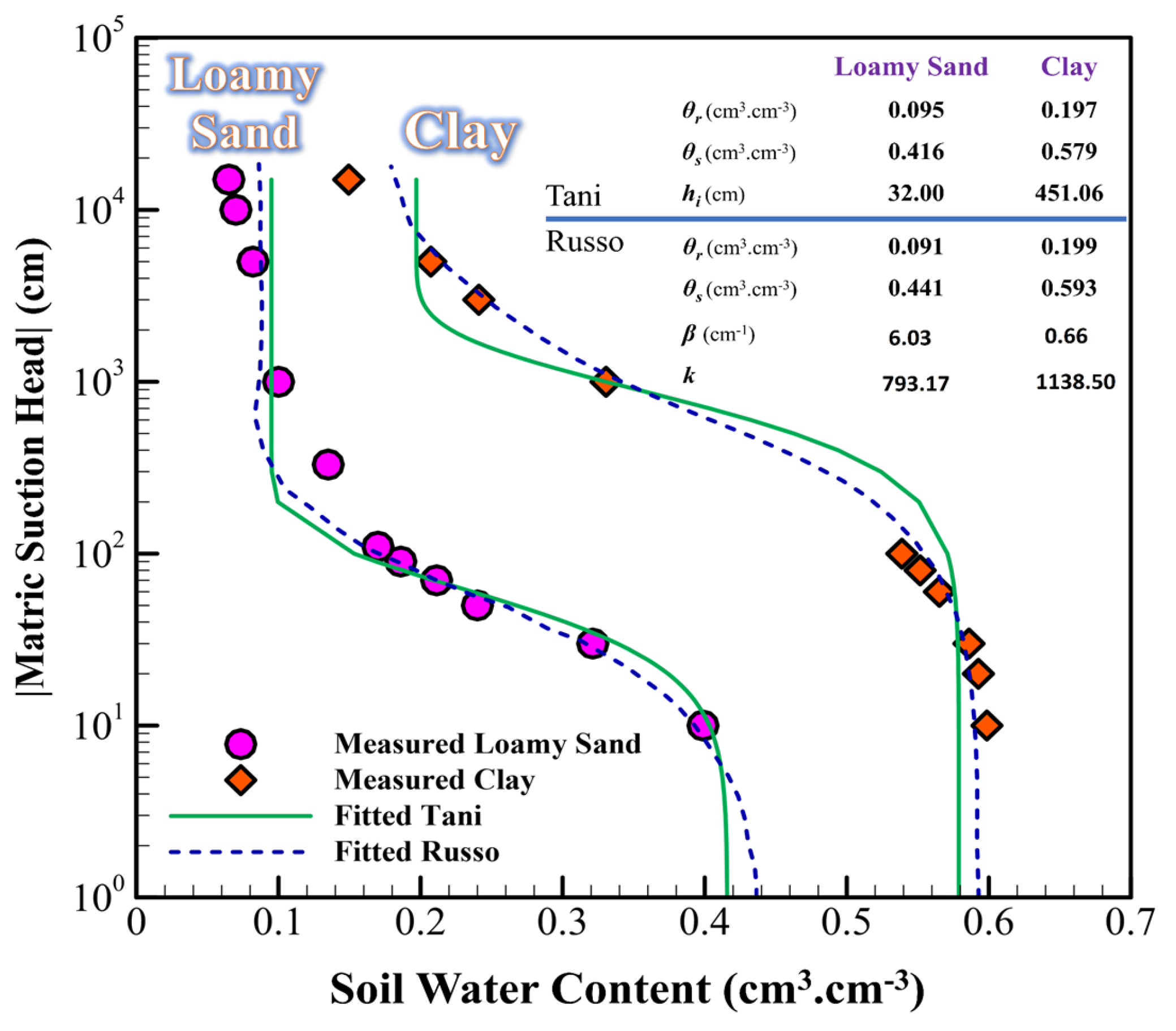
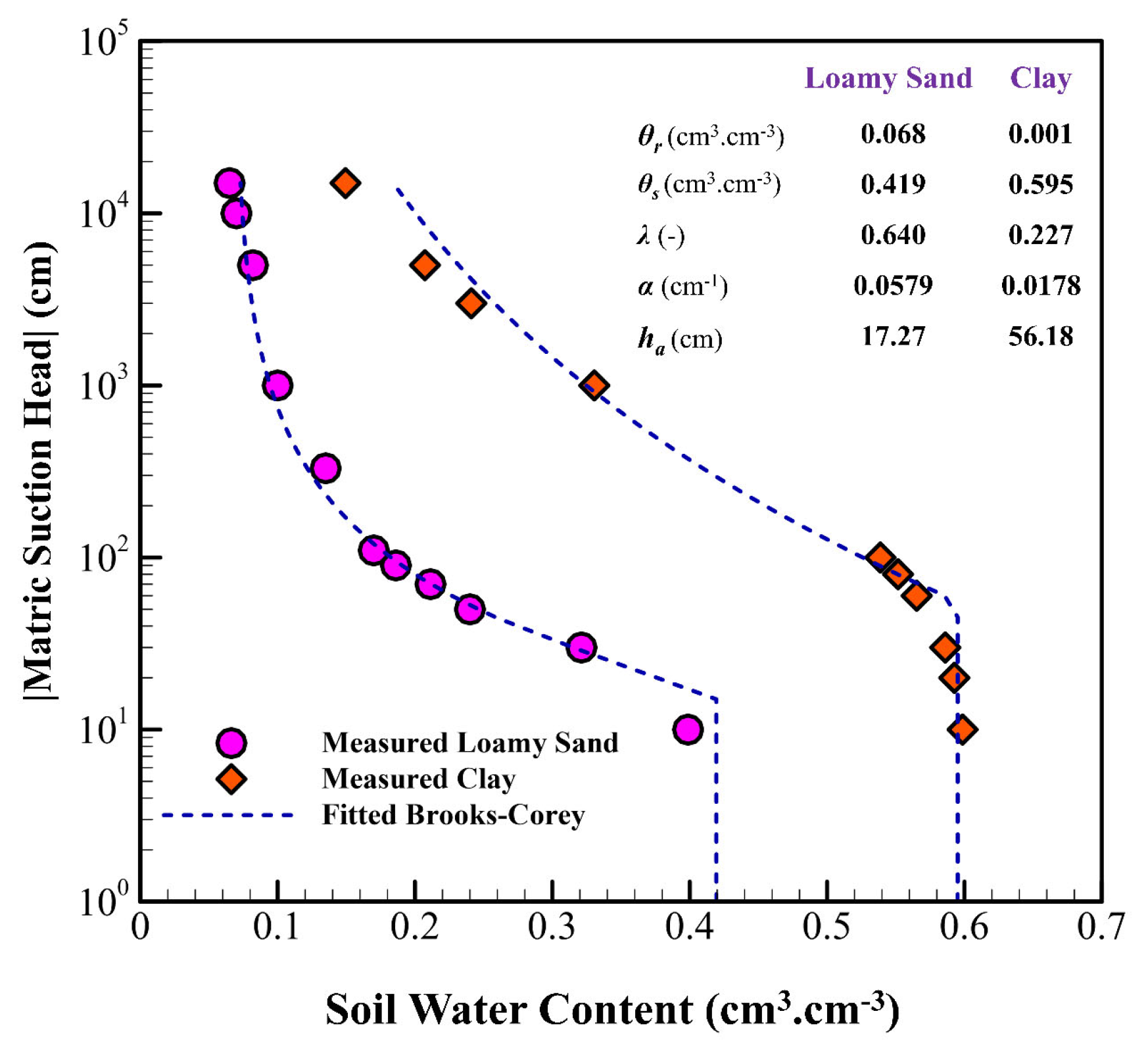
2. SWRC Models
- Soil particle size distribution, which directly influences soil structure, is a result of a process of uniform random fragmentation.
- The conversion of solid particle volume to pore volume follows a power function, with the equation constant being proportional to the particle shape produced by fragmentation.
3. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Ket, P.; Oeurng, C.; Degré, A. Estimating Soil Water Retention Curve by Inverse Modelling from Combination of In Situ Dynamic Soil Water Content and Soil Potential Data. Soil Syst. 2018, 2, 55. [Google Scholar] [CrossRef]
- Rasoulzadeh, A.; Nasiri, N. Investigation of Saline Drainage Water Reuse Effect on Soil Hydraulic Properties Using Inverse Method (Case Study: Moghan Plain). J. Civ. Environ. Eng. 2013, 43, 33–44. (In Persian) [Google Scholar]
- Rashid, N.S.A.; Askari, M.; Tanaka, T.; Simunek, J.; van Genuchten, M.T. Inverse estimation of soil hydraulic properties under oil palm trees. Geoderma 2015, 241–242, 306–312. [Google Scholar] [CrossRef]
- Dobriyal, P.; Qureshi, A.; Badola, R.; Hussain, S.A. A review of the methods available for estimating soil moisture and its implications for water resource management. J. Hydrol. 2012, 458–459, 110–117. [Google Scholar] [CrossRef]
- Pollacco, J.A.P.; Fernández-Gálvez, J.; Carrick, S. Improved prediction of water retention curves for fine texture soils using an intergranular mixing particle size distribution model. J. Hydrol. 2020, 584, 124597. [Google Scholar] [CrossRef]
- Fernández-Gálvez, J.; Pollacco, J.A.P.; Lassabatere, L.; Angulo-Jaramillo, R.; Carrick, S. A general Beerkan Estimation of Soil Transfer parameters method predicting hydraulic parameters of any unimodal water retention and hydraulic conductivity curves: Application to the Kosugi soil hydraulic model without using particle size distribution data. Adv. Water Resour. 2019, 129, 118–130. [Google Scholar] [CrossRef]
- Zakizadeh Abkenar, F.; Rasoulzadeh, A.; Asghari, A. Performance evaluation of different soil water retention functions for modeling of water flow under transient condition. Bragantia 2019, 78, 119–130. [Google Scholar] [CrossRef]
- Rasoulzadeh, A.; Yaghoubi, A. Inverse modeling approach for determining soil hydraulic properties as affected by application of cattle manure. Int. J. Agric. Biol. Eng. 2014, 7, 27–35. [Google Scholar]
- Verbist, K.; Cornelis, W.M.; Gabriels, D.; Alaerts, K.; Soto, G. Using an inverse modelling approach to evaluate the water retention in a simple water harvesting technique. Hydrol. Earth Syst. Sci. 2009, 13, 1979–1992. [Google Scholar] [CrossRef]
- Le Bourgeois, O.; Bouvier, C.; Brunet, P.; Ayral, P.A. Inverse modeling of soil water content to estimate the hydraulic properties of a shallow soil and the associated weathered bedrock. J. Hydrol. 2016, 541, 116–126. [Google Scholar] [CrossRef]
- Rasoulzadeh, A.; Sepaskhah, A.R. Advanced Topics in Soil Water Physics; Soil Water Characteristic Curve; University of Mohaghegh Ardabili Press: Ardabil, Iran, 2022; Volume 1, p. 304. (In Persian) [Google Scholar]
- Smagin, A.V. Column-centrifugation method for determining water retention curves of soils and disperse sediments. Eurasian Soil Sci. 2012, 45, 416–422. [Google Scholar] [CrossRef]
- Solone, R.; Bittelli, M.; Tomei, F.; Morari, F. Errors in water retention curves determined with pressure plates: Effects on the soil water balance. J. Hydrol. 2012, 470–471, 65–74. [Google Scholar] [CrossRef]
- Wang, M.; Kong, L.; Zang, M. Effects of sample dimensions and shapes on measuring soil–water characteristic curves using pressure plate. J. Rock Mech. Geotech. Eng. 2015, 7, 463–468. [Google Scholar] [CrossRef]
- Latorre, B.; Moret-Fernández, D.; Peña, C. Estimate of Soil Hydraulic Properties from Disc Infiltrometer Three-dimensional Infiltration Curve: Theoretical Analysis and Field Applicability. Procedia Environ. Sci. 2013, 19, 580–589. [Google Scholar] [CrossRef]
- Degré, A.; van der Ploeg, M.J.; Caldwell, T.; Gooren, H.P.A. Comparison of Soil Water Potential Sensors: A Drying Experiment. Vadose Zone J. 2017, 16, 1–8. [Google Scholar] [CrossRef]
- Fernández-Gálvez, J.; Verhoef, A.; Barahona, E. Estimating soil water fluxes from soil water records obtained using dielectric sensors. Hydrol. Process. 2007, 21, 2785–2793. [Google Scholar] [CrossRef]
- Arya, L.M.; Paris, J.F. A Physicoempirical Model to Predict the Soil Moisture Characteristic from Particle-Size Distribution and Bulk Density Data. Soil Sci. Soc. Am. J. 1981, 45, 1023–1030. [Google Scholar] [CrossRef]
- Shang, S.H.; Mao, X.M. A Physicoempirical Model for Soil Water Simulation in Crop Root Zone. Pedosphere 2011, 21, 512–521. [Google Scholar] [CrossRef]
- Mohammadi, M.H.; Meskini-Vishkaee, F. Predicting Soil Moisture Characteristic Curves from Continuous Particle-Size Distribution Data. Pedosphere 2013, 23, 70–80. [Google Scholar] [CrossRef]
- da Silva, A.C.; Armindo, R.A.; Prevedello, C.L. Splintex 2.0: A physically-based model to estimate water retention and hydraulic conductivity parameters from soil physical data. Comput. Electron. Agric. 2020, 169, 105157. [Google Scholar] [CrossRef]
- Zakizadeh Abkenar, F.; Rasoulzadeh, A. Functional Evaluation of Pedotransfer Functions For Simulation of Soil Profile Drainage. Irrig. Drain. 2019, 68, 573–587. [Google Scholar] [CrossRef]
- van den Berg, M.; Klamt, E.; van Reeuwijk, L.P.; Sombroek, W.G. Pedotransfer functions for the estimation of moisture retention characteristics of Ferralsols and related soils. Geoderma 1997, 78, 161–180. [Google Scholar] [CrossRef]
- Cueff, S.; Coquet, Y.; Aubertot, J.N.; Bel, L.; Pot, V.; Alletto, L. Estimation of soil water retention in conservation agriculture using published and new pedotransfer functions. Soil Tillage Res. 2021, 209, 104967. [Google Scholar] [CrossRef]
- Huang, G.H.; Zhang, R.D.; Huang, Q.Z. Modeling Soil Water Retention Curve with a Fractal Method. Pedosphere 2006, 16, 137–146. [Google Scholar] [CrossRef]
- Perfect, E.; Kay, B.D. Applications of fractals in soil and tillage research: A review. Soil Tillage Res. 1995, 36, 1–20. [Google Scholar] [CrossRef]
- Veltri, M.; Severino, G.; De Bartolo, S.; Fallico, C.; Santini, A. Scaling Analysis of Water Retention Curves: A Multi-fractal Approach. Procedia Environ. Sci. 2013, 19, 618–622. [Google Scholar] [CrossRef][Green Version]
- Huang, G.; Zhang, R. Evaluation of soil water retention curve with the pore–solid fractal model. Geoderma 2005, 127, 52–61. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal processes in soil water retention. Water Resour. Res. 1990, 26, 1047–1054. [Google Scholar] [CrossRef]
- Leij, F.J.; Russell, W.B.; Lesch, S.M. Closed-form expressions for water retention and conductivity data. Groundwater 1997, 35, 848–858. [Google Scholar] [CrossRef]
- Wöhling, T.; Vrugt, J.A.; Barkle, G.F. Comparison of Three Multiobjective Optimization Algorithms for Inverse Modeling of Vadose Zone Hydraulic Properties. Soil Sci. Soc. Am. J. 2008, 72, 305–319. [Google Scholar] [CrossRef]
- Osorio-Murillo, C.A.; Over, M.W.; Savoy, H.; Ames, D.P.; Rubin, Y. Software framework for inverse modeling and uncertainty characterization. Environ. Model. Softw. 2015, 66, 98–109. [Google Scholar] [CrossRef]
- Rasoulzadeh, A. Evaluation of parameters estimation using inverse method in unsaturated porous media. In Proceedings of the 10th International Agricultural Engineering Conference, Bangkok, Thailand, 7–10 December 2009. [Google Scholar]
- Buckingham, E. Studies on the Movement of Soil Moisture; Bulletin (no.38); USDA, Bureau of Soils: Washington DC, USA, 1907; ISBN 9788578110796. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media, 3rd ed.; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Brutsaert, W. Probability laws for pore-size distributions. Soil Sci. 1966, 101, 85–92. [Google Scholar] [CrossRef]
- Laliberte, G.E. A mathematical function for describing capillary pressure-desaturation data. Int. Assoc. Sci. Hydrol. Bull. 1969, 14, 131–149. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Hutson, J.L.; Cass, A. A retentivity function for use in soil–water simulation models. J. Soil Sci. 1987, 38, 105–113. [Google Scholar] [CrossRef]
- Vogel, T.; Cislerova, M. On the reliability of unsaturated hydraulic conductivity calculated from the moisture retention curve. Transp. Porous Media 1988, 3, 1–15. [Google Scholar] [CrossRef]
- Campbell, G.S.; Shiozawa, S. Prediction of hydraulic properties of soils using particle-size distribution and bulk density data. In International Workshop on Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils; University of California: Oakland, CA, USA, 1992; pp. 317–328. [Google Scholar]
- Mehta, B.K.; Shiozawa, S.H.O.; Nakano, M. Hydraulic properties of a sandy soil at low water contents. Soil Sci. 1994, 157, 208–214. [Google Scholar] [CrossRef]
- Rossi, C.; Nimmo, J.R. Modeling of soil water retention from saturation to oven dryness. Water Resour. Res. 1994, 30, 701–708. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Kosugi, K. Three-parameter lognormal distribution model for soil water retention. Water Resour. Res. 1994, 30, 891–901. [Google Scholar] [CrossRef]
- Fayer, M.J.; Simmons, C.S. Modified Soil Water Retention Functions for All Matric Suctions. Water Resour. Res. 1995, 31, 1233–1238. [Google Scholar] [CrossRef]
- Kosugi, K. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Assouline, S.; Tessier, D.; Bruand, A. A conceptual model of the soil water retention curve. Water Resour. Res. 1998, 34, 223–231. [Google Scholar] [CrossRef]
- Webb, S.W. A simple extension of two-phase characteristic curves to include the dry region. Water Resour. Res. 2000, 36, 1425–1430. [Google Scholar] [CrossRef]
- Groenevelt, P.H.; Grant, C.D. A new model for the soil-water retention curve that solves the problem of residual water contents. Eur. J. Soil Sci. 2004, 55, 479–485. [Google Scholar] [CrossRef]
- Khlosi, M.; Cornelis, W.M.; Gabriels, D.; Sin, G. Simple modification to describe the soil water retention curve between saturation and oven dryness. Water Resour. Res. 2006, 42, 1–5. [Google Scholar] [CrossRef]
- Ippisch, O.; Vogel, H.J.; Bastian, P. Validity limits for the van Genuchten-Mualem model and implications for parameter estimation and numerical simulation. Adv. Water Resour. 2006, 29, 1780–1789. [Google Scholar] [CrossRef]
- Dexter, A.R.; Czyz, E.A.; Richard, G.; Reszkowska, A. A user-friendly water retention function that takes account of the textural and structural pore spaces in soil. Geoderma 2008, 143, 243–253. [Google Scholar] [CrossRef]
- Omuto, C.T. Biexponential model for water retention characteristics. Geoderma 2009, 149, 235–242. [Google Scholar] [CrossRef]
- Grant, C.D.; Groenevelt, P.H.; Robinson, N.I. Application of the Groenevelt—Grant soil water retention model to predict the hydraulic conductivity. Soil Res. 2010, 48, 447. [Google Scholar] [CrossRef]
- Romano, N.; Nasta, P.; Severino, G.; Hopmans, J.W. Using Bimodal Lognormal Functions to Describe Soil Hydraulic Properties. Soil Sci. Soc. Am. J. 2011, 75, 468–480. [Google Scholar] [CrossRef]
- Peters, A. Simple consistent models for water retention and hydraulic conductivity in the complete moisture range. Water Resour. Res. 2013, 49, 6765–6780. [Google Scholar] [CrossRef]
- Iden, S.C.; Durner, W. Comment on “Simple consistent models for water retention and hydraulic conductivity in the complete moisture range” by A. Peters. Water Resour. Res. 2014, 50, 7530–7534. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Pachepsky, Y.A.; Pederera-Parrilla, A.; Martínez, G.; Espejo-Pérez, A.J.; Perea, F.; Giráldez, J.V. Water Retention and Preferential States of Soil Moisture in a Cultivated Vertisol. Soil Sci. Soc. Am. J. 2017, 81, 1–9. [Google Scholar] [CrossRef]
- Du, C. A novel segmental model to describe the complete soil water retention curve from saturation to oven dryness. J. Hydrol. 2020, 584, 124649. [Google Scholar] [CrossRef]
- King, L.G. Description of Soil Characteristics for Partially Saturated Flow. Soil Sci. Soc. Am. J. 1965, 29, 359–362. [Google Scholar] [CrossRef]
- Visser, W.C. An empirical expression for the desorption curve. In Water in the Unsaturated Zone: Proceedings of the Wageningen Symposium; Rijtema, P.E., Wassink, H., Eds.; IASH/AIHS; UNESCO: Paris, France, 1966; Volume 1, pp. 329–335. [Google Scholar]
- Gardner, W.R.; Hillel, D.; Benyamini, Y. Post-Irrigation Movement of Soil Water: 1. Redistribution. Water Resour. Res. 1970, 6, 851–861. [Google Scholar] [CrossRef]
- Campbell, G.S. A Simple Method For Determining Unsaturated Conductivity From Moisture Retention Data. Soil Sci. 1974, 117, 311–314. [Google Scholar] [CrossRef]
- Gillham, R.W.; Klute, A.; Heermann, D.F. Hydraulic Properties of a Porous Medium: Measurement and Empirical Representation. Soil Sci. Soc. Am. J. 1976, 40, 203–207. [Google Scholar] [CrossRef]
- Tani, M. The properties of a water-table rise produced by a one-dimen-sional, vertical, unsaturated flow. J. Jpn. For. Soc. 1982, 64, 409–418. [Google Scholar] [CrossRef]
- McKee, C.R.; Bumb, A.C. The importance of unsaturated flow parameters in designing a monitoring system for hazardous wastes and environmental emergencies. In Proceedings of the Hazardous Materials Control Research Institute, National Conference, Washington, DC, USA, 7–9 November 1984; pp. 50–58. [Google Scholar]
- Russo, D. Determining soil hydraulic properties by parameter estimation: On the selection of a model for the hydraulic properties. Water Resour. Res. 1988, 24, 453–459. [Google Scholar] [CrossRef]
- Zhang, R.; Van Genuchten, M.T. New Models For Unsaturated Soil Hydraulic Properties. Soil Sci. 1994, 158, 77–85. [Google Scholar] [CrossRef]
- Farrell, D.A.; Larson, W.E. Modeling the pore structure of porous media. Water Resour. Res. 1972, 8, 699–706. [Google Scholar] [CrossRef]
- Rogowski, A.S. Estimation of soil water characteristics and hydraulic conductivity: Comparison of models. Soil Sci. 1972, 114, 423–429. [Google Scholar] [CrossRef]
- Vauclin, M.; Haverkamp, M.; Vachaud, G. Resolution Numerique d’une Equation de Diffusion Non-Lineaire: Application a L’infiltration de l’eau dans les sols Non-Satures; Presses Universitaires de Grenoble: Grenoble, France, 1979; p. 183. [Google Scholar]
- D’Hollander, E.H. Estimation of the pore size distribution from the moisture characteristic. Water Resour. Res. 1979, 15, 107–112. [Google Scholar] [CrossRef]
- Globus, A.M. Soil-Hydrophysical Support of Agroecological Mathematical Models; Hydrometeoizdat: St. Petersburg, Russia, 1987. [Google Scholar]
- Ross, P.J.; Smettem, K.R.J. Describing Soil Hydraulic Properties with Sums of Simple Functions. Soil Sci. Soc. Am. J. 1993, 57, 26–29. [Google Scholar] [CrossRef]
- Ross, P.J.; Williams, J.; Bristow, K.L. Equation for Extending Water-Retention Curves to Dryness. Soil Sci. Soc. Am. J. 1991, 55, 923–927. [Google Scholar] [CrossRef]
- Pachepsky, Y.A.A.; Shcherbakov, R.A.; Korsunskaya, L.P. Scaling of soil water retention using a fractal model. Soil Sci. 1995, 159, 99–104. [Google Scholar] [CrossRef]
- Bruce, R.R.; Luxmoore, R.J. Water Retention: Field Methods. Methods Soil Anal. Part 1 Phys. Mineral. Methods 1986, 5, 663–686. [Google Scholar] [CrossRef]
- Simmons, C.S.; Nielsen, D.R.; Biggar, J.W. Scaling of field-measured soil-water properties: II. Hydraulic conductivity and flux. Hilgardia 1979, 47, 103–174. [Google Scholar] [CrossRef]
- Simmons, C.S.; Nielsen, D.R.; Biggar, J.W. Scaling of field-measured soil-water properties: I. Methodology. Hilgardia 1979, 47, 75–102. [Google Scholar] [CrossRef]
- Driessen, P.M.; Konijn, N.T. Land-Use Systems Analysis; ISRIC: Wageningen, The Netherlands, 1992; pp. 1–230. [Google Scholar]
- Haverkamp, R.; Leij, F.J.; Fuentes, C.; Sciortino, A.; Ross, P.J. Soil Water Retention. Soil Sci. Soc. Am. J. 2005, 69, 1881–1890. [Google Scholar] [CrossRef]
- Rasoulzadeh, A.; Homapoor Ghoorabjiri, M. Comparing hydraulic properties of different forest floors. Hydrol. Process. 2014, 28, 5122–5130. [Google Scholar] [CrossRef]
- Su, C.; Brooks, R.H. Soil Hydraulic properties from infiltration tests. Watershed Management Proceedings, Irrigation and Drainage Div. In Proceedings of the Watershed Management, Logan, UT, USA, 11–13 August 1975; Proceedings of a Symposium; ASCE: Reston, VA, USA, 1975; pp. 516–542. [Google Scholar]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef]
- Ahuja, L.R.; Swartzendruber, D. An Improved Form of Soil-Water Diffusivity Function. Soil Sci. Soc. Am. J. 1972, 36, 9–14. [Google Scholar] [CrossRef]
- Endelman, F.J.; Box, G.E.P.; Boyle, J.R.; Hughes, R.R.; Keeney, D.R.; Northup, M.L.; Saffigna, P.G. Mathematical Modeling of Soil-Water-Nitrogen Phenomena; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1974. [Google Scholar]
- Varallyay, G.; Mironenko, E.V. Soil-water relationships in saline and alkali conditions. Agrokémia Talajt. 1979, 28, 33–82. [Google Scholar]
- van Genuchten, M.T.; Nielsen, D. On describing and predicting the hydraulic properties. Ann. Geophys. 1985, 3, 615–628. [Google Scholar]
- Fernández-Gálvez, J.; Pollacco, J.A.P.; Lilburne, L.; McNeill, S.; Carrick, S.; Lassabatere, L.; Angulo-Jaramillo, R. Deriving physical and unique bimodal soil Kosugi hydraulic parameters from inverse modeling. Adv. Water Resour. 2021, 153, 103933. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Kosugi, K. General Model for Unsaturated Hydraulic Conductivity for Soils with Lognormal Pore-Size Distribution. Soil Sci. Soc. Am. J. 1999, 63, 270–277. [Google Scholar] [CrossRef]
- Pollacco, J.A.P.; Webb, T.; McNeill, S.; Hu, W.; Carrick, S.; Hewitt, A.; Lillburne, L. Saturated hydraulic conductivity model computed from bimodal water retention curves for a range of New Zealand soils. Hydrol. Earth Syst. Sci. 2017, 21, 2725–2737. [Google Scholar] [CrossRef]
- Milly, P.C.D. Estimation of Brooks-Corey Parameters from water retention data. Water Resour. Res. 1987, 23, 1085–1089. [Google Scholar] [CrossRef]
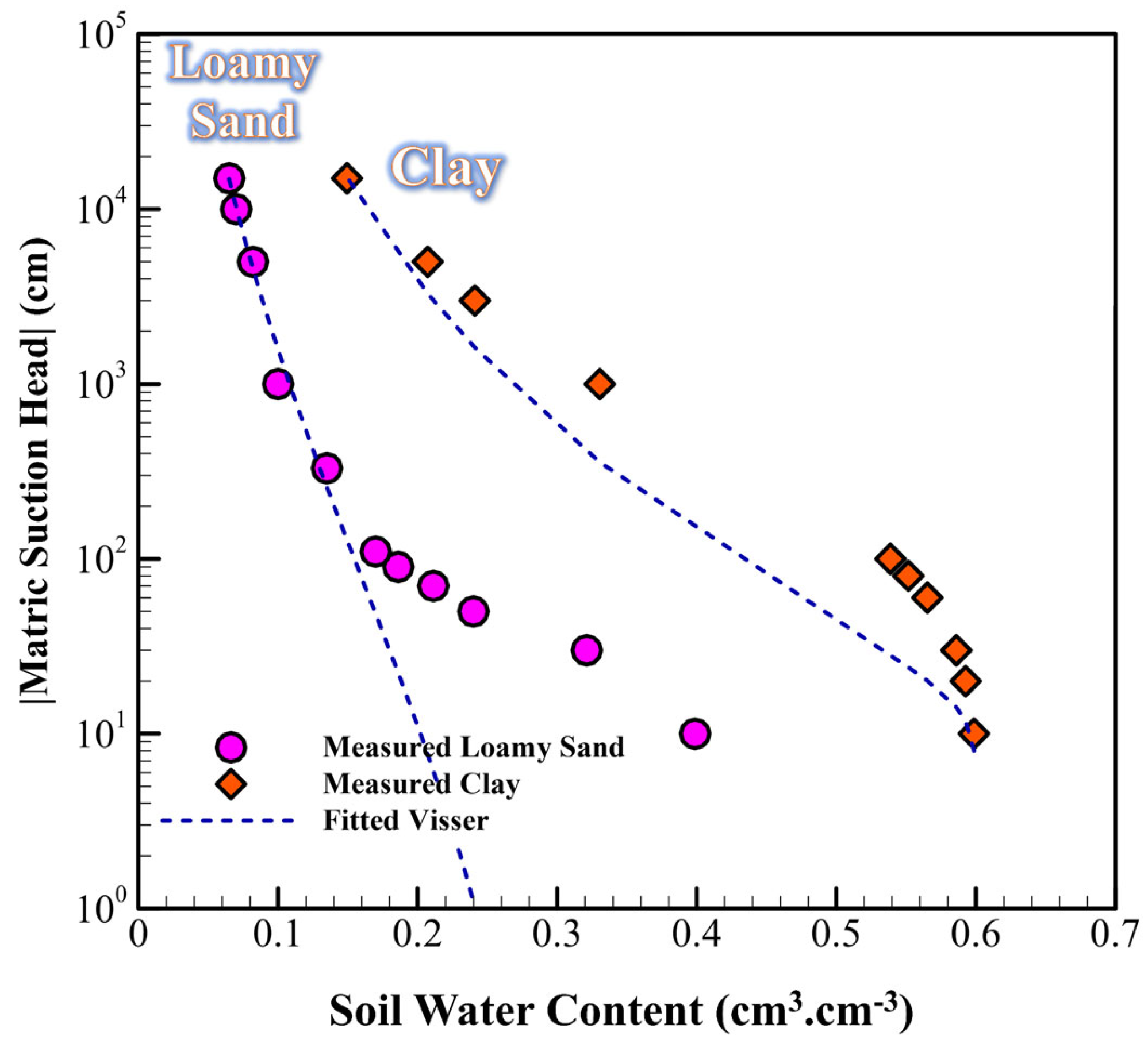
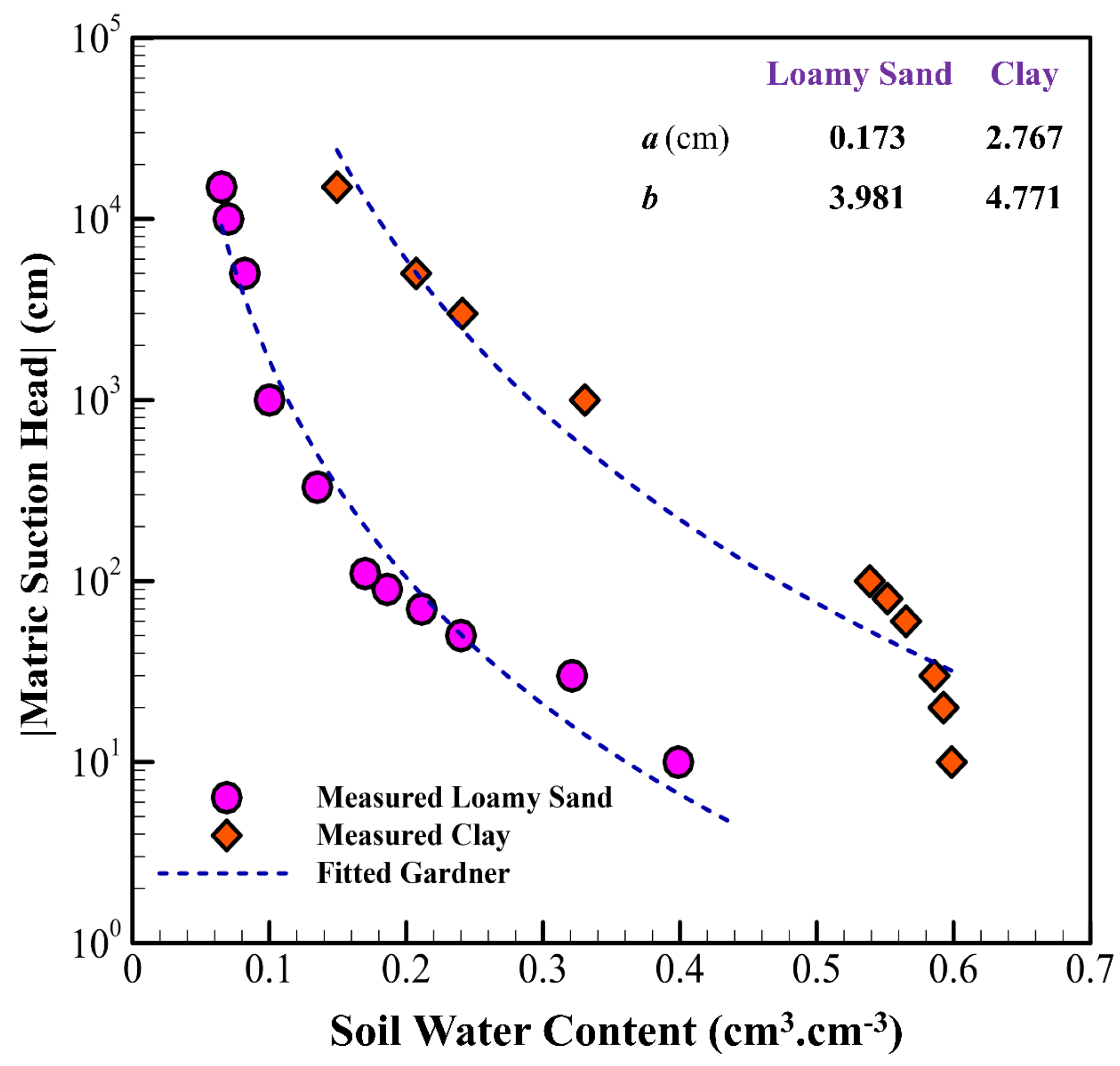
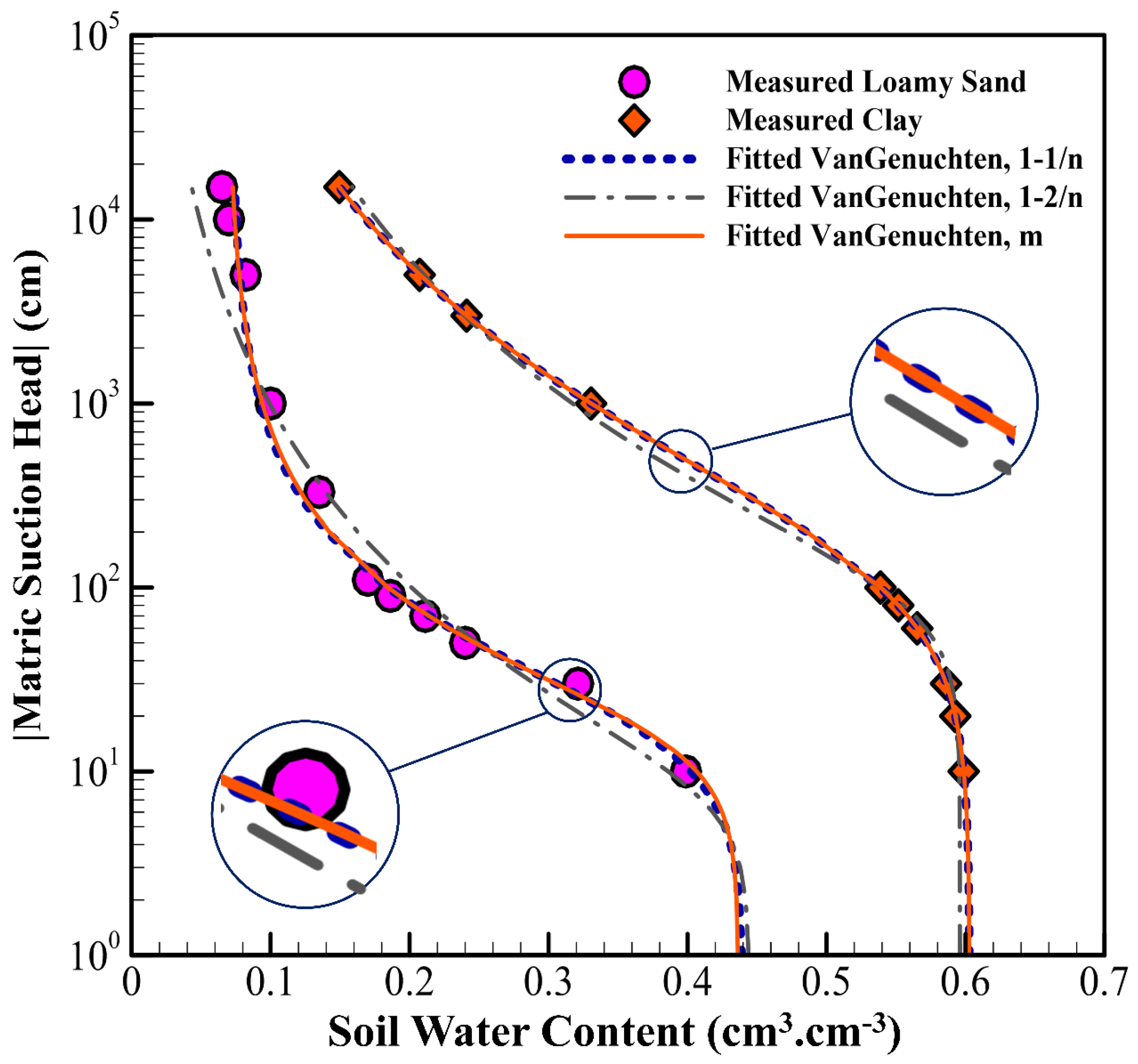
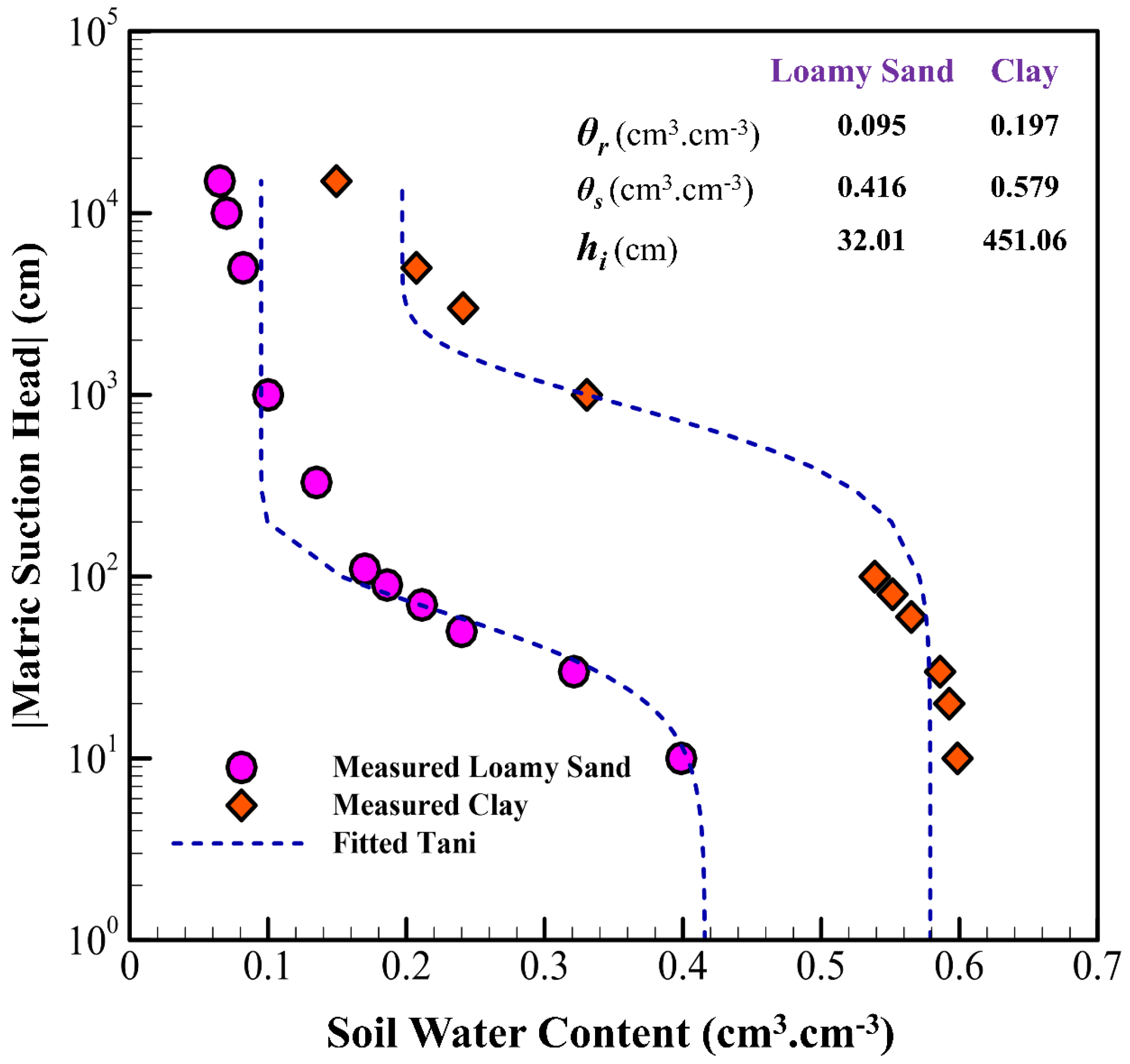
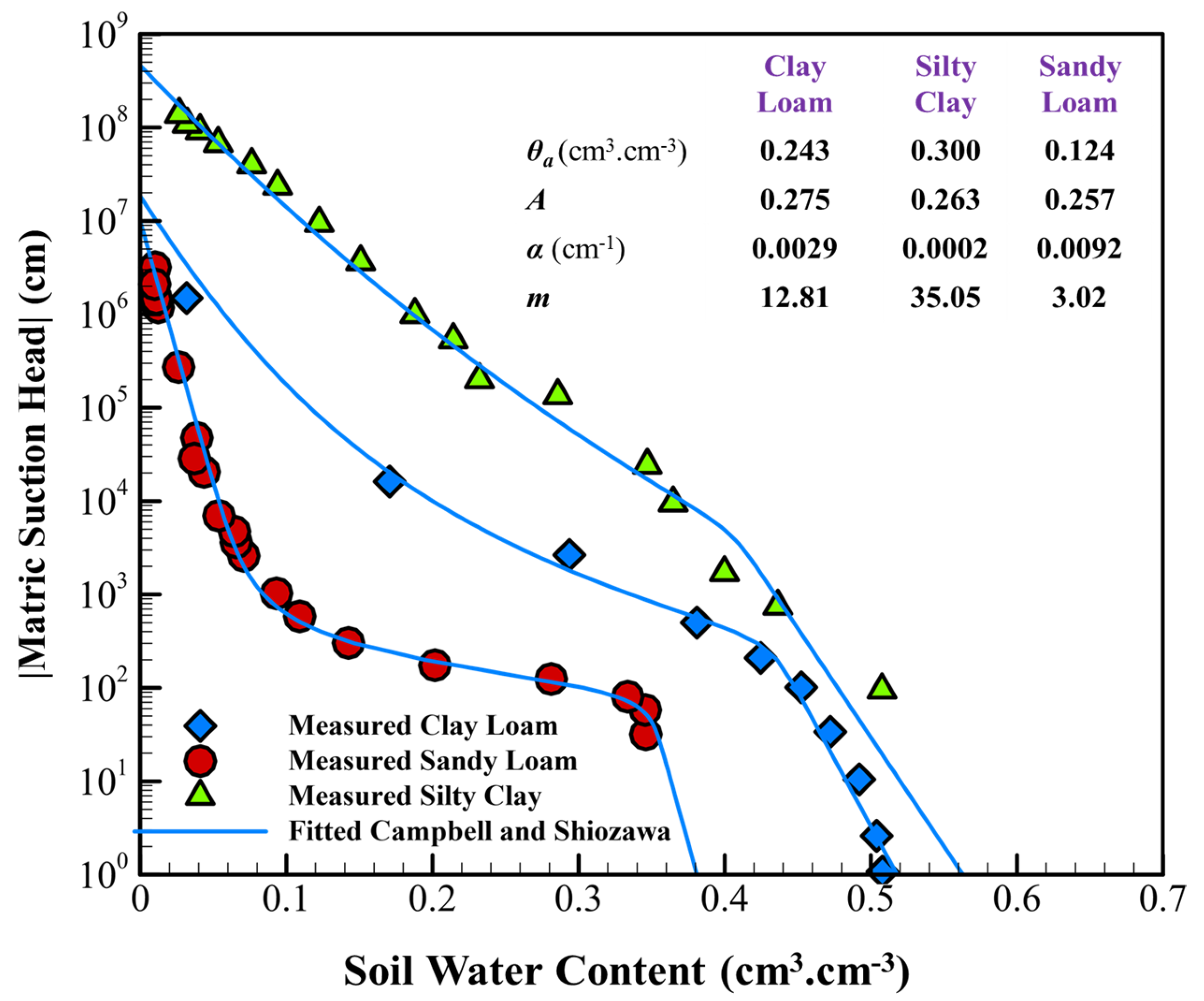
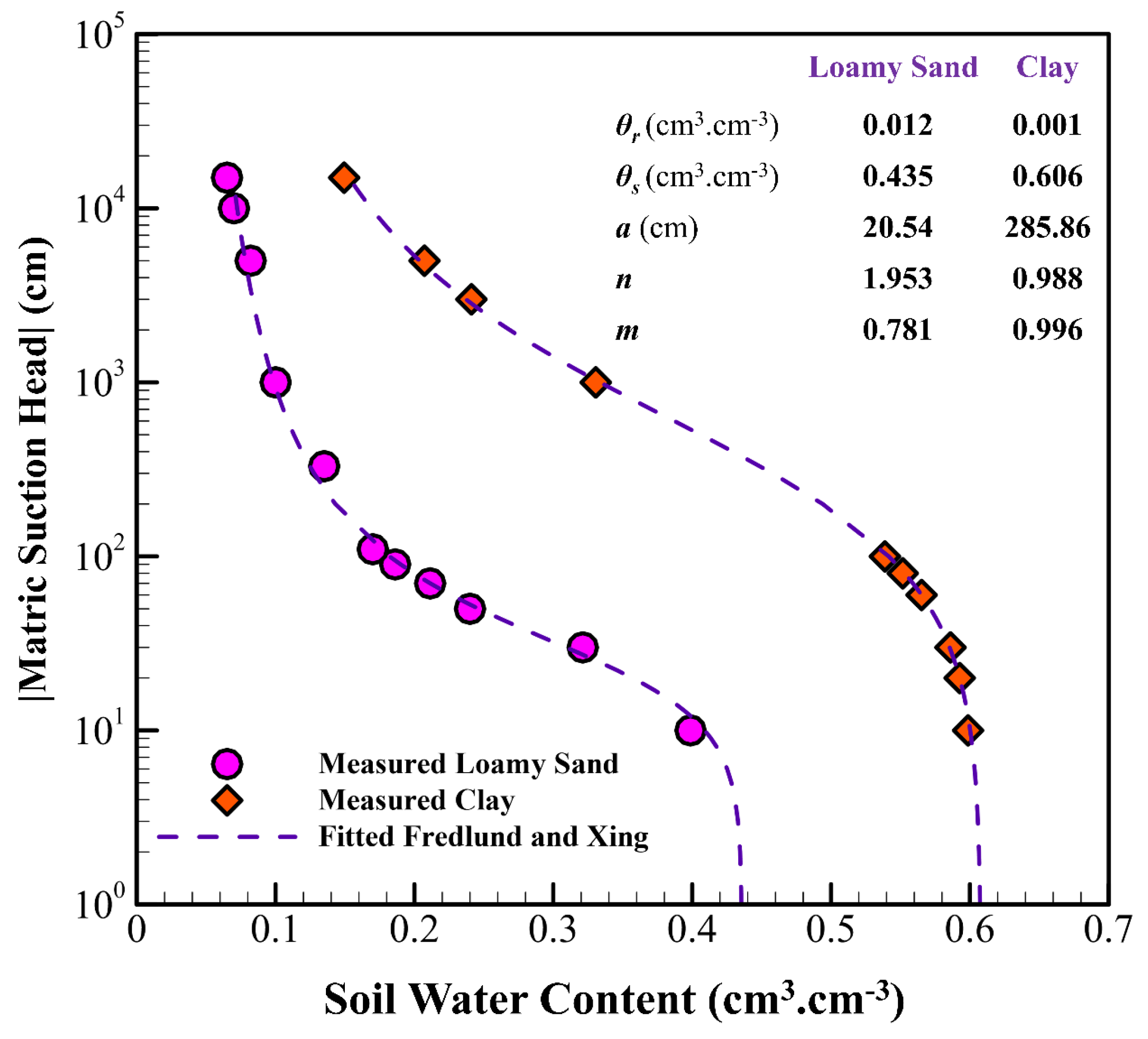
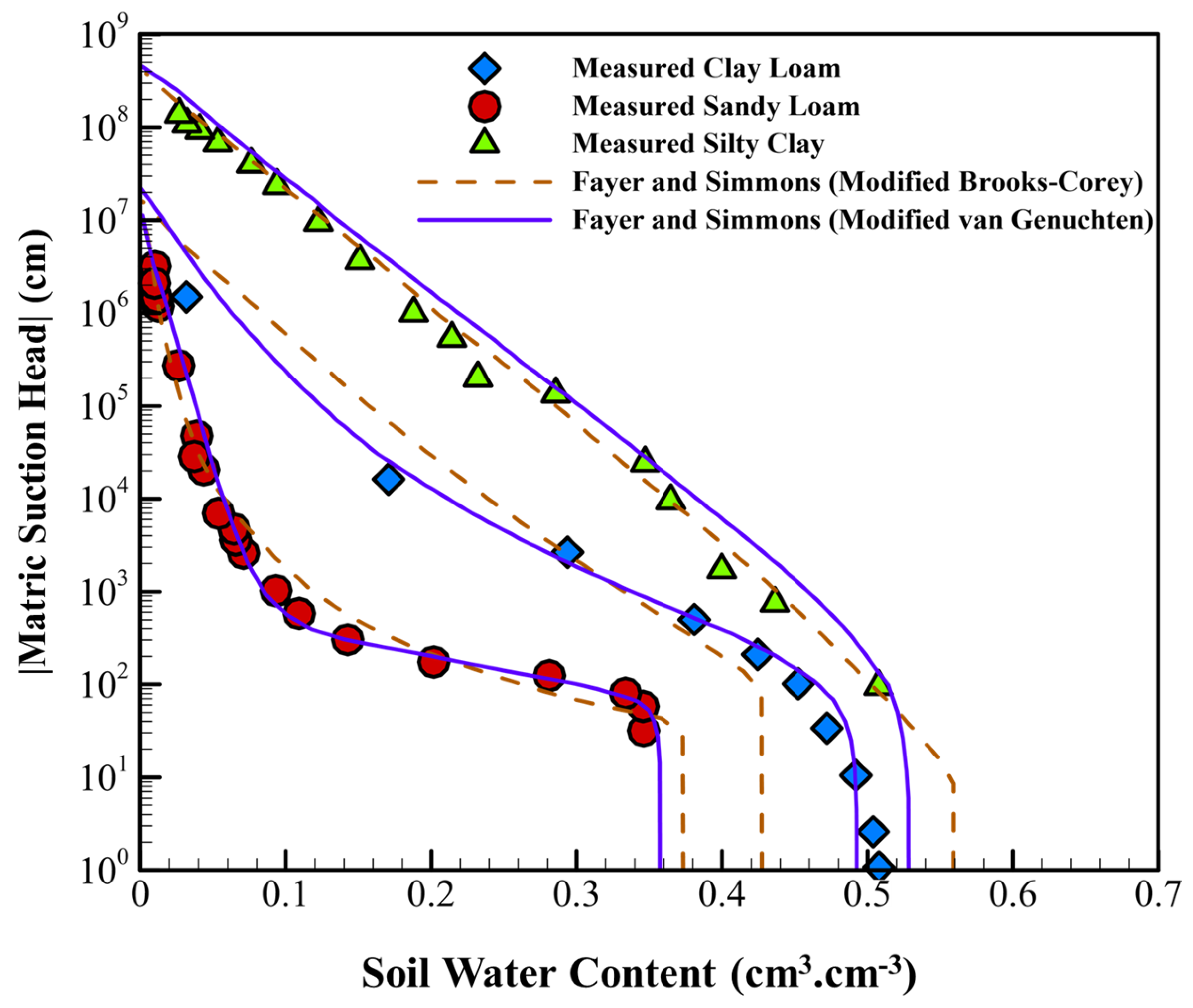
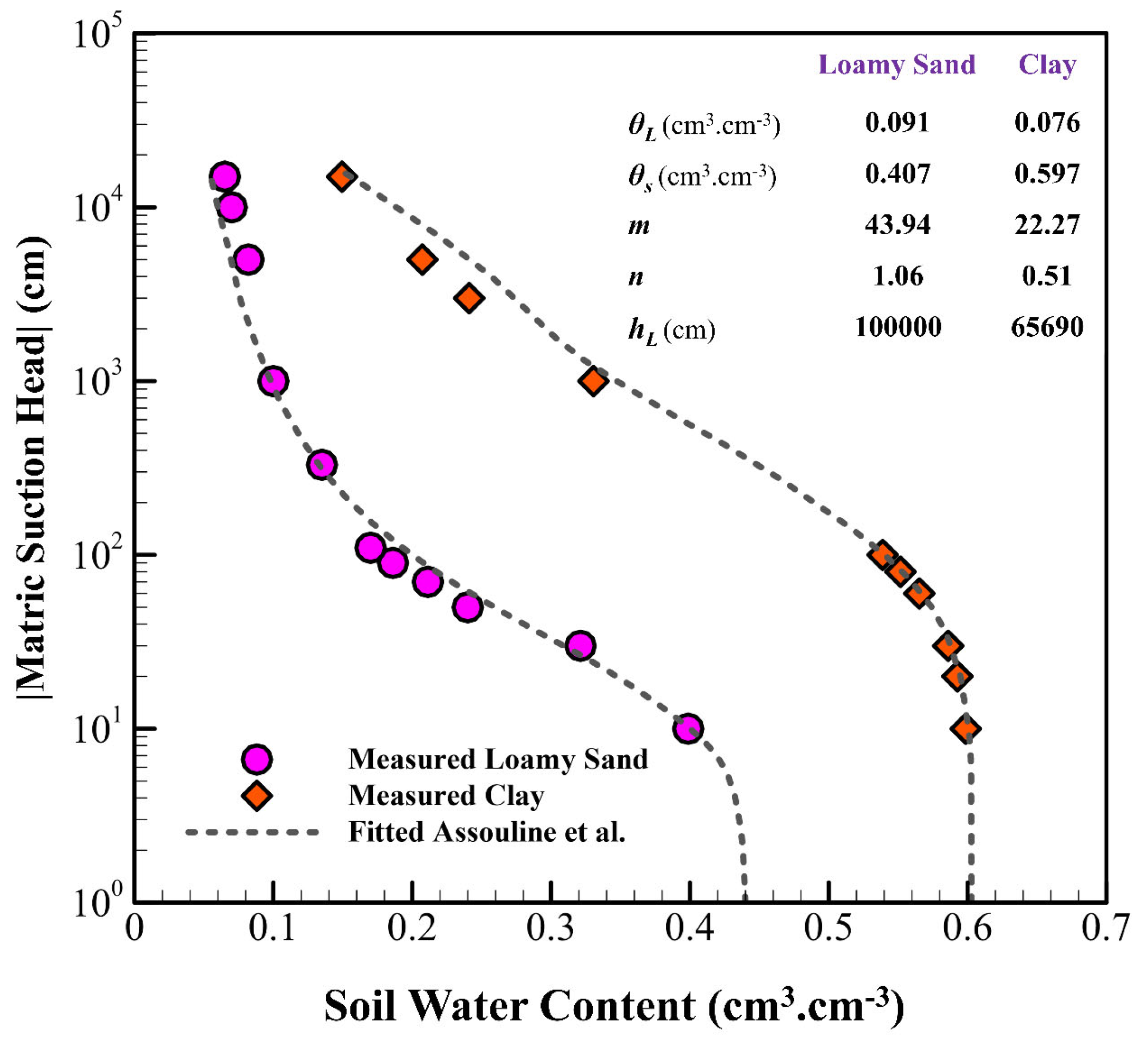
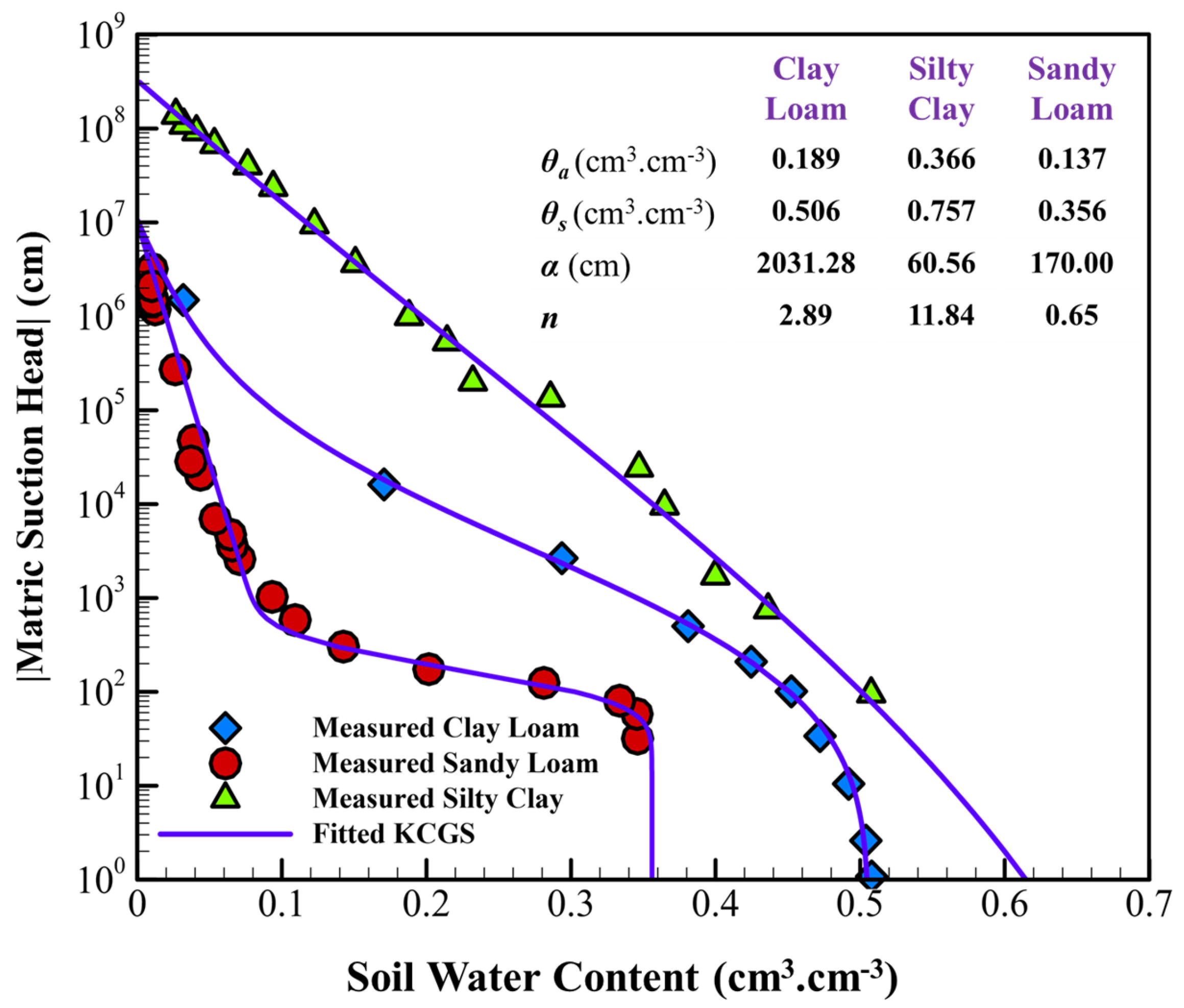
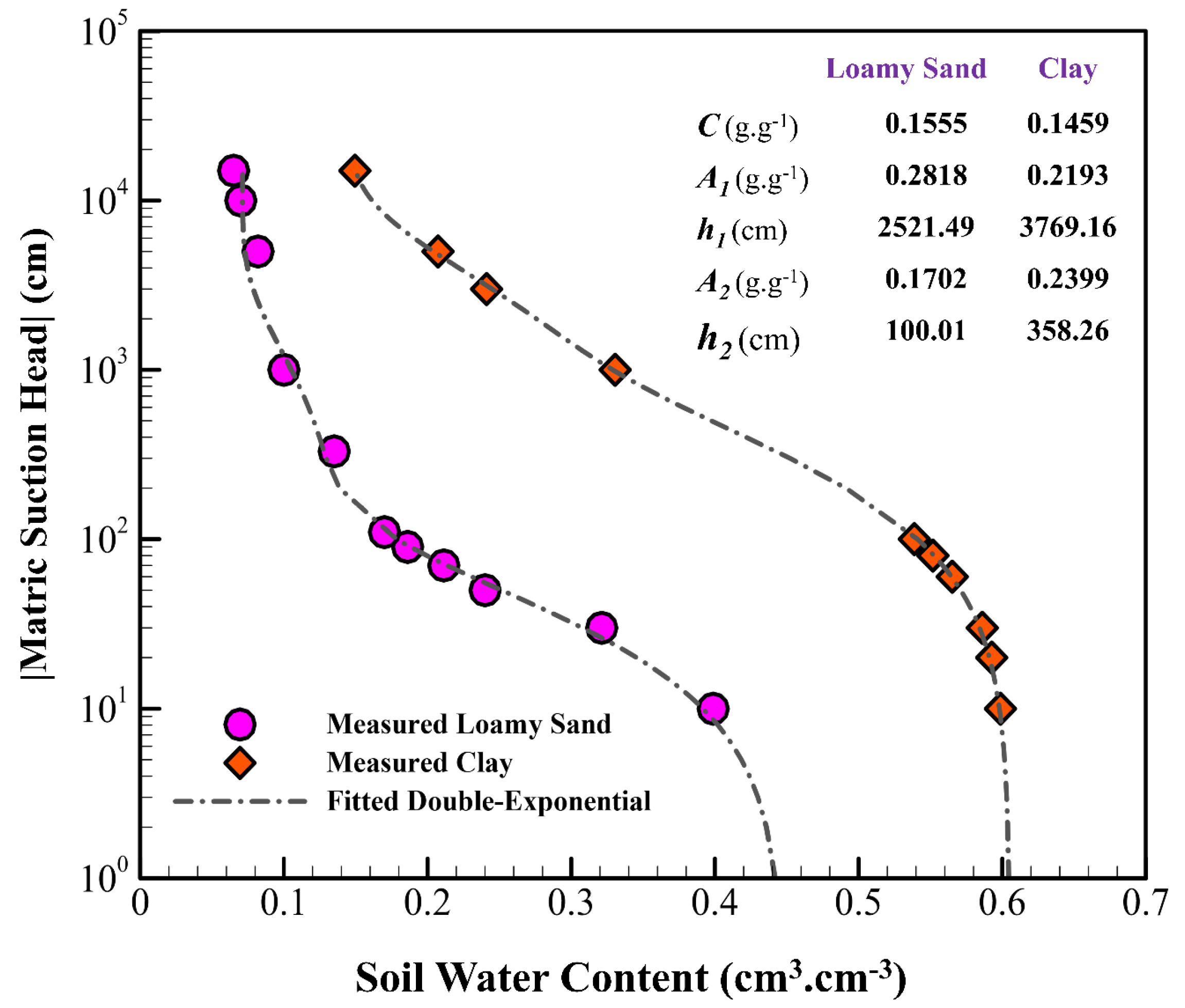
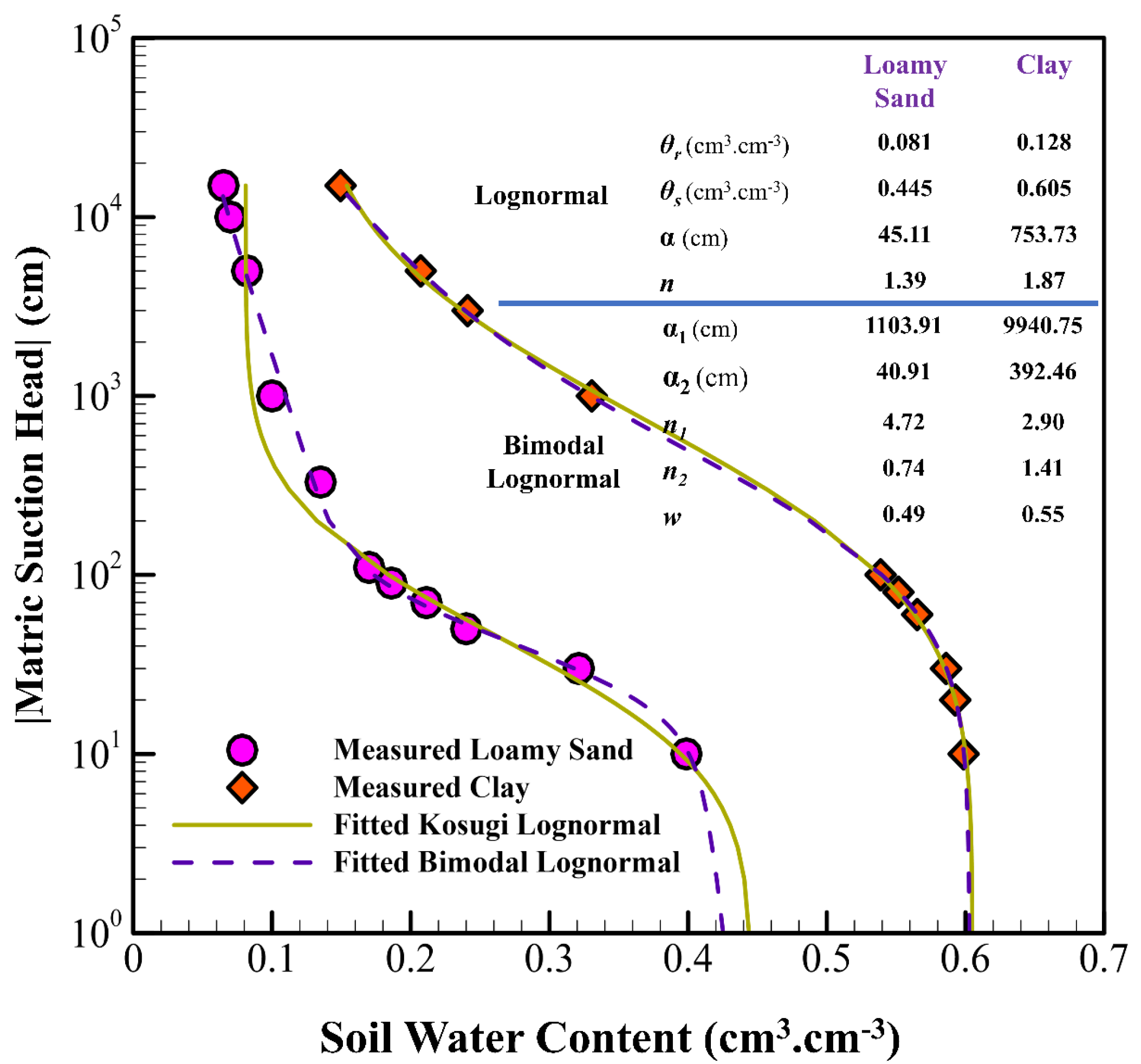
| Clay | Loamy Sand | |||||||
|---|---|---|---|---|---|---|---|---|
| a | b | c | a | b | c | |||
| a | 1.00 | 1.00 | ||||||
| b | 0.97 | 1.00 | 0.97 | 1.00 | ||||
| c | −0.98 | −0.88 | 1.00 | −1.00 | −0.97 | 1.00 | ||
| 0.94 | 0.98 | −0.91 | 1.00 | 0.95 | 1.00 | −0.94 | 1.00 | |
| Clay | Loamy Sand | |||||||
|---|---|---|---|---|---|---|---|---|
| CL | CL | |||||||
| Value | SE | Lower | Upper | Value | SE | Lower | Upper | |
| a | 29.42 | 12.04 | −4.01 | 62.86 | 2.46 | 110.39 | −252.10 | 257.03 |
| b | 0.01 | 0.21 | −0.58 | 0.61 | 2.98 | 124.48 | −284.1 | 290.04 |
| c | 3.28 | 0.13 | 2.93 | 3.64 | 4.25 | 5.39 | −8.18 | 16.69 |
| 0.59 | 0.05 | 0.46 | 0.71 | 0.44 | 11.58 | −26.27 | 27.15 | |
| Clay | Loamy Sand | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| θs | α | n | θr | θs | α | n | ||||
| θs | 1.00 | θr | 1.00 | |||||||
| α | 0.71 | 1.00 | θs | −0.17 | 1.00 | |||||
| n | −0.51 | −0.88 | 1.00 | α | −0.39 | 0.63 | 1.00 | |||
| n | 0.67 | −0.37 | −0.86 | 1.00 | ||||||
| Variable m | ||||||||||
| θs | α | n | m | θr | θs | α | n | m | ||
| θs | 1.00 | θr | 1.00 | |||||||
| α | −0.21 | 1.00 | θs | 0.08 | 1.00 | |||||
| n | −0.62 | 0.82 | 1.00 | α | −0.63 | −0.06 | 1.00 | |||
| m | 0.53 | −0.91 | −0.98 | 1.00 | n | −0.42 | −0.47 | 0.77 | 1.00 | |
| m | 0.59 | 0.38 | −0.90 | −0.96 | 1.00 | |||||
| Clay | Loamy Sand | |||||||
|---|---|---|---|---|---|---|---|---|
| CL | CL | |||||||
| Value | SE | Lower | Upper | Value | SE | Lower | Upper | |
| θs | 0.59 | 0.02 | 0.55 | 0.63 | 0.44 | 0.02 | 0.40 | 0.48 |
| θr | 0.20 | 0.02 | 0.16 | 0.24 | 0.09 | 0.01 | 0.07 | 0.11 |
| β | 0.66 | 0.00 | 0.66 | 0.67 | 6.03 | 0.01 | 6.01 | 6.06 |
| k | 1138.50 | 801.57 | −756.92 | 3033.92 | 793.17 | 98.31 | 566.47 | 1019.88 |
| Year | Model | Parameters |
|---|---|---|
| 1964 | Brooks and Corey | θr, θs, α, λ |
| 1965 | King | θs, ho, b, ε, γ |
| 1966 | Visser | a, b, c, φ |
| 1969 | Laliberte | a, b, c, θr, θs, ha |
| 1970 | Gardner | a, b |
| 1974 | Campbell | θs, ha, b |
| 1976 | Gillham et al. | θs, ho, b, γ |
| 1980 | van Genuchten | θr, θs, α, n, m |
| 1982 | Tani | θr, θs, hi |
| 1984 | McKee and Bumb | θr, θs, hi |
| 1987 | Hutson and Cass | θs, θi, α, b |
| 1988 | Russo | θr, θs, β, k |
| 1988 | Vogel and Cislerova | θr, θm, α, n, m |
| 1992 | Campbell and Shiozawa | θa, ho, A, α, m |
| 1994 | Shiozawa et al. | a, b, c, α, n, m |
| 1994 | Rossi and Nimmo | θs, α, β, he, ho |
| 1994 | Fredlund and Xing | θs, a, n, m |
| 1994 | Zhang and van Genuchten | θr, θs, C1, C2, δ |
| 1994 | Kosugi | θr, θs, ho, ha, n |
| 1995 | Fayer and Simmons (FSVG) | θa, θs, ho, α, n, m |
| 1995 | Fayer and Simmons (FSBC) | θa, θs, ho, α, λ |
| 1996 | Kosugi | θr, θs, ho, n |
| 1998 | Assouline et al. | θL, θs, hL, n, m |
| 2000 | Webb | k, hm, θm |
| 2004 | Groenevelt and Grant | θa, k0, k1, ha, n |
| 2006 | Khlosi et al. (KCGS) | θa, θs, ho, α, n |
| 2006 | Ippisch et al. | θr, θs, α, n, m, ha |
| 2008 | Dexter et al. | C, A1, A2, h1, h2 |
| 2009 | Omuto | θr, θs, α1, α2, θ1 |
| 2010 | Groenevelt et al. | θa, k0, k1, ha, n |
| 2011 | Romano et al. | θr, θs, w, α1, α2, n1, n2 |
| 2013 | Peters | w, α, ho, n |
| 2014 | Iden et al. (PDI) | θr, θs, α, ho, n |
| 2017 | Vanderlinden et al. | A1, A2, h1, h2, k0, k1 |
| 2020 | Du | θs, α, n, ho, λ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasoulzadeh, A.; Bezaatpour, J.; Azizi Mobaser, J.; Fernández-Gálvez, J. Half-Century Review and Advances in Closed-Form Functions for Estimating Soil Water Retention Curves. Hydrology 2025, 12, 164. https://doi.org/10.3390/hydrology12070164
Rasoulzadeh A, Bezaatpour J, Azizi Mobaser J, Fernández-Gálvez J. Half-Century Review and Advances in Closed-Form Functions for Estimating Soil Water Retention Curves. Hydrology. 2025; 12(7):164. https://doi.org/10.3390/hydrology12070164
Chicago/Turabian StyleRasoulzadeh, Ali, Javad Bezaatpour, Javanshir Azizi Mobaser, and Jesús Fernández-Gálvez. 2025. "Half-Century Review and Advances in Closed-Form Functions for Estimating Soil Water Retention Curves" Hydrology 12, no. 7: 164. https://doi.org/10.3390/hydrology12070164
APA StyleRasoulzadeh, A., Bezaatpour, J., Azizi Mobaser, J., & Fernández-Gálvez, J. (2025). Half-Century Review and Advances in Closed-Form Functions for Estimating Soil Water Retention Curves. Hydrology, 12(7), 164. https://doi.org/10.3390/hydrology12070164