Abstract
Extreme rainfall events directly increase flood risks and further trigger environmental geological hazards (i.e., landslides and debris flows). Meanwhile, rainfall-induced risks are determined by climate and geographical factors and spatial socioeconomic factors (e.g., population density and gross domestic product). However, the middle stream of Yellow River Basin, where geological hazards frequently occur, lacks systematic analyses of rainfall-induced risks. In this study, we propose a comprehensive quantification framework and apply it to the Loess Plateau of northern China based on 40 years of climate data, streamflow measurements, and multiple spatial and geographical attribute datasets. A deep learning algorithm of long short-term memory (LSTM) was used to predict runoff, and the analytic hierarchy index was utilized to evaluate the comprehensive spatial risk considering natural and socioeconomic factors. Despite a decrease in annual precipitation in our study area of 1.46 mm per year, the intensity of heavy rainfall has increased since the 1980s, characterized by increases in rainstorm intensity (+4.68%), rainfall intensity (+7.07%), and rainfall amount (+5.34%). A comprehensive risk assessment indicated that high-risk areas accounted for 20.30% of the total area, with rainfall, geographical factors, and socioeconomic variables accounting for 53.90%, 29.72%, and 16.38% of risk areas, respectively. Rainfall was the dominant factor that determined the risk, and geographical and socioeconomic properties characterized the vulnerability and resilience of disasters. Our study provided an evaluation framework for multi-hazard risk assessment and insights for the development of disaster prevention and reduction policies.
1. Introduction
Rainfall is one of the most important triggers of geo-hazards, which are harmful to human life, damage key infrastructure, and destroy cultural and natural heritage [1]. In the event of heavy or persistent rainfall, river discharge can rapidly occur and cause flooding, landslides, and debris flows [2,3]. In addition, global warming increases the spatial heterogeneity of rainfall events in terms of the total amount of rainfall, frequency of rainfall events, and maximum amount of rainfall [4,5,6]. Consequently, disasters are more likely to occur in arid and semi-arid regions where disaster management and control capabilities are inadequate [7]. According to the National Geological Disaster Bulletin 2009–2016, there are approximately 14,000 geological disasters in China annually. Natural factors (e.g., rainfall, earthquakes, and the freezing and thawing of snow and ice) cause 93.4% of these disasters, which result in an average annual economic loss of 4.84 billion yuan [8]. Heavy rainfall causes intense surface runoff scouring and seepage erosion, which pre-existing drainage systems originally designed for semi-arid and arid regions are ill-equipped to manage [9,10]. In addition, debris flows and landslides caused by excessive rainfall result in heavy losses of life and property for existing communities [11,12]. Accordingly, it is crucial to assess the risks associated with multiple hazards resulting from rainfall, particularly in semi-arid and arid regions.
The risk evaluations for floods and the induced geo-hazards of landslides and debris flows show differences in scale and methodology. Flood risk is typically evaluated at a regional scale, ranging from less than 100 km2 to over 10,000 km2, whereas landslides and debris flows are evaluated at the location or slope level; the majority of relevant studies are conducted within 10 km2 on average for one to occur [13,14,15]. Both types of hazards were assessed and projected using physical-based or data-driven models in conjunction with observed records and remote sensing imagery, but at different time scales. Models for flood prediction focus on dynamic runoff simulations for months to years, characterizing the flow components and geographical attributes (i.e., precipitation, evaporation, soil, and land use or land cover type) of the hydrological cycle [16,17]. Models for landslides simulate the moving volumes and velocities, but models for debris flows are concerned with the volume of mobilized flow, with resolutions ranging from seconds to years, requiring extensive computations [18]. These predictions are based on rainfall frequency and intensity [19]. Although the current research on both types of hazards is beneficial in theory and practice, they are typically viewed as independent. They are rarely combined to provide a comprehensive assessment of both risks.
The early detection of rainfall-induced hazards can be acquired by analyzing and simulating floods, landslides, and debris flows caused by natural drivers. In contrast, risk assessment and management should consider spatial socioeconomic factors. Risk vulnerability evaluations at the regional level apply to urban areas, population density, economic status (i.e., gross domestic product, GDP), and other infrastructure and cultural heritage [20]. These socioeconomic factors are highly heterogeneous. For flood risk, socioeconomic vulnerability assessments have been developed and adopted in previous studies, whereas the vulnerability of landslides and debris flows is primarily focused on mortality and damage to structures at the site of occurrence because of the research scale [21,22]. There are substantial scientific and practical challenges associated with developing a comprehensive framework that integrates hazards on different scales with socioeconomic vulnerability to identify spatial risk patterns.
To evaluate the regional spatial risks of multiple rainfall-caused hazards, we selected the Guanzhong Basin in the Middle Yellow River Basin of northern China as a representative case for the following reasons. The selection of the Guanzhong Basin as a case study is underpinned by several key considerations: it is a typical semi-arid region characterized by a dense population, significant agricultural activity, and an exceptionally rich cultural and natural heritage of international importance, making it highly sensitive to environmental changes and disaster impacts. Furthermore, the basin frequently experiences heavy summer rainfall which markedly increases the risk of concurrent flooding, landslides, and debris flows, particularly in its mountainous southern and western areas [23,24,25,26]. As this region has experienced more frequent heavy rainfall events in recent years, the existing urban drainage systems in urban areas have become inadequate [27,28]. In the meantime, the spatial risks of landslides and debris flows in this region are yet to be quantified. The existing research has made significant contributions to understanding and assessing various hazard risks. For instance, studies in the Yellow River Basin have focused on modeling rainstorm-induced floods and large-scale flooding events [24,26,28]. In terms of geological hazards, significant work has been completed on landslide susceptibility and risk in Shaanxi Province and the Loess Plateau using various GIS-based, statistical, and machine learning techniques, often complemented by field investigations [29,30,31], and furthermore, national-level disaster risk indexing and frameworks integrating socioeconomic factors into flood disaster risk in the Yellow River Basin [32,33].
However, the current approaches often address these components in isolation or lack a robust method for combining diverse data sources into a unified multi-hazard risk structure. This study aims to address this gap by proposing and applying an integrated multi-hazard risk assessment framework. The novelty herein lies in the unique combination of deep learning (LSTM for runoff prediction) with the analytic hierarchy process (AHP) to systematically integrate diverse factors including rainfall characteristics (based on daily rainfall records from 43 stations), geographical attributes, and critical socioeconomic variables. Furthermore, we compared our results with those from the locations of geo-hazards occurrences identified by field survey records. Major tourism destinations in high-risk areas were also noted. This comprehensive framework for assessing rainfall-induced hazards provides an effective tool for other regions, and the results of spatial patterns provide novel insights for the planning of urban infrastructure and the management of risks.
2. Materials and Methods
2.1. Description of the Study Area
The Guanzhong Basin is the core of the Loess Plateau and is situated in the hinterland of China in the middle stream of the Yellow River Basin (Figure 1). It encompasses a total area of 20,576.57 km2 and constitutes a narrow corridor between the Qinling Mountains in the south and the Bei Mountains in the north. The Guanzhong Basin is a part of the lower drainage basin of the Wei River, which is a tributary of the Yellow River. It contains four catchments: Linjiacun (LJC), Zhangjiashan (ZJS), Zhuangtou (ZT), and Huaxian (HX). The mean annual rainfall is approximately 590.1 mm/year, and the surface runoff is 81.47 mm/year. The Loess Plateau is densely populated in the Guanzhong Basin, which contains Xi’an, the largest and most historically important city in northern China. The study area varies in elevation from 1779 m in the southern Qinling Mountains to 323 m in the center oases. The mean annual temperature varies between −3 °C in January and 27 °C in July.
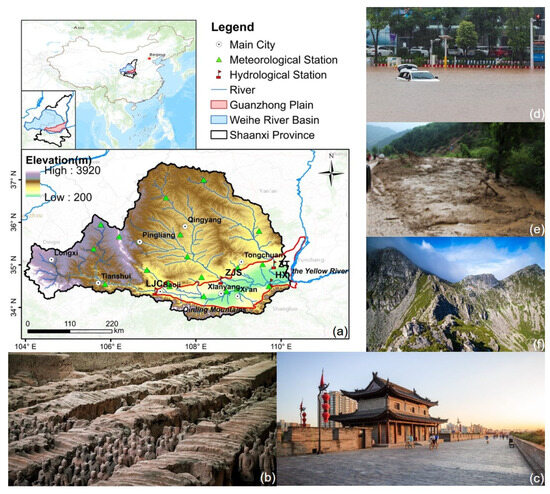
Figure 1.
(a) Study area; the historical heritage of (b) the mausoleum of the first Qin emperor and (c) the ancient city wall; and the hazards of (d) flooding, (e) debris flows, and (f) landslides occurring within the study area.
Because the Guanzhong Basin is an encompassing drainage area, the surge of river flow induced by heavy summer rainfall discharges into this area, increasing the risk of flooding. Furthermore, rainfall is often responsible for triggering geological hazards (e.g., landslides and debris flows) in the southern mountains. There are 764.8 km2 of main urban land, 1636.9 km2 of rural settlements and historical sites, and 142 tourist attractions.
2.2. Rainfall Analysis and Runoff Simulation
2.2.1. Rainfall Analysis
We collected the 1980–2019 daily rainfall data for 43 stations from the National and Shaanxi Meteorological Bureaus. The spatial pattern of rainfall variation was examined using four variables: rainfall days, which was the total number of days with daily rainfall greater than 0.1 mm; rainfall intensity, which represented the mean amount of daily rainfall; maximum daily rainfall amount; and the rainstorm amount, which was the daily rainfall amount greater than 50 mm per day [34,35,36].
The Mann–Kendall trend test [37] was applied to each station to determine the changing trends in rainfall days, rainfall intensity, maximum daily rainfall, and rainstorm amount.
2.2.2. Runoff Simulation
Runoff was simulated using an LSTM network, a type of recurrent neural network adept at learning temporal dependencies from time-series data [38,39,40,41]. The core LSTM architecture comprised an input layer, a single LSTM layer with 256 hidden units, and an output linear layer. Key hyperparameters for training included 1000 epochs a mini-batch size of 128, a learning rate of 0.001, and the Adam optimizer. In addition to an LSTM trained solely on local sub-basin data, six transfer learning (TL) configurations were evaluated. These TL models were pre-trained on either the full CAMELS US dataset (671 catchments; models TL_A, TL_B, TL_C) or a selected subset of 531 CAMELS catchments (models TL_A_531, TL_B_531, TL_C_531). The TL strategies differed in their fine-tuning approach on local data; TL_A involved freezing core LSTM weights and fine-tuning only input/output layers; TL_B allowed the fine-tuning of LSTM recurrent connections and output layers; and TL_C allowed full fine-tuning of all pre-trained weights. The inputs to LSTM for the simulations included climate forcing (e.g., precipitation, solar radiation, maximum temperature, and minimum temperature), as well as attribute data (e.g., soil type, land cover, and geology). The training period spanned from 1971 to 1978, the validating period from 1979 to 1986, and the predicting period between 1987 and 2019. The Nash–Sutcliffe efficiency coefficient (NSE) was used as a goodness-of-fit measure for runoff prediction by LSTM [42]. In order to evaluate the performance of the models in extreme cases, we calculated the percentage deviation between the top 2% high-flow range (FHV) and the bottom 30% low-flow range (FLV) [43]. The FHV and FLV were calculated using the following equation:
where represents the simulated runoff value and denotes the observed runoff value.
2.3. Risk Evaluation
2.3.1. Risk of Hazards and Vulnerability Index
We adopted a comprehensive risk index (R) to assess the hazards caused by rainfall and the vulnerability to socioeconomic effects [44]. R could be expressed using the following equation:
where represents the indicator of hazards and vulnerability and denotes the weight identified to that indicator, . The sum of all the weights is equal to 1.
Three types of indicators were identified in this study, as shown in Figure 2 [45]. The first was climate-relevant indicators, which included climate-forcing variables. Climate forcing primarily consisted of annual rainfall, rainfall days, rainfall intensity, rainstorm intensity, and maximum rainfall amount. The second type comprised geographic attribute indicators, which comprised landscape (i.e., elevation and slope), geology (i.e., soil type), and hydrology (i.e., drainage density) indicators. The third component is the Socio-Hazard Risk Index, which, in this study, quantifies the risk arising from the exposure and concentration of socioeconomic elements (e.g., population density, GDP, urban areas, historical sites) to potential rainfall-induced natural hazards. A higher index value signifies areas where a natural hazard event would likely lead to greater societal and economic losses due to the characteristics of the elements at risk. This index therefore focuses on the societal consequences and susceptibility to damage rather than societal factors as primary hazard triggers, and is related to the broader concept of socioeconomic vulnerability [46].
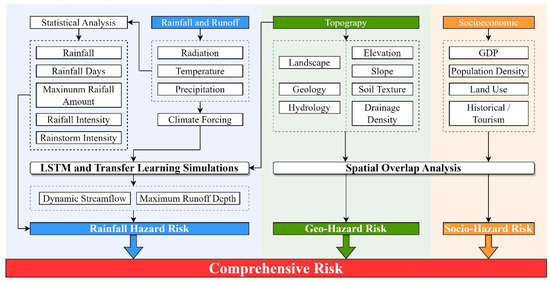
Figure 2.
Framework of evaluation for rainfall-induced risk.
2.3.2. Determining Risk Weights
The AHP was employed in this study to determine the weights for each indicator in the composite index of R, as this index simultaneously considered multiple indicators of an interrelated nature and human systems. The AHP is a multi-criteria decision-making model that is capable of integrating the effects of multiple factors into a single conclusion [47,48]. It is applied in risk assessment for natural hazards [49,50]. Factors can be qualitative, quantitative, independent, or dependent on one another [51], such as the interrelated factors of rainfall amount and surface runoff.
The AHP procedure for identifying the weights is summarized in Table 1. In this study, climate-relevant attributes, geographic attributes, and socioeconomic indicators were organized into a unified hierarchy. Then, a pairwise comparison matrix was constructed based on a comparative scale [48], which included integer numbers between 1 and 9, with 1 signifying that the indicators were of equal importance and 9 indicating that one indicator was much more important than its pairwise indicator [52].

Table 1.
Procedure for AHP calculation.
The discordances in the pairwise comparison results were then evaluated using the consistency ratio (CR), and the weights were accepted when the CR was less than 0.1. CR could be expressed as follows:
where CI represents the consistency index in Equation (4) and RI denotes the random index, which serves as the average random consistency index and is obtained from Table 2.
where is the maximum eigenvalue of the judgment matrix and denotes the order of the matrix. The method for assigning the value of n is based on Table 2.

Table 2.
Mean random consistency index RI value [53].
When the CR < 0.10, the consistency of the judgment matrix was regarded as within an acceptable range; otherwise, the elements in the judgment matrix should have been properly revised to ensure adequate consistency.
2.3.3. Data Integration
Data sources and descriptions are provided in Table 3. The data for climate-relevant indicators consisted of time-series datasets that included 43 rainfall stations and 20 meteorological stations. The indicators of geographic attribution were primarily spatial datasets in a grid format, as depicted in Figure 3. The described dataset was converted into numeric values for evaluation purposes. Soil texture was expressed as a percentage of the soil/sand content ratio. A digital elevation model (DEM) was used in conjunction with a grid system in a geographic information system (GIS) to extract data about river networks, which were then represented as drainage density for evaluation purposes. Statistical datasets from national and provincial statistical yearbooks, as well as spatial data with grids, were used for socioeconomic indicators. Land use types were categorized on a scale from 1 to 6 and normalized based on forest land, grassland, cultivated land, housing development, undeveloped land, and water area. Spatial distribution data of geological hazard locations from 1960 to 2019 were collected in order to validate the calculated risk area, which covered seven types of geo-hazards (i.e., collapse, debris flow, land subsidence, ground fissures, landslides, and slopes). During the data integration process for constructing the AHP framework and for LSTM model inputs, careful attention was paid to data quality and completeness. For time-series data such as daily rainfall from meteorological stations, short, isolated periods of missing values were imputed using linear interpolation or data from the nearest neighboring station with a high correlation, where appropriate.

Table 3.
Overview of data sources and descriptions.
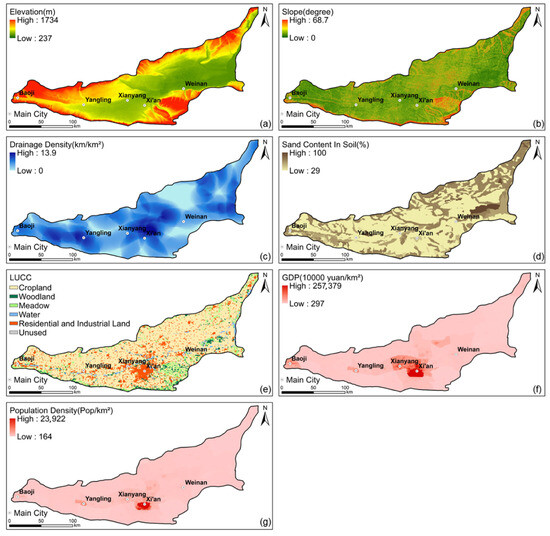
Figure 3.
Spatial pattern of geographical and socioeconomic indicators. (a) Elevation (m), (b) slope (°), (c) drainage density (km/km2), (d) sand content in soil (%), (e) land use, (f) gross domestic product (10,000 yuan/km2), and (g) population density (Pop/km2).
As the three types of indicators had distinct units, we converted each indicator into a standardized value for calculation. The standard normalization method that was used to map the data to a range of 0–1 was as follows [54]:
where represents the value of the indicator and and are the maximum and minimum values of , respectively.
3. Results
3.1. Spatiotemporal Variation in Rainfall
The changing trend in rainfall from the 43 meteorological stations and the spatial patterns of the annual average are presented in Figure 4. In this study, we adopted a significance level of 95% and a critical test value of ±1.96. Annual rainfall in the Guanzhong Basin ranged from 723.5 mm in the southern mountains to 503.1 mm in the northern alluvial plain. The annual rainfall trend analysis using the Mann–Kendall trend test indicated a decreasing trend for the entire study area between 1980 and 2019, with a mean z-statistic of −0.64; nevertheless, the rainfall in the southern mountains exhibited an increasing trend, with a z-statistic ranging between 0.20 and 1.22 (Figure 4a). Annual rainfall days varied from 105 d in the southwestern region to 77 d in the northeastern region. Over the past 40 y, the annual rainfall days in the study area showed a downward trend, with an average z-value of −1.83. Since the 1980s, the average number of rainfall days for the entire study area has decreased by 9.96%. Over the past 40 y, the annual rainfall days in the entire study area have decreased, with an average z-value of −1.83 (Figure 4b).
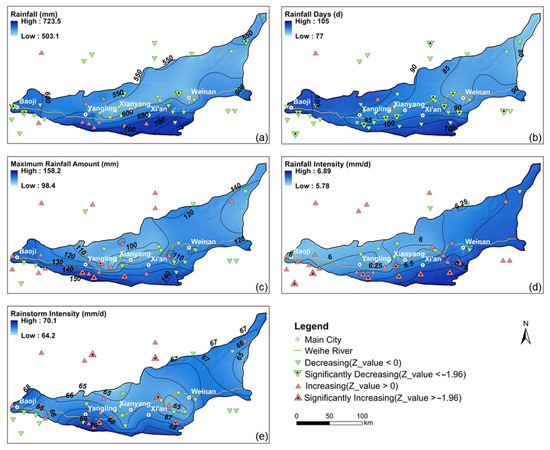
Figure 4.
Spatiotemporal variation in rainfall between 1980 and 2019. (a) Annual rainfall (mm), (b) rainfall days (d), (c) maximum rainfall amount (mm), (d) rainfall intensity (mm/d), and (e) rainstorm intensity (mm/d). The triangle indicates the result of the Mann–Kendall trend test, with red indicating an upward trend and green indicating a downward trend. The size of the triangle reflects the statistical significance of the trend at a 95% confidence level.
The difference in the spatial distribution of the maximum rainfall amount (the day with the maximum rainfall) ranged from 98.4 mm to 158.2 mm. In contrast to the decreasing trend in annual rainfall, the maximum amount of precipitation for the entire study area showed an upward trend, with a mean z-statistic of 0.52 between 1980 and 2019. The maximum rainfall at 22 of the 43 meteorological stations showed an upward trend, particularly in the southern and western mountainous regions, as shown in Figure 4c. From the western to the eastern part of the study area, rainfall intensity (mean rainfall amount for rain days) decreased. The rainfall intensity for the entire study area showed a significant increase between 1980 and 2019, with a mean z-value of 2.37. The rainfall intensity has increased by 9.20% over the past decade (2010–2019) (Figure 4d). Similar to the maximum rainfall amount, the intensity of rainstorms across the entire study area exhibited a significant upward trend during the test period, with an average z-value of 1.94 (Figure 4e).
Figure 5 illustrates the seasonal variation in monthly rainfall. The average annual rainfall was 590 mm, with the highest rainfall occurring in July and August. A total of 52.4% of the annual rainfall occurred between July and September. In addition, the intensity of rainfall and rainstorms reached their peaks in August. A summer rainfall of 46.5% implied the characteristics of a continental climate on the Loess Plateau.
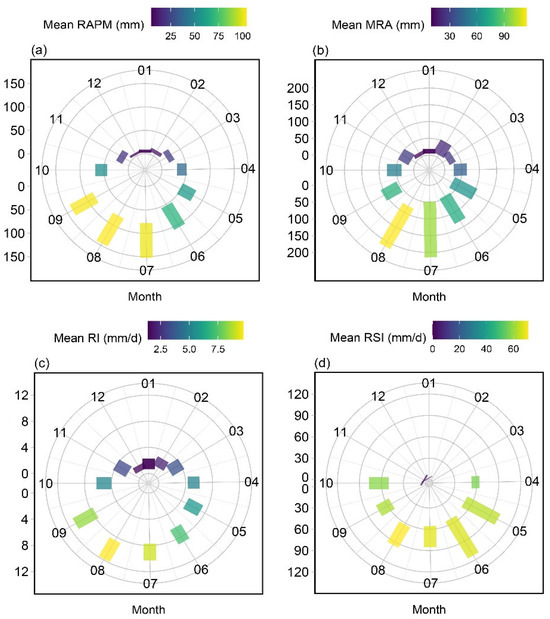
Figure 5.
Seasonal variation in rainfall. (a) Rainfall amount per month (mm); (b) maximum rainfall amount (mm); (c) rainfall intensity (mm/d); and (d) rainstorm intensity (mm/d). The histogram represents the range, and the colors represent the average.
3.2. Variation in Runoff
The Weihe River Basin mainly includes four sub-basins, and the four hydrological stations are the outlets along the upstream tributaries (i.e., LJC, ZJS, and ZT) and mainstream (i.e., HX). The results of the runoff simulation and prediction for all sub-basins are depicted in Figure 6. The application of transfer learning generally led to an improved runoff simulation performance compared to LSTM, although the optimal TL strategy varied by sub-basin. At the LJC station, the highest NSE of 0.67 was achieved by the TL_C model (pre-trained on 671 catchments with full fine-tuning). For the ZJS station, the TL_A_531 model (pre-trained on 531 catchments with minimal core fine-tuning) demonstrated the best performance with an NSE of 0.67. At the ZT station, the TL_A model (pre-trained on 671 catchments with minimal core fine-tuning) provided the highest NSE of 0.63. Finally, at the HX mainstream station, the TL_A_531 model again proved most effective, achieving a robust NSE of 0.78. While these models were selected based on their optimal NSE, an examination of their corresponding FHV and FLV metrics reveals varied performance in simulating extreme flows. For instance, the TL_C model at LJC, despite its high NSE (0.67), showed an underestimation of peak flows (FHV −23.13%) but reasonable low-flow simulation (FLV 4.85%). The TL_A_531 model at ZJS (NSE 0.67) slightly overestimated peak flows (FHV 17.36%) and slightly underestimated low-flows (FLV −5.19%). At ZT, the best NSE model (TL_A, NSE 0.63) simulated peak flows accurately (FHV −1.92%) but underestimated low-flows (FLV −20.29%). Finally, the TL_A_531 model at HX (NSE 0.78) also tended to underestimate peak flows (FHV −19.43%) while significantly overestimating low-flows (FLV 67.54%). This indicates that even models performing well on overall water balance (high NSE) may exhibit different biases for high- and low-flow extremes, underscoring the importance of multi-metric assessment for specific applications. The performance of our simulations using LSTM (NSE is 0.78) was consistent with the results obtained using physical hydrological models (NSE from 0.76 to 0.82) [55,56,57]. The results showed that the runoff varied from 44.2 m3/s (42 mm/year) in the upstream to 187 m3/s (169.29 mm/year) in the downstream. During the wet season (i.e., between July and September), the upstream runoff increased to 76 m3/s (71.2 mm/year), while the downstream runoff increased to 344 m3/s. Despite these observed variations and specific biases in peak-flow and low-flow simulations, the ability of the best-performing models to capture the overall hydrological regime and seasonal runoff dynamics (evidenced by NSE values above 0.63 for all sub-basins and 0.78 for mainstream HX) provides a sufficiently robust and quantitative basis for their use in evaluating the relative risk of rainfall-induced flooding across the study area.
Figure 6.
Streamflow simulations and predictions for sub-basins. According to the trend of the river and the distribution of hydrological stations, the (a) Weihe River Basin is divided into four sub-basins: Linjiacun (LJC), Zhangjiashan (ZJS), Zhuangtou (ZT), and Huaxian (HX). Runoff simulation and prediction in the (b) LJC, (c) ZJS, (d) ZT, and (e) HX watersheds. The purple lines represent the measured runoff curves, whereas the red lines denote the runoff prediction curves.
Figure 7 shows the monthly variations in runoff for four sub-basins. From 1980 to 2019, the annual average runoff depth in the upper stream of the Weihe River was 59.0 mm for LJC, 37.4 mm for ZJS, and 29.6 mm for ZT, and it was 169.3 mm for downstream HX. The runoff from July to September accounted for 42.00% of the total runoff.
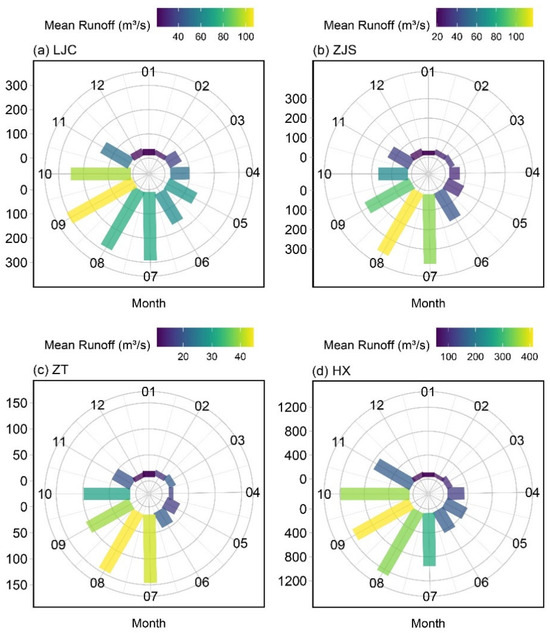
Figure 7.
Monthly variations in runoff for four sub-basins: (a) Linjiacun (LJC); (b) Zhangjiashan (ZJS); (c) Zhuangtou (ZT); and (d) Huaxian (HX). The histogram represents the range, and the colors represent the average.
Over the period 1980–2019, the upper stream of the Weihe River averaged 1.81 billion m3 of runoff for LJC, 1.62 billion m3 for ZJS, and 0.76 billion m3 for ZT, while it averaged 5.92 billion m3 for downstream HX. Approximately 42.00% of the total runoff occurred between July and September. Converted to runoff depth, the annual average runoff depth in the upper stream of the Weihe River was 59.0 mm for LJC, 37.4 mm for ZJS, and 29.6 mm for ZT, while it was 169.3 mm for downstream HX.
3.3. Spatial Risk Assessment
The risk patterns for rainfall hazards, geo-hazards, and socio-hazards are shown in Figure 8. In accordance with the normalization principle and natural breakpoint grading method, the risk index was graded from 0 to 1, with 1 representing the highest level of risk, as shown in Table 4. The rainfall hazard risk map was based on rainfall and flooding, including annual rainfall, rainfall days, rainfall intensity, rainstorm intensity, maximum rainfall amount, average runoff depth, and flood season runoff depth. The map indicated a high risk of climate-related areas in the western and middle regions, which reflected the high rainfall and induced flooding in these areas. There was a 6.87% share of the total area that was deemed to have high- and very-high risk. Geo-hazard risk maps were based on several geographic attributes, including elevation, slope, soil type, and drainage density. The distribution of high-risk areas was relatively dispersed, reflecting that disasters were affected by multiple factors. The area at risk from geological attributes accounted for 29.72% of the total area. The socio-hazard risk map (Figure 8c), derived from indicators reflecting socioeconomic exposure (GDP, population density, land cover, historical sites), highlights areas where potential societal and economic impacts from natural hazards would be most significant. As expected under this definition, high socio-hazard risk areas are predominantly located in urban centers such as Xi’an, reflecting the concentration of valuable assets and population. Only 13.43% of the total area was considered high-risk.
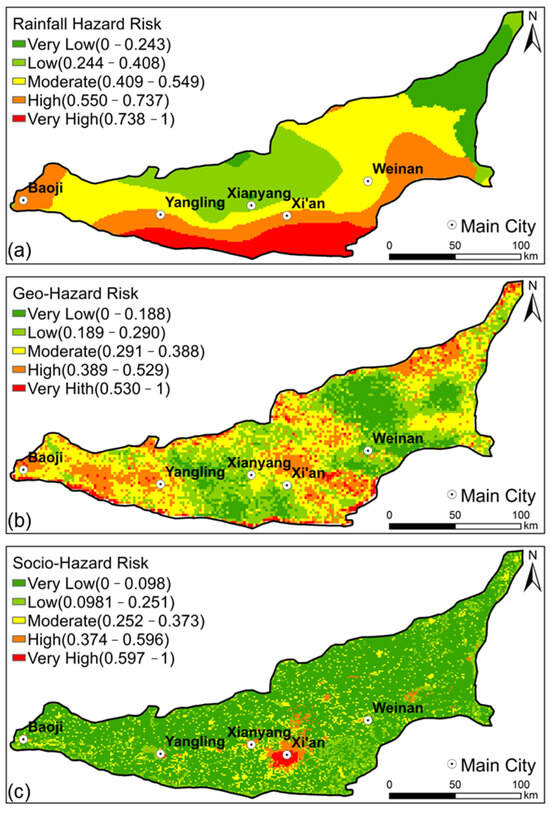
Figure 8.
Risk map of (a) rainfall hazards, (b) geo-hazards, and (c) socio-hazards.

Table 4.
Grading of various risk levels.
The weights for each type of factor and the comprehensive weight were calculated, as shown in Table 5. The sum of the comprehensive weights for each type of factor represented their contribution to the cause of the hazards. Thus, rainfall and runoff contributed 53.9%, geographical attributes contributed 29.72%, and socioeconomic variables contributed 16.38% of the hazards. Figure 9 depicts the comprehensive risk distribution and corresponding area statistics for each risk level, which were calculated by superimposing the comprehensive weight. The high-risk area encompassed 2762.56 km2, which represented 13.43% of the total study area. The very high-risk area was 1414.4 km2, which represented 6.87% of the total study area. High-risk and very high-risk areas were concentrated in the southern mountainous area and were primarily located over valley terrain. Generally, the northern region was subject to a low level of risk owing to its relatively flat terrain and steady rainfall.

Table 5.
Calculation of the weights of factors.
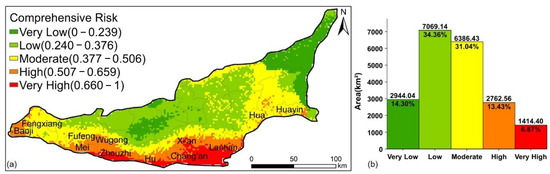
Figure 9.
Comprehensive risk overlaying rainfall, geo-hazard, and socio-hazard risks based on calculated weight. (a) Spatial risk map, and (b) area statistics for each risk level.
Figure 10 illustrates a comparison of our findings with historical geo-hazard locations identified by field surveys, and Table 6 displays the number of identified geo-hazard locations within regions with varying levels of risk. Approximately 91.76% of historical geological disasters occurred in moderate, high, and very high-risk areas, whereas no disasters occurred in very low-risk areas. The 8.24% of historical geological disasters that occurred in our defined low-risk areas caused a limited degree of damage to houses and roads, which was within the acceptable range. This comparison demonstrated that our risk map, which combined climate, geographic, and social factors, was reliable for providing a spatial assessment to control and prevent rainfall-induced hazards.
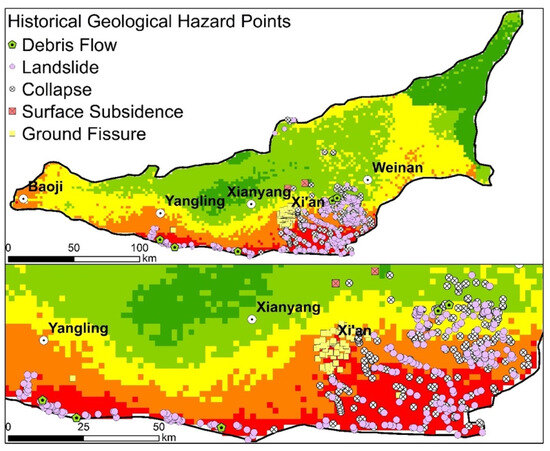
Figure 10.
A comparison between mapped risk areas and identified historical geological hazard locations via field surveys. The 1960–2019 spatial distribution data of geological disaster points were compiled by the data center of resource and environmental science and data (https://www.resdc.cn/).

Table 6.
Proportion of historical disaster points in each risk level.
4. Discussion and Implications
The analysis of historical rainfall trends facilitates the assessment of the impacts of spatiotemporal rainfall changes on geo-hazards as a result of climate change. In this study, our application of the Mann–Kendall trend test to rainfall data from 1980 to 2019 (Figure 4) revealed significant overall shifts in rainfall patterns across the study area. Specifically, for annual rainfall, the Mann–Kendall test yielded an average z-statistic of −0.64 across all stations, indicating a statistically significant general decreasing trend. This trend has resulted in an approximate 11.63% reduction in the characteristic magnitude of annual rainfall over the 40-year period. Similarly, a statistically significant and substantial decreasing trend was identified for annual rainfall days (average z-statistic of −1.83), which has led to an approximate 25.58% reduction in the number of rain days per year. Conversely, average rainfall intensity exhibited a statistically significant increasing trend (average z-statistic of +2.37), causing an approximate 20.93% increase. Average rainstorm intensity also showed a statistically significant increasing trend (average z-statistic of +1.94), resulting in an approximate 11.63% increase. This indicated that the frequency of rainfall in the study area decreased, and the amount of rainfall became more concentrated. The increased frequency of extreme rainfall events resulted in landslides, and debris flows as a result of the increased concentration and rainstorm intensity. Other computationally complex and data-demanding mechanistic models, as well as extensive field surveys and experiments in the study area and surrounding areas, also illuminate the impact of rainfall changes [31,58,59]. While this study did not use specific local hazard models to distinguish between hazard types or rainfall-induced hazards, rainfall analysis could serve as an initial early warning approach for geological hazards.
Flooding is a form of hydrological hazard that responds directly to changes in rainfall. The risk of flooding can be determined by simulating the river runoff and the depth of runoff from upstream to downstream. As shown in Figure 6 and Figure 7, peak flows may occur from July to September and could exceed three to four times the monthly median flow in the upstream region (LJC, ZJS, and ZT stations), whereas the flood risk may persist into October for the downstream HX station. Although there was a high risk of overbank flooding in the study area because of the confluence of the three rivers on the three sides, the occurrence frequency of peak flows for the HX station was reduced. This was consistent with previous conclusions [58,60]. Additionally, this result could be used as spatial attribute data to overlay analyses with other types of risks associated with hazards.
Hazards, such as debris flows caused by rainfall, were heavily influenced by geological factors such as lithology, elevation, slope, and aspect. Land use was also an important risk factor, and the dense distribution of mountains and water networks in the study area provided physical prerequisites for mudflow origination. Rainfall and geo-environmental factors represented measures of hazard risk, whereas socioeconomic factors (population and land use) denoted measures of the vulnerability of the carrier itself. In the study area, the spatial distribution of precipitation and its geo-environmental and socioeconomic impacts varied widely. Rainfall-driven impacts were mainly concentrated in the southern mountainous areas, geo-environmental impacts were more widespread, and socioeconomic factors were mainly clustered in urban areas (Figure 8). Additionally, the results after overlaying the AHP weight reflected the composite spatial distribution of disaster risk. The resulting map in Figure 9 indicates that this distribution is highly correlated with rainfall. The greater the indicator weight coefficient, the more significant the influence of the indicator on the occurrence of geo-hazards. In this study, runoff depth, rainstorm intensity, and drainage density were the main factors influencing the risk assessment outcomes, based on the comprehensive indicator weight calculation.
Our socioeconomic analysis focused primarily on population and GDP, whereas the study area, as a historical city in western China, contained a large number of historical heritage sites. By superimposing a map of tourist attractions of heritage sites on the comprehensive risk results map, we determined that 39 tourist attractions were located within the high-risk and the very high-risk areas (Figure 11). Tourist attractions in high-risk areas represented 27.46% of the total number of tourist attractions included in the entire study area. According to statistics, more than 60% of global heritage sites are under threat from geological hazards [61]. Historical sites demand special attention in disaster assessment, mainly because of their irreplaceable cultural value and difficult recovery. Our risk assessment indicated the risk faced by the current spatial distribution of heritage sites in the study area and implied that this issue should be incorporated in comprehensive risk index evaluations in future hazard assessments.
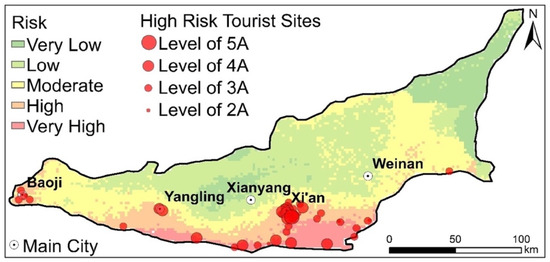
Figure 11.
Distribution of high-risk tourist destinations. The size of red dots represents the level of tourist attractions.
5. Conclusions
In this study, we evaluated the risk index of rainfall-induced disasters on the Loess Plateau using integrated approaches of deep learning, AHP, and statistical analysis. The main conclusions were as follows:
- (1)
- Over the past four decades, the annual rainfall in the Guanzhong Basin of the Loess Plateau decreased at a rate of 1.46 mm/year, rainfall days decreased by 10.89%, the maximum rainfall amount increased by 5.34%, rainfall intensity increased by 7.66%, and rainstorm intensity increased by 4.68%.
- (2)
- The performance of our simulations using LSTM was acceptable, which indicated that runoff varied between 44.2 m3/s (42 mm/year) in the upstream and 187 m3/s (169.29 mm/year) in the downstream. A peak flow period was observed between July and September, which could exceed three to four times the monthly median flow in the upstream region. The downstream region could be at risk of flooding until October.
- (3)
- The high-risk and very high-risk areas encompassed 4176.96 km2, which covered 20.3% of the total study area and were mainly located in the southern Qinglin Mountain terrain. Rainfall and runoff dominated the risk of hazards with a weight fraction of 53.9%, while geographical attributes contributed 29.72% and socioeconomic contributed 16.38%.
Our study provided a comprehensive evaluation framework that quantified the spatial–temporal variations in rainfall and runoff, geographical attributes, and socioeconomic factors in order to assess the multiple rainfall-induced geo-hazards. The results provided valuable insights for the development of future geo-hazard monitoring networks, as well as for the protection of historical and cultural heritage monuments on the Loess Plateau and other global historical cities.
Author Contributions
Conceptualization, Y.Y.; methodology, Y.Z., X.W. and Y.Y.; resources, S.X.; writing—original draft preparation, Y.Z., S.X. and Y.Y.; writing—review and editing, Y.Z., S.X., X.W., S.G. and Y.Y.; visualization, Y.Z. and X.W.; supervision, Y.Y.; project administration, Y.Y.; funding acquisition, S.X. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (Grant No. 42422701, 42171158, 41771220) and the Young Top Talents Support Program of Xi’an Jiaotong University (Grant No. HJ6J011).
Data Availability Statement
The data supporting the findings of this research are available in the manuscript, as shown in Table 3.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dano, U.L. An AHP-based assessment of flood triggering factors to enhance resiliency in Dammam, Saudi Arabia. GeoJournal 2022, 87, 1945–1960. [Google Scholar] [CrossRef]
- Borga, M.; Stoffel, M.; Marchi, L.; Marra, F.; Jakob, M. Hydrogeomorphic response to extreme rainfall in headwater systems: Flash floods and debris flows. J. Hydrol. 2014, 518, 194–205. [Google Scholar] [CrossRef]
- Tang, C.; Zhu, J.; Ding, J.; Cui, X.F.; Chen, L.; Zhang, J.S. Catastrophic debris flows triggered by a 14 August 2010 rainfall at the epicenter of the Wenchuan earthquake. Landslides 2011, 8, 485–497. [Google Scholar] [CrossRef]
- Dominguez, F.; Rivera, E.; Lettenmaier, D.; Castro, C. Changes in winter precipitation extremes for the western United States under a warmer climate as simulated by regional climate models. Geophys. Res. Lett. 2012, 39, 5. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, D.; Guo, X. Regional climate response to global warming in the source region of the Yellow River and its impact on runoff. Sci. China Earth Sci. 2024, 67, 843–855. [Google Scholar] [CrossRef]
- Lu, J.; Qin, T.; Yan, D.; Zhang, X.; Jiang, S.; Yuan, Z.; Xu, S.; Gao, H.; Liu, H. Drought and wetness events encounter and cascade effect in the Yangtze River and Yellow River Basin. J. Hydrol. 2024, 639, 131608. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, M.; Deng, Y.; Dong, Y.; Wu, X.; Kuang, X. Evaluation of environmental engineering geology issues caused by rising groundwater levels in Xi’an, China. Eng. Geol. 2021, 294, 106350. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, L.; Wang, Y.; Wang, C. Review on Forecast Methods of Rainfall-induced Geo-hazards. J. Appl. Meteorol. Sci. 2019, 30, 142–153. [Google Scholar] [CrossRef]
- Jiang, W.; Tan, Y. Heavy rainfall-related excavation failures in China during 1994 to 2018: An overview. Eng. Fail. Anal. 2021, 129, 105695. [Google Scholar] [CrossRef]
- Yao, Y.; Khan, Z.A. Predicting Pakistan’s next flood. Science 2022, 378, 483. [Google Scholar] [CrossRef]
- Chong, Y.; Chen, G.; Meng, X.; Yang, Y.; Shi, W.; Bian, S.; Zhang, Y.; Yue, D. Quantitative analysis of artificial dam failure effects on debris flows—A case study of the Zhouqu ‘8.8’debris flow in northwestern China. Sci. Total Environ. 2021, 792, 148439. [Google Scholar] [CrossRef] [PubMed]
- Wang, G. Lessons learned from protective measures associated with the 2010 Zhouqu debris flow disaster in China. Nat. Hazards 2013, 69, 1835–1847. [Google Scholar] [CrossRef]
- Herrera, G.; Mateos, R.M.; García-Davalillo, J.C.; Grandjean, G.; Poyiadji, E.; Maftei, R.; Filipciuc, T.-C.; Jemec Auflič, M.; Jež, J.; Podolszki, L. Landslide databases in the Geological Surveys of Europe. Landslides 2018, 15, 359–379. [Google Scholar] [CrossRef]
- Miao, Q.; Yang, D.; Yang, H.; Li, Z. Establishing a rainfall threshold for flash flood warnings in China’s mountainous areas based on a distributed hydrological model. J. Hydrol. 2016, 541, 371–386. [Google Scholar] [CrossRef]
- O’Connor, J.E.; Costa, J.E. Spatial distribution of the largest rainfall-runoff floods from basins between 2.6 and 26,000 km2 in the United States and Puerto Rico. Water Resour. Res. 2004, 40, 1. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, H.; Liang, Q. A coupled hydrological and hydrodynamic model for flood simulation. Hydrol. Res. 2019, 50, 589–606. [Google Scholar] [CrossRef]
- Liu, S.; Yao, Y.; Kuang, X.; Zheng, C. A preliminary investigation on the climate-discharge relationship in the upper region of the Yarlung Zangbo River basin. J. Hydrol. 2021, 603, 127066. [Google Scholar] [CrossRef]
- Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Wang, X.; Huang, G.; Liu, J. Projected increases in intensity and frequency of rainfall extremes through a regional climate modeling approach. J. Geophys. Res. Atmos. 2014, 119, 13271–13286. [Google Scholar] [CrossRef]
- Mallick, J.; Alqadhi, S.; Talukdar, S.; AlSubih, M.; Ahmed, M.; Khan, R.A.; Kahla, N.B.; Abutayeh, S.M. Risk assessment of resources exposed to rainfall induced landslide with the development of GIS and RS based ensemble metaheuristic machine learning algorithms. Sustainability 2021, 13, 457. [Google Scholar] [CrossRef]
- Papathoma-Köhle, M.; Gems, B.; Sturm, M.; Fuchs, S. Matrices, curves and indicators: A review of approaches to assess physical vulnerability to debris flows. Earth Sci. Rev. 2017, 171, 272–288. [Google Scholar] [CrossRef]
- Pollock, W.; Wartman, J. Human vulnerability to landslides. GeoHealth 2020, 4, e2020GH000287. [Google Scholar] [CrossRef] [PubMed]
- Riedel, J.L.; Sarrantonio, S.M. Debris flow magnitude, frequency, and precipitation threshold in the eastern North Cascades, Washington, USA. Nat. Hazards 2021, 106, 2519–2544. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, Q.; Singh, V.P.; Wang, G.; He, C.; Zhao, J. Escalating rainstorm-induced flood risks in the Yellow River Basin, China. Environ. Res. Lett. 2024, 19, 064006. [Google Scholar] [CrossRef]
- Lan, H.; Zhao, Z.; Li, L.; Li, J.; Fu, B.; Tian, N.; Lai, R.; Zhou, S.; Zhu, Y.; Zhang, F. Climate change drives flooding risk increases in the Yellow River Basin. Geogr. Sustain. 2024, 5, 193–199. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Q.; Singh, V.P. Flooding in the Yellow River Basin, China: Spatiotemporal patterns, drivers and future tendency. J. Hydrol. Reg. Stud. 2024, 52, 101706. [Google Scholar] [CrossRef]
- Myhre, G.; Alterskjær, K.; Stjern, C.W.; Hodnebrog, Ø.; Marelle, L.; Samset, B.H.; Sillmann, J.; Schaller, N.; Fischer, E.; Schulz, M. Frequency of extreme precipitation increases extensively with event rareness under global warming. Sci. Rep. 2019, 9, 16063. [Google Scholar] [CrossRef]
- Zhao, Z.; Huo, A.; Liu, Q.; Yang, L.; Luo, C.; Ahmed, A.; Elbeltagi, A. Assessment of urban inundation and prediction of combined flood disaster in the middle reaches of Yellow river basin under extreme precipitation. J. Hydrol. 2024, 640, 131707. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, M.; Ma, Y.; Liu, J.; Wang, Y.; Ma, X.; Chen, J. Multiclassification method of landslide risk assessment in consideration of disaster levels: A case study of Xianyang City, Shaanxi Province. ISPRS Int. J. Geo-Inf. 2021, 10, 646. [Google Scholar] [CrossRef]
- Liang, S.; Chen, D.; Li, D.; Qi, Y.; Zhao, Z. Spatial and temporal distribution of geologic hazards in Shaanxi Province. Remote Sens. 2021, 13, 4259. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, J.; Wang, G.; Javed, I.; Wang, Y.; Li, W. Distribution and characteristics of landslide in Loess Plateau: A case study in Shaanxi province. Eng. Geol. 2018, 236, 89–96. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Wu, W.; Li, N. Integrated risk assessment of multi-hazards in China. Nat. Hazards 2015, 78, 257–280. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, Q.; Wang, G.; Singh, V.P.; Wu, W.; Fan, K.; Shen, Z. Flood disaster risk and socioeconomy in the Yellow River Basin, China. J. Hydrol. Reg. Stud. 2022, 44, 101272. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Z.; Charles, S.P.; Fu, G.; Liu, L. Evaluation of two statistical downscaling models for daily precipitation over an arid basin in China. Int. J. Climatol. 2011, 31, 2006–2020. [Google Scholar] [CrossRef]
- Ma, S.; Zhou, T.; Dai, A.; Han, Z. Observed changes in the distributions of daily precipitation frequency and amount over China from 1960 to 2013. J. Clim. 2015, 28, 6960–6978. [Google Scholar] [CrossRef]
- Penalba, O.C.; Robledo, F.A. Spatial and temporal variability of the frequency of extreme daily rainfall regime in the La Plata Basin during the 20th century. Clim. Chang. 2010, 98, 531–550. [Google Scholar] [CrossRef]
- Neeti, N.; Eastman, J.R. A contextual mann-kendall approach for the assessment of trend significance in image time series. Trans. GIS 2011, 15, 599–611. [Google Scholar] [CrossRef]
- Feng, D.; Fang, K.; Shen, C. Enhancing streamflow forecast and extracting insights using long-short term memory networks with data integration at continental scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Gauch, M.; Mai, J.; Lin, J. The proper care and feeding of CAMELS: How limited training data affects streamflow prediction. Environ. Model. Softw. 2021, 135, 104926. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Benchmarking a catchment-aware long short-term memory network (LSTM) for large-scale hydrological modeling. Hydrol. Earth Syst. Sci. Discuss 2019, 2019, 5089–5110. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, Y.; Li, X.; Feng, D.; Shen, C.; Liu, C.; Kuang, X.; Zheng, C. Can transfer learning improve hydrological predictions in the alpine regions? J. Hydrol. 2023, 625, 130038. [Google Scholar] [CrossRef]
- Man, Y.; Yang, Q.; Shao, J.; Wang, G.; Bai, L.; Xue, Y. Enhanced LSTM Model for Daily Runoff Prediction in the Upper Huai River Basin, China. Engineering 2022, 24, 229–238. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44, 9. [Google Scholar] [CrossRef]
- Aydin, M.C.; Sevgi Birincioğlu, E. Flood risk analysis using gis-based analytical hierarchy process: A case study of Bitlis Province. Appl. Water Sci. 2022, 12, 122. [Google Scholar] [CrossRef]
- He, Y.; Wang, Q.; Xu, Y.; Li, Z.; Yuan, J.; Lu, M.; Lin, Z. Climate change increased the compound extreme precipitation-flood events in a representative watershed of the Yangtze River Delta, China. Stoch. Environ. Res. Risk Assess. 2022, 36, 3803–3813. [Google Scholar] [CrossRef]
- Zhang, Y.; You, W. Social vulnerability to floods: A case study of Huaihe River Basin. Nat. Hazards 2014, 71, 2113–2125. [Google Scholar] [CrossRef]
- Saaty, T.L. What is the analytic hierarchy process. In Mathematical Models for Decision Support; Springer: Berlin/Heidelberg, Germany, 1988; pp. 109–121. [Google Scholar]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Lyu, H.; Sun, W.; Shen, S.; Arulrajah, A. Flood risk assessment in metro systems of mega-cities using a GIS-based modeling approach. Sci. Total Environ. 2018, 626, 1012–1025. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Stefanidis, S.; Stathis, D. Assessment of flood hazard based on natural and anthropogenic factors using analytic hierarchy process (AHP). Nat. Hazards 2013, 68, 569–585. [Google Scholar] [CrossRef]
- Salo, A.A.; Hämäläinen, R.P. On the measurement of preferences in the analytic hierarchy process. J. Multi-Crit. Decis. Anal. 1997, 6, 309–319. [Google Scholar] [CrossRef]
- Tang, J. Prioritizing User Requirements based on Analytic Hierarchy Process. Proc. J. Phys. Conf. Ser. 2021, 1861, 012021. [Google Scholar] [CrossRef]
- Pollesch, N.L.; Dale, V.H. Normalization in sustainability assessment: Methods and implications. Ecol. Econ. 2016, 130, 195–208. [Google Scholar] [CrossRef]
- Chang, J.; Wang, Y.; Istanbulluoglu, E.; Bai, T.; Huang, Q.; Yang, D.; Huang, S. Impact of climate change and human activities on runoff in the Weihe River Basin, China. Quat. Int. 2015, 380, 169–179. [Google Scholar] [CrossRef]
- Li, Y.; Chang, J.; Jin, W.; Guo, A.; Wang, D. Runoff simulation in subzones of the Wei River Basin based on the SWAT model. J. Northwest A F Univ. (Nat. Sci. Ed.) 2017, 45, 204–212. [Google Scholar]
- Yang, S.; Kang, T.; Bu, J.; Chen, J.; Wang, Z.; Gao, Y. Detection and Attribution of Runoff Reduction of Weihe River over Different Periods during 1961–2016. Water 2020, 12, 1416. [Google Scholar] [CrossRef]
- Qi, Q.; Ju, Y.W. Study on Rainfall-induced Loess Geological Hazards Characteristics and Preventive Measures in Shanxi Province. Proc. Appl. Mech. Mater. 2015, 744–746, 1741–1744. [Google Scholar] [CrossRef]
- Zhuang, J.; Iqbal, J.; Peng, J.; Liu, T. Probability prediction model for landslide occurrences in Xi’an, Shaanxi Province, China. J. Mt. Sci. 2014, 11, 345–359. [Google Scholar] [CrossRef]
- Tian, S.; Luo, W.; Jia, Z.; Butalia, R.S. Temporal variation of over-bank flooding of Wei River and its impact on a riparian wetland in Xi’an, China. Hydrol. Process. 2010, 24, 1296–1307. [Google Scholar] [CrossRef]
- Pavlova, I.; Makarigakis, A.; Depret, T.; Jomelli, V. Global overview of the geological hazard exposure and disaster risk awareness at world heritage sites. J. Cult. Herit. 2017, 28, 151–157. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).