Forecasting Model for Danube River Water Temperature Using Artificial Neural Networks

Abstract

The objective of this paper is to propose an artificial neural network (ANN) model to forecast the Danube River temperature at Chiciu–Călărași, Romania, bordered by Romanian and Bulgarian ecological sites, and situated upstream of the Cernavoda nuclear power plant. Given the temperature increase trend, the potential of thermal pollution is rising, impacting aquatic and terrestrial ecosystems. The available data covered a period of eight years, between 2008 and 2015. Using as input data actual air and water temperatures, and discharge, as well as air temperature data provided by weather forecasts, the ANN model predicts the Danube water temperature one week in advance with a root mean square deviation (RMSE) of 0.954 °C for training and 0.803 °C for testing. The ANN uses the Levenberg–Marquardt feedforward backpropagation algorithm. This feature is useful for the irrigation systems and for the power plants in the area that use river water for different purposes. The results are encouraging for developing similar studies in other locations and extending the ANN model to include more parameters that can have a significant influence on water temperature.

1. Introduction

Water temperature is a powerful parameter that triggers the initiation and development of complex biogeochemical processes in watercourses [1], influencing water quality and changes in ecosystems [2]. Regrettably, global warming has led to a considerable increase in the mean temperature at the surface of the Earth [3]. As well, recent data provided by NASA indicate a 1.36 °C increase in 2023 compared to the preindustrial average (an aggregate of the second half of the 19th century, 1850–1900). The same NASA source stressed that during the last decade the hottest years from all records were registered [4]. In this established climate change context, and considering the rapid increase in anthropogenic impacts, water temperature forecasting has become a practice of utmost necessity to correctly evaluate the quality of water courses and their supporting land ecosystems [5]. This leads to deeper insight into temperature fluctuations, allowing identification of the most suitable strategies to better adapt to climate change.

Over time, several types of mathematical models have been used to forecast the temperature of water courses. These range in complexity from statistical to process-based and artificial intelligence (AI) models [6]. Due to their reliability and optimization capacity, AI techniques have gained precedence with respect to previous classical methods [5,7,8]. Replacing statistical models with AI ones brings at least a 20% improvement in the accuracy of predicting river temperature [8]. Thus, ref. [9] proposed an extreme learning machine (ELM) AI model to estimate the daily river water temperature based on the air temperature, the day of the year, and the water discharge. Long short-term memory (LSTM) deep learning neural networks were used by [5,10] to predict mean daily river temperatures.

River water temperature was also modelled using a hybrid model integrating long short-term memory and a transformer encoder [11]. Another hybrid model forecasts the daily river water temperature by combining a nonlinear autoregressive neural network with a Bayesian Optimization algorithm [12]. A different model, using measured data from five stations in Poland, predicts water temperature based on signal decomposition algorithms (wavelet transform, maximum overlap discrete wavelet transform) and machine learning (feedforward neural network, optimally pruned extreme learning, adaptive boosting, bootstrap aggregating) [13].

An extensive review on river water temperature modelling, including machine learning, is conducted by [14]. Also, the use of machine learning in hydrologic sciences applications is discussed by [15]. The article focusses on issues dealing with controlling factors influencing hydrological parameters.

The Danube River’s water temperature was statistically analysed by [16] to assess its monthly changes and forecast its values in certain locations. Other researchers studied the trends in the mean annual water temperature in a location at the confluence of the Sava and Danube Rivers [17].

Among different AI models (artificial neural networks, wavelet–artificial intelligence integrated models, Gaussian process regression, adaptive neuro-fuzzy inference systems, adapting boosting, hybrid machine learning [8,18]) provided by the scientific literature, artificial neural network (ANN) models are among the best suited to approach unknown nonlinear functions and to tackle noisy data [19,20,21]. Also, even though ANN models require big data sets and extensive power for computing, these disadvantages are increasingly overcome by advancements in computing technology [22]. The stability and fast convergence of the Levenberg–Marquardt algorithm makes it fit for implementation in ANN models for forecasting procedures, including for river water temperatures [23,24].

River temperature forecast several days in advance based on artificial neural networks [25,26] still encounters certain difficulties and gaps, such as (i) data quality and availability; (ii) model generalization to different locations; (iii) integrating environmental and climatic drivers; (iv) model complexity; and (v) lack of interdisciplinary collaboration between scientists from different fields.

The objective of this paper is to develop a tool addressing the problem of Danube water temperature prediction in a certain location (Chiciu–Călărași) over a time span. This prediction is useful because it is more reliable to forecast the air temperature than the water, with the latter depending on many other factors (such as discharge, solar radiation, nebulosity, wind, etc.). Air temperature can be predicted over a 7-day period with an accuracy of 80%. If this period further increases, the accuracy drops. The place was selected due to its proximity to sensitive locations: ecological areas in Romania and Bulgaria, irrigation stations, and the only nuclear power plant in Romania, for which the cooling water for the reactor is supplied from the Danube River.

The ANN model used in the paper builds on the Levenberg–Marquardt feedforward backpropagation algorithm, as it is considered by researchers to outperform other machine learning algorithms [23,27]. The model provides a useful tool for Danube River water temperature prediction at Chiciu–Călărași, offering a valuable input for the nuclear power plant at Cernavoda. Knowing in advance the temperature of the water from the Danube that is used as cooling water, the power plant can be safely operated.

2. Materials and Methods

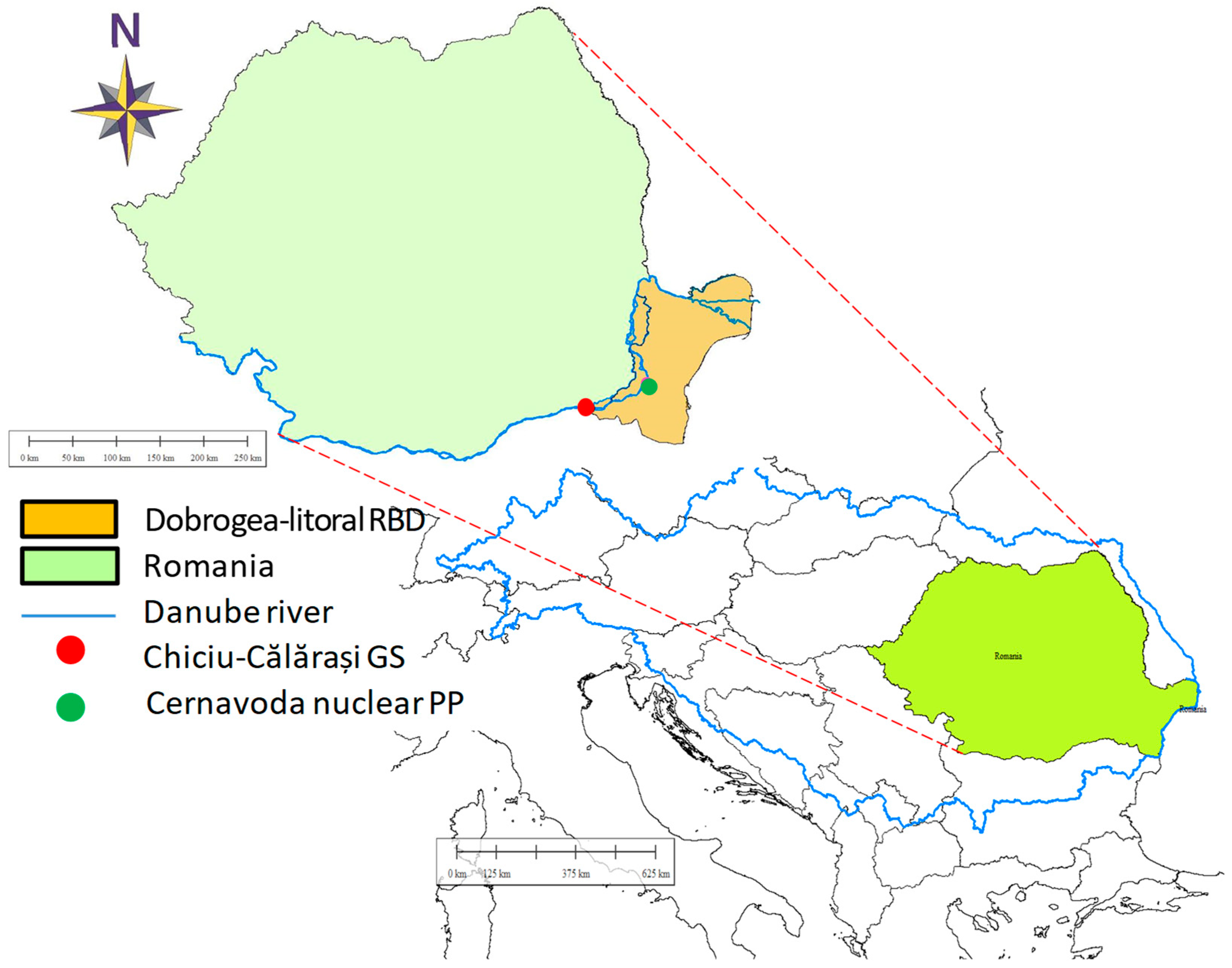
2.1. Study Area and Hydrometeorological Data

The Danube River is the second-longest fluvial system in Europe (about 11% of the continent’s surface), flowing through 19 countries. The ecosystems of the Danube are subject to increasing human impact. Its lower stretch can be divided into four sections from Baziaș to the downstream Danube River mouth (rkm 0) into the Black Sea:

• Baziaș (rkm 1072)–Drobeta Turnu Severin (rkm 931);
• Iron Gate II (rkm 863)–Călărași (rkm 370);
• Călărași–Ceatal Ismail (delta apex at rkm 80);
• Ceatal Ismail–Black Sea.

The upstream mountain section Baziaș–Drobeta Turnu Severin is characterized by a narrow and deep channel, with high flow velocities. Downstream, the Iron Gates II dam (Iron Gates–Călărași section), the river channel becomes wider, less deep, with major islands and embankment dikes along the left Romanian bank floodplain, modifying the hydrodynamic regime.

The tectonic uplift from river km 370 (from the river mouth at the Black Sea), near Călărași, is considered the cause for the abrupt bend in the river course towards the north and a reduced bed slope of the channel. These led to a split of the river channel into two branches, and to diminished velocities after the split [28]. The S–N-oriented reach of the Danube (Figure 1) is the border between the Dobrogea–Litoral River basin district (RBD) and the rest of Romania.

The most downstream section (Ceatal Ismail–Black Sea) is the Danube delta, with three main branches, where the hydrodynamics and water quality parameters change dramatically.

While mean annual precipitation in Romania is about 637 mm, Dobrogea–Litoral is the region with the lowest precipitation (less than 400 mm mean annual rainfall), with the smallest density of surface water resources. In terms of air temperature, the Dobrogea region has an arid climate with mean multiannual temperatures of 10–11 °C, compared to the 8.5–9 °C towards the central and northern parts of the country. This is why this region is usually affected by drought during summers.

Chiciu–Călărași represents an important gauging station (GS) on the left bank of the Danube River. Measured data consist of daily water temperatures at Călărași GS, where the mean multiannual water temperature is 14.2 °C, with annual variation between 0 and 28 °C [29]. The mean multiannual flow at Chiciu GS (rkm 371) is 6107 m³/s [30].

The mean multiannual air temperature in Călărași City is 11.2 °C, with the lowest value on 8 January 1938, of −30 °C, and the highest on 10 August 1951, of 41.4 °C. Mean annual precipitation is 500 mm. Summers are hot in the area, with the hottest July in history being in 2012, when the mean monthly temperature was 27.1 °C, with a peak temperature of 42 °C. Solar radiation in the area is high at 1454 kW/m² [29].

In addition to the natural climate, the industrial, agricultural, and transport activities performed along the Danube River heavily affect the water’s temperature and the other physical and chemical parameters.

A study on the lower Danube River conducted over 16 years showed an increasing trend in the water temperature, specifically identified at the Chiciu–Călărași gauging station [31].

These influences should be closely monitored due to the proximity of many of the Natura 2000 sites, located on both banks of the Danube River (Figure 2). Some of the natural sites in the proximity of Chiciu–Călărași GS in Romania are Iezerul–Călărași, Danube–Ostroave, Oltenița–Ulmeni, Danube–Oltenița, Valea Mostiștea, Galațui Lake, Ciocănești–Danube, Oltenița–Mostiștea–Chiciu, Eseschioi forest, Bugeac Lake, Borcea Danube branch, Canaraua Feții forest–Iortmac, Oltina Lake, and Vederoasa Lake. In Bulgaria, in the proximity of Silistra (the city on the right bank of the Danube, across from Călărași) the Natura 2000 sites are Srebarna and Ludogorie, Pozharevo–Garvan, and Ostrov–Chayka.

The Oltenița–Mostiștea–Chiciu site is located in the central–south area of Călărași county and has an area of 11,540 hectares. Its ecological value resides in the wetlands along the Oltenița–Călărași reach of the Danube River, renowned for its diverse habitats. The Srebarna Nature Reserve, including the Srebarna Lake, extending over 600 hectares, is an important wetland adjacent to the Danube River, being listed in the World Heritage and protected under the Ramsar Convention and as a UNESCO Biosphere Reserve.

High water temperatures during summers affect the natural areas, irrigation processes, and the cooling of the nuclear power plant reactor. It is important to know several days in advance what the water temperature will be, so that the power plant operators are able to take the appropriate measures. This is because such a reactor needs several days to be stopped. For example, due to the drought in the summer of 2003, Unit 1 of the Cernavoda nuclear power plant (NPP), with a power of 706 MW, was stopped on 23 August, when the Danube water levels dropped (below 2.5 m above Baltic Sea level), discharge reached 1800 m³/s, and water temperatures increased over the restricted levels.

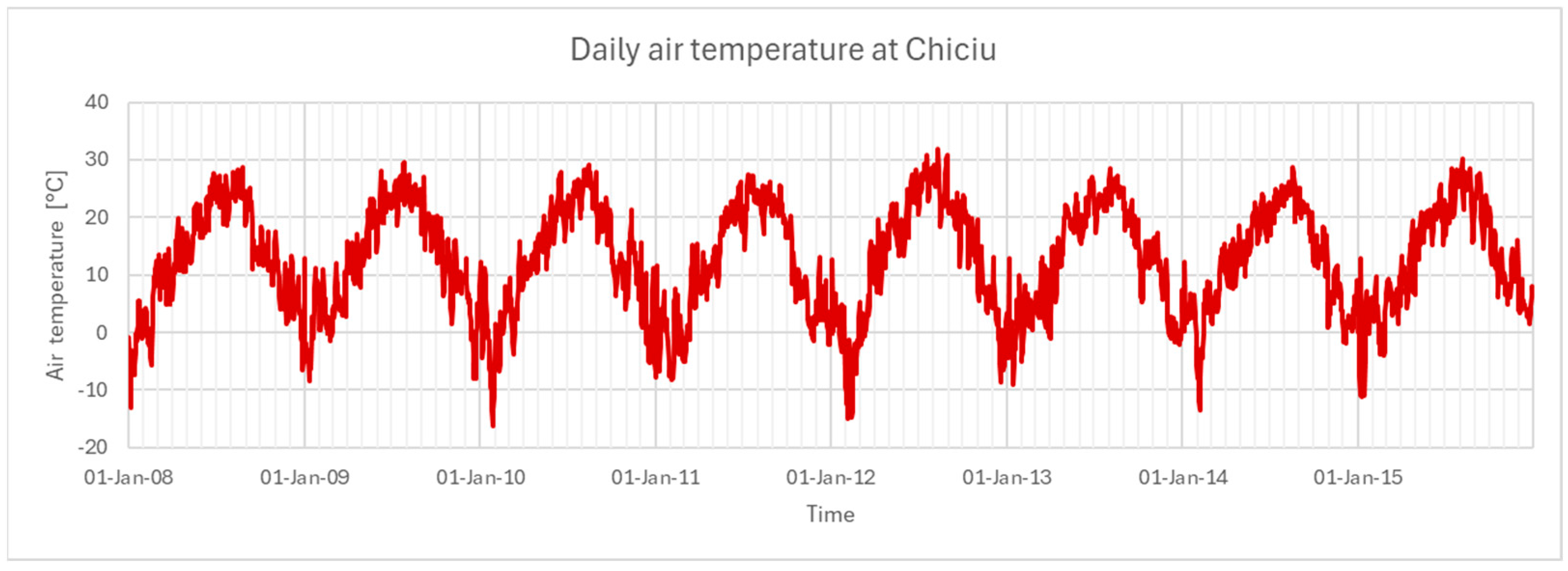
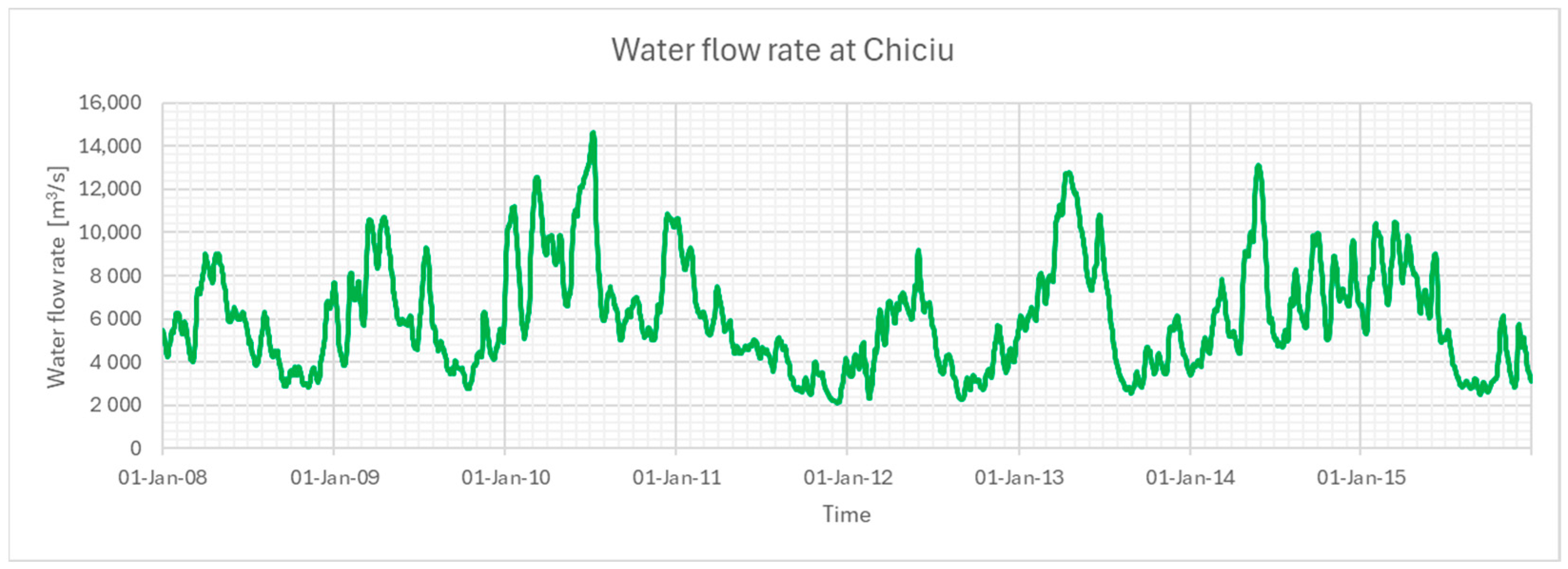
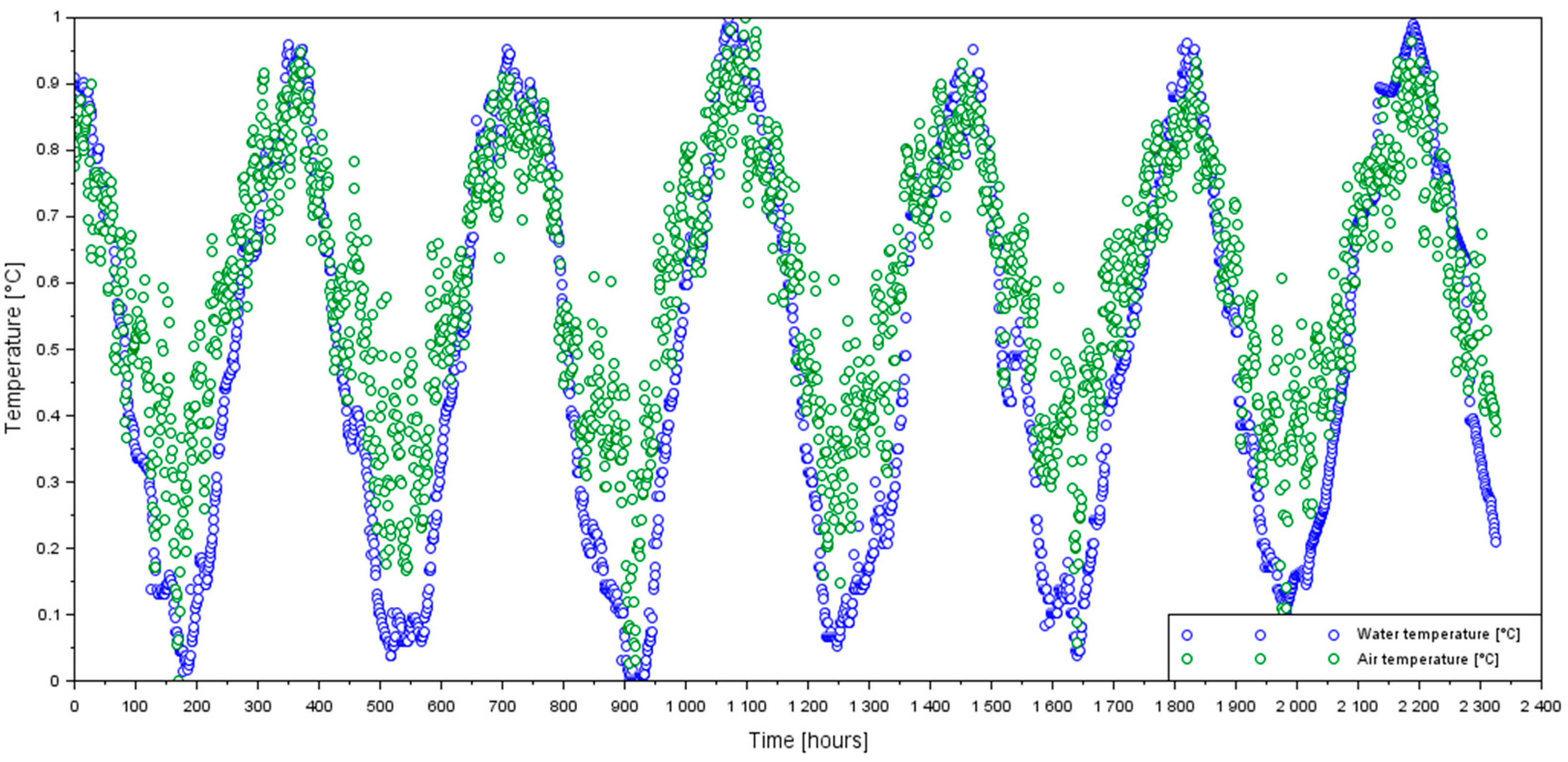
2.2. Air and Water Data

The data range period to forecast the Danube water temperature was 2008–2015, selected to cover both extreme flood (2010, 2013, and 2014) and drought (2011 and 2015) events, in addition to the normal hydrological years.

Hourly mean air temperature data for the period 2008–2015 were downloaded from OpenWeather [32] and averaged to obtain daily mean values. Daily Danube River temperature data were obtained from the edelta.ro website [33], while discharges were provided by the National Administration “Romanian Waters” for the same period.

Figure 3 presents the daily mean variation in air temperature between 1 January 2008 and 31 December 2015 at Chiciu. Figure 4 and Figure 5 show the daily river water discharge and temperature at Chiciu–Călărași, respectively, for the same period.

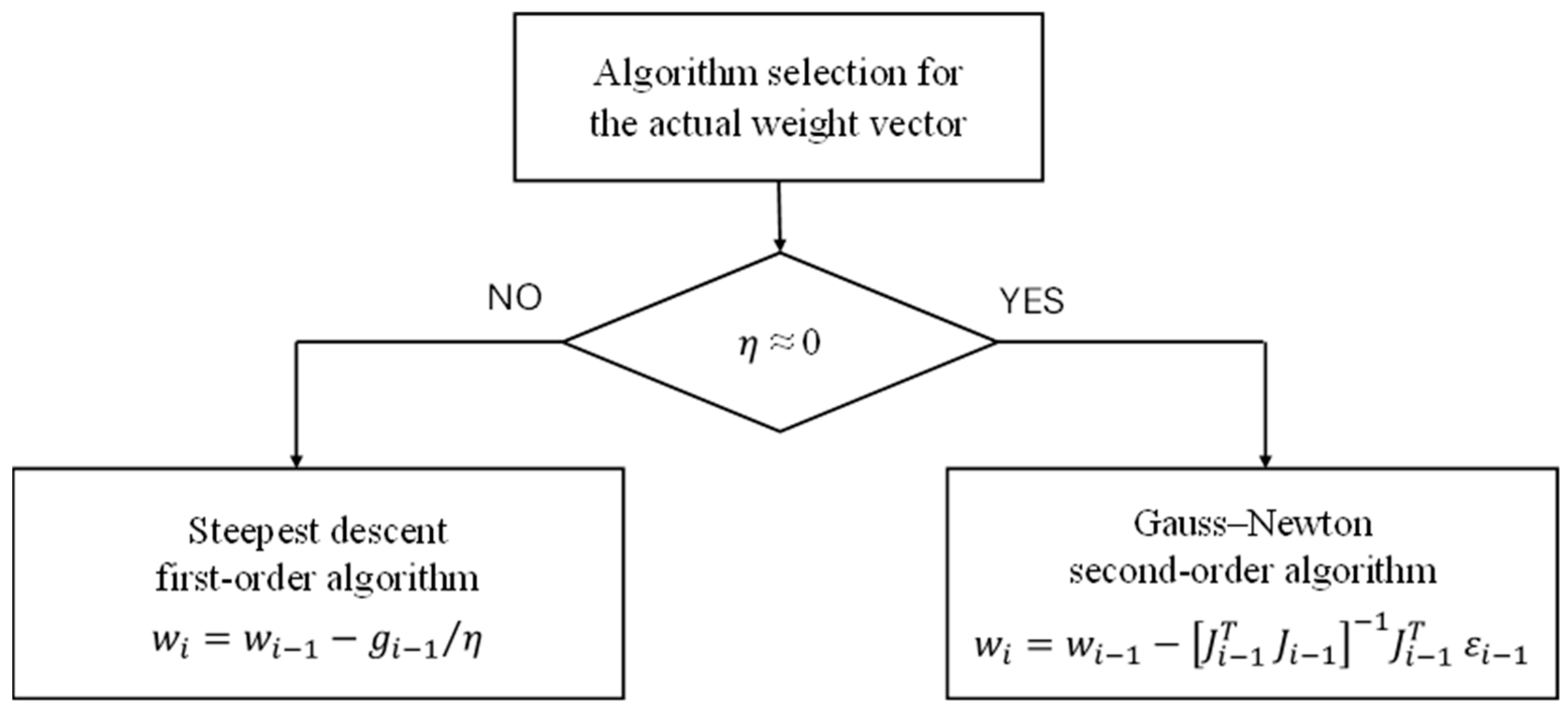
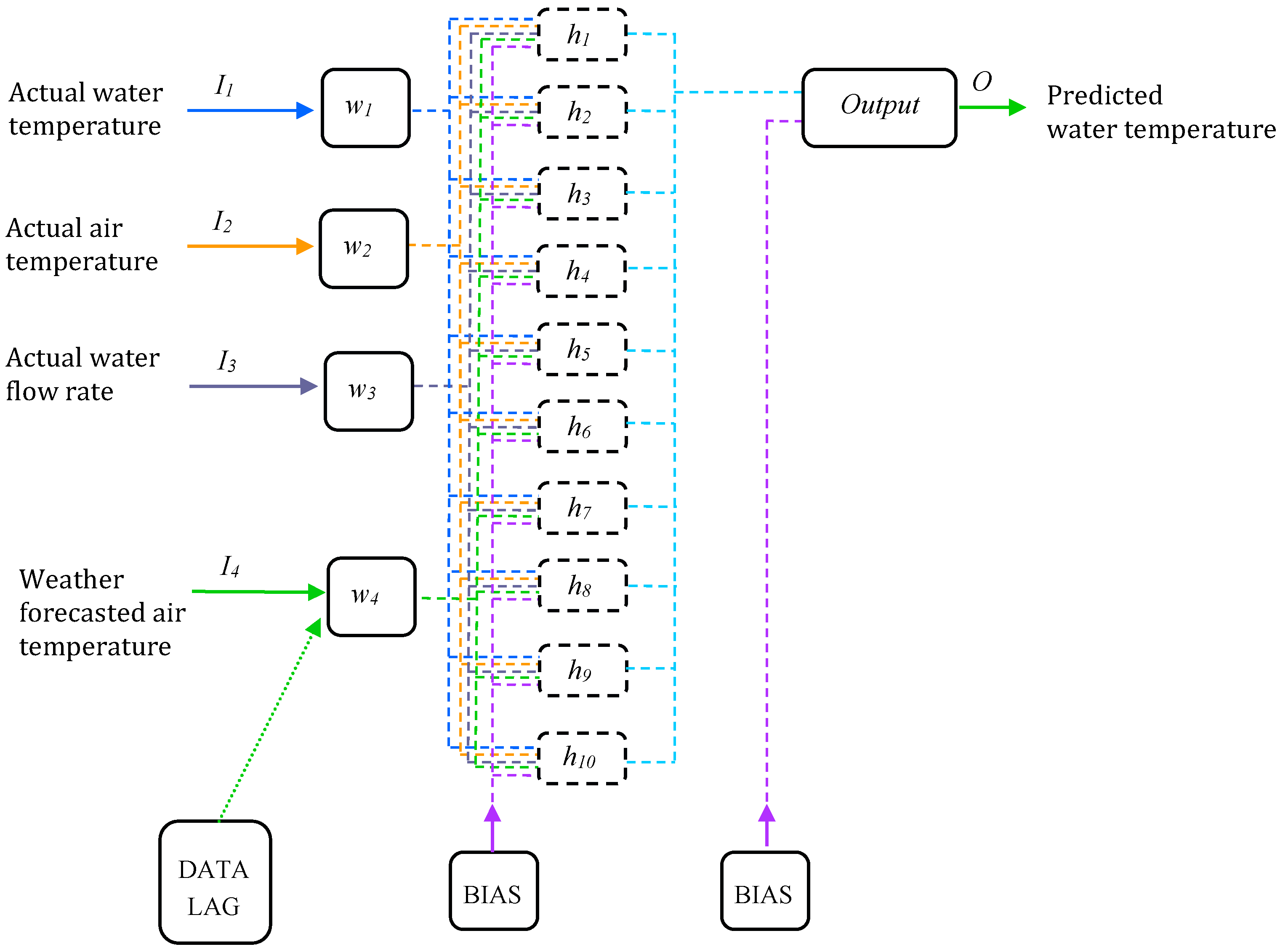
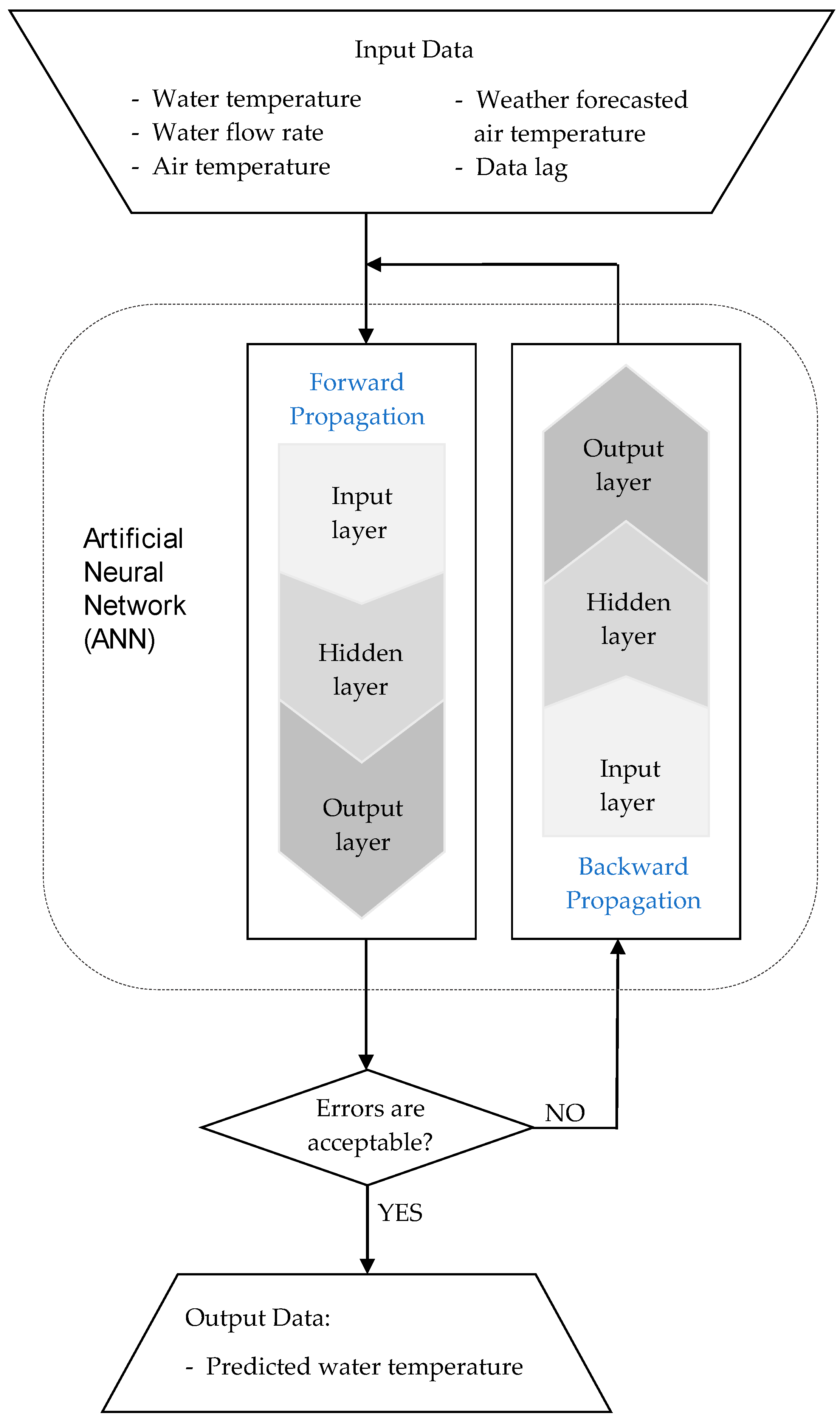
2.3. ANN Arhitecture

An ANN contains three or more layers: one input layer, at least one intermediate (hidden) layer, and one output layer. In turn, these layers include a number of neurons. The neurons of the input layer are connected to the input parameters, and the neurons from the output layer correspond to the output parameters. The number of hidden layers, and their number of neurons, depend on the ANN model. To each neuron, from any of the layers, a weight is assigned. The value of the weight ranges from 0 to 1, showing the influence the neuron has over the network.

To make a prediction, the ANN passes sequentially through all the layers, starting from the input layer towards the last output layer (Figure 6). Through this process, the neurons generate output information by using the input information received from the neurons within the previous layer, in accordance with their assigned weights. A bias is also introduced as an overall adjustment of the weights to better fit the data.

The output of the neurons from a layer is given by a function that depends on the inputs and a bias:

$$Out=f\left({\sum }_{i=1}^n{In}_i·w_i+BIAS\right)$$

(1)

where f is the activation function used by the ANN algorithm to calculate the output value; n is the number of input values from previous neurons; ${In}_i$ are variables from the input that are connected to the neurons; $w_i$ are the weights associated with each input variable; and BIAS is a bias value.

The neurons that belong to the same layer are calculated by the same activation function, independently, without influencing each other [34].

To allow high-accuracy ANN results, the weights $w_i$ are calculated by training the network through Feedforward Backpropagation (FB) [23,35]. This process includes forward and backward calculation of the weights until the error between the actual and ANN-predicted values is acceptable. Using an initial estimation of the weights, by forward propagation (from the input layer towards the output layer), the errors are calculated using an algorithm based on second-order derivatives. Next, by backward propagation (from the output layer towards the input layer), the errors are used to adjust the weights using an algorithm based on first-order derivatives. These forward–backward propagation iterations are repeated until the condition of maximum prediction error is met [36].

The Levenberg–Marquardt (LM) algorithm is a good choice for training ANNs by FB based on its advantages of being a robust algorithm with good optimization characteristics. To adjust and refine the weights, the LM algorithm uses linear interpolation between two methods: the gradient descent method (the steepest descent method) and the Gauss–Newton method [37,38].

If the calculated weights are far from the optimum values and the gradient is steep, a first-order algorithm is used, due to its very good convergence [39]. Although it has a slow convergence, it is a simple algorithm that facilitates the convergence to the optimum values of the weights. Therefore, the LM algorithm uses the gradient descent method to reduce the sum of the squared errors and adjust the weights towards the steepest descent direction. When the weights come closer to their optimum values, the LM algorithm uses the Gauss–Newton method, a second-order algorithm. This algorithm has a very fast convergence because it has the capability to adjust its step sizes while evaluating the curvature of the error surface pending on the quadratic approximation of the error function. Otherwise, the scheme becomes divergent.

The LM algorithm is therefore used to develop the ANN forecast water temperature model. Thus, the relationship linking a Hessian and a Jacobian matrix in the LM algorithm is [38,40]

$$∆w_{i,i-1}={w_i-w}_{i-1}={\left[J_{i-1}^T J_{i-1}+\eta I\right]}^{-1}{J}_{i-1}^T {\epsilon }_{i-1}$$

(2)

where i is the actual iteration; $∆w_{i,i-1}$ is the change in the weight vector between two consecutive iterations; $w_i$ is the actual weight vector; $w_{i-1}$ is the previous weight vector; J is the Jacobian matrix with the derivative of the network error; ${\epsilon }_{i-1}$ is the error vector given by the difference between the actual and the previous output; η is the combination coefficient that can be zero or positive; and I is the identity matrix.

From (2), the actual weight vector can be written as

$$w_i=w_{i-1}-{\left[H_{i-1}+\eta I\right]}^{-1}{J}_{i-1}^T {\epsilon }_{i-1}$$

(3)

where H is the Hessian matrix, defined as

$$H=J_{i-1}^T{J}_{i-1},$$

(4)

The selection between two algorithms is influenced by the η parameter [41]. The flowchart in Figure 7 summarizes the training selection algorithm of the ANN model. When η tends to zero, the Gauss–Newton second-order algorithm is used, while for larger η values the steepest descent first-order algorithm applies. In Figure 7, $g_{i-1}$ is the first-order derivative of the total error vector and 1/η represents the step size (the learning coefficient).

The training algorithm runs until the output weights show predefined acceptable results.

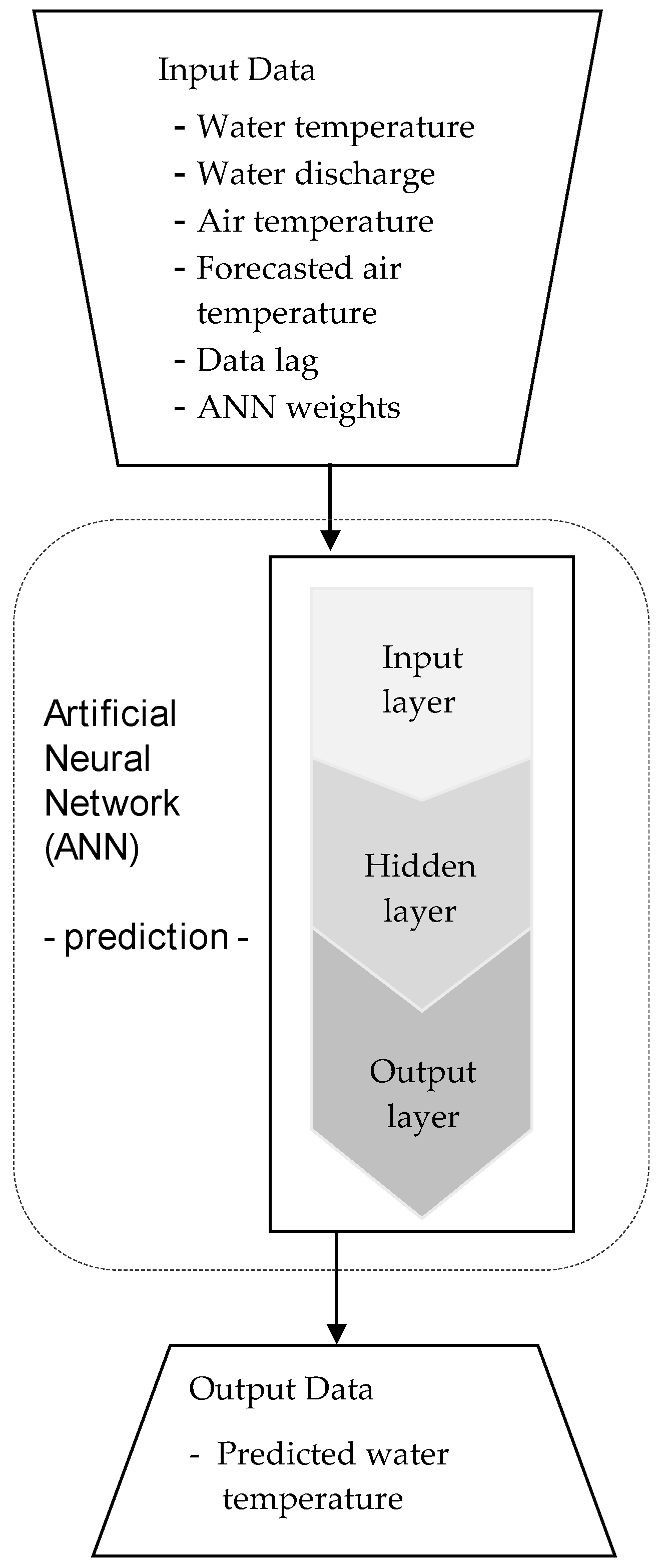
2.4. ANN Danube Water Temperature Prediction Model at Chiciu–Călărași

Given the benefits provided by ANN models in predicting water temperature variation with respect to time, a model was set up for the Danube River at Chiciu–Călărași GS. In this location, daily mean air and water temperatures, as well as water discharge values, were available for eight years (Figure 3, Figure 4 and Figure 5), making it possible to develop a reliable neural model.

In addition to air temperature, which is the dominant physical quantity that has the greatest influence on river water temperature, discharge is the second critical factor exerting significant impact on water temperature [5]. These two input variables together with the water temperature are suitable and adequate for a sound ANN prediction [42]. As well, as previously mentioned, the ANN can handle the noisiness of the meteorological data [19,20,21].

Figure 8 presents the chosen architecture of the ANN forecasting model for the Danube River temperature. The network has three layers: the input layer, the intermediate hidden layer, and the output layer. The input layer contains four neurons. These designate the actual data for air and water temperature, flowrate, and the weather forecasted air temperature. A lag time is linked to the weather forecasted air temperature neuron.

For the type of problem to be solved, involving the Levenberg–Marquardt algorithm, one hidden layer is considered to be sufficient for the ANN architecture [43]. The intermediate hidden layer contains ten neurons connected to the input and the output layer. The number of intermediate neurons was determined by trial and error to obtain good results and also avoid overfitting.

In the output layer is the neuron corresponding to the predicted water temperature, having the same lag time as the weather forecasted air temperature.

The input is represented by a matrix of size 5 × 2335 for the training stage and 4 × 584 for the testing stage. The entire data range consists of 2919 value sets (meteorological and hydrological), chronologically ranked. In the training stage, the four input parameters (Figure 8) and the output parameter (predicted water temperature) are used. In the testing stage, only the four input parameters are used, with the output parameter (predicted water temperature) being computed.

The matrix stores the actual daily data as well as the forecasted data. The data lag is used to obtain the forecast with a specified delay. The parameters (I₁, I₂, I₃) are the terms of the matrix corresponding to the values of the actual day. The parameter I₄ and the output O (the forecasted ones) are terms of the matrix corresponding to a day in the future, specified by the data lag.

The Scilab open software (version 6.0.1) [44] was used to develop the ANN forecast model. The feedforward backpropagation simulation was performed in two steps. For the ANN training and weights computation the ann_ffbp_init(N,r) function was used, while for the ANN run and temperature prediction the ann_FFBP_run(X,W) function was used. Figure 9 and Figure 10 present the flowcharts for the ANN training with the feedforward backpropagation algorithm and the ANN prediction steps.

2.5. Input Data for the ANN Model

The input data for the ANN model consists of 2919 daily mean values for each of the three parameters (air and water temperature and discharge; Figure 3, Figure 4 and Figure 5), spanning 8 years.

To test the prediction capability of the model, a data lag of seven days was considered feasible for a river like the Danube, since seven days is a threshold between short- and long-term forecasting of air temperature. Beyond this threshold, the prediction accuracy drops significantly [45,46].

The available data were split into two different sets: 80% (2335 values) for training and the remaining 20% (584 values) for testing. The 80% used for training were selected as the first ones from the investigated 8-year period, since they contained the whole range of discharge and temperature data. The normalized input data were computed using

$$x_k^N={\displaystyle \frac{x_k-x_{MIN}}{x_{MAX}-x_{MIN}}},$$

(5)

where $x_k^N$ is the normalized value, and $x_{MIN}$ and $x_{MAX}$ are the minimum and maximum values of $x_k$, respectively, from the entire study period. The interval ranges for the considered variables were obtained from the available data: (0.1–28.4) °C for the Danube water temperature; (−16.22 to 31.82) °C for air temperature; and (2120–14,600) m³/s for the discharge.

Figure 11 and Figure 12 depict the normalized variation with respect to time for each of the considered values for training.

The discharge presents a much more pronounced variability over the study period as compared to the air and water temperatures.

2.6. Simple Statistical Models for Danube River Temperature Prediction

To estimate the accuracy and the usefulness of the ANN model, four simple models were used.

2.6.1. Statistical Model 1

The predicted water temperature is assumed to have the same value as the actual river water temperature, and therefore the linear dependence is identified by the first bisection line:

$$t_P=t_M$$

(6)

where $t_P$ is the predicted water temperature considering the given lag time, in °C, and $t_M$ is the actual measured water temperature, in °C.

The model does not consider the influence of air temperature and discharge variations during the lag time period (a week).

2.6.2. Statistical Model 2

The predicted water temperature is also assumed to have a linear dependence, given by

$$t_P=a_{0\_2}+{a_{1\_2}·t}_M,$$

(7)

where $a_{0\_2}$ and $a_{1\_2}$ are the intercept and the slope that define the linear regression.

Also, the model neglects the air temperature and discharge variability.

2.6.3. Statistical Model 3

The water temperature variation linearly depends on the air temperature variation:

$${∆t}_w=a_{0\_3}+{a_{1\_3}·∆t}_{air},$$

(8)

where $a_{0\_3}$ and $a_{1\_3}$ are the coefficients that define the linear regression line, and ${∆t}_{air}$ is the air temperature variation, defined by

$${∆t}_{air}=t_{P\_air}-t_{M\_air},$$

(9)

where $t_{P\_air}$ is the predicted air temperature, in °C, and $t_{M\_air}$ is the actual measured air temperature, in °C.

Using Equations (8) and (9), the predicted water temperature, in °C, is

$$t_P=t_M+{∆t}_w,$$

(10)

The model neglects the discharge variation during the lag time period (a week).

2.6.4. Statistical Model 4

The water temperature change is calculated by multiple linear regression, depending on air temperature and discharge variations:

$${∆t}_{w\_4}=a_{0\_4}+{a_{1\_4}·∆t}_{air}+a_{2\_4}·Q,$$

(11)

where $a_{0\_4}$, $a_{1\_4}$, and $a_{2\_4}$ are the coefficients that define the multiple linear regression, and $Q$ is the discharge, in m³/s.

The predicted water temperature results from adding the water temperature variation ${∆t}_{w\_4}$ to the actual water temperature $t_M$, similar to (11).

2.7. Evaluation Metrics

To evaluate the model performance, the following indicators were used:

• The correlation coefficient (R):

$$R={\displaystyle \frac{n\sum t_{Mi}·t_{Pi}-\sum t_{Mi}·\sum t_{Pi}}{\sqrt{n\sum t_{Mi}^2-{\left(\sum t_{Mi}\right)}^2}·\sqrt{n\sum t_{Pi}^2-{\left(\sum t_{Pi}\right)}^2}}}$$

(12)

where $t_{Mi},t_{Pi}$—measured and predicted water temperatures, in °C; $n$—the number of values;

• The root mean square error (RMSE),

  $$RMSE=\sqrt{{\displaystyle \frac{\sum {\left(t_{Mi}-t_{Pi}\right)}^2}{n}}},$$

  (13)

  representing the standard deviation of the predicted value;

• The root mean square error corresponding to a confidence level of 95% (RMSE 95%):

  $$RMSE 95\%=2·RMSE.$$

  (14)

3. Results and Discussion

A linear regression algorithm was used to assess the prediction accuracy of the water temperature during the training and validation steps.

As the ANN model uses normalized values, the resulting values are presented both as normalized and dimensional values. Relation (6) was used for normalizing the input parameters and conversely to obtain the dimensional value of the output water temperature.

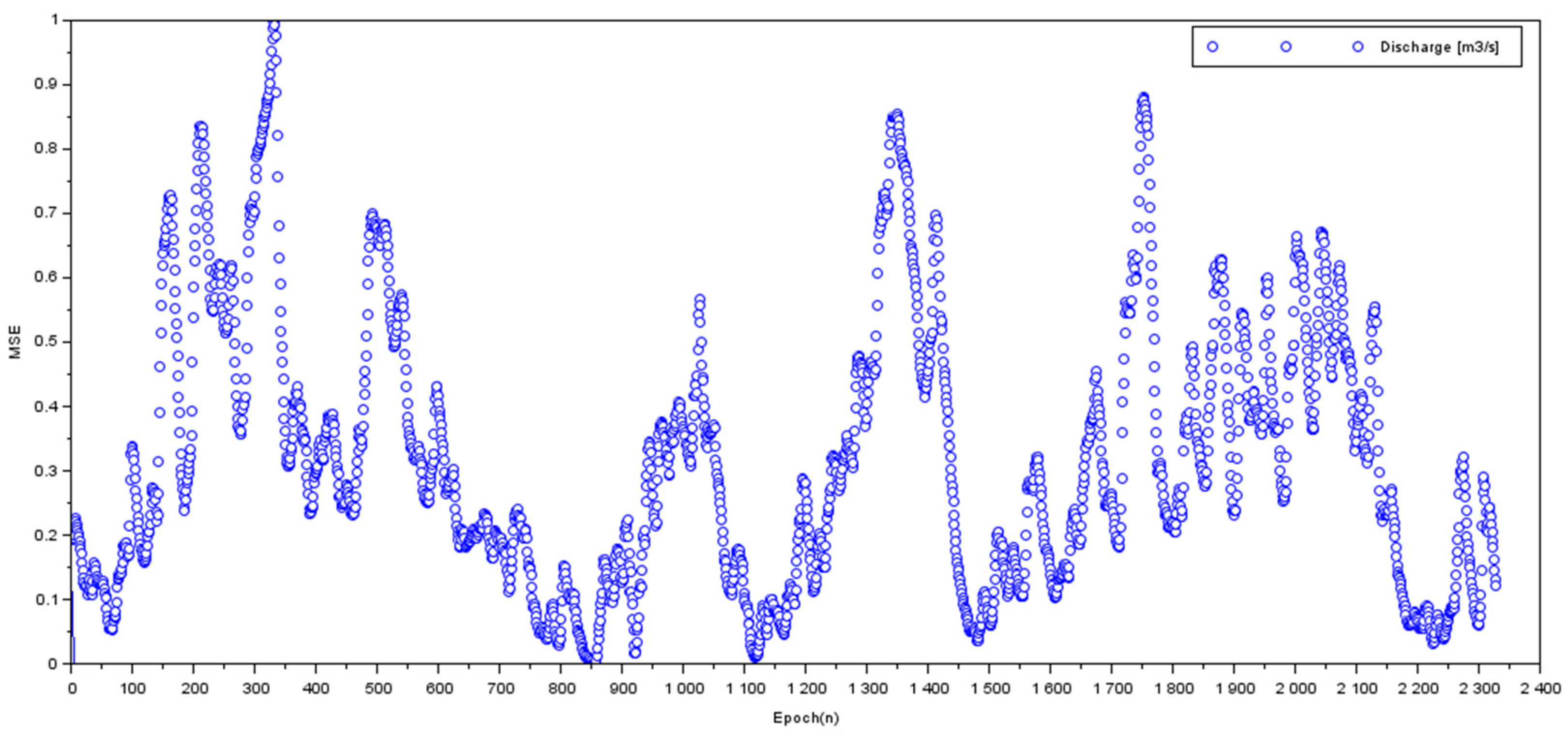
3.1. Results of the Training Stage of the ANN Danube Water Temperature Model at Chiciu–Călărași

As shown by the equations in Figure 13 (normalized temperature values) and Figure 14 (temperature values), a very good correlation is established between the input (measured) temperatures, $y_M$, and the predicted ones, $y_P$, one week later. The two values are almost equal, and the Pearson correlation coefficient has a very high value, R = 0.993, showing that the regression is statistically significant. The prediction regression line fits on the bisection line, $y_P$, getting very close to $y_M$.

For the training stage the standard deviation of the water temperatures predicted values, the RMSE, is 0.954 °C, showing that the model has a good performance. Considering a 95% confidence level, the RMSE is 1.908 °C.

3.2. Results of the Testing Stage of the ANN Danube Water Temperature Model at Chiciu–Călărași

Similar results were obtained by evaluating the model’s prediction capability when inputting new data. The equations in Figure 15 and Figure 16 (normalized temperature values and temperature values, respectively) show an even better correlation between the measured and predicted temperatures 7 days later. The data fit close to the bisection line, with a Pearson correlation coefficient of R = 0.995.

In Figure 15, the regression line presents a deviation from the bisection, one that increases with increasing temperature.

The predicted water temperatures a week later mimic the actual measured data, as depicted in Figure 17. They fall within 68% and 95% confidence intervals, corresponding to RMSEs of 0.803 °C and 1.606 °C, respectively. The small values of the standard deviation of the predicted values show the small differences between the predicted and the actual water temperatures values.

3.3. Comparison of the Testing Stage of the ANN Danube Water Temperature Model with Simple Statistical Models

Table 1. Statistical metrics of prediction water temperature models.

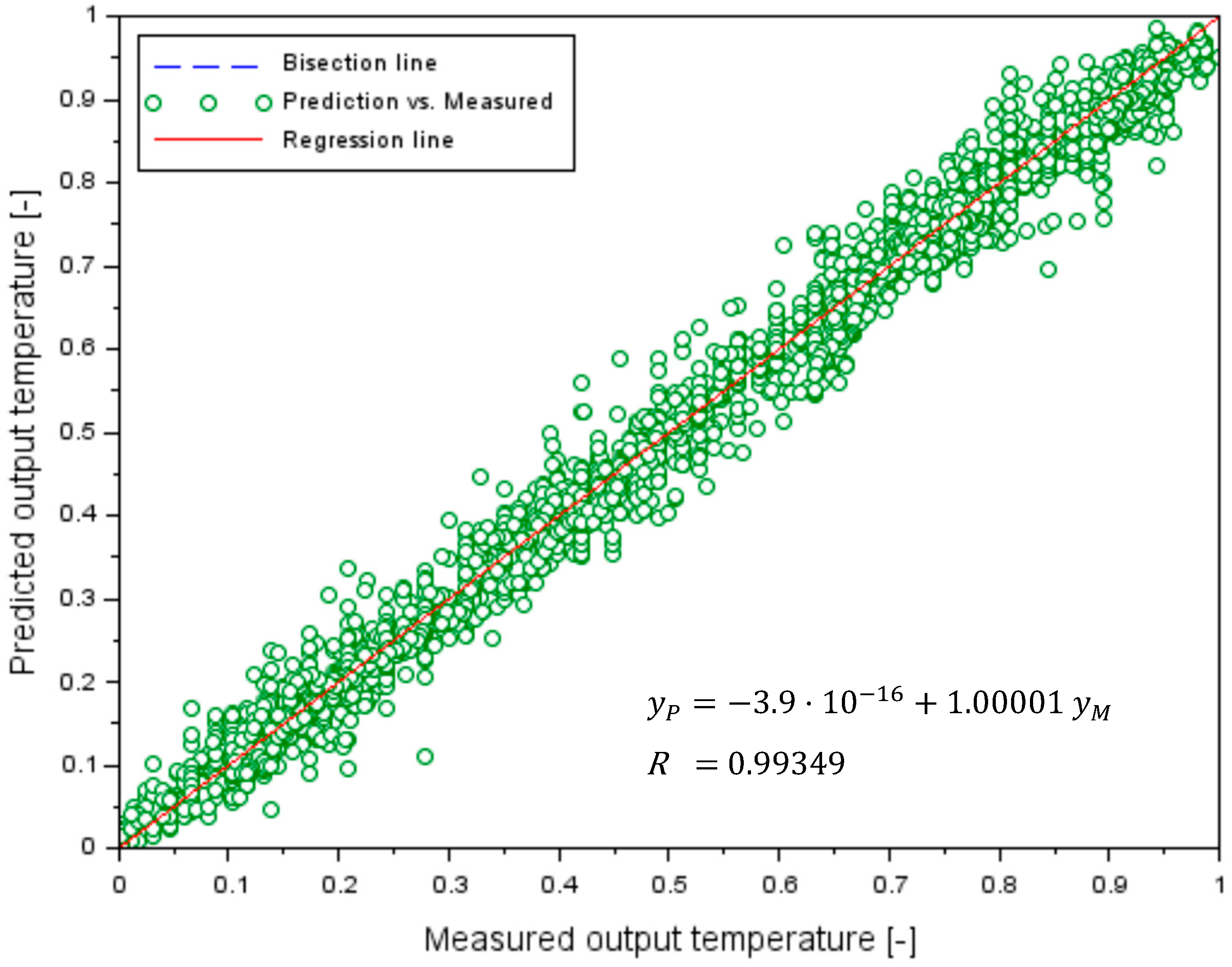
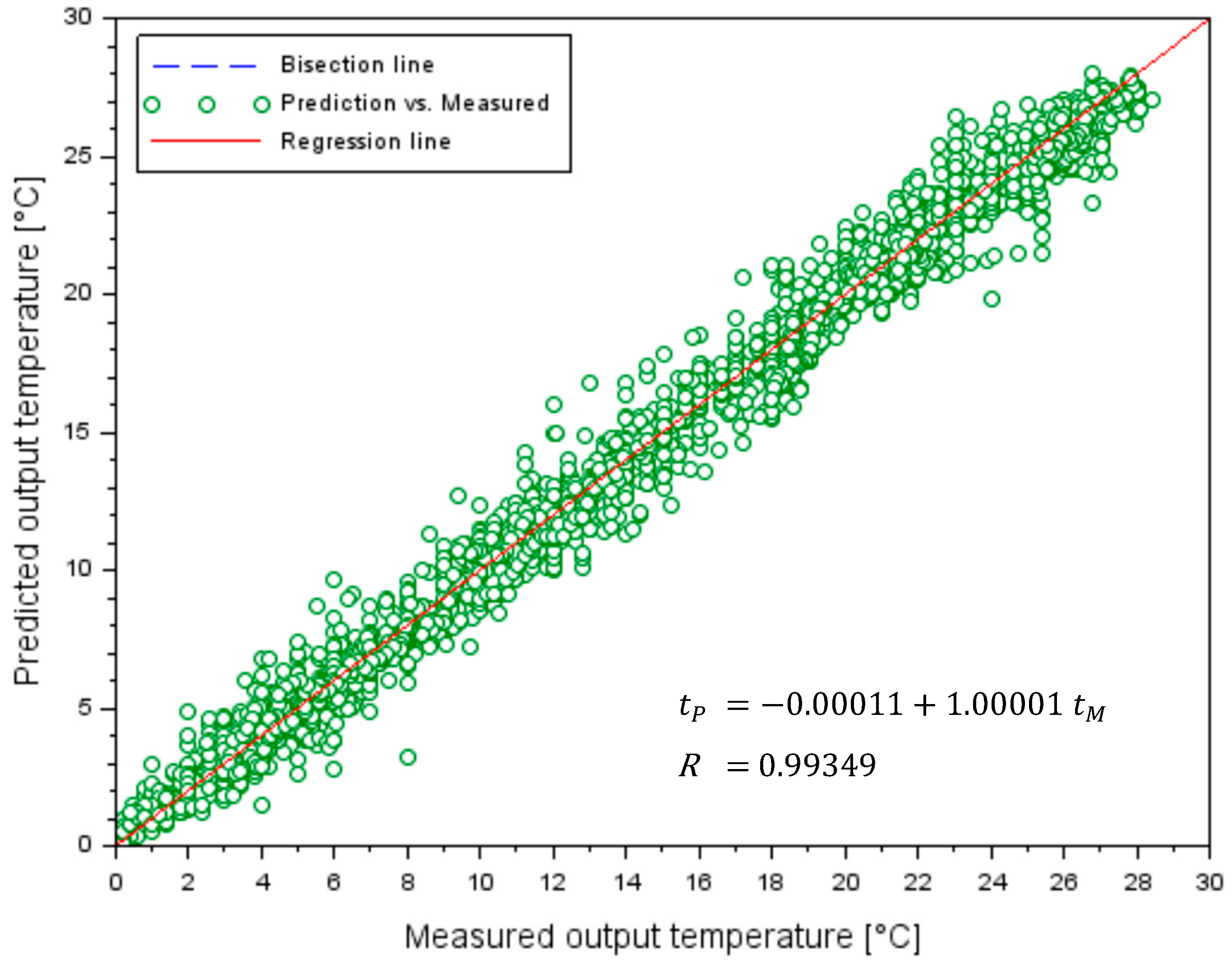
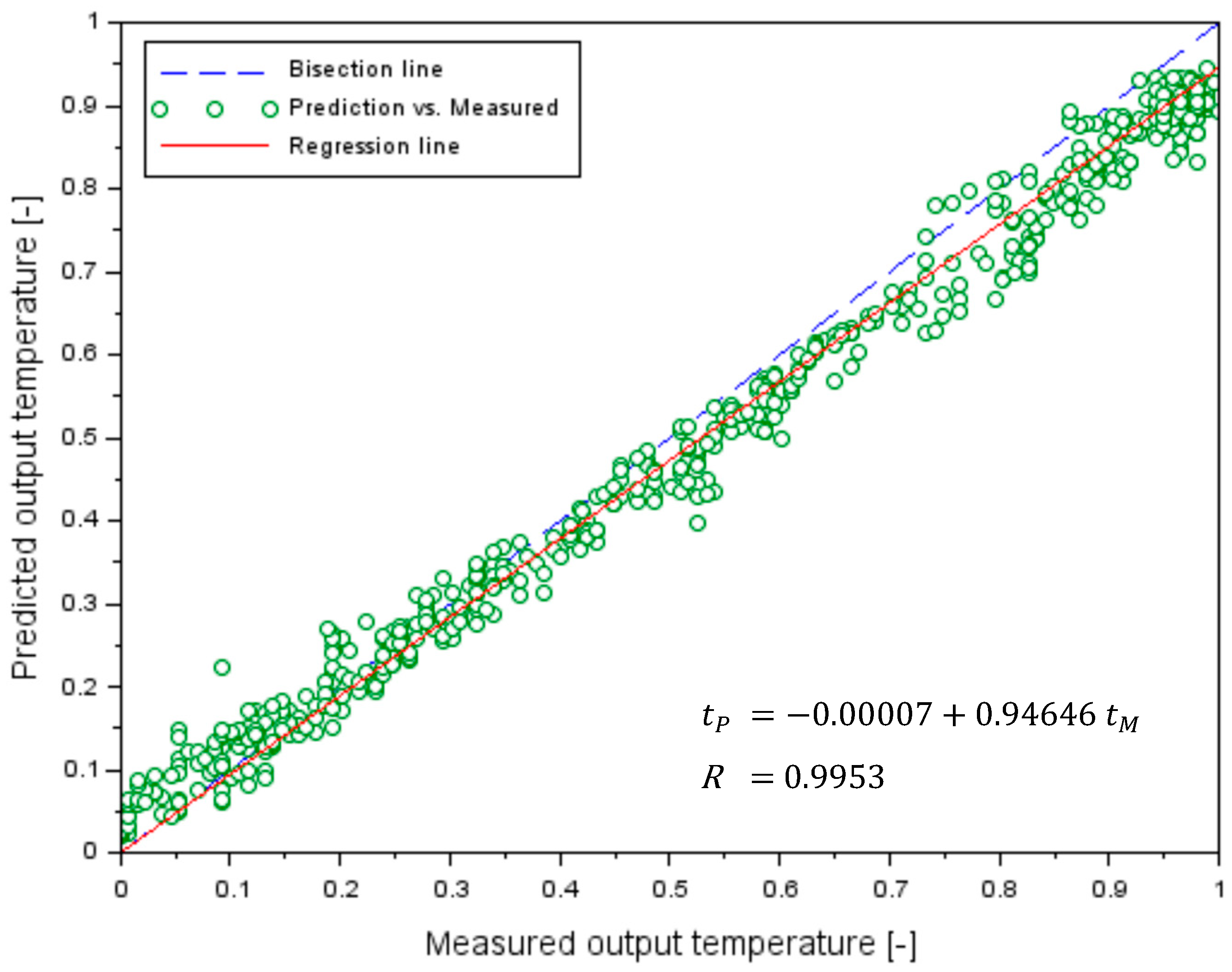
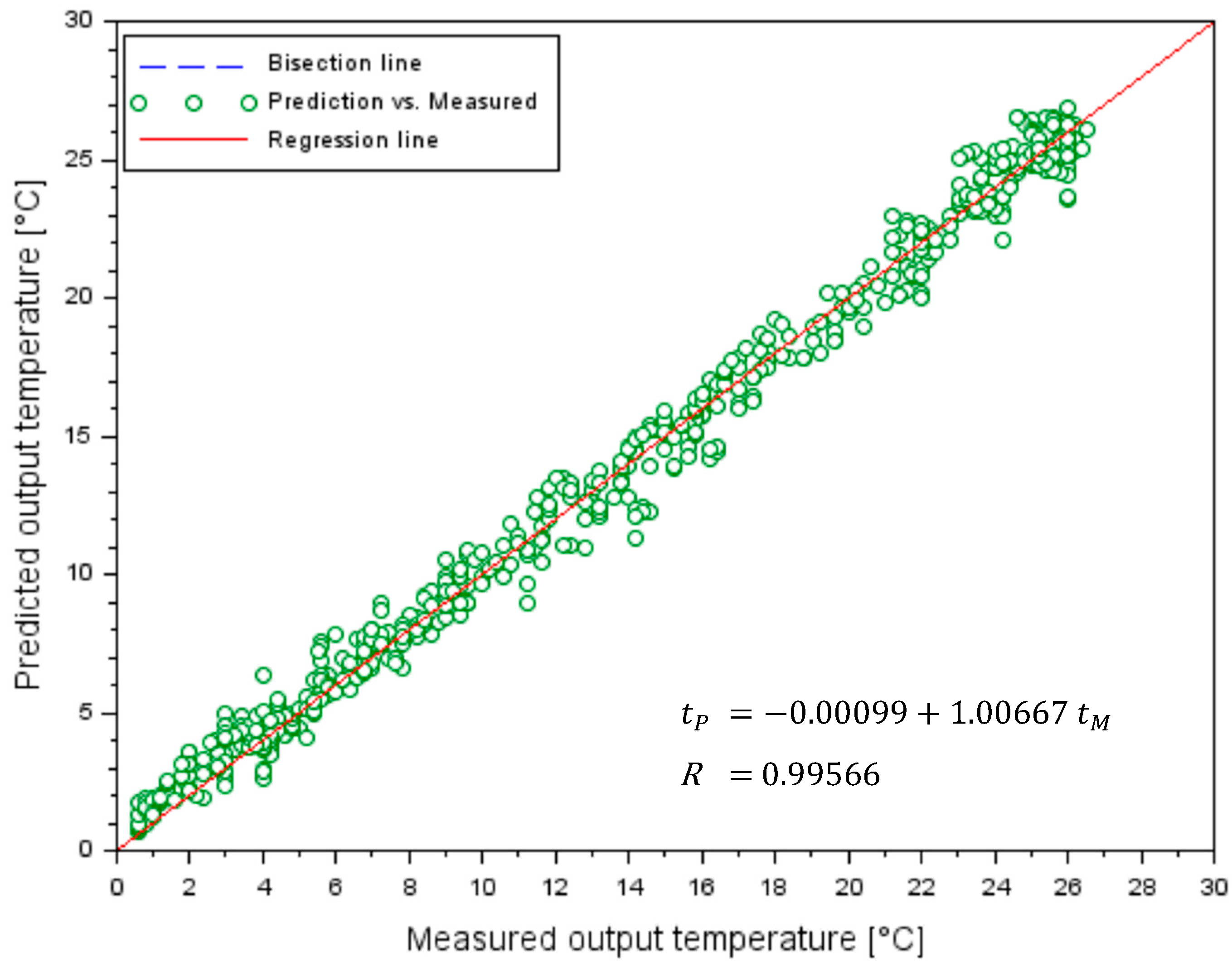
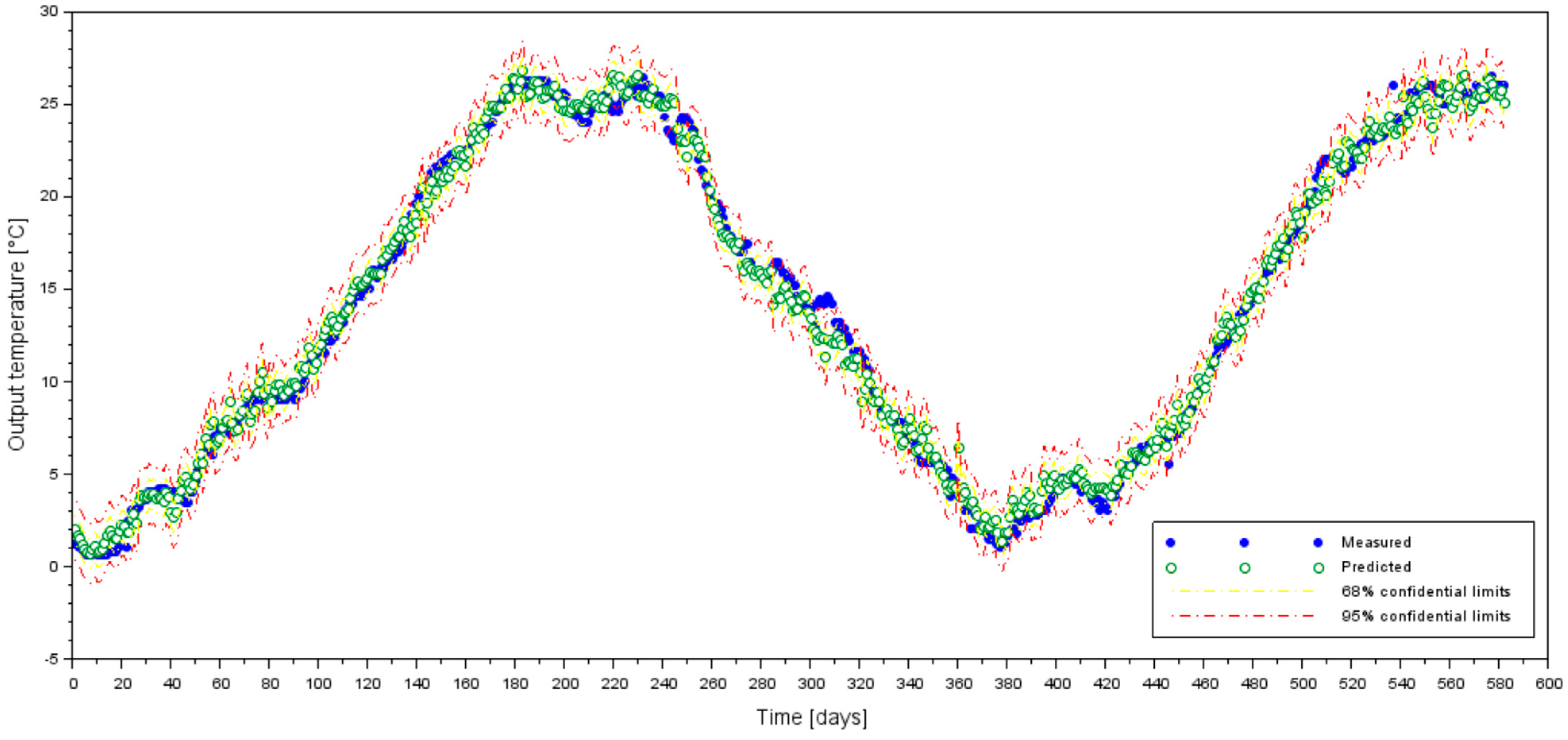
Model	Predicted Water Temperature, in °C	R [-]	RMSE [°C]
ANN	$t_P=ANN\left(t_M,t_{M\_air},Q_M,t_{P\_air}\right)$	0.995	0.803
Model 1	$t_P=t_M$	0.989	1.288
Model 2	$t_P=-0.00119+{1.02082t}_M$	0.989	1.283
Model 3	$t_P=t_M+1.231981-2.702\left(t_{P\_air}-t_{M\_air}\right)$	0.578	13.159
Model 4	$t_P=t_M+0.10155+0.06295\left(t_{P\_air}-t_{M\_air}\right)+0.01168Q$	0.989	1.217

presents the results provided by the ANN model and simple statistical models. For each model, the correlation coefficient (R) and the root mean square deviation at confidence levels of 68% and 95% (RMSE and RMSE 95%) are computed, with the ANN showing the highest performance.

The findings show that the ANN model outperforms all the other statistical models, having the highest R and the lowest RMSE. Among the statistical models, a better performance is obtained if only water temperature or if water temperature and discharge are considered. This can be attributed both to the high thermal inertia of water and to the large and unpredictable air temperature variations from one week to another. The weak correlation between the water and air temperature variation leads to a high RMSE.

In

Table 2. Comparison of the ANN Danube Water Temperature Model with other models.

Reference	Model	Training		Testing
		R	RMSE [°C]	R	RMSE [°C]
[47]	WTAI 1	0.919–0.984	1.127–2.471	0.916–0.980	1.286–2.350
[11]	LSTMTE 2	0.931	0.567 °C	0.845	0.625 °C
[12]	FFNN 3 OPELM 4 AdaBoost 5 Bagging 6	0.938 0.937 0.939 0.941	2.634 2.655 2.618 2.580	0.941 0.942 0.941 0.939	2.605 2.583 2.615 2.660
Danube River ANN model	LMFB 7	0.993	0.954	0.995	0.803

¹ WTAI—integration of wavelet transformation with AI (multilayer perceptron neural network, adaptive neural fuzzy inference); ² LSTMTE—integration of long short-term memory and transformer encoder; ³ FFNN—feedforward neural network; ⁴ OPELM—optimally pruned extreme learning machine; ⁵ AdaBoost—adaptive boosting; ⁶ Bagging—bootstrap aggregating; ⁷ LMFB—Levenberg–Marquardt feedforward backpropagation.

, a comparison is made between the ANN Danube Water Temperature Model performance and other models from the scientific literature.

The values of the correlation coefficient and the mean square root error obtained with the ANN developed in this paper fall in the range of the values specified in the scientific literature, indicating a good performance among the other models.

4. Conclusions

The paper proposes an ANN model to estimate the Danube River Temperature at Chiciu–Călărași, located in the vicinity of many sensitive ecological areas (nature reserves) in Romania and Bulgaria. The temperature trend in this location was found by previous research to show a significant increase over the last sixteen years. If this trend continues, the thermal pollution potential will increase, which in turn will impact both aquatic and terrestrial ecosystems.

Moreover, due to the downstream proximity of Cernavoda nuclear power plant and its expected extension with two new units in the near future, two important risks arise. Firstly, the increased temperature of the water supplied as cooling water to the power plant could be ineffective in providing the necessary steam condensing pressure in the condenser. Secondly, the thermal pollution of the river will be worsened due to the heated water released from the power plant condenser. Therefore, knowing the water temperature a few days in advance will allow the power plant operators to take informed decisions.

The study used an eight-year data range, between 2008 and 2015. The input data consisted of observed air and water temperatures, discharges, and air temperature data provided by weather forecasts. The model ANN used to predict the Danube water temperature is based on the Levenberg–Marquardt feedforward backpropagation algorithm. The output of the ANN model is the forecasted Danube water temperature one week in advance. The water temperature was estimated with a root mean square deviation (RMSE) of 0.954 °C for training and 0.803 °C for testing.

The ANN Danube Water Temperature Model predicts the water temperature with good accuracy with a lag time of one week. This result is an encouraging start for extending the ANN model to include more parameters that can have a significant influence on water temperature. The method can also be tested for monitoring stations on other rivers, provided similar data sets are available.