TopEros: An Integrated Hydrology and Multi-Process Erosion Model—A Comparison with MUSLE
Abstract
1. Introduction
2. Materials and Methods
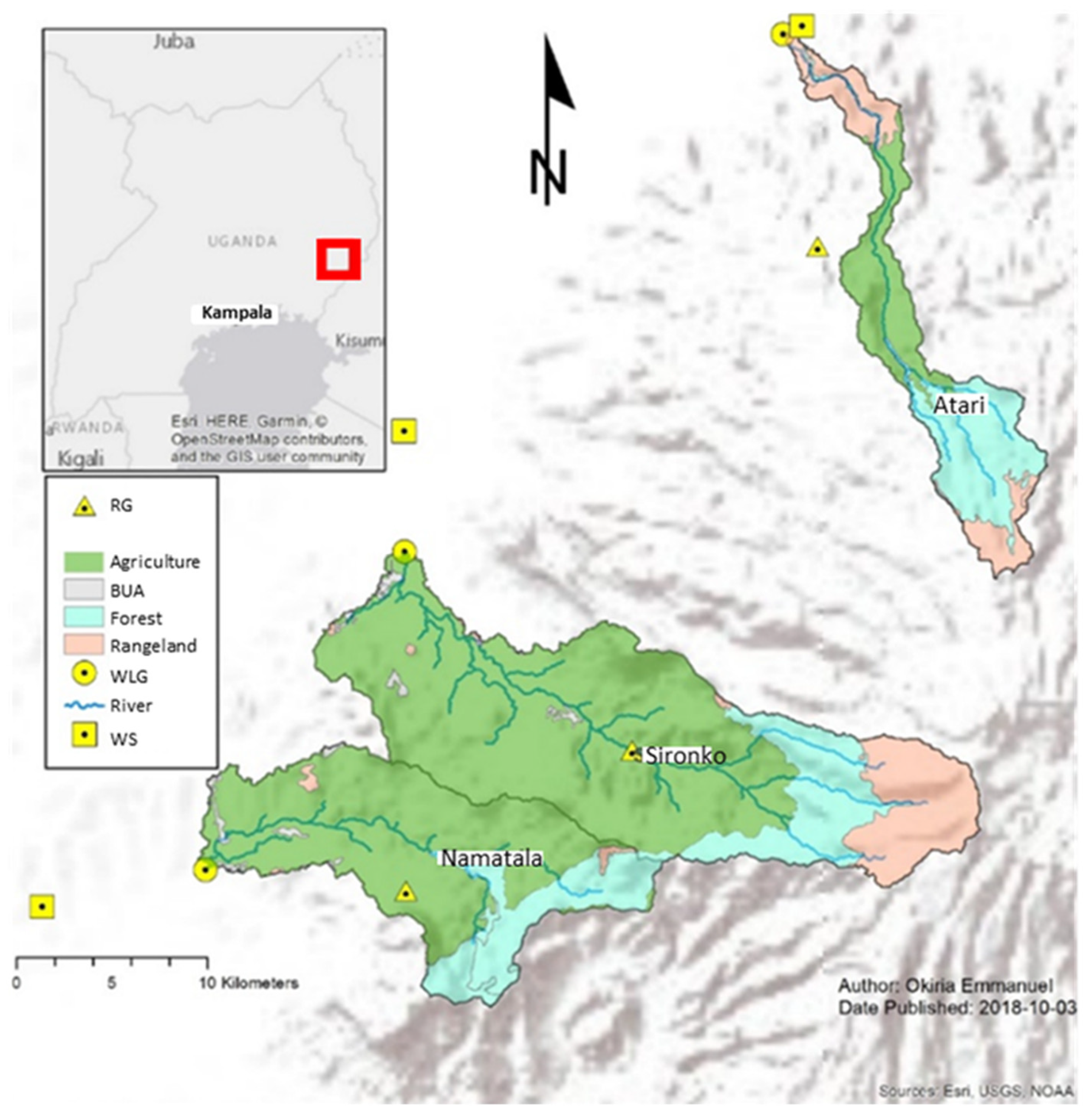
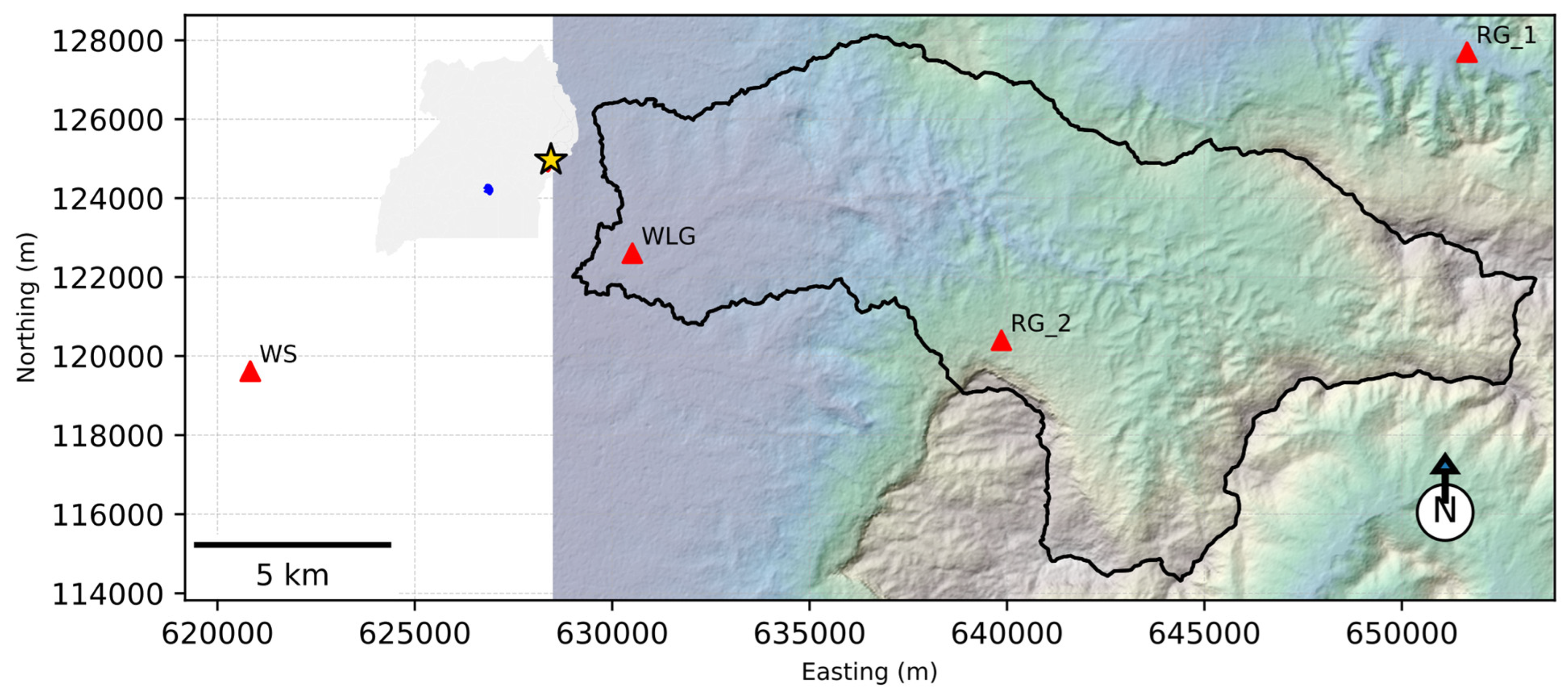
2.1. The Study Area
2.2. TopEros Model
2.2.1. Hydrologic Model Component
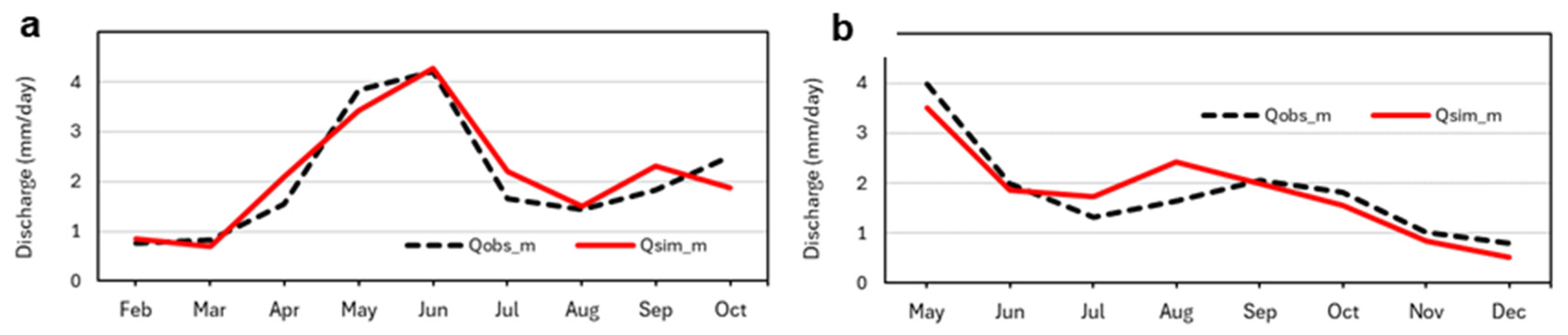
Calibration Strategy
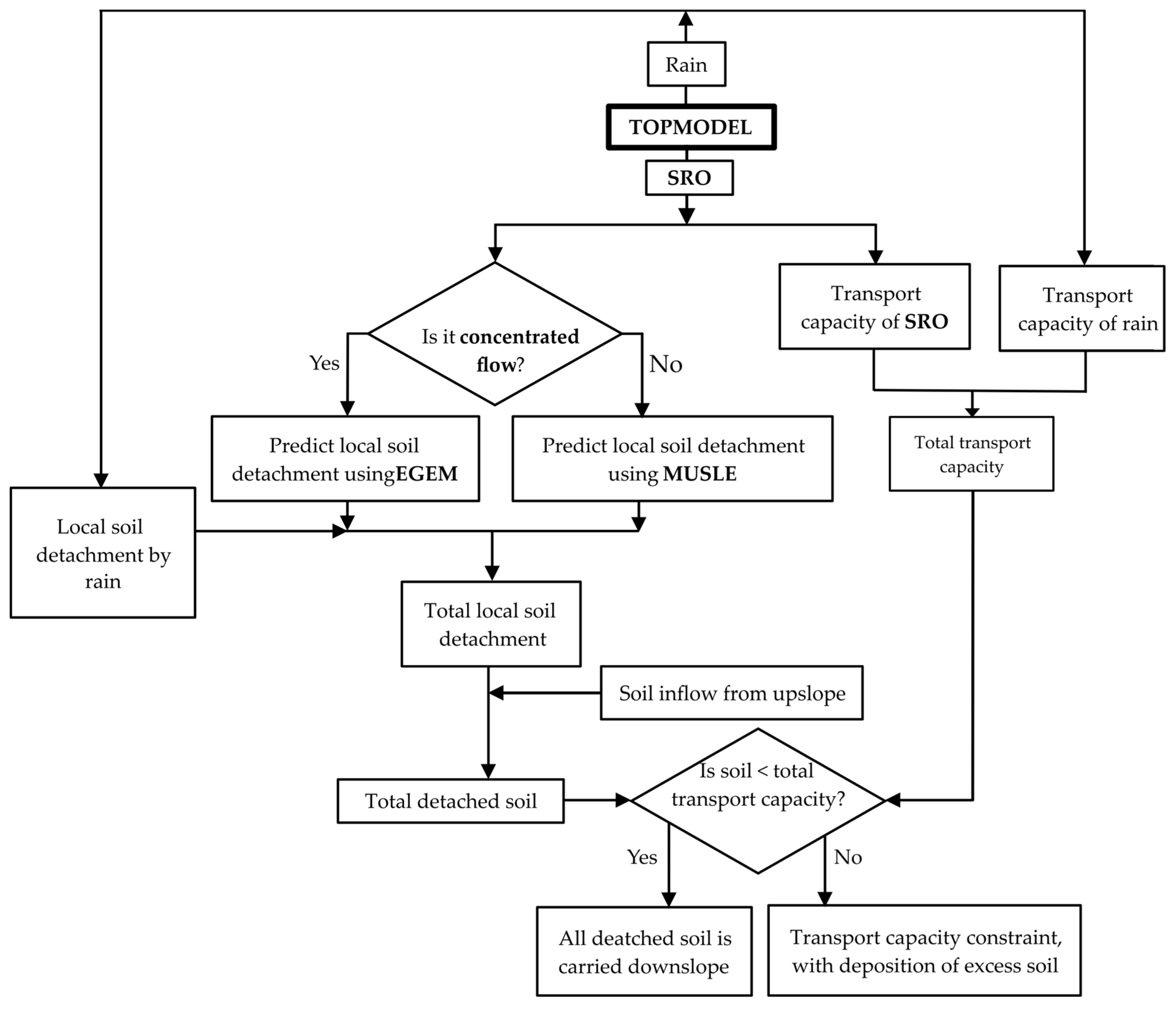
2.2.2. The Soil Erosion Component
- Each cell has an assumed channel, whose width is expressed by Equation (13) [21].
- Grid cells whose topographic indices exceed a certain threshold have zones of concentrated flow and exhibit a duality of sheet + raindrop splash erosion and gully erosion, i.e., sheet erosion due to diffuse runoff in the non-channel zone of the cell, raindrop splash erosion when the soil is not saturated, and gully erosion within the channel section of the cell.
- The hypothetical channel in each cell receives runoff and its entrained sediment for routing to a downstream cell.
| Erosion Risk | Threshold (Mgha−1yr−1) |
|---|---|
| Very low | Soil Loss ≤ 2 |
| Low | 2 ≤ Soil Loss ≤ 10 |
| Moderate | 10 ≤ Soil Loss ≤ 50 |
| High | 50 ≤ Soil Loss ≤ 100 |
| Very high | Soil Loss ≥ 100 |
| Parameter Set | m (mm) | Te (mm2h−1) | td (hmm−1) | SRmax (mm) | SRZinitial (mm) | NSE | RSR | PBIAS (%) | NSE_v | RSR_v | PBIAS_v |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 30.847 | 6879 | 0.014 | 2.871 | 0.000 | 0.616 | 0.619 | −4.576 | 0.503 | 0.705 | 1.462 |
| 2 | 33.532 | 7335 | 0.012 | 3.485 | 0.000 | 0.611 | 0.624 | −6.519 | 0.503 | 0.705 | −1.109 |
| 3 | 30.882 | 6318 | 0.013 | 4.241 | 0.000 | 0.608 | 0.626 | −8.091 | 0.500 | 0.707 | 1.108 |
| 4 | 19.172 | 9575 | 0.027 | 0.331 | 0.000 | 0.601 | 0.631 | −5.371 | 0.486 | 0.717 | 6.753 |
| 5 | 21.879 | 6328 | 0.020 | 3.267 | 0.000 | 0.600 | 0.633 | −2.513 | 0.479 | 0.722 | 8.378 |
| 6 | 28.402 | 7295 | 0.020 | 0.681 | 0.000 | 0.589 | 0.641 | 4.554 | 0.491 | 0.713 | 7.673 |
| 7 | 20.713 | 6593 | 0.025 | 2.928 | 0.000 | 0.583 | 0.646 | 11.930 | 0.446 | 0.744 | 19.357 |
| 8 | 17.975 | 9069 | 0.026 | 3.605 | 0.000 | 0.579 | 0.649 | 9.893 | 0.429 | 0.756 | 21.818 |
| 9 | 23.433 | 1489 | 0.026 | 9.426 | 0.000 | 0.553 | 0.668 | 10.509 | 0.387 | 0.783 | 22.468 |
| 10 | 30.605 | 6169 | 0.011 | 5.547 | 0.000 | 0.545 | 0.675 | −17.212 | 0.465 | 0.731 | −6.767 |
| 11 | 28.797 | 7571 | 0.015 | 9.678 | 0.000 | 0.541 | 0.677 | 16.338 | 0.434 | 0.752 | 22.765 |
| 12 | 18.436 | 8702 | 0.024 | 1.719 | 0.000 | 0.537 | 0.681 | −9.384 | 0.473 | 0.726 | 7.540 |
| 13 | 47.187 | 6869 | 0.008 | 7.066 | 0.000 | 0.520 | 0.693 | 5.980 | 0.500 | 0.707 | −1.375 |
| 14 | 41.631 | 6231 | 0.012 | 0.120 | 0.000 | 0.518 | 0.694 | −23.872 | 0.426 | 0.758 | −20.933 |
| 15 | 48.838 | 2800 | 0.010 | 6.340 | 0.000 | 0.501 | 0.706 | 5.916 | 0.470 | 0.728 | −1.303 |
| 16 | 20.733 | 3611 | 0.022 | 2.884 | 0.000 | 0.452 | 0.740 | −16.854 | 0.438 | 0.749 | 0.629 |
| Year | NSE | RSR | PBIAS (%) | |
|---|---|---|---|---|
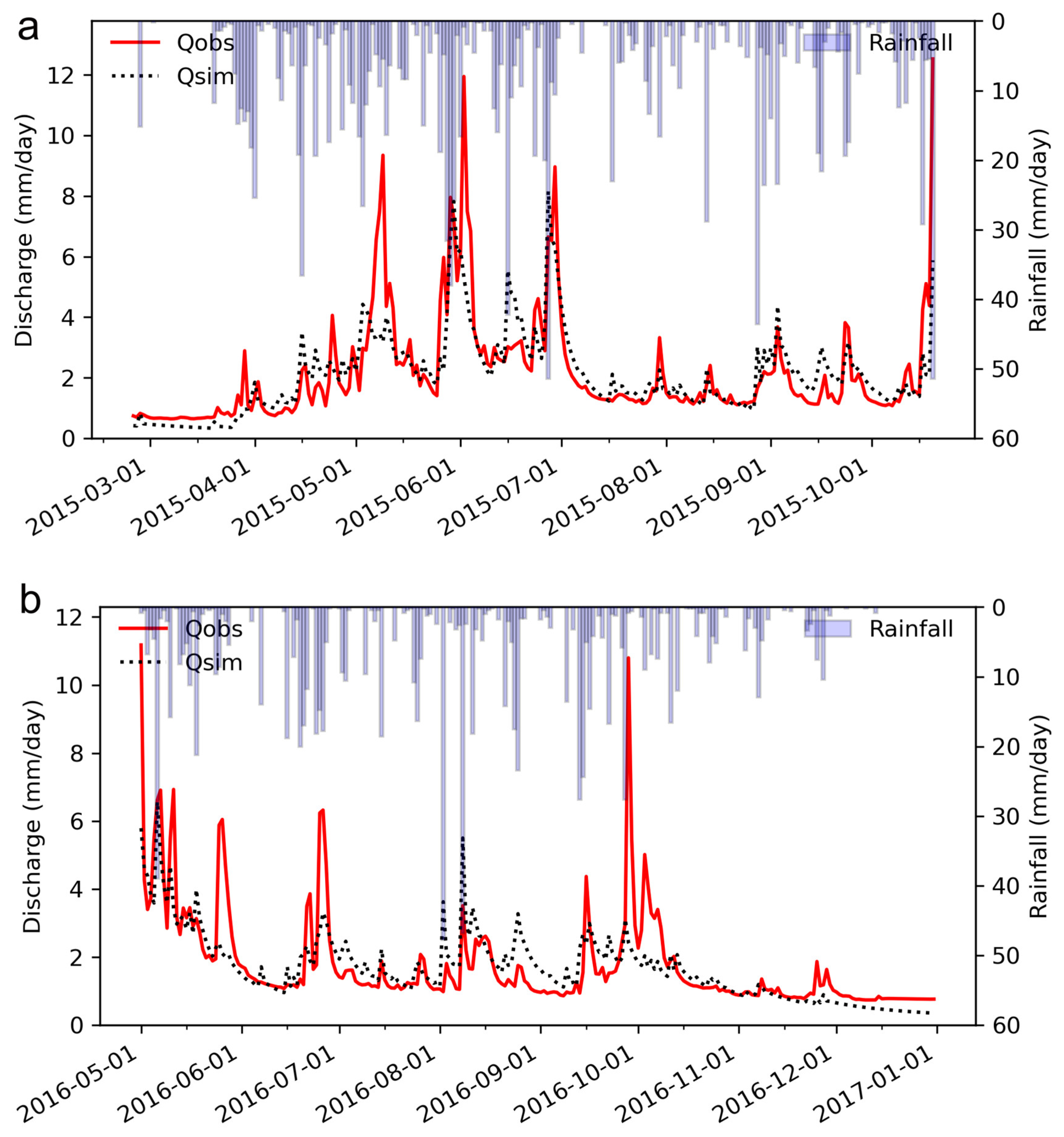
| Calibration | 2015 | 0.881 | 0.345 | −3.268 |
| Validation | 2016 | 0.879 | 0.347 | 1.529 |
Detachment by Raindrop
Sheet Erosion
Soil Erosion by Concentrated Flow
Identification of the Location of Gully Erosion
Calculation of Gully Erosion
Transport Capacity of Flow
2.3. Data
2.3.1. Meteorological Data
2.3.2. Streamflow
2.3.3. Sediment
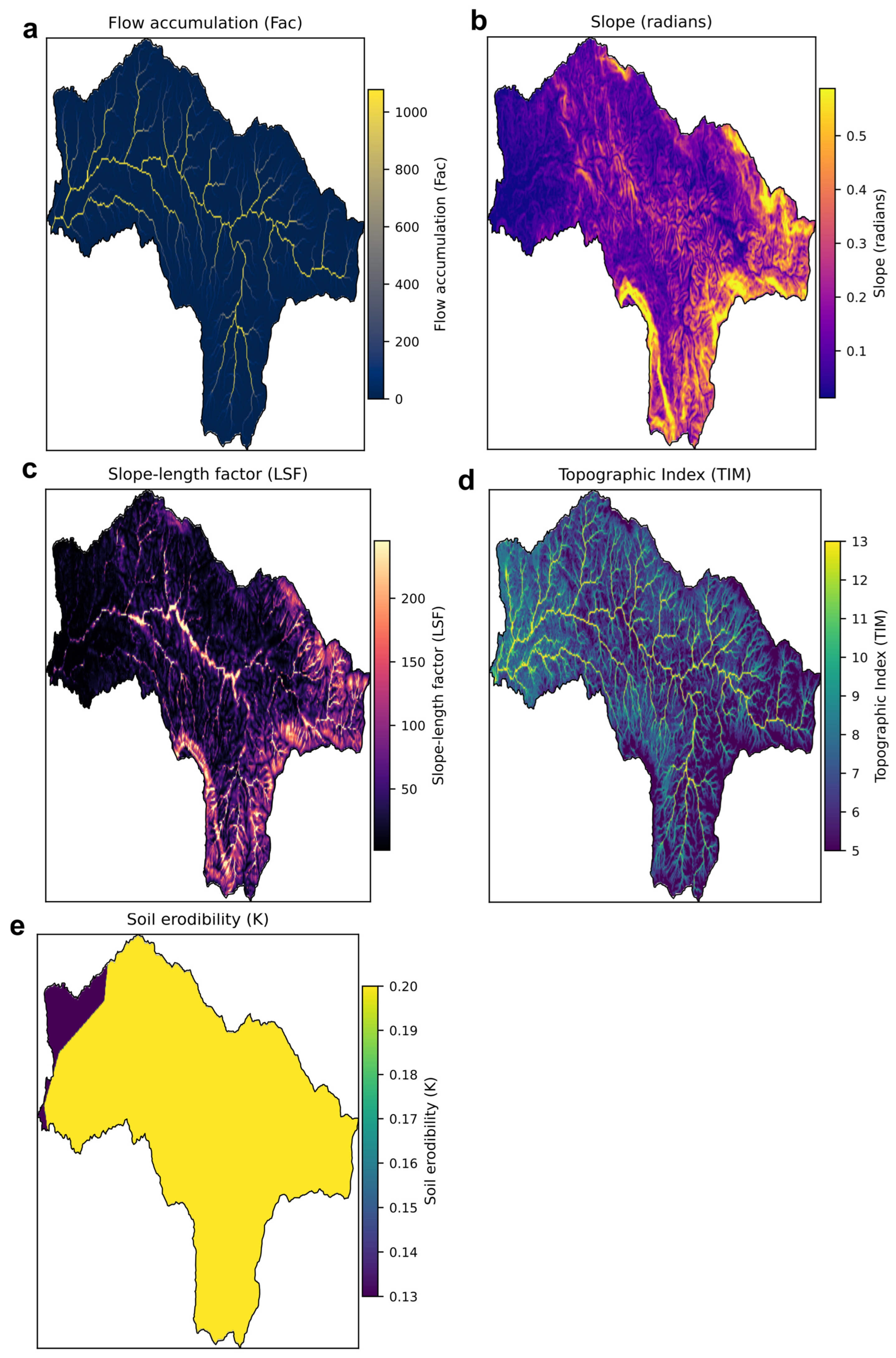
2.3.4. Geo-Spatial Data
2.4. Validation of the Erosion Model
- Comparison against running MUSLE across the entire catchment.
- Comparison of TopEros sediment delivery ratios against those predicted by established empirical relationships (refer to Section 3.2.5).
- Comparison of the erosion values against those from similar catchments in previous studies.
3. Results and Discussion
3.1. Calibration and Validation of TOPMODEL
3.2. TopEros Erosion Module
3.2.1. MUSLE Parameters
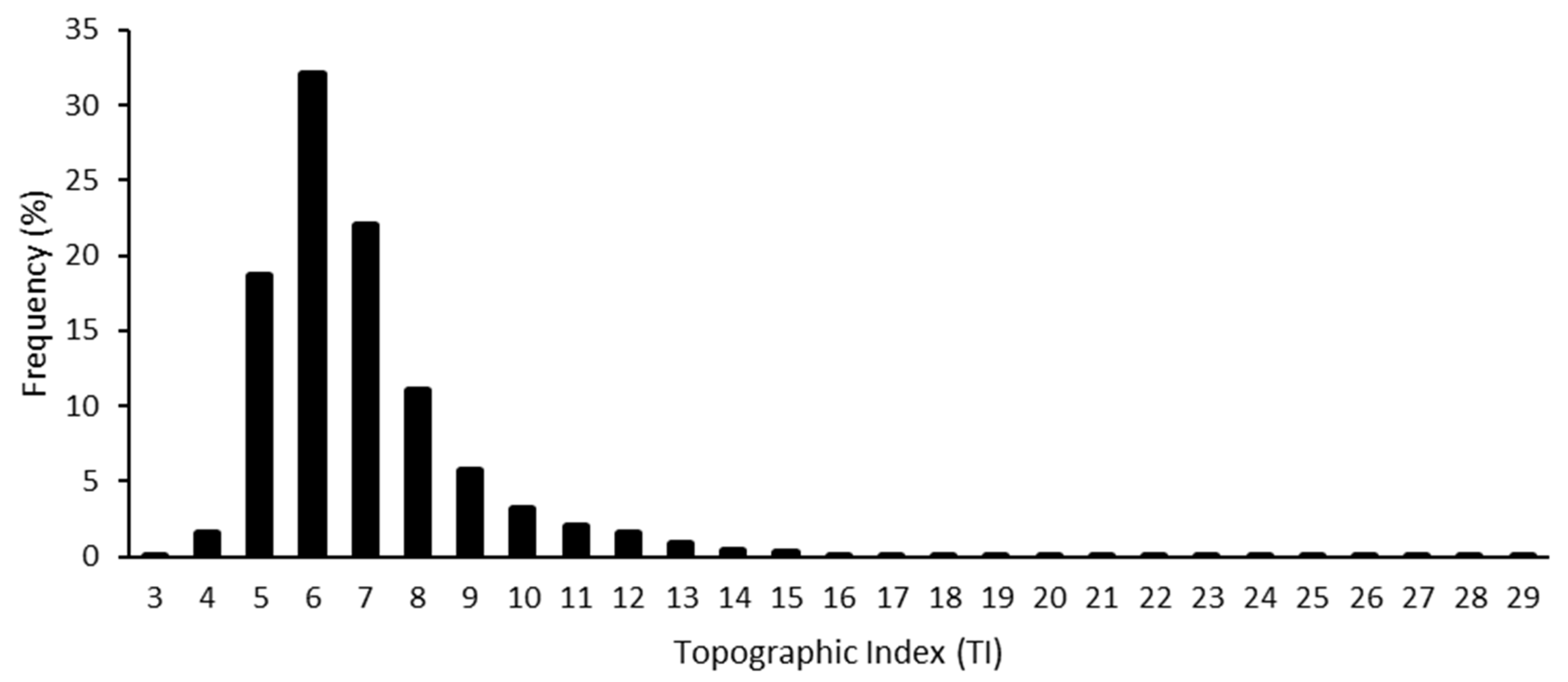
3.2.2. Threshold Values of the Topographic Indices
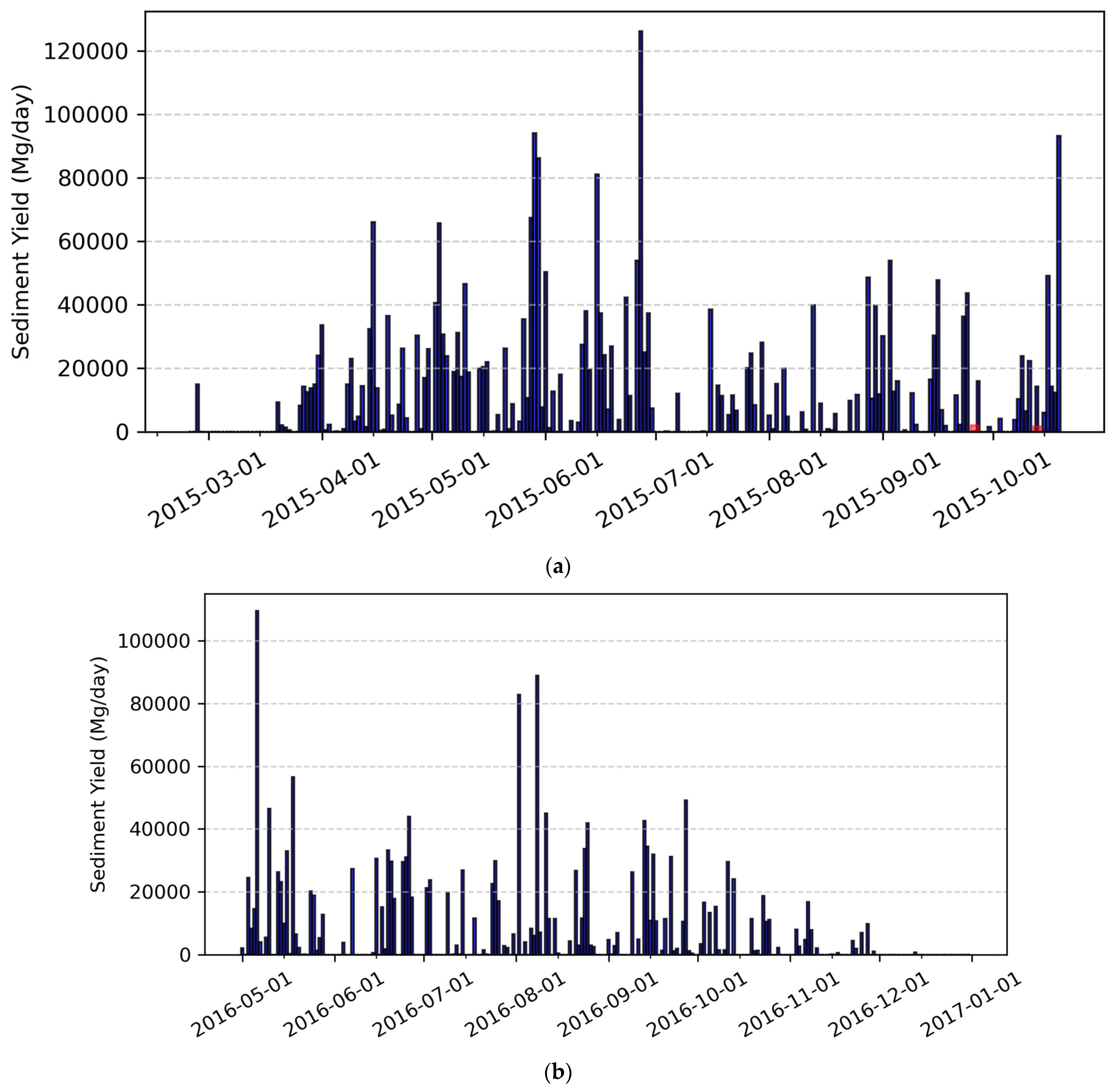
3.2.3. Sediment Yield at the Catchment Outlet
3.2.4. Partitioning of the Erosion Process
3.2.5. Specific Erosion and Sediment Delivery Ratios
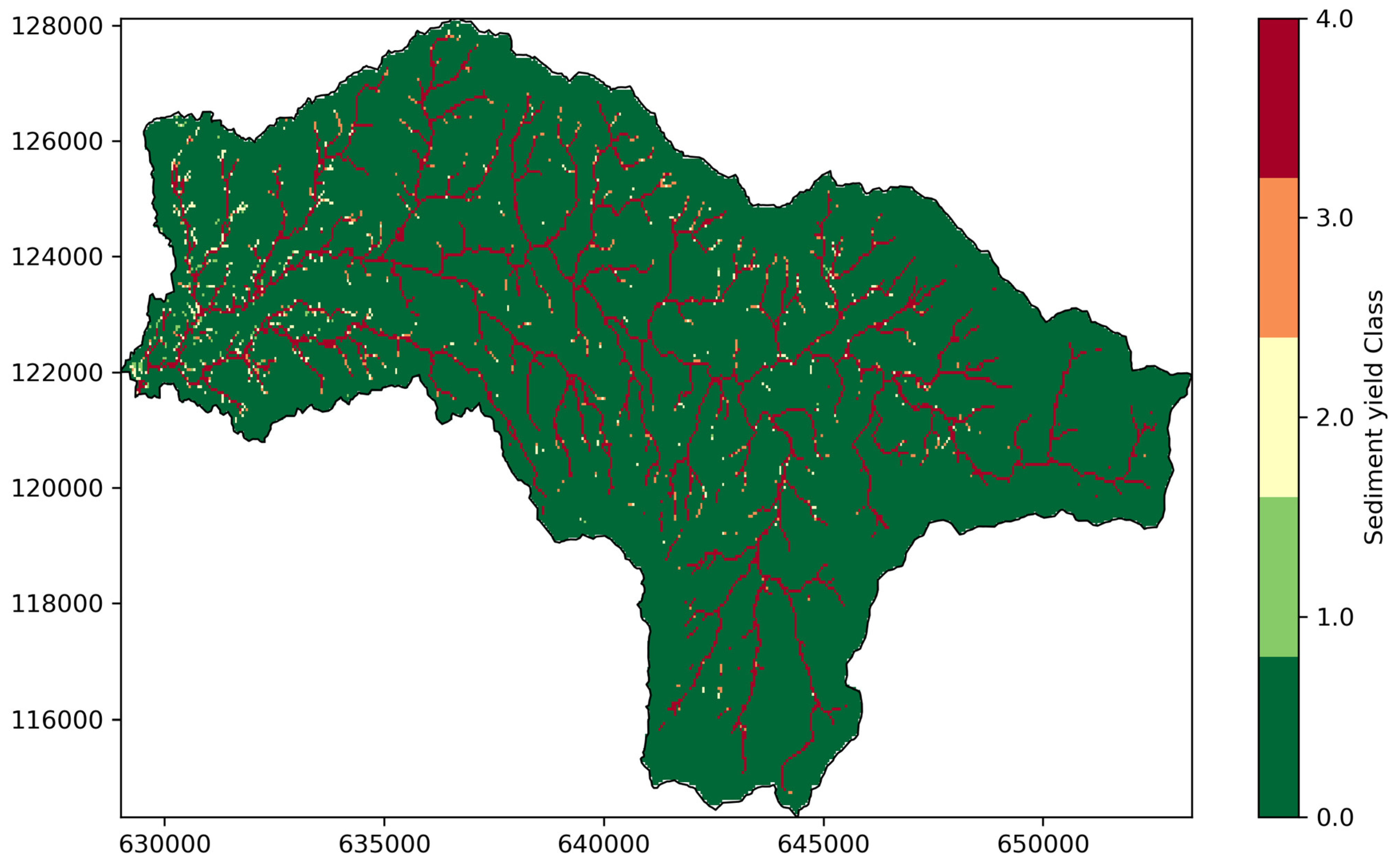
3.2.6. Spatial Patterns and Risk Classification
3.2.7. Model Validation and Implications
3.3. Limitations and Future Directions
4. Conclusions
- Cross-catchment validation with observed sediment-yield records to quantify TopEros’ predictive gains over conventional models.
- Enhanced gully detection, leveraging high-resolution optical and DEM data, topographic-wetness indices, and targeted field surveys to improve the delineation of ephemeral features.
- Integration of flow-routing modules to extend the model’s applicability to larger basins and facilitate eventual upscaling to regional or global soil erosion assessments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
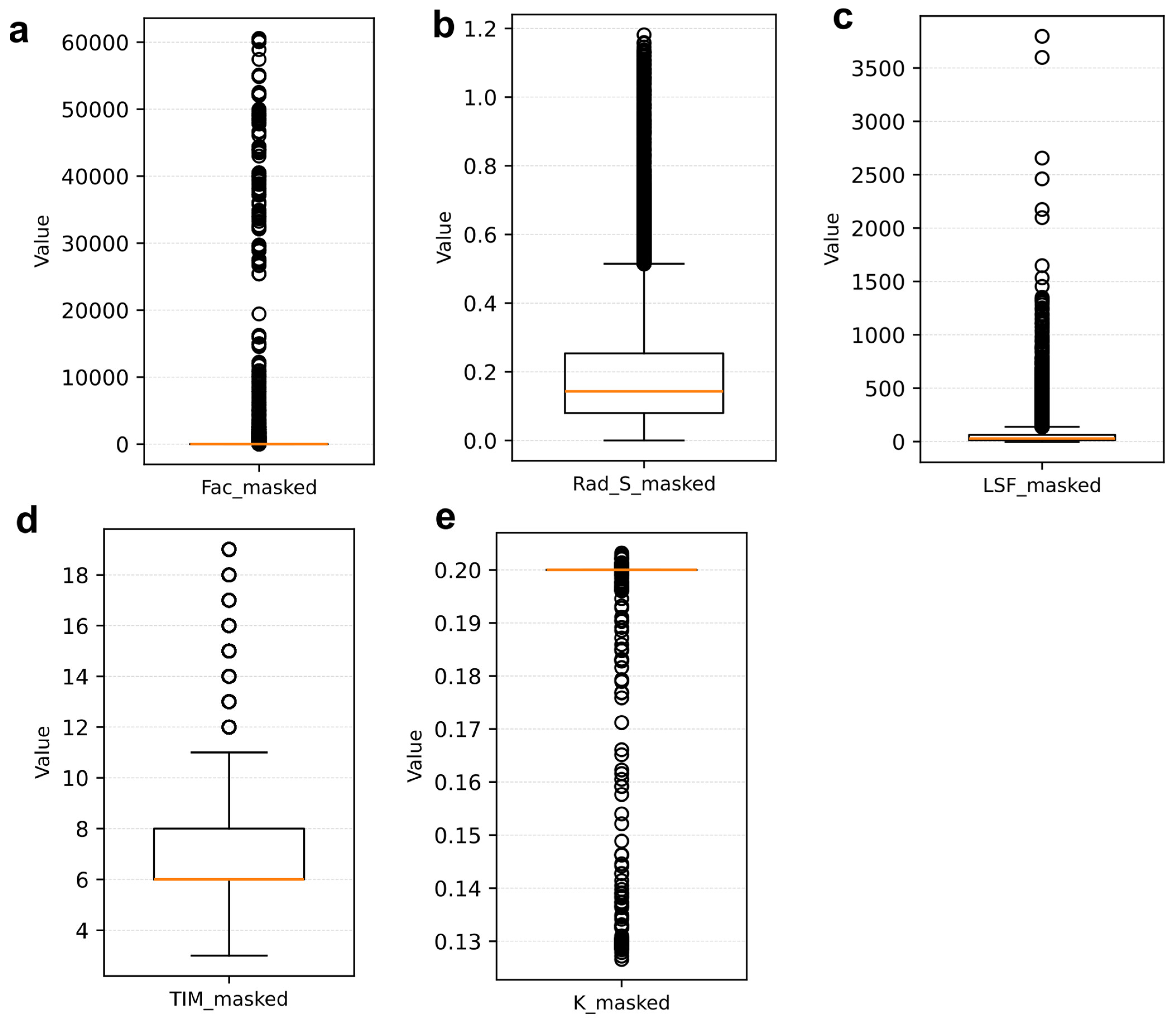
References
- Gruver, J.B. Prediction, Prevention and Remediation of Soil Degradation by Water Erosion. Nat. Educ. Knowl. 2013, 4, 2. [Google Scholar]
- Labrière, N.; Locatelli, B.; Laumonier, Y.; Freycon, V.; Bernoux, M. Soil Erosion in the Humid Tropics: A Systematic Quantitative Review. Agric. Ecosyst. Environ. 2015, 203, 127–139. [Google Scholar] [CrossRef]
- Nkonge, L.K.; Gathenya, J.M.; Kiptala, J.K.; Cheruiyot, C.K.; Petroselli, A. An Ensemble of Weight of Evidence and Logistic Regression for Gully Erosion Susceptibility Mapping in the Kakia-Esamburmbur Catchment, Kenya. Water 2023, 15, 1292. [Google Scholar] [CrossRef]
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully Erosion and Environmental Change: Importance and Research Needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; No. 537; Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1978.
- Renard, K.G.; Foster, G.R.; Yoder, G.C.; McCool, D.K. RUSLE Revisited: Status, Questions, Answers and the Future. J. Soil Water Conserv. 1994, 49, 213–220. [Google Scholar] [CrossRef]
- Williams, J.R. Testing the Modified Universal Soil Loss Equation. In Proceedings of the Workshop on Estimating Erosion and Sediment Yield on Rangelands, Tucson, AZ, USA, 7–9 March 1981; Burroughs, E.R., Jr., Chugg, J.C., Dissmeyer, G.E., Farrell, D.A., Foster, G.R., Gebhardt, K.A., Hart, G.E., Johnson, C.W., Laflen, J.M., Lane, L.J., et al., Eds.; U.S. Department of Agriculture, Agricultural Research Service, Agricultural Reviews and Manuals ARM-W: Tucson, AZ, USA, 1982; pp. 157–165. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil & Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011; pp. 1–647. [CrossRef]
- Beasley, D.B.; Huggins, L.F.; Monke, E.J. ANSWERS: A Model for Watershed Planning. Trans. Am. Soc. Agric. Eng. 1980, 23, 938–944. [Google Scholar] [CrossRef]
- Wicks, J.M.; Bathurst, J.C. SHESED: A Physically Based, Distributed Erosion and Sediment Yield Component for the SHE Hydrological Modelling System. J. Hydrol. 1996, 175, 213–238. [Google Scholar] [CrossRef]
- Ewen, J.; Parkin, G.; O’Connell, P.E. SHETRAN: Distributed River Basin Flow and Transport Modeling System. J. Hydrol. Eng. 2000, 5, 250–258. [Google Scholar] [CrossRef]
- Cerdà, A.; Brazier, R.; Nearing, M.; de Vente, J. Scales and Erosion. Catena 2013, 102, 1–2. [Google Scholar] [CrossRef]
- Foster, G.R. Modeling the Erosion Process. In Hydrologic Modeling of Small Watersheds; Haan, C.T., Johnson, H.P., Brakensiek, D.L., Eds.; ASAE: Washington, DC, USA, 1982; pp. 295–380. [Google Scholar]
- Wang, G.; Jiang, H.; Xu, Z.; Wang, L.; Yue, W. Evaluating the Effect of Land Use Changes on Soil Erosion and Sediment Yield Using a Grid-Based Distributed Modelling Approach. Hydrol. Process 2012, 26, 3579–3592. [Google Scholar] [CrossRef]
- Sadeghi, S.H.R.; Mizuyama, T. Applicability of the Modified Universal Soil Loss Equation for Prediction of Sediment Yield in Khanmirza Watershed, Iran. Hydrol. Sci. J. 2007, 52, 1068–1075. [Google Scholar] [CrossRef]
- Sadeghi, S.H.R.; Gholami, L.; Khaledi Darvishan, A.; Saeidi, P. A Review of the Application of the MUSLE Worldwide. Hydrol. Sci. J. 2014, 59, 365–375. [Google Scholar] [CrossRef]
- Gwapedza, D.; Hughes, D.A.; Slaughter, A.R. Spatial Scale Dependency Issues in the Application of the Modified Universal Soil Loss Equation (MUSLE). Hydrol. Sci. J. 2018, 63, 1890–1900. [Google Scholar] [CrossRef]
- Thakuriah, G. GIS-Based Revised Universal Soil Loss Equation for Estimating Annual Soil Erosion: A Case of Lower Kulsi Basin, India. SN Appl. Sci. 2023, 5, 81. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P.; Ciesiolka, C.A. Soil Erosion Prediction and GIS: Linking Theory and Practice. In Proceedings of the International Conference on Application of Geographic Information Systems to Soil Erosion Management, Taiyuan, China, 2–11 June 1992; pp. 31–48. [Google Scholar]
- Desmet, P.J.J.; Govers, G. A GIS Procedure for Automatically Calculating the USLE LS Factor on Topographically Complex Landscape Units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar] [CrossRef]
- Wang, G.; Hapuarachchi, H.A.P.; Takeuchi, K.; Ishidaira, H. Grid-Based Distribution Model for Simulating Runoff and Soil Erosion from a Large-Scale River Basin. Hydrol. Process 2010, 24, 641–653. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A Physically Based, Variable Contributing Area Model of Basin Hydrology. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Moore, I.D.; Burch, G.J.; Mackenzie, D.H. Topographic Effects on the Distribution of Surface Soil Water and the Location of Ephemeral Gullies. Trans. ASAE 1988, 31, 1098–1107. [Google Scholar] [CrossRef]
- Japan Aerospace Exploration Agency (JAXA); Ministry of Economy, Trade and Industry (METI). ALOS PALSAR Radiometric Terrain Corrected (RTC)—High Resolution; Alaska Satellite Facility Distributed Active Archive Center (ASF DAAC). 2014. Available online: https://www.earthdata.nasa.gov/data/catalog/asf-alos-psr-rtc-high-1 (accessed on 18 October 2023).
- Ferguson, C.R.; Pan, M.; Oki, T. The Effect of Global Warming on Future Water Availability: CMIP5 Synthesis. Water Resour. Res. 2018, 54, 7791–7819. [Google Scholar] [CrossRef]
- Singh, V.P. Watershed Modeling. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 1–20. ISBN 0-918334-91-8. [Google Scholar]
- Allen, R.G.; Luis, S.P.; RAES, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56. Crop Evapotranspiration (Guidelines for Computing Crop Water Requirements). Irrig. Drain. 1998, 300, 300. [Google Scholar] [CrossRef]
- Foster, G.R.; Lombardi, F.; Moldenhauer, W.C. Evaluation of Rainfall-Runoff Erosivity Factors for Individual Storms. Trans. ASAE 1982, 25, 124–129. [Google Scholar] [CrossRef]
- Foster, G.R.; Meyer, L.D.; Onstad, C.A. Erosion Equation Derived From Basic Erosion Principles. Trans. ASAE 1977, 20, 678–682. [Google Scholar] [CrossRef]
- Quinn, P.F.; Beven, K.J.; Lamb, R. The Ln(a/Tanβ) Index: How to Calculate It and How to Use It Within the TOPMODEL Framework. Hydrol. Process. 1995, 9, 161–182. [Google Scholar] [CrossRef]
- Speight, J.G. The Role of Topography in Controlling Throughflow Generation: A Discussion. Earth Surf. Process. 1980, 5, 187–191. [Google Scholar] [CrossRef]
- Pradhan, N.R.; Ogden, F.L.; Tachikawa, Y.; Takara, K. Scaling of Slope, Upslope Area, and Soil Water Deficit: Implications for Transferability and Regionalization in Topographic Index Modeling. Water Resour. Res. 2008, 44, 1–12. [Google Scholar] [CrossRef]
- Okiria, E.; Okazawa, H.; Noda, K.; Kobayashi, Y.; Suzuki, S.; Yamazaki, Y. A Comparative Evaluation of Lumped and Semi-Distributed Conceptual Hydrological Models: Does Model Complexity Enhance Hydrograph Prediction? Hydrology 2022, 9, 89. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: West Sussex, UK, 2012; ISBN 978-0-470-71459-1. [Google Scholar]
- Hornberger, G.M.; Wiberg, P.L.; Raffensperger, J.P.; D’Odorico, P. Elements of Physical Hydrology, 2nd ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2014; ISBN 978-1-4214-1373-0. [Google Scholar]
- Mukae, K.; Miwa, K.; Okazawa, H. Ecosystem Service Assessment in Agricultural Watershed by Using TOPMODEL. AGROFO Int. J. 2017, 2, 27–36. [Google Scholar] [CrossRef]
- Foglia, L.; Hill, M.C.; Mehl, S.W.; Burlando, P. Sensitivity Analysis, Calibration, and Testing of a Distributed Hydrological Model Using Error-Based Weighting and One Objective Function. Water Resour. Res. 2009, 45, W06427. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Am. Soc. Agric. Eng. 2007, 50, 885–900. [Google Scholar]
- Jiang, B.; Bamutaze, Y.; Pilesjö, P. Climate Change and Land Degradation in Africa: A Case Study in the Mount Elgon Region, Uganda. Geo-Spat. Inf. Sci. 2014, 17, 39–53. [Google Scholar] [CrossRef]
- van der Knijff, J.M.; Jones, R.J.A.; Montanarella, L. Soil Erosion Risk Assessment in Italy; EUR 19022 EN; Joint Research Centre, European Commission, European Soil Bureau: Luxembourg, 1999; 54p. [Google Scholar]
- Williams, J.R. The EPIC Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 909–1000. ISBN 0-918334-91-8. [Google Scholar]
- Moore, I.D.; Burch, G.J. Physical Basis of the Length-Slope Factor in the Universal Soil Loss Equation. Soil Sci. Soc. Am. J. 1986, 50, 1294–1298. [Google Scholar] [CrossRef]
- Nachtergaele, F.; Van Velthuizen, H.; Verelst, L.; Batjes, N.; Dijkshoorn, K.; Van Engelen, V.; Fischer, G.; Jones, A.; Montanarella, L.; Petri, M.; et al. Harmonized World Soil Database—Version 1.1; FAO: Rome, Italy; IIASA: Laxenburg, Austria, 2009. [Google Scholar]
- Moore, I.D.; Wilson, J.P. Length-Slope Factors for the Revised Universal Soil Loss Equation: Simplified Method of Estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar] [CrossRef]
- Thorne, C.R.; Zevenbergen, L.W.; Grissinger, E.H.; Murphey, J.B. Ephemeral Gullies as Sources of Sediment. In Proceedings of the Fourth Federal Interagency Sedimentation Conference, Las Vegas, NV, USA, 24–27 March 1986; pp. 3.152–3.161. [Google Scholar]
- Flanagan, D.C.; Livingston, S.J. WEPP User Summary; NSERL Report No. 11; USADA-ARS National Soil Erosion Research Laboratory: West Lafayette, IN, USA, 1995; 141p.
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Automatic Calibration of Conceptual Rainfall-Runoff Models: Sensitivity to Calibration Data. J. Hydrol. 1996, 181, 23–48. [Google Scholar] [CrossRef]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of Rainfall-Runoff Models: Application of Global Optimization to the Sacramento Soil Moisture Accounting Model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Sugawara, M. Automatic Calibration of the Tank Model/L’étalonnage Automatique d’un Modèle à Cisterne Automatic Calibration of the Tank Model. Hydrol. Sci. Bull. 1979, 24, 375–388. [Google Scholar] [CrossRef]
- Takido, K.; Saavedra Valeriano, O.C.; Ryo, M.; Tanuma, K.; Ushio, T.; Kubota, T. Spatiotemporal Evaluation of the Gauge-Adjusted Global Satellite Mapping of Precipitation at the Basin Scale. J. Meteorol. Soc. Jpn. 2016, 94, 185–195. [Google Scholar] [CrossRef]
- Li, J.; He, H.; Zeng, Q.; Chen, L.; Sun, R. A Chinese Soil Conservation Dataset Preventing Soil Water Erosion from 1992 to 2019. Sci. Data 2023, 10, 319. [Google Scholar] [CrossRef]
- Vandaele, K.; Poesen, J.; Marques da Silva, J.R.; Desmet, P.P.J. Rates and Predictability of Ephemeral Gully Erosion in Two Contrasting Environments. Géomorphologie Relief Process. Environ. 1996, 2, 83–95. [Google Scholar] [CrossRef]
- Daggupati, P.; Sheshukov, A.Y.; Douglas-Mankin, K.R. Evaluating Ephemeral Gullies with a Process-Based Topographic Index Model. Catena 2014, 113, 177–186. [Google Scholar] [CrossRef]
- Daggupati, P.; Douglas-Mankin, K.R.; Sheshukov, A.Y. Predicting Ephemeral Gully Location and Length Using Topographic Index Models. Trans. ASABE 2013, 56, 1427–1440. [Google Scholar] [CrossRef]
- Owor, M.; Tindimugaya, C.; Brown, L.; Upton, K.; Ó Dochartaigh, B.É.; Bellwood-Howard, I. Africa Groundwater Atlas: Hydrogeology of Uganda. Available online: http://earthwise.bgs.ac.uk/index.php/Hydrogeology_of_Uganda (accessed on 12 February 2020).
- Benavidez, R.; Jackson, B.; Maxwell, D.; Norton, K. A Review of the (Revised) Universal Soil Loss Equation ((R)USLE): With a View to Increasing Its Global Applicability and Improving Soil Loss Estimates. Hydrol. Earth Syst. Sci. 2018, 22, 6059–6086. [Google Scholar] [CrossRef]
- Boardman, J.; Poesen, J. Soil Erosion in Europe: Major Processes, Causes and Consequences. In Soil Erosion in Europe; Boardman, J., Poesen, J., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; pp. 479–487. [Google Scholar]
- Vanoni, V.A. (Ed.) Sedimentation Engineering; ASCE Manuals and Reports on Engineering Practice No. 54; American Society of Civil Engineers: New York, NY, USA, 1975. [Google Scholar]
- Dhakal, A.; Tsuchiya, S.; Ohsaka, O. Application of the USLE and Sediment Delivery Models in a Mountainous Catchment. J. Jpn. Soc. Eros. Control. Eng. 2006, 59, 43–48. [Google Scholar]
- Ouyang, D.; Bartholic, J. Predicting Sediment Delivery Ratio in Saginaw Bay Watershed. In Proceedings of the 22nd National Association of Environmental Professional Conference, Orlando, FL, USA, 19–23 May 1997; pp. 659–671. [Google Scholar]
- Karamage, F.; Zhang, C.; Ndayisaba, F.; Shao, H.; Kayiranga, A.; Fang, X.; Nahayo, L.; Nyesheja, E.M.; Tian, G. Extent of Cropland and Related Soil Erosion Risk in Rwanda. Sustainability 2016, 8, 609. [Google Scholar] [CrossRef]
- Morgan, R.P.C. Soil Erosion & Conservation, 3rd ed.; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2005; ISBN 1-4051-1781-8. [Google Scholar]
- Henrique Lima Alencar, P.; De Araujo, J.C.; Dos Santos Teixeira, A. Physically Based Model for Gully Simulation: Application to the Brazilian Semiarid Region. Hydrol. Earth Syst. Sci. 2020, 24, 4239–4255. [Google Scholar] [CrossRef]
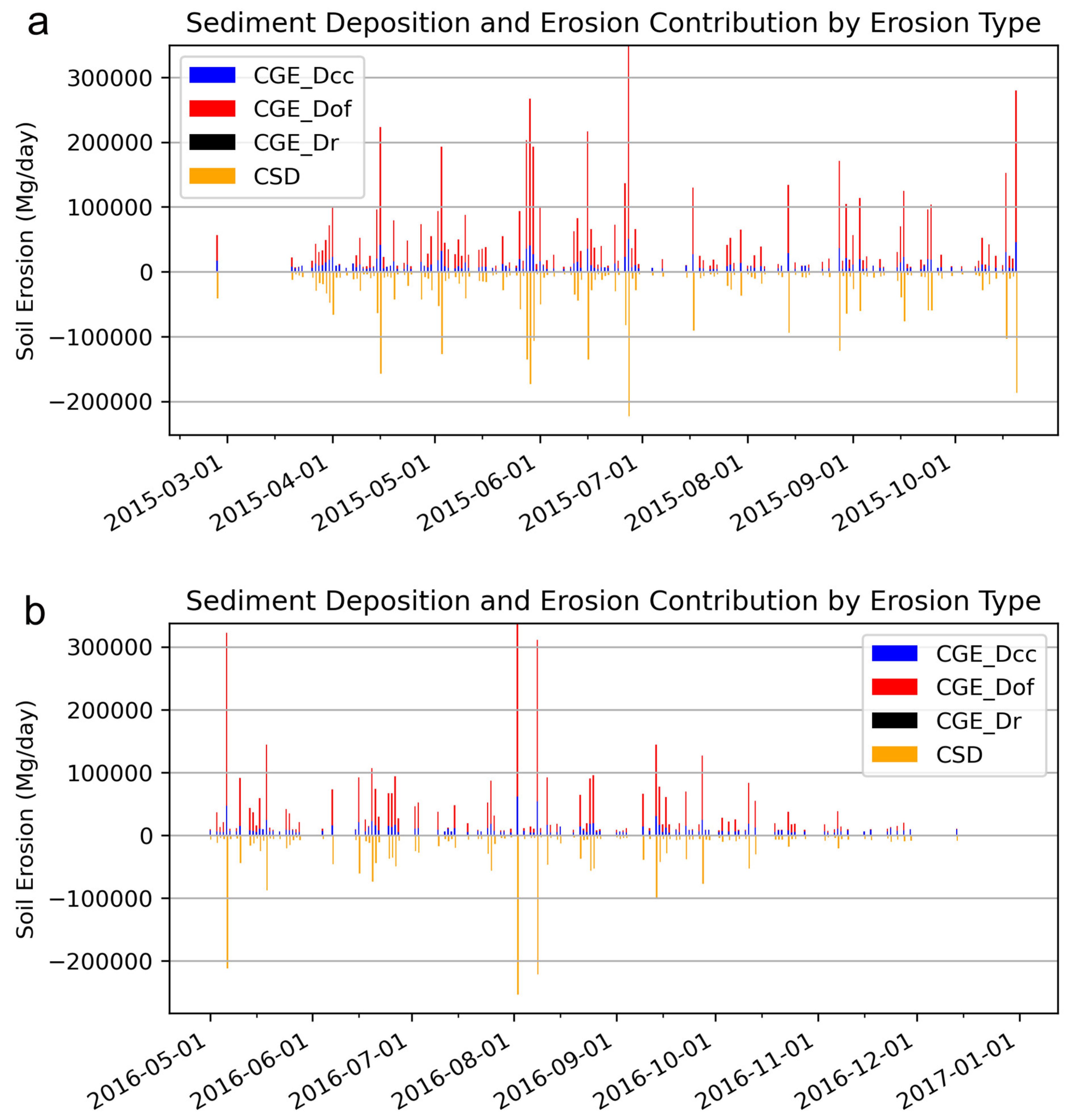
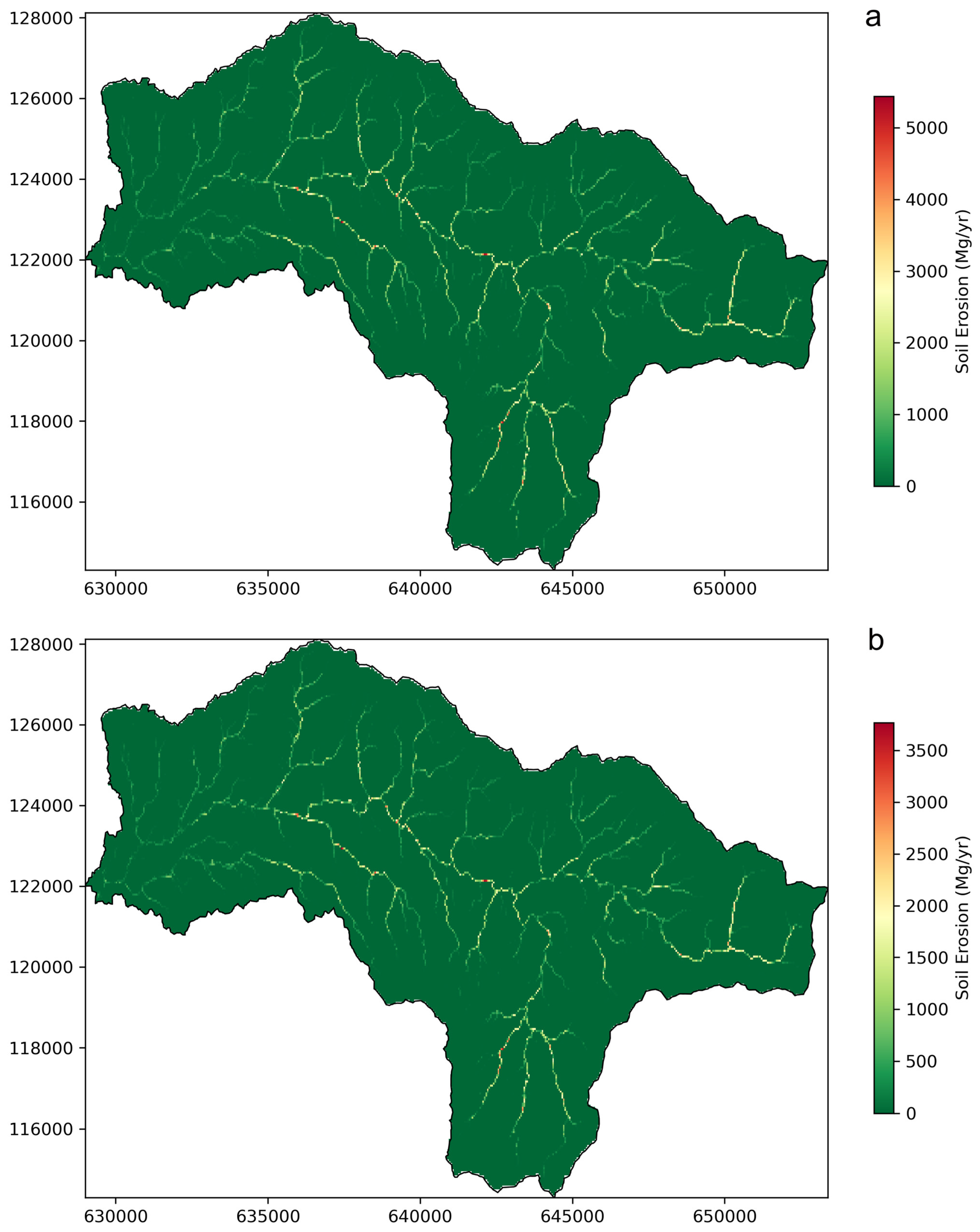
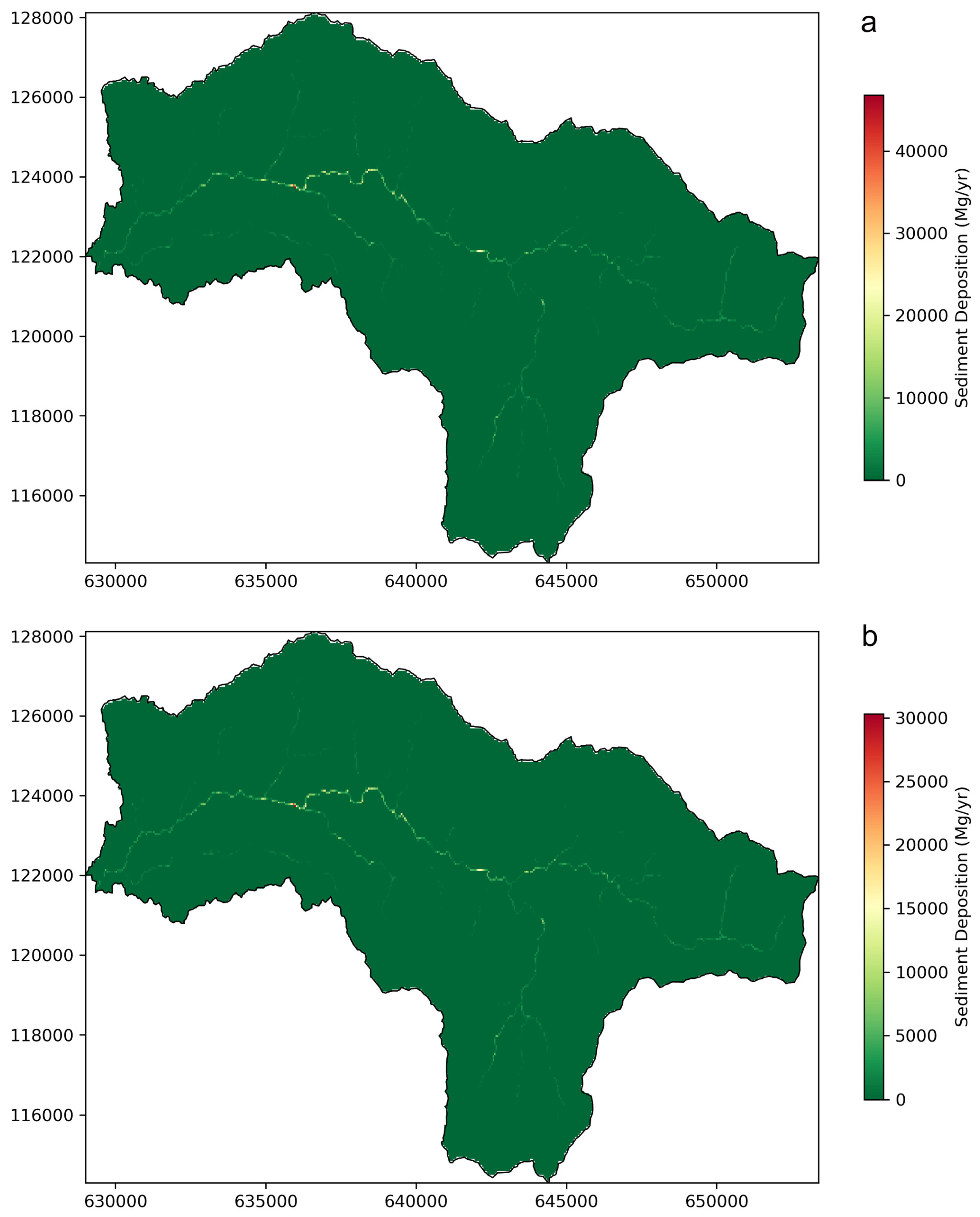
| Year | CSY (Mgyr−1) ×106 | CSD (Mgyr−1) ×106 | CGE_Dof (Mgyr−1) ×106 | CGE_Dr (Mgyr−1) | CGE_Df (Mgyr−1) ×106 | Model |
|---|---|---|---|---|---|---|
| 2015 | 2.387 | 4.141 | 4.438 | 2.510 | 2.090 | TopEros |
| 2015 | 2.915 | 3.697 | — | — | — | MUSLE |
| 2016 | 1.443 | 3.110 | 2.714 | 1.719 | 1.839 | TopEros |
| 2016 | 1.774 | 3.697 | — | — | — | MUSLE |
| Year | CSY (Mgha−1yr−1) | CSD (Mgha−1yr−1) | SDR* | SDR** | Model |
|---|---|---|---|---|---|
| 2015 | 155 | 270 | 0.366 | 0.252 | TopEros |
| 2015 | 190 | 241 | 0.441 | 0.252 | MUSLE |
| 2016 | 94 | 202 | 0.317 | 0.252 | TopEros |
| 2016 | 115 | 137 | 0.456 | 0.252 | MUSLE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okiria, E.; Keigo, N.; Nishimura, S.-i.; Kobayashi, Y. TopEros: An Integrated Hydrology and Multi-Process Erosion Model—A Comparison with MUSLE. Hydrology 2025, 12, 309. https://doi.org/10.3390/hydrology12110309
Okiria E, Keigo N, Nishimura S-i, Kobayashi Y. TopEros: An Integrated Hydrology and Multi-Process Erosion Model—A Comparison with MUSLE. Hydrology. 2025; 12(11):309. https://doi.org/10.3390/hydrology12110309
Chicago/Turabian StyleOkiria, Emmanuel, Noda Keigo, Shin-ichi Nishimura, and Yukimitsu Kobayashi. 2025. "TopEros: An Integrated Hydrology and Multi-Process Erosion Model—A Comparison with MUSLE" Hydrology 12, no. 11: 309. https://doi.org/10.3390/hydrology12110309
APA StyleOkiria, E., Keigo, N., Nishimura, S.-i., & Kobayashi, Y. (2025). TopEros: An Integrated Hydrology and Multi-Process Erosion Model—A Comparison with MUSLE. Hydrology, 12(11), 309. https://doi.org/10.3390/hydrology12110309






