Impact Analysis of Climate Change on Hydropower Resource Development in the Vakhsh River Basin of Tajikistan
Abstract
1. Introduction
2. Materials and Methods
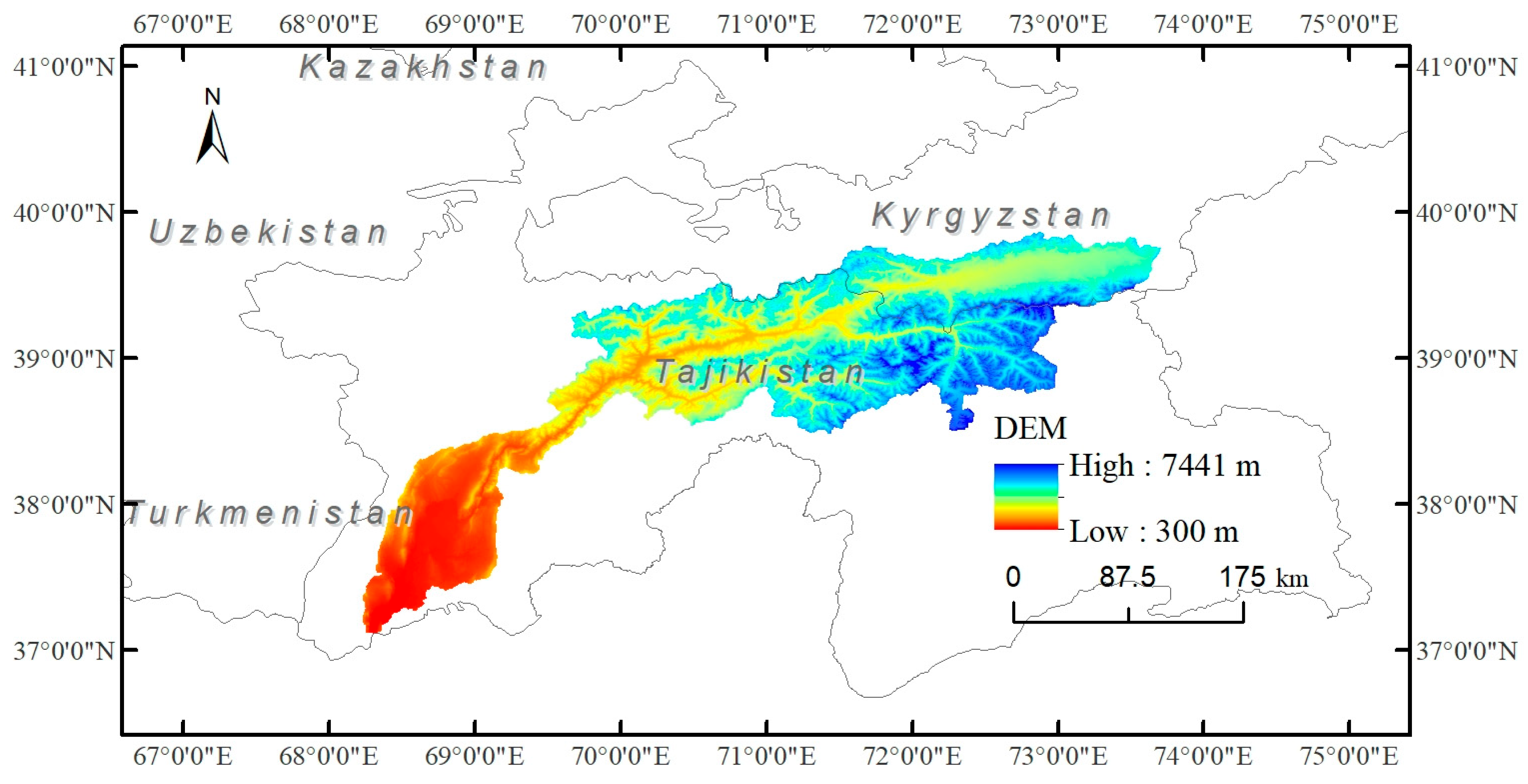
2.1. Study Area
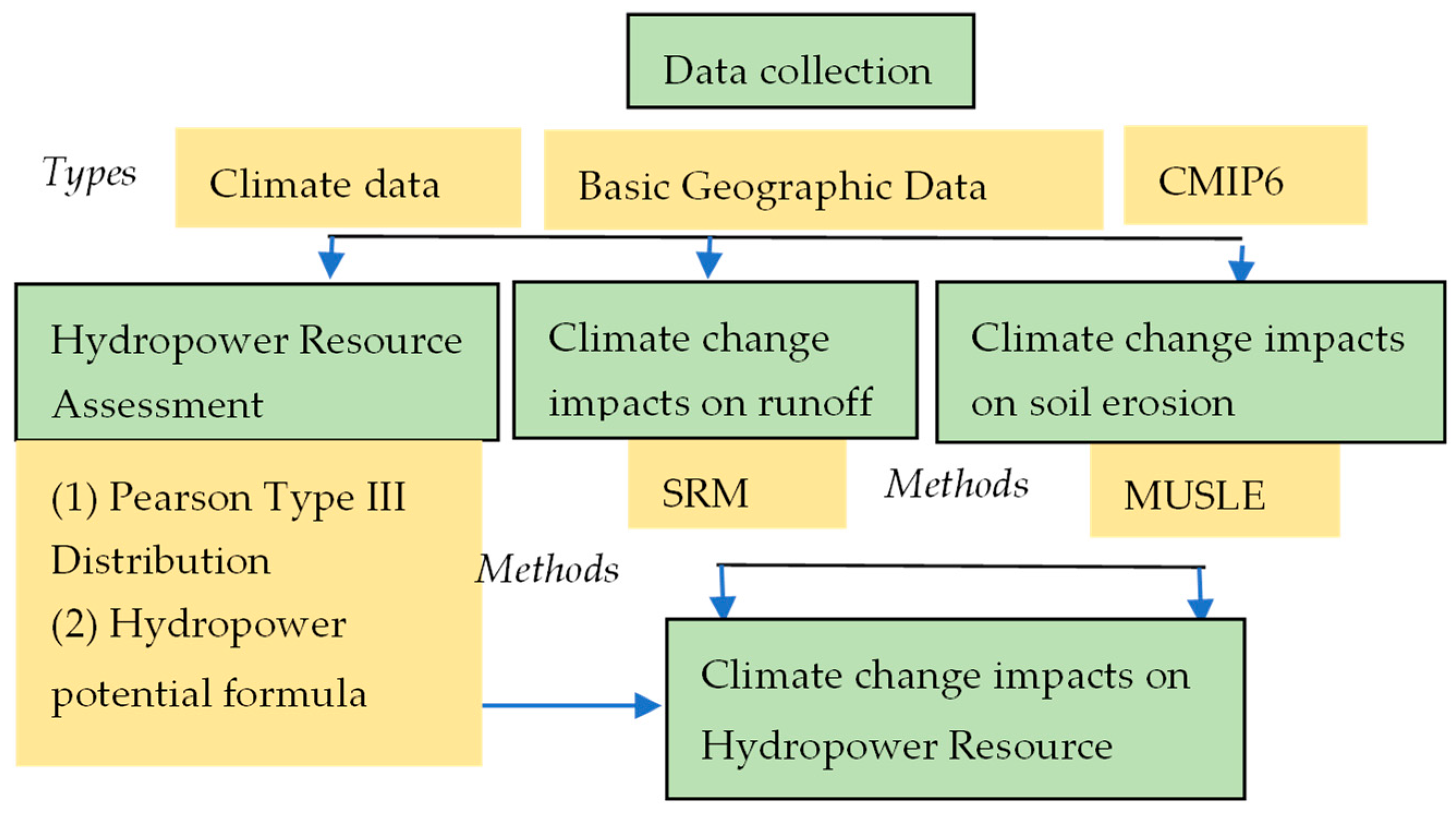
2.2. Research Framework
2.3. Data Collection
2.4. Hydropower Resource Assessment
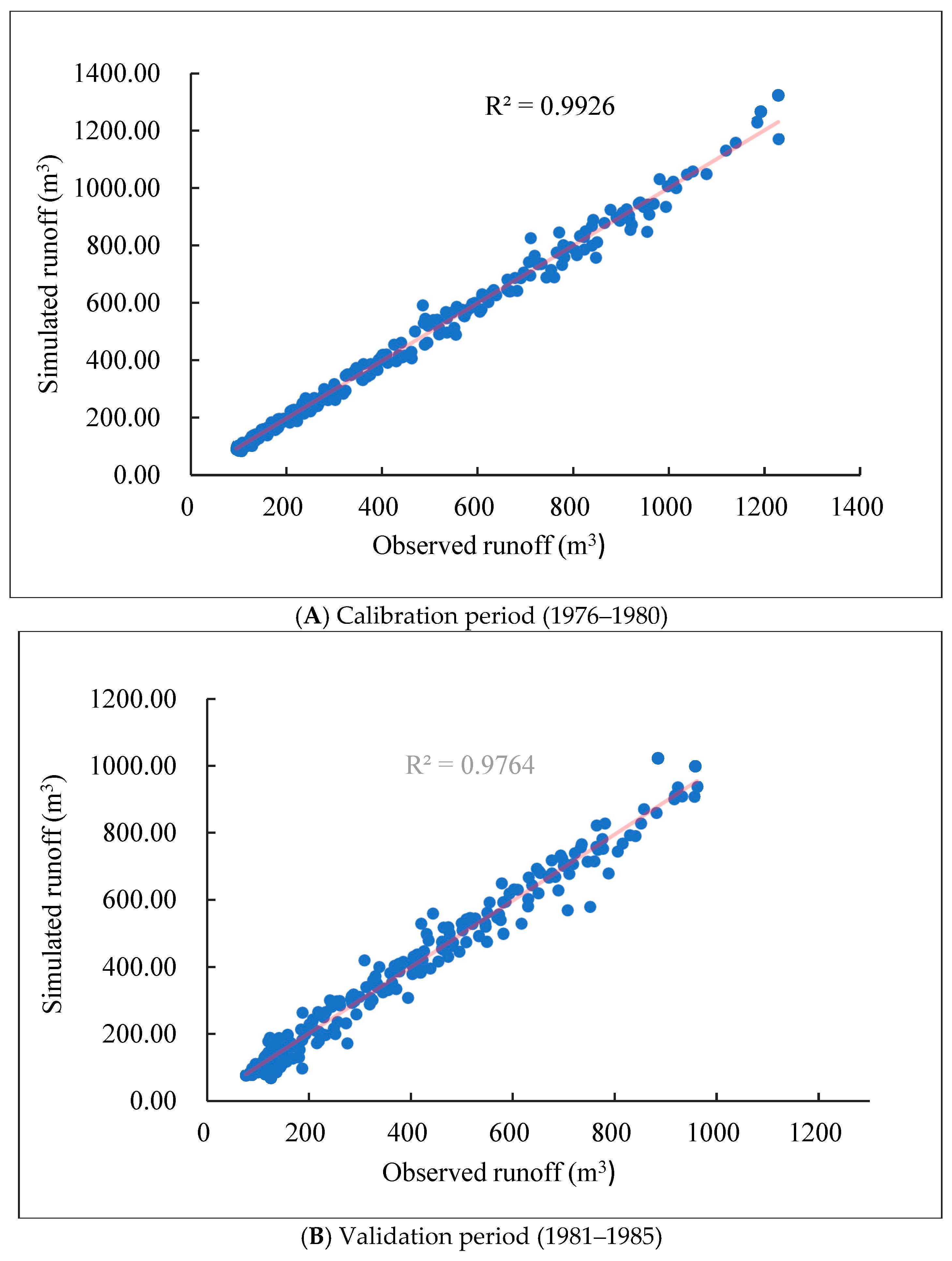
2.5. Simulation of Climate Change Impacts on Runoff
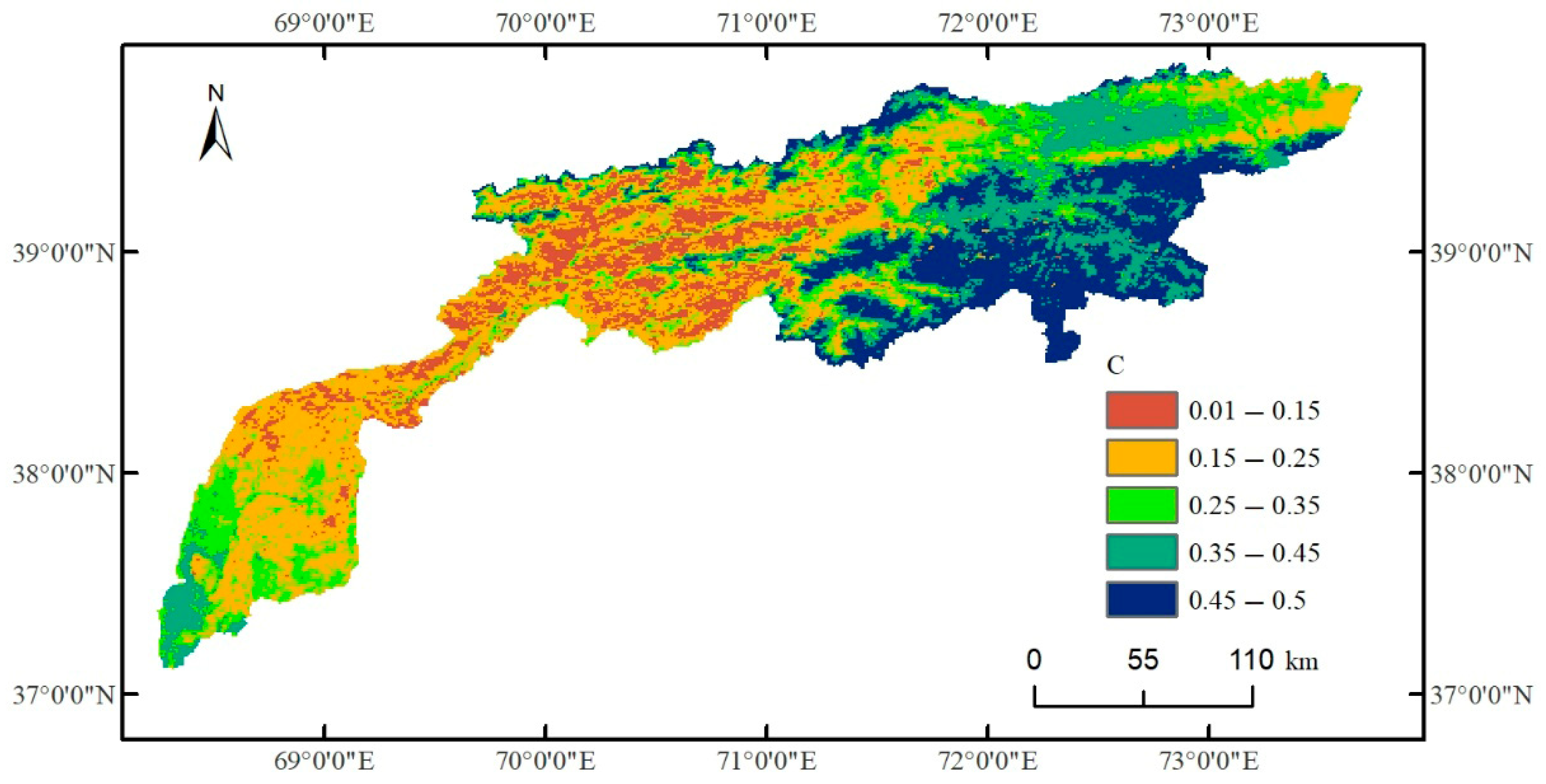
2.6. Impact of Soil Erosion on Hydropower Resources Under Climate Change
2.7. Pearson Type III Distribution
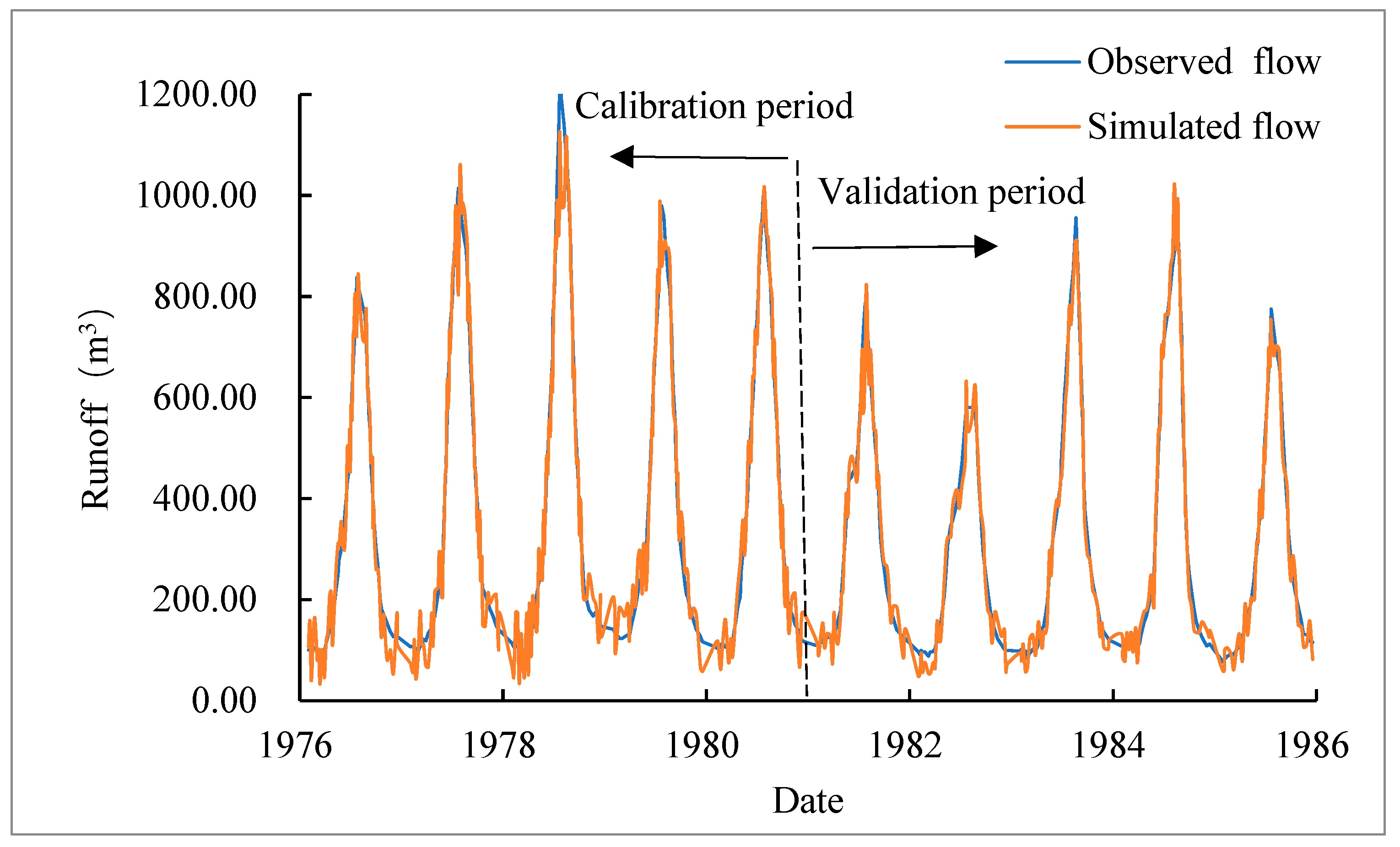
2.8. Simulation and Analysis Software
3. Results and Discussion
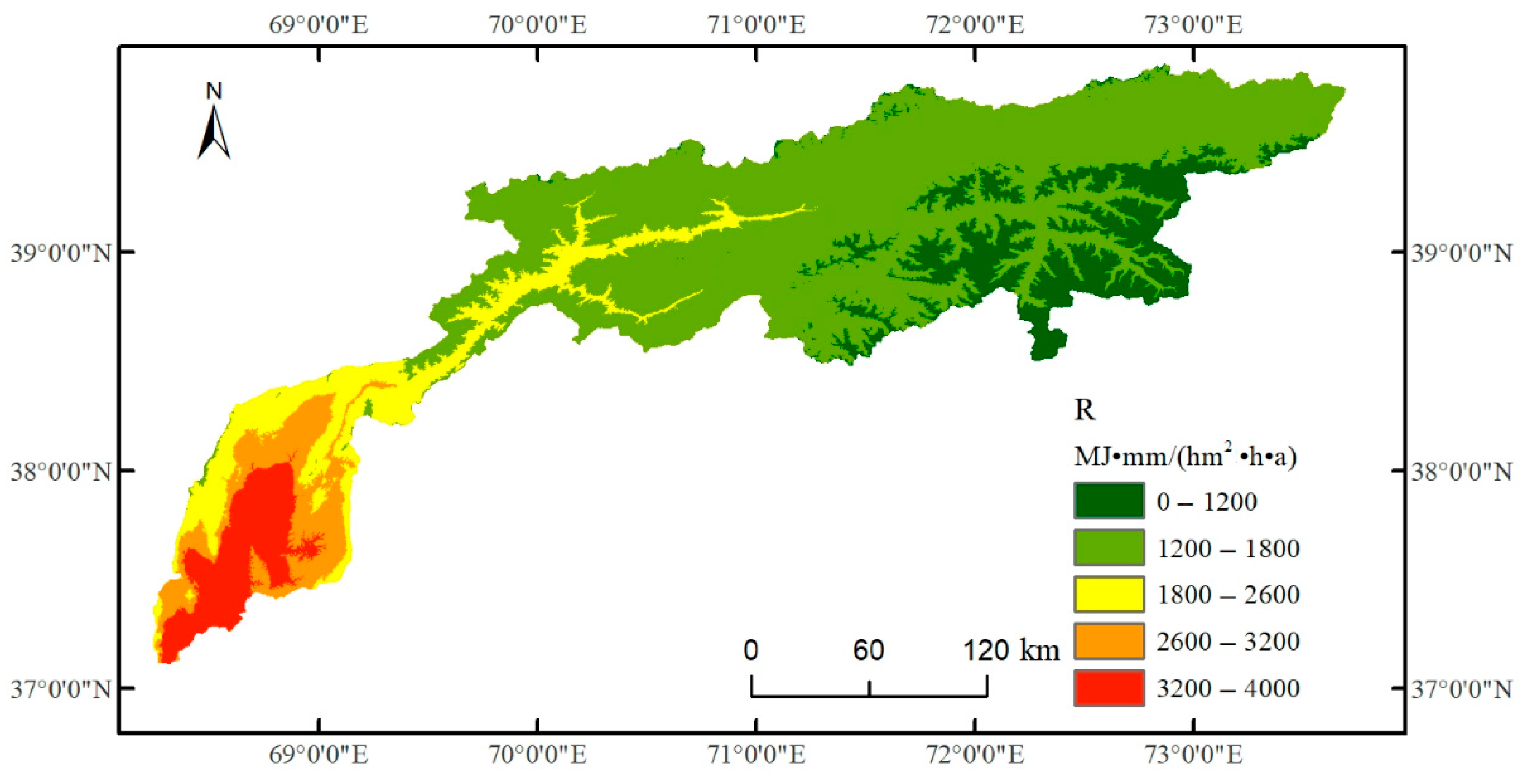
3.1. Water Energy Resource Assessment in the Vakhsh River Basin
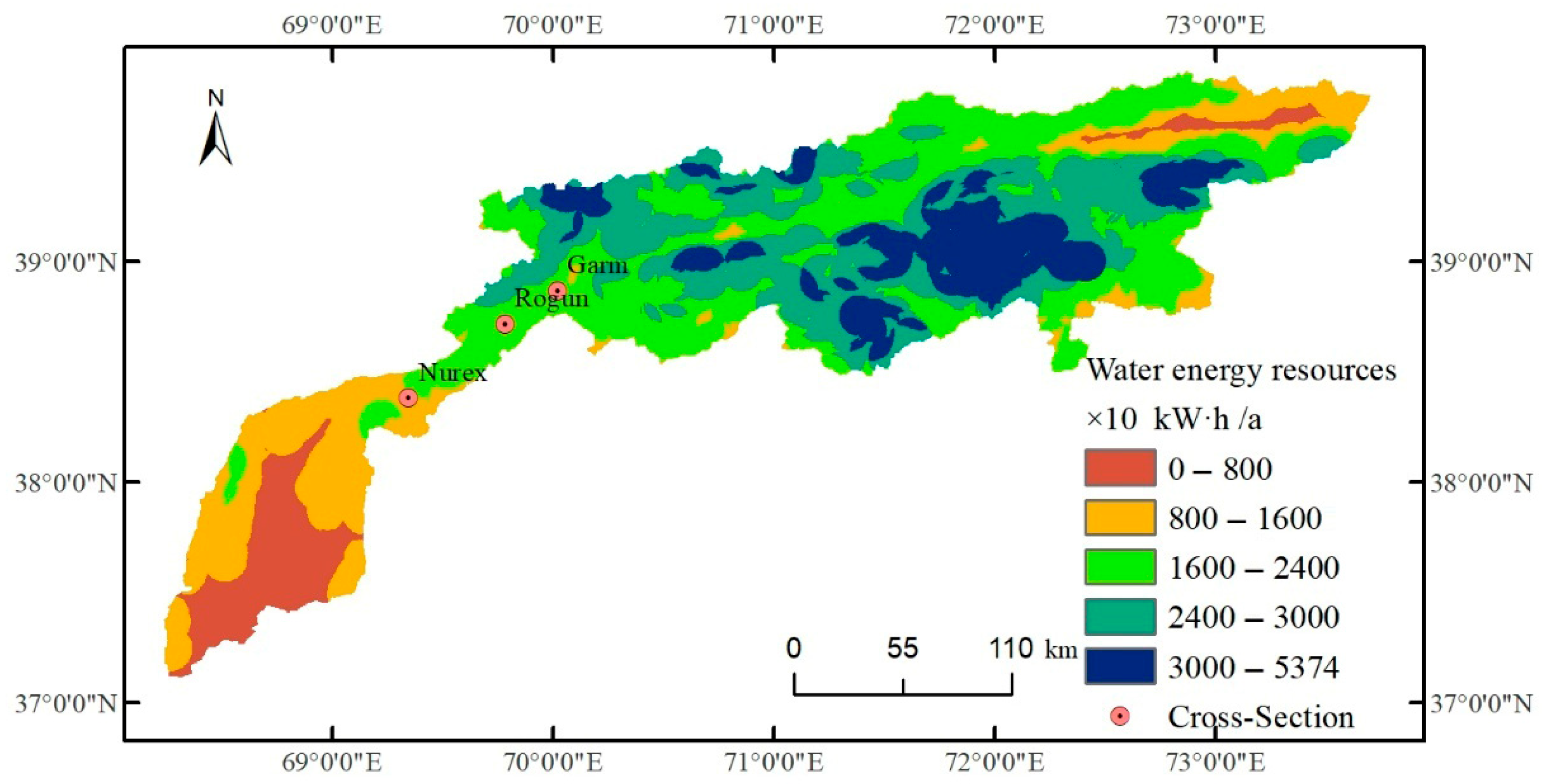
3.1.1. Spatial Distribution of Hydropower Resources
3.1.2. Frequency Distribution Characteristics of Hydropower Resources
3.1.3. Intra-Annual Distribution Characteristics of Hydropower Resources
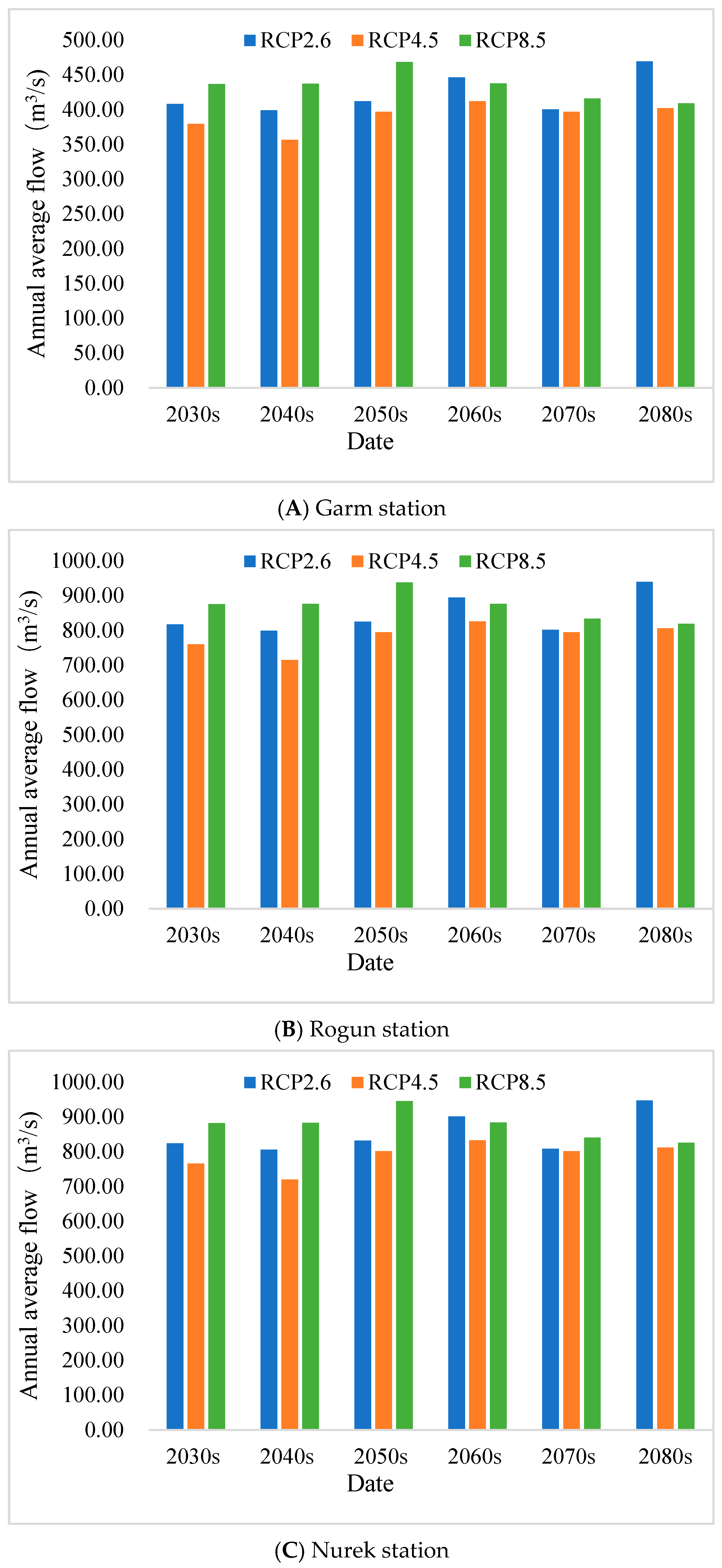
3.2. Impact of Climate Change on Hydropower Resources
3.2.1. Impact of Climate Change on Runoff
3.2.2. Impact of Climate Change on Hydropower Resources
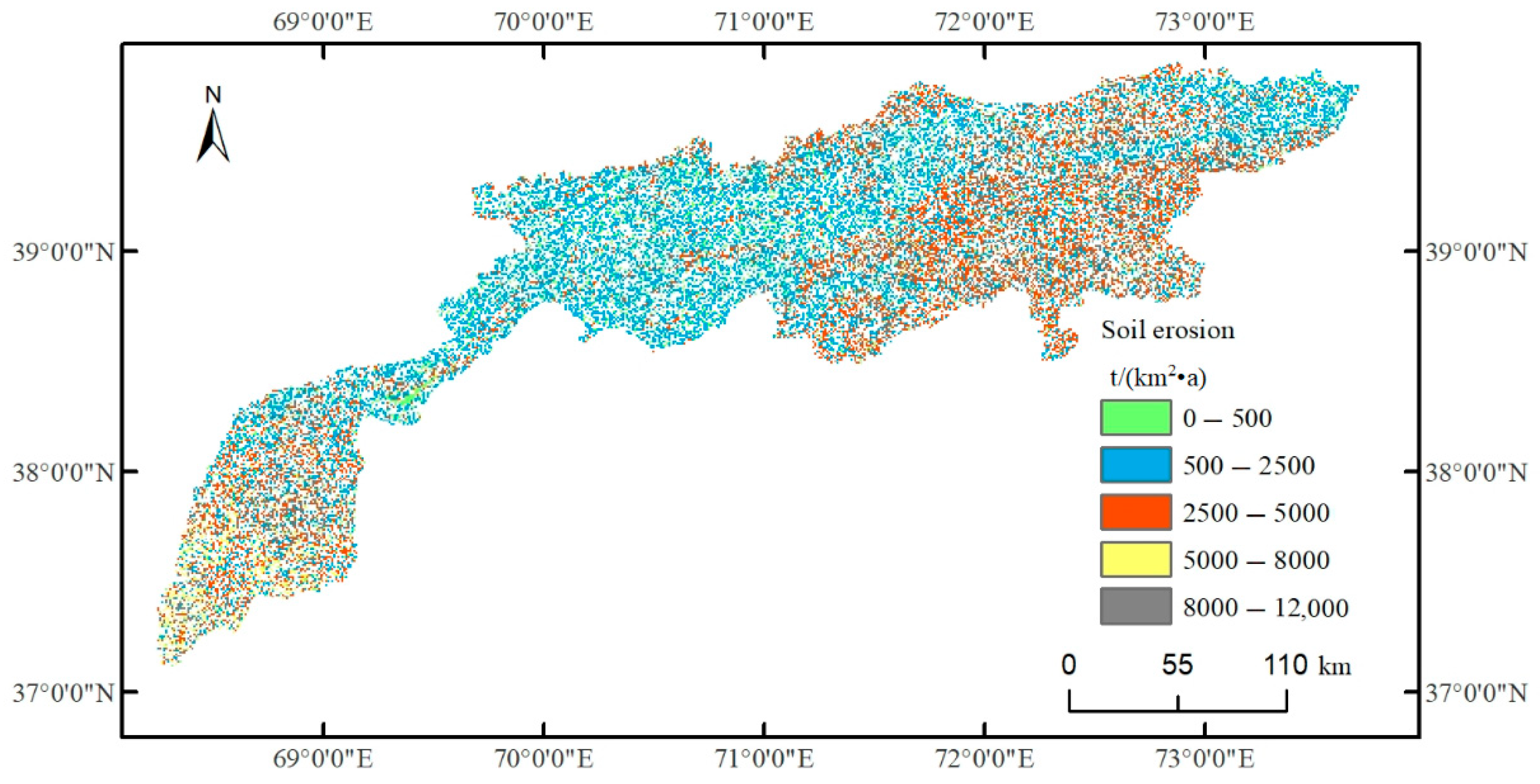
3.2.3. Estimation of Soil Erosion
3.2.4. Impact of Soil Erosion Changes on Hydropower Development
3.2.5. Uncertainty Analysis
- (1)
- Multi-source input data. The analysis utilizes DEM (Digital Elevation Model), remote sensing data, climate change scenario data, and observed data. Uncertainties arise from the resolution differences among these data sources and the impact of cloud cover on remote sensing data, with climate change scenario data exhibiting particularly prominent uncertainties.
- (2)
- Hydrological model parameters. The spatial distributotal, tion of three hydrological meteorological stations in the basin is insufficient to accurately represent spatial variations in the Vakhsh River Basin, which features complex topography. Although most model parameters are derived from field observations and information inversion, data errors and calibrated parameters still introduce significant uncertainties.
- (3)
- MUSLE factor parameters. In practical applications of the MUSLE model, many scholars adapt it to specific scenarios, leading to variations in thresholds across different contexts. Given the study area’s elevation range from low to high altitudes, high-altitude regions are characterized by steeper terrain and significant differences in soil erosion due to snow and glacier influence. This study does not classify these variations, introducing uncertainties into the results.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gilland, B. Population, economic growth, and energy demand, 1985–2020. Popul. Dev. Rev. 1988, 14, 233–244. [Google Scholar] [CrossRef]
- Holdren, J.P. Population and the energy problem. Popul. Env. 1991, 12, 231–255. [Google Scholar] [CrossRef]
- van Ruijven, B.J.; De Cian, E.; Wing, I.S. Amplification of future energy demand growth due to climate change. Nat. Commun. 2019, 10, 2762. [Google Scholar] [CrossRef]
- Siri, R.; Mondal, S.R.; Das, S. Hydropower: A renewable energy resource for sustainability in terms of climate change environmental protection. In Alternative Energy Resources; The handbook of environmental chemistry; Pathak, P., Srivastava, R.R., Eds.; Springer: Cham, Switzerland, 2020; Volume 99. [Google Scholar] [CrossRef]
- Andronova, I.V.; Kuzmin, V.V.; Tinkova, A.A. Global Hydropower as the main driver of sustainable development in the context of industry 40. In Industry 4.0; Zavyalova, E.B., Popkova, E.G., Eds.; Palgrave Macmillan: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Othman, M.E.F.; Sidek, L.M.; Basri, H.; El-Shafie, A.; Ahmed, A.N. Climate challenges for sustainable hydropower development and operational resilience: A review. Renew. Sustain. Energy Rev. 2025, 209, 115108. [Google Scholar] [CrossRef]
- Viers, J.H. Hydropower relicensing and climate change. J. Am. Water Resour. Assoc. 2011, 47, 655–661. [Google Scholar] [CrossRef]
- Falchetta, G.; David, E.H.J.; Gernaat, J.H.; Sebastian, S. Hydropower dependency and climate change in sub-Saharan Africa: A nexus framework and evidence-based review. J. Clean. Prod. 2019, 231, 1399–1417. [Google Scholar] [CrossRef]
- Neupane, P.; Khanal, A.; Kafle, M.; Bhattarai, S.; Khanal, A. Climate change influence on hydropower energy output variability. J. Appl. Water Eng. Res. 2025, 13, 251–268. [Google Scholar] [CrossRef]
- Vliet, M.V.; Wiberg, D.; Leduc, S.; Riahi, K. Power-generation system vulnerability and adaptation to changes in climate and water resources. Nat. Clim. Change 2016, 6, 375–380. [Google Scholar] [CrossRef]
- Shu, J.; Qu, J.J.; Motha, R.; Dong, D.F. Impacts of climate change on hydropower development and sustainability: A review. IOP Conf. Ser. Earth Environ. Sci. 2018, 163, 012126. [Google Scholar] [CrossRef]
- Zhang, Q.; Kang, S.; Chen, F. Glacier variations in the Fedchenko basin, Tajikistan, 1992–2006: Insights from remote-sensing images. Mt. Res. Dev. 2014, 34, 56–65. [Google Scholar] [CrossRef]
- Guay, C.; Minville, M.; Braun, M. A global portrait of hydrological changes at the 2050 horizon for the province of Québec. Can. Water Resour. J. Rev. Can. Des Ressour. Hydr. 2015, 40, 285–302. [Google Scholar] [CrossRef]
- Fu, X.; Wang, X.; Gong, Y.; Wang, Y.; Zhang, Y. Impact of snow weather on PV power generation and improvement of power forecasting. In Proceedings of the 2023 International Conference on Power Energy Systems and Applications (ICoPESA), Nanjing, China, 24–26 February 2023; pp. 448–453. [Google Scholar] [CrossRef]
- Chen, F.; Chen, J.; Huang, W.; Chen, S.; Huang, X.; Jin, L.; Jia, J.; Zhang, X.; An, C.; Zhang, J.; et al. Westerlies Asia and monsoonal Asia: Spatiotemporal differences in climate change and possible mechanisms on decadal to sub-orbital timescales. Earth-Sci. Rev. 2019, 192, 337–354. [Google Scholar] [CrossRef]
- Dilinuer, T.; Yao, J.-Q.; Chen, J.; Mao, W.-Y.; Yang, L.-M.; Yeernaer, H.; Chen, Y.-H. Regional drying and wetting trends over Central Asia based on Köppen climate classification in 1961–2015. Adv. Clim. Change Res. 2021, 12, 363–372. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Env. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Li, H.; Liu, Y.; Wang, C. Analysis of drought change and its impact in Central Asia. Adv. Earth Sci. 2022, 37, 37–50. [Google Scholar] [CrossRef]
- Jalilov, S.M.; Keskinen, M.; Varis, O.; Amer, S.; Ward, F.A. Managing the water–energy–food nexus: Gains and losses from new water development in Amu Darya river basin. J. Hydrol. 2016, 539, 648–661. [Google Scholar] [CrossRef]
- Yu, J.; Gao, B.; Li, M.; Xiao, P. Improving runoff modelling through strengthened snowmelt and glacier module enhances runoff attribution in a large watershed in Central Asia. J. Hydrol. 2025, 660, 133528. [Google Scholar] [CrossRef]
- Tan, Z.; Liu, H.; Gao, F. Experimental research on reduction measures of sediment Deposition of the power plant port under the long period wave. Procedia Eng. 2015, 116, 229–236. [Google Scholar] [CrossRef]
- Timmerman, J.G.; Koeppel, S.; Bernardini, F.; Buntsma, J.J. Adaptation to climate change: Challenges for transboundary water management. In The Economic, Social and Political Elements of Climate Change; Climate Change Management; Leal Filho, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Abuduwaili, J.; Issanova, G.; Saparov, G. Water resources in Tajikistan. In Hydrology and Limnology of Central Asia; Water Resources Development and Management; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Fallah, B.; Didovets, I.; Rostami, M.; Hamidi, M. Climate change impacts on Central Asia: Trends, extremes and future projections. Int. J. Climatol. 2024, 44, 3191–3213. [Google Scholar] [CrossRef]
- Chen, M.; Zeng, S.; Yang, L.; Ren, Y.; Xia, J. Statistical insights into the water exchange process in the Yangtze-Poyang System: The YPWES model. J. Hydrol. Reg. Stud. 2022, 40, 101054. [Google Scholar] [CrossRef]
- Bilal, H.; Siwar, C.; Mokhtar, M.B.; Lahlou, F.Z.; Kanniah, K.D.; Al-Ansari, T. Snow runoff modelling in the upper Indus River Basin and its implication to energy water food nexus. Ecol. Model. 2024, 498, 110871. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment-yield prediction with universal equation using runoff energy factor. In Present and Prospective Technology for Predicting Sediment Yield and Sources; US Department of Agriculture, Agriculture Research Service: Washington, DC, USA, 1975; pp. 244–252. [Google Scholar]
- Sadeghi, S.H.R.; Gholami, L.; Darvishan, A.K.; Saeidi, P. A review of the application of the MUSLE model worldwide. Hydrol. Sci. J. 2014, 59, 365–375. [Google Scholar] [CrossRef]
- Yang, L.; Gao, M.; Chen, J.; Shi, W.; Hou, C.; Liu, Z.; Luo, C.; Yu, J.; Yang, X.; Dong, J. Effects of climate variables and human activities on groundwater level fluctuations in unconsolidated sedimentary aquifers: A data-driven approach. Hydrology 2025, 12, 215. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, R.; Jiang, Y.; Zhang, W.; Liu, C.; Zhou, L. Soil erosion in Qilian Mountain National Park: Dynamics and driving mechanisms. J. Hydrol. Reg. Stud. 2022, 42, 101144. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Mannering, J.V. Relation of soil properties to its erodibility. Soil Sci. Soc. Am. Proc. 1963, 33, 131–137. [Google Scholar] [CrossRef]
- Williams, J.R.; Renard, K.G.; Dyke, P.T. A new method for assessing erosions effect on soil Productivity. J. Soil Water Conserv. 1983, 38, 38–383. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, J.C.; Yang, Q.K.; Baartman, J.E.M.; Gai, L.; Yang, X.; Li, S.Q.; Yu, J.; Ritsema, C.J.; Geissen, V. An improved method for calculating slope length(λ) and the LS parameters of the revised universal soil loss equation for large watersheds. Geoderma 2017, 308, 36–45. [Google Scholar] [CrossRef]
- Cai, C.; Ding, S.; Shi, Z.; Huang, L.; Zhang, G.Y. Study of applying USLE and geographical information system IDRISI to predict soil erosion in small watershed. J. Soil Water Conserv. 2000, 14, 19–24. [Google Scholar]
- Bhagwat, N.; Kumar, R.; Qureshi, M.; Nagisetty, R.M.; Zhou, X. The Status, Applications, and Modifications of the Snowmelt Runoff Model (SRM): A Comprehensive Review. Hydrology 2025, 12, 156. [Google Scholar] [CrossRef]
- Phien, H.N.; Ajirajah, T.J. Applications of the log Pearson type-3 distribution in hydrology. J. Hydrol. 1984, 73, 359–372. [Google Scholar] [CrossRef]
- Paul, J.; Pilon, K. Adamowski, Asymptotic variance of flood quantile in log Pearson Type III distribution with historical information. J. Hydrol. 1993, 143, 481–503. [Google Scholar] [CrossRef]
- Asghari, F.B.; Mohammadi, A.A.; Dehghani, M.H.; Yousefi, M. Data on assessment of groundwater quality with application of ArcGIS in Zanjan, Iran. Data Brief. 2018, 18, 375–379. [Google Scholar] [CrossRef] [PubMed]





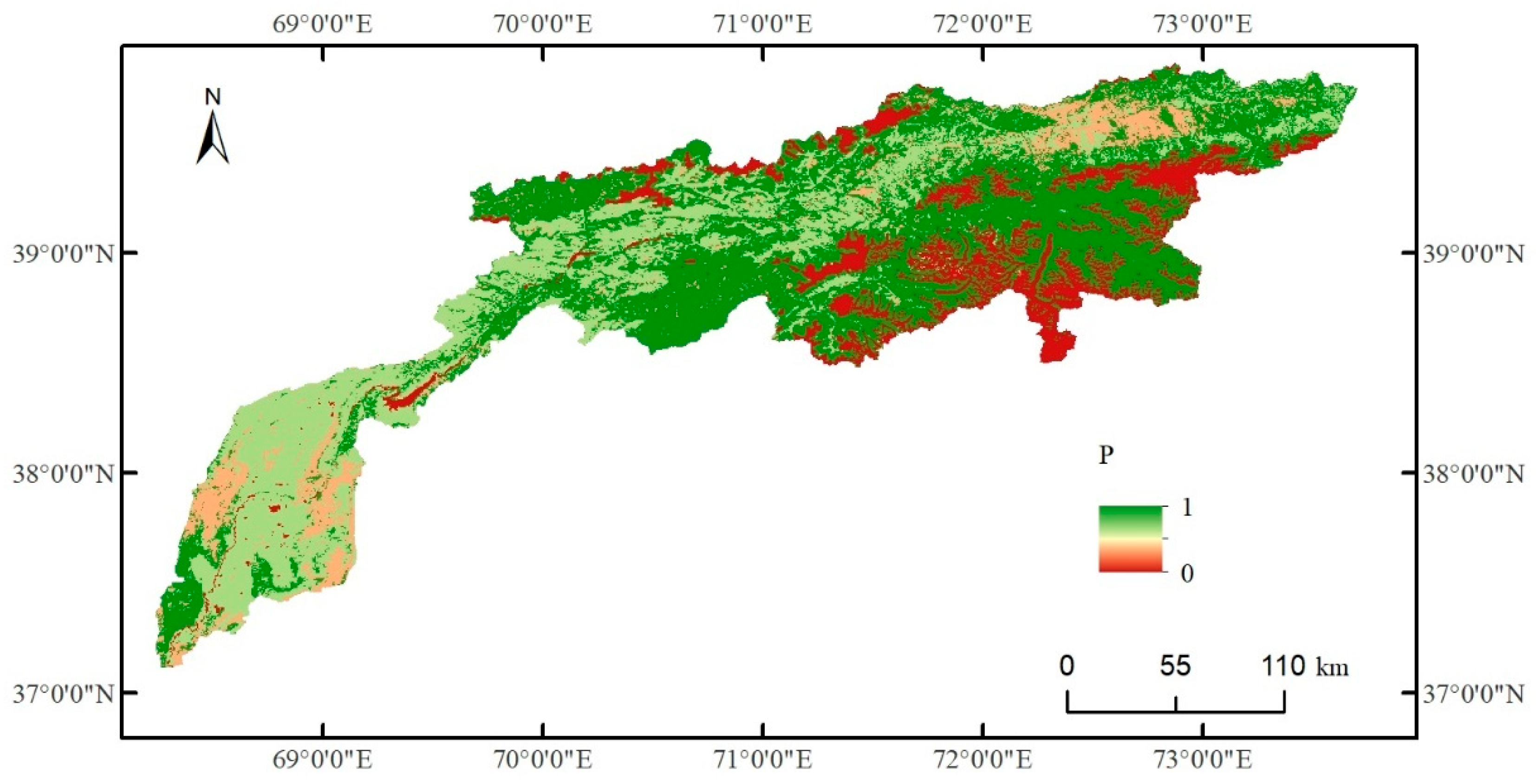
| Land Use Type | p |
|---|---|
| Farmland | 0.01 |
| Forestland | 0.2 |
| Grassland | 0.6 |
| Water Body | 0 |
| Built-up Area | 1 |
| Bare Land | 0.8 |
| Name | Elevation Difference (m) | Mean Annual Flow (m3/s) | Hydropower Resources (×108 kWh/a) |
|---|---|---|---|
| Garm | 2007 | 321.92 | 554.65 |
| Rogun | 2036 | 645.0 | 1127.37 |
| Nurek | 1413 | 650.05 | 788.53 |
| Variable | Scenario | 2030s | 2040s | 2050s | 2060s | 2070s | 2080s |
|---|---|---|---|---|---|---|---|
| TMax (°C) | RCP2.6 | 0.19 | 0.18 | 0.33 | 0.46 | 0.44 | 0.27 |
| RCP4.5 | 0.20 | 0.28 | 0.36 | 0.52 | 0.62 | 0.61 | |
| RCP8.5 | 0.21 | 0.51 | 0.76 | 0.83 | 1.19 | 1.40 | |
| TMin (°C) | RCP2.6 | 0.22 | 0.22 | 0.35 | 0.40 | 0.44 | 0.27 |
| RCP4.5 | 0.26 | 0.32 | 0.33 | 0.50 | 0.49 | 0.51 | |
| RCP8.5 | 0.19 | 0.46 | 0.63 | 0.70 | 1.04 | 1.15 | |
| Tav (°C) | RCP2.6 | 0.21 | 0.20 | 0.34 | 0.43 | 0.44 | 0.27 |
| RCP4.5 | 0.23 | 0.30 | 0.35 | 0.51 | 0.56 | 0.56 | |
| RCP8.5 | 0.20 | 0.49 | 0.69 | 0.76 | 1.12 | 1.28 | |
| p (mm) | RCP2.6 | 6.67 | 5.96 | 6.97 | 9.60 | 6.06 | 11.41 |
| RCP4.5 | 6.27 | 3.79 | 8.18 | 9.86 | 8.16 | 8.75 | |
| RCP8.5 | 8.19 | 8.22 | 10.44 | 8.25 | 6.72 | 6.21 |
| Item | Reservoir Capacity (×108 m3) | Accumulation of Sediment (m3) | Head Loss (m) | Hydropower Energy Loss (kWh/a) |
|---|---|---|---|---|
| p (Multi-year average) | 133 | 329,818.71 | (8.31 ± 1.15) × 10−3 | (1.57 ± 0.22) × 106 |
| p ↑ + 1 mm | ↑ 1978.91 | ↑ (4.98 ± 0.69) × 10−5 | ↑ 939.93 ± 130.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Gulakhmadov, A.; Shaimuradov, F. Impact Analysis of Climate Change on Hydropower Resource Development in the Vakhsh River Basin of Tajikistan. Hydrology 2025, 12, 294. https://doi.org/10.3390/hydrology12110294
Liu H, Gulakhmadov A, Shaimuradov F. Impact Analysis of Climate Change on Hydropower Resource Development in the Vakhsh River Basin of Tajikistan. Hydrology. 2025; 12(11):294. https://doi.org/10.3390/hydrology12110294
Chicago/Turabian StyleLiu, Hailong, Aminjon Gulakhmadov, and Firdavs Shaimuradov. 2025. "Impact Analysis of Climate Change on Hydropower Resource Development in the Vakhsh River Basin of Tajikistan" Hydrology 12, no. 11: 294. https://doi.org/10.3390/hydrology12110294
APA StyleLiu, H., Gulakhmadov, A., & Shaimuradov, F. (2025). Impact Analysis of Climate Change on Hydropower Resource Development in the Vakhsh River Basin of Tajikistan. Hydrology, 12(11), 294. https://doi.org/10.3390/hydrology12110294







