Long-Term Hydrodynamic Modeling of Low-Flow Conditions with Groundwater–River Interaction: Case Study of the Rur River
Abstract
1. Introduction
- Improve the representation of groundwater–river dynamics by explicitly incorporating bidirectional exchange processes.
- Enable the assessment of the spatio-temporal patterns of groundwater–river interactions.
- Ensure consistent accuracy, stability, and computational efficiency over extended simulation periods.
2. Materials and Methods
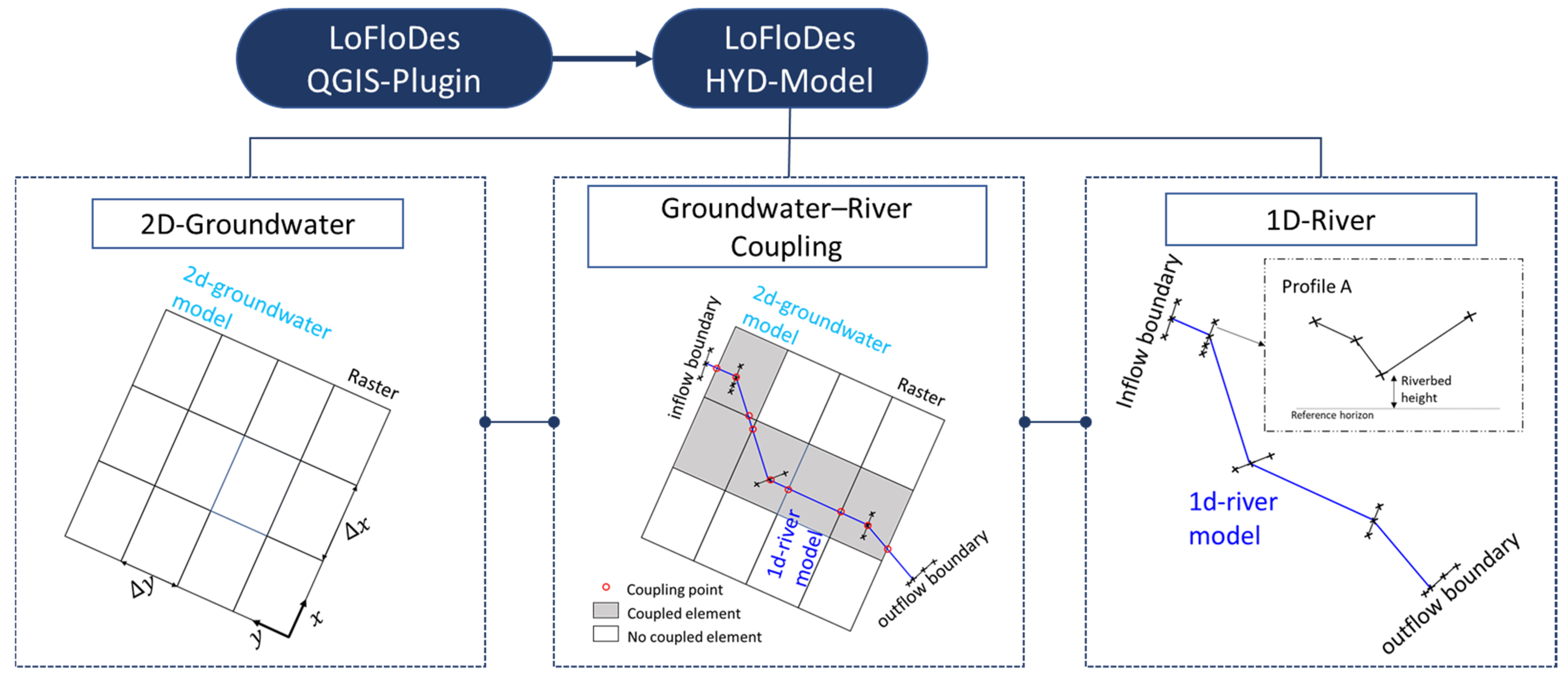
2.1. Software LoFloDes
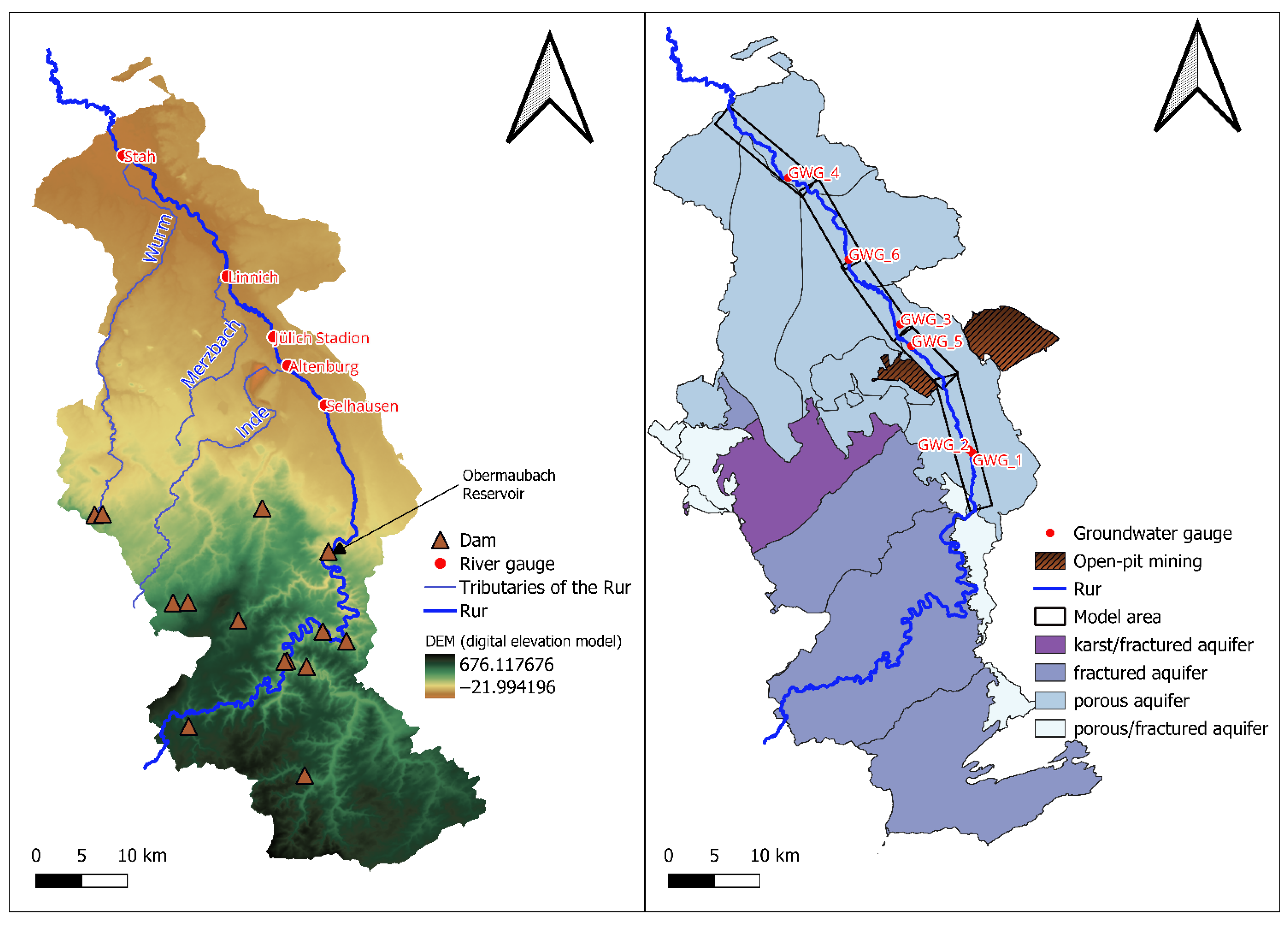
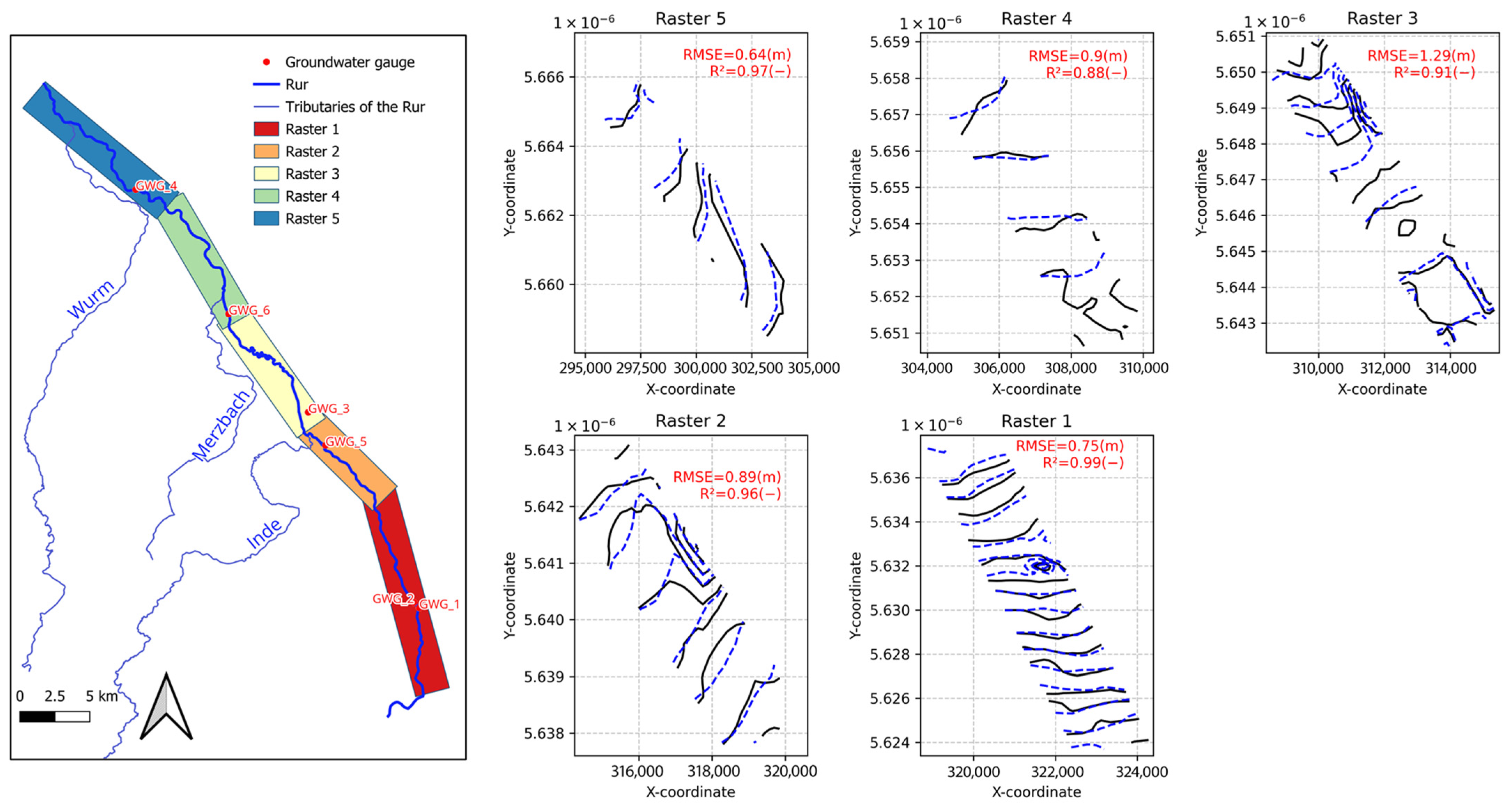
2.2. Study Area: The Rur River Basin
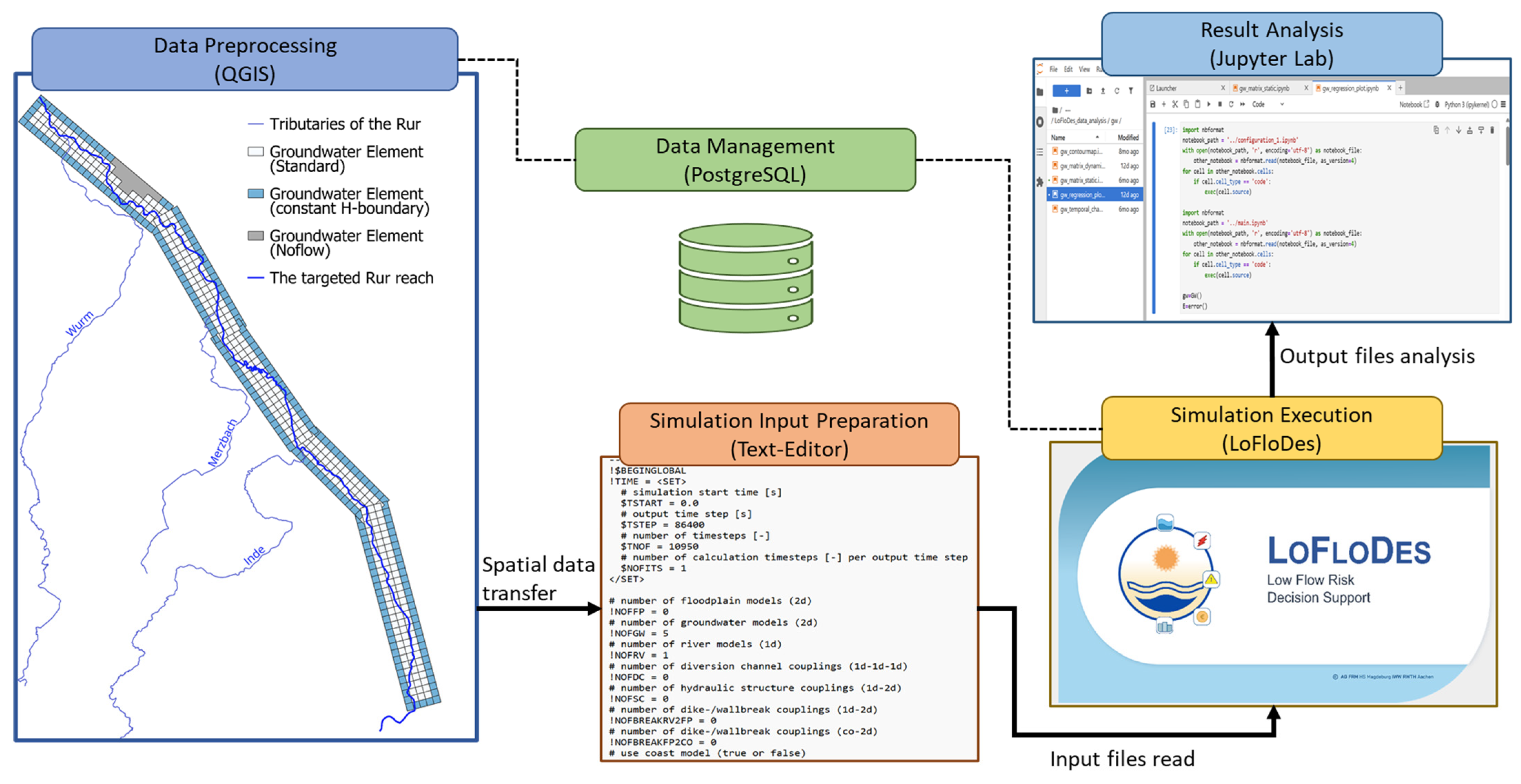
2.3. Coupled Model in the Rur River Basin
2.4. Initial Simulation, Calibration, and Validation
3. Results
3.1. Calibration 2002–2005
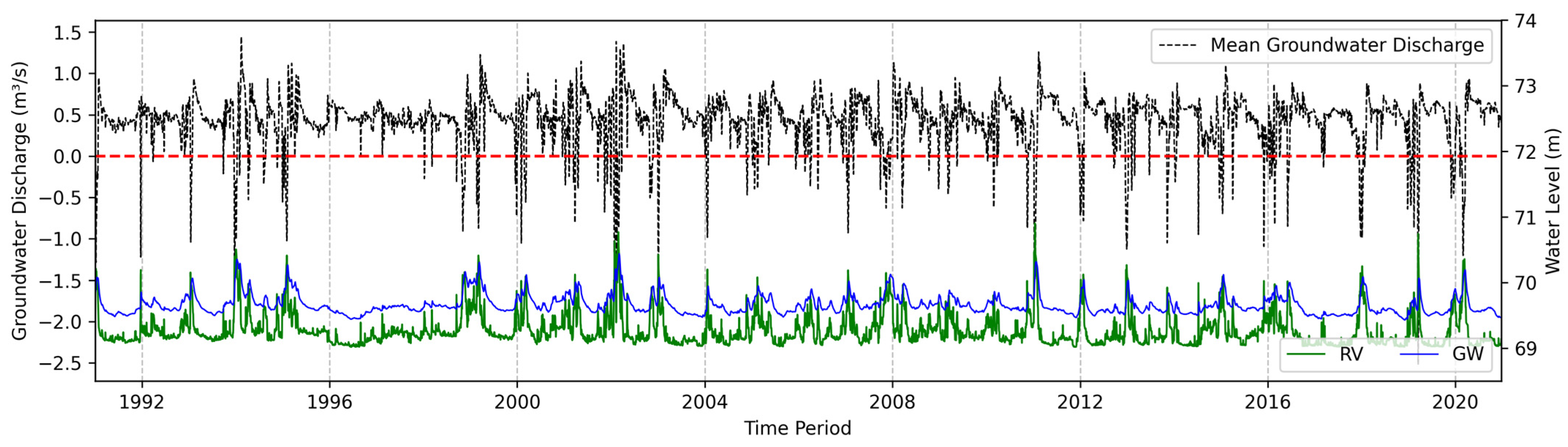
3.2. Long-Term Simulation for 1991–2020
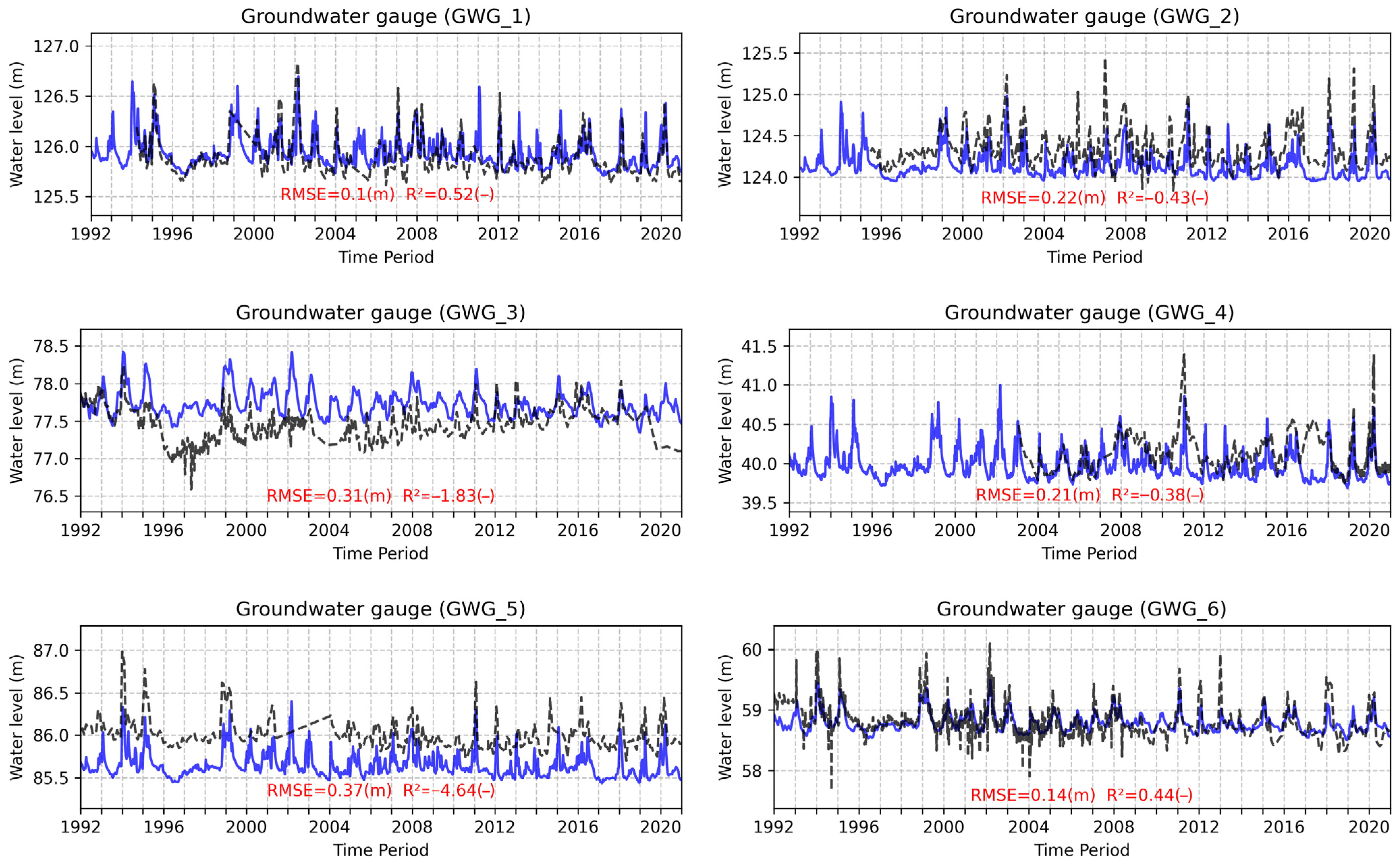
3.2.1. Groundwater Results
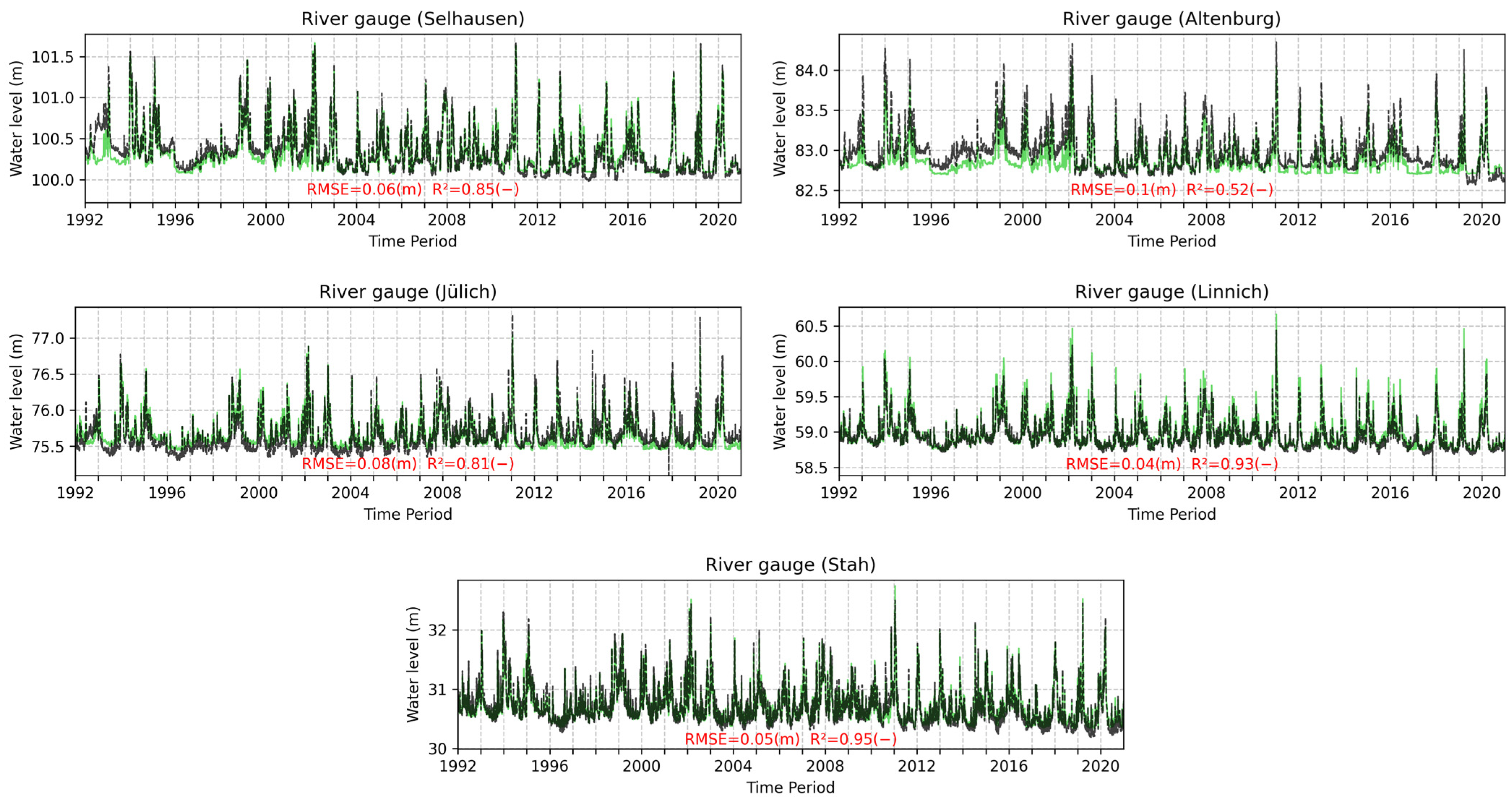
3.2.2. River Results
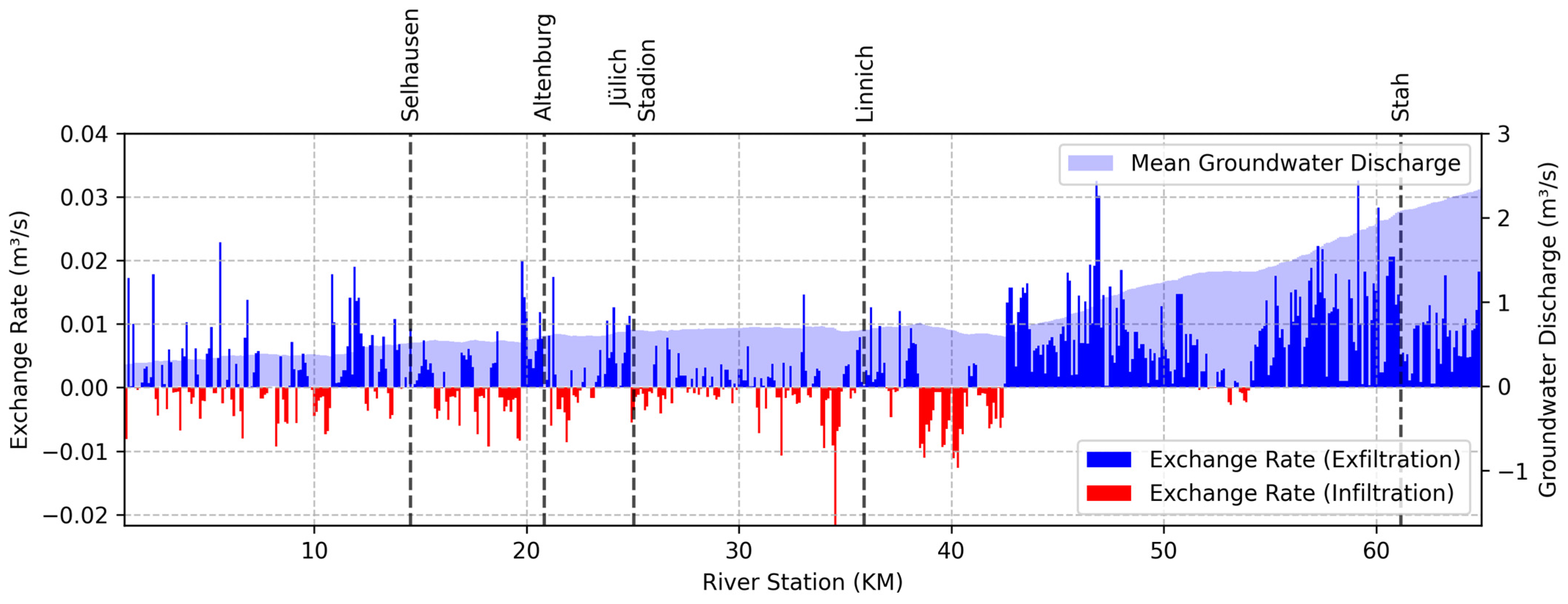
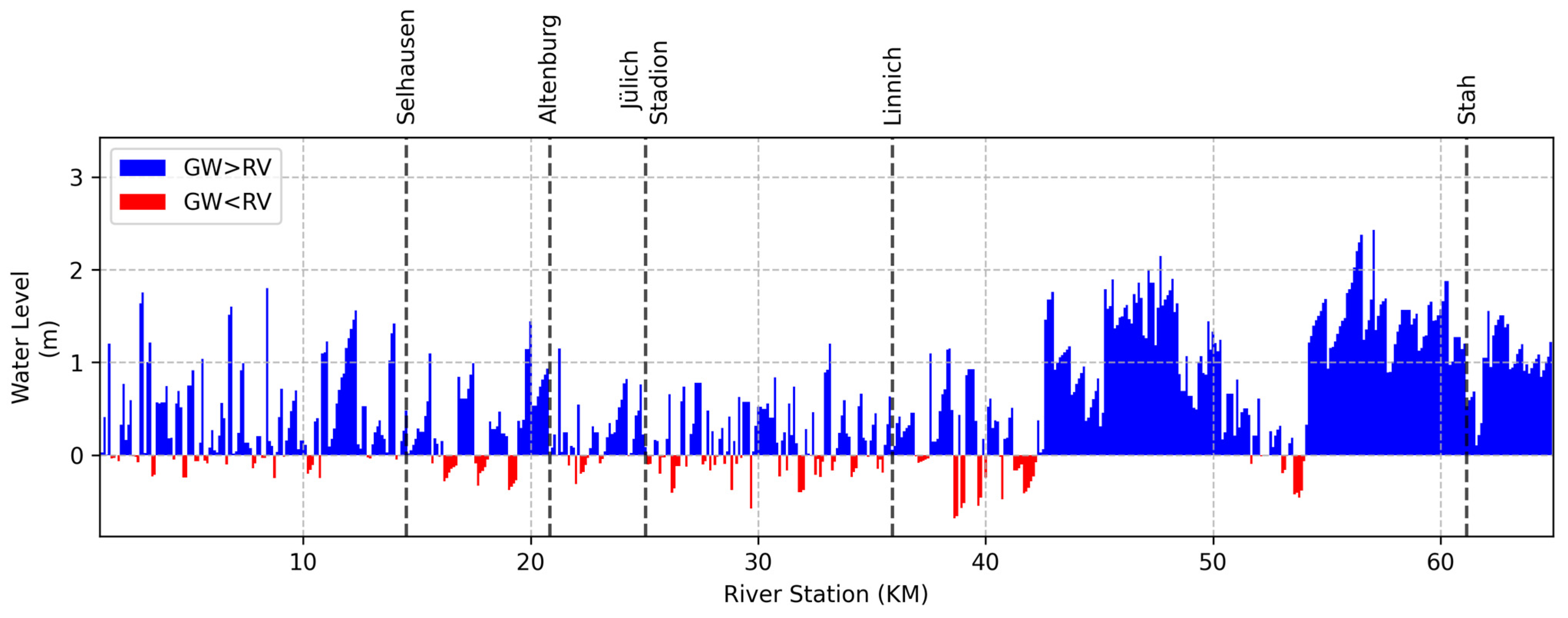
3.2.3. Exchange Between Groundwater and River Systems
4. Discussion
4.1. The Long-Term Simulation Along the Rur Reach
4.2. Discussion on Software Usability and Further Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LoFloDes | Low Flow Decision Support Tool |
| ProMaiDes | Protection Measures against Inundation Decision Support Tool |
| RV | River Water |
| GW | Groundwater |
| HK | Hydrogeological Map |
| AI | Artificial Intelligence |
References
- Van Loon, A.F. Hydrological drought explained. WIREs Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Cenobio-Cruz, O.; Quintana-Seguí, P.; Barella-Ortiz, A.; Zabaleta, A.; Garrote, L.; Clavera-Gispert, R.; Habets, F.; Beguería, S. Improvement of low flows simulation in the SASER hydrological modeling chain. J. Hydrol. X 2023, 18, 100147. [Google Scholar] [CrossRef]
- Laaha, G.; Demuth, S.; Hisdal, H.; Kroll, C.N.; van Lanen, H.A.J.; Nester, T.; Rogger, M.; Sauquet, E.; Tallaksen, L.M.; Woods, R.A.; et al. Prediction of low flows in ungauged basins. In Runoff Prediction in Ungauged Basins; Blöschl, G., Sivapalan, M., Wagener, T., Viglione, A., Savenije, H., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 163–188. ISBN 9781139235761. [Google Scholar]
- Nalbantis, I.; Tsakiris, G. Assessment of Hydrological Drought Revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- van Loon, A.F.; van Lanen, H.A.J. A process-based typology of hydrological drought. Hydrol. Earth Syst. Sci. 2012, 16, 1915–1946. [Google Scholar] [CrossRef]
- Stahl, K.; Kohn, I.; Blauhut, V.; Urquijo, J.; De Stefano, L.; Acácio, V.; Dias, S.; Stagge, J.H.; Tallaksen, L.M.; Kampragou, E.; et al. Impacts of European drought events: Insights from an international database of text-based reports. Nat. Hazards Earth Syst. Sci. 2016, 16, 801–819. [Google Scholar] [CrossRef]
- Condon, L.E.; Kollet, S.; Bierkens, M.F.P.; Fogg, G.E.; Maxwell, R.M.; Hill, M.C.; Fransen, H.-J.H.; Verhoef, A.; Van Loon, A.F.; Sulis, M.; et al. Global Groundwater Modeling and Monitoring: Opportunities and Challenges. Water Resour. Res. 2021, 57, e2020WR029500. [Google Scholar] [CrossRef]
- Marchionni, V.; Daly, E.; Manoli, G.; Tapper, N.J.; Walker, J.P.; Fatichi, S. Groundwater Buffers Drought Effects and Climate Variability in Urban Reserves. Water Resour. Res. 2020, 56, e2019WR026192. [Google Scholar] [CrossRef]
- Hellwig, J. Grundwasserdürren in Deutschland von 1970 bis 2018. Korresp. Wasserwirtsch. 2019, 12, 10. [Google Scholar]
- Haque, A.; Salama, A.; Lo, K.; Wu, P. Surface and Groundwater Interactions: A Review of Coupling Strategies in Detailed Domain Models. Hydrology 2021, 8, 35. [Google Scholar] [CrossRef]
- Lewandowski, J.; Meinikmann, K.; Krause, S. Groundwater–Surface Water Interactions: Recent Advances and Interdisciplinary Challenges. Water 2020, 12, 296. [Google Scholar] [CrossRef]
- Kelly, L.; Kalin, R.M.; Bertram, D.; Kanjaye, M.; Nkhata, M.; Sibande, H. Quantification of Temporal Variations in Base Flow Index Using Sporadic River Data: Application to the Bua Catchment, Malawi. Water 2019, 11, 901. [Google Scholar] [CrossRef]
- Zink, M.; Samaniego, L.; Kumar, R.; Thober, S.; Mai, J.; Schäfer, D.; Marx, A. The German drought monitor. Environ. Res. Lett. 2016, 11, 74002. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Chung, S.Y.; Kim, G.-B.; Senapathi, V. Drought and Groundwater Development. Water 2023, 15, 1908. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Van Lanen, H.A.J. (Eds.) Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater, 1st ed.; Reprint; Elsevier: Amsterdam, The Netherlands, 2004; ISBN 0444517677. [Google Scholar]
- Haslinger, K.; Koffler, D.; Schöner, W.; Laaha, G. Exploring the link between meteorological drought and streamflow: Effects of climate-catchment interaction. Water Resour. Res. 2014, 50, 2468–2487. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Marchant, B.P. Analysis of groundwater drought building on the standardised precipitation index approach. Hydrol. Earth Syst. Sci. 2013, 17, 4769–4787. [Google Scholar] [CrossRef]
- Stoelzle, M.; Stahl, K.; Morhard, A.; Weiler, M. Streamflow sensitivity to drought scenarios in catchments with different geology. Geophys. Res. Lett. 2014, 41, 6174–6183. [Google Scholar] [CrossRef]
- Hellwig, J.; Stahl, K. An assessment of trends and potential future changes in groundwater-baseflow drought based on catchment response times. Hydrol. Earth Syst. Sci. 2018, 22, 6209–6224. [Google Scholar] [CrossRef]
- Carlier, C.; Wirth, S.B.; Cochand, F.; Hunkeler, D.; Brunner, P. Exploring Geological and Topographical Controls on Low Flows with Hydrogeological Models. Ground Water 2019, 57, 48–62. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W. A review of regional groundwater flow modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef]
- Guevara-Ochoa, C.; Medina-Sierra, A.; Vives, L. Spatio-temporal effect of climate change on water balance and interactions between groundwater and surface water in plains. Sci. Total Environ. 2020, 722, 137886. [Google Scholar] [CrossRef]
- Huo, A.-D.; Dang, J.; Song, J.-X.; Chen, X.H.; Mao, H.-R. Simulation modeling for water governance in basins based on surface water and groundwater. Agric. Water Manag. 2016, 174, 22–29. [Google Scholar] [CrossRef]
- Surinaidu, L.; Muthuwatta, L.; Amarasinghe, U.A.; Jain, S.K.; Ghosh, N.C.; Kumar, S.; Singh, S. Reviving the Ganges Water Machine: Accelerating surface water and groundwater interactions in the Ramganga sub-basin. J. Hydrol. 2016, 540, 207–219. [Google Scholar] [CrossRef]
- Amanambu, A.C.; Obarein, O.A.; Mossa, J.; Li, L.; Ayeni, S.S.; Balogun, O.; Oyebamiji, A.; Ochege, F.U. Groundwater system and climate change: Present status and future considerations. J. Hydrol. 2020, 589, 125163. [Google Scholar] [CrossRef]
- Singh, A. Groundwater modelling for the assessment of water management alternatives. J. Hydrol. 2013, 481, 220–229. [Google Scholar] [CrossRef]
- Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing regional-scale spatio-temporal patterns of groundwater–surface water interactions using a coupled SWAT-MODFLOW model. Hydrol. Process. 2016, 30, 4420–4433. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.N.; Gowda, P.H.; Steiner, J.L.; Starks, P.J.; Arnold, J.G.; Srinivasan, R. A model integration framework for linking SWAT and MODFLOW. Environ. Model. Softw. 2015, 73, 103–116. [Google Scholar] [CrossRef]
- Rodriguez, L.B.; Cello, P.A.; Vionnet, C.A.; Goodrich, D. Fully conservative coupling of HEC-RAS with MODFLOW to simulate stream–aquifer interactions in a drainage basin. J. Hydrol. 2008, 353, 129–142. [Google Scholar] [CrossRef]
- Miro, M.E.; Groves, D.; Tincher, B.; Syme, J.; Tanverakul, S.; Catt, D. Adaptive water management in the face of uncertainty: Integrating machine learning, groundwater modeling and robust decision making. Clim. Risk Manag. 2021, 34, 100383. [Google Scholar] [CrossRef]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 3904. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D.; et al. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Langevin, C.D.; Hughes, J.D.; Banta, E.R.; Niswonger, R.G.; Panday, S.; Provost, A.M. Techniques and Methods; US Geological Survey: Reston, VA, USA, 2017. [Google Scholar]
- DHI. MIKE SHE Fully Integrated Exercises; Danish Hydraulic Institute: Hørsholm, Denmark, 2025. [Google Scholar]
- Aquanty Inc. HydroGeoSphere (HGS) Theory Manual; Aquanty Inc.: Waterloo, ON, Canada, 2025. [Google Scholar]
- Maxwell, R.M.; Kollet, S.J.; Smith, S.G.; Woodward, C.S.; Falgout, R.D.; Ferguson, I.M.; Baldwin, C.; Bosl, W.J.; Hornung, R.; Ashby, S.; et al. ParFlow User’s Manual. Available online: https://parflow.readthedocs.io/en/latest/index.html (accessed on 26 September 2025).
- Satzinger, U.; Bachmann, D. Conceptual approach for a holistic low-flow risk analysis. Hydrol. Process. 2024, 38, e15217. [Google Scholar] [CrossRef]
- Bachmann, D. Beitrag zur Entwicklung eines Entscheidungsunterstützungssystems zur Bewertung und Planung von Hochwasserschutzmaßnahmen; RWTH Aachen University: Aachen, Germany, 2012. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005 : The U.S. Geological Survey modular ground-water model—the ground-water flow process: Techniques and Methods. Tech. Methods 2005, 6-A16. [Google Scholar] [CrossRef]
- Hindmarsh, A.; Serban, R. User Documentation for CVODES v2.1.0; United States. Department of Energy by the University of California: Washington, DC, USA, 2009. [Google Scholar]
- Wolf, S.S. The Long-Term-Memory of a Typical Mid-European Upland to Lowland River |b or Why We Struggle to Reach a Good Ecological State for Our Rivers; RWTH Aachen University: Aachen, Germany, 2023. [Google Scholar]
- Nilson, E. Flusslandschaften im Wandel. In Grenzüberschreitendes Integratives Gewässermanagement; Reineke, T., Lehmkuhl, F., Und Blümel, H., Eds.; Sankt Augustin, Academia-Verl.: Sankt Augustin, Germany, 2006. [Google Scholar]
- Forschungszentrum Jülich. MOSYRUR: Water Balance Analysis in the Rur Basin, 1st ed.; Forschungszentrum, Zentralbibliothek: Jülich, Germany, 2005; ISBN 3893363858. [Google Scholar]
- Eurostat. CNTR_RG_20M_2024_4326.shp. Available online: https://ec.europa.eu/eurostat/de/web/gisco/geodata/administrative-units/countries (accessed on 10 July 2025).
- Johann, P. Grenzen der Belastbarkeit: Die Flüsse Rur (Roer) und Inde im Industriezeitalter; Verlag der Joseph-Kuhl-Gesellschaft: Jülich, Germany, 1994; ISBN 3980398803. [Google Scholar]
- WVER. Die Talsperren in der Nordeifel. In 100 Jahre Wasserwirtschaft in der Nordeifel; Wasserverband Eifel-Rur: Düren, Germany, 1999; pp. 64–72. [Google Scholar]
- Kufeld, M.; Lange, J.; Hausmann, B. Das Einzugsgebiet der Rur: Ergebnisbericht der im Rahmen des AMICE-Projekts Durchgeführten Literaturrecherche; AMICE, meus, maas; INTERREG IVB North West Europe Project (number 074C); Lehrstuhl und Institut für Wasserbau und Wasserwirtschaft RWTH-CONV-008445: Aachen, Germany, 2010; Available online: https://publications.rwth-aachen.de/record/48070 (accessed on 5 July 2025).
- Land NRW. ELWAS-WEB. 2024. Available online: https://www.elwasweb.nrw.de/elwas-web/index.xhtml;jsessionid=B23452E6234727BFB72FCBA00E256060 (accessed on 10 December 2024).
- Bezirksregierung Köln. Hydraulik Rur: Hydraulischer Längsschnitt; Bezirksregierung Köln: Köln, Germany, 2019. [Google Scholar]
- LANUV NRW. Landesweite Grundwasseroberfläche (Grundwassergleichen) für Mittlere Verhältnisse (2006–2015); LANUV NRW: Düsseldorf, Germany, 2023. [Google Scholar]
- DWD Climate Data Center. Grids of Monthly Total Precipitation Over Germany, Version v1.0.; DWD Climate Data Center: Offenbach, Germany, 2018. [Google Scholar]
- DWD Climate Data Center. Monthly Grids of the Accumulated Actual Evapotranspiration over Grass and Sandy Loam, Version 0.x; DWD Climate Data Center: Offenbach, Germany, 2018. [Google Scholar]
- BGR & SGD. Hydrogeological Map of Germany 1:250,000 (HÜK250); The German State Geological Surveys (SGD) and The Federal Institute for Geosciences and Natural Resources (BGR): Hannover, Germany, 2019. [Google Scholar]
- Bucher, B.; Denneborg, M. Infiltrationsverhalten der Rur. In Wasser und Boden; Wasser und Boden GmbH: Boppard, Germany, 1993; pp. 173–177. ISBN 0043-0951. [Google Scholar]
- Bollrich, G. Technische Hydromechanik, 4th ed.; Verl. Bauwesen: Berlin, Germany, 1996; ISBN 3345006081. [Google Scholar]
- Ntona, M.M.; Busico, G.; Mastrocicco, M.; Kazakis, N. Modeling groundwater and surface water interaction: An overview of current status and future challenges. Sci. Total Environ. 2022, 846, 157355. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Li, X.; Li, G.; Zhang, Y. Identifying Major Factors Affecting Groundwater Change in the North China Plain with Grey Relational Analysis. Water 2014, 6, 1581–1600. [Google Scholar] [CrossRef]
- Ren, X.; Li, P.; Wang, D.; Zhang, Q.; Ning, J. Drivers and characteristics of groundwater drought under human interventions in arid and semiarid areas of China. J. Hydrol. 2024, 631, 130839. [Google Scholar] [CrossRef]
- Doppler, T.; Franssen, H.-J.H.; Kaiser, H.-P.; Kuhlman, U.; Stauffer, F. Field evidence of a dynamic leakage coefficient for modelling river–aquifer interactions. J. Hydrol. 2007, 347, 177–187. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, G.; Mao, H.; Liao, F.; Shi, Z.; Huang, H. Numerical modeling for the temporal variations of the water interchange between groundwater and surface water in a regional great lake (Poyang Lake, China). J. Hydrol. 2022, 610, 127827. [Google Scholar] [CrossRef]
- Rahimi, M.; Essaid, H.I.; Wilson, J.T. The role of dynamic surface water-groundwater exchange on streambed denitrification in a first-order, low-relief agricultural watershed. Water Resour. Res. 2015, 51, 9514–9538. [Google Scholar] [CrossRef]
- Riedel, T.; Nolte, C.; Beek, T.; Liedtke, J.; Sures, B.; Grabner, D. Niedrigwasser, Dürre und Grundwasserneubildung—Be-standsaufnahme zur Gegen-Wärtigen Situation in Deutsch-land, den Klimaprojektionen und den Existierenden Maß-Nahmen und Strategien; Umweltbundesamt: Dessau-Roßlau, Germany, 2021. [Google Scholar]
- Folkens, L.; Bachmann, D.; Satzinger, U.; Schneider, P. The Hydro-Economic Modeling of Low-Flow Events on the Middle Elbe: Assessing Socio-Economic Impacts on River Navigation. Water 2024, 16, 3497. [Google Scholar] [CrossRef]

| Parameter | Unit | Explanation | Linked Equations |
|---|---|---|---|
| m | riverbed elevation | (2) | |
| m | absolute river water level | (2) | |
| manning values | (2) | ||
| river flow area | (1) and (2) | ||
| m | river hydraulic radius | (2) | |
| m | river wetted perimeter | (7) | |
| exchange discharge between two adjacent groundwater elements | (3) | ||
| exchange discharge between groundwater element and river profile | (7) | ||
| inflow and outflow of the control volume, e.g., river profile or groundwater element | (1) and (6) | ||
| additional sources and sinks as boundary conditions | (1) and (6) | ||
| exchange discharges from other coupled sub-models | (1) and (6) | ||
| groundwater transmissivity | (3)–(5) | ||
| m | absolute groundwater level | (3) and (5) | |
| m/s | groundwater hydraulic conductivity | (4) and (5) | |
| m | groundwater thickness | (3) and (4) | |
| m | groundwater bottom elevation | (3) | |
| eP | - | effective porosity | (6) |
| 1/s | leakage factor | (7) | |
| m | coupled river length | (7) | |
| m | riverbed thickness | (7) | |
| m | hydraulic gradient for groundwater and river: | (7) |
| Groundwater Rasters | Kfgw (m/s) | eP (-) | River Segments | Kfrv (1/s) | n (s/m1/3) |
|---|---|---|---|---|---|
| Raster_1 | 10−3 | 0.2 | inlet-Selhausen | 5 × 10−6 | 0.02 |
| Raster_2 | 5 × 10−4 | 0.2 | Selhausen-Altenburg | 5 × 10−6 | 0.02 |
| Raster_3 | 10−3 | 0.2 | Altenburg-Jülich Stadion | 5 × 10−6 | 0.01 |
| Raster_4 | 10−3 | 0.2 | Jülich Stadion-Linnich | 5 × 10−6 | 0.01 |
| Raster_5 | 10−3 | 0.2 | Linnich-Stah | 5 × 10−6 | 0.028 |
| Stah-outlet | 5 × 10−6 | 0.02 |
| Groundwater Rasters | 2003, 2004 | River Gauges | 2003, 2004 | ||
|---|---|---|---|---|---|
| RMSE (m) | R2 (−) | RMSE (m) | R2 (−) | ||
| Raster_1 | 1.16 | 0.98 | Selhausen | 0.03 | 0.98 |
| Raster_2 | 1.27 | 0.90 | Altenburg | 0.05 | 0.93 |
| Raster_3 | 1.77 | 0.87 | Jülich Stadion | 0.08 | 0.88 |
| Raster_4 | 1.20 | 0.75 | Linnich | 0.03 | 0.94 |
| Raster_5 | 0.90 | 0.94 | Stah | 0.04 | 0.98 |
| River Gauges | RMSE (m) | (−) | ||
|---|---|---|---|---|
| With GW | No GW | With GW | No GW | |
| Selhausen | 0.066 | 0.070 | 0.65 | 0.60 |
| Altenburg | 0.090 | 0.102 | 0.50 | 0.37 |
| Jülich Stadion | 0.075 | 0.074 | 0.59 | 0.60 |
| Linnich | 0.030 | 0.028 | 0.88 | 0.90 |
| Stah | 0.051 | 0.070 | 0.90 | 0.83 |
| Study | Software | Interaction Type | Spatial Resolution GW Model | Spatial Resolution RV Model | Computation Time; Time Step | Normalized Computation Time |
|---|---|---|---|---|---|---|
| This study | HYD module LoFloDes | Bidirectional | 500 m (550 Elements) | 100 m (524 Profiles) | 9900 s for 30 Years; Daily | 0.0016 s per Step-element |
| [32] | MODFLOW | Unidirectional (RV → GW) | 1000 m (21,120 Elements) | 1000 m (Unknown) | 1898 s for 22 Years; Monthly | 0.00034 s per Step-element |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Bachmann, D.; Schüttrumpf, H. Long-Term Hydrodynamic Modeling of Low-Flow Conditions with Groundwater–River Interaction: Case Study of the Rur River. Hydrology 2025, 12, 270. https://doi.org/10.3390/hydrology12100270
Wu Y, Bachmann D, Schüttrumpf H. Long-Term Hydrodynamic Modeling of Low-Flow Conditions with Groundwater–River Interaction: Case Study of the Rur River. Hydrology. 2025; 12(10):270. https://doi.org/10.3390/hydrology12100270
Chicago/Turabian StyleWu, You, Daniel Bachmann, and Holger Schüttrumpf. 2025. "Long-Term Hydrodynamic Modeling of Low-Flow Conditions with Groundwater–River Interaction: Case Study of the Rur River" Hydrology 12, no. 10: 270. https://doi.org/10.3390/hydrology12100270
APA StyleWu, Y., Bachmann, D., & Schüttrumpf, H. (2025). Long-Term Hydrodynamic Modeling of Low-Flow Conditions with Groundwater–River Interaction: Case Study of the Rur River. Hydrology, 12(10), 270. https://doi.org/10.3390/hydrology12100270