Runoff Prediction in the Songhua River Basin Based on WEP Model
Abstract
1. Introduction
2. Data and Methods
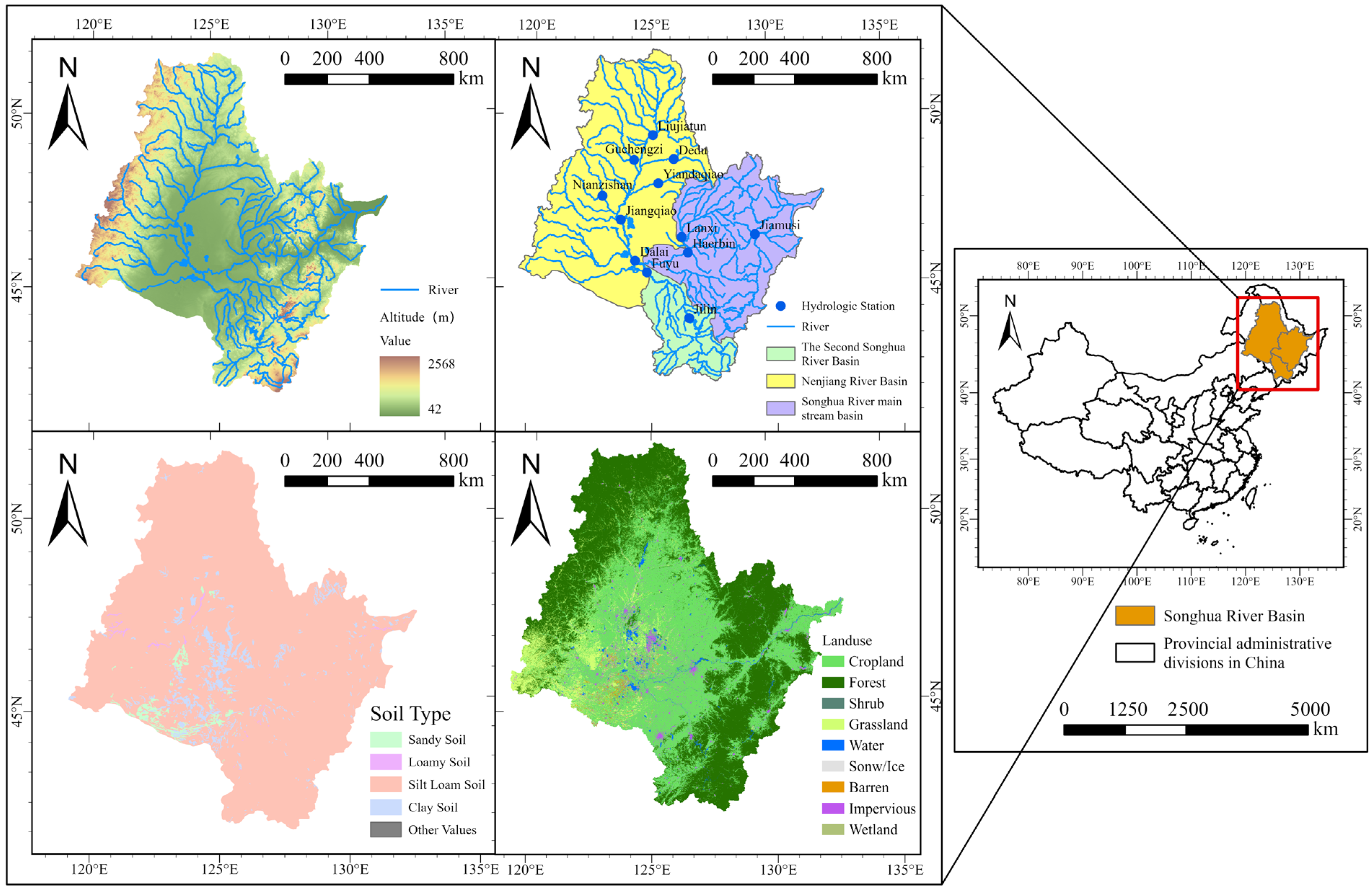
2.1. Study Area
2.2. Data
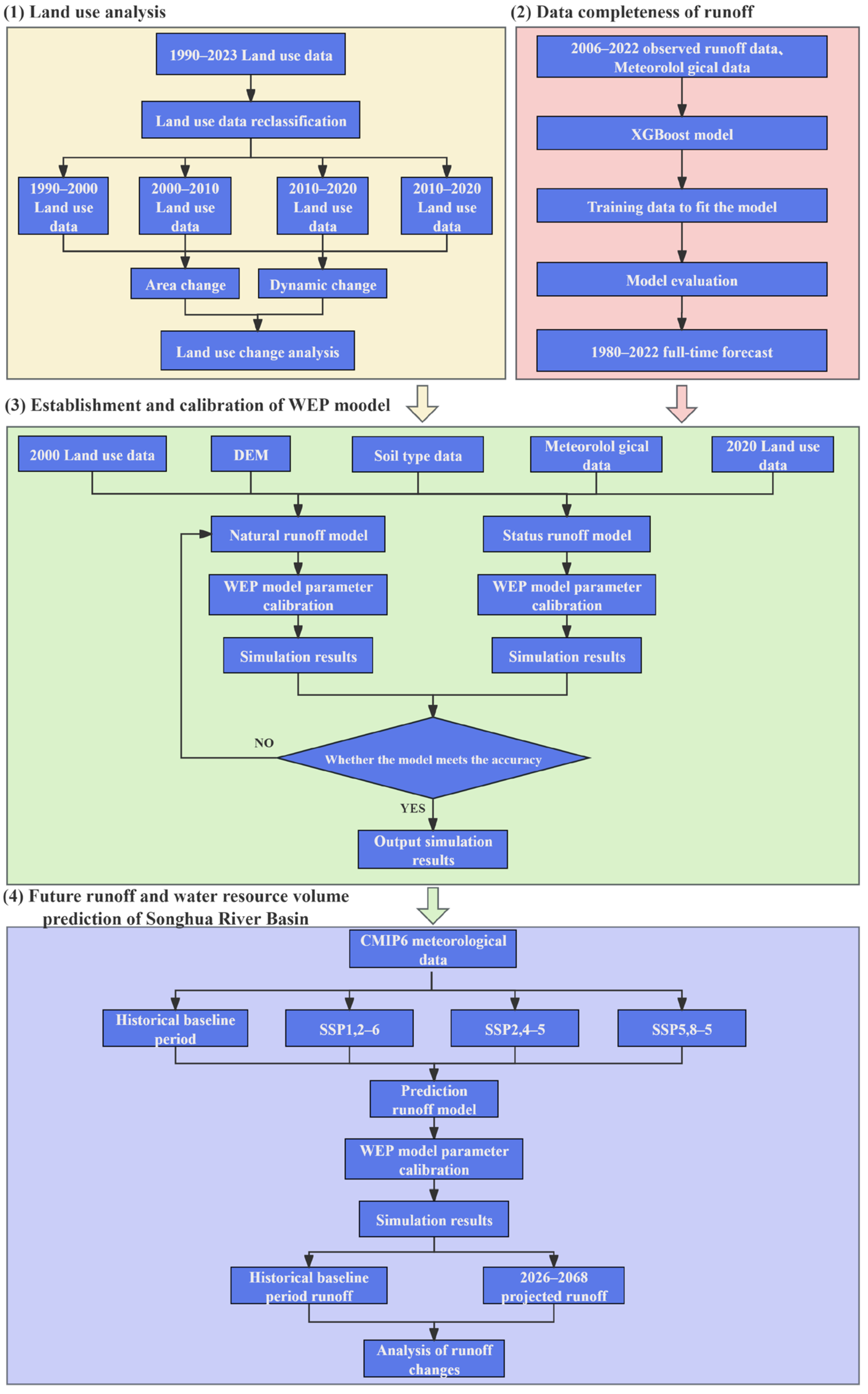
2.3. Methods
2.3.1. Land Use Change
Land Use Dynamic Degree (LUD) Index
Land Use Transfer Matrix
2.3.2. The Extreme Gradient Boosting Model
2.3.3. The WEP Model
Model Principle and Calculation Unit
2.3.4. Methods of Evaluation
The eXtreme Gradient Boosting Model Accuracy Evaluation
The WEP Model Accuracy Evaluation
Correlation Test
3. Results
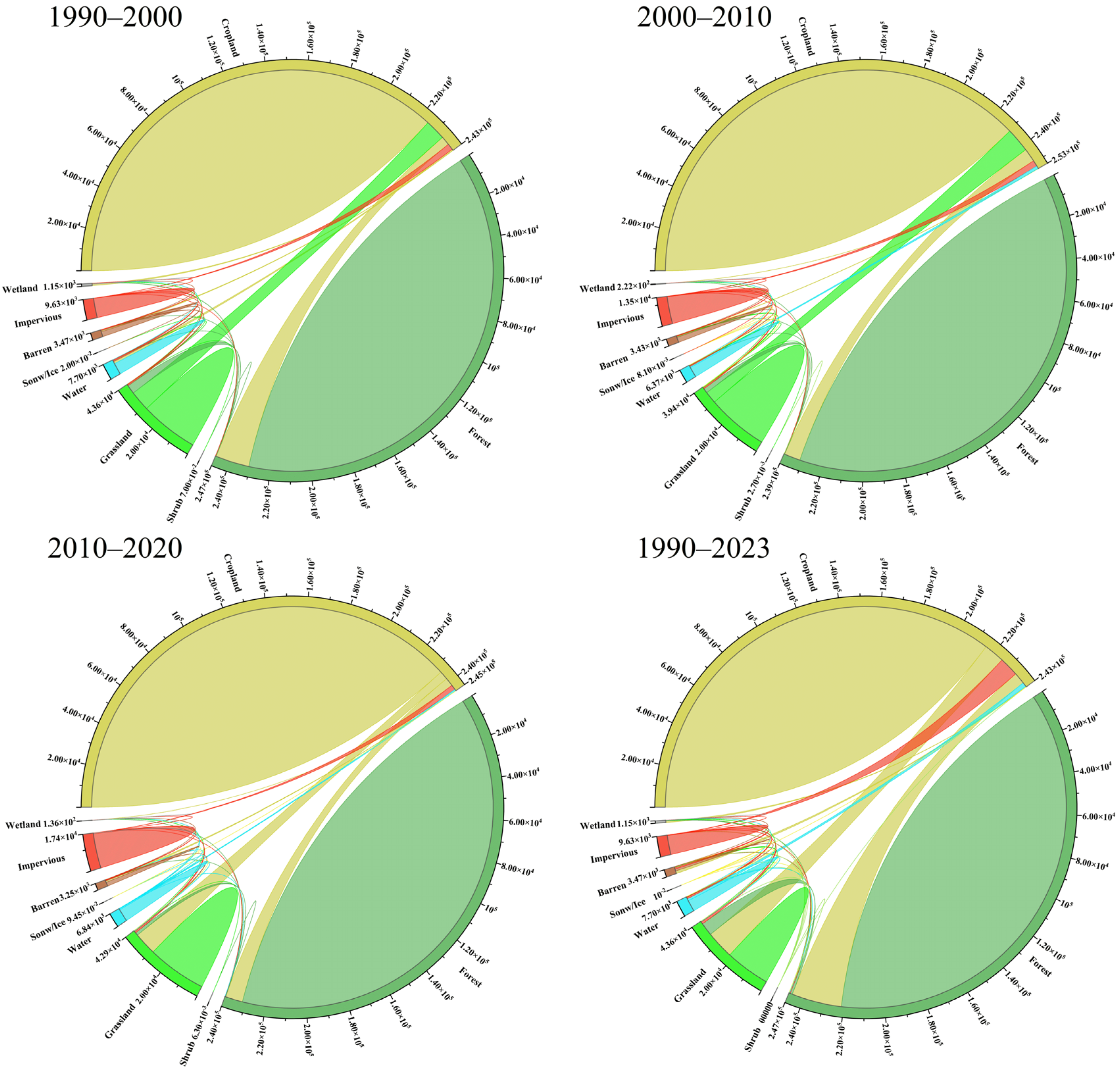
3.1. Land Use Change Analysis
3.2. Completed Measured Runoff
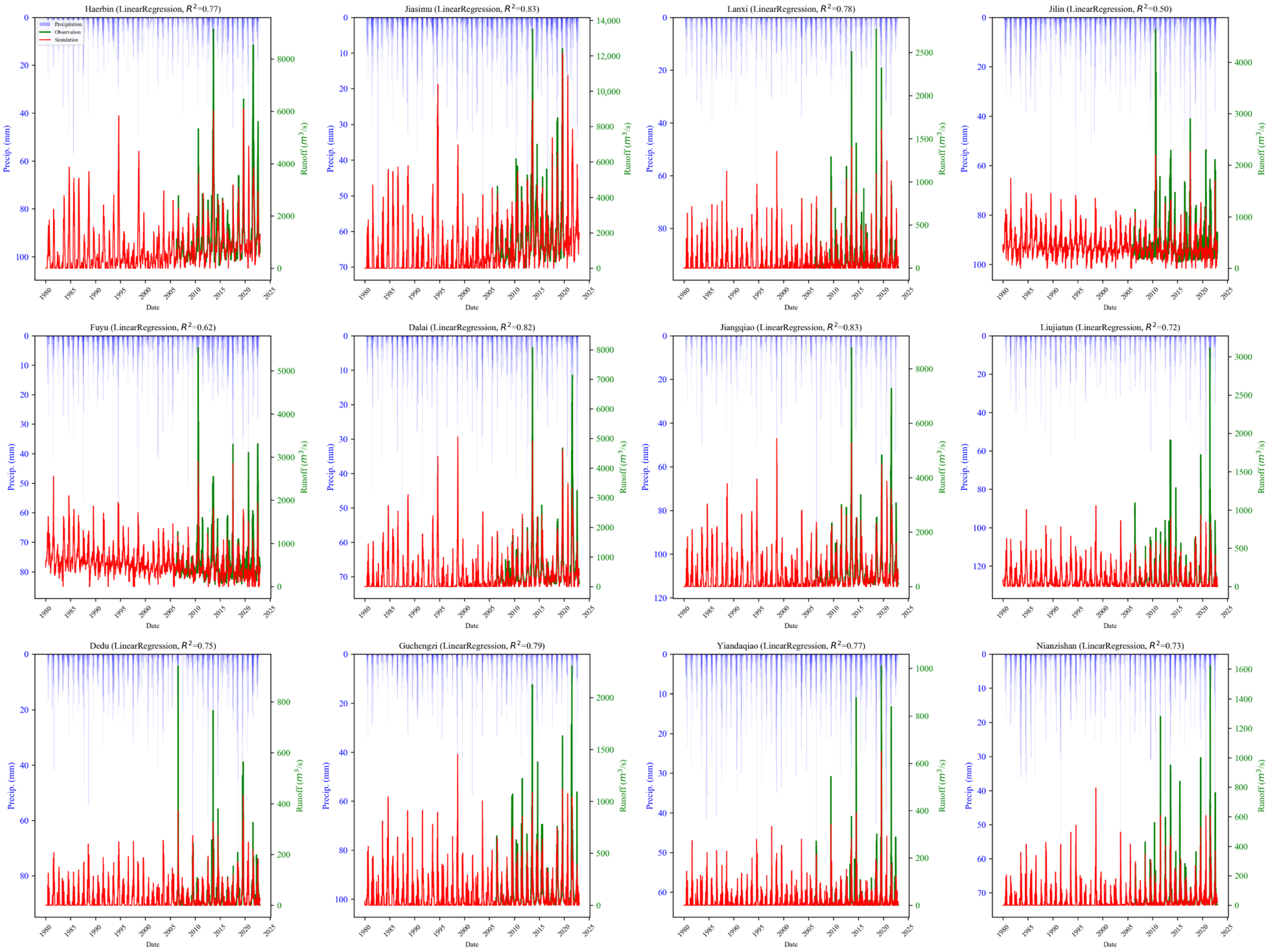
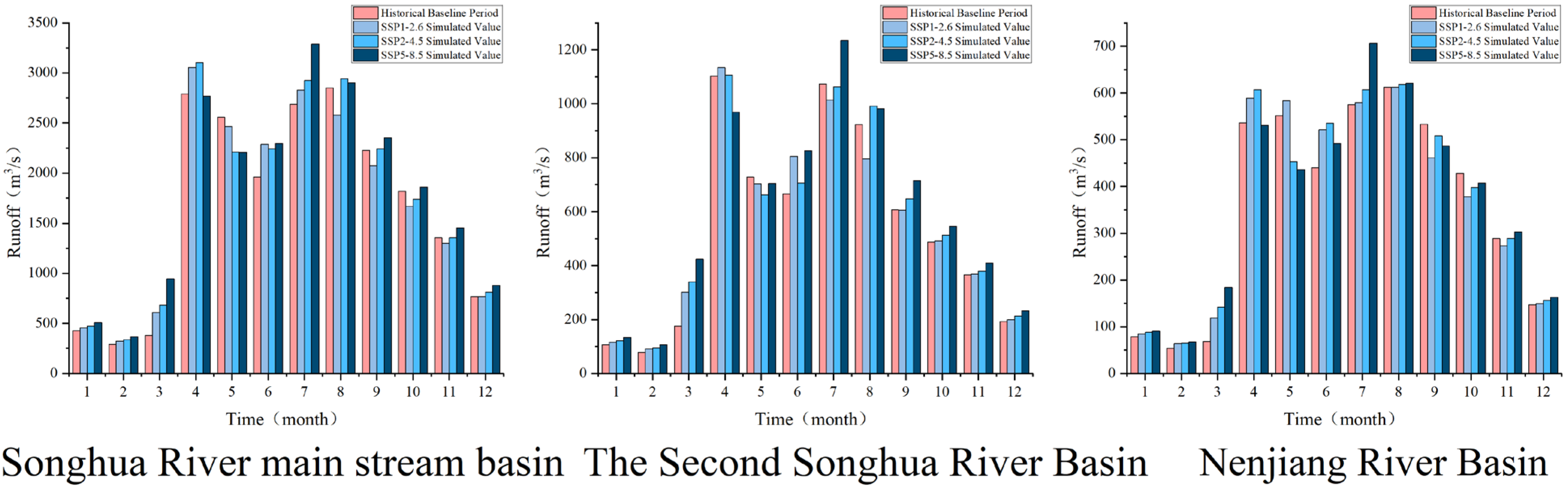
3.3. Results of Runoff Simulation
3.4. Key Parameters of the Model
- Aquifer Thickness Adjustment Factor: The aquifer thickness, defined as the vertical distance between the land surface and the underlying impermeable layer, determines the subsurface water storage capacity of a watershed. Modifying this coefficient primarily affects the peak flow and total volume of simulated runoff. Generally, increasing the aquifer thickness adjustment factor enhances groundwater storage, leading to a reduction in both the peak flow and the total volume of simulated surface runoff.
- Soil Layer Thickness: Adjusting this parameter predominantly influences simulated soil evaporation, vegetation transpiration, and runoff volume. Typically, increasing the soil layer thickness, particularly that of the uppermost layer, increases root-zone water storage capacity and consequently enhances evapotranspiration (ET), which reduces the volume of surface runoff.
- Stomatal Resistance Adjustment Factor: Modifying this coefficient mainly affects simulated vegetation transpiration and runoff. Generally, increasing the stomatal resistance adjustment factor restricts plant transpiration, thereby reducing total evapotranspiration and resulting in an increase in simulated runoff volume.
- Saturated Hydraulic Conductivity Adjustment Factor: Adjusting this coefficient primarily influences simulated infiltration capacity and peak runoff. Typically, increasing this factor enhances infiltration, thereby reducing surface runoff and peak flow. However, beyond a critical threshold, further increases can lead to rapid saturation of the soil profile. Under saturated conditions, infiltration capacity diminishes, paradoxically leading to an increase in surface runoff and peak flow.
- Streambed Hydraulic Conductivity Adjustment Factor: Modifying this coefficient chiefly affects simulated baseflow contribution to the stream channel. Generally, increasing the streambed hydraulic conductivity coefficient enhances groundwater exfiltration into the channel (or stream-aquifer exchange), resulting in increased baseflow and higher simulated discharge during dry periods.
- Aquifer Lateral Hydraulic Conductivity Adjustment Factor: Adjusting this coefficient primarily governs the rate of lateral groundwater movement within the aquifer. Typically, increasing the aquifer lateral hydraulic conductivity facilitates faster subsurface flow, leading to an increase in simulated baseflow contribution to the stream network.
- Surface Depression Storage Capacity: Adjusting this parameter primarily affects simulated surface runoff generation and volume. Generally, increasing the surface depression storage capacity allows for greater retention of rainfall and surface water, thereby reducing the volume and rate of surface runoff generation.
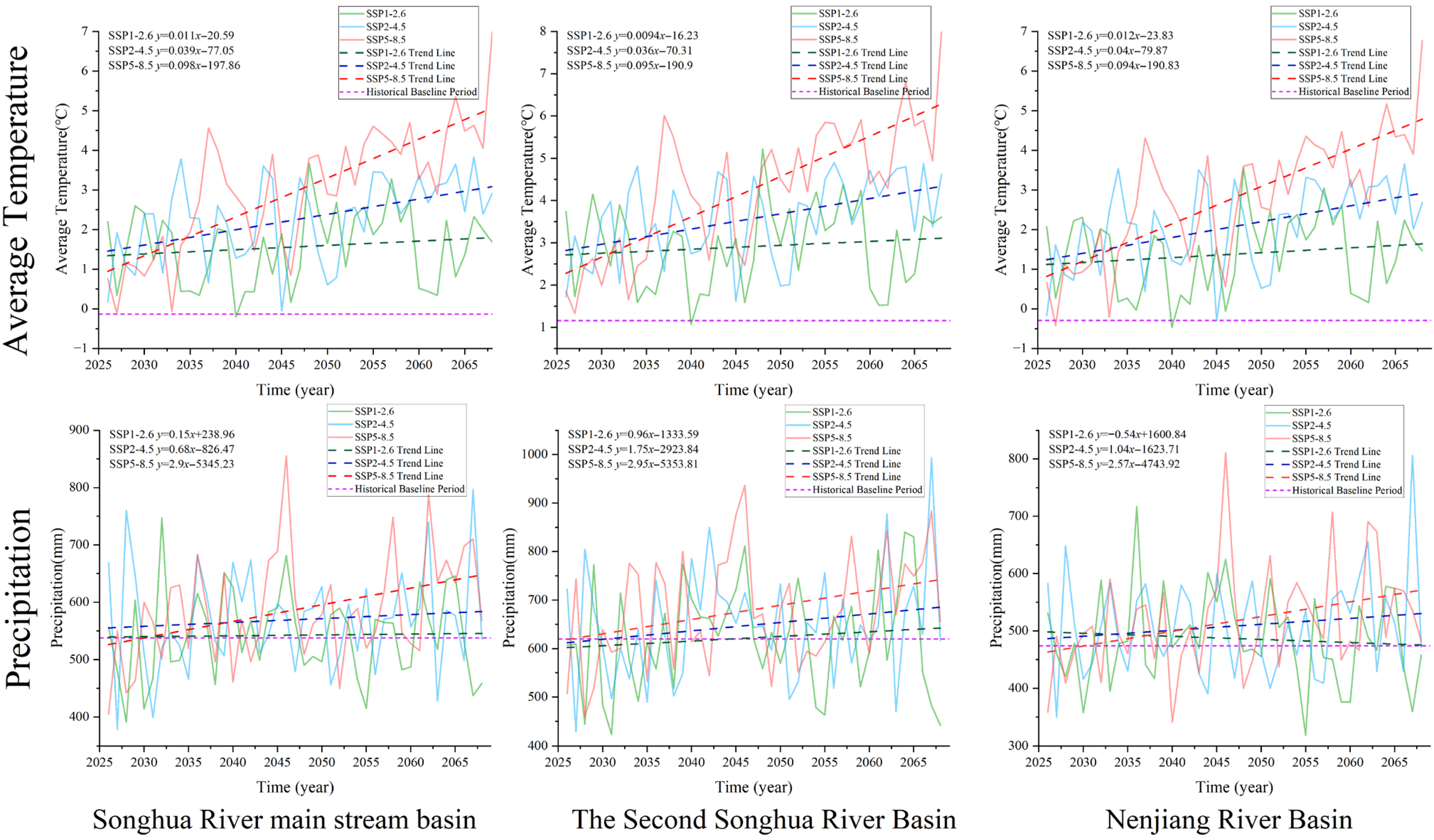
3.5. Future Trends in Temperature and Precipitation
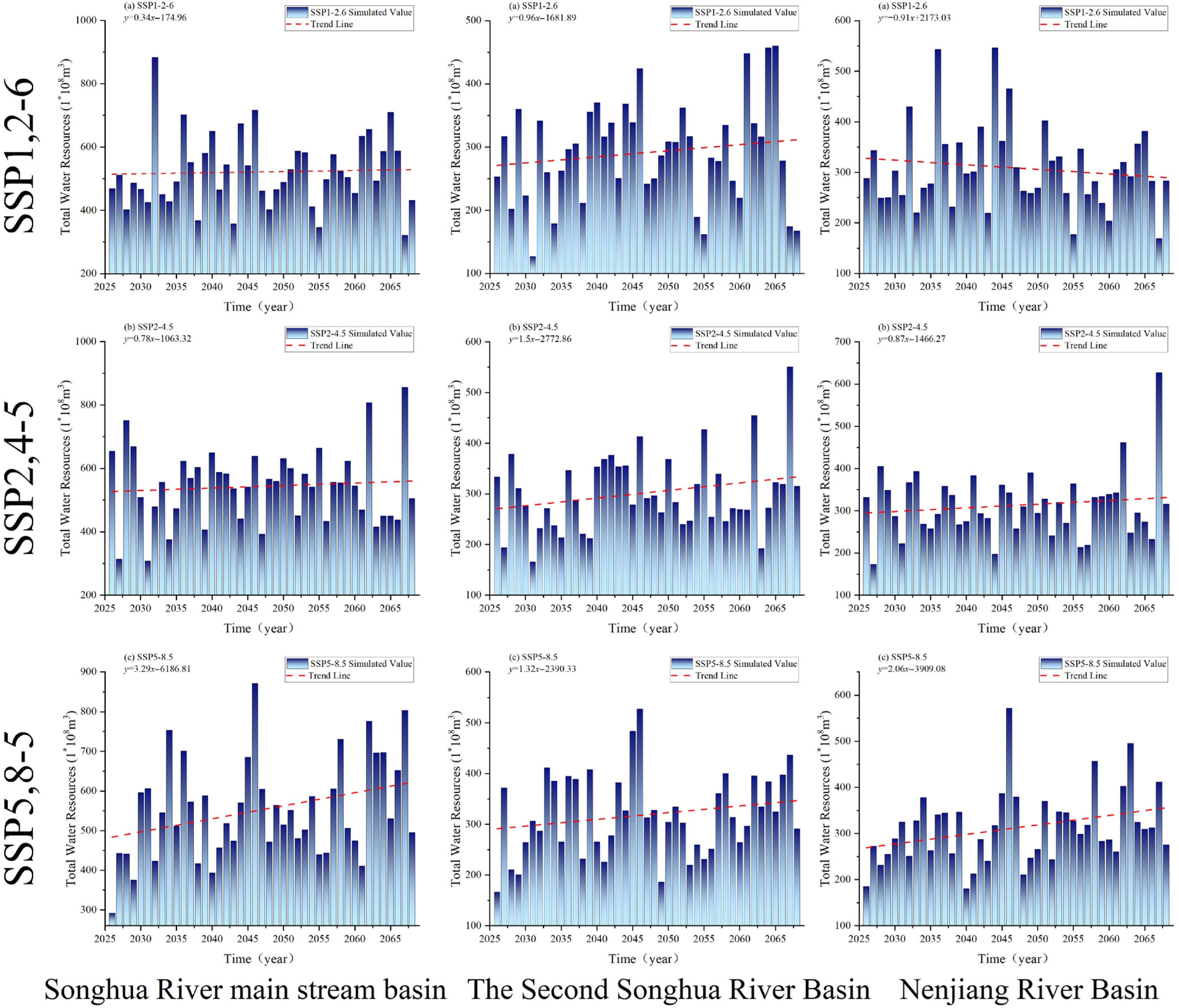
3.6. Changes in Future Runoff and Total Water Resources
3.6.1. Interannual Trends of Future Runoff Under Different Scenarios
3.6.2. Trends of Runoff and Total Water Resources Under Different Scenarios
3.6.3. Correlation Analysis Between Runoff and Temperature and Precipitation
4. Discussion
4.1. Application of Machine Learning in Hydrological Modeling
4.2. Distributed Hydrological Models
4.3. Wep Model’s Broader Applications
4.4. Future Climate Change Hydrological Impacts
4.5. Uncertainties of the Study
4.6. Policy and Water-Resources Management Implications
5. Conclusions
- Major shifts in land use occurred between 1990 and 2000, primarily reflected as a marked expansion of cultivated land and a considerable reduction in forest area.
- The integrated XGBoost–Savitzky–Golay hybrid algorithm achieved high-precision simulation of complex hydrological processes, demonstrating strong generalization capability under varying climate conditions.
- The WEP model, based on physical mechanisms, effectively simulated both natural and human-influenced hydrological patterns across basin subsystems, showing consistently robust performance.
- Future projections indicate rising temperatures across all scenarios, with the most pronounced warming under high-emission pathways. Precipitation changes exhibit spatial heterogeneity, alongside increased probability of extreme rainfall events under higher emissions.
- Runoff is projected to increase throughout the basin, predominantly driven by precipitation changes, with seasonal and regional variability. Southern sub-basins show heightened sensitivity to warming, approaching critical thresholds under intense warming scenarios.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Dimension | RF + XGBoost (Savitzky–Golay) | Linear Regression (Savitzky–Golay) |
|---|---|---|
| Principle | Integrated decision trees/gradient boosting | Ordinary least squares |
| Advantage | Nonlinear, interactive effects, high precision | Fast computation, interpretability, and non-overfitting. |
| Shortcoming | Black box, slow training, prone to overfitting | Limited by linear assumptions and low precision. |
| Model | Metrics | Haerbin | Jiasimu | Lanxi | Jilin | Fuyu | Dalai | Jiangqiao | Liujiatun | Dedu | Guchengzi | Yiandaqiao | Nianzishan |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| XGBoost Model | R2 | 1.00 | 1.00 | 0.99 | 0.97 | 0.99 | 1.00 | 1.00 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 |
| MAE | 36.82 | 85.39 | 9.46 | 41.8 | 34.0 | 21.7 | 24.68 | 8.29 | 2.85 | 8.69 | 2.63 | 3.98 | |
| RMSE | 56.03 | 118.72 | 18.71 | 63.0 | 46.4 | 35.2 | 34.54 | 27.50 | 9.81 | 19.53 | 7.39 | 10.52 | |
| Linear Regression Model | R2 | 0.77 | 0.83 | 0.78 | 0.50 | 0.62 | 0.82 | 0.83 | 0.72 | 0.75 | 0.79 | 0.77 | 0.77 |
| MAE | 355.05 | 570.02 | 65.09 | 186.19 | 187.21 | 202.66 | 205.15 | 48.40 | 18.18 | 53.82 | 15.39 | 15.39 | |
| RMSE | 492.43 | 784.75 | 116.01 | 273.69 | 275.8 | 315.7 | 322.22 | 92.68 | 34.39 | 94.08 | 31.42 | 31.42 |
| Station Name | Model | Period | R2 | NSE |
|---|---|---|---|---|
| Jiamusi | Natural model | Calibration | 0.85 | 0.71 |
| Validation | 0.85 | 0.69 | ||
| Status quo model | Calibration | 0.78 | 0.61 | |
| Validation | 0.82 | 0.65 | ||
| Fuyu | Natural model | Calibration | 0.87 | 0.79 |
| Validation | 0.89 | 0.8 | ||
| Status quo model | Calibration | 0.85 | 0.69 | |
| Validation | 0.87 | 0.82 | ||
| Dalai | Natural model | Calibration | 0.84 | 0.81 |
| Validation | 0.89 | 0.85 | ||
| Status quo model | Calibration | 0.83 | 0.74 | |
| Validation | 0.85 | 0.7 |
| Scenario | SSP1-2.6 | SSP2-4.5 | SSP5-8.5 | |||
|---|---|---|---|---|---|---|
| Basin | Annual Average Temperature | Annual Precipitation | Annual Average Temperature | Annual Precipitation | Annual Average Temperature | Annual Precipitation |
| Songhua River main stream basin | −0.335 * | 0.858 ** | −0.177 | 0.846 ** | 0.104 | 0.898 ** |
| The Second Songhua River Basin | −0.358 * | 0.916 ** | −0.077 | 0.882 ** | 0.032 | 0.906 ** |
| Nenjiang River Basin | −0.326 * | 0.847 ** | −0.234 | 0.852 ** | 0.044 | 0.870 ** |
References
- Zhang, B.; Ouyang, C.; Cui, P.; Xu, Q.; Wang, D.; Zhang, F.; Li, Z.; Fan, L.; Lovati, M.; Liu, Y.; et al. Deep Learning for Cross-Region Streamflow and Flood Forecasting at a Global Scale. Innovation 2024, 5, 100617. [Google Scholar] [CrossRef]
- Nearing, G.; Cohen, D.; Dube, V.; Gauch, M.; Gilon, O.; Harrigan, S.; Hassidim, A.; Klotz, D.; Kratzert, F.; Metzger, A.; et al. Global Prediction of Extreme Floods in Ungauged Watersheds. Nature 2024, 627, 559–563. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, M.; Chen, K.; Xing, L.; Jin, R.; Jordan, M.I.; Wang, J. Skilful Nowcasting of Extreme Precipitation with NowcastNet. Nature 2023, 619, 526–532. [Google Scholar] [CrossRef]
- Gaertner, B. Geospatial Patterns in Runoff Projections Using Random Forest Based Forecasting of Time-Series Data for the Mid-Atlantic Region of the United States. Sci. Total Environ. 2024, 912, 169211. [Google Scholar] [CrossRef] [PubMed]
- Niazkar, M.; Menapace, A.; Brentan, B.; Piraei, R.; Jimenez, D.; Dhawan, P.; Righetti, M. Applications of XGBoost in Water Resources Engineering: A Systematic Literature Review (Dec 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
- Shekar, P.R.; Mathew, A.; S, A.P.; Gopi, V.P. Rainfall-Runoff Modelling Using SWAT and Eight Artificial Intelligence Models in the Murredu Watershed, India. Environ. Monit. Assess. 2023, 195, 1041. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ai, P.; Xiong, C.; Song, Y. Coupled Intelligent Prediction Model for Medium- to Long-Term Runoff Based on Teleconnection Factors Selection and Spatial-Temporal Analysis. PLoS ONE 2024, 19, e0313871. [Google Scholar] [CrossRef]
- Xia, R.; Liu, Q.; Li, T.; Liu, X.; Gao, Y.; Wu, D. Runoff prediction in ungauged basins of the Yellow River using ensemble learning. J. Basic Sci. Eng. 2020, 28, 740–749. [Google Scholar] [CrossRef]
- Liu, W.; Wu, J.; Xu, F.; Mu, D.; Zhang, P. Modeling the Effects of Land Use/Land Cover Changes on River Runoff Using SWAT Models: A Case Study of the Danjiang River Source Area, China. Environ. Res. 2024, 242, 117810. [Google Scholar] [CrossRef] [PubMed]
- Das, P.C.; Esraz-Ul-Zannat, M. Assessing the Impacts of Land Use–Land Cover Changes on Direct Surface Runoff: A Remote Sensing Approach in Khulna City. Water Sci. Technol. 2022, 85, 3122–3144. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Dai, C.; Jing, J.; Liu, G.; Ru, Q.; Li, J.; Liu, P. Study on the Relationship between Surface Water and Groundwater Transformation in the Middle and Lower Reaches of Songhua River Basin. Sci. Rep. 2025, 15, 8088. [Google Scholar] [CrossRef]
- Zhai, R.; Tao, F.; Chen, Y.; Dai, H.; Liu, Z.; Fu, B. Future Water Security in the Major Basins of China under the 1.5 °C and 2.0 °C Global Warming Scenarios. Sci. Total Environ. 2022, 849, 157928. [Google Scholar] [CrossRef]
- Mayou, L.A.; Alamdari, N.; Ahmadisharaf, E.; Kamali, M. Impacts of Future Climate and Land Use/Land Cover Change on Urban Runoff Using Fine-Scale Hydrologic Modeling. J. Environ. Manage. 2024, 362, 121284. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Liu, Z.; Woods, R.; McVicar, T.R.; Yang, D.; Wang, T.; Hou, Y.; Guo, Y.; Li, C.; Yang, Y. Streamflow Seasonality in a Snow-Dwindling World. Nature 2024, 629, 1075–1081. [Google Scholar] [CrossRef]
- Feldman, A.F.; Konings, A.G.; Gentine, P.; Cattry, M.; Wang, L.; Smith, W.K.; Biederman, J.A.; Chatterjee, A.; Joiner, J.; Poulter, B. Large Global-Scale Vegetation Sensitivity to Daily Rainfall Variability. Nature 2024, 636, 380–384. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Wang, H.; Zhou, Z.; Qiu, Y.; Luo, X.; Wang, J.; Yan, D.; Qin, D. Development of the WEP-L Distributed Hydrological Model and Dynamic Assessment of Water Resources in the Yellow River Basin. J. Hydrol. 2006, 331, 606–629. [Google Scholar] [CrossRef]
- Gan, Y.; Zhao, S.; Zheng, L. Distributed Hydrological Model Considering Influence of Two-flow Zone and Its Application. China Rural Water Hydropower 2023, 03, 8–14. [Google Scholar] [CrossRef]
- Zhou, X.; Shen, Y.; Bai, Y.; Liu, L.; Li, J.; Huo, Z. Joint Modeling of Surface-Groundwater in the Agro-pastoral Ecotone—A Case Study of the Mu Us Sandy Land. China Rural Water Hydropower 2023, 56–64. [Google Scholar] [CrossRef]
- Xu, F.; Jia, Y.; Niu, C.; Liu, J. Multi Temporal-Spatial Scale Characteristics of Water Cycle Process in Jumahe River Basin. Water Resour. Power 2022, 40, 18–20. [Google Scholar]
- Xu, F.; Jia, Y.; Niu, C.; Liu, J. Study on Response of Runoff to Land Use and Climate Changes in the Qingshui River Basin of Beijing. Water Resour. Power 2019, 37, 17–20. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Z.; Liu, J.; Xia, J.; Wang, K.; Li, J.; Wang, P.; You, J.; Wang, H.; Jia, Y. Analysis of Runoff Evolution in the Source Region of the Yellow River in the Past 65 Years Based on the WEP⁃QTP Model. Yellow River 2024, 46, 41–48. [Google Scholar] [CrossRef]
- Su, H.; Jia, Y.; Liu, H.; Li, Y.; Du, J.; Niu, C.; Gan, Y.; Zeng, Q. Runoff evolution simulation and attribution analysis in cold region basin based on WEP-L model. J. Glaciol. Geocryol. 2021, 43, 1523–1530. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, Q.; Wei, R.; Liu, J.; Yan, J.; Wang, P.; Jia, Y.; Wang, H. Research on Parameter Classification and Optimization Method of Distributed Hydrological Model based on RAGA. J. China Hydrol. 2023, 43, 28–33. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, Y.; Liu, S.; Zheng, X. Simulation Analysis of Field Water Circulation in Cold Region Based on WEP—Take Qinggang County as an Example. J. Heilongjiang Bayi Agric. Univ. 2024, 36, 99–105. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, H.; Jiang, Y.; Jia, Y.; Du, J.; Liu, J.; Xu, F. An improved method of parameter range selection and its application to WEP-L model. South North Water Transf. Water Sci. Technol. 2018, 16, 50–57. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Cheng, F.; Li, K.; Wang, G. Research progress and reference for the impact of environmental change on water resources. Hydro Sci. Cold Zone Eng. 2020, 3, 1–6. [Google Scholar]
- Pokhrel, Y.; Felfelani, F.; Satoh, Y.; Boulange, J.; Burek, P.; Gädeke, A.; Gerten, D.; Gosling, S.N.; Grillakis, M.; Gudmundsson, L.; et al. Global Terrestrial Water Storage and Drought Severity under Climate Change. Nat. Clim. Change 2021, 11, 226–233. [Google Scholar] [CrossRef]
- Anwar, H.; Khan, A.U.; Ullah, B.; Taha, A.T.B.; Najeh, T.; Badshah, M.U.; Ghanim, A.A.J.; Irfan, M. Intercomparison of Deep Learning Models in Predicting Streamflow Patterns: Insight from CMIP6. Sci. Rep. 2024, 14, 17468. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Xu, X.; Li, M.; Zhang, X.; Cao, K. Risk Regulation of Water Allocation in Irrigation Areas under Changing Water Supply and Demand Conditions. J. Environ. Manage. 2022, 313, 114945. [Google Scholar] [CrossRef] [PubMed]
- Jing, W.; Yao, L.; Zhao, X.; Zhang, P.; Liu, Y.; Xia, X.; Song, J.; Yang, J.; Li, Y.; Zhou, C. Understanding Terrestrial Water Storage Declining Trends in the Yellow River Basin. J. Geophys. Res. Atmos. 2019, 124, 12963–12984. [Google Scholar] [CrossRef]
- Qiao, B.; Nie, B.; Liang, C.; Xiang, L.; Zhu, L. Spatial Difference of Terrestrial Water Storage Change and Lake Water Storage Change in the Inner Tibetan Plateau. Remote Sens. 2021, 13, 1984. [Google Scholar] [CrossRef]
- Climate Change 2021—The Physical Science Basis. Available online: https://www.cambridge.org/core/books/climate-change-2021-the-physical-science-basis/415F29233B8BD19FB55F65E3DC67272B (accessed on 7 May 2025).
- Ma, C.; Pei, W.; Liu, J.; Fu, G. Long-Term Trends and Variability of Hydroclimate Variables and Their Linkages with Climate Indices in the Songhua River. Atmosphere 2024, 15, 174. [Google Scholar] [CrossRef]
- Liu, Z.H.; Xu, H.; Ju, Q.; Wu, G.; Xing, R. Climate Simulation and Estimation of Songhua River Basin Based on Model Integration. Water Power 2020, 46, 14–18. [Google Scholar]
- Li, G.; Chen, W.; Cui, Y.; Wang, H.; Chi, Y. The Adaptability and Irrigation Constraints Analysis of the WOFOST Model for Grain Production in the Songhua River Basin. J. Sci. Food Agric. 2024, 104, 7996–8007. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, X.; Liu, Z.; Wang, Y.; Shen, Y. Spatial and temporal variations of extreme climate index in the Songhua River Basin during 1961–2020. Chin. J. Appl. Ecol. 2023, 34, 1091–1101. [Google Scholar] [CrossRef]
- Wang, G.; Yang, J.; Hu, Y.; Li, J.; Yin, Z. Application of a Novel Artificial Neural Network Model in Flood Forecasting. Environ. Monit. Assess. 2022, 194, 125. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, Z.; Liu, J.; Li, J.; Jia, Y.; Wang, H.; Xu, C. Impact of Climate Change on Water Quality Evolution in Cold Regions Using a Water–Heat–Nitrogen Processes Coupled Model. Environ. Sci. Pollut. Res. 2024, 31, 22395–22409. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Wang, H.; Tong, J.; Bai, Y.; Alatalo, J.M.; Liu, G.; Fang, Z.; Zhang, F. Impacts of Environment and Human Activity on Grid-Scale Land Cropping Suitability and Optimization of Planting Structure, Measured Based on the MaxEnt Model. Sci. Total Environ. 2022, 836, 155356. [Google Scholar] [CrossRef]
- Xi, J.; Wang, X.; Kong, Q.; Zhang, N. Spatial Morphology Evolution of Rural Settlements Induced by Tourism: A Comparative Study of Three Villages in Yesanpo Tourism Area, China. J. Geogr. Sci. 2015, 25, 497–511. [Google Scholar] [CrossRef]
- Hu, S.; Chen, L.; Li, L.; Wang, B.; Yuan, L.; Cheng, L.; Yu, Z.; Zhang, T. Spatiotemporal Dynamics of Ecosystem Service Value Determined by Land-Use Changes in the Urbanization of Anhui Province, China. Int. J. Environ. Res. Public. Health 2019, 16, 5104. [Google Scholar] [CrossRef] [PubMed]
- Shen, G.; Yang, X.; Jin, Y.; Luo, S.; Xu, B.; Zhou, Q. Land Use Changes in the Zoige Plateau Based on the Object-Oriented Method and Their Effects on Landscape Patterns. Remote Sens. 2019, 12, 14. [Google Scholar] [CrossRef]
- Huang, C.; Huang, X.; Peng, C.; Zhou, Z.; Teng, M.; Wang, P. Land Use/Cover Change in the Three Gorges Reservoir Area, China: Reconciling the Land Use Conflicts between Development and Protection. Catena 2019, 175, 388–399. [Google Scholar] [CrossRef]
- Zheng, J.; Zhou, Z.; Liu, J.; Yan, Z.; Li, G.; Wang, Q. Impact mechanism of agricultural drought in Fuhe River Basin. Yangtze River 2023, 54, 70–76, 105. [Google Scholar] [CrossRef]
- Qin, Z.; Zhou, Z.; Liu, M.; Xiang, D.; Liu, J. Investigation on Temporal⁃Spatial Discretization Parallel Computing Method for Distributed Hydrological Model. Yellow River 2020, 42, 15–20. [Google Scholar]
- Guan, T.; Liu, J.; Zhou, Z.; Du, C.; Jing, Y.; Wang, P. Research on the Division Method of Calculation Unit Considering Hill-Plain Area to Distributed Hydrological Model. J. China Hydrol. 2022, 42, 7–13. [Google Scholar] [CrossRef]
- Zhou, Z.; Jia, Y.; Qiu, Y.; Liu, J.; Wang, H.; Xu, C.-Y.; Li, J.; Liu, L. Simulation of Dualistic Hydrological Processes Affected by Intensive Human Activities Based on Distributed Hydrological Model. J. Water Resour. Plan. Manag. 2018, 144, 04018077. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, J.; Yan, Z.; Wang, H.; Jia, Y. Attribution analysis of the natural runoff evolution in the Yellow River basin. Adv. WATER Sci. 2022, 33, 27–37. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another Look at Measures of Forecast Accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Armstrong, J.S.; Collopy, F. Error Measures for Generalizing about Forecasting Methods: Empirical Comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef]
- Adler, J.; Parmryd, I. Quantifying Colocalization by Correlation: The Pearson Correlation Coefficient Is Superior to the Mander’s Overlap Coefficient. Cytom. A 2010, 77A, 733–742. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y. Study on Comprehensive Assessment and Evolution Law of Water Resources. Ph.D. Thesis, China Institute of Water Resources & Hydropower Research, Beijing, China, 2006. [Google Scholar]
- Li, J. Modeling of Hydrological Processes in Cold Regions and Its Application in Songhua River Basin. Ph.D. Thesis, Donghua University, Shanghai, China, 2017. [Google Scholar]
- Jia, Y.; Wang, H.; Yan, D. Distributed model of hydrological cycle system in Heihe River basin I.Model development and Verification. J. Hydraul. Eng. 2006, 37, 534–542. [Google Scholar]
- WEP: Watershed Distributed Binary Water Cycle Model Software User Manual, Version 1.0.
- Yao, M. Uncertainty Analysis and Optimization Method for SWAT Model Parameters and its Application to the Shitoukoumen Basin. Master’s Thesis, Jilin University, Changchun, China, 2023. [Google Scholar]
- Wang, S.; Peng, H.; Hu, Q.; Jiang, M. Analysis of Runoff Generation Driving Factors Based on Hydrological Model and Interpretable Machine Learning Method. J. Hydrol. Reg. Stud. 2022, 42, 101139. [Google Scholar] [CrossRef]
- Feng, D.; Fang, K.; Shen, C. Enhancing Streamflow Forecast and Extracting Insights Using Long-short Term Memory Networks with Data Integration at Continental Scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Chang, F.-J. Explore an Evolutionary Recurrent ANFIS for Modelling Multi-Step-Ahead Flood Forecasts. J. Hydrol. 2019, 570, 343–355. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Wang, D.; Jia, Y.; Niu, C.; Sui, Y.; Yan, X. Evaluation method for main functions of water retention based on WEP⁃L model: A case of water retention area in Wei River. ACTA Ecol. Sin. 2024, 44, 4342–4352. [Google Scholar] [CrossRef]
- Ji, S.; Du, J.; Qiu, Y.; Liu, H.; Lyu, X.; Wang, W. Attribution analysis of river runoff variation in the upper basin of Miyun Reservoir based on dualistic water cycle simulation. Water Resour. Hydropower Eng. 2022, 53, 116–127. [Google Scholar] [CrossRef]
- Wang, P.; Zhou, Z.; Liu, J.; Xu, C.; Wang, K.; Liu, Y.; Li, J.; Li, Y.; Jia, Y.; Wang, H. Application of an Improved Distributed Hydrological Model Based on the Soil–Gravel Structure in the Niyang River Basin, Qinghai–Tibet Plateau. Hydrol. Earth Syst. Sci. 2023, 27, 2681–2701. [Google Scholar] [CrossRef]
- Chen, W.; Wu, H.; Kimball, J.S.; Alfieri, L.; Nanding, N.; Li, X.; Jiang, L.; Wu, W.; Tao, Y.; Zhao, S.; et al. A Coupled River Basin-Urban Hydrological Model (DRIVE-Urban) for Real-Time Urban Flood Modeling. Water Resour. Res. 2022, 58, e2021WR031709. [Google Scholar] [CrossRef]
- Zhang, W.; Che, W.; Liu, D.K.; Gan, Y.P.; Lv, F.F. Characterization of Runoff from Various Urban Catchments at Different Spatial Scales in Beijing, China. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2012, 66, 21–27. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Zhang, G.; Zhang, X. Simulation of Hydrological Processes in the Jing River Basin Based on the WEP Model. Water 2023, 15, 2989. [Google Scholar] [CrossRef]
- Lyu, J.; Luo, P.; Mo, S.; Zhou, M.; Shen, B.; Fan, L.; Nover, D. Towards Sustainable Water Regulation Based on a Distributed Hydrological Model for a Heavily Polluted Urban River, Northwest China. Hydrol. Res. 2019, 50, 961–973. [Google Scholar] [CrossRef]
- Dorjsuren, B.; Yan, D.; Yuheng, Y.; Zemtsov, V.A.; Dong, N.; Gao, H.; Shiikhar, D.; Zhou, H.; Demberel, O. Advancing Hydrological Understanding in Cold Regions: Development and Application of the WEP Model for Lateral Flow Estimation in the Great Lakes Depression of Mongolia. Hydrol. Res. 2025, 56, 244–259. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Z.; Wang, H.; Liu, J.; Jia, Y.; Hu, P.; Xu, C.-Y. Development of WEP-COR Model to Simulate Land Surface Water and Energy Budgets in a Cold Region. Hydrol. Res. 2019, 50, 99–116. [Google Scholar] [CrossRef]
- Gu, H.; Yu, Z.; Yang, C.; Ju, Q.; Yang, T.; Zhang, D. High-Resolution Ensemble Projections and Uncertainty Assessment of Regional Climate Change over China in CORDEX East Asia. Hydrol. Earth Syst. Sci. 2018, 22, 3087–3103. [Google Scholar] [CrossRef]
- Huang, S.; Zang, W.; Xu, M.; Li, X.; Xie, X.; Li, Z.; Zhu, J. Study on Runoff Simulation of the Upstream of Minjiang River under Future Climate Change Scenarios. Nat. Hazards 2015, 75, 139–154. [Google Scholar] [CrossRef]
- Wu, T.; Lu, Y.; Fang, Y.; Xin, X.; Li, L.; Li, W.; Jie, W.; Zhang, J.; Liu, Y.; Zhang, L.; et al. The Beijing Climate Center Climate System Model (BCC-CSM): The Main Progress from CMIP5 to CMIP6. Geosci. Model Dev. 2019, 12, 1573–1600. [Google Scholar] [CrossRef]
- Wang, D.; Liu, J.; Wang, H.; Shao, W.; Mei, C.; Ding, X. Performance Evaluations of CMIP6 and CMIP5 Models for Precipitation Simulation over the Hanjiang River Basin, China. J. Water Clim. Change 2022, 13, 2089–2106. [Google Scholar] [CrossRef]
- Liu, Y.-W.; Zhao, L.; Tan, G.-R.; Shen, X.-Y.; Nie, S.-P.; Li, Q.-Q.; Zhang, L. Evaluation of Multidimensional Simulations of Summer Air Temperature in China from CMIP5 to CMIP6 by the BCC Models: From Trends to Modes. Adv. Clim. Change Res. 2022, 13, 28–41. [Google Scholar] [CrossRef]
- Song, M.; Pei, Y.; Zhang, S.; Wu, T. Simulation Performance and Case Study of Extreme Events in Northwest China Using the BCC-CSM2 Model. Remote Sens. 2022, 14, 4922. [Google Scholar] [CrossRef]
- Huang, D.; Liu, A.; Zheng, Y.; Zhu, J. Inter-Model Spread of the Simulated East Asian Summer Monsoon Rainfall and the Associated Atmospheric Circulations from the CMIP6 Models. J. Geophys. Res. Atmos. 2022, 127, e2022JD037371. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, P. Uncertainty of the Future Changes in Interannual Precipitation Variability under Global Warming Based on Single-Model Initial-Condition Large Ensembles and CMIP6. Adv. Atmos. Sci. 2025, 42, 2279–2289. [Google Scholar] [CrossRef]
- Chu, Z.; Guo, J.; Zhao, J. Impacts of Future Climate Change on Agroclimatic Resources in Northeast China. J. Geogr. Sci. 2017, 27, 1044–1058. [Google Scholar] [CrossRef]
- Luo, M.; Liu, T.; Frankl, A.; Duan, Y.; Meng, F.; Bao, A.; Kurban, A.; De Maeyer, P. Defining Spatiotemporal Characteristics of Climate Change Trends from Downscaled GCMs Ensembles: How Climate Change Reacts in Xinjiang, China. Int. J. Climatol. 2018, 38, 2538–2553. [Google Scholar] [CrossRef]
- Steinschneider, S.; Brown, C. Dynamic Reservoir Management with Real-option Risk Hedging as a Robust Adaptation to Nonstationary Climate. Water Resour. Res. 2012, 48, 2011WR011540. [Google Scholar] [CrossRef]
- Ouyang, F.; Zhu, Y.; Fu, G.; Lü, H.; Zhang, A.; Yu, Z.; Chen, X. Impacts of Climate Change under CMIP5 RCP Scenarios on Streamflow in the Huangnizhuang Catchment. Stoch. Environ. Res. Risk Assess. 2015, 29, 1781–1795. [Google Scholar] [CrossRef]
- Eum, H.-I.; Gachon, P.; Laprise, R. Developing a Likely Climate Scenario from Multiple Regional Climate Model Simulations with an Optimal Weighting Factor. Clim. Dyn. 2014, 43, 11–35. [Google Scholar] [CrossRef]
- Zhu, B.; Xue, L.; Wei, G.; Zhang, L.; Chen, X. CMIP5 Projected Changes in Temperature and Precipitation in Arid and Humid Basins. Theor. Appl. Climatol. 2019, 136, 1133–1144. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Ducharne, A.; Thiery, W.; Cheruy, F.; Lawrence, D. The Role of Irrigation Expansion on Historical Climate Change: Insights from CMIP6. Earths Future 2022, 10, e2022EF002859. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Capturing the influence of groundwater dynamics on land surface processes using an integrated, distributed watershed model. Water Resour. Res. 2008, 44, 252–261. [Google Scholar] [CrossRef]
- Knutti, R.; Furrer, R.; Tebaldi, C.; Cermak, J.; Meehl, G.A. Challenges in Combining Projections from Multiple Climate Models. J. Clim. 2010, 23, 2739–2758. [Google Scholar] [CrossRef]
- Kuffour, B.N.O.; Engdahl, N.B.; Woodward, C.S.; Condon, L.E.; Kollet, S.; Maxwell, R.M. Simulating Coupled Surface–Subsurface Flows with ParFlow v3.5.0: Capabilities, Applications, and Ongoing Development of an Open-Source, Massively Parallel, Integrated Hydrologic Model. Geosci. Model Dev. 2020, 13, 1373–1397. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of Input Uncertainty in Hydrologic Modeling: Doing Hydrology Backward with Markov Chain Monte Carlo Simulation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Blasone, R.-S.; Vrugt, J.A.; Madsen, H.; Rosbjerg, D.; Robinson, B.A.; Zyvoloski, G.A. Generalized Likelihood Uncertainty Estimation (GLUE) Using Adaptive Markov Chain Monte Carlo Sampling. Adv. Water Resour. 2008, 31, 630–648. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global Sensitivity Analysis in Hydrological Modeling: Review of Concepts, Methods, Theoretical Framework, and Applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ Sensitivity Analysis of a Complex Environmental Model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. arxiv 2017, arXiv:1705.07874. [Google Scholar]
- Mushtaq, H.; Akhtar, T.; Hashmi, M.Z.U.R.; Masood, A.; Saeed, F. Hydrologic Interpretation of Machine Learning Models for 10-Daily Streamflow Simulation in Climate Sensitive Upper Indus Catchments. Theor. Appl. Climatol. 2024, 155, 5525–5542. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly Proper Scoring Rules, Prediction, and Estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Flood Control Law of the People’s Republic of China. 2002. Available online: http://www.mwr.gov.cn/english/Documents/LawsAndRegulations/202311/P020231102622099053893.pdf (accessed on 20 September 2025).
- Hailun, Z. The Associated Programme on Flood Management. Available online: https://www.floodmanagement.info/publications/casestudies/cs_china_full.pdf?utm_source (accessed on 1 July 2025).
- Wu, Y.; Ju, H.; Qi, P.; Li, Z.; Zhang, G.; Sun, Y. Increasing Flood Risk under Climate Change and Social Development in the Second Songhua River Basin in Northeast China. J. Hydrol. Reg. Stud. 2023, 48, 101459. [Google Scholar] [CrossRef]
- Yang, K.; Yao, J.; Huang, Y.; Ling, H.; Yang, Y.; Zhang, L.; Chen, D.; Liu, Y. Evaluating the Effectiveness of the “River Chief System”: An Empirical Study Based on the Water Quality Data of Coastal Rivers in Guangdong Province. Water 2024, 16, 790. [Google Scholar] [CrossRef]
- Xu, X.; Wu, F.; Zhang, L.; Gao, X. Assessing the Effect of the Chinese River Chief Policy for Water Pollution Control under Uncertainty—Using Chaohu Lake as a Case. Int. J. Environ. Res. Public. Health 2020, 17, 3103. [Google Scholar] [CrossRef] [PubMed]



| Type | Data Source | Period | Resolution |
|---|---|---|---|
| DEM | Geospatial Date Cloud (https://www.gscloud.cn) URL (accessed on 1 July 2025) | - | 30 m |
| Climatic forcing data | Institute of Tibetan Plateau Research Chinese Academy of Sciences (TPDC) (https://data.tpdc.ac.cn) URL (accessed on 1 July 2025) | 1980–2022 | Daily |
| CMIP6 meteorological data | The Earth System Grid Federation (ESGF) (https://aims2.llnl.gov/search/cmip6) URL (accessed on 1 July 2025) | 1980–2068 | Daily |
| Land use data | China Multi-period Land Use Remote Sensing Monitoring Data Set (CNLUCC) of the Chinese Academy of Sciences Resource and Environmental Science and Data Center (http://www.resdc.cn) URL (accessed on 1 July 2025) | 1985–2023 | 30 m |
| Soil-type data | The second national soil census and the “Chinese Soil Records” | - | - |
| River discharge data | Actual measurement data from 12 hydrological stations in the Songhua River Basin, including Harbin, Jiamusi, Lanxi, Jilin, Fuyu, Dalai, Jiangqiao, Liujiatun, Dedu, Guchengzi, Yanqiao, and Nianzishan | 2006–2022 | Daily |
| Land Use Type | 1990 | 2000 | 2010 | 2020 | 2023 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Area (km2) | % | Area (km2) | % | Area (km2) | % | Area (km2) | % | Area (km2) | % | |
| Cropland | 242,849.82 | 44.17 | 253,487.84 | 46.11 | 245,176.16 | 44.59 | 254,337.91 | 46.26 | 256,661.45 | 46.68 |
| Forest | 247,375.42 | 44.99 | 239,351.96 | 43.53 | 240,103.73 | 43.67 | 236,843.73 | 43.08 | 233,568.31 | 42.48 |
| Shrub | 0.07 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 50.89 | 0.01 |
| Grassland | 43,616.03 | 7.93 | 39,424.24 | 7.17 | 42,914.14 | 7.81 | 33,759.21 | 6.14 | 33,854.25 | 6.16 |
| Water | 7700.71 | 1.40 | 6365.23 | 1.16 | 6843.97 | 1.24 | 7616.34 | 1.39 | 8280.23 | 1.51 |
| Snow/Ice | 0.02 | 0.00 | 0.01 | 0.00 | 0.09 | 0.00 | 0.19 | 0.00 | 0.22 | 0.00 |
| Barren | 3473.24 | 0.63 | 3427.09 | 0.62 | 3253.96 | 0.59 | 2429.08 | 0.44 | 1743.38 | 0.32 |
| Impervious | 9630.08 | 1.75 | 13,517.96 | 2.46 | 17,368.72 | 3.16 | 20,701.80 | 3.77 | 21,493.62 | 3.91 |
| Wetland | 1151.38 | 0.21 | 222.46 | 0.04 | 135.99 | 0.02 | 108.51 | 0.02 | 144.43 | 0.03 |
| Land Use Type | 1990–2000 | 2000–2010 | 2010–2020 | 1990–2023 | ||||
|---|---|---|---|---|---|---|---|---|
| Area Change (km2) | Single LUD Index (%) | Area Change (km2) | Single LUD Index (%) | Area Change (km2) | Single LUD Index (%) | Area Change (km2) | Single LUD Index (%) | |
| Cropland | 10,637.97 | 0.44 | −8311.91 | −0.33 | 9161.43 | 0.37 | 13,811.77 | 0.57 |
| Forest | −8023.54 | −0.32 | 751.88 | 0.03 | −3260.05 | −0.14 | −13,806.89 | −0.56 |
| Shrub | −0.07 | −9.63 | 0.00 | 13.33 | −0.01 | −8.57 | 50.82 | 6885.85 |
| Grassland | −4191.65 | −0.96 | 3490.10 | 0.89 | −9154.58 | −2.13 | −9761.98 | −2.24 |
| Water | −1335.46 | −1.73 | 478.72 | 0.75 | 772.37 | 1.13 | 579.49 | 0.75 |
| Snow/Ice | −0.01 | −5.50 | 0.09 | 106.67 | 0.10 | 10.48 | 0.21 | 114.50 |
| Barren | −46.16 | −0.13 | −173.13 | −0.51 | −824.89 | −2.54 | −1729.88 | −4.98 |
| Impervious | 3887.85 | 4.04 | 3850.73 | 2.85 | 3333.10 | 1.92 | 11,863.42 | 12.32 |
| Wetland | −928.92 | −8.07 | −86.47 | −3.89 | −27.48 | −2.02 | −1006.95 | −8.75 |
| CLUD Index (%) | 0.26 | 0.15 | 0.24 | 0.47 | ||||
| Parameter | Sandy Soil | Loamy Soil | Silt Loam Soil | Clay Soil |
|---|---|---|---|---|
| Saturated water content | 0.4 | 0.466 | 0.475 | 0.479 |
| Field capacity | 0.174 | 0.278 | 0.365 | 0.387 |
| Residual water content | 0.077 | 0.120 | 0.170 | 0.250 |
| Soil water suction at the wetting front (cm) | 6.1 | 8.9 | 12.5 | 17.5 |
| Mualem constant n | 3.37 | 3.97 | 3.97 | 4.38 |
| Saturated hydraulic conductivity (cm/s) | 2.5 × 103 | 7.0 × 104 | 2.0 × 104 | 3.0 × 10−5 |
| Parameter | Forest Land | Grass Land | Farm Land | Bare Land | Bare Rock, and Urban Surfaces | Water Bodies |
|---|---|---|---|---|---|---|
| Manning coefficient | 0.3 | 0.1 | 0.2 | 0.05 | 0.02 | 0.01 |
| Parameter | Forest Land | Grass Land | Urban Land Use | Bare Land | Snowfield |
|---|---|---|---|---|---|
| Degree-Day Factor (mm/°C/day) | 1 | 2 | 5 | 3 | 1 |
| Factors | Basin | Songhua River Main Stream Basin | The Second Songhua River Basin | Nenjiang River Basin | |||
|---|---|---|---|---|---|---|---|
| Average temperature | Scenario | Annual average temperature (°C) | Increase speed (°C/10a) | Annual average temperature(°C) | Increase speed (°C/10a) | Annual average temperature (°C) | Increase speed (°C/10a) |
| Historical Baseline Period | −0.134 | 1.16 | −0.29 | ||||
| SSP1-2.6 | 1.57 | 0.34 | 2.91 | 0.35 | 1.38 | 0.33 | |
| SSP2-4.5 | 2.27 | 0.48 | 3.57 | 0.48 | 2.08 | 0.47 | |
| SSP5-8.5 | 3 | 0.62 | 4.28 | 0.62 | 2.8 | 0.62 | |
| precipitation | Scenario | Annual Average Precipitation (mm) | Increase speed (mm/10a) | Annual Average Precipitation (mm) | Increase speed (mm/10a) | Annual Average Precipitation (mm) | Increase speed (mm/10a) |
| Historical Baseline Period | 537.79 | 619.85 | 474.16 | ||||
| SSP1-2.6 | 542.54 | 0.95 | 622.15 | 0.46 | 486.81 | 2.53 | |
| SSP2-4.5 | 569.62 | 6.37 | 648.7 | 5.77 | 508.42 | 6.85 | |
| SSP5-8.5 | 586.98 | 9.84 | 680.43 | 12.11 | 517.32 | 8.63 | |
| Basin | 1980–2014 Historical Baseline Period | 2026–2068 Future Climate Scenarios | |||
|---|---|---|---|---|---|
| SSP1-2.6 | SSP2-4.5 | SSP5-8.5 | |||
| Songhua River main stream basin | Average Annual Runoff (m3/s) | 1682.17 | 1706.25 | 1760.75 | 1825.45 |
| Change Values (m3/s) | 24.09 | 78.58 | 143.29 | ||
| change rate (%) | 1.43 | 4.67 | 8.52 | ||
| The Second Songhua River Basin | Average Annual Runoff (m3/s) | 543.95 | 553.51 | 571.85 | 609.35 |
| Change Values (m3/s) | 9.56 | 27.90 | 65.40 | ||
| change rate (%) | 1.76 | 5.13 | 12.02 | ||
| Nenjiang River Basin | Average Annual Runoff (m3/s) | 360.50 | 369.28 | 373.36 | 375.36 |
| Change Values (m3/s) | 8.78 | 12.86 | 14.86 | ||
| change rate (%) | 2.44 | 3.57 | 4.12 | ||
| Basin | 1980–2014 Historical Baseline Period | 2026–2068 Future Climate Scenarios | |||
|---|---|---|---|---|---|
| SSP1-2.6 | SSP2-4.5 | SSP5-8.5 | |||
| Songhua River main stream basin | Average Annual Runoff (1 × 108 m3) | 510.14 | 521.57 | 543.48 | 553.01 |
| Change Values (1 × 108 m3) | 11.43 | 33.34 | 42.87 | ||
| Change Rate (%) | 2.24 | 6.54 | 8.40 | ||
| The Second Songhua River Basin | Average Annual Runoff (1 × 108 m3) | 286.86 | 291.36 | 302.15 | 319.01 |
| Change Values (1 × 108 m3) | 4.50 | 15.29 | 32.15 | ||
| Change Rate (%) | 1.57 | 5.33 | 11.21 | ||
| Nenjiang River Basin | Average Annual Runoff (1 × 108 m3) | 302.27 | 308.67 | 312.94 | 312.54 |
| Change Values (1 × 108 m3) | 6.40 | 10.67 | 10.27 | ||
| Change Rate (%) | 2.12 | 3.53 | 3.40 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Dai, C.; Liu, G.; Yang, X.; Jing, J.; Ru, Q. Runoff Prediction in the Songhua River Basin Based on WEP Model. Hydrology 2025, 12, 266. https://doi.org/10.3390/hydrology12100266
Wang X, Dai C, Liu G, Yang X, Jing J, Ru Q. Runoff Prediction in the Songhua River Basin Based on WEP Model. Hydrology. 2025; 12(10):266. https://doi.org/10.3390/hydrology12100266
Chicago/Turabian StyleWang, Xinyu, Changlei Dai, Gengwei Liu, Xiao Yang, Jianyu Jing, and Qing Ru. 2025. "Runoff Prediction in the Songhua River Basin Based on WEP Model" Hydrology 12, no. 10: 266. https://doi.org/10.3390/hydrology12100266
APA StyleWang, X., Dai, C., Liu, G., Yang, X., Jing, J., & Ru, Q. (2025). Runoff Prediction in the Songhua River Basin Based on WEP Model. Hydrology, 12(10), 266. https://doi.org/10.3390/hydrology12100266






