GMesh: A Flexible Voronoi-Based Mesh Generator with Local Refinement for Watershed Hydrological Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. GMesh Architecture
2.1.1. Network Pre-Processing
2.1.2. Mesh Generation
2.1.3. Polygon Definition
2.1.4. Localized Mesh Refinement
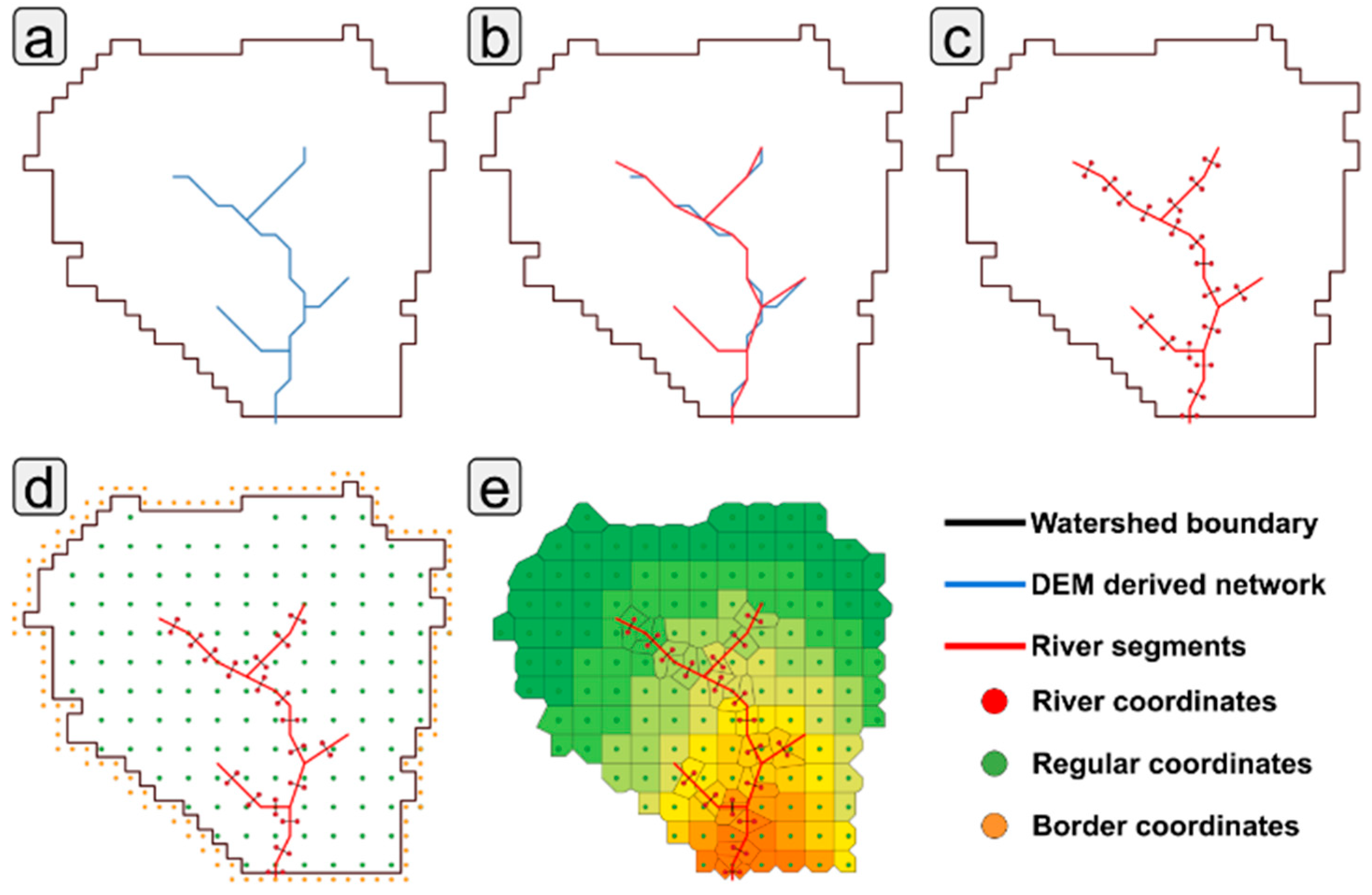
2.2. Functions and Usage
- Get_segments_topology: Obtains the connectivity between the new channel segments (Figure 1b).
- Get_mesh_river_points: Obtains the coordinates of the points surrounding each network segment. It extracts two points per segment, one over the left and the other over the right (Figure 1c).
- Get_mesh_grid_points: Defines the coordinates of a regular grid used to populate the mesh inside the watershed (Figure 1d).
- Get_vornoi_polygons: Derives the polygons using the river, regular grid, and border mesh points. Also, it differentiates between them.
- Define_polygons_topology: Defines the valid polygons, the connectivity between them, their connectivity with the segments network, and their properties (Figure 1e).
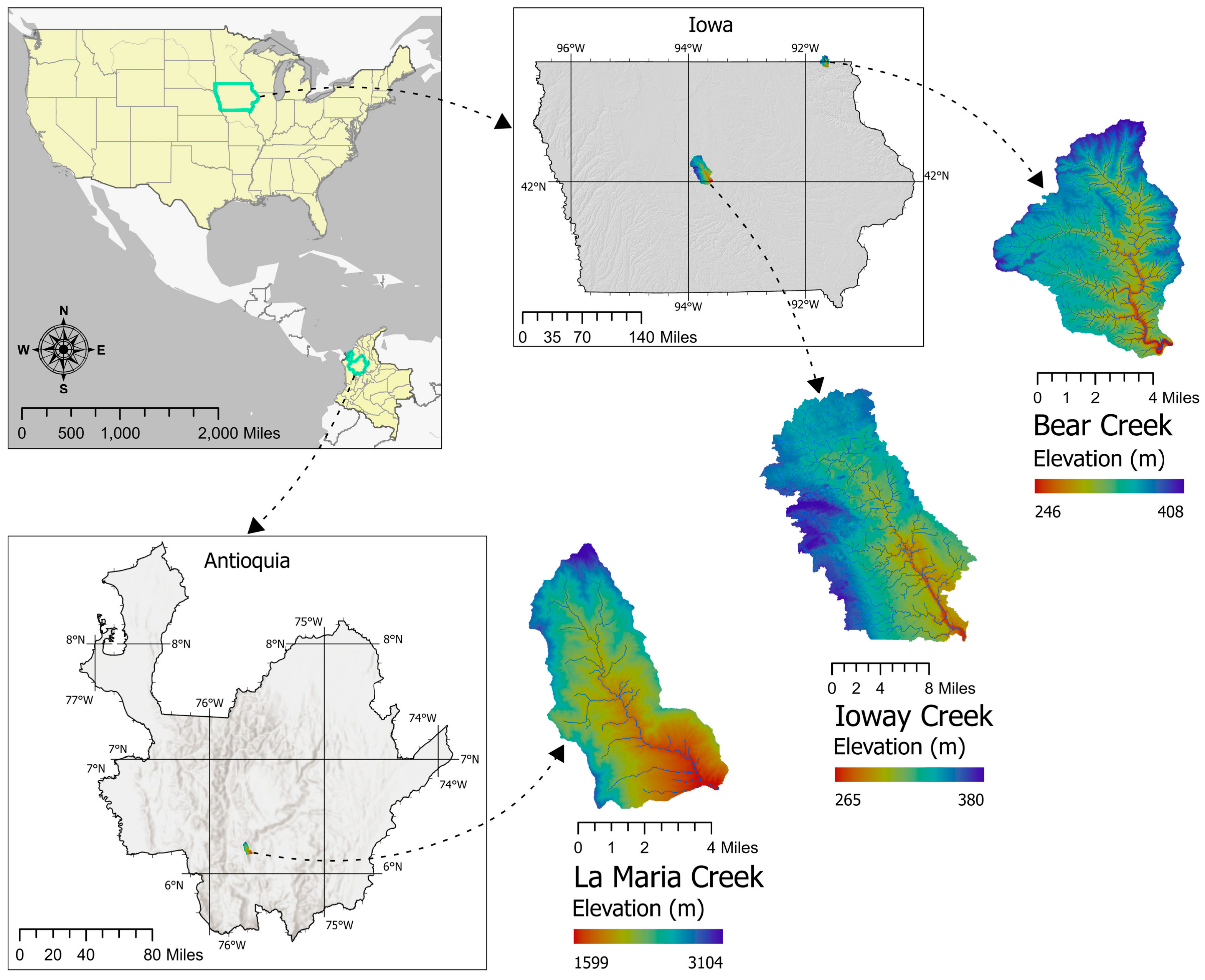
2.3. Data and Regions of Implementation
2.3.1. Bear Creek
2.3.2. Iowa Creek
2.3.3. La Maria Creek
3. Results
3.1. GMesh over Three Different Watersheds
3.2. Bear Creek Results
3.2.1. Mesh Stability Evaluation
3.2.2. Local Mesh Refinement for Bear Creek
3.3. Iowa Creek Results
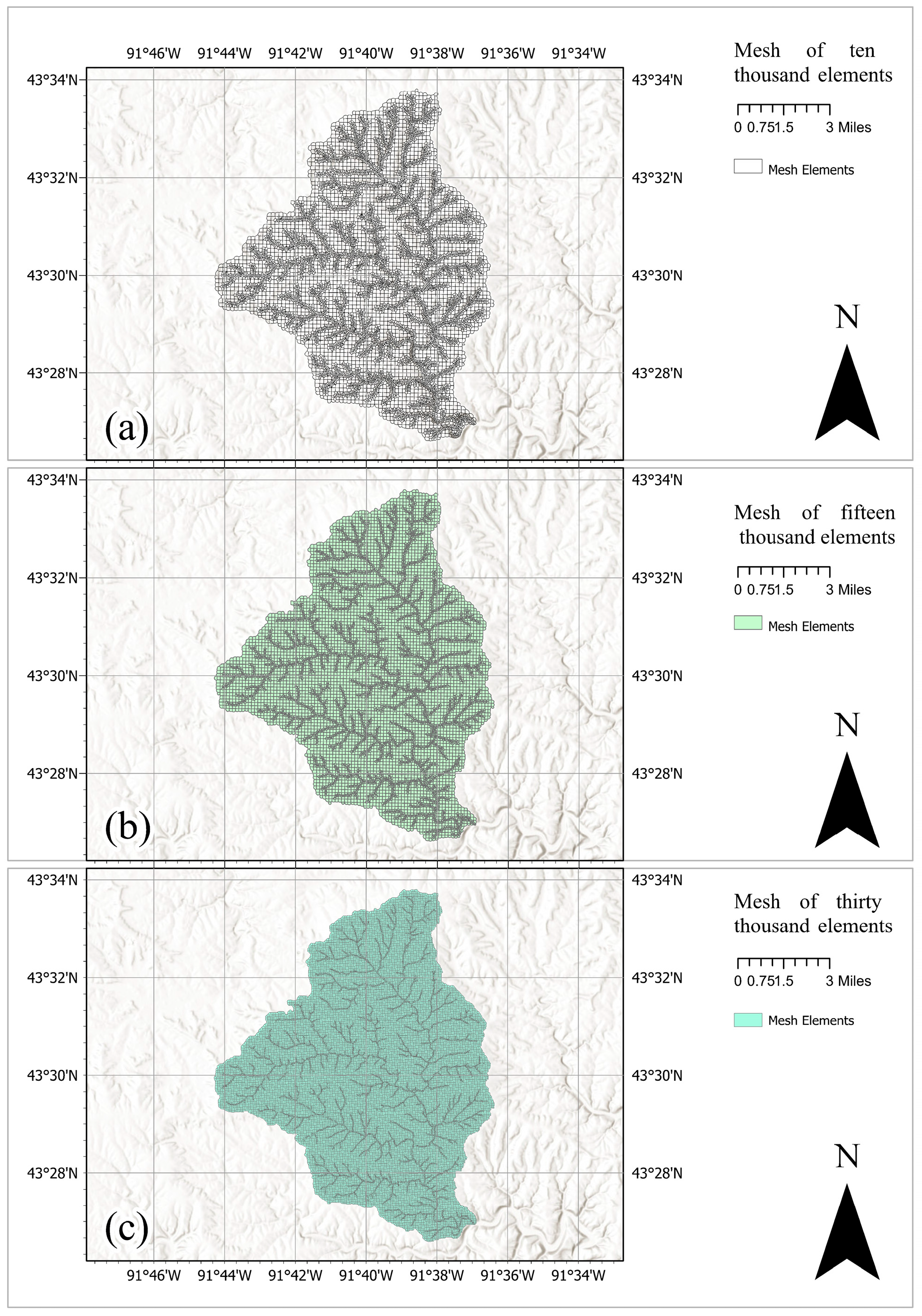
3.3.1. Local Mesh Refinement for Iowa Creek
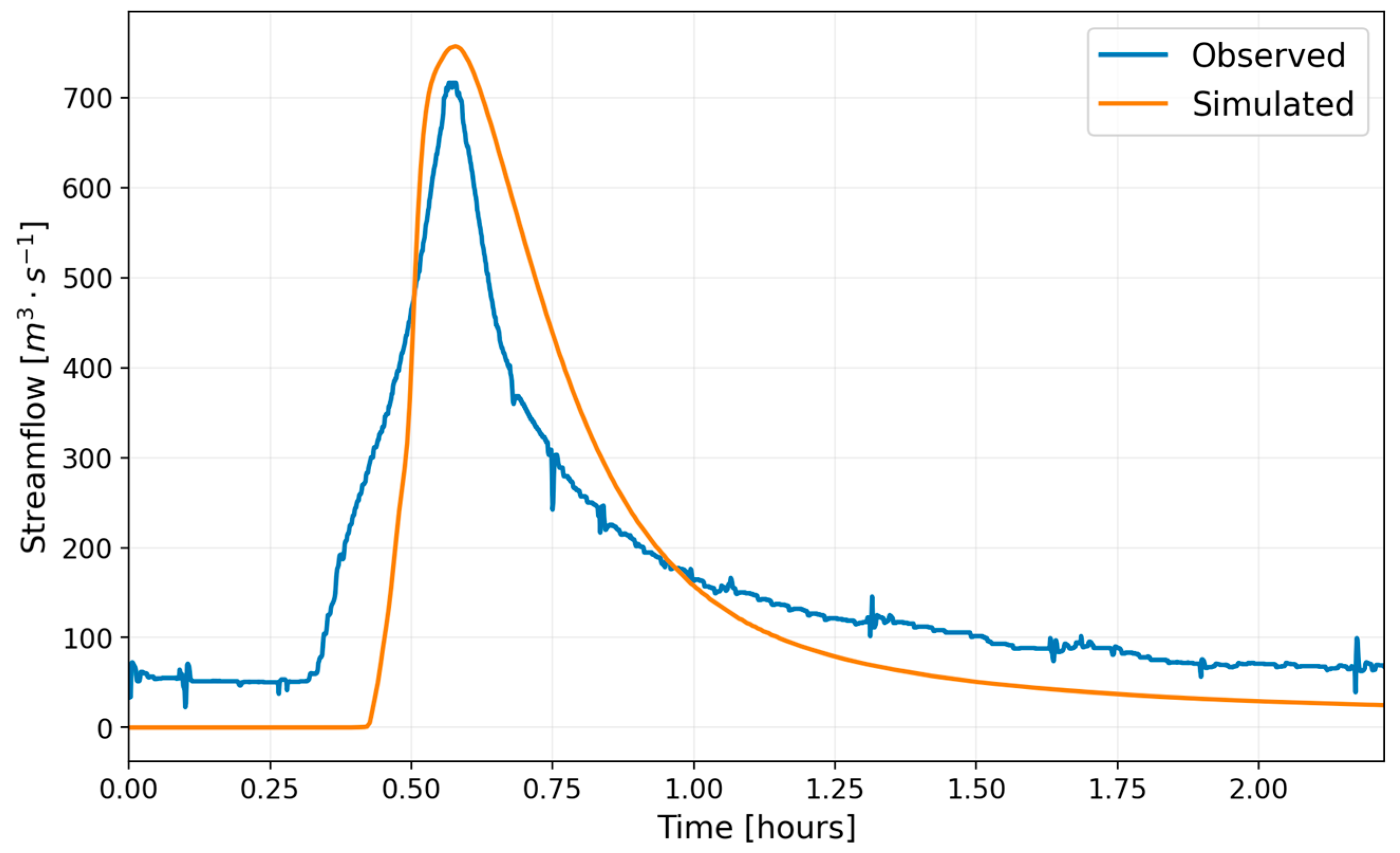
3.3.2. Streamflow Simulation Validation
3.4. Comparison with Pyflowline
4. Discussion
4.1. GMesh Advantages and Limitations
- In contrast with other available tools, GMesh preserves hydrological features, distinguishing between network and hillslope elements. Additionally, it identifies the connectivity between them.
- GMesh open license and the way it presents the information using known Python variables such as arrays and dataframes, allowing for easy customization.
- GMesh allows for the definition of different levels of refinement within the same project.
- The GMesh connectivity with Google Earth Engine (GEE) allows an easy retrieval of land use and soil properties, enhancing the implementation of the model in different regions.
- Once executed, GMesh writes the files required for GHOST and writes the vector maps of the watershed, including the mesh and the network. Moreover, GMesh allows the definition of the variables that will be contained in the vector layers.
- While optimized for the GHOST model, adapting GMesh for use with other hydrological models may require additional customization.
- High-resolution meshes can lead to increased computational requirements, potentially limiting scalability for extensive watershed analyses. However, this issue applies to other mesh generators and to hydrological PDE models where modelers need to define relatively large simulation elements.
- GMesh execution time could be improved by implementing parallel approaches, adapting the usage of graphics processing units (GPUs), and migrating some of its code to Fortran or C (as has been done in the WMF).
4.2. Comparison with Similar Tools
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GHOST | Generic Hydrologic Overland-Subsurface Toolkit |
| WMF | Watershed Modelling Framework |
| GMesh | GHOST Mesh generator |
References
- Freeze, R.A.; Harlan, R.L. Blueprint for a Physically-Based, Digitally-Simulated Hydrologic Response Model. J. Hydrol. 1969, 9, 237–258. [Google Scholar] [CrossRef]
- Politano, M.; Arenas, A.; Weber, L. A Process-Based Hydrological Model for Continuous Multi-Year Simulations of Large-Scale Watersheds. Int. J. River Basin Manag. 2023, 23, 15–28. [Google Scholar] [CrossRef]
- Simmons, C.T.; Brunner, P.; Therrien, R.; Sudicky, E.A. Commemorating the 50th Anniversary of the Freeze and Harlan (1969) Blueprint for a Physically-Based, Digitally-Simulated Hydrologic Response Model. J. Hydrol. 2020, 584, 124309. [Google Scholar] [CrossRef]
- Sanzana, P.; Jankowfsky, S.; Branger, F.; Braud, I.; Vargas, X.; Hitschfeld, N.; Gironás, J. Computer-Assisted Mesh Generation Based on Hydrological Response Units for Distributed Hydrological Modeling. Comput. Geosci. 2013, 57, 32–43. [Google Scholar] [CrossRef]
- Díaz García, M.Á.; Santos Granados, G.R. Modelación del Flujo en 3D en el Proceso de Sedimentación Primaria para el Tratamiento de aguas Residuales Domesticas Utilizando ANSYS-FLUENT. Master’s Thesis, Escuela Colombiana de Ingenieria Julio Garavito, Bogota, Colombia, 2022. [Google Scholar]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; Contractor Report (CR); NASA Langley Research Center: Hampton, VA, USA, 2014. [Google Scholar]
- Donnelly, C.; Rosberg, J.; Isberg, K. A Validation of River Routing Networks for Catchment Modelling from Small to Large Scales. Hydrol. Res. 2013, 44, 917–925. [Google Scholar] [CrossRef]
- Rojas, R.; Velleux, M.; Julien, P.Y.; Johnson, B.E. Grid Scale Effects on Watershed Soil Erosion Models. J. Hydrol. Eng. 2008, 13, 793–802. [Google Scholar] [CrossRef]
- Marsh, C.B.; Spiteri, R.J.; Pomeroy, J.W.; Wheater, H.S. Multi-Objective Unstructured Triangular Mesh Generation for Use in Hydrological and Land Surface Models. Comput. Geosci. 2018, 119, 49–67. [Google Scholar] [CrossRef]
- Shewchuk, J.R. Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator. In Applied Computational Geometry Towards Geometric Engineering; Lin, M.C., Manocha, D., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1148, pp. 203–222. ISBN 978-3-540-61785-3. [Google Scholar]
- Brunner, P.; Simmons, C.T. HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model. Groundwater 2012, 50, 170–176. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.; Šejna, M. Development and Applications of the HYDRUS and STANMOD Software Packages and Related Codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-Dimensional Finite Element Mesh Generator with Built-in Pre- and Post-Processing Facilities. Int. J. Numer. Meth. Engng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Deltares. D-Flow Flexible Mesh User Manual; Deltares: Delft, The Netherlands, 2024. [Google Scholar]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An Overview of Current Applications, Challenges, and Future Trends in Distributed Process-Based Models in Hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef]
- Kang, Y.; Kubatko, E.J. An Automatic Mesh Generator for Coupled 1D–2D Hydrodynamic Models. Geosci. Model Dev. 2024, 17, 1603–1625. [Google Scholar] [CrossRef]
- Velásquez, N.; Vélez, J.I.; Álvarez-Villa, O.D.; Salamanca, S.P. Comprehensive Analysis of Hydrological Processes in a Programmable Environment: The Watershed Modeling Framework. Hydrology 2023, 10, 76. [Google Scholar] [CrossRef]
- Vélez, J.I. Desarrollo de Un Modelo Hidrológico Conceptual y Distribuido Orientado a La Simulación de Crecidas. Ph.D. Thesis, Universidad Politécnica de Valencia, Valencia, Spain, 2001. [Google Scholar]
- Francés, F.; Vélez, J.I.; Vélez, J.J. Split-Parameter Structure for the Automatic Calibration of Distributed Hydrological Models. J. Hydrol. 2007, 332, 226–240. [Google Scholar] [CrossRef]
- Mantilla, R.; Krajewski, W.F.; Velasquez, N.; Small, S.J.; Ayalew, T.B.; Quintero, F.; Jadidoleslam, N.; Fonley, M. The Hydrological Hillslope-Link Model for Space-Time Prediction of Streamflow: Insights and Applications at the Iowa Flood Center. Extrem. Weather Forecast. 2022, 200. [Google Scholar]
- Tarboton, D.G.; Bras, R.L. The Analysis of River Basins and Channel Networks Using Digital Terrain Data. Dep. Civ. Eng. 1989, 252. [Google Scholar]
- Özgen-Xian, I.; Kesserwani, G.; Caviedes-Voullième, D.; Molins, S.; Xu, Z.; Dwivedi, D.; Moulton, J.D.; Steefel, C.I. Wavelet-Based Local Mesh Refinement for Rainfall–Runoff Simulations. J. Hydroinformatics 2020, 22, 1059–1077. [Google Scholar] [CrossRef]
- Wright, K.; Passalacqua, P.; Simard, M.; Jones, C.E. Integrating Connectivity Into Hydrodynamic Models: An Automated Open-Source Method to Refine an Unstructured Mesh Using Remote Sensing. J. Adv. Model Earth Syst. 2022, 14, e2022MS003025. [Google Scholar] [CrossRef]
- Cosgrove, B.A.; Lohmann, D.; Mitchell, K.E.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Marshall, C.; Sheffield, J.; Duan, Q.; et al. Real-time and Retrospective Forcing in the North American Land Data Assimilation System (NLDAS) Project. J. Geophys. Res. 2003, 108, 2002JD003118. [Google Scholar] [CrossRef]
- OpenTopography. USGS 1/3 Arc-Second Digital Elevation Models 2021. Available online: https://portal.opentopography.org/datasetMetadata?otCollectionID=OT.012021.4269.1 (accessed on 15 September 2025).
- Horritt, M.S.; Bates, P.D.; Mattinson, M.J. Effects of Mesh Resolution and Topographic Representation in 2D Finite Volume Models of Shallow Water Fluvial Flow. J. Hydrol. 2006, 329, 306–314. [Google Scholar] [CrossRef]
- Dehotin, J.; Braud, I. Which Spatial Discretization for Distributed Hydrological Models? Proposition of a Methodology and Illustration for Medium to Large-Scale Catchments. Hydrol. Earth Syst. Sci. 2008, 12, 769–796. [Google Scholar] [CrossRef]
- Gurtz, J.; Zappa, M.; Jasper, K.; Lang, H.; Verbunt, M.; Badoux, A.; Vitvar, T. A Comparative Study in Modelling Runoff and Its Components in Two Mountainous Catchments. Hydrol. Process. 2003, 17, 297–311. [Google Scholar] [CrossRef]
- Horton, P.; Schaefli, B.; Kauzlaric, M. Why Do We Have so Many Different Hydrological Models? A Review Based on the Case of Switzerland. WIREs Water 2022, 9, e1574. [Google Scholar] [CrossRef]
- Liao, C.; Zhou, T.; Xu, D.; Cooper, M.G.; Engwirda, D.; Li, H.; Leung, L.R. Topological Relationship-Based Flow Direction Modeling: Mesh-Independent River Networks Representation. J. Adv. Model Earth Syst. 2023, 15, e2022MS003089. [Google Scholar] [CrossRef]
- Mantilla, R.; Fonley, M.; Velasquez, N. Technical Note: Testing the Connection Between Hillslope Scale Runoff Fluctuations and Streamflow Hydrographs at the Outlet of Large River Basins. Hydrol. Earth Syst. Sci. 2023, 28, 1373–1382. [Google Scholar] [CrossRef]
- FEATool Multiphysics. Fully Integrated Simulation Platform. Available online: https://www.featool.com/?srsltid=AfmBOop749G_bZPQ-pnRnWYdcYKsu11vacA-swEMyrhXG0F6gg3h9llg (accessed on 15 September 2025).
- Liao, C.; Cooper, M.G. Pyflowline: A Mesh-Independent River Network Generatorfor Hydrologic Models. JOSS 2023, 8, 5446. [Google Scholar] [CrossRef]
- Troupin, C.; Barth, A.; Sirjacobs, D.; Ouberdous, M.; Brankart, J.-M.; Brasseur, P.; Rixen, M.; Alvera-Azcárate, A.; Belounis, M.; Capet, A.; et al. Generation of Analysis and Consistent Error Fields Using the Data Interpolating Variational Analysis (DIVA). Ocean Model 2012, 52–53, 90–101. [Google Scholar] [CrossRef]

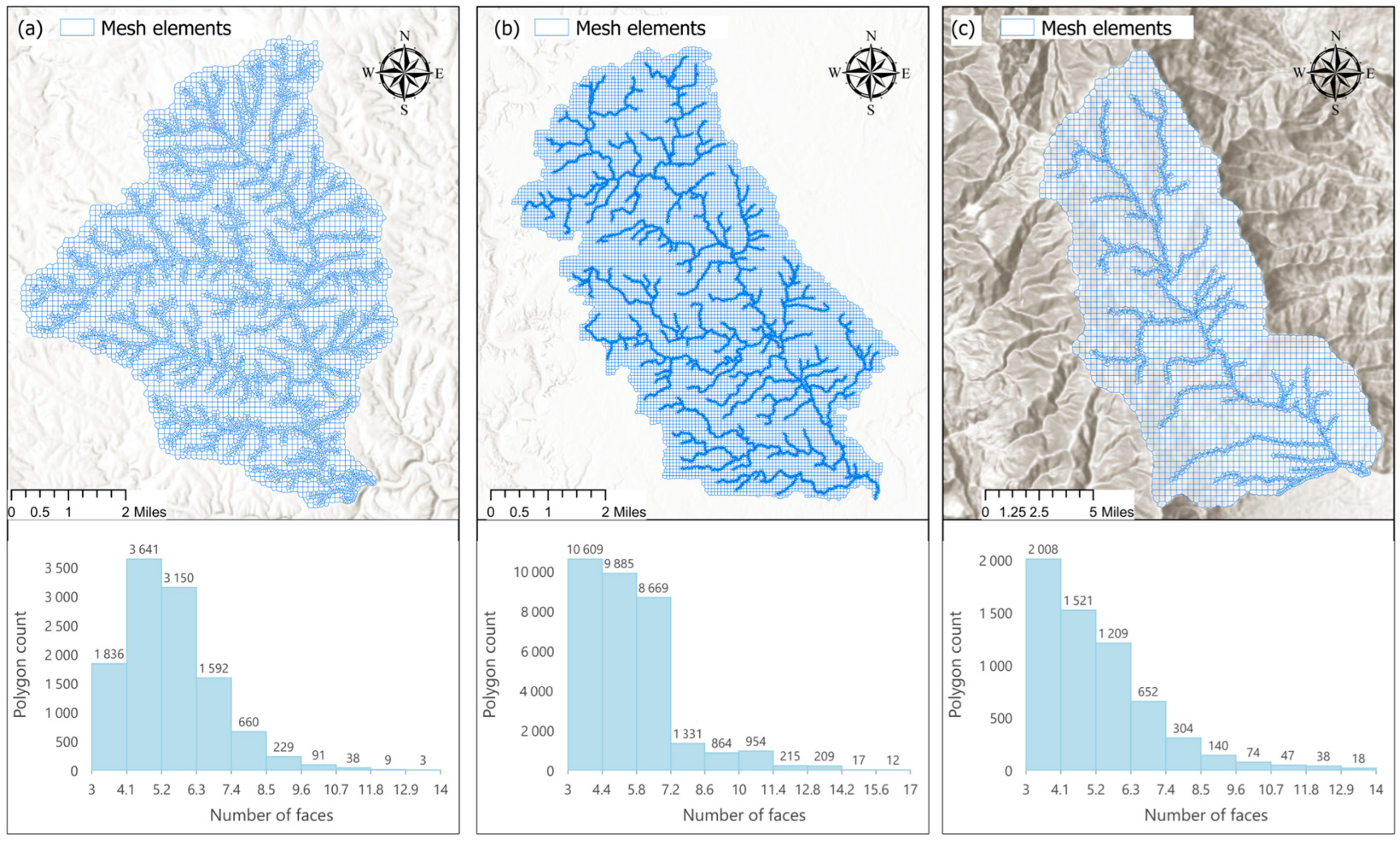
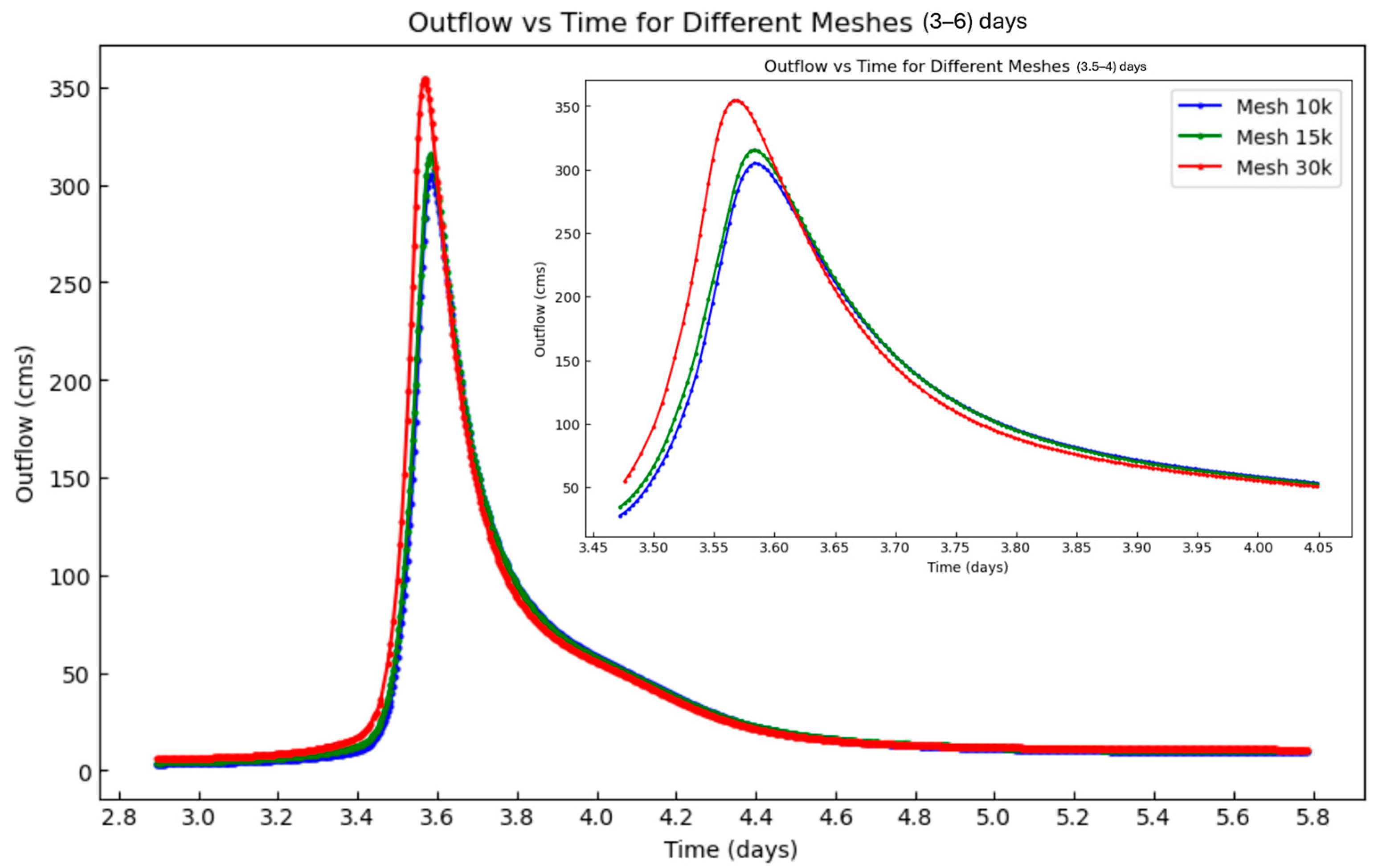
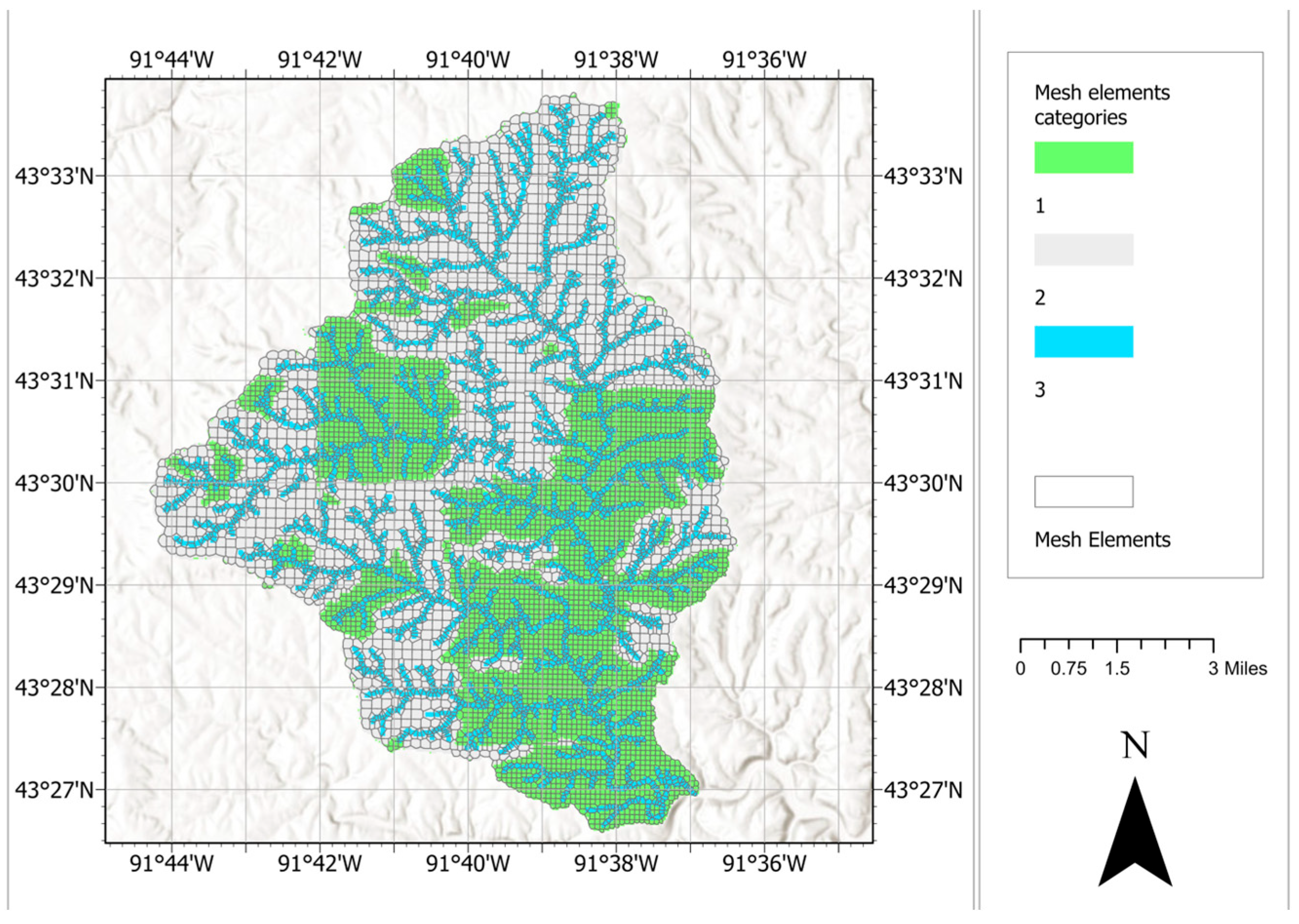
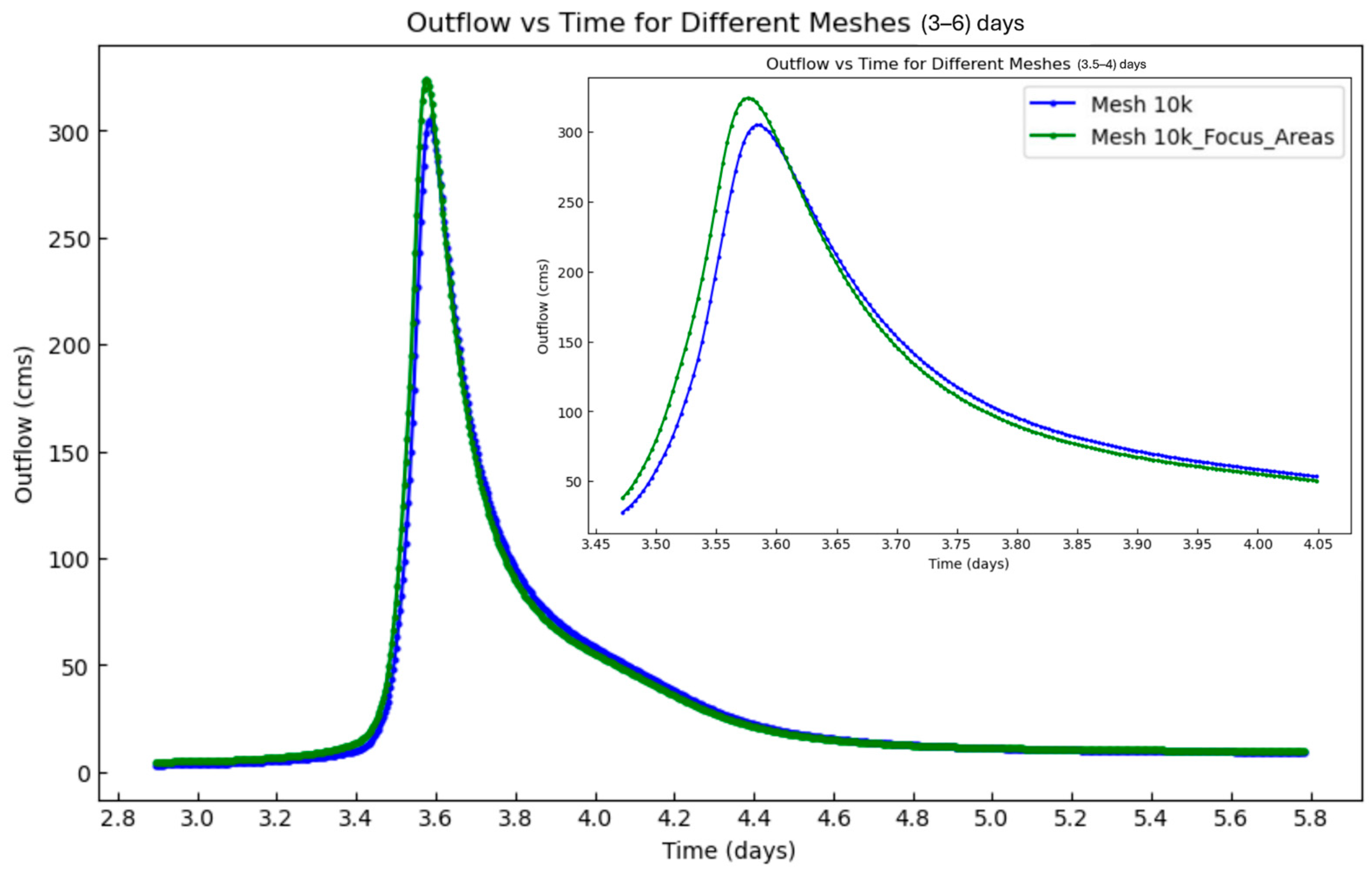
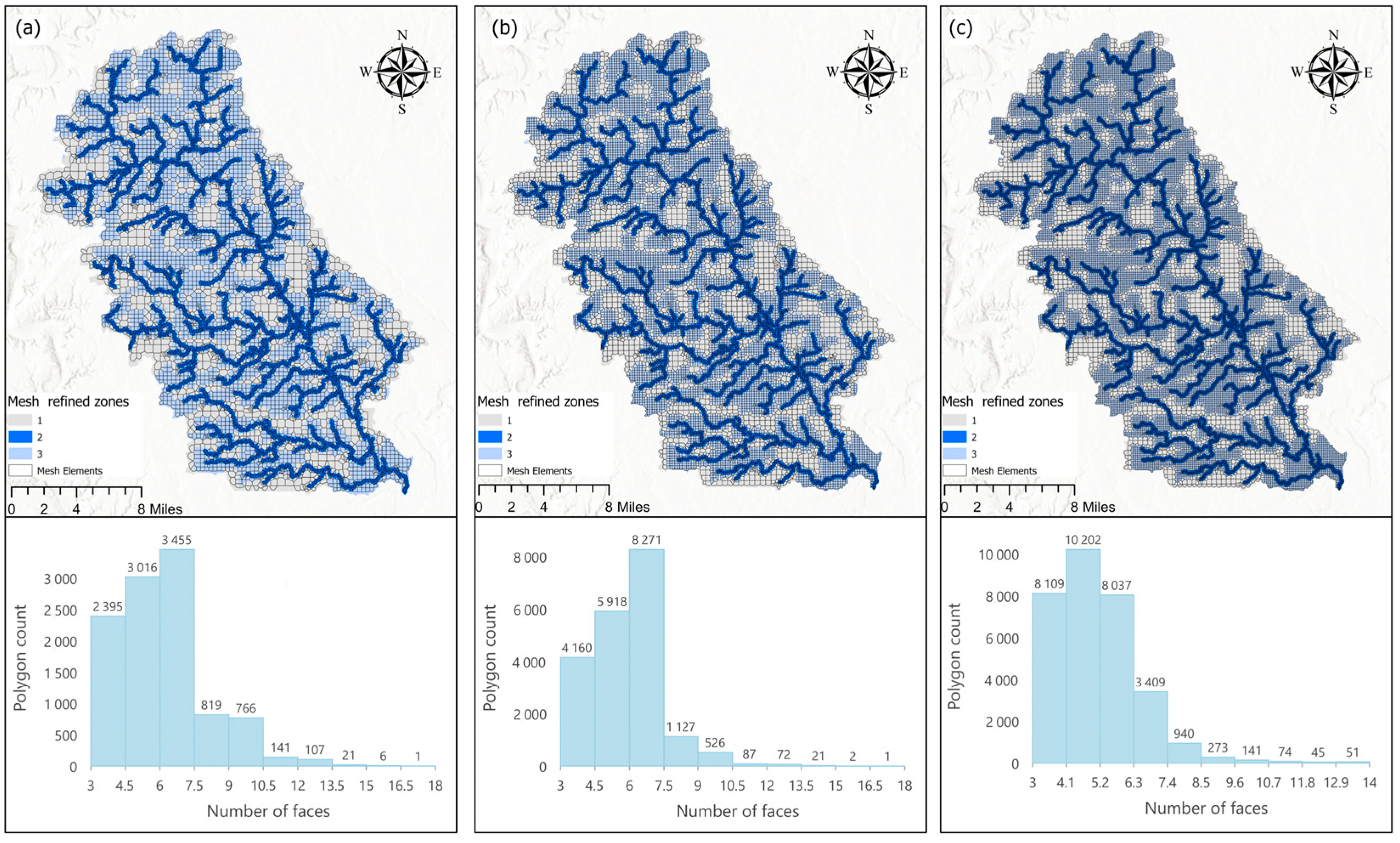
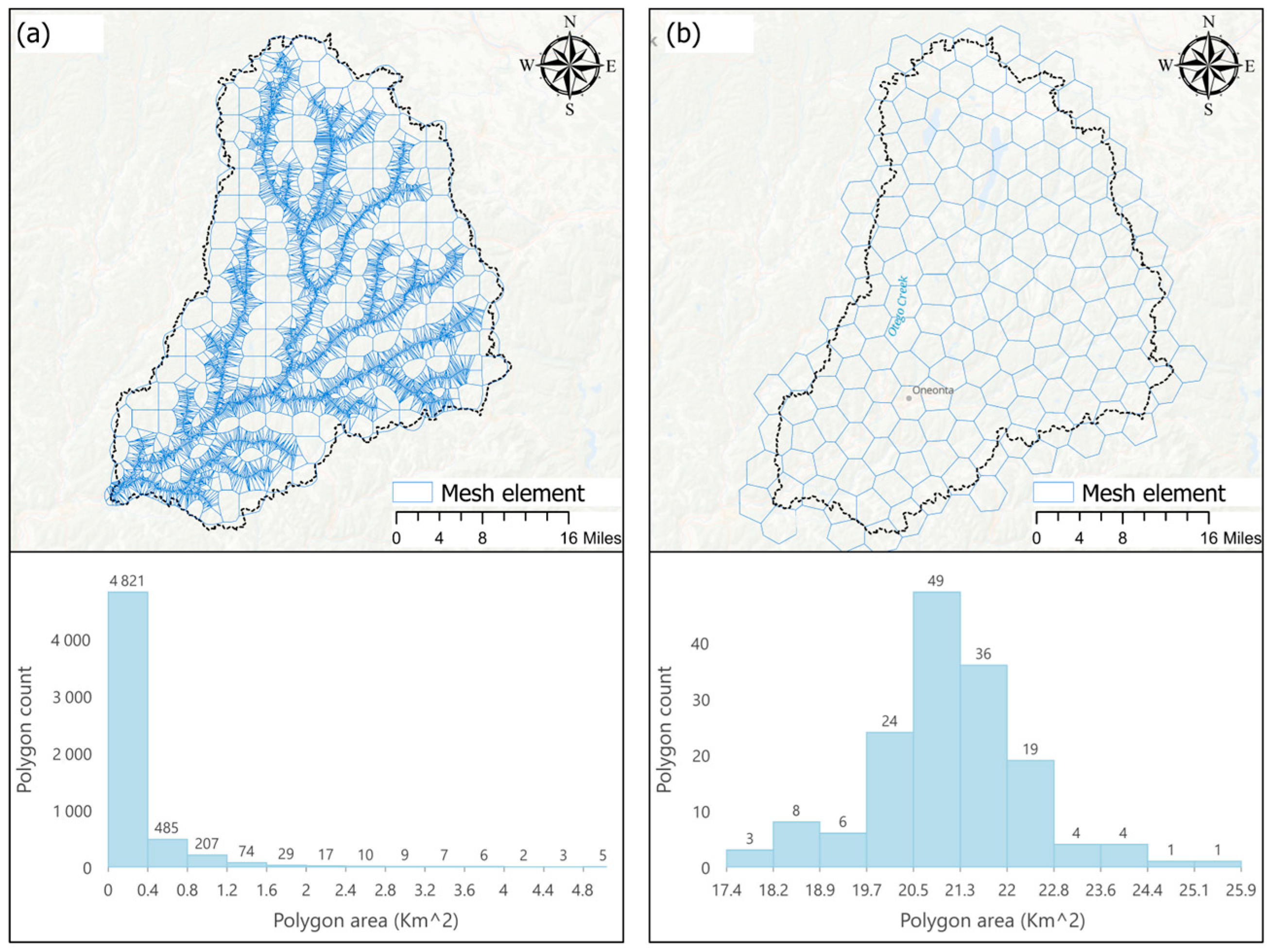
| Watershed | Area (square km) | Number of Elements | Generation Time (min) | Average Number of Faces | Max Number of Faces |
|---|---|---|---|---|---|
| Ioway Creek | 533.58 | 32,765 (32k) | 52 | 5 | 17 |
| Bear Creek | 82.25 | 11,248 (11k) | 10 | 5 | 14 |
| La Maria Creek | 62.41 | 6010 (6k) | 1.5 | 6 | 14 |
| Number of Elements | Generation Time (min) | Average Number of Faces |
|---|---|---|
| 10,000 (10k) | 10 | 11 |
| 15,000 (15k) | 20 | 8 |
| 30,000 (30k) | 35 | 7 |
| Number of Elements | GHOST Computational Time (h) |
|---|---|
| 10,000 (10k) | 0.5 |
| 15,000 (15k) | 1 |
| 30,000 (30k) | 7 |
| Item | Computational Time (h) |
|---|---|
| Mesh generation | 0.2 |
| GHOST execution | 0.4 |
| Number of Elements | Generation Time (min) | Average Number of Faces | Max Number of Faces |
|---|---|---|---|
| 10,726 (10k) | 15 | 6 | 18 |
| 20,184 (20k) | 65 | 6 | 18 |
| 31,281 (31k) | 118 | 5 | 14 |
| Tool | Description | Advantages | Limitations | License |
|---|---|---|---|---|
| GMesh | Automated watershed-oriented mesh generator | Preserves river-hillslope connectivity, local refinement, and support GEE support | Currently tied to GHOST, computationally intensive | GNU V3.0 |
| Gmsh | General-purpose 3D finite element mesh generator | Versatile, GUI interaction, community support | Not tailored for hydrology and requires manual integration | GPL |
| ADMESH+ | Mesh generation for 1 and 2D hydrodynamic models. | Integrates DEM, land-water data and refines around hydrological features | Focused on hydraulics and is less flexible for hydrological simulations | MIT |
| PyFlowline | Mesh generation for hydraulic simulations | River-network-focused and works with structured/unstructured meshes | Is it not a full mesh generator. Supplies riverine data | MIT |
| FEATool Multiphysics | Integrated modeling tool with support for multiple physics including flow and mesh generation | Has a GUI and is scriptable, supports several physics and exports to OpeanFOAM and COMSOL | General purpose not focused on hydrological modeling | Free with paid upgrades |
| HydroGeoSphere | Fully integrated 3D physically based hydrological model | It is well tested for soil moisture and ground water modeling | Has commercial limitations | Free for 1/2D and paid for 3D |
| D-Flow Flexible Mesh [14] | Unstructured mesh generator for hydrodynamics | High-quality GUI, integration with Deltf3D products, and has coastal and riverine applications | It is GUI-focused, paid for advanced features, and not open | Freemium/Paid |
| DIVA [34] | Spatial gridding and interpolation tool for coastlines and sub-basins | Good for marine/coastal applications | Not a mesh generator per se | GNU V3.0 |
| Hydrus 3D | Software package for simulating water, heat, and solute movement in 3D variably saturated media | It is well tested for soil moisture and ground water modeling | Is it not specialized in hydrological network structure | Free for 1/2D and paid for 3D |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velásquez, N.; Díaz, M.; Arenas, A. GMesh: A Flexible Voronoi-Based Mesh Generator with Local Refinement for Watershed Hydrological Modeling. Hydrology 2025, 12, 255. https://doi.org/10.3390/hydrology12100255
Velásquez N, Díaz M, Arenas A. GMesh: A Flexible Voronoi-Based Mesh Generator with Local Refinement for Watershed Hydrological Modeling. Hydrology. 2025; 12(10):255. https://doi.org/10.3390/hydrology12100255
Chicago/Turabian StyleVelásquez, Nicolás, Miguel Díaz, and Antonio Arenas. 2025. "GMesh: A Flexible Voronoi-Based Mesh Generator with Local Refinement for Watershed Hydrological Modeling" Hydrology 12, no. 10: 255. https://doi.org/10.3390/hydrology12100255
APA StyleVelásquez, N., Díaz, M., & Arenas, A. (2025). GMesh: A Flexible Voronoi-Based Mesh Generator with Local Refinement for Watershed Hydrological Modeling. Hydrology, 12(10), 255. https://doi.org/10.3390/hydrology12100255








