Exploring the Added Value of Sub-Daily Bias Correction of High-Resolution Gridded Rainfall Datasets for Rainfall Erosivity Estimation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.2.1. Rainfall Observations
2.2.2. Rainfall Products (RPs)
2.3. Steps of the Methodology
2.3.1. Selection of a Reference RP for Bias Correction of Rainfall Data
2.3.2. Sub-Daily Bias Correction of RPs
2.3.3. Impact of Bias Correction on Rainfall Estimation across the RPs
2.3.4. Calculation of Rainfall Erosivity
2.3.5. Comparison of Rainfall Erosivity with Reference Values
2.3.6. Trend Analysis of Rainfall Erosivity over the Period 2001–2020
3. Results
3.1. Sub-Daily Bias Correction of RPs
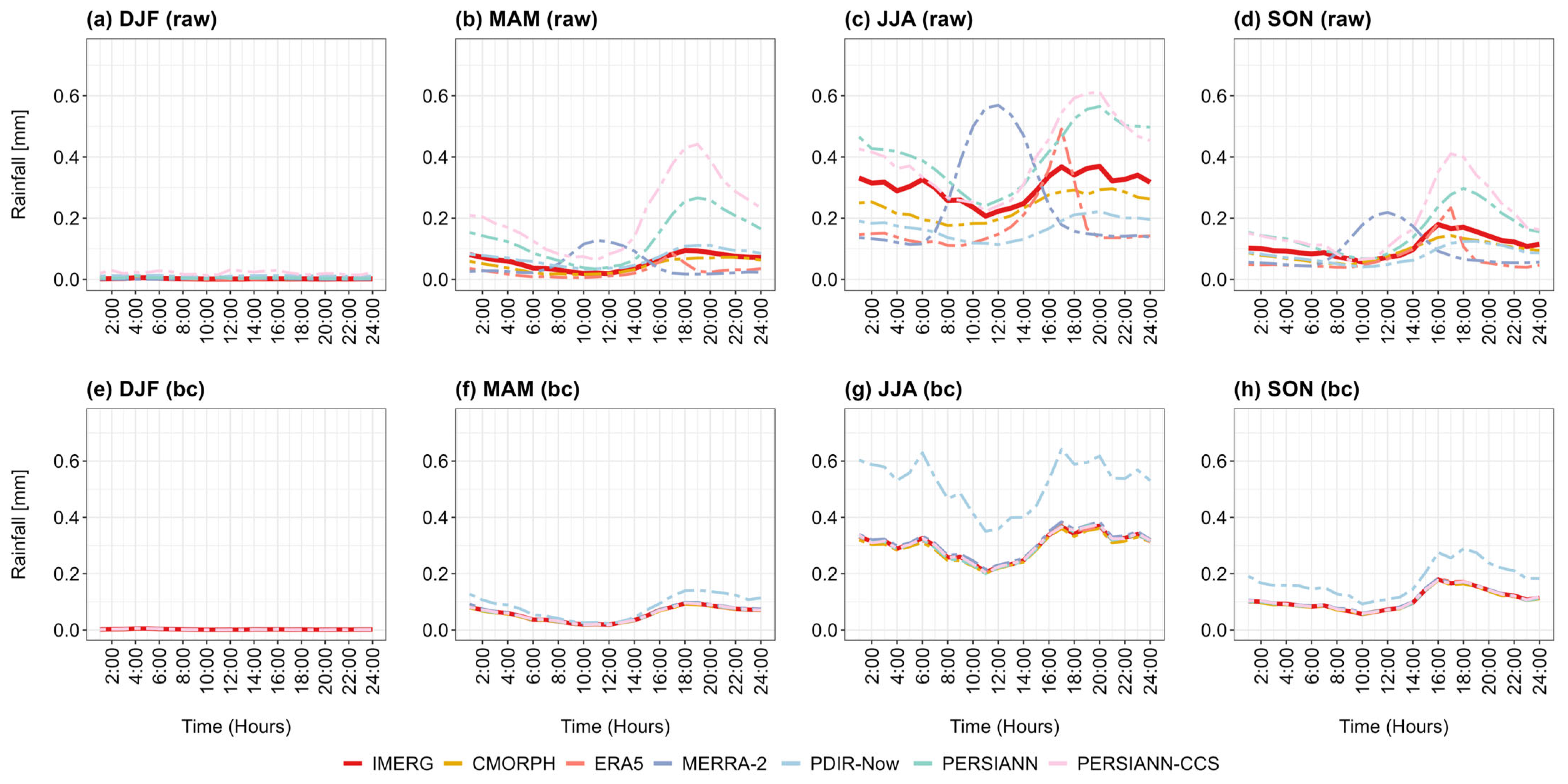
3.2. Impact of Bias Correction on Rainfall
3.2.1. Comparison of Rainfall at Daily, Monthly, and Annual Timescales
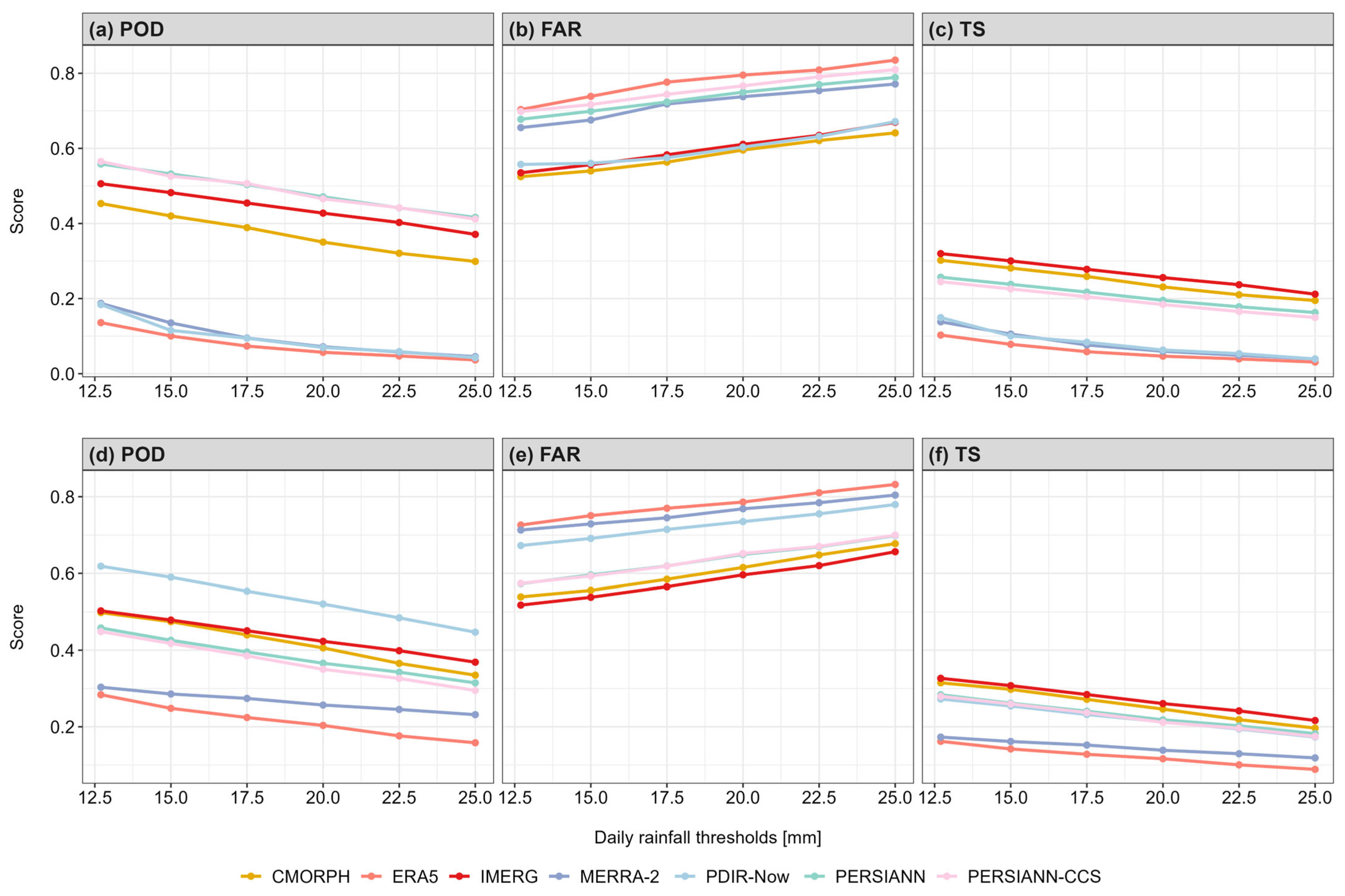
3.2.2. Categorical Metrics
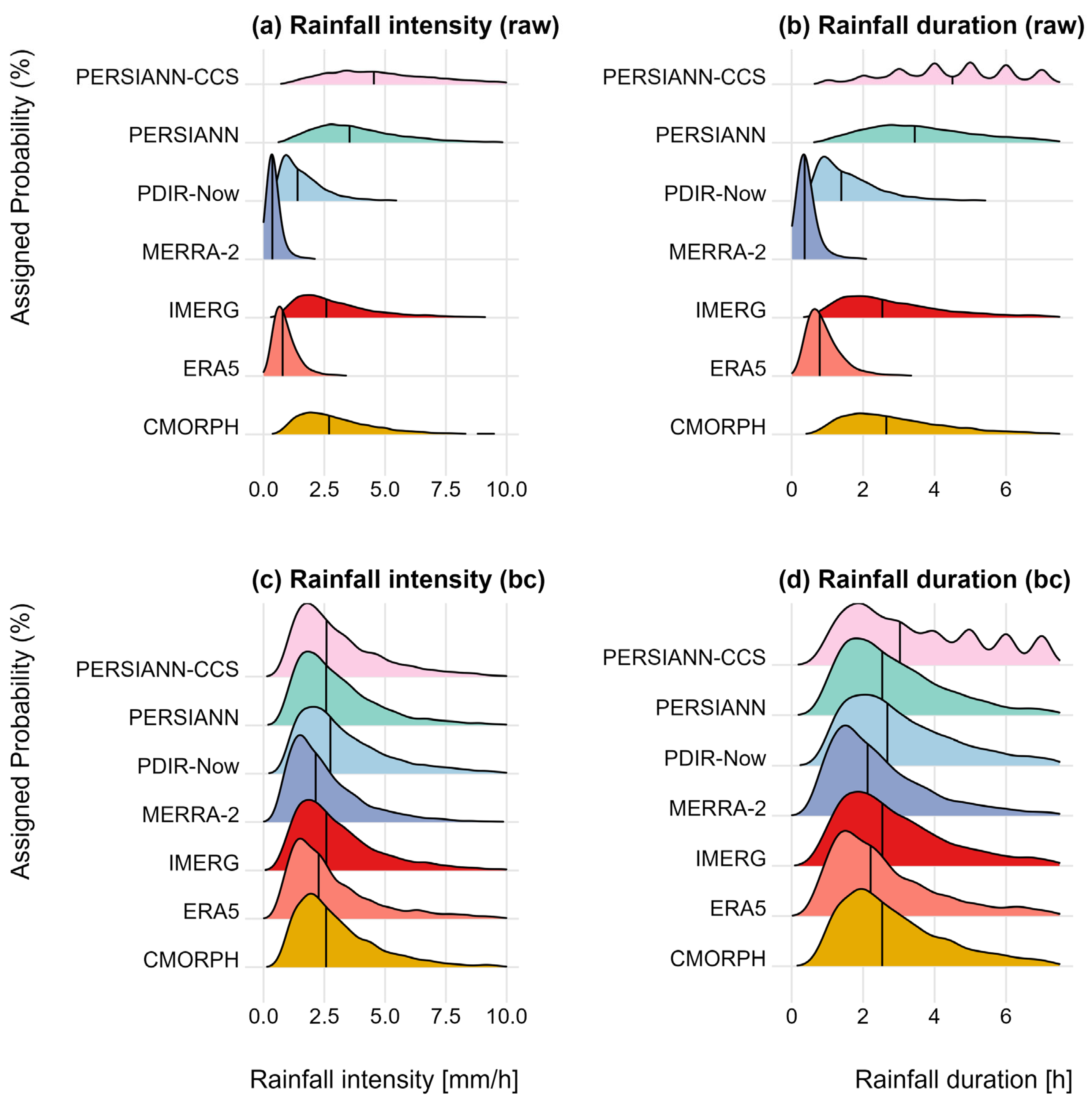
3.2.3. Distribution of Rainfall Events Intensity and Duration
3.2.4. Spatial Patterns in Annual Rainfall
3.3. Impact of Bias Correction on Rainfall Erosivity Estimates from RPs
3.3.1. Estimation of Half-Hourly to Hourly Calibration Factors
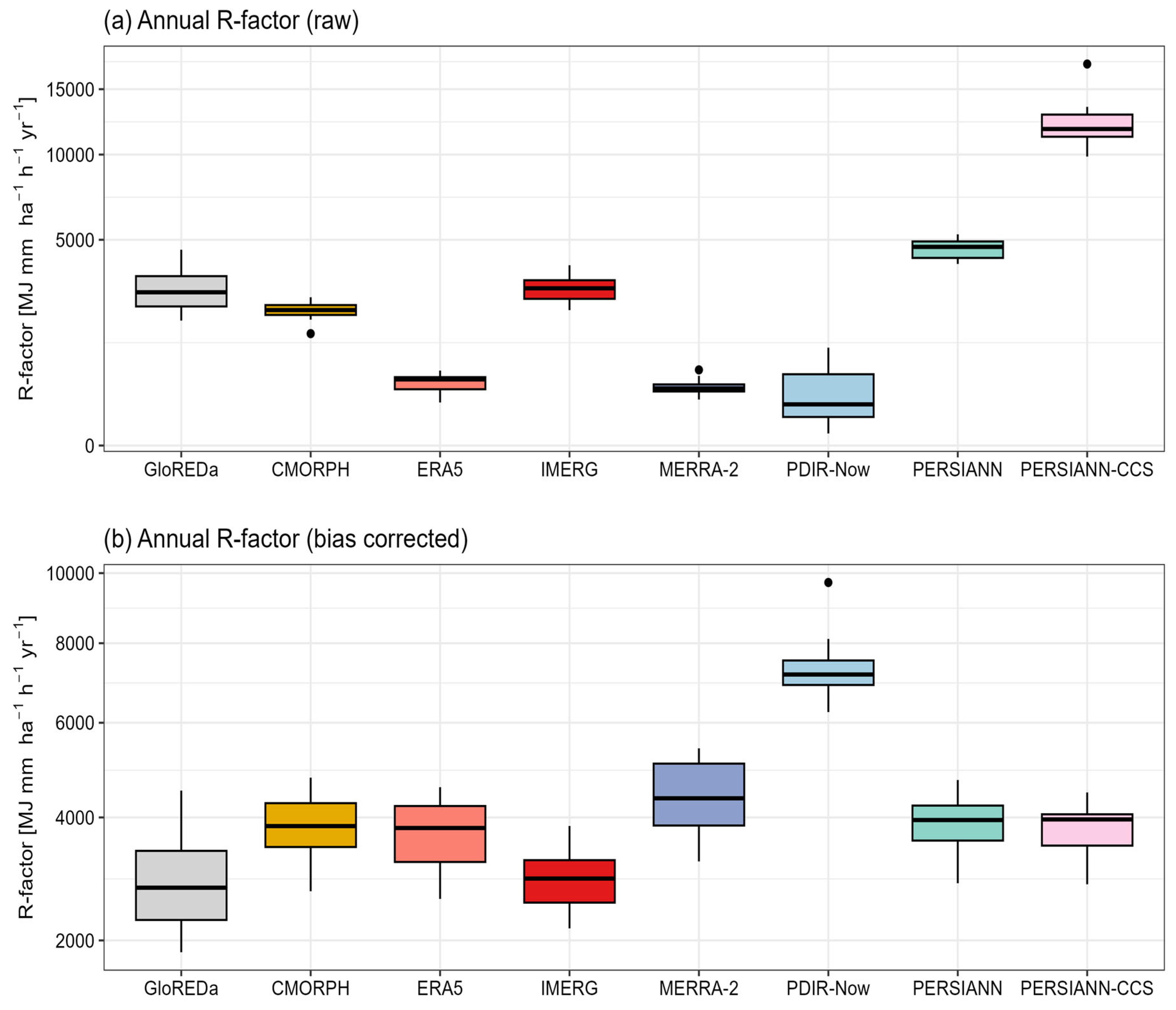
3.3.2. Annual Rainfall Erosivity R-Factor
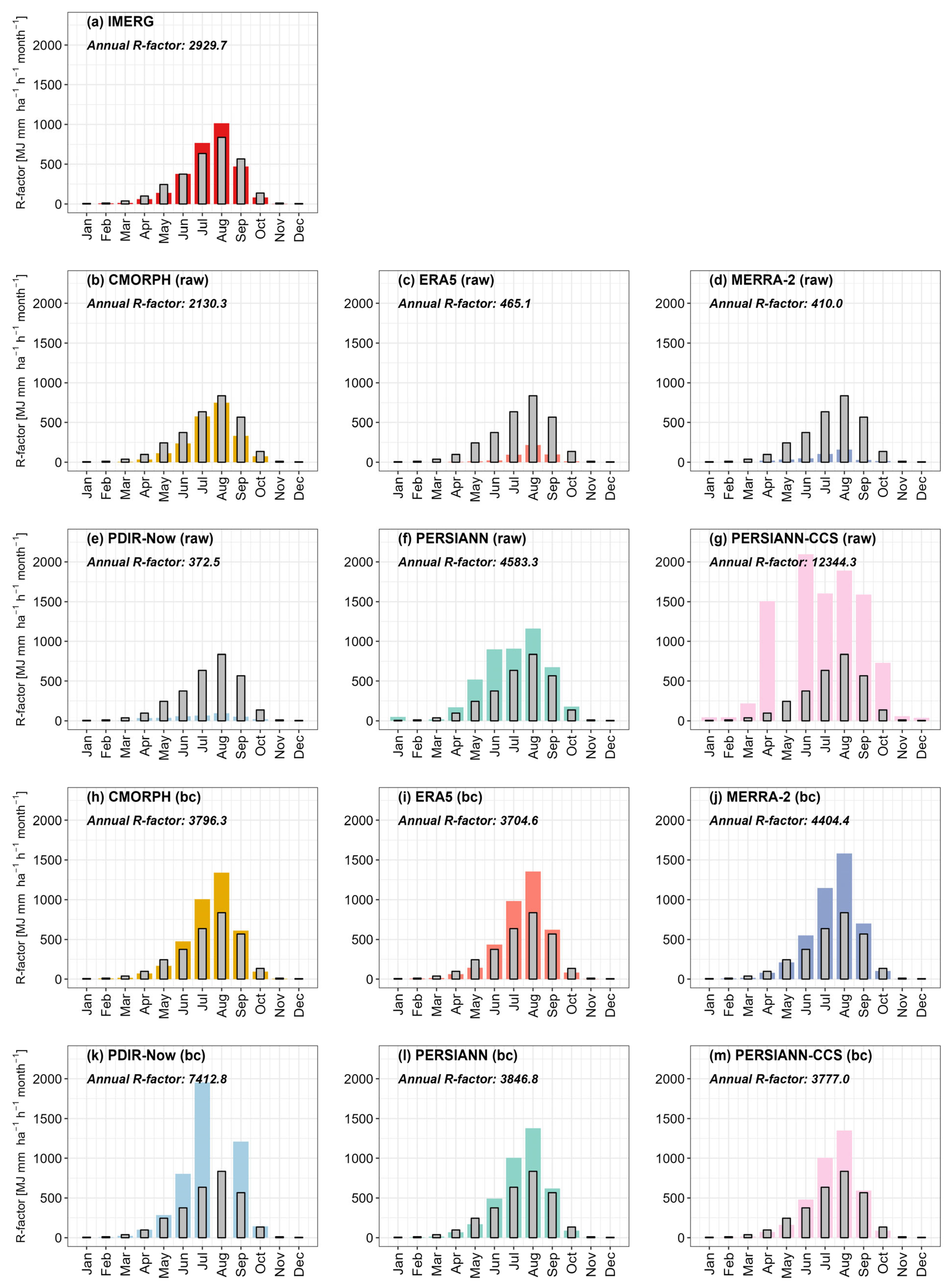
3.3.3. Monthly Rainfall Erosivity R-Factors
3.3.4. Spatial Patterns in Annual Rainfall Erosivity R-Factor
3.4. Impact of Bias Correction on Annual Trends in Rainfall and Rainfall Erosivity
4. Discussion
4.1. Key Findings in This Study
4.2. Study Limitations and Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amanambu, A.C.; Li, L.; Egbinola, C.N.; Obarein, O.A.; Mupenzi, C.; Chen, D. Spatio-Temporal Variation in Rainfall-Runoff Erosivity Due to Climate Change in the Lower Niger Basin, West Africa. CATENA 2019, 172, 324–334. [Google Scholar] [CrossRef]
- Lèye, B.; Zouré, C.O.; Yonaba, R.; Karambiri, H. Water Resources in the Sahel and Adaptation of Agriculture to Climate Change: Burkina Faso. In Climate Change and Water Resources in Africa; Diop, S., Scheren, P., Niang, A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 309–331. ISBN 978-3-030-61224-5. [Google Scholar]
- Salako, F.K. Development of Isoerodent Maps for Nigeria from Daily Rainfall Amount. Geoderma 2010, 156, 372–378. [Google Scholar] [CrossRef]
- Vrieling, A.; Sterk, G.; De Jong, S.M. Satellite-Based Estimation of Rainfall Erosivity for Africa. J. Hydrol. 2010, 395, 235–241. [Google Scholar] [CrossRef]
- Vrieling, A.; Hoedjes, J.C.B.; Van Der Velde, M. Towards Large-Scale Monitoring of Soil Erosion in Africa: Accounting for the Dynamics of Rainfall Erosivity. Glob. Planet. Chang. 2014, 115, 33–43. [Google Scholar] [CrossRef]
- Rutebuka, J.; De Taeye, S.; Kagabo, D.; Verdoodt, A. Calibration and Validation of Rainfall Erosivity Estimators for Application in Rwanda. CATENA 2020, 190, 104538. [Google Scholar] [CrossRef]
- Serdeczny, O.; Adams, S.; Baarsch, F.; Coumou, D.; Robinson, A.; Hare, W.; Schaeffer, M.; Perrette, M.; Reinhardt, J. Climate Change Impacts in Sub-Saharan Africa: From Physical Changes to Their Social Repercussions. Reg. Environ. Chang. 2017, 17, 1585–1600. [Google Scholar] [CrossRef]
- Roose, E.J. Use of the Universal Ssil Loss Equation to Predict Erosion in West Africa. In Soil Erosion: Prediction and Control; Soil Conservation Society of America: Ankeny, IA, USA, 1977. [Google Scholar]
- Roose, E. Approach to the Definition of Rain Erosivity and Soil Erodibility in West Africa. In Assessment of Erosion; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 1980. [Google Scholar]
- Renard, K.G. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); Agriculture Handbook; U.S. Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1997; ISBN 978-0-16-048938-9.
- Nearing, M.A.; Yin, S.; Borrelli, P.; Polyakov, V.O. Rainfall Erosivity: An Historical Review. CATENA 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised Universal Soil Loss Equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- USDA-ARS Revised Universal Soil Loss Equation Version 2—User’s Reference Guide 2008. Available online: https://www.ars.usda.gov/ARSUserFiles/60600505/RUSLE/RUSLE2_User_Ref_Guide.pdf (accessed on 24 April 2024).
- Kinnell, P.I.A. Event Soil Loss, Runoff and the Universal Soil Loss Equation Family of Models: A Review. J. Hydrol. 2010, 385, 384–397. [Google Scholar] [CrossRef]
- Diodato, N. Estimating RUSLE’s Rainfall Factor in the Part of Italy with a Mediterranean Rainfall Regime. Hydrol. Earth Syst. Sci. 2004, 8, 103–107. [Google Scholar] [CrossRef]
- Vernimmen, R.R.E.; Hooijer, A.; Mamenun; Aldrian, E.; Van Dijk, A.I.J.M. Evaluation and Bias Correction of Satellite Rainfall Data for Drought Monitoring in Indonesia. Hydrol. Earth Syst. Sci. 2012, 16, 133–146. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Jae Lim, K.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global Rainfall Erosivity Assessment Based on High-Temporal Resolution Rainfall Records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef] [PubMed]
- Bezak, N.; Borrelli, P.; Panagos, P. Exploring the Possible Role of Satellite-Based Rainfall Data in Estimating Inter- and Intra-Annual Global Rainfall Erosivity. Hydrol. Earth Syst. Sci. 2022, 26, 1907–1924. [Google Scholar] [CrossRef]
- Borrelli, P.; Ballabio, C.; Yang, J.E.; Robinson, D.A.; Panagos, P. GloSEM: High-Resolution Global Estimates of Present and Future Soil Displacement in Croplands by Water Erosion. Sci. Data 2022, 9, 406. [Google Scholar] [CrossRef]
- Fenta, A.A.; Tsunekawa, A.; Haregeweyn, N.; Yasuda, H.; Tsubo, M.; Borrelli, P.; Kawai, T.; Sewale Belay, A.; Ebabu, K.; Liyew Berihun, M.; et al. Improving Satellite-Based Global Rainfall Erosivity Estimates through Merging with Gauge Data. J. Hydrol. 2023, 620, 129555. [Google Scholar] [CrossRef]
- Yin, S.; Xie, Y.; Nearing, M.A.; Wang, C. Estimation of Rainfall Erosivity Using 5- to 60-Minute Fixed-Interval Rainfall Data from China. CATENA 2007, 70, 306–312. [Google Scholar] [CrossRef]
- Beguería, S.; Serrano-Notivoli, R.; Tomas-Burguera, M. Computation of Rainfall Erosivity from Daily Precipitation Amounts. Sci. Total Environ. 2018, 637–638, 359–373. [Google Scholar] [CrossRef]
- Benavidez, R.; Jackson, B.; Maxwell, D.; Norton, K. A Review of the (Revised) Universal Soil Loss Equation (R/USLE): With a View to Increasing Its Global Applicability and Improving Soil Loss Estimates. Hillslope Hydrol. Model. Approaches 2018, 22, 6059–6086. [Google Scholar] [CrossRef]
- Lee, M.-H.; Hsu, I.-P. Estimation of the Annual Rainfall Erosivity Index Based on Hourly Rainfall Data in a Tropical Region. Soil Water Res. 2021, 16, 74–84. [Google Scholar] [CrossRef]
- Fowé, T.; Yonaba, R.; Mounirou, L.A.; Ouédraogo, E.; Ibrahim, B.; Niang, D.; Karambiri, H.; Yacouba, H. From Meteorological to Hydrological Drought: A Case Study Using Standardized Indices in the Nakanbe River Basin, Burkina Faso. Nat. Hazards 2023, 119, 1941–1965. [Google Scholar] [CrossRef]
- Yonaba, R.; Tazen, F.; Cissé, M.; Mounirou, L.A.; Belemtougri, A.; Ouedraogo, V.A.; Koïta, M.; Niang, D.; Karambiri, H.; Yacouba, H. Trends, Sensitivity and Estimation of Daily Reference Evapotranspiration ET0 Using Limited Climate Data: Regional Focus on Burkina Faso in the West African Sahel. Theor. Appl. Climatol. 2023, 153, 947–974. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Meusburger, K.; Spinoni, J.; Alewell, C.; Borrelli, P. Towards Estimates of Future Rainfall Erosivity in Europe Based on REDES and WorldClim Datasets. J. Hydrol. 2017, 548, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Panagos, P.; Hengl, T.; Wheeler, I.; Marcinkowski, P.; Rukeza, M.B.; Yu, B.; Yang, J.E.; Miao, C.; Chattopadhyay, N.; Sadeghi, S.H.; et al. Global Rainfall Erosivity Database (GloREDa) and Monthly R-Factor Data at 1 Km Spatial Resolution. Data Brief 2023, 50, 109482. [Google Scholar] [CrossRef] [PubMed]
- Diodato, N.; Knight, J.; Bellocchi, G. Reduced Complexity Model for Assessing Patterns of Rainfall Erosivity in Africa. Glob. Planet. Chang. 2013, 100, 183–193. [Google Scholar] [CrossRef]
- Yonaba, R.; Belemtougri, A.; Fowé, T.; Mounirou, L.A.; Nkiaka, E.; Dembélé, M.; Komlavi, A.; Coly, S.M.; Koïta, M.; Karambiri, H. Rainfall Estimation in the West African Sahel: Comparison and Cross-Validation of Top-down vs. Bottom-up Precipitation Products in Burkina Faso. Geocarto Int. 2024, 39, 2391956. [Google Scholar] [CrossRef]
- Satgé, F.; Defrance, D.; Sultan, B.; Bonnet, M.-P.; Seyler, F.; Rouché, N.; Pierron, F.; Paturel, J.-E. Evaluation of 23 Gridded Precipitation Datasets across West Africa. J. Hydrol. 2020, 581, 124412. [Google Scholar] [CrossRef]
- Raj, R.; Saharia, M.; Chakma, S.; Rafieinasab, A. Mapping Rainfall Erosivity over India Using Multiple Precipitation Datasets. CATENA 2022, 214, 106256. [Google Scholar] [CrossRef]
- Dai, Q.; Zhu, J.; Lv, G.; Kalin, L.; Yao, Y.; Zhang, J.; Han, D. Radar Remote Sensing Reveals Potential Underestimation of Rainfall Erosivity at the Global Scale. Sci. Adv. 2023, 9, eadg5551. [Google Scholar] [CrossRef]
- Gutierrez, L.; Huerta, A.; Sabino, E.; Bourrel, L.; Frappart, F.; Lavado-Casimiro, W. Rainfall Erosivity in Peru: A New Gridded Dataset Based on GPM-IMERG and Comprehensive Assessment (2000–2020). Remote Sens. 2023, 15, 5432. [Google Scholar] [CrossRef]
- Emberson, R.A. Dynamic Rainfall Erosivity Estimates Derived from IMERG Data. Hydrol. Earth Syst. Sci. 2023, 27, 3547–3563. [Google Scholar] [CrossRef]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of Several Rainfall Products Used for Hydrological Applications over West Africa Using Two High-resolution Gauge Networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Casse, C.; Gosset, M.; Peugeot, C.; Pedinotti, V.; Boone, A.; Tanimoun, B.A.; Decharme, B. Potential of Satellite Rainfall Products to Predict Niger River Flood Events in Niamey. Atmos. Res. 2015, 163, 162–176. [Google Scholar] [CrossRef]
- Dembélé, M.; Zwart, S.J. Evaluation and Comparison of Satellite-Based Rainfall Products in Burkina Faso, West Africa. Int. J. Remote Sens. 2016, 37, 3995–4014. [Google Scholar] [CrossRef]
- Atiah, W.A.; Tsidu, G.M.; Amekudzi, L.K. Investigating the Merits of Gauge and Satellite Rainfall Data at Local Scales in Ghana, West Africa. Weather Clim. Extrem. 2020, 30, 100292. [Google Scholar] [CrossRef]
- Dembélé, M.; Schaefli, B.; van de Giesen, N.; Mariéthoz, G. Suitability of 17 Gridded Rainfall and Temperature Datasets for Large-Scale Hydrological Modelling in West Africa. Hydrol. Earth Syst. Sci. 2020, 24, 5379–5406. [Google Scholar] [CrossRef]
- Gbohoui, Y.P.; Paturel, J.-E.; Tazen, F.; Mounirou, L.A.; Yonaba, R.; Karambiri, H.; Yacouba, H. Impacts of Climate and Environmental Changes on Water Resources: A Multi-Scale Study Based on Nakanbé Nested Watersheds in West African Sahel. J. Hydrol. Reg. Stud. 2021, 35, 100828. [Google Scholar] [CrossRef]
- Echeta, O.C.; Adjei, K.A.; Andam-Akorful, S.A.; Gyamfi, C.; Darko, D.; Odai, S.N.; Kwarteng, E.V.S. Performance Evaluation of Near-Real-Time Satellite Rainfall Estimates over Three Distinct Climatic Zones in Tropical West-Africa. Environ. Process. 2022, 9, 59. [Google Scholar] [CrossRef]
- Garba, J.N.; Diasso, U.J.; Waongo, M.; Sawadogo, W.; Daho, T. Performance Evaluation of Satellite-Based Rainfall Estimation across Climatic Zones in Burkina Faso. Theor. Appl. Climatol. 2023, 154, 1051–1073. [Google Scholar] [CrossRef]
- Houngnibo, M.C.M.; Minoungou, B.; Traore, S.B.; Maidment, R.I.; Alhassane, A.; Ali, A. Validation of High-Resolution Satellite Precipitation Products over West Africa for Rainfall Monitoring and Early Warning. Front. Clim. 2023, 5, 1185754. [Google Scholar] [CrossRef]
- Di Lena, B.; Curci, G.; Vergni, L. Analysis of Rainfall Erosivity Trends 1980–2018 in a Complex Terrain Region (Abruzzo, Central Italy) from Rain Gauges and Gridded Datasets. Atmosphere 2021, 12, 657. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Mohammed, S.A.; Hamouda, M.A.; Mohamed, M.M. Impact of Topography and Rainfall Intensity on the Accuracy of IMERG Precipitation Estimates in an Arid Region. Remote Sens. 2020, 13, 13. [Google Scholar] [CrossRef]
- Hashemi, H.; Fayne, J.; Lakshmi, V.; Huffman, G.J. Very High Resolution, Altitude-Corrected, TMPA-Based Monthly Satellite Precipitation Product over the CONUS. Sci. Data 2020, 7, 74. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of Satellite Precipitation Retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Li, Z.; Wen, Y.; Schreier, M.; Behrangi, A.; Hong, Y.; Lambrigtsen, B. Advancing Satellite Precipitation Retrievals With Data Driven Approaches: Is Black Box Model Explainable? Earth Space Sci. 2021, 8, e2020EA001423. [Google Scholar] [CrossRef]
- Zinner, T.; Wind, G.; Platnick, S.; Ackerman, A.S. Testing Remote Sensing on Artificial Observations: Impact of Drizzle and 3-D Cloud Structure on Effective Radius Retrievals. Atmos. Chem. Phys. 2010, 10, 9535–9549. [Google Scholar] [CrossRef]
- Kim, J.; Han, H.; Kim, B.; Chen, H.; Lee, J.-H. Use of a High-Resolution-Satellite-Based Precipitation Product in Mapping Continental-Scale Rainfall Erosivity: A Case Study of the United States. CATENA 2020, 193, 104602. [Google Scholar] [CrossRef]
- Faghih, M.; Brissette, F.; Sabeti, P. Impact of Correcting Sub-Daily Climate Model Biases for Hydrological Studies. Hydrol. Earth Syst. Sci. 2022, 26, 1545–1563. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correcting Climate Change Simulations—A Critical Review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef]
- Li, J.; Johnson, F.; Evans, J.; Sharma, A. A Comparison of Methods to Estimate Future Sub-Daily Design Rainfall. Adv. Water Resour. 2017, 110, 215–227. [Google Scholar] [CrossRef]
- Bagré, P.M.; Yonaba, R.; Sirima, A.B.; Somé, Y.C.S. Influence Des Changements d’utilisation Des Terres Sur Les Débits Du Bassin Versant Du Massili à Gonsé (Burkina Faso). Vertigo 2023, 23, 1–26. [Google Scholar] [CrossRef]
- Dayamba, S.; D’haen, S.; Coulibaly, O.; Korahiré, J. Étude de La Vulnérabilité Des Systèmes de Production Agro-Sylvo-Pastoraux Face Aux Changements Climatiques Dans Les Provinces Du Houet et Du Tuy Au Burkina Faso. Report Produced under the Project “Projet d’Appui Scientifique Aux Processus de Plans Nationaux d’Adaptation Dans Les Pays Francophones Les Moins Avancés d’Afrique Subsaharienne”; Climate Analytics gGmbH: Berlin, Germany, 2019. [Google Scholar]
- Zougmoré, F.; Damiba, L.; D’Haen, S.; Dayamba, S.D. Projet d’Appui Scientifique Aux Processus de Plans Nationaux d’Adaptation (PAS-PNA)—État Des Lieux Des Connaissances Scientifiques Sur Les Ressources En Eau Au Burkina Faso et de l’impact Des Changements Climatiques Sur Ces Ressources (Scientific Support Project for National Adaptation Plan Processes—State of Scientific Knowledge on Water Resources in Burkina Faso and the Impact of Climate Change on These Resources); Climate Analytics gGmbH: Berlin, Germany, 2019. [Google Scholar]
- Basson, F.; Dayamba, D.S.; Korahire, J.; Dipama, J.M.; Zougmore, F.; Neya, T. Institutional Barriers to Climate Change Adaptation in Burkina Faso: How Could We Go around Them? JSD 2020, 13, 67. [Google Scholar] [CrossRef]
- Nyamekye, C.; Thiel, M.; Schönbrodt-Stitt, S.; Zoungrana, B.; Amekudzi, L. Soil and Water Conservation in Burkina Faso, West Africa. Sustainability 2018, 10, 3182. [Google Scholar] [CrossRef]
- Zouré, C.; Queloz, P.; Koïta, M.; Niang, D.; Fowé, T.; Yonaba, R.; Consuegra, D.; Yacouba, H.; Karambiri, H. Modelling the Water Balance on Farming Practices at Plot Scale: Case Study of Tougou Watershed in Northern Burkina Faso. CATENA 2019, 173, 59–70. [Google Scholar] [CrossRef]
- Yonaba, R. Spatio-Temporal Land Use and Land Cover Dynamics and Impact on Surface Runoff in a Sahelian Landscape: Case of Tougou Watershed (Northern Burkina Faso). Ph.D. Thesis, International Institute for Water and Environmental Engineering (2iE), Ouagadougou, Burkina Faso, 2020. [Google Scholar]
- INSD 5ème Rescensement Général de la Population et de l’Habitation du Burkina Faso—Résultats Préliminaires (5th General Census of Population and Housing in Burkina Faso—Preliminary Results); Institut National de la Statistique et de la Démographie (INSD): Ouagadougou, Burkina Faso, 2020.
- Kafando, M.B.; Koïta, M.; Le Coz, M.; Yonaba, O.R.; Fowe, T.; Zouré, C.O.; Faye, M.D.; Leye, B. Use of Multidisciplinary Approaches for Groundwater Recharge Mechanism Characterization in Basement Aquifers: Case of Sanon Experimental Catchment in Burkina Faso. Water 2021, 13, 3216. [Google Scholar] [CrossRef]
- Kafando, M.B.; Koïta, M.; Zouré, C.O.; Yonaba, R.; Niang, D. Quantification of Soil Deep Drainage and Aquifer Recharge Dynamics According to Land Use and Land Cover in the Basement Zone of Burkina Faso in West Africa. Sustainability 2022, 14, 14687. [Google Scholar] [CrossRef]
- Mounirou, L.A.; Sawadogo, B.; Yanogo, H.; Yonaba, R.; Zorom, M.; Faye, M.D.; Kafando, M.B.; Biaou, A.C.; Koïta, M.; Karambiri, H. Estimation of the Actual Specific Consumption in Drinking Water Supply Systems in Burkina Faso (West Africa): Potential Implications for Infrastructure Sizing. Water 2023, 15, 3423. [Google Scholar] [CrossRef]
- Faye, M.D.; Loyara, V.Y.B.; Biaou, A.C.; Yonaba, R.; Koita, M.; Yacouba, H. Modelling Groundwater Pollutant Transfer Mineral Micropollutants in a Multi-Layered Aquifer in Burkina Faso (West African Sahel). Heliyon 2024, 10, e23557. [Google Scholar] [CrossRef]
- Zouré, C.O.; Kiema, A.; Yonaba, R.; Minoungou, B. Unravelling the Impacts of Climate Variability on Surface Runoff in the Mouhoun River Catchment (West Africa). Land 2023, 12, 2017. [Google Scholar] [CrossRef]
- UNCCD Country Profile Burkina Faso. Investing in Land Degradation Neutrality: Making the Case. An Overview of Indicators and Assessments; Country Profile; UNCCD: Bonn, Germany, 2018. [Google Scholar]
- Barbier, B.; Yacouba, H.; Karambiri, H.; Zoromé, M.; Somé, B. Human Vulnerability to Climate Variability in the Sahel: Farmers’ Adaptation Strategies in Northern Burkina Faso. Environ. Manag. 2009, 43, 790–803. [Google Scholar] [CrossRef]
- Hawker, L.; Neal, J. FABDEM V1-0 2021. Available online: https://data.bris.ac.uk/data/dataset/25wfy0f9ukoge2gs7a5mqpq2j7 (accessed on 24 April 2024).
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Yonaba, R.; Mounirou, L.A.; Tazen, F.; Koïta, M.; Biaou, A.C.; Zouré, C.O.; Queloz, P.; Karambiri, H.; Yacouba, H. Future Climate or Land Use? Attribution of Changes in Surface Runoff in a Typical Sahelian Landscape. Comptes Rendus. Géoscience 2023, 355, 411–438. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1940 to Present. 2023. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.adbb2d47?tab=overview (accessed on 24 April 2024).
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-Satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Advances in Global Change Research; Springer International Publishing: Cham, Switzerland, 2020; Volume 67, pp. 343–353. ISBN 978-3-030-24567-2. [Google Scholar]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.; Shearer, E.J.; Tran, H.; Ombadi, M.; Hayatbini, N.; Palacios, T.; Huynh, P.; Braithwaite, D.; Updegraff, G.; Hsu, K.; et al. The CHRS Data Portal, an Easily Accessible Public Repository for PERSIANN Global Satellite Precipitation Data. Sci. Data 2019, 6, 180296. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.; Ombadi, M.; Gorooh, V.A.; Shearer, E.J.; Sadeghi, M.; Sorooshian, S.; Hsu, K.; Bolvin, D.; Ralph, M.F. PERSIANN Dynamic Infrared–Rain Rate (PDIR-Now): A Near-Real-Time, Quasi-Global Satellite Precipitation Dataset. J. Hydrometeorol. 2020, 21, 2893–2906. [Google Scholar] [CrossRef]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN Family of Global Satellite Precipitation Data: A Review and Evaluation of Products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef]
- Lober, C.; Fayne, J.; Hashemi, H.; Smith, L.C. Bias Correction of 20 Years of IMERG Satellite Precipitation Data over Canada and Alaska. J. Hydrol. Reg. Stud. 2023, 47, 101386. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Cannon, A.J. MBC: Multivariate Bias Correction of Climate Model Outputs 2023. Available online: https://cran.r-project.org/web/packages/MBC/index.html (accessed on 24 April 2024).
- Zambrano-Bigiarini, M. hydroGOF: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series 2020. Available online: https://github.com/hzambran/hydroGOF (accessed on 24 April 2024).
- Gilleland, E. Verification: Weather Forecast Verification Utilities 2015. Available online: https://cran.r-project.org/web/packages/verification/index.html (accessed on 24 April 2024).
- Brown, L.C.; Foster, G.R. Storm Erosivity Using Idealized Intensity Distributions. Trans. ASAE 1987, 30, 0379–0386. [Google Scholar] [CrossRef]
- Lu, H.; Yu, B. Spatial and Seasonal Distribution of Rainfall Erosivity in Australia. Soil Res. 2002, 40, 887. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall Erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef]
- Chang, Y.; Lei, H.; Zhou, F.; Yang, D. Spatial and Temporal Variations of Rainfall Erosivity in the Middle Yellow River Basin Based on Hourly Rainfall Data. CATENA 2022, 216, 106406. [Google Scholar] [CrossRef]
- ESRI ArcGIS Desktop|ArcCatalog 2016. Available online: https://www.esri.com/en-us/arcgis/products/arcgis-desktop/resources?srsltid=AfmBOoo3LmnALO49gZM8lVzsvEnkgm03C5vBXUQObpxvUY_svJy8UBac (accessed on 24 April 2024).
- Kassambara, A. Ggpubr: “ggplot2” Based Publication Ready Plots 2023. Available online: https://rpkgs.datanovia.com/ggpubr/ (accessed on 24 April 2024).
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Kendall, M.G. Multivariate Analysis; Griffin: London, UK, 1975; ISBN 978-0-85264-234-4. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The Influence of Autocorrelation on the Ability to Detect Trend in Hydrological Series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; O’Brien, N. Modifiedmk: Modified Versions of Mann Kendall and Spearman’s Rho Trend Tests 2021. Available online: https://cran.r-project.org/web/packages/modifiedmk/index.html (accessed on 24 April 2024).
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. In Henri Theil’s Contributions to Economics and Econometrics; Raj, B., Koerts, J., Eds.; Advanced Studies in Theoretical and Applied Econometrics; Springer: Dordrecht, The Netherlands, 1992; Volume 23, pp. 345–381. ISBN 978-94-010-5124-8. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Wilke, C.O. Ggridges: Ridgeline Plots in “Ggplot2” 2023. Available online: https://cran.r-project.org/web/packages/ggridges/ (accessed on 24 April 2024).
- Mounirou, L.A.; Zouré, C.O.; Yonaba, R.; Paturel, J.-E.; Mahé, G.; Niang, D.; Yacouba, H.; Karambiri, H. Multi-Scale Analysis of Runoff from a Statistical Perspective in a Small Sahelian Catchment under Semi-Arid Climate. Arab. J. Geosci. 2020, 13, 154. [Google Scholar] [CrossRef]
- Mounirou, L.A.; Yonaba, R.; Koïta, M.; Paturel, J.-E.; Mahé, G.; Yacouba, H.; Karambiri, H. Hydrologic Similarity: Dimensionless Runoff Indices across Scales in a Semi-Arid Catchment. J. Arid. Environ. 2021, 193, 104590. [Google Scholar] [CrossRef]
- Mounirou, L.A.; Yonaba, R.; Tazen, F.; Ayele, G.T.; Yaseen, Z.M.; Karambiri, H.; Yacouba, H. Soil Erosion across Scales: Assessing Its Sources of Variation in Sahelian Landscapes under Semi-Arid Climate. Land 2022, 11, 2302. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.; Hong, J.; Lee, D.; Bae, J.H.; Yang, J.E.; Kim, J.; Lim, K.J. Evaluation of Rainfall Erosivity Factor Estimation Using Machine and Deep Learning Models. Water 2021, 13, 382. [Google Scholar] [CrossRef]
- Lee, S.; Bae, J.H.; Hong, J.; Yang, D.; Panagos, P.; Borrelli, P.; Yang, J.E.; Kim, J.; Lim, K.J. Estimation of Rainfall Erosivity Factor in Italy and Switzerland Using Bayesian Optimization Based Machine Learning Models. CATENA 2022, 211, 105957. [Google Scholar] [CrossRef]
- Vergni, L.; Todisco, F. A Random Forest Machine Learning Approach for the Identification and Quantification of Erosive Events. Water 2023, 15, 2225. [Google Scholar] [CrossRef]
- Bhagat, S.K.; Tiyasha, T.; Al-khafaji, Z.; Laux, P.; Ewees, A.A.; Rashid, T.A.; Salih, S.; Yonaba, R.; Beyaztas, U.; Yaseen, Z.M. Establishment of Dynamic Evolving Neural-Fuzzy Inference System Model for Natural Air Temperature Prediction. Complexity 2022, 2022, 1–17. [Google Scholar] [CrossRef]
- Renard, K.G.; Freimund, J.R. Using Monthly Precipitation Data to Estimate the R-Factor in the Revised USLE. J. Hydrol. 1994, 157, 287–306. [Google Scholar] [CrossRef]
- Yonaba, R.; Koïta, M.; Mounirou, L.A.; Tazen, F.; Queloz, P.; Biaou, A.C.; Niang, D.; Zouré, C.; Karambiri, H.; Yacouba, H. Spatial and Transient Modelling of Land Use/Land Cover (LULC) Dynamics in a Sahelian Landscape under Semi-Arid Climate in Northern Burkina Faso. Land Use Policy 2021, 103, 105305. [Google Scholar] [CrossRef]
- Yonaba, R.; Biaou, A.C.; Koïta, M.; Tazen, F.; Mounirou, L.A.; Zouré, C.O.; Queloz, P.; Karambiri, H.; Yacouba, H. A Dynamic Land Use/Land Cover Input Helps in Picturing the Sahelian Paradox: Assessing Variability and Attribution of Changes in Surface Runoff in a Sahelian Watershed. Sci. Total Environ. 2021, 757, 143792. [Google Scholar] [CrossRef]
- Yameogo, A.; Some, Y.S.C.; Pale, S.; Sirima, B.A.; Da, D.É.C. Application of GIS/RUSLE to the Estimation of Erosion by Sheet Runoff in the Upper Sissili Watershed (Burkina Faso)—Application de SIG/RUSLE à l’estimation de l’érosion Par Ruissellement En Nappe Dans Le Bassin Versant Supérieur de La Sissili (Burkina Faso). Geo-Eco-Trop. 2021, 45, 299–310. [Google Scholar]
- Ouedraogo, B.; Kabore, O.; Kabore, M. Quantitative Mapping of Soil Erosion Using a GIS/RUSLE Approach in the Commune of Karangasso Vigué (Burkina Faso)—Cartographie Quantitative de l’érosion Des Sols Par Approche SIG/RUSLE Dans La Commune de Karangasso Vigué (Burkina Faso). Int. J. Biol. Chem. Sci. 2019, 13, 1638–1653. [Google Scholar] [CrossRef]
- Fenta, A.A.; Tsunekawa, A.; Haregeweyn, N.; Yasuda, H.; Tsubo, M.; Borrelli, P.; Kawai, T.; Belay, A.S.; Ebabu, K.; Berihun, M.L.; et al. An Integrated Modeling Approach for Estimating Monthly Global Rainfall Erosivity. Sci. Rep. 2024, 14, 8167. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Luca, D.L.D.; Napolitano, F. A User-Friendly Software for Modelling Extreme Values: EXTRASTAR (EXTRemes Abacus for STAtistical Regionalization). Environ. Model. Softw. 2023, 161, 105622. [Google Scholar] [CrossRef]





| WMO Code 1 | Name | Latitude, Longitude (Decimal Degrees) | Altitude (m) | Annual Rainfall (mm) 2 | Climate Type 3 |
|---|---|---|---|---|---|
| 1200010000 | Dori | 14.0333, −0.0333 | 288 | 528.2 ± 127.6 | BWh |
| 1200024100 | Ouahigouya | 13.5833, −2.4333 | 329 | 764.7 ± 145.0 | BSh |
| 1200004300 | Bogande | 12.9833, −0.1333 | 250 | 643.8 ± 121.6 | BSh |
| 1200007900 | Dedougou | 12.4667, −3.4667 | 308 | 859.7 ± 115.1 | BSh |
| 1200000100 | Ouagadougou | 12.3500, −1.5167 | 304 | 816.1 ± 115.0 | BSh |
| 1200010300 | Fada | 12.0333, 0.3667 | 308 | 833.3 ± 103.5 | BSh |
| 1200005200 | Boromo | 11.7500, −2.9333 | 270 | 920.1 ± 129.2 | BSh |
| 1200004000 | Bobo-Dioulasso | 11.1667, −4.3167 | 459 | 1043.4 ± 197.1 | Aw |
| 1200026200 | Po | 11.1667, −1.1500 | 326 | 1024.9 ± 128.0 | Aw |
| 1200011200 | Gaoua | 10.3333, −3.1833 | 333 | 1088.4 ± 150.2 | Aw |
| Source | Type 1 | Spatial Resolution | Temporal Resolution | Spatial Coverage | Temporal Coverage | References |
|---|---|---|---|---|---|---|
| CMORPH (CPC MORPHing technique) | S | 0.25° × 0.25° (~28 km) | 1 h | 60°N/S | 1998-present | [74,75] |
| ERA5 (5th generation of the European Centre for Medium-Range Weather Forecasts (ECMWF) atmospheric reanalysis) | R | 0.25° × 0.25° (~28 km) | 1 h | Global | 1940-present | [76,77] |
| IMERG (Integrated multi-satellite retrievals for the global precipitation measurement)-Late run (v6) | S | 0.1° × 0.1° (~11 km) | 0.5 h | Global | 2000-present | [78] |
| MERRA-2 (modern-era retrospective analysis for research and applications, Version 2) | R | 0.5° × 0.685° (~60 km) | 1 h | Global | 1980-present | [79] |
| PERSIANN-PDIR-Now (precipitation estimation from remotely sensed information using artificial neural networks-dynamic infrared rain rate near real-time) | S + G | 0.04° × 0.04° (~4.44 km) | 1 h | 60°N/S | 2000-present | [80,81] |
| PERSIANN (precipitation estimation from remotely sensed information using artificial neural Networks) | S + G | 0.25° × 0.25° (~28 km) | 1 h | 60°N/S | 2000-present | [80,82] |
| PERSIANN-CCS (precipitation estimation from remotely sensed information using artificial neural networks-cloud classification system) | S + G | 0.04° × 0.04° (~4.44 km) | 1 h | 60°N/S | 2003-present | [80,82] |
| Metric | Description | Formula 1 | Range |
|---|---|---|---|
| Probability of detection (POD) | Fraction of events correctly identified to the total rainfall events occurrences | 0 (no skill)–1 (perfect score) | |
| False alarm ratio (FAR) | Fraction of predicted rainfall events which did not occur in gauge measurements | 0 (perfect score)–1 (no skill) | |
| Threat score (TS) or critical success index (CSI) | Fraction of observed and/or predicted events that were correctly predicted | 0 (no skill)–1 (perfect score) |
| Timescale | Type | RP | R [-] | MAE [mm/timescale] | RMSE [mm/timescale] | PBIAS [%] | KGE [-] |
|---|---|---|---|---|---|---|---|
| Daily | reference | IMERG | 0.85 | 6.49 | 8.58 | 6.20 | 0.83 |
| raw | CMORPH | 0.50 | 13.56 | 18.06 | 0.70 | 0.40 | |
| raw | ERA5 | 0.32 | 17.89 | 24.05 | −18.70 | 0.07 | |
| raw | MERRA-2 | 0.40 | 23.96 | 33.18 | −38.80 | 0.01 | |
| raw | PDIR-Now | 0.26 | 24.34 | 33.80 | −45.90 | −0.07 | |
| raw | PERSIANN | 0.50 | 15.65 | 19.64 | 39.00 | 0.29 | |
| raw | PERSIANN-CCS | 0.46 | 16.17 | 20.61 | 42.10 | 0.27 | |
| bc | CMORPH | 0.81 | 6.38 | 8.42 | 8.60 | 0.78 | |
| bc | ERA5 | 0.75 | 5.59 | 7.18 | 15.80 | 0.57 | |
| bc | MERRA-2 | 0.81 | 5.42 | 6.75 | 16.10 | 0.69 | |
| bc | PDIR-Now | 0.78 | 5.67 | 7.48 | 18.10 | 0.57 | |
| bc | PERSIANN | 0.82 | 6.28 | 8.18 | 6.00 | 0.80 | |
| bc | PERSIANN-CCS | 0.84 | 6.35 | 8.40 | 4.50 | 0.83 | |
| Monthly | reference | IMERG | 0.91 | 17.76 | 35.40 | −5.50 | 0.88 |
| raw | CMORPH | 0.88 | 21.64 | 38.96 | 14.90 | 0.77 | |
| raw | ERA5 | 0.73 | 37.84 | 66.90 | 178.50 | −1.03 | |
| raw | MERRA-2 | 0.75 | 36.91 | 64.02 | 156.10 | −0.75 | |
| raw | PDIR-Now | 0.64 | 42.78 | 76.03 | 262.70 | −2.13 | |
| raw | PERSIANN | 0.79 | 56.07 | 92.16 | −46.80 | 0.37 | |
| raw | PERSIANN-CCS | 0.65 | 84.19 | 137.29 | −56.10 | 0.18 | |
| bc | CMORPH | 0.91 | 19.98 | 36.35 | −7.10 | 0.85 | |
| bc | ERA5 | 0.80 | 28.89 | 54.51 | −2.50 | 0.76 | |
| bc | MERRA-2 | 0.81 | 34.55 | 68.11 | −18.40 | 0.60 | |
| bc | PDIR-Now | 0.86 | 65.54 | 123.90 | −51.40 | 0.25 | |
| bc | PERSIANN | 0.89 | 22.15 | 41.05 | −7.30 | 0.83 | |
| bc | PERSIANN-CCS | 0.85 | 25.62 | 47.88 | −3.80 | 0.80 | |
| Annual | reference | IMERG | 0.76 | 105.26 | 132.70 | −7.50 | 0.78 |
| raw | CMORPH | 0.69 | 132.35 | 166.36 | 14.90 | 0.64 | |
| raw | ERA5 | 0.63 | 428.93 | 453.91 | 178.50 | −0.96 | |
| raw | MERRA-2 | 0.62 | 407.95 | 437.27 | 156.10 | −0.62 | |
| raw | PDIR-Now | 0.67 | 485.18 | 505.83 | 262.70 | −1.66 | |
| raw | PERSIANN | 0.48 | 589.38 | 625.33 | −46.80 | 0.29 | |
| raw | PERSIANN-CCS | 0.40 | 969.96 | 1026.92 | −56.10 | −0.07 | |
| bc | CMORPH | 0.80 | 106.58 | 133.72 | −7.10 | 0.78 | |
| bc | ERA5 | 0.61 | 142.89 | 185.66 | −2.50 | 0.58 | |
| bc | MERRA-2 | 0.63 | 249.06 | 318.77 | −18.40 | 0.37 | |
| bc | PDIR-Now | 0.41 | 718.46 | 768.25 | −51.40 | 0.12 | |
| bc | PERSIANN | 0.73 | 124.00 | 152.57 | −7.30 | 0.72 | |
| bc | PERSIANN-CCS | 0.58 | 179.99 | 244.99 | −3.80 | 0.44 |
| Type | Product | Annual Mean (±sd) R-Factor (MJ mm ha−1 h−1 yr−1) | RMSE 1 (MJ mm ha−1 h−1 yr−1) | MAE 1 (MJ mm ha−1 h−1 yr−1) | PBIAS 1 (%) |
|---|---|---|---|---|---|
| GloREDa | 2964.9 ± 886.9 | ||||
| IMERG | 2929.7 ± 543.8 | 494.1 | 365.0 | 1.2 | |
| raw | CMORPH | 2130.3 ± 312.5 | 1192.8 | 897.6 | 39.2 |
| raw | ERA5 | 465.1 ± 142.6 | 2605.9 | 2499.7 | 537.4 |
| raw | MERRA-2 | 410.0 ± 132.8 | 2682.9 | 2554.8 | 623.1 |
| raw | PDIR-Now | 372.5 ± 396.1 | 2638.6 | 2592.3 | 695.8 |
| raw | PERSIANN | 4583.3 ± 468.4 | 1951.9 | 1744.9 | −35.3 |
| raw | PERSIANN-CCS | 12,344.3 ± 2014.2 | 9472.8 | 9379.4 | −76.0 |
| bc | CMORPH | 3796.3 ± 678.4 | 934.6 | 862.0 | −21.9 |
| bc | ERA5 | 3704.6 ± 682.5 | 861.5 | 793.2 | −20.0 |
| bc | MERRA-2 | 4404.4 ± 782.5 | 1495.9 | 1439.5 | −32.7 |
| bc | PDIR-Now | 7412.8 ± 955.9 | 4663.0 | 4447.9 | −60.0 |
| bc | PERSIANN | 3846.8 ± 631.5 | 1004.0 | 930.9 | −22.9 |
| bc | PERSIANN-CCS | 3777.0 ± 569.8 | 966.8 | 906.2 | −21.5 |
| Product | DORI | OUAHIGOUYA | BOGANDE | DEDOUGOU | OUAGADOUGOU | FADA | BOROMO | BOBO | PO | GAOUA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Rainfall | Observed | 3.3 (0.263) | 12.6 (0.069) | 1.9 (0.675) | 4.6 (0.294) | 9.9 (0.014) | −3.8 (0.234) | 8.1 (0.142) | 18.5 (0.080) | −0.0 (1.000) | 10.1 (0.294) |
| IMERG | 13.2 (0.208) | 8.2 (0.401) | 5.3 (0.576) | 10.2 (0.234) | 17.0 (0.030) | 9.8 (0.401) | 15.5 (0.069) | 17.0 (0.042) | 6.6 (0.401) | 6.2 (0.401) | |
| CMORPH (raw) | 10.1 (0.069) | 19.3 (0.002) | 9.2 (0.124) | 14.8 (0.036) | 9.4 (0.025) | 11.3 (0.080) | 11.1 (0.162) | 20.4 (0.008) | 7.3 (0.327) | 8.1 (0.108) | |
| ERA5 (raw) | 3.8 (0.263) | 2.1 (0.484) | 5.4 (0.080) | 6.9 (0.080) | 11.9 (0.021) | 5.4 (0.142) | 8.5 (0.162) | 6.0 (0.363) | 8.1 (0.069) | 7.8 (0.142) | |
| MERRA-2 (raw) | 10.4 (0.000) | 8.1 (0.010) | 11.1 (0.005) | 11.4 (0.002) | 17.7 (0.003) | 7.2 (0.208) | 17.8 (0.014) | 13.5 (0.030) | 9.7 (0.142) | 13.4 (0.030) | |
| PDIR-Now (raw) | −1.0 (0.944) | 2.3 (0.576) | −1.2 (0.889) | 3.2 (0.726) | 0.6 (0.944) | −1.4 (0.675) | 2.6 (0.441) | −3.2 (0.726) | −4.5 (0.401) | −9.4 (0.184) | |
| PERSIANN (raw) | 8.1 (0.294) | 12.1 (0.069) | −0.3 (1.000) | 9.4 (0.184) | −2.3 (0.675) | −3.8 (0.576) | 4.8 (0.675) | 4.5 (0.780) | −8.9 (0.675) | −11.6 (0.093) | |
| PERSIANN-CCS (raw) | 49.0 (0.050) | 16.1 (0.234) | 35.4 (0.080) | 18.4 (0.484) | 2.8 (0.889) | −3.4 (0.834) | 5.0 (0.780) | 4.7 (0.726) | 3.0 (0.889) | 21.2 (0.363) | |
| CMORPH (bc) | 13.5 (0.059) | 7.7 (0.327) | 10.8 (0.142) | 10.7 (0.108) | 13.0 (0.059) | 4.1 (0.327) | 14.0 (0.080) | 12.6 (0.093) | 6.9 (0.576) | 5.7 (0.401) | |
| ERA5 (bc) | 2.1 (0.780) | 9.4 (0.025) | 11.6 (0.184) | 4.9 (0.441) | 22.5 (0.030) | 5.2 (0.263) | 9.9 (0.234) | 12.5 (0.184) | 9.1 (0.108) | 6.5 (0.441) | |
| MERRA-2 (bc) | 26.9 (0.001) | 30.9 (0.010) | 36.2 (0.006) | 38.7 (0.008) | 42.2 (0.003) | 30.2 (0.059) | 44.6 (0.008) | 60.7 (0.001) | 49.1 (0.001) | 32.5 (0.036) | |
| PDIR-Now (bc) | 9.5 (0.401) | 8.9 (0.624) | 4.1 (0.675) | 4.8 (0.675) | 12.6 (0.327) | 3.6 (0.726) | 7.0 (0.780) | −1.1 (0.944) | 8.0 (0.401) | 0.0 (1.000) | |
| PERSIANN (bc) | 3.2 (0.327) | 2.5 (0.726) | 5.6 (0.294) | 4.7 (0.401) | −0.1 (1.000) | 0.8 (0.944) | −3.5 (0.675) | 1.7 (0.780) | −1.5 (0.889) | −0.4 (1.000) | |
| PERSIANN-CCS (bc) | 16.9 (0.050) | 5.9 (0.484) | 9.5 (0.208) | 15.0 (0.263) | 10.0 (0.363) | 0.2 (0.944) | 13.1 (0.327) | 12.6 (0.441) | 8.4 (0.401) | 3.8 (0.726) | |
| R-factor | IMERG | 50.9 (0.363) | 6.1 (0.889) | 31.6 (0.484) | 42.8 (0.263) | 88.7 (0.036) | −23.3 (0.726) | 51.4 (0.363) | −0.0 (1.000) | −8.5 (0.889) | 20.9 (0.363) |
| CMORPH (raw) | 37.7 (0.263) | 78.5 (0.042) | 15.3 (0.780) | 30.9 (0.184) | 61.7 (0.014) | −6.5 (1.000) | 38.7 (0.184) | 51.9 (0.108) | 13.5 (0.484) | 24.3 (0.484) | |
| ERA5 (raw) | 5.2 (0.441) | 4.2 (0.529) | −0.4 (0.944) | −1.7 (0.944) | 11.0 (0.162) | −7.4 (0.484) | 10.8 (0.441) | 2.9 (0.726) | 12.9 (0.184) | 3.3 (0.624) | |
| MERRA-2 (raw) | 24.1 (0.000) | 26.6 (0.000) | 14.1 (0.021) | 49.3 (0.001) | 29.5 (0.010) | 11.4 (0.208) | 33.9 (0.050) | 25.3 (0.001) | 14.5 (0.017) | 24.3 (0.001) | |
| PDIR-Now (raw) | −0.2 (0.675) | 4.4 (0.069) | 2.4 (0.142) | 1.7 (0.726) | 5.3 (0.263) | 3.8 (0.327) | 6.2 (0.484) | −0.5 (1.000) | 9.8 (0.576) | −7.1 (0.576) | |
| PERSIANN (raw) | 172.3 (0.003) | 175.7 (0.030) | 77.9 (0.162) | 120.8 (0.017) | 123.2 (0.059) | 97.0 (0.036) | 112.1 (0.012) | 124.5 (0.012) | 51.0 (0.401) | 94.8 (0.017) | |
| PERSIANN-CCS (raw) | 526.1 (0.108) | 286.9 (0.124) | 529.9 (0.093) | 371.6 (0.124) | 200.8 (0.294) | 99.7 (0.780) | 219.4 (0.263) | 167.4 (0.484) | 92.9 (0.675) | 431.5 (0.263) | |
| CMORPH (bc) | 88.4 (0.208) | 64.8 (0.363) | 69.0 (0.025) | 33.7 (0.529) | 117.4 (0.030) | −53.6 (0.401) | 95.9 (0.080) | −6.0 (0.944) | −1.3 (1.000) | 35.9 (0.401) | |
| ERA5 (bc) | −74.0 (0.401) | 74.9 (0.184) | 59.5 (0.363) | 3.8 (0.944) | 133.6 (0.162) | 22.4 (0.780) | 70.9 (0.401) | 105.1 (0.234) | 21.6 (0.889) | −7.6 (0.944) | |
| MERRA-2 (bc) | 155.2 (0.069) | 189.4 (0.124) | 146.9 (0.059) | 229.8 (0.002) | 167.8 (0.069) | 129.7 (0.208) | 188.5 (0.050) | 383.0 (0.008) | 318.3 (0.003) | 114.0 (0.208) | |
| PDIR-Now (bc) | 82.0 (0.441) | −28.6 (0.834) | −23.6 (0.780) | −16.5 (0.889) | 1.3 (0.944) | −56.1 (0.441) | 131.0 (0.162) | −151.7 (0.108) | 41.4 (0.726) | 18.4 (0.780) | |
| PERSIANN (bc) | 5.8 (0.944) | 38.9 (0.529) | 66.4 (0.093) | 43.9 (0.484) | 50.7 (0.363) | −71.5 (0.263) | 25.9 (0.944) | −25.0 (0.441) | 19.6 (0.889) | −5.7 (1.000) | |
| PERSIANN-CCS (bc) | 79.8 (0.234) | 6.1 (0.780) | 50.5 (0.363) | 74.5 (0.484) | 94.9 (0.184) | −35.1 (0.726) | 86.3 (0.263) | 36.4 (0.944) | 110.9 (0.363) | 94.6 (0.184) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yonaba, R.; Mounirou, L.A.; Keïta, A.; Fowé, T.; Zouré, C.O.; Belemtougri, A.; Kafando, M.B.; Koïta, M.; Karambiri, H.; Yacouba, H. Exploring the Added Value of Sub-Daily Bias Correction of High-Resolution Gridded Rainfall Datasets for Rainfall Erosivity Estimation. Hydrology 2024, 11, 132. https://doi.org/10.3390/hydrology11090132
Yonaba R, Mounirou LA, Keïta A, Fowé T, Zouré CO, Belemtougri A, Kafando MB, Koïta M, Karambiri H, Yacouba H. Exploring the Added Value of Sub-Daily Bias Correction of High-Resolution Gridded Rainfall Datasets for Rainfall Erosivity Estimation. Hydrology. 2024; 11(9):132. https://doi.org/10.3390/hydrology11090132
Chicago/Turabian StyleYonaba, Roland, Lawani Adjadi Mounirou, Amadou Keïta, Tazen Fowé, Cheick Oumar Zouré, Axel Belemtougri, Moussa Bruno Kafando, Mahamadou Koïta, Harouna Karambiri, and Hamma Yacouba. 2024. "Exploring the Added Value of Sub-Daily Bias Correction of High-Resolution Gridded Rainfall Datasets for Rainfall Erosivity Estimation" Hydrology 11, no. 9: 132. https://doi.org/10.3390/hydrology11090132
APA StyleYonaba, R., Mounirou, L. A., Keïta, A., Fowé, T., Zouré, C. O., Belemtougri, A., Kafando, M. B., Koïta, M., Karambiri, H., & Yacouba, H. (2024). Exploring the Added Value of Sub-Daily Bias Correction of High-Resolution Gridded Rainfall Datasets for Rainfall Erosivity Estimation. Hydrology, 11(9), 132. https://doi.org/10.3390/hydrology11090132







