Estimation of Incoming Sediments and Useful Life of Haditha Reservoir with Limited Measurements Using Hydrological Modeling
Abstract
1. Introduction
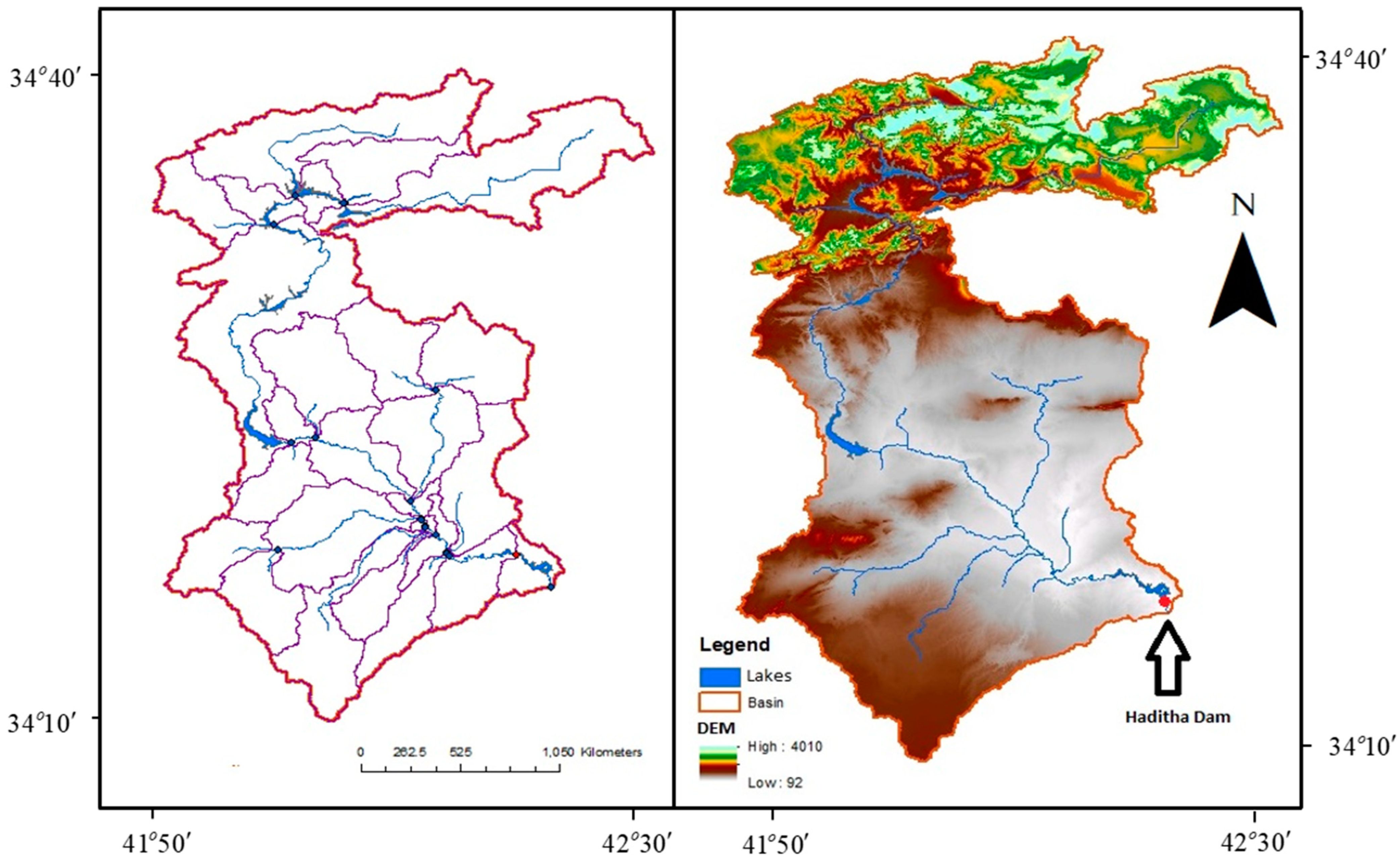
2. Study Area
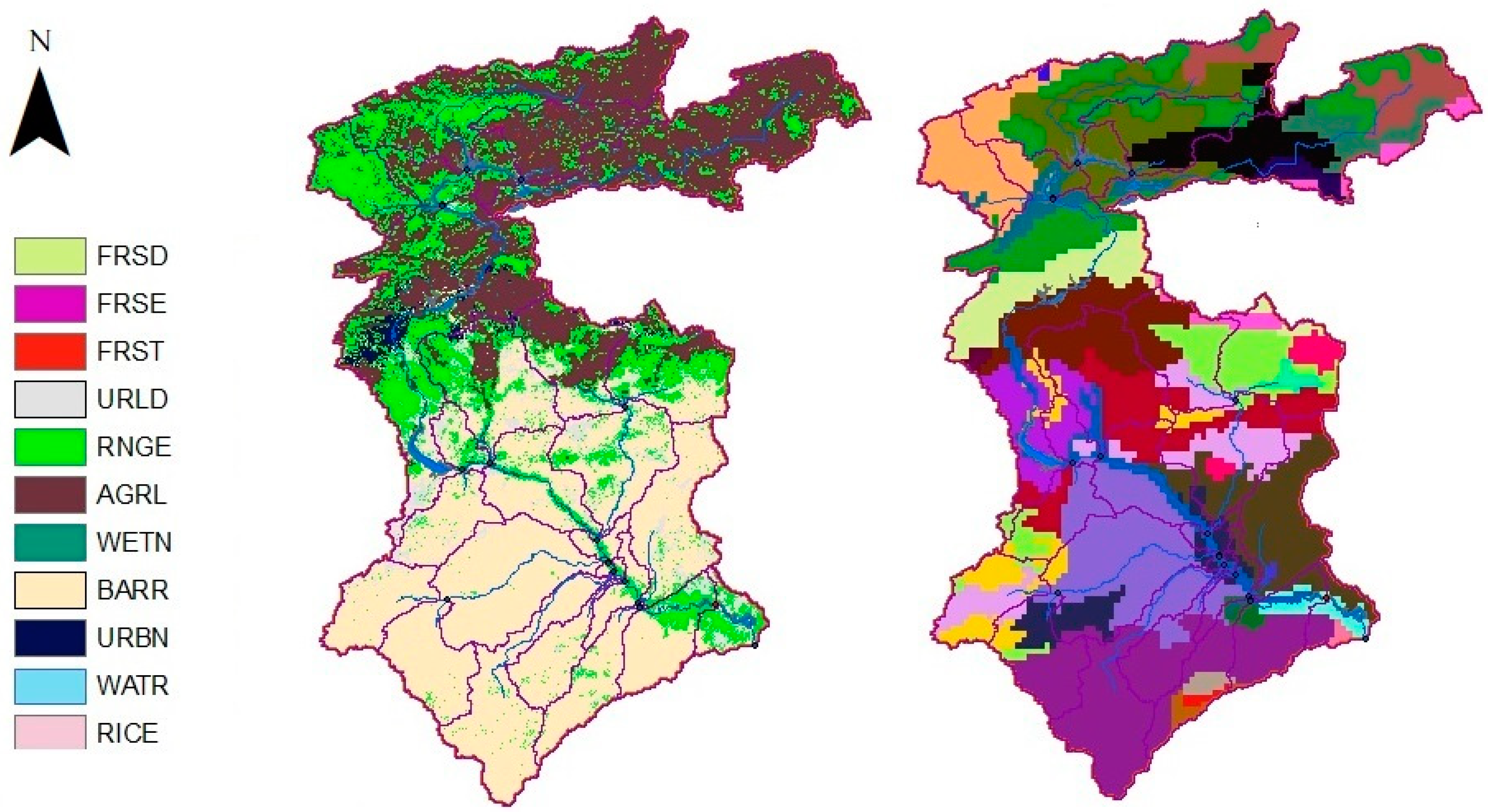
3. Model Data Inputs
4. Methodology
4.1. SWAT Model Setup and Calibration
4.2. Trap Efficiency and Sediment Accumulation
4.3. SWAT Hydrologic Model
4.4. The Trap Efficiency Function (TEF)
- The appropriate mean sedimentation factor, , is 0.00688 [8].
- The values of and for the inflow sediment mixture are estimated to be 1100 kg/m3 and 0.85, respectively [52].
- Gill’s number, , was obtained from Equation (8), discussed later.
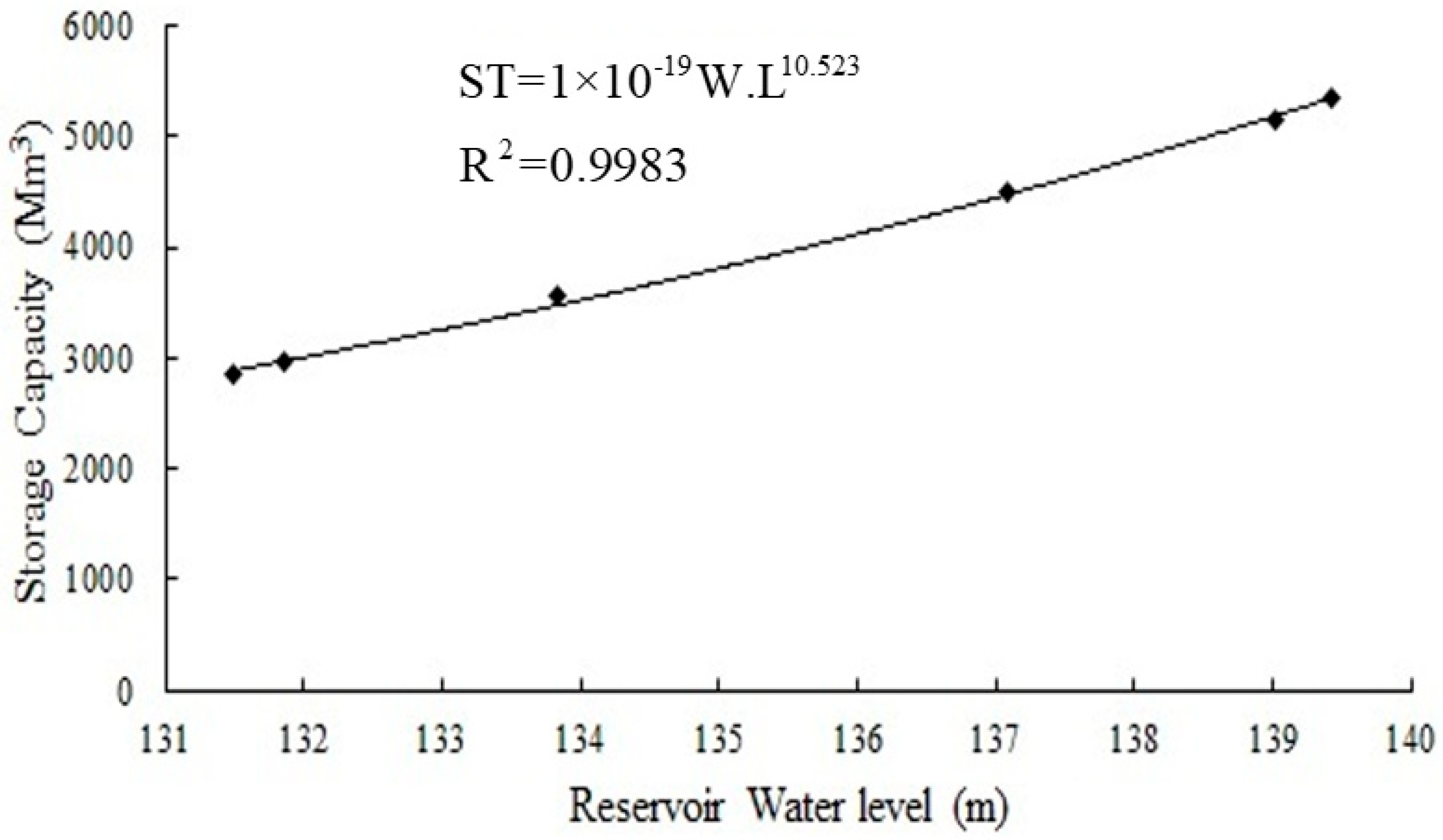
- Equation (7) is solved by trial and error to determine the remaining capacity of the reservoir after years of operation, noting that is the original volume of the reservoir.
- The sediment accumulated in the reservoir is calculated as the difference between base line capacity () and the computed capacity () at the specified levels during the specific survey.
- The average , measured at nine cross sections of the Euphrates River upstream of the HR, is estimated to be 0.23 mm [36].
5. Results and Discussion
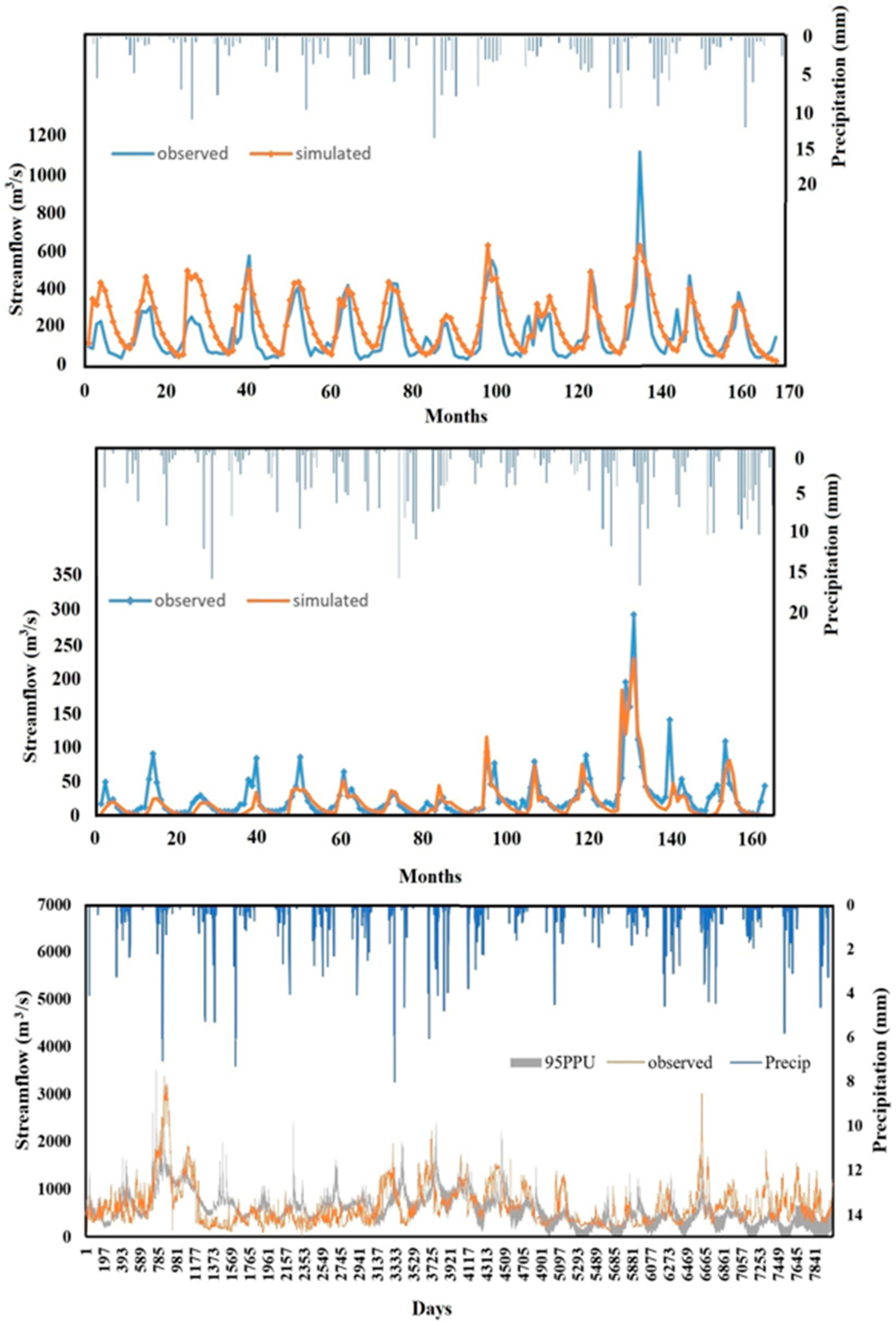
5.1. Calibration and Uncertainties in SWAT Model Outputs
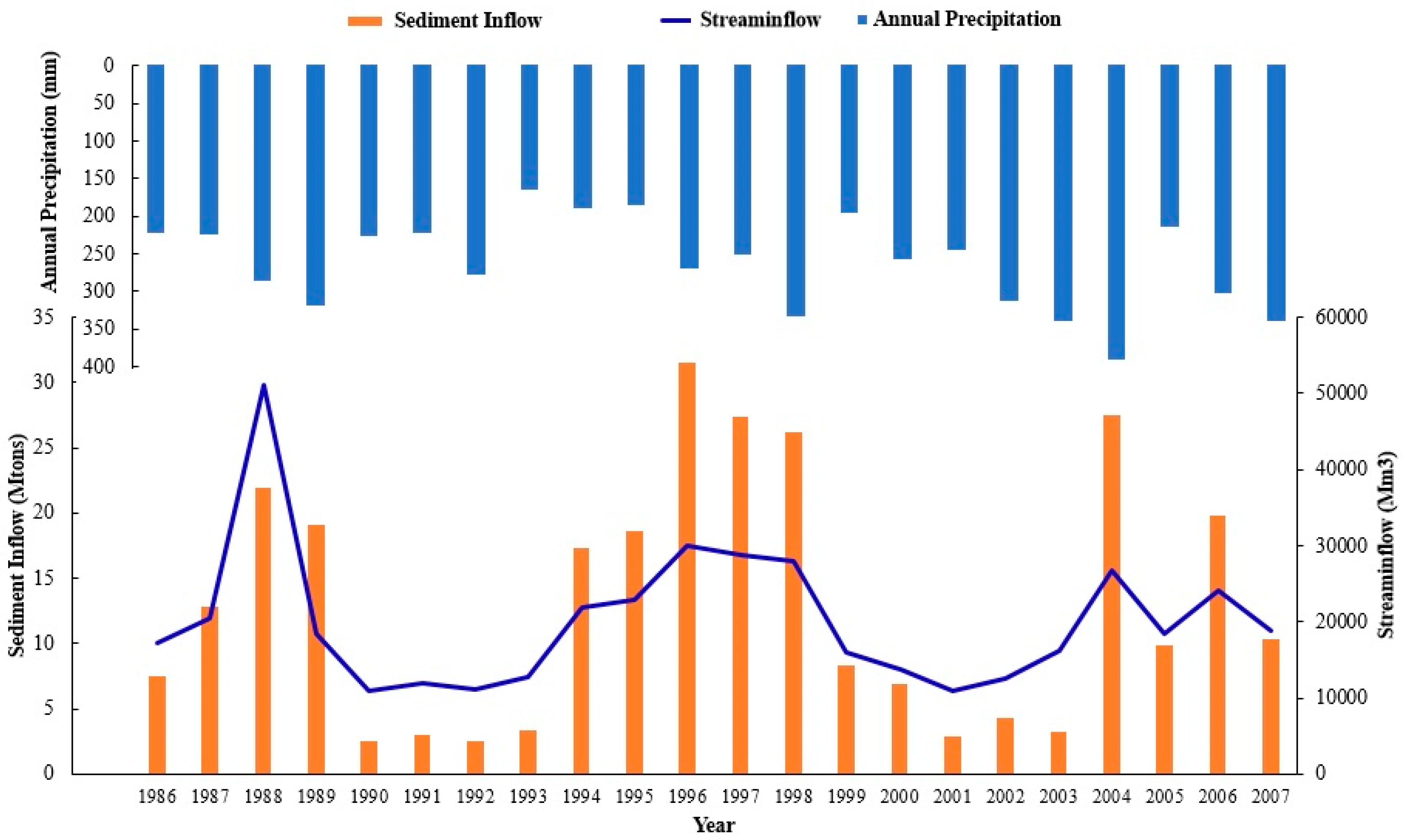
5.2. Simulation of Streamflow and Sediment Inflow
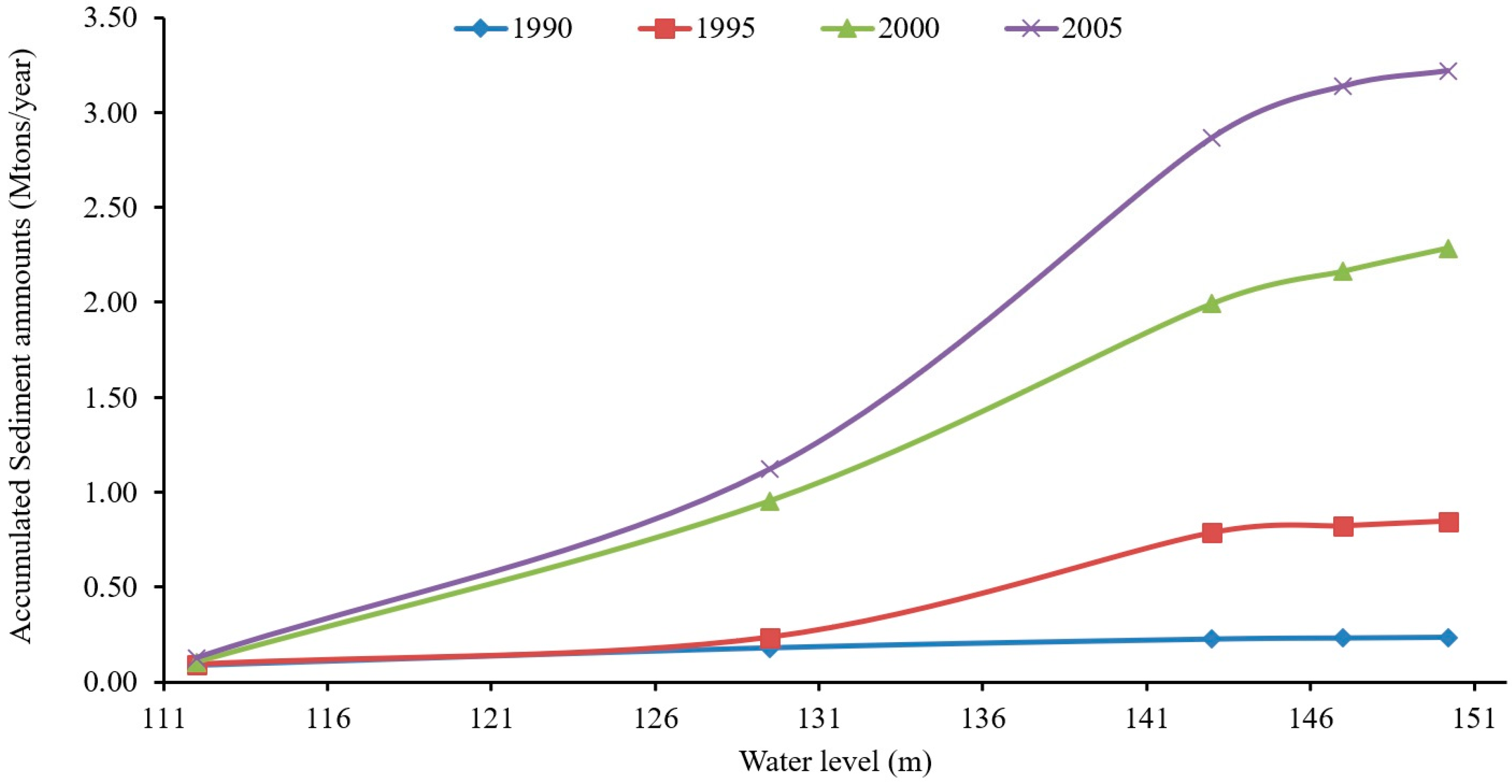
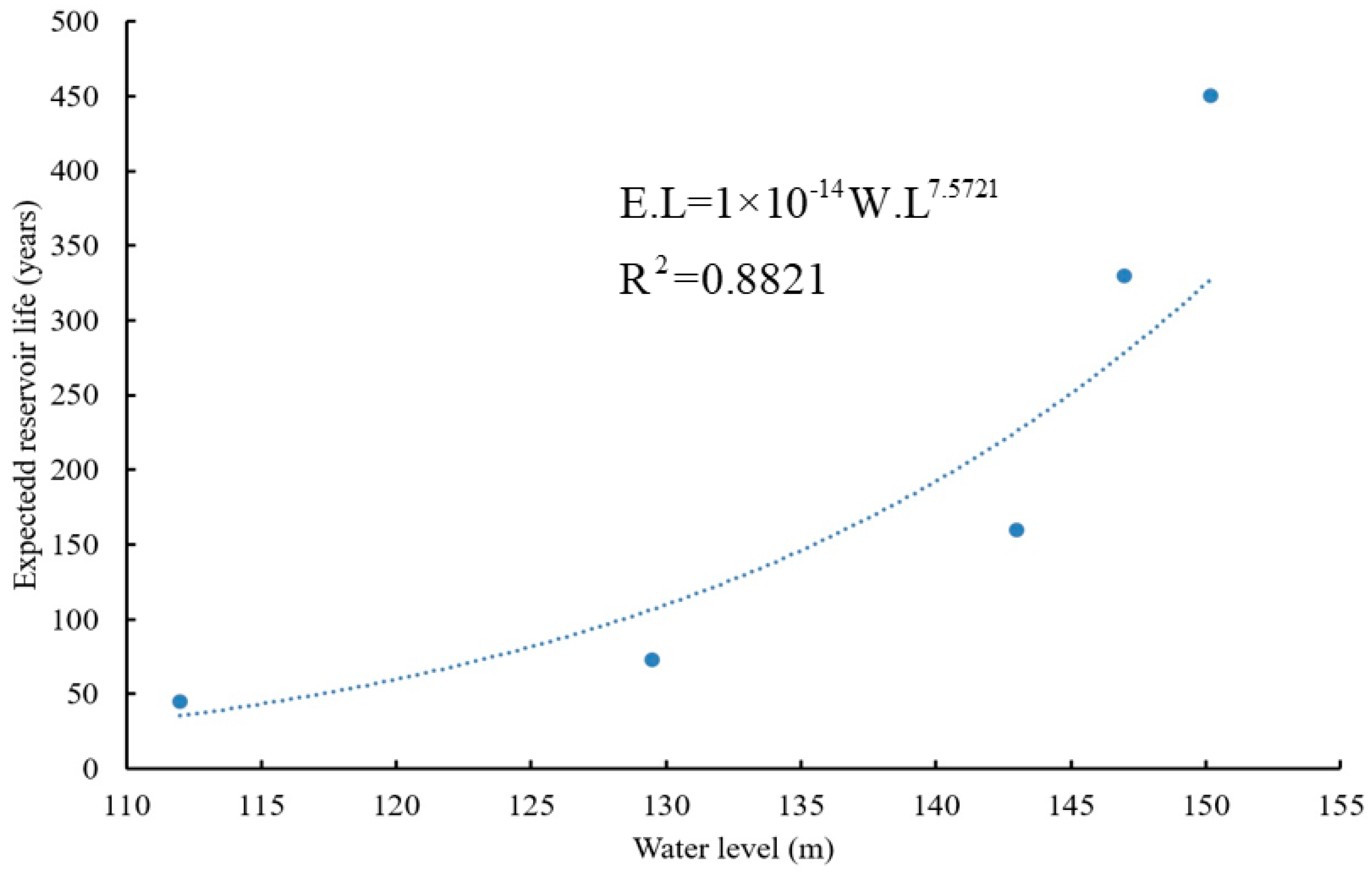
5.3. Sediment Accumulation in HR
6. Conclusions
- Based on the statistical measures adopted, the performance of the SWAT model in predicting streamflows was better during calibration than validation for all three locations.
- The SWAT model predictive ability was higher on a monthly time scale than a daily time scale.
- The daily sediment loads during calibration and validation were predicted at lower R2 and NSE values than the daily streamflows.
- The storage capacity during the period ranging from 1986 to 2005 was continuously decreasing with time for all operating water surface levels in the reservoir. For 1986, the initial storage capacity at water level 112 m was established to be 188 m-m3 and the loss of capacity for this level in 2005 was 15% from the initial storage, while the initial capacity for the 147 m water level was established to be 8200 m-m3, and the storage loss for this level was 35% in 2005.
- After 19 years of operation (1986–2005) at 147 m water level, it is predicted that the quantity of accumulated sediment deposited in the reservoir is 3.20 m-ts, with about 0.98 m-ts added during the years 2000 to 2005. This suggests an increasing rate of sedimentation over time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Ajaaj, A.A.; Mishra, A.K.; Khan, A.A. Comparison of BIAS correction techniques for GPCC rainfall data in semi-arid climate. Stoch. Environ. Res. Risk Assess. 2016, 30, 1659–1675. [Google Scholar]
- Mustafa, A.S.; Sulaiman, S.O.; Hussein, O.M. Application of swat model for sediment loads from valleys transmitted to Haditha Reservoir. J. Eng. 2016, 22, 184–197. [Google Scholar]
- Ozdogan, M.; Salvucci, G.D. Irrigation-induced changes in potential evapotranspiration in southeastern Turkey: Test and application of Bouchet’s complementary hypothesis. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Olcay Unver, I.H. Southeastern Anatolia Project (GAP). Int. J. Water Resour. Dev. 1997, 13, 453–484. [Google Scholar]
- Morris, G.L.; Fan, J. Reservoir Sedimentation Handbook: Design and Management of Dams, Reservoirs, and Watersheds for Sustainable Use; McGraw Hill: New York, NY, USA, 1998. [Google Scholar]
- Wang, J.; Watts, D.B.; Meng, Q.; Ma, F.; Zhang, Q.; Zhang, P.; Way, T.R. Influence of soil wetting and drying cycles on soil detachment. AgriEngineering 2022, 4, 533–543. [Google Scholar] [CrossRef]
- Siyam, A.M.; Mirghani, M.; Elzein, S.; Golla, S.; El-Sayed, S. Assessment of the Current State of the Nile Basin Reservoir Sedimentation Problems; Nile Basin Capacity Building Network (NBCBN), River morphology Research Cluster, Group1: Cairo, Egypt, 2005. [Google Scholar]
- Brune, G.M. Trap efficiency of reservoirs. Trans. Am. Geophys. Union 1953, 34, 407–418. [Google Scholar]
- Curchill, M. Discussion of Analysis and use of reservoir sedimentation data by Gottschalk L. C. In Proceedings of the Federal Interagency Sedimentation Conference, Denver, FL, USA, 6–8 May 1947; pp. 139–140. [Google Scholar]
- Alighalehbabakhani, F.; Miller, C.J.; Baskaran, M.; Selegean, J.P.; Barkach, J.H.; Dahl, T.; Abkenar, S.M.S. Forecasting the remaining reservoir capacity in the Laurentian Great Lakes watershed. J. Hydrol. 2017, 555, 926–937. [Google Scholar]
- Deletic, A. Modelling of water and sediment transport over grassed areas. J. Hydrol. 2001, 248, 168–182. [Google Scholar]
- Reinwarth, B.; Riddell, E.S.; Glotzbach, C.; Baade, J. Estimating the sediment trap efficiency of intermittently dry reservoirs: Lessons from the Kruger National Park, South Africa. Earth Surf. Process. Landf. 2018, 43, 463–481. [Google Scholar]
- Samson-Dô, M.; St-Hilaire, A. Characterizing and modelling the trapping efficiency of sedimentation basins downstream of harvested peat bog. Can. J. Civ. Eng. 2018, 45, 478–488. [Google Scholar]
- Lewis, S.E.; Bainbridge, Z.T.; Kuhnert, P.M.; Sherman, B.S.; Henderson, B.; Dougall, C.; Cooper, M.; Brodie, J.E. Calculating sediment trapping efficiencies for reservoirs in tropical settings: A case study from the Burdekin Falls Dam, NE Australia. Water Resour. Res. 2013, 49, 1017–1029. [Google Scholar]
- Garg, V.; Jothiprakash, V. Estimation of useful life of a reservoir using sediment trap efficiency. J. Spat. Hydrol. 2008, 8. [Google Scholar]
- Verstraeten, G.; Poesen, J. Estimating trap efficiency of small reservoirs and ponds: Methods and implications for the assessment of sediment yield. Prog. Phys. Geogr. 2000, 24, 219–251. [Google Scholar]
- Heinemarm, H.G. A new sediment trap efficiency curve for small reservoirs. J. Am. Water Resour. Assoc. 1981, 17, 825–830. [Google Scholar]
- Yeoh, J.; Loveless, J.; Siyam, A. New approach in determining useful life of reservoirs. In Hydraulics of Dams and River Structures: Proceedings of the International Conference, Tehran, Iran, 26–28 April 2004; Yadandoost, F., Attari, J., Eds.; CRC Press: Boca Raton, FL, USA, 2004; pp. 229–236. [Google Scholar]
- Environmental Protection Authority. FDR Ethiopia. National Action Programme to Combat Desertification; FDR Ethiopia: Addis Ababa, Ethiopia, 1998. [Google Scholar]
- Haan, C.T.; Barfield, B.J.; Hayes, J.C. Design Hydrology and Sedimentology for Small Catchments; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Azari, M.; Moradi, H.R.; Saghafian, B.; Faramarzi, M. Climate change impacts on streamflow and sediment yield in the North of Iran. Hydrol. Sci. J. 2016, 61, 123–133. [Google Scholar]
- Dutta, S. Soil erosion, sediment yield and sedimentation of reservoir: A review. Model. Earth Syst. Environ. 2016, 2, 123. [Google Scholar]
- Arnold, J.G.; Fohrer, N. SWAT2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 1211–1250. [Google Scholar]
- Vigiak, O.; Malagó, A.; Bouraoui, F.; Vanmaercke, M.; Obreja, F.; Poesen, J.; Habersack, H.; Fehér, J.; Grošelj, S. Modelling sediment fluxes in the Danube River Basin with SWAT. Sci. Total Environ. 2017, 599–600, 992–1012. [Google Scholar]
- Gassman, P.W.; Sadeghi, A.M.; Srinivasan, R. Applications of the SWAT model special section: Overview and insights. J. Environ. Qual. 2014, 43, 1–8. [Google Scholar] [PubMed]
- Najafi, M.R.; Moradkhani, H.; Jung, I.W. Assessing the uncertainties of hydrologic model selection in climate change impact studies. Hydrol. Process. 2011, 25, 2814–2826. [Google Scholar]
- Pechlivanidis, I.G.; Jackson, B.M.; McIntyre, N.R.; Wheater, H.S. Catchment scale hydrological modelling: A review of model types, calibration approaches and uncertainty analysis methods in the context of recent developments in technology and applications. Glob. NEST J. 2011, 13, 193–214. [Google Scholar]
- Dutta, D.; Das, R.; Mazumdar, A. Assessment of runoff and sediment yield in the Tilaya Reservoir, India using SWAT model. Asian J. Water Environ. Pollut. 2017, 14, 9–18. [Google Scholar]
- Setegn, S.G.; Dargahi, B.; Srinivasan, R.; Melesse, A.M. Modeling of sediment yield from Anjeni-gauged watershed, Ethiopia using SWAT model. J. Am. Water Resour. Assoc. 2010, 46, 514–526. [Google Scholar]
- Duru, U.; Wohl, E.; Ahmadi, M. Factors controlling sediment load in The Central Anatolia Region of Turkey: Ankara River Basin. Environ. Manag. 2017, 59, 826–841. [Google Scholar]
- Licciardello, F.; Govers, G.; Cerdan, O.; Kirkby, M.J.; Vacca, A.; Kwaad, F.J.P.M. Evaluation of the PESERA model in two contrasting environments. Earth Surf. Process. Landf. 2009, 34, 629–640. [Google Scholar]
- Al-Ansari, N.A.; Assad, N.M.; Walling, D.E.; Hussan, S.A. The suspended sediment discharges of the River Euphrates at Haditha, Iraq: An assessment of the potential for establishing sediment rating curves. Geogr. Annaler. Ser. A Phys. Geogr. 1988, 70, 203–213. [Google Scholar]
- Al-Hadithi, K.I.M. Hydrology and Hydrogeochemistry of Al-Qadisiya Dam Reservoir-Iraq. Ph.D. Thesis, University of Baghdad, Baghdad, Iraq, 1994. [Google Scholar]
- Ministry of Water Resources, Iraq. (2020). Private Communications with Aws Ajaaj.
- Khassaf, S.I.; Abde Al-Rahman, K.Z. Sediment transport upstream of reservoir of Haditha Dam. Eng. Dev. 2005, 9, 45–66. [Google Scholar]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar]
- Tateishi, R.; Uriyangqai, B.; Al-Bilbisi, H.; Ghar, M.A.; Tsend-Ayush, J.; Kobayashi, T.; Kasimu, A.; Hoan, N.T.; Shalaby, A.; Alsaaideh, B.; et al. Production of global land cover data–GLCNMO. Int. J. Digit. Earth 2011, 4, 22–49. [Google Scholar]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: An application in the Blue Nile River Basin. J. Am. Water Resour. Assoc. 2014, 50, 1226–1241. [Google Scholar]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the climate forecast system reanalysis as weather input data for watershed models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar]
- Bargaoui, Z.K.; Chebbi, A. Comparison of two kriging interpolation methods applied to spatiotemporal rainfall. J. Hydrol. 2009, 365, 56–73. [Google Scholar]
- Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT Calibration and Uncertainty Programs. A User Manual; Swiss Federal Institute of Aquatic Science and Technology: Eawag, Switzerland, 2015; Volume 103, pp. 17–66. [Google Scholar]
- Duru, U.; Arabi, M.; Wohl, E.E. Modeling stream flow and sediment yield using the SWAT model: A case study of Ankara River Basin, Turkey. Phys. Geogr. 2018, 39, 264–289. [Google Scholar]
- Rostamian, R.; Jaleh, A.; Afyuni, M.; Mousavi, S.F.; Heidarpour, M.; Jalalian, A.; Abbaspour, K.C. Application of a SWAT model for estimating runoff and sediment in two mountainous basins in central Iran. Hydrol. Sci. J. 2008, 53, 977–988. [Google Scholar]
- Wible, T. Enhanced Watershed Modeling and Data Analysis with a Fully Coupled Hydrologic Model and Cloud-Based Flow Analysis. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2014. [Google Scholar]
- Dalton, J., III. On the absorption of gases by water and other liquids. Philos. Mag. 1806, 24, 15–24. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar]
- Wang, X.; Melesse, A. Evaluation of the SWAT model’s snowmelt hydrology in a northwestern Minnesota watershed. Trans. ASAE 2005, 48, 1359–1376. [Google Scholar]
- Arnold, J.G.; Allen, P.M.; Muttiah, R.; Bernhardt, G. Automated base flow separation and recession analysis techniques. Groundwater 1995, 33, 1010–1018. [Google Scholar]
- William, J.R. Sediment yield prediction with universal equation using runoff energy factor. In Present and Prospective Technology for Predicting Sediment Yields and Sources, Proceeding of the Sediment Yield Workshop, USDA Sedimentation Laboratory, Oxford, MO, USA, 28–30 November 1972; Agricultural Research Service, US Department of Agriculture: Washington, DC, USA, 1975; ARS-S-40; pp. 244–252. [Google Scholar]
- Punmia, B.C.; Jain, A.K.; Jain, A.K. Soil Mechanics and Foundations; Laxmi Publications: New Delhi, India, 2005. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar]
- Cardoso de Salis, H.H.; Monteiro da Costa, A.; Moreira Vianna, J.H.; Azeneth Schuler, M.; Künne, A.; Sanches Fernandes, L.F.; Leal Pacheco, F.A. Hydrologic modeling for sustainable water resources management in urbanized karst areas. Int. J. Environ. Res. Public Health 2019, 16, 2542. [Google Scholar] [CrossRef]
- Mukundan, R.; Radcliffe, D.; Risse, L. Spatial resolution of soil data and channel erosion effects on SWAT model predictions of flow and sediment. J. Soil Water Conserv. 2010, 65, 92–104. [Google Scholar]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. Am. Soc. Agric. Biol. Eng. 2012, 55, 1491–1508. [Google Scholar]
- Chawanda, C.J.; Nkwasa, A.; Thiery, W.; van Griensven, A. Combined impacts of climate and land-use change on future water resources in Africa. Hydrol. Earth Syst. Sci. 2024, 28, 117–138. [Google Scholar]
- Sissakian, V.K.; Al-Ansari, N.; Knutsson, S. Sand and dust storm events in Iraq. J. Nat. Sci. 2013, 5, 1084–1094. [Google Scholar]
- Breshears, D.D.; Whicker, J.J.; Johansen, M.P.; Pinder, J.E. Wind and water erosion and transport in semi-arid shrubland, grassland and forest ecosystems: Quantifying dominance of horizontal wind-driven transport. Earth Surf. Process. Landf. 2003, 28, 1189–1209. [Google Scholar]
- Lavee, H.; Imeson, A.C.; Sarah, P. The impact of climate change on geomorphology and desertification along a mediterranean-arid transect. Land Degrad. Dev. 1998, 9, 407–422. [Google Scholar]
- Gill, M.A. Sedimentation and useful life of reservoirs. J. Hydrol. 1979, 44, 89–95. [Google Scholar]
- Mulu, A.; Dwarakish, G.S. Different approach for using trap efficiency for estimation of reservoir sedimentation. An overview. Aquat. Procedia 2015, 4, 847–852. [Google Scholar]

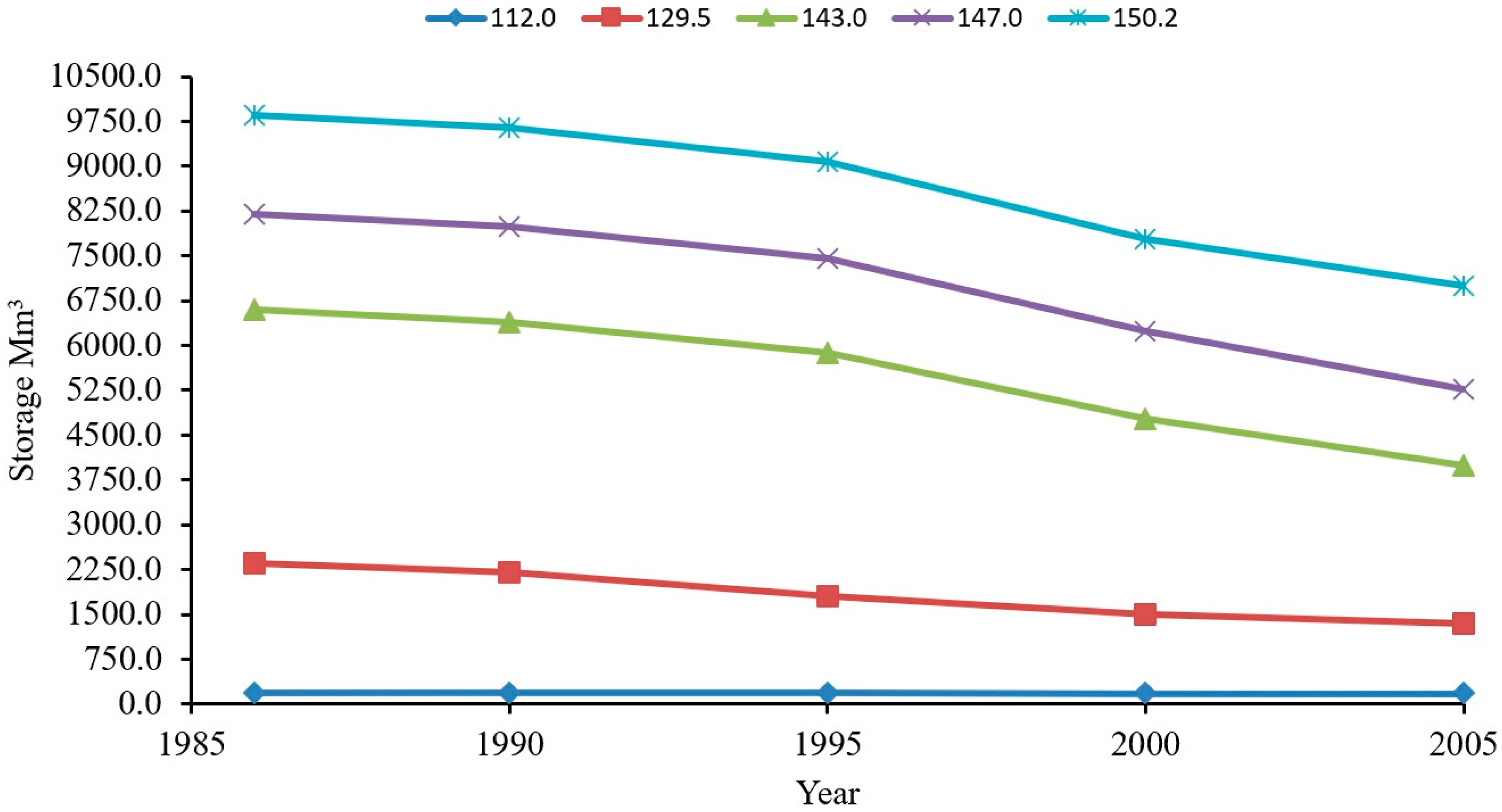
| Water Level Description | WL (m) | 1986 | 1990 | 1995 | 2000 | 2003 |
|---|---|---|---|---|---|---|
| Lower Water level | 112 | 188 | 169.95 | 149.03 | 130.03 | 119.6 |
| Lower working water level | 129.5 | 2362 | 2330.08 | 2290.23 | 2250.43 | 2226.56 |
| Normal working water level | 143 | 6591 | 6558.1 | 6516.99 | 6475.89 | 6451.24 |
| Design working water level | 147 | 8200 | 8166.99 | 8125.74 | 8084.51 | 8059.77 |
| Maximum water level | 150.2 | 9850 | 9816.91 | 9775.57 | 9734.24 | 9709.45 |
| Location | Name | Time Step | Drainage Area (km2) | Latitude | Longitude | Data Type |
|---|---|---|---|---|---|---|
| Euphrates River Upstream of HR | UERBQ_1 | Daily | - | - | - | Streamflow and Sediment |
| Euphrates River at Hussaybah | UERBQ_2 | Monthly | 221,000 | 34.42 | 41.01 | Streamflow |
| Euphrates River at Hit | UERBQ_3 | Monthly | 264,100 | 33.61 | 42.84 | Streamflow |
| Euphrates River Downstream of Hindiyah Barrage | UERBQ_4 | Monthly | 274,100 | 32.72 | 44.27 | Streamflow |
| Rank | Parameter_Name | Fitted Value | Min. Value | Max. Value | t-Stat | p-Value |
|---|---|---|---|---|---|---|
| 1 | R__GWQMN.gw | −0.601 | −0.736 | −0.466 | −9.561 | 0.000 |
| 2 | R__CN2.mgt | −0.644 | −0.777 | −0.512 | −3.774 | 0.001 |
| 3 | R__GW_REVAP.gw | −0.046 | −0.120 | 0.028 | −2.257 | 0.031 |
| 4 | R__BIOMIX.mgt | −0.066 | −0.150 | 0.018 | −1.974 | 0.057 |
| 5 | R__EPCO.hru | 0.030 | −0.036 | 0.096 | 1.307 | 0.201 |
| 6 | R__CH_N2.rte | 0.062 | −0.020 | 0.144 | 0.168 | 0.427 |
| 7 | R__CH_K2.rte | −0.090 | −0.186 | 0.006 | 0.804 | 0.427 |
| 8 | R__ALPHA_BF.gw | −0.426 | −0.906 | 0.053 | −0.803 | 0.428 |
| 9 | R__CANMX.hru | 0.070 | −0.016 | 0.156 | −0.678 | 0.503 |
| 10 | R__OV_N.hru | −0.022 | −0.084 | 0.040 | −0.669 | 0.508 |
| 11 | R__SOL_BD(..).sol | −0.090 | −0.186 | 0.006 | −0.634 | 0.531 |
| Station | Variable Calibrated | p-Factor | r-Factor | R2 | NSE |
|---|---|---|---|---|---|
| UERBQ_1 | Daily-Streamflow | 0.36/0.32 | 0.59/0.54 | 0.45/0.39 | 0.35/0.33 |
| UERBQ_1 | Daily-Sediment | 0.34/0.30 | 0.43/0.42 | 0.37/0.34 | 0.30/0.32 |
| UERBQ_2 | Monthly-Streamflow | 0.43/0.42 | 0.37/0.32 | 0.64/0.62 | 0.60/0.55 |
| UERBQ_3 | Monthly-Streamflow | 0.45/0.46 | 0.4/0.41 | 0.56/0.66 | 0.36/0.34 |
| UERBQ_4 | Monthly-Streamflow | 0.36/0.34 | 0.31/0.30 | 0.64/0.56 | 0.61/0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajaaj, A.A.; Khan, A.A.; Mishra, A.K.; Alhathloul, S.H. Estimation of Incoming Sediments and Useful Life of Haditha Reservoir with Limited Measurements Using Hydrological Modeling. Hydrology 2024, 11, 128. https://doi.org/10.3390/hydrology11080128
Ajaaj AA, Khan AA, Mishra AK, Alhathloul SH. Estimation of Incoming Sediments and Useful Life of Haditha Reservoir with Limited Measurements Using Hydrological Modeling. Hydrology. 2024; 11(8):128. https://doi.org/10.3390/hydrology11080128
Chicago/Turabian StyleAjaaj, Aws A., Abdul A. Khan, Ashok K. Mishra, and Saleh H. Alhathloul. 2024. "Estimation of Incoming Sediments and Useful Life of Haditha Reservoir with Limited Measurements Using Hydrological Modeling" Hydrology 11, no. 8: 128. https://doi.org/10.3390/hydrology11080128
APA StyleAjaaj, A. A., Khan, A. A., Mishra, A. K., & Alhathloul, S. H. (2024). Estimation of Incoming Sediments and Useful Life of Haditha Reservoir with Limited Measurements Using Hydrological Modeling. Hydrology, 11(8), 128. https://doi.org/10.3390/hydrology11080128






