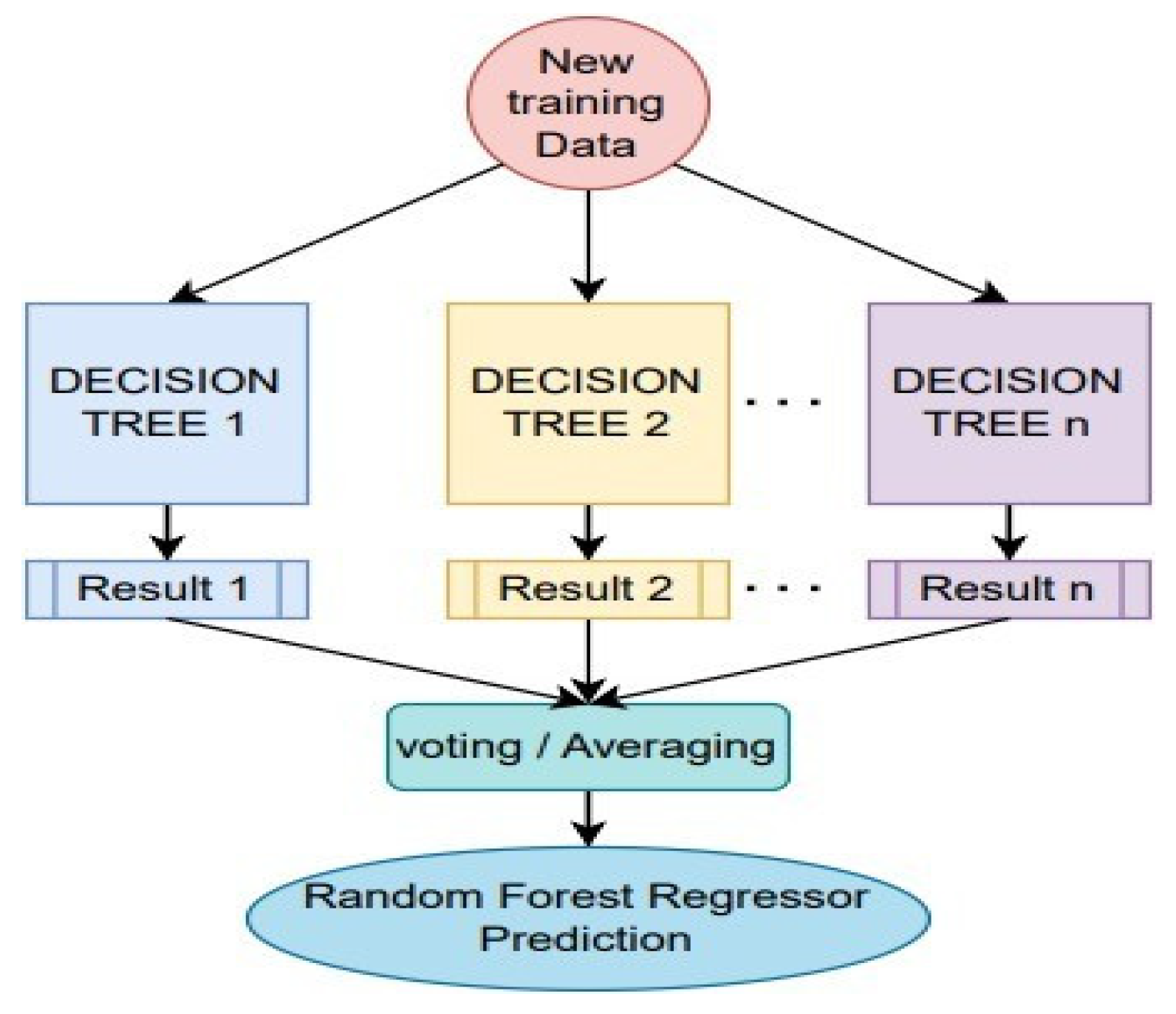
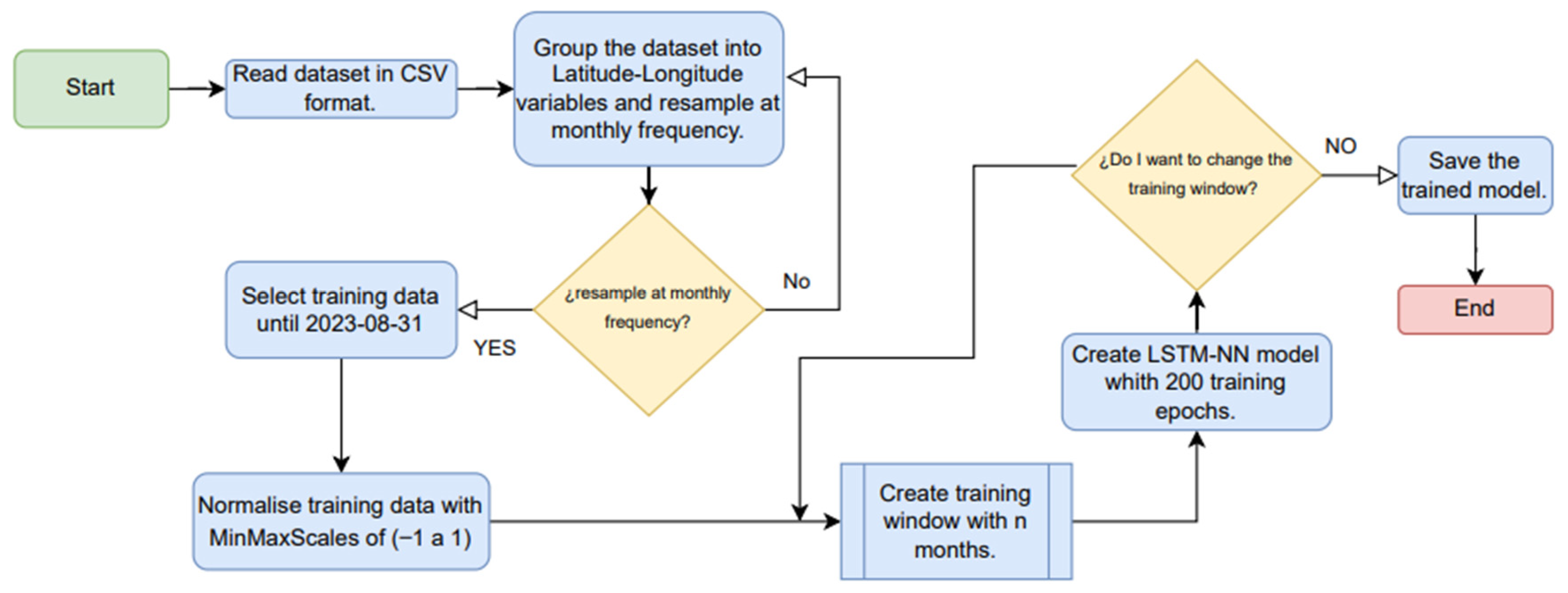
1. Introduction
In Colombia, the Institute of Hydrology, Meteorology and Environmental Studies (IDEAM) knows climate change, indicating that throughout the 21st century, precipitation will increase toward the center and north of the Pacific region and decrease between 15% and 36% in the Caribbean and Andean regions. This prolonged increase in precipitation was reflected in 2022, with permanent precipitation events and, according to [
1], persisted until late 2022 and early 2023. This would mark the first “triple episode” La Niña of this century, spanning three consecutive northern hemisphere winters, corresponding to summer in the southern hemisphere. This project aims to implement a methodology to develop predictive models of total monthly precipitation using new cutting-edge technologies, such as deep learning, for water supply consumption in the department of Boyacá.
With the rise of artificial intelligence, the importance of massive data for science, and in particular geography, stands out. Remote sensing plays an important role, allowing the acquisition of images of the earth’s surface from aerial or space sensors [
2,
3], which complements the acquisition of information from different sensors or meteorological devices necessary to know the spatiotemporal behavior of precipitation, such as surface weather stations, altitude stations, and hundreds of weather radars, in addition to some 200 research satellites among others [
4]. From the aforementioned devices, one can gain an idea of the magnitude of the global network of meteorological and hydrological observations. This abundance of information facilitates analysis, modeling, and prediction of this phenomenon by using various emerging technologies focused on artificial intelligence, such as machine learning (ML) and deep learning (DL).
The effects of climate change have led to an increase in global precipitation, a phenomenon known as La Niña. This is particularly evident in Colombia, affecting the Andean, Pacific, and Caribbean regions.
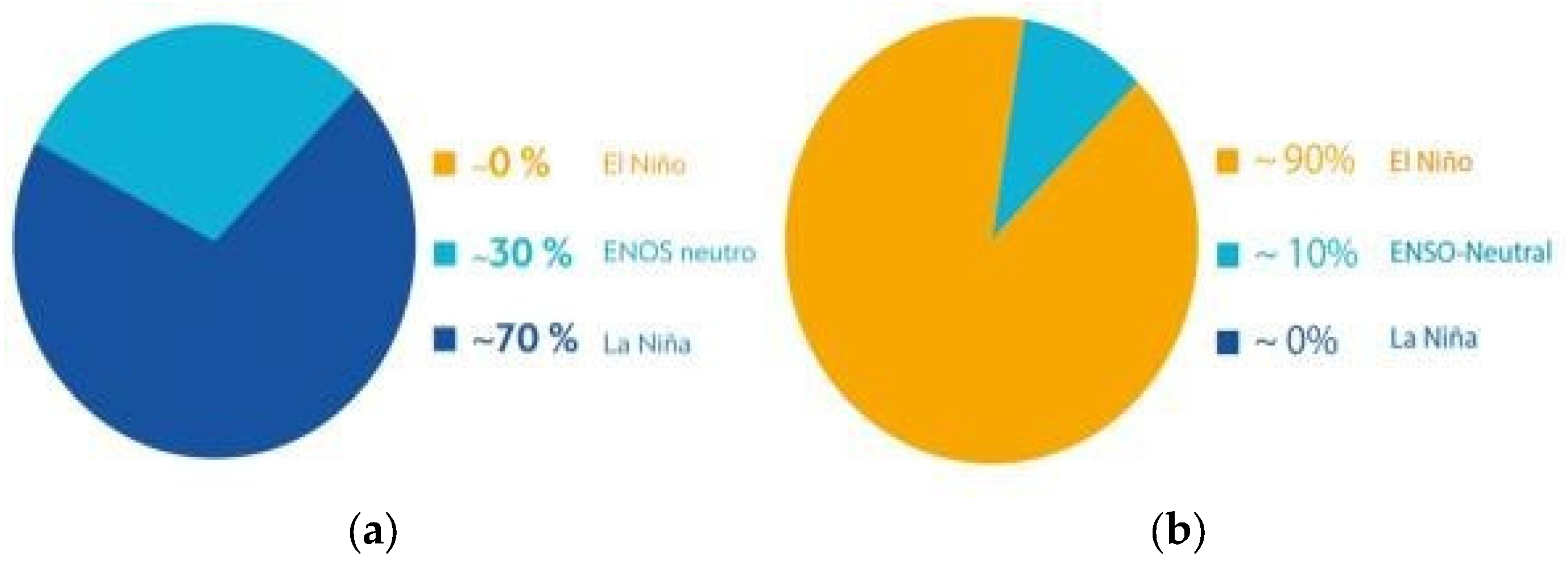
Figure 1a illustrates the occurrence of the third triple episode of La Niña (ENSO), which had a 70% probability of persisting until the end of March 2023. Forecasts indicated a 60% probability of an El Niño event from May through July 2023, with a 90% probability of continuing through October 2023, as shown in
Figure 1b. This left a 10% probability of an ENSO neutral period and virtually no chance of another La Niña event by the end of October 2023.
Statistical and numerical applications are often not as effective in predicting precipitation accurately and timely, and although weather stations offer short-term predictions, forecasting long-term precipitation remains challenging [
6,
7]. Therefore, advancements are being made by integrating them with emerging technologies, like artificial intelligence. For instance, Ref. [
8] implemented machine learning and observed that the forecast achieved better precipitation prediction compared to a deviation between 46% and 91% experienced in June 2019 in India. This progress involves leveraging historical data and using time series models to implement various machine learning (ML) and deep learning (DL) models, such as the OP-ELM algorithm, which demonstrated successful monthly rainfall predictions in China [
9].
In the field of meteorological and hydrological prediction, the accuracy of long-term forecasts tends to decrease, especially when predicting higher intensities. However, new artificial intelligence techniques have significantly improved these predictions. Ref. [
10] introduced a spatiotemporal feature fusion transformer that enhances the accuracy of precipitation nowcasting by effectively fusing spatial and temporal features. This model’s innovative approach to feature fusion and attention mechanisms is particularly relevant for developing methods aimed at monthly precipitation prediction.
Similarly, Ref. [
11] presented a comprehensive framework for predicting the monthly runoff in the Xijiang River using gated recurrent units (GRUs), discrete wavelet transforms (DWTs), and variational modal decomposition (VMD). By leveraging antecedent monthly runoff, water levels, and precipitation data, this approach demonstrates substantial improvements in prediction accuracy, highlighting its applicability to monthly precipitation forecasting. Additionally, Ref. [
12] used long short-term memory (LSTM) and neural hierarchical interpolation for time series forecasting (N-HiTS) to predict the standardized precipitation index (SPI) across various regions in Zacatecas, Mexico. Their combined modeling approach enhances the ability to predict SPI values, offering a valuable method for monthly precipitation prediction.
There are several ML versions, as demonstrated by [
13] in their study predicting the normalized precipitation index using monthly data from 1949 to 2013 at four meteorological stations. Techniques included M5tree, extreme learning machine (ELM), and online sequential ELM (OSELM). The ELM model made the best predictions for months 3, 6, and 12, with the lowest root mean square error (RMSE) value, except for the predicted values for month 1, where the M5tree model obtained the best result.
DL is an emerging technique for dealing with complex systems, such as the prediction of meteorological variables. Therefore, Ref. [
14] proposed a hybrid DL approach using a combination of a one-dimensional convolutional neural network (Conv1D) and a multilayer perceptron (MLP) (hereafter Conv1D-MLP) to predict precipitation applied to 12 different locations. The result was better and was compared with a support vector regression (SVM) machine learning approach. Similarly, using 92 meteorological stations in China, Ref. [
15] combined the surface altitudes of the stations with the precipitation prediction, grouping by the k-means method, as implemented by [
16], the stations surrounding the target and using a convolutional neural network (CNN), thus obtaining better results in the existing threat index and mean squared error (MSE).
Finding the best method for modeling the precipitation variable and the different parameters surrounding it is complicated. For this reason, Ref. [
6] evaluated a model in Australia based on ML optimized with DL to predict daily rainfall and used GridSearchCV (version 1.5.1) to find the best parameters for the different models over a daily span of 10 years from 2007 to 2017 from 26 geographically diverse rain gauge locations. With the rise of ML and DL systems, remote sensing plays an important role since, according to [
17], it allows the acquisition of terrestrial information from sensors installed on space platforms and the use of satellite images to perform multi-temporal analyses, understood as spatiotemporal changes [
18,
19]. In 2020, a CNN model was used with different architectures, such as GoogLeNet, AlexNet, and LeNet, among others [
20], on 2D images as input precipitation data with three different heights: 100, 3000, and 5500 m above sea level. The output variable was an image that indicates to which class it belongs, converting the model to a binary class defined by a rainfall probability threshold between 0 and 100%. The main result was that CNNs can predict precipitation with lower computational capacity than traditional methods [
21]. Two data sources were used for training and testing the CNN model. The first was the CEH, and the second was the Centre for Ecology and Hydrology Gridded Estimate of Areal Rainfall (GEAR), providing data on the monthly rainfall across Britain between 1890 and 2017. The results obtained from video-based rainfall prediction using different CNN architectures can provide valuable post-processing to traditional numerical weather prediction models.
The main concern for researchers studying precipitation in different geographical areas and climates worldwide has been the selection of suitable ML and DL methods. Hence, [
22,
23,
24,
25] have also presented various approaches for predicting precipitation.
Table 1 evaluates techniques such as the Lagrangian convolutional neural network (L-CNN), the ELM model, the LSTM model, the multilayer perceptron (MLP) model, and the CNN model.
3. Results
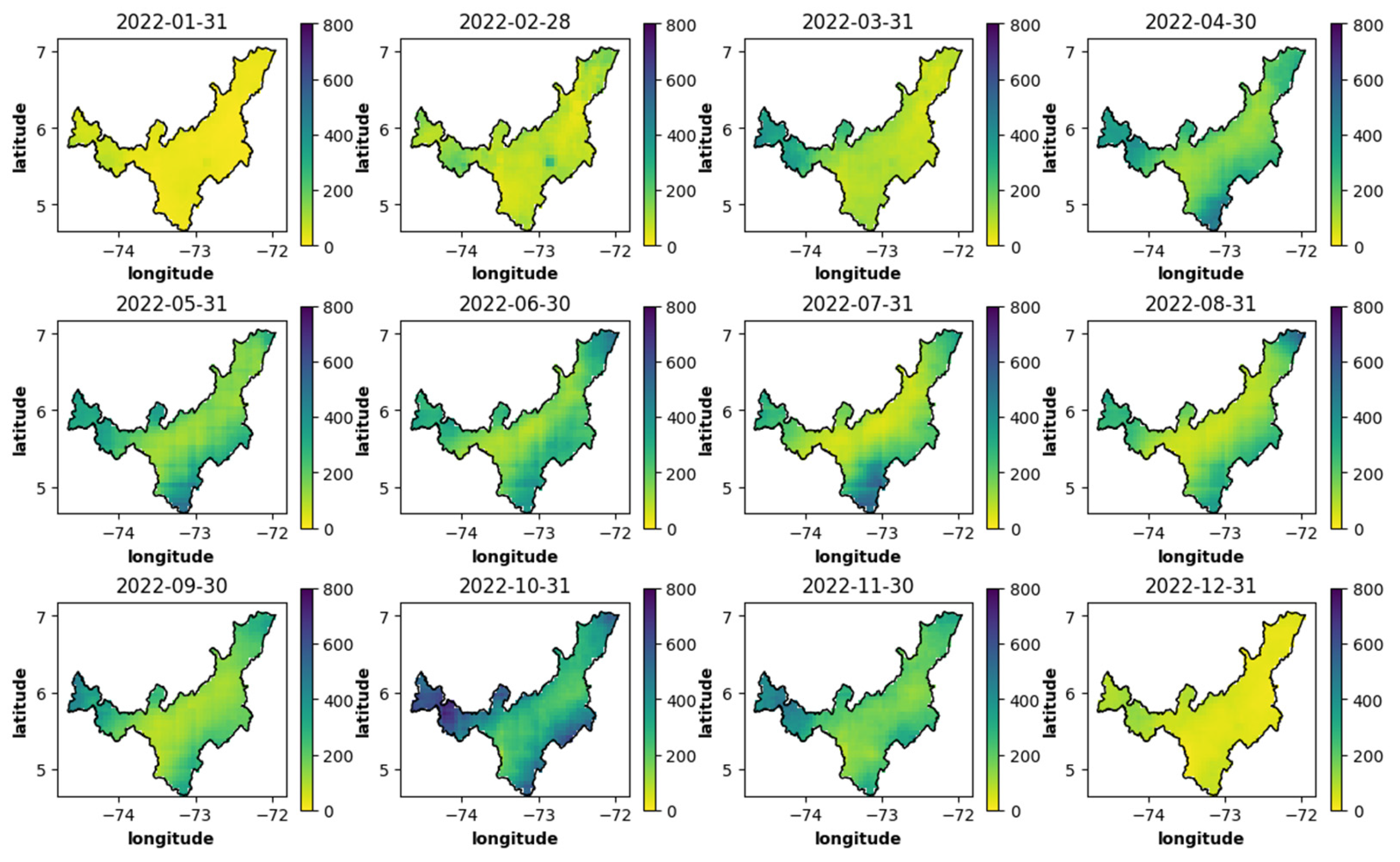
In surveying and geography, spatial analysis is a widely used technique for collecting information from specific sampling points. The coordinates were used to filter the CHIRPS precipitation data for Boyacá, Colombia, using the department’s polygon. Subsequently, the dataset was organized to visualize the spatiotemporal dimension for climate analysis through time, as depicted in
Figure 7, illustrating the spatiotemporal precipitation of Boyacá in the year 2022.
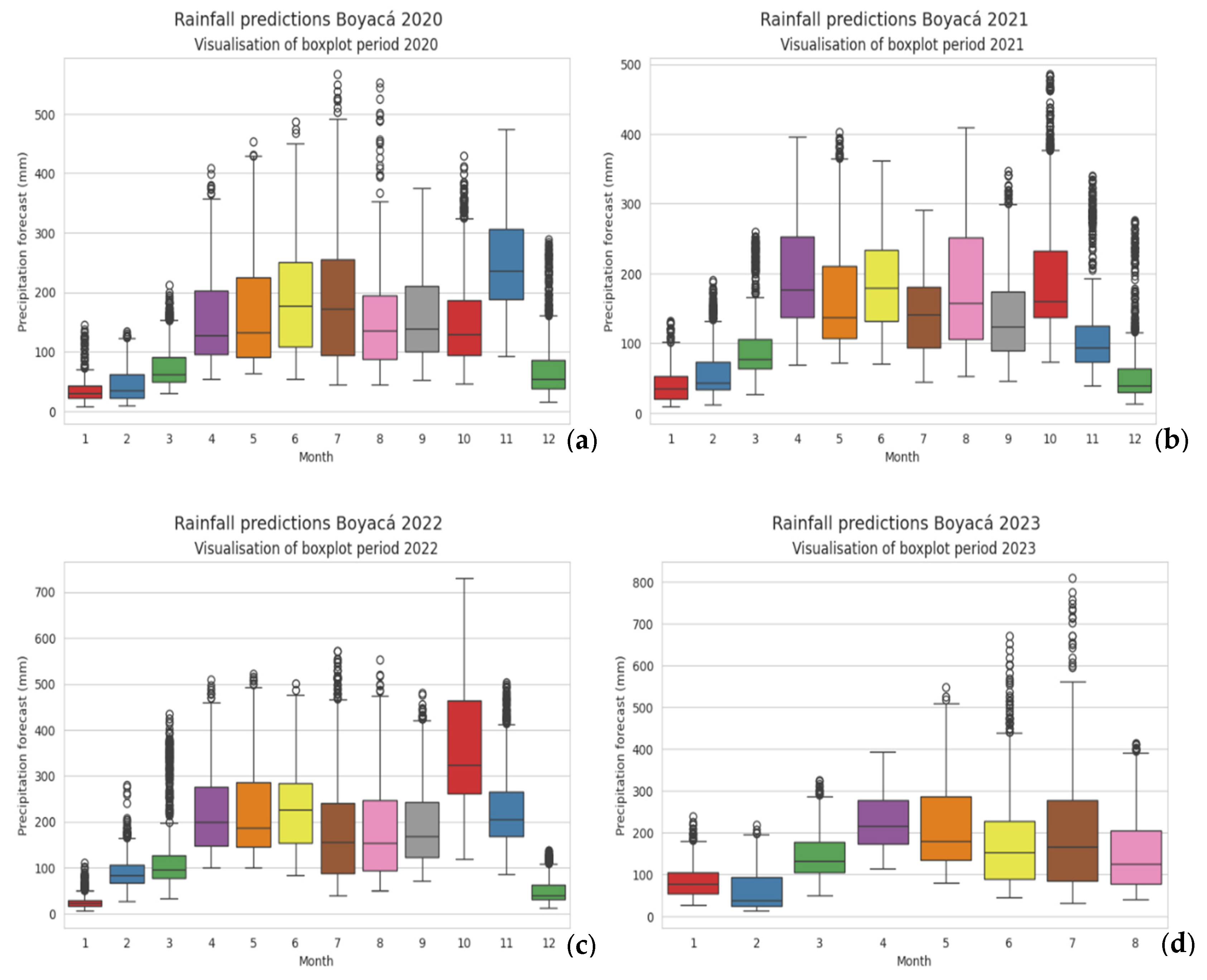
An analysis of historical precipitation values from 2020 to 2023 was conducted using box-and-whisker plots, presenting quantitative distribution through quartiles, as shown in
Figure 8a–d. Based on the acquired and organized stationary precipitation data, along with statistical analysis, patterns and trends in and relationships between the dataset’s characteristics can be identified. According to [
40], the box-and-whisker plot facilitates the establishment of relationships between samples and the identification of outliers.
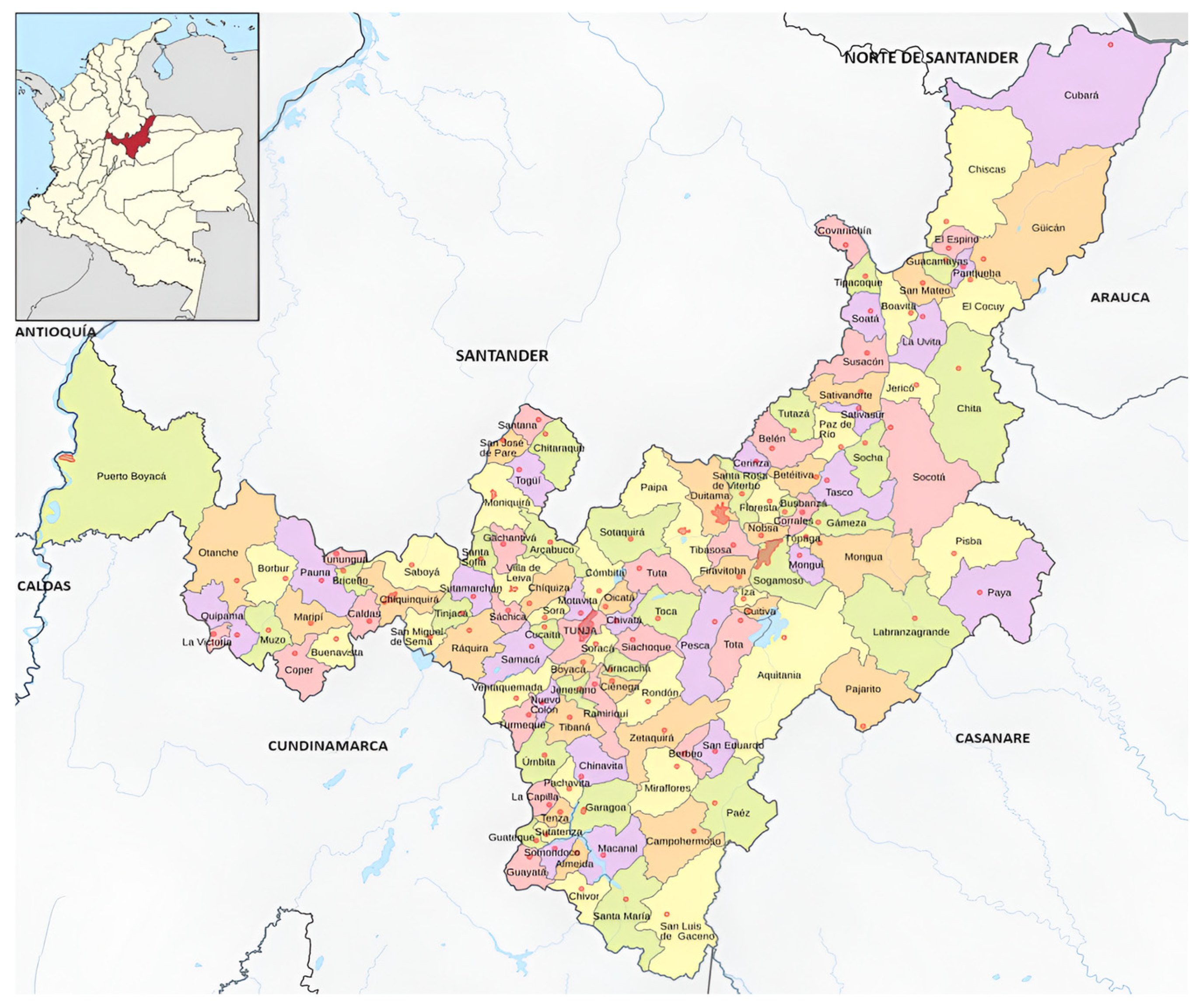
Examining the distribution of precipitation in Boyacá, it was observed that in the year 2020, the maximum precipitation occurred in July, reaching approximately 500 mm. Additionally, some outlier precipitation points exceeded this value, suggesting the presence of a geographical area with significant monthly precipitation, such as a moor or an anomaly within the dataset for that year. Upon investigating these outliers, it was found that the coordinates corresponding to latitude 7.024998 and longitude −72.125008, located in the municipality of Cubará, Boyacá (see
Figure 3), in the northeast of the region, experience high rainfall. This indicates that it is not an outlier but rather a location with a high probability of significant precipitation.
In 2021, the dry-season months (January to March) did not exceed an average of 100 mm of monthly rainfall, although March saw rainfall exceeding 200 mm. The rainy season, with precipitation averaging between 150 and 200 mm, persisted from April to October, with October being the wettest month, recording rainfall over 400 mm.
In 2022, the effects of climate change were evident, with maximum precipitation values from May to November exceeding 400 mm and in some months reaching approximately 500 mm. In October, some data showed values exceeding 700 mm, without any outliers, representing a significant increase compared to previous years, when precipitation values did not exceed 400–450 mm per month.
For 2023, rainfall ranged between 150 mm and a maximum of 300 mm until March. From April to October, the El Niño phenomenon was expected, resulting in decreased departmental precipitation, averaging 200 mm per month. This analysis indicates that the dry season occurs between January and March, with December having moderate rainfall. Months with average rainfall are between April and August, while the highest rainfall occurs from September to November, with October experiencing the highest rainfall in the two years 2021 and 2022.
3.1. Development of Predictive Models
The dataset for each of the models was divided into 70% for training and 30% for testing. The results of the ARIMA, RFR, and LSTM models are presented next.
3.1.1. ARIMA Model Design
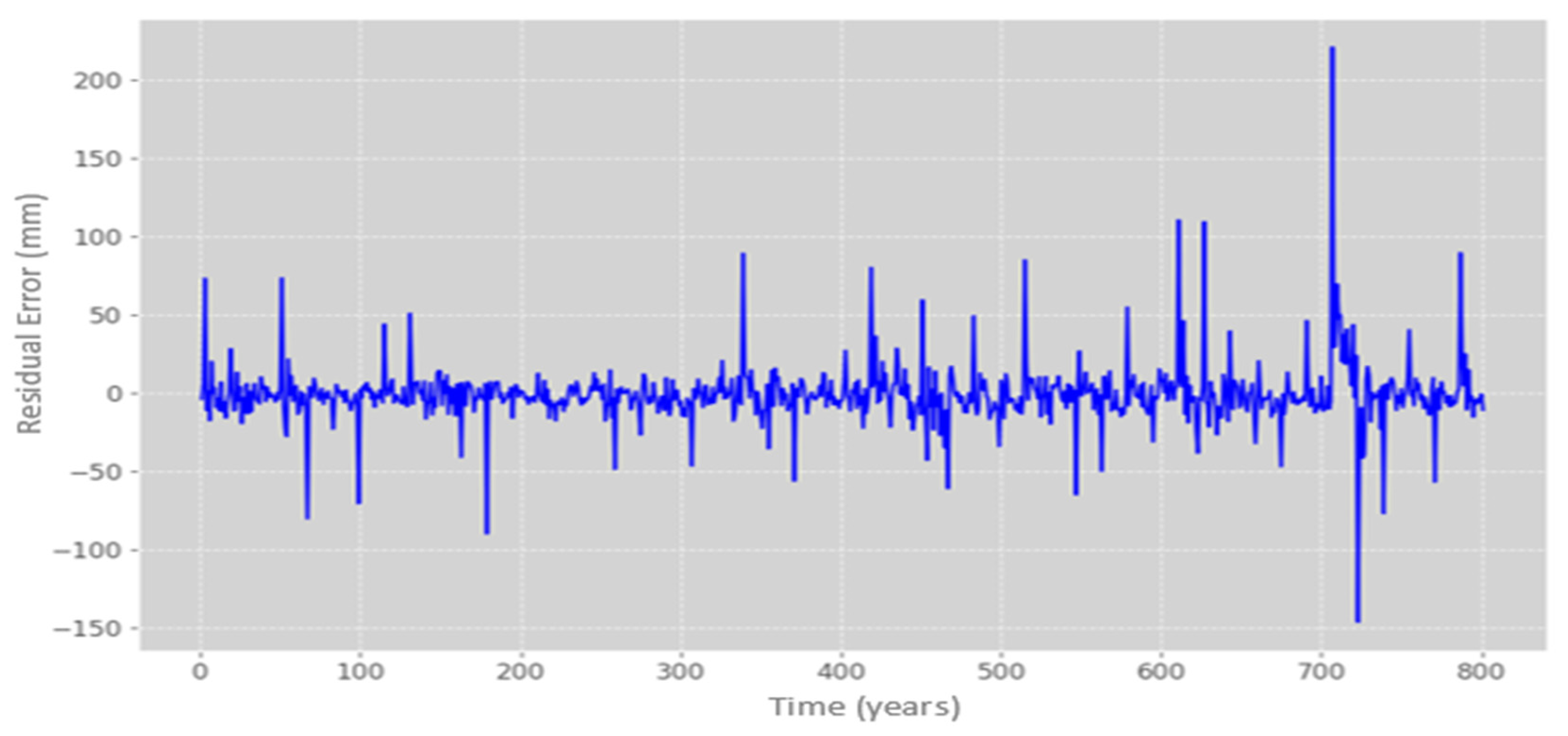
A Dickey–Fuller (DF) test was conducted on the time series to determine whether the data adhere to a unit root autoregressive process [
32], indicating the stationarity of the model. Once the time series rejected the null hypothesis and the data were stationary, precipitation was selected as the target variable. The best model for the training set was identified as the autoregressive and differenced ARIMA model (4,1,0) (2,1,0) (12), lacking moving average characteristics (i.e., a stationary model), with four lag observations in the autoregressive model and one degree of differencing.
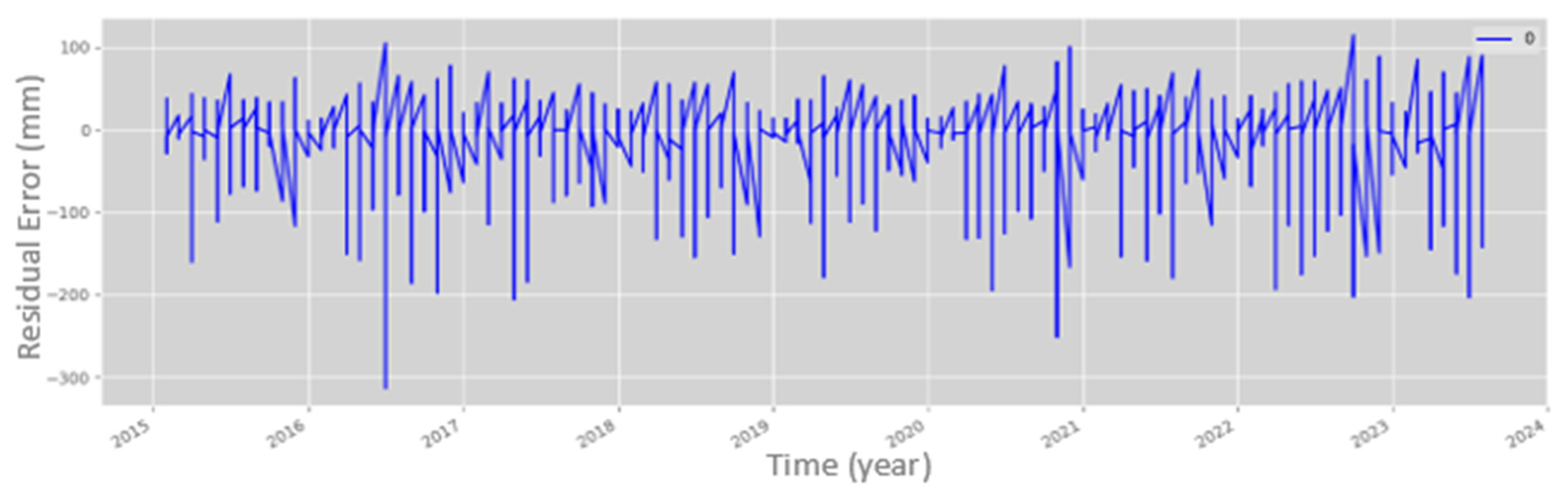
Finally, the model’s predictions were evaluated, achieving an 81% similarity to the observed precipitation in both training and test datasets, with residual errors averaging 27.98 mm compared to the actual measurements. The error trend across most data points exhibited a mean of zero and a uniform variance, although there were instances where the residual error exceeded 200 mm, as illustrated in
Figure 9.
3.1.2. Random Forest Regression Design
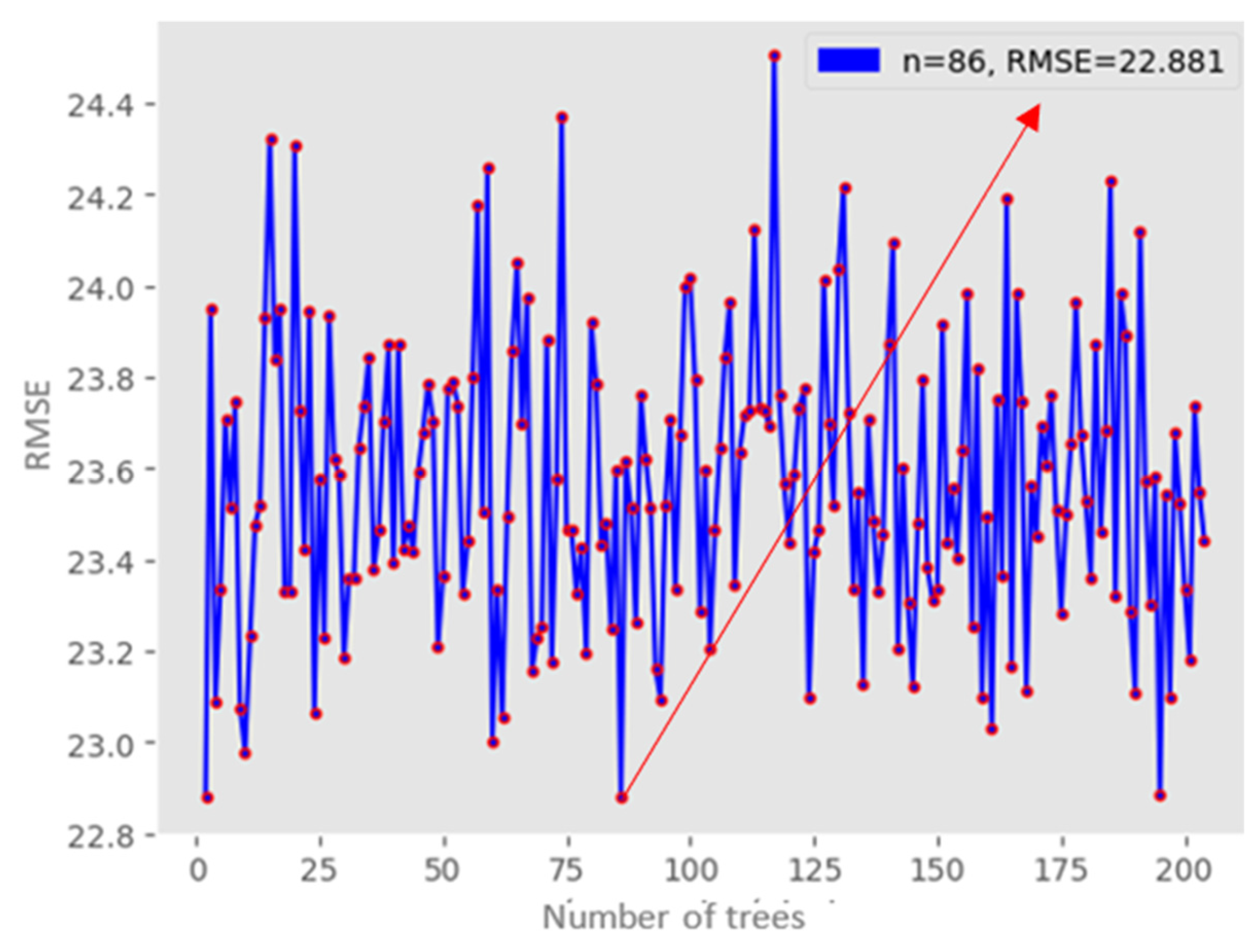
In this model, seasonal variables of year and month were included in each observation of the input dataset. Additionally, one year’s worth of data were included for each observation. Consequently, a dataset with 17 variables (latitude, longitude, precipitation, year, month, L1, …, L12) was obtained, where precipitation served as the target variable and the other variables acted as labels for prediction.
A random forest regression model with 83 decision trees was created. This specific number of trees was chosen as it produced the lowest RMSE value among the 0 to 205 trees evaluated, as shown in
Figure 10.
The study achieved an 87% similarity between the model’s precipitation predictions and the observations from the training and test datasets. When plotting the model’s response against the test dataset, it was observed that the predictions closely matched the actual behavior in most instances. However, there were a few outliers where the predictions deviated by approximately 12 mm from the actual values, resulting in an overall error of 23.21 mm, as illustrated in
Figure 11.
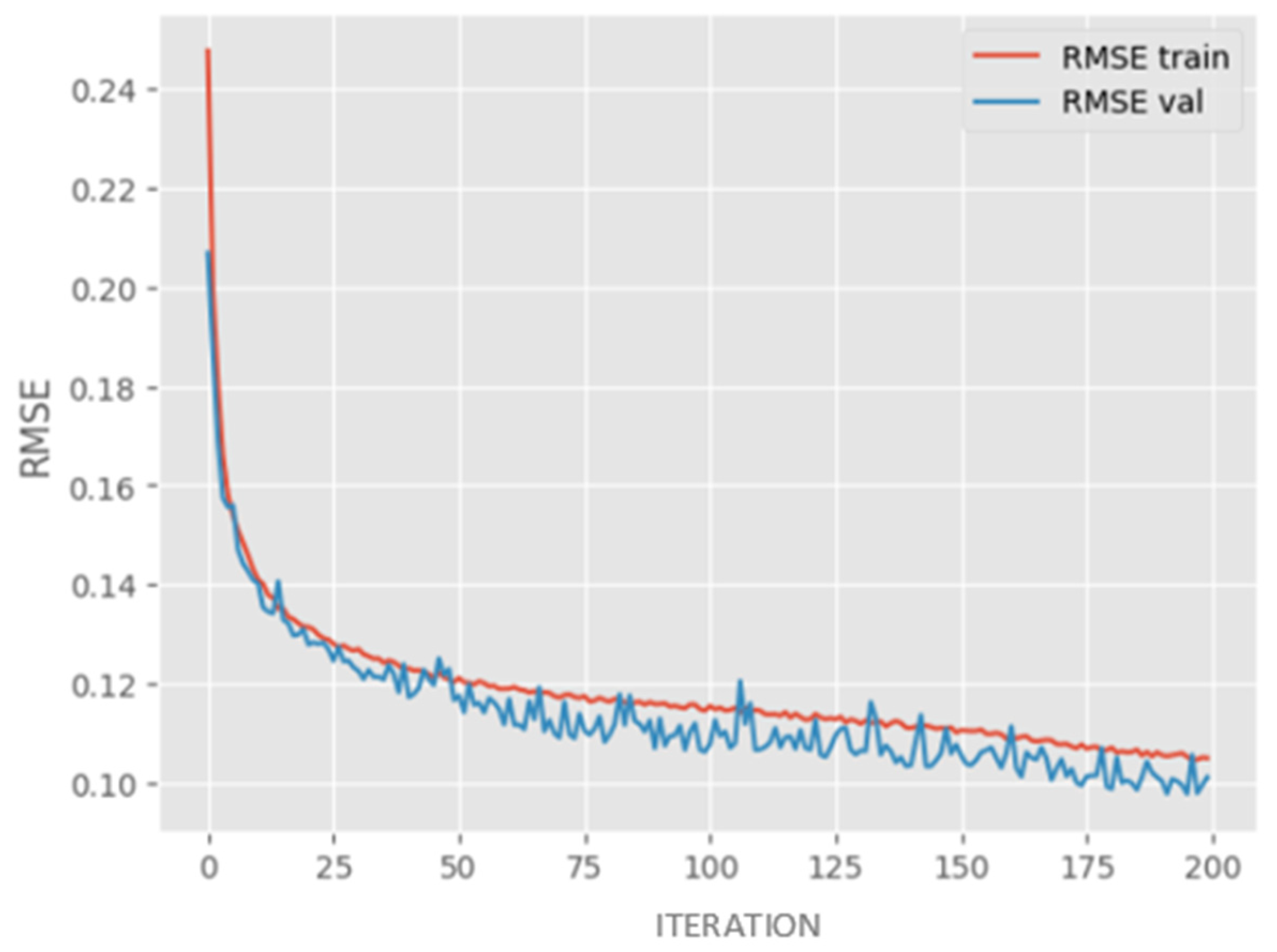
3.1.3. LSTM-NN Model Design
Several training runs were conducted for the LSTM model, exploring different hyperparameter values. The best model achieved included a sequential class instance with 128 memory units in the hidden layers, using a linear activation function and a mean squared error (MSE) loss function, with a learning rate set to RMSprop.
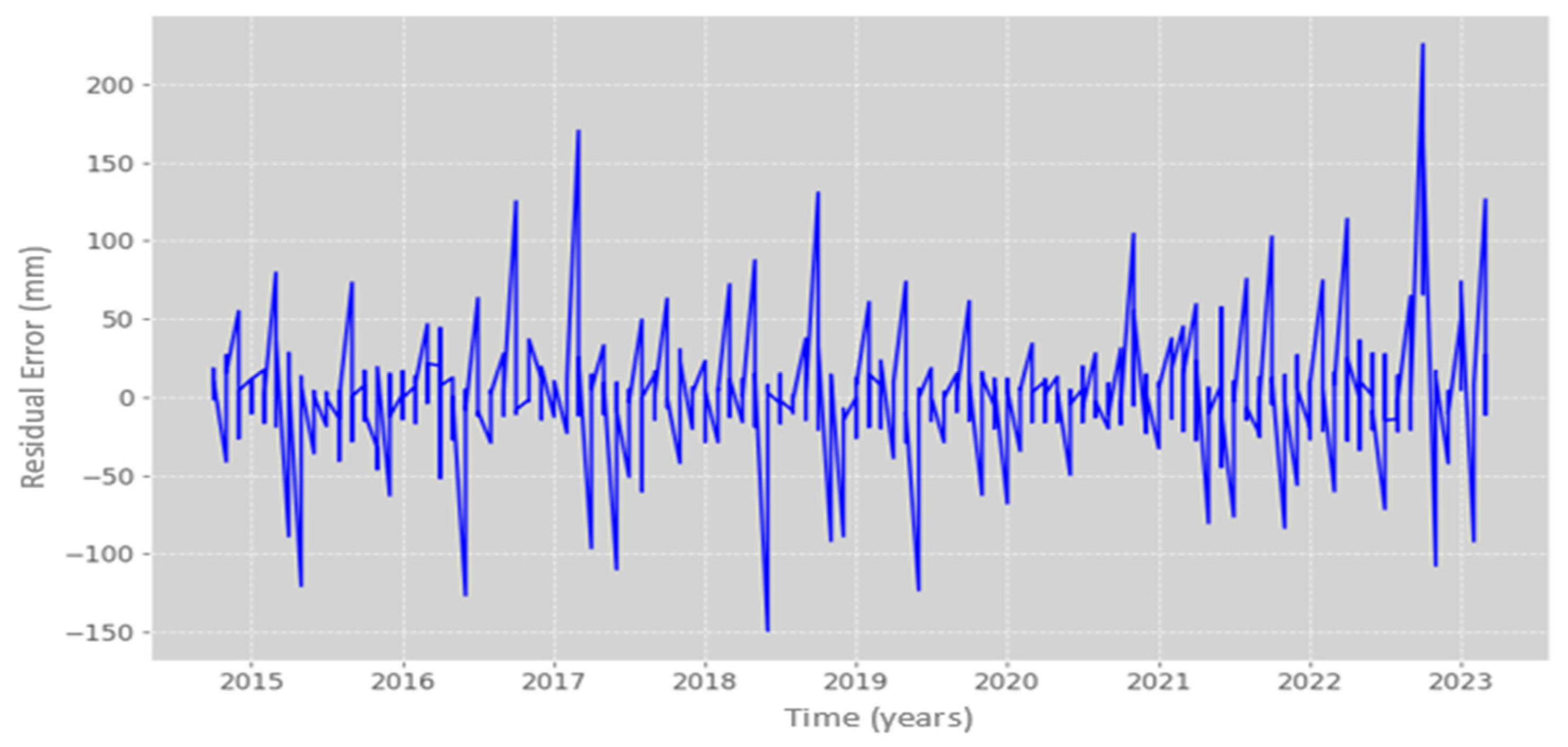
Furthermore, validation for overfitting was performed on the training and test datasets, as illustrated in
Figure 12. Upon converting the predictions to full scale, the LSTM model demonstrated 92% effectiveness in reproducing the precipitation values of the dataset. This resulted in a 16-percentage point reduction in the residual error compared to the random forest regression (RF-R) model. Additionally, the LSTM model showed a decrease in the number of significant errors, with only a few iterations exhibiting values above 100 mm and one instance of approximately 200 mm, as shown in
Figure 13.
In the evaluation metrics, three models were compared: the ARIMA model, the LSTM-NN model, and the random forest regressor. The ARIMA model demonstrated efficiency but exhibited 10% lower reliability in predictions compared to the LSTM-NN model, as detailed in
Table 2. Additionally, the root mean square error (RMSE) of the ARIMA model was more than 10% higher than that of the other two evaluated models. Consequently, the LSTM-NN emerged as the best model for reproducing observations from the dataset, with an error rate of 0.8% and a superior RMSE metric compared to the second-best model, the random forest regressor. The monthly precipitation errors, whether above or below the actual measurements, were approximately 10 mm.
Based on the evaluated results, the LSTM-NN model is the most effective in reproducing precipitation observations from the training and test datasets. Consequently, this model was implemented to predict precipitation over the next 48 months, starting from the last month, which was August 2023.
3.2. LSTM-NN Model Implementation
The implementation was based on the LSTM-NN model capturing spatiotemporal patterns of monthly precipitation data for the Boyacá department with the following architecture:
The decision to use an LSTM layer with 128 units was based on its ability to yield the best results, leading to an improvement in the RMSE value. It is worth noting that increasing the number of hidden layers in the model tends to result in more accurate predictions. However, it is important to exercise caution, as the number of layers determines the amount of information the layer can learn. Therefore, there is a risk of overfitting of the training and test data if this number is increased excessively.
This function was used so that training would be fast and there would be no saturation, as occurs with functions such as sigmoidal and hyperbolic tangent, and it is computationally simpler to implement.
The objective of prediction was to perform a regression; therefore, a dense layer with a unit was used, which was the prediction on the precipitation variable.
It is a method to accelerate the training of neural networks and achieve a near-linear acceleration rate with the increase in computational nodes [
41]. It was selected to speed up the LSTM model, as it can adapt to learning each parameter individually and can lead to a lower prediction error compared to other algorithms.
The MSE loss function gives more importance to large errors or outliers by providing a quadratic loss function as it squares and subsequently averages the values. This method is used in many identifications, prediction, and optimal filtering applications [
42].
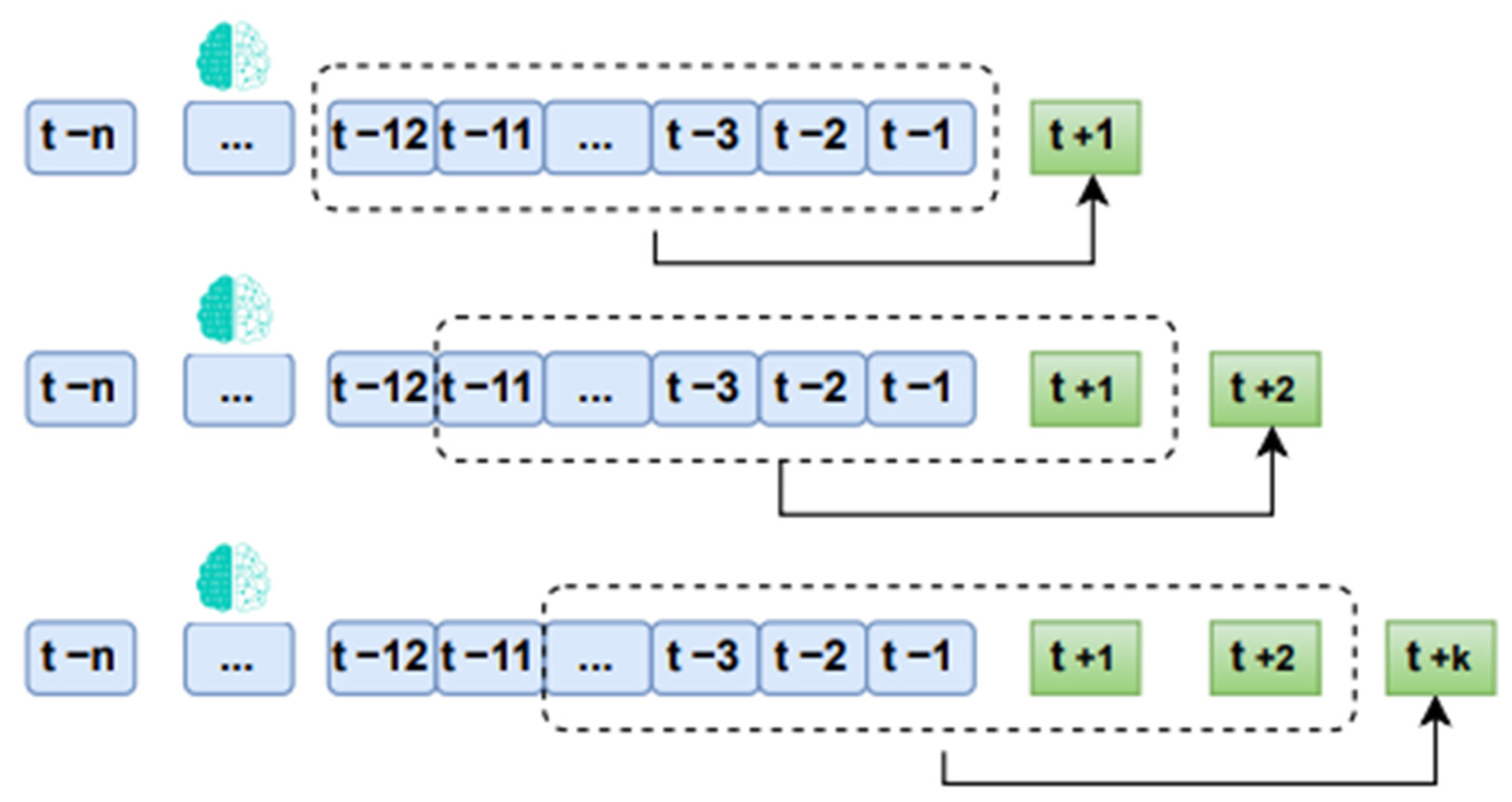
A sliding windows approach was used, wherein several previous months (t + n) were used to make predictions. This concept, known as sliding windows, was used to repair the input data for the training model. Subsequently, an algorithm was developed to construct a dataset comprising n number of previous months, with the output obtained for k following months using the architecture of the LSTM model mentioned before (refer to
Figure 14).
The sliding windows model significantly enhances the accuracy of short-term monthly precipitation prediction when using deep long short-term memory (LSTM) recurrent neural networks, which segment the input data [
43]. In this project, the 48-month window size was reconsidered to account for the El Niño and La Niña phenomena present in the region. Therefore, a 48-month window was established to predict at (t + 16), the first prediction commencing in September 2023 for each dataset and concluding in December 2024. The process detailing the handling of training data windows is illustrated in
Figure 15.
The dataset contained a total of 757 geographical points of latitude and longitude of the Boyacá Department. Once validated, the model was trained and run on Google Collaboratory, which has the advantage of running Python 3 code in a runtime environment that uses T4 GPU hardware acceleration and high RAM capacity. A CSV-type dataset was generated with the columns latitude, longitude, time, and precipitation prediction in millimeters (mm), which allowed the generation of heat maps and box-and-whisker plots for each month.
LSTM-NN Forecast with a 48-Month Window
The training of this model was conducted in Google Collaboratory, following the specified configurations and using 200 epochs, lasting approximately 2 h.
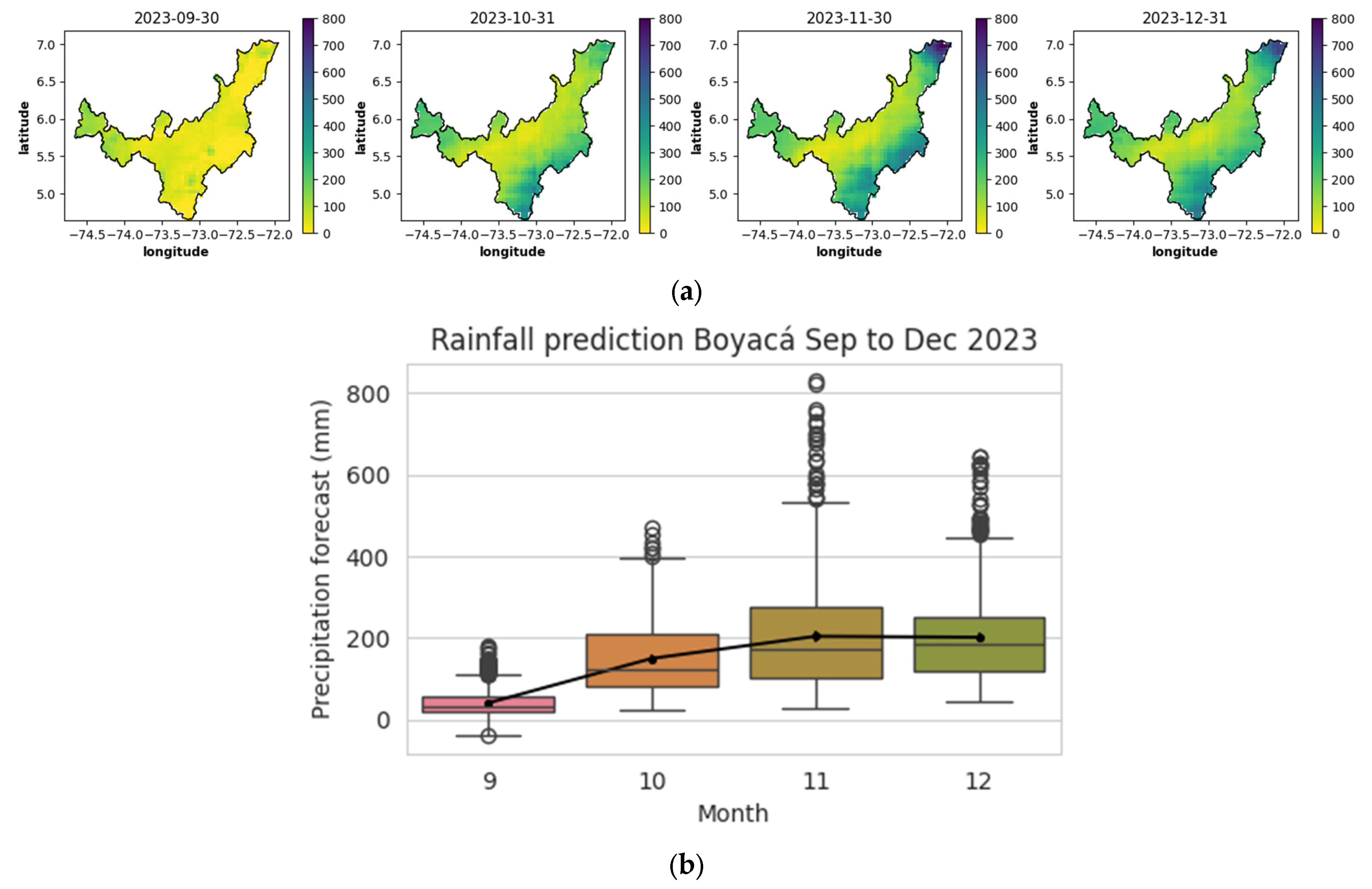
Figure 16a illustrates the spatiotemporal precipitation data, and
Figure 16b represents the predicted values in box-and-whisker plots obtained for the remaining 4 months of the year 2023, starting in September.
The data indicated that precipitation levels for September were relatively low, as evidenced by the median, which fell below the 50th percentile of the data distribution. Forecasted precipitation values were expected to remain low, not exceeding 150 mm. However, the mean suggested a right-skewed distribution, with higher precipitation values leading to potential increases up to 200 mm per month across the entire Boyacá Department. This value was close to the average precipitation for this month.
For October, an increase in precipitation was expected, indicating a wetter month compared to September. The mean was slightly higher than the median, suggesting once again a right-skewed distribution, with some extreme values influencing the mean. The box-and-whisker plots (see
Figure 16b) showed that from October to December, there were outliers exceeding 400 mm, and in October, these values ranged from 600 to 800 mm. However, when these results were compared with the spatiotemporal diagrams in
Figure 16a, it became evident that these were not outliers but rather represent potential precipitation data in municipalities located on the borders and boundaries with the Departments of Antioquia, Caldas, Cundinamarca, and Norte de Santander (see
Figure 3).
Regarding November, the mean continued to rise, while in December, it slightly decreased, indicating persistently high precipitation levels in the municipalities bordering the department and a trend of moderate precipitation, around 200 mm, in the central region.
A spatiotemporal prediction of precipitation for 2024 was conducted, revealing, as shown in
Figure 17a, that during the first quarter, precipitation was expected to range from low to moderate, between 100 and 300 mm, with a slight decreasing trend. In
Figure 17b, it is observed that during the first quarter, the median and mean precipitation values remained relatively close to each other, suggesting a symmetrical distribution of the data with few outliers. March was projected to end with the lowest precipitation levels, below 200 mm, indicating a particularly dry start to the second quarter.
As observed in the first quarter, March exhibited a decreasing trend in precipitation values. This trend continued into the second quarter, with a notable decline, particularly in May and June, where the average precipitation was approximately 70 mm, reaching maximum values of up to 200 mm across the three months. In the third quarter, a shift from the dry conditions of the previous quarter was expected, with July experiencing low-to-moderate rainfall, averaging around 230 mm, similar to the levels seen at the beginning of the year. Higher precipitation values were anticipated near the department’s borders, with some outliers exceeding 400 mm.
August was projected to be the wettest month, with intense rainfall ranging from 400 to 500 mm, and certain municipalities within the department could record peaks of up to 700 mm. The mean precipitation surpassed the median, indicating a potential presence of extreme high values.
For the final quarter, precipitation values are expected to remain relatively constant, with the mean and median being close, suggesting a uniform distribution of rainfall of around 200 mm per month. In the northeastern and southeastern parts of the department, precipitation levels may fluctuate between 350 and 400 mm per month.
4. Discussion
When compared with traditional models, such as ARIMA and random forest regression, the LSTM model demonstrates superior performance in accurately predicting precipitation, particularly in capturing the nuances of outlier data, which in the Boyacá region are not entirely outliers but rather data from municipalities or areas with high precipitation, mostly located at the department’s borders or extremities. The effectiveness of the LSTM model can be attributed to its ability to retain and learn from sequential dependencies within time series data, enabling it to better model the complex and nonlinear patterns inherent in precipitation datasets.
The results from the LSTM model indicated significant seasonal variations in precipitation, with a notable dry period forecasted for the second quarter of 2024, particularly in May and June, followed by a transition to wetter conditions in the third quarter. The model’s ability to predict such transitions is crucial for water resource management, agricultural planning, and disaster mitigation strategies, especially in regions with variable climatic conditions, like Boyacá, where 24% of Colombia’s páramo areas are located. The accuracy of the LSTM model in predicting extreme precipitation events, such as those expected in August, with up to 700 mm of precipitation, will be highly beneficial for early-warning systems in flood risk management.
Despite the strengths of the LSTM model, our study reveals limitations in current prediction approaches, particularly given the diverse topography of Boyacá, which includes mountainous areas, valleys, and plains that significantly influence precipitation patterns. The model’s performance could be enhanced by incorporating additional topographic features, as demonstrated in the study by [
11] on the monthly runoff prediction for the Xijiang River. By using a combination of GRU, DWT, and VMD, their research highlights substantial improvements in accuracy by leveraging historical data on runoff, water levels, and precipitation.
Integrating additional topographic variables during training, such as altitude, water levels, and runoff, could improve the spatial resolution of our model and reduce residual errors. This would not only enhance the prediction of extreme precipitation events but also better capture microclimatic variations in a region as diverse as Boyacá.
The comparison with ARIMA and random forest regression models underscores the robustness of the LSTM model in handling time series data with long-term complexities. Although ARIMA models are traditionally preferred for their simplicity and interpretability in forecasting linear time series, their limitations become evident when faced with nonlinear climatic data. Random forest regression offers strong predictive performance with the advantage of feature importance evaluation; however, it struggles with the temporal dependencies that LSTM models manage effectively. This confirms the use of neural networks, as also demonstrated by a study conducted in Zacatecas, Mexico [
12], where a combined modeling approach for predicting the Standardized Precipitation Index (SPI) enhanced the ability to predict SPI values, providing a valuable method for monthly precipitation forecasting. This further validates the efficacy of advanced neural network models in handling the long-term complexities of climatic data. The strength of this method lies in the hierarchical interpolation of time series, enabling the effective capture of temporal patterns across multiple scales.
The application of the LSTM model in this study has broad implications beyond the department of Boyacá. The methodology demonstrated here can be adapted for precipitation prediction in different regions, provided that local geographic and climatic conditions are considered in the model-training process. This adaptability makes the LSTM model a powerful tool for regional climate modeling and water resource management, as it integrates spatiotemporal features. This contrasts with the spatiotemporal feature fusion transformer implemented by [
10], which enhances the prediction of complex precipitation patterns. This reaffirms that the use of spatiotemporal variables can potentially reduce residual errors and improve the accuracy of long-term forecasts.
Future work should explore the potential of combining LSTM models with other advanced machine learning techniques, such as hybrid models, to further improve prediction accuracy and reduce residual errors. Additionally, expanding the model to include dynamic climate variables, such as the sea surface temperature anomalies associated with El Niño and La Niña phenomena, could enhance long-term forecasting capabilities. As climate change continues to impact precipitation patterns globally, these advancements in predictive modeling are essential for proactive adaptation and mitigation strategies.
5. Conclusions
The implementation of the LSTM-NN model, leveraging the sliding windows method, achieved accurate predictions of precipitation patterns in Boyacá for the 16 months spanning September 2023 to December 2024. The results demonstrated the model’s superiority in capturing the subtleties of outlier data and seasonal variations, attributed to its ability to learn from sequential dependencies in time series data. This capability enables precise long-term predictions, crucial for informing water resource management, agricultural planning, and disaster mitigation strategies in Boyacá, Colombia.
The findings also underscore the importance of considering local geographic and climatic conditions during model training, as well as the potential for enhancement through the integration of topographic features and dynamic climatic variables.
Future research should focus on combining models to mitigate residual errors, incorporating altitude and other pertinent variables, and expanding the model to encompass dynamic climate variables. By building upon these results, we can enhance predictive modeling capabilities, enabling proactive adaptation and mitigation strategies to address climate-related challenges in Boyacá and other departments of Colombia.