Significance of Multi-Variable Model Calibration in Hydrological Simulations within Data-Scarce River Basins: A Case Study in the Dry-Zone of Sri Lanka
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Hydro-Meteorological Data Collection and Preprocessing
| Dataset | Resolution | Source |
|---|---|---|
| Rainfall (six stations) | Daily | Meteorological Department, Sri Lanka |
| Temperature (two stations) | Daily | Meteorological Department, Sri Lanka |
| Streamflow (one station) | Daily | Irrigation Department, Sri Lanka |
| SMAP L4 root zone soil moisture | 3 hourly (9 km × 9 km) | National Snow and Ice Data Centre Distributed Active Archive Center (NSIDC DAAC), USA |
| Digital Elevation Model | 30 m × 30 m | Shuttle Radar Topography Mission (SRTM) |
2.3. Hydrological Model Set-Up
2.4. Objective Function for Model Optimisation
2.5. Model Calibration and Optimisation
2.5.1. Single-Variable Calibration
2.5.2. Multi-Variable Calibration
3. Results
3.1. Parameter Sensitivity
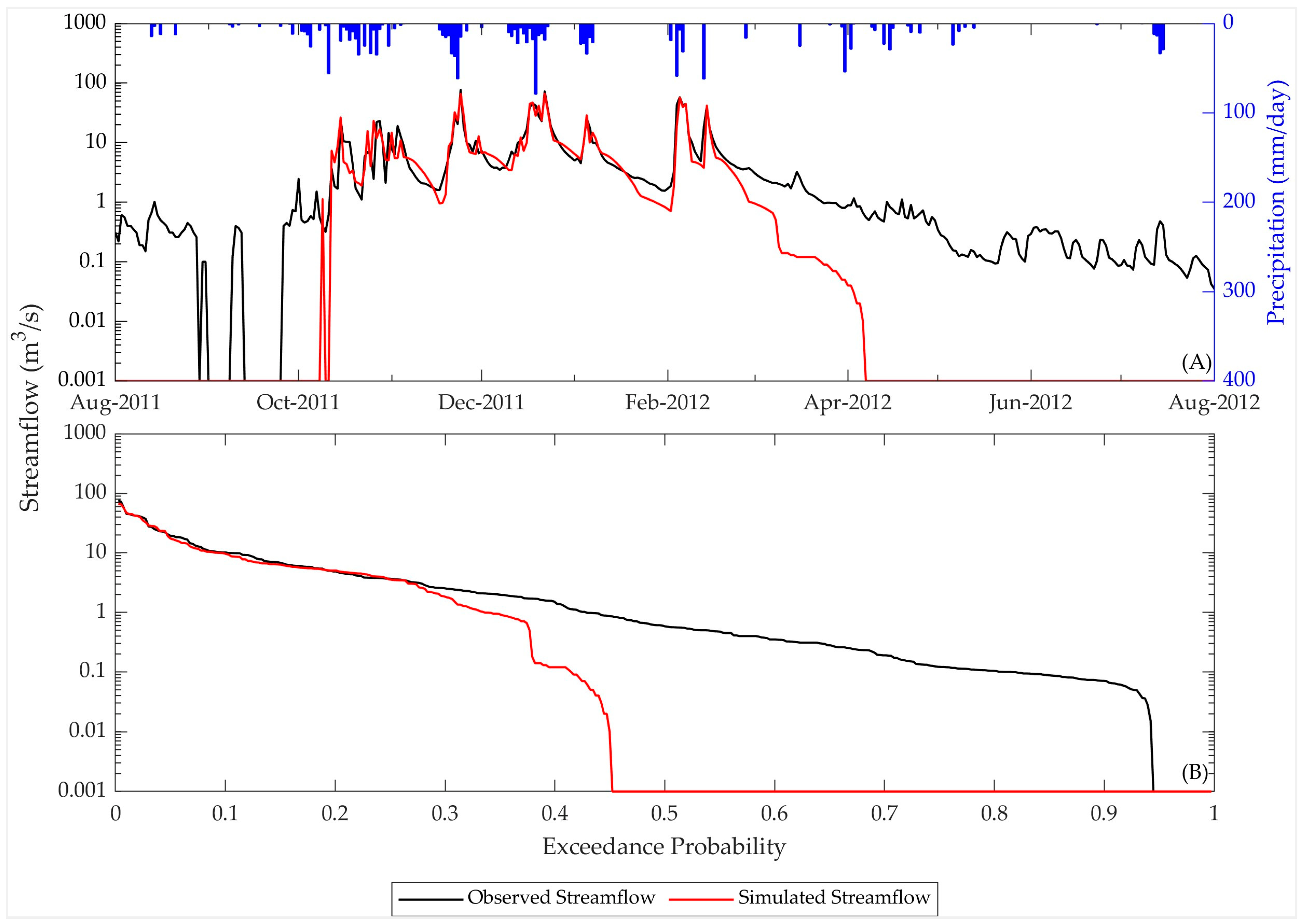
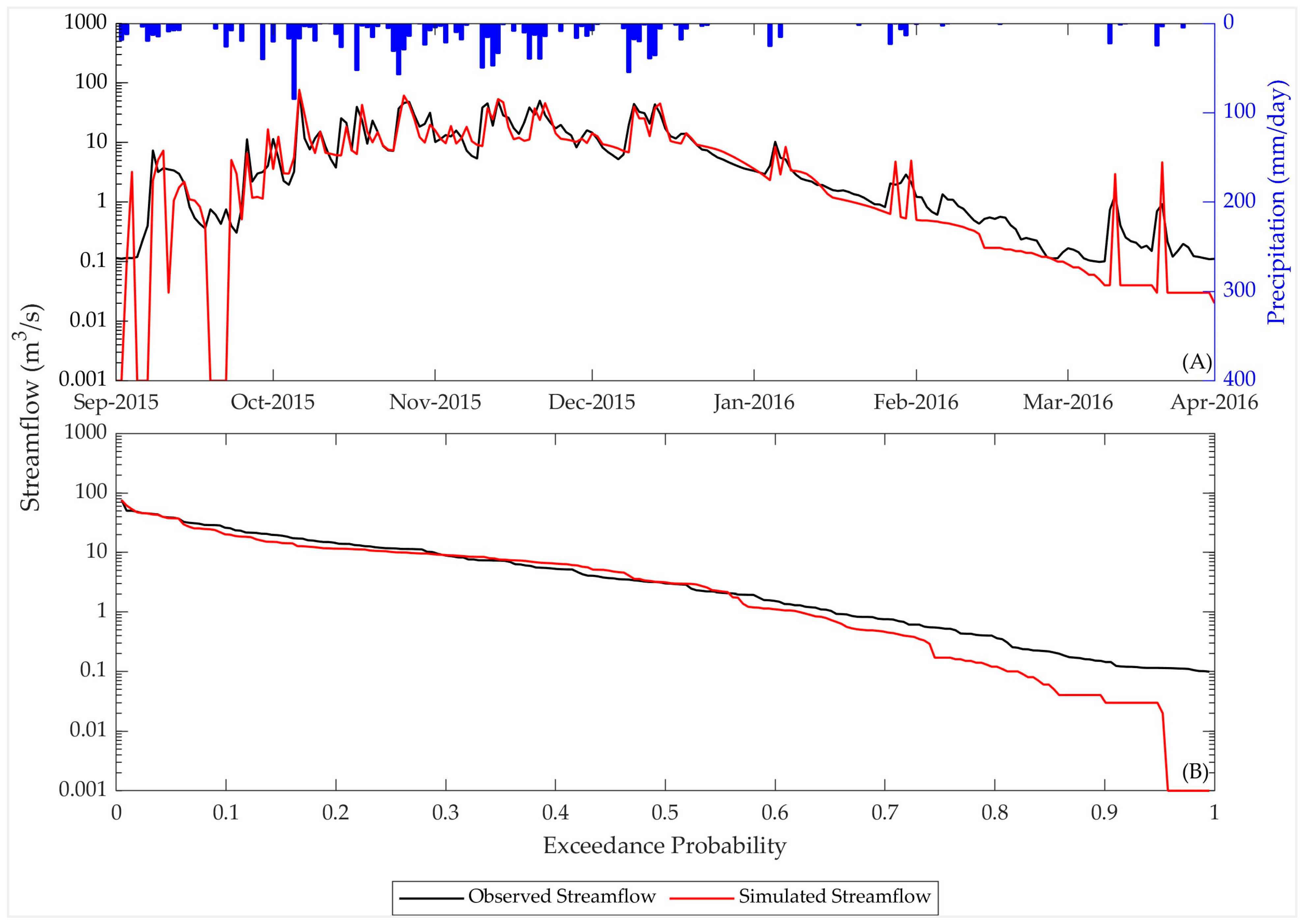
3.2. Model Performances in Single-Variable Calibration
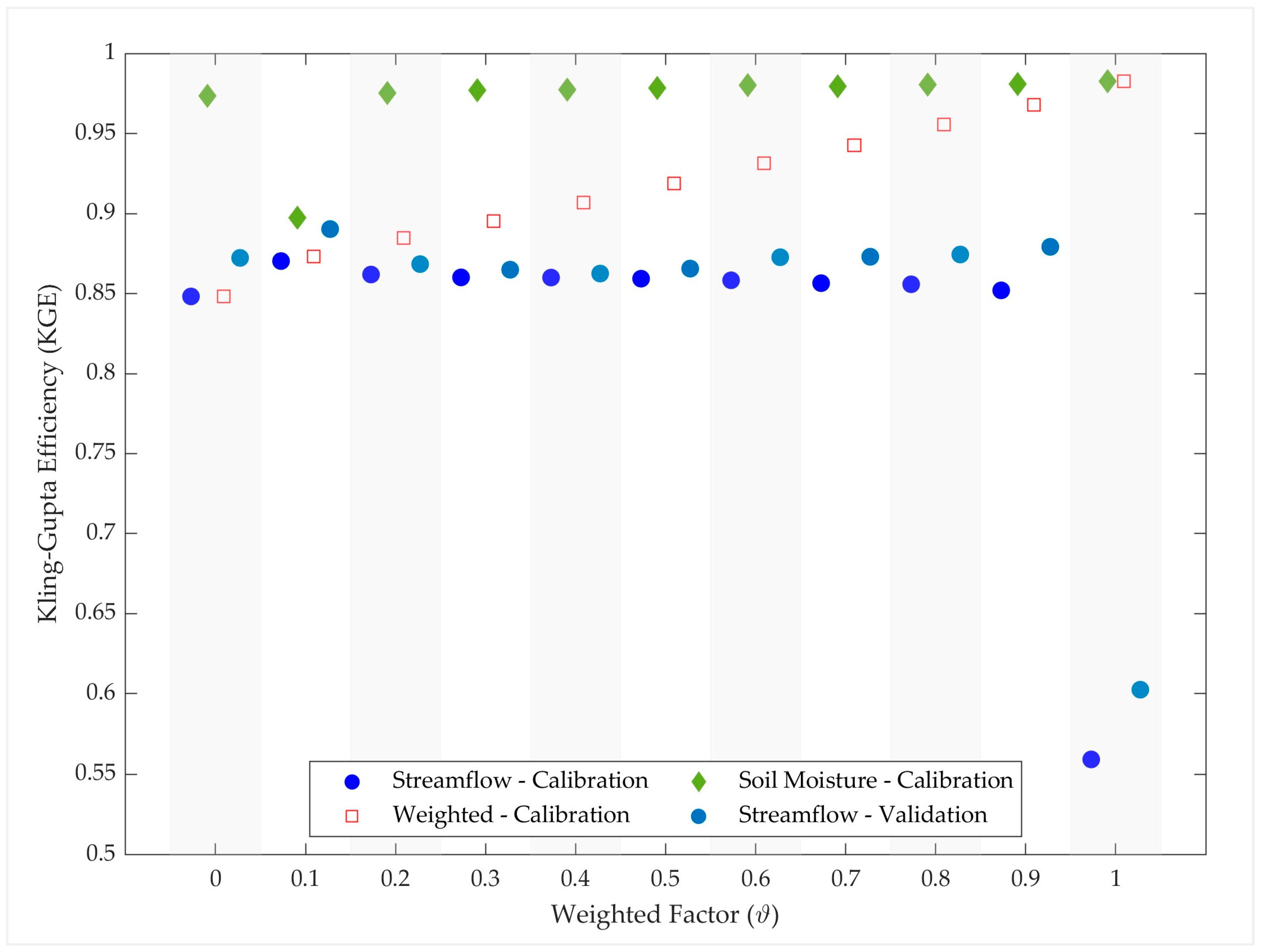
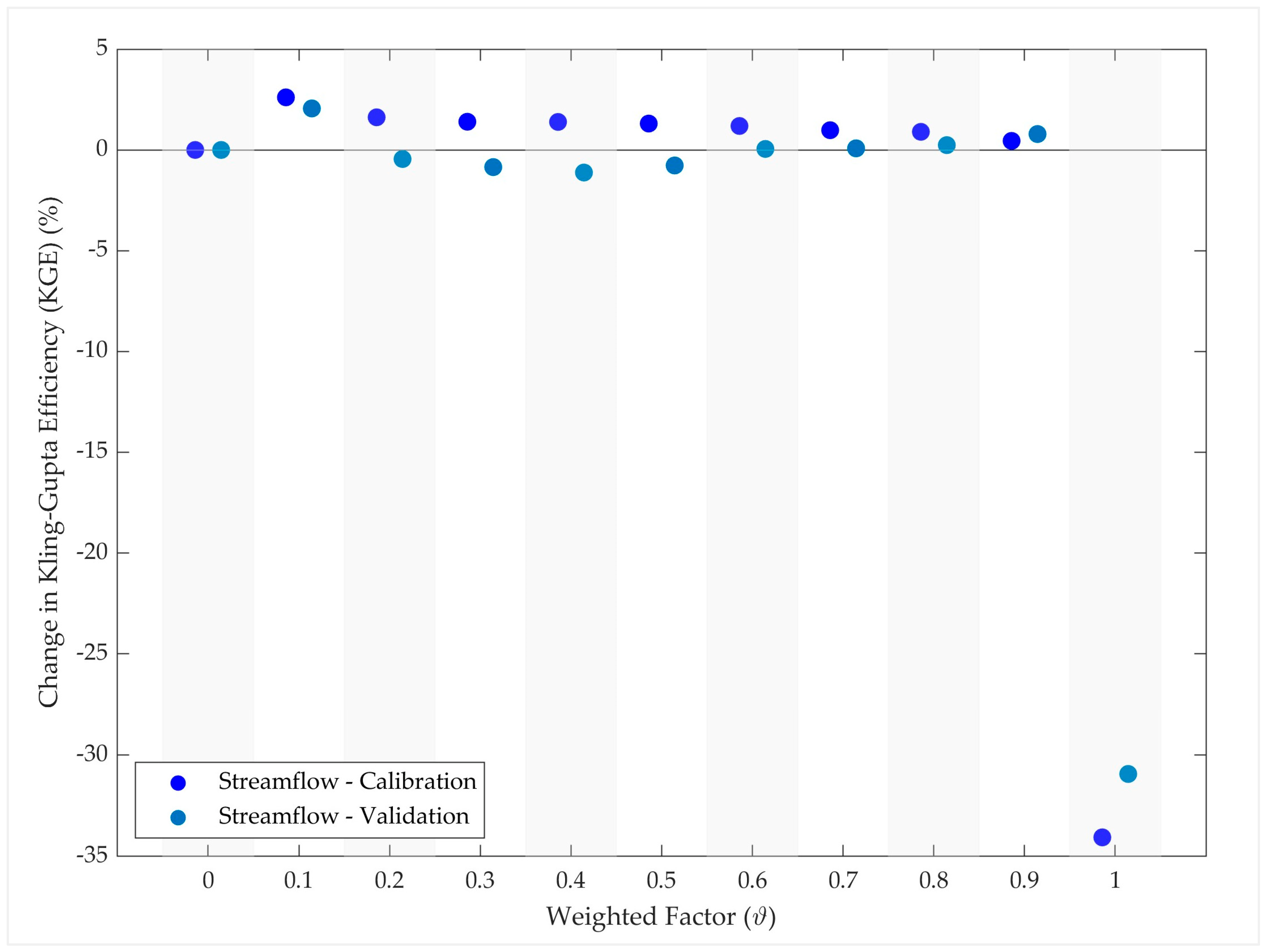
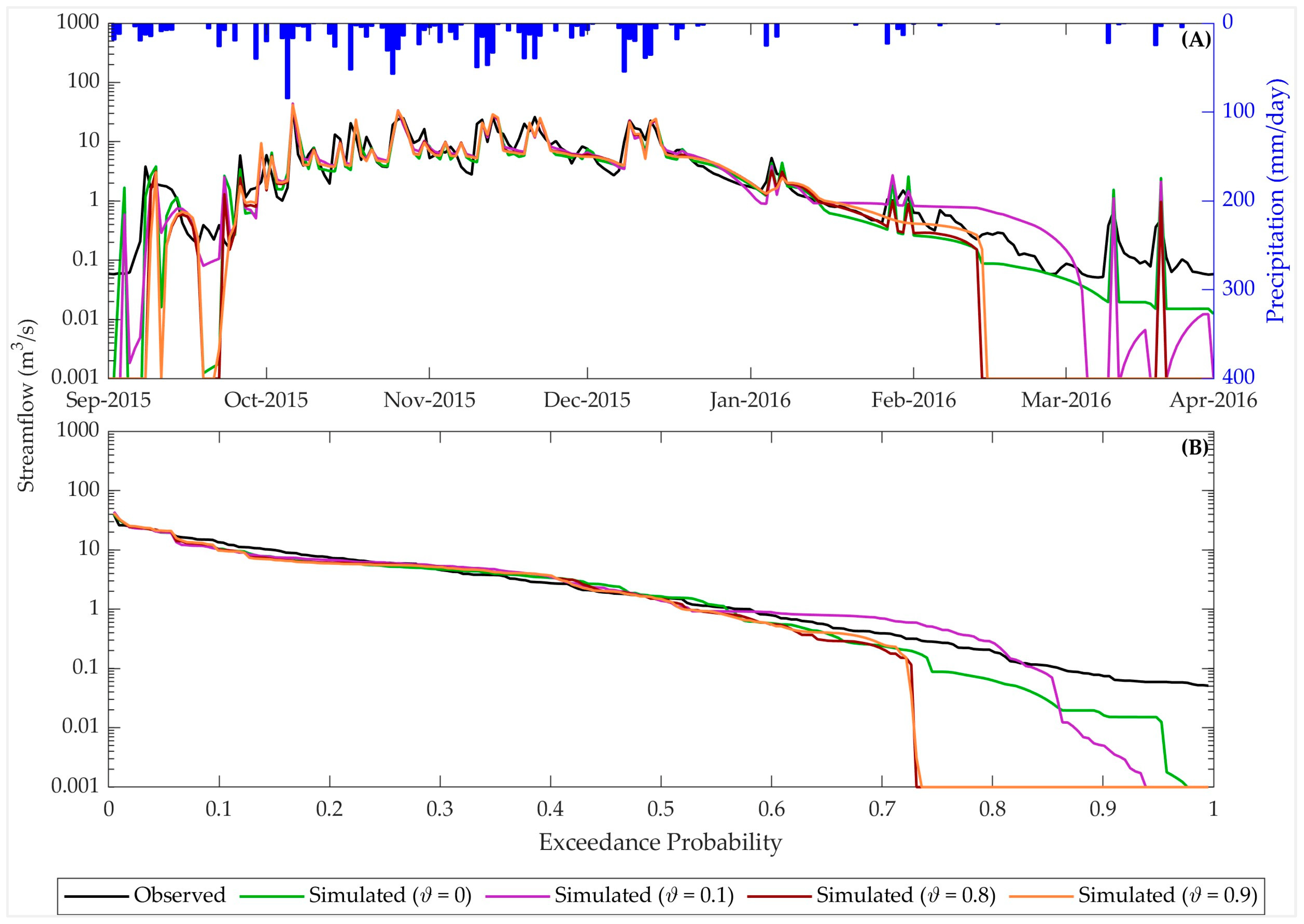
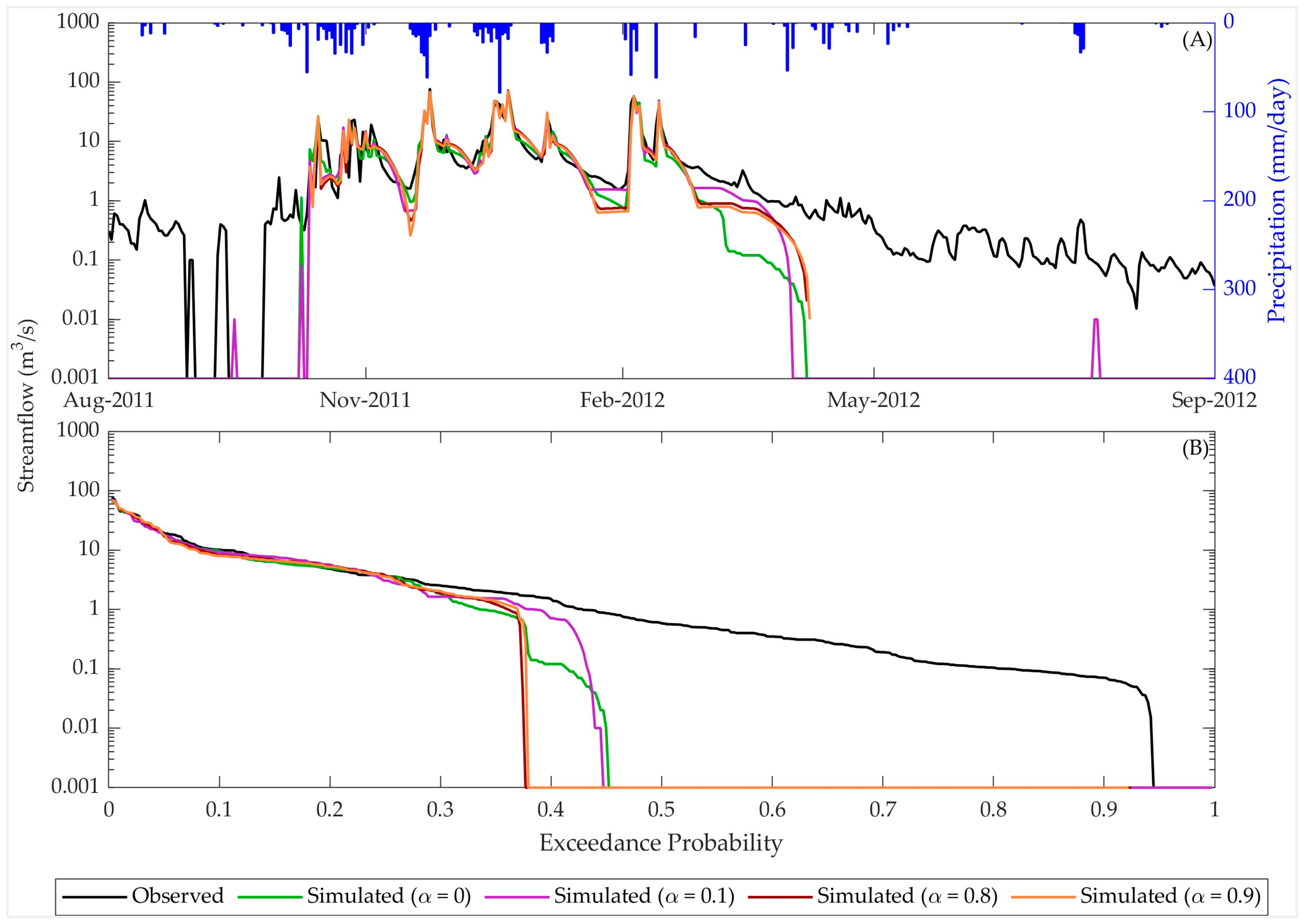
3.3. Model Performances in Multi-Variable Calibration
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
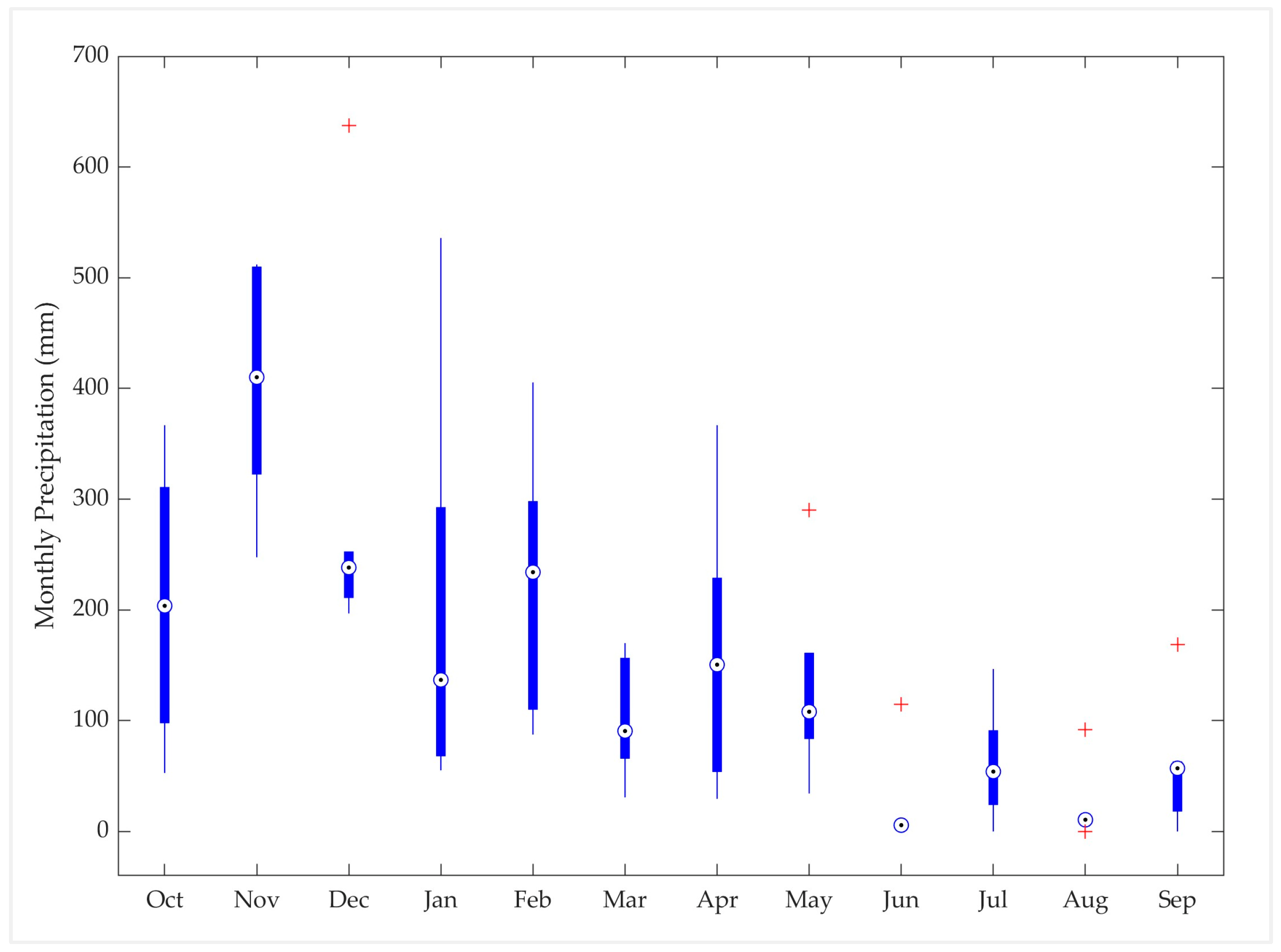
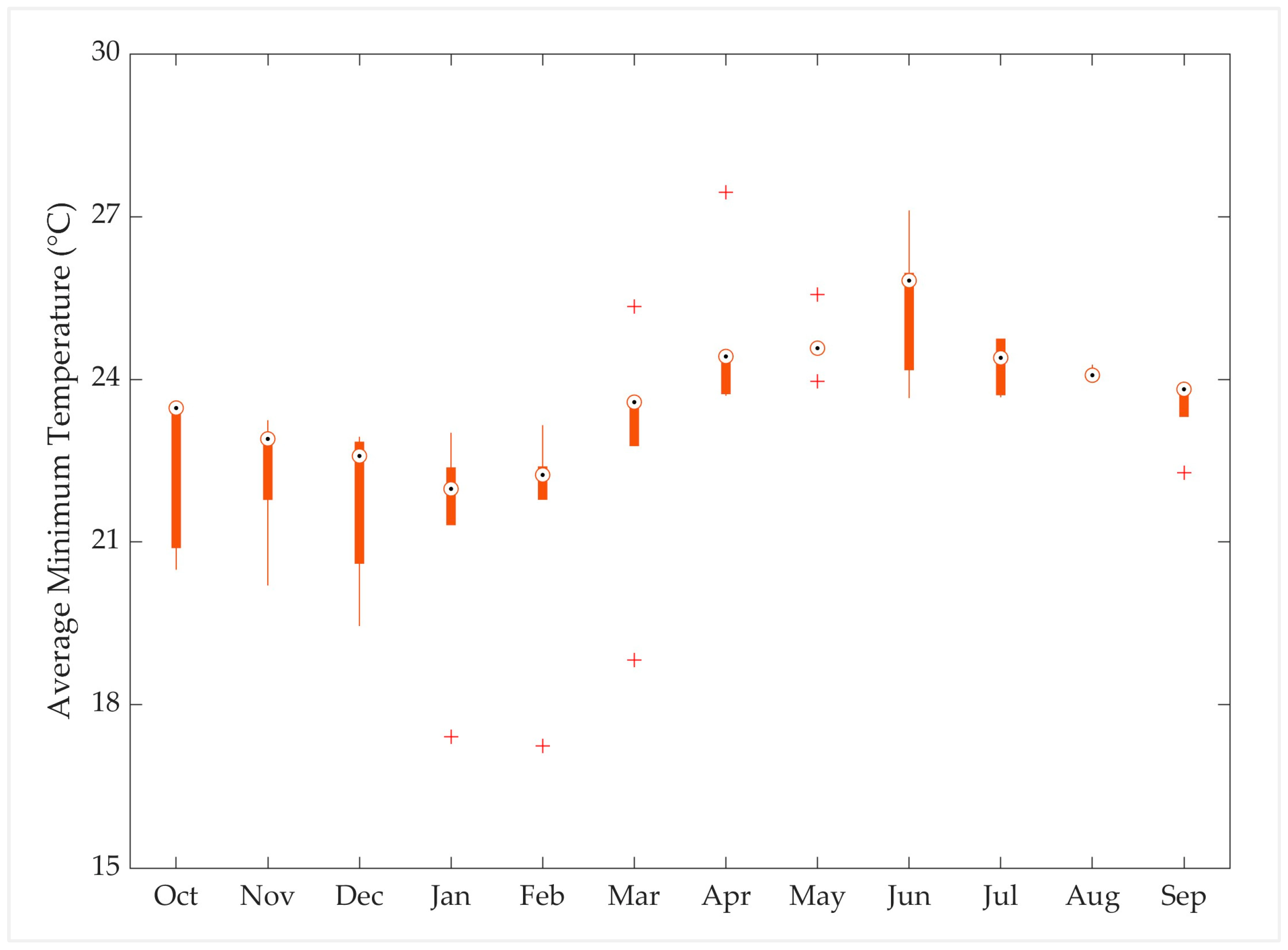
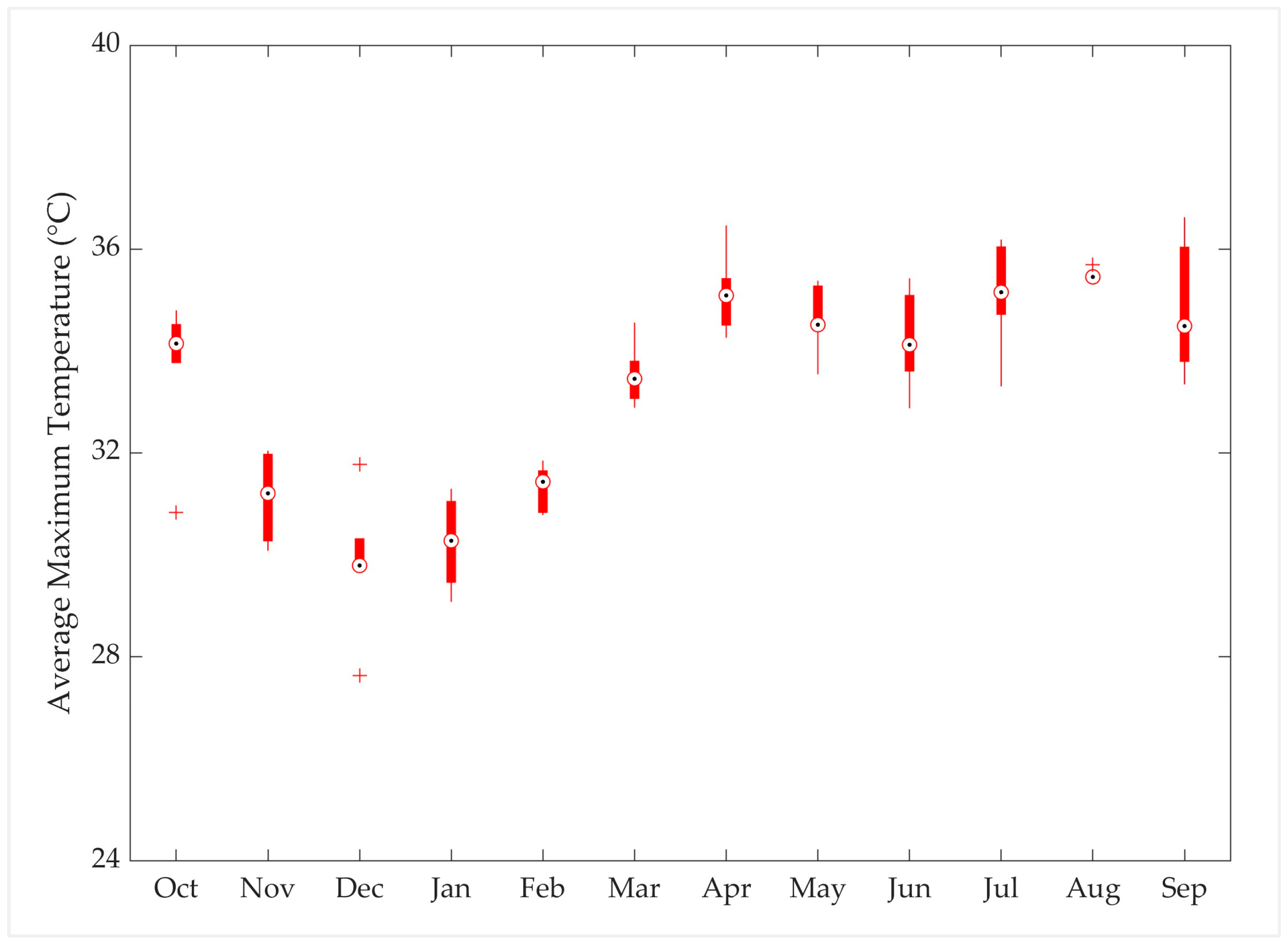
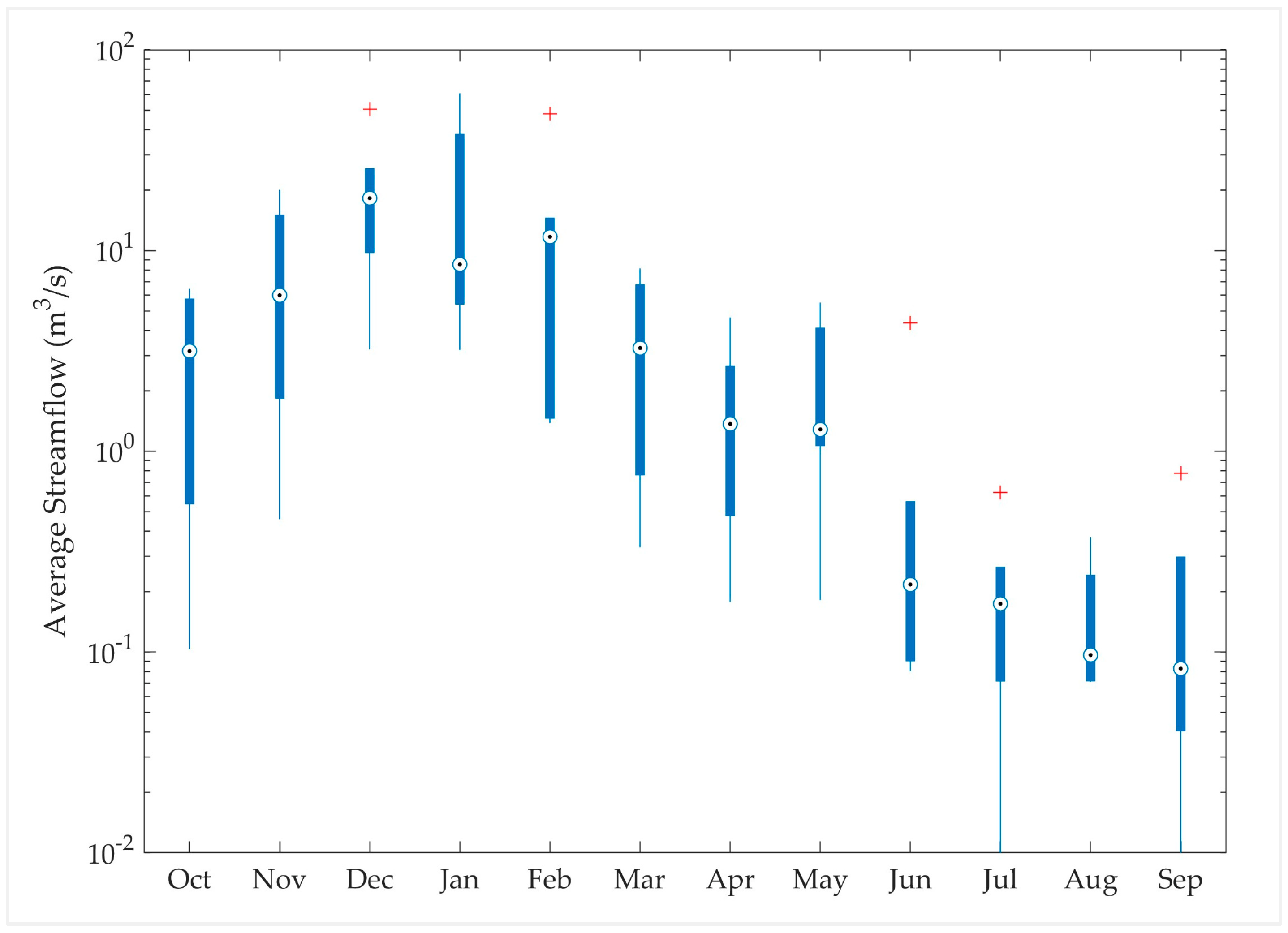
Appendix B
| Month | Observed Pan Evaporation (mm) | Simulated ET0 (mm) | Evaporation Coefficient |
|---|---|---|---|
| October | 117 | 145 | 0.65 |
| November | 87 | 130 | 0.54 |
| December | 72 | 136 | 0.42 |
| January | 79 | 143 | 0.44 |
| February | 90 | 134 | 0.54 |
| March | 126 | 158 | 0.64 |
| April | 124 | 163 | 0.61 |
| May | 133 | 165 | 0.65 |
| June | 153 | 156 | 0.78 |
| July | 165 | 162 | 0.82 |
| August | 161 | 153 | 0.84 |
| September | 145 | 145 | 0.8 |
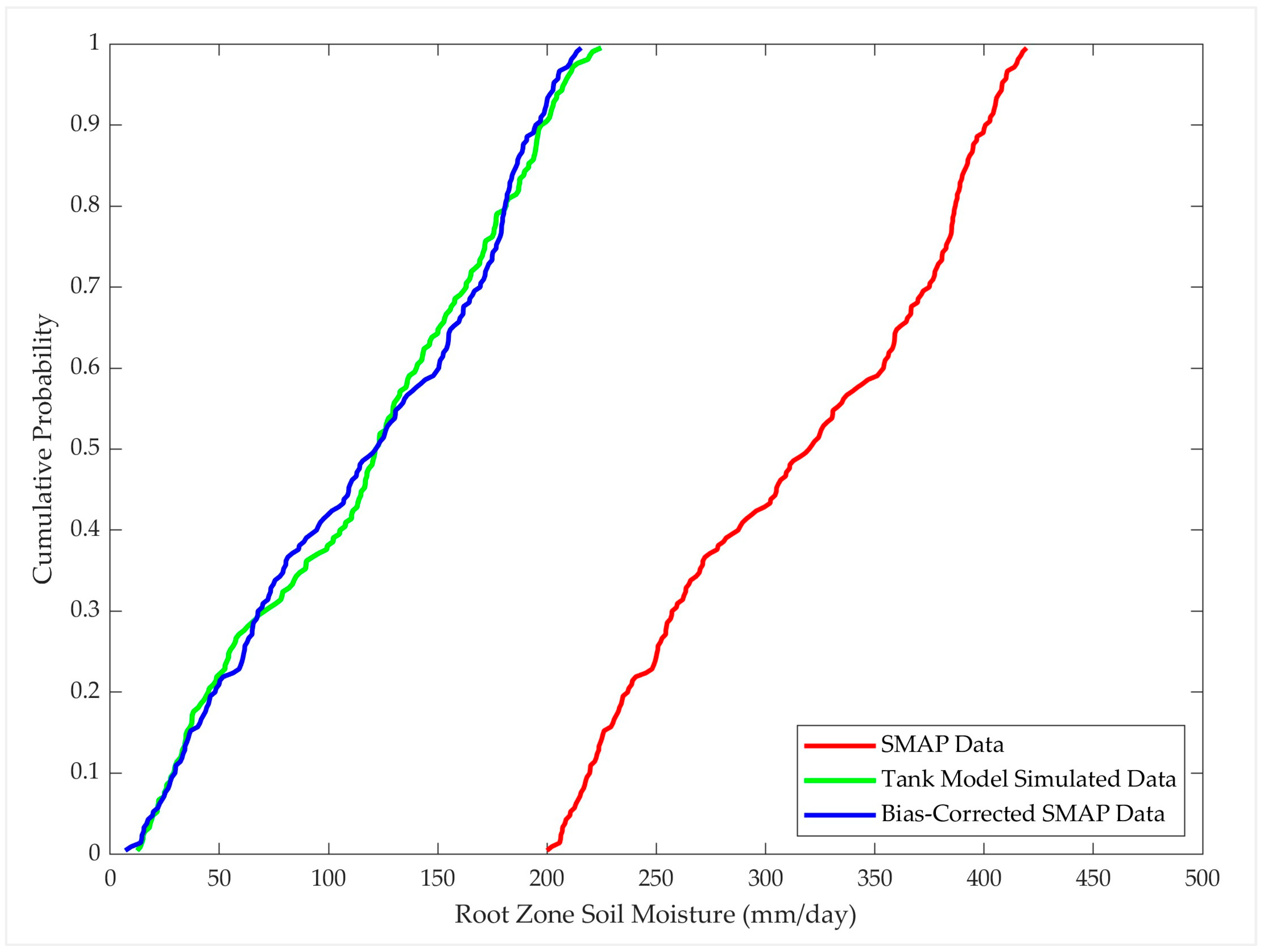
Appendix C
| Weighted Factor (ϑ) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| 0.85 | 0.87 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.85 | 0.56 | |
| 0.97 | 0.90 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | |
| 0.85 | 0.87 | 0.88 | 0.90 | 0.91 | 0.92 | 0.93 | 0.94 | 0.96 | 0.97 | 0.98 | |
| 0.25 | 0.37 | 0.33 | 0.34 | 0.35 | 0.31 | 0.30 | 0.31 | 0.29 | 0.26 | 0.14 | |
| 0.34 | 0.39 | 0.45 | 0.42 | 0.41 | 0.40 | 0.43 | 0.41 | 0.46 | 0.53 | 0.01 | |
| 0.19 | 0.21 | 0.13 | 0.16 | 0.18 | 0.16 | 0.13 | 0.16 | 0.08 | 0.00 | 1.00 | |
| 14.99 | 16.62 | 21.74 | 19.13 | 18.34 | 19.31 | 19.95 | 18.98 | 20.02 | 23.92 | 15.16 | |
| 38.77 | 39.04 | 41.88 | 39.18 | 39.24 | 38.96 | 40.13 | 38.75 | 38.72 | 36.93 | 38.74 | |
| 0.02 | 0.03 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | |
| 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.04 | 0.06 | 0.05 | 0.05 | 0.06 | 0.03 | |
| 30.56 | 31.38 | 37.62 | 33.02 | 33.16 | 33.11 | 37.70 | 33.25 | 35.48 | 34.68 | 30.64 | |
| 0.02 | 0.10 | 0.05 | 0.07 | 0.07 | 0.06 | 0.01 | 0.02 | 0.02 | 0.01 | 0.02 | |
| 0.04 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.06 | 0.07 | 0.06 | 0.05 | 0.09 | |
| 10.59 | 11.14 | 15.65 | 12.51 | 12.40 | 12.39 | 15.26 | 12.36 | 13.54 | 12.98 | 10.64 | |
| 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| * | 0.87 | 0.89 | 0.87 | 0.86 | 0.86 | 0.87 | 0.87 | 0.87 | 0.87 | 0.88 | 0.60 |
References
- Hishinuma, S.; Takeuchi, K.; Magome, J. Challenges of Hydrological Analysis for Water Resource Development in Semi-Arid Mountainous Regions: Case Study in Iran. Hydrol. Sci. J. 2014, 59, 1718–1737. [Google Scholar] [CrossRef]
- IDMP. Drought and Water Scarcity; WMO No. 1284; Global Water Partnership: Stockholm, Sweden; World Meteorological Organization: Geneva, Switzerland, 2022. [Google Scholar]
- Khaki, M. Land Surface Model Calibration Using Satellite Remote Sensing Data. Sensors 2023, 23, 1848. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Grimaldi, S.; Pauwels, V.R.N.; Walker, J.P. Hydrologic Model Calibration Using Remotely Sensed Soil Moisture and Discharge Measurements: The Impact on Predictions at Gauged and Ungauged Locations. J. Hydrol. 2018, 557, 897–909. [Google Scholar] [CrossRef]
- Westerberg, I.K.; Sikorska-Senoner, A.E.; Viviroli, D.; Vis, M.; Seibert, J. Hydrological Model Calibration with Uncertain Discharge Data. Hydrol. Sci. J. 2022, 67, 2441–2456. [Google Scholar] [CrossRef]
- Rajat, A.P. Calibration of Hydrological Models Considering Process Interdependence: A Case Study of SWAT Model. Environ. Model. Softw. 2021, 144, 105131. [Google Scholar] [CrossRef]
- Fenicia, F.; Savenije, H.H.G.; Matgen, P.; Pfister, L. A Comparison of Alternative Multi-objective Calibration Strategies for Hydrological Modeling. Water Resour. Res. 2007, 43, WR005098. [Google Scholar] [CrossRef]
- Sirisena, T.A.J.G.; Maskey, S.; Ranasinghe, R. Hydrological Model Calibration with Streamflow and Remote Sensing Based Evapotranspiration Data in a Data Poor Basin. Remote Sens. 2020, 12, 3768. [Google Scholar] [CrossRef]
- Döll, P.; Hasan, H.M.M.; Schulze, K.; Gerdener, H.; Börger, L.; Shadkam, S.; Ackermann, S.; Hosseini-Moghari, S.-M.; Schmied, H.M.; Güntner, A.; et al. Multi-Variable Parameter Estimation for a Global Hydrological Model: Comparison and Evaluation of Three Ensemble-Based Calibration Methods for the Mississippi River Basin. Hydrol. Earth Syst. Sci. Discuss. 2023. in review. [Google Scholar]
- Ahlmer, A.-K.; Cavalli, M.; Hansson, K.; Koutsouris, A.J.; Crema, S.; Kalantari, Z. Soil Moisture Remote-Sensing Applications for Identification of Flood-Prone Areas along Transport Infrastructure. Environ. Earth Sci. 2018, 77, 533. [Google Scholar] [CrossRef]
- Azimi, S.; Dariane, A.B.; Modanesi, S.; Bauer-Marschallinger, B.; Bindlish, R.; Wagner, W.; Massari, C. Assimilation of Sentinel 1 and SMAP—Based Satellite Soil Moisture Retrievals into SWAT Hydrological Model: The Impact of Satellite Revisit Time and Product Spatial Resolution on Flood Simulations in Small Basins. J. Hydrol. 2020, 581, 124367. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A.; Herrero-Jiménez, C.M. Satellite Soil Moisture for Agricultural Drought Monitoring: Assessment of the SMOS Derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Zhu, Q.; Luo, Y.; Xu, Y.-P.; Tian, Y.; Yang, T. Satellite Soil Moisture for Agricultural Drought Monitoring: Assessment of SMAP-Derived Soil Water Deficit Index in Xiang River Basin, China. Remote Sens. 2019, 11, 362. [Google Scholar] [CrossRef]
- Sungmin, O.; Xinyuan, H.; Rene, O. Observational Evidence of Wildfire-Promoting Soil Moisture Anomalies. Sci. Rep. 2020, 10, 11008. [Google Scholar] [CrossRef]
- Chaleplis, K.; Walters, A.; Fang, B.; Lakshmi, V.; Gemitzi, A. A Soil Moisture and Vegetation-Based Susceptibility Mapping Approach to Wildfire Events in Greece. Remote Sens. 2024, 16, 1816. [Google Scholar] [CrossRef]
- Gupta, M.; Srivastava, P.K.; Islam, T. Chapter 14—Integrative Use of Near-Surface Satellite Soil Moisture and Precipitation for Estimation of Improved Irrigation Scheduling Parameters. In Satellite Soil Moisture Retrieval; Srivastava, P.K., Petropoulos, G.P., Kerr, Y.H., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 271–288. ISBN 978-0-12-803388-3. [Google Scholar]
- Fontanet, M.; Fernàndez-Garcia, D.; Ferrer, F. The Value of Satellite Remote Sensing Soil Moisture Data and the DISPATCH in Irrigation Fields. Hydrol. Earth Syst. Sci. 2018, 22, 5889–5900. [Google Scholar] [CrossRef]
- Sakai, T.; Iizumi, T.; Okada, M.; Nishimori, M.; Grünwald, T.; Prueger, J.; Cescatti, A.; Korres, W.; Schmidt, M.; Carrara, A.; et al. Varying Applicability of Four Different Satellite-Derived Soil Moisture Products to Global Gridded Crop Model Evaluation. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 51–60. [Google Scholar] [CrossRef]
- White, J.; Berg, A.A.; Champagne, C.; Zhang, Y.; Chipanshi, A.; Daneshfar, B. Improving Crop Yield Forecasts with Satellite-Based Soil Moisture Estimates: An Example for Township Level Canola Yield Forecasts over the Canadian Prairies. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102092. [Google Scholar] [CrossRef]
- Srivastava, P.K. Satellite Soil Moisture: Review of Theory and Applications in Water Resources. Water Resour. Manag. 2017, 31, 3161–3176. [Google Scholar] [CrossRef]
- Xiong, L.; Zeng, L. Impacts of Introducing Remote Sensing Soil Moisture in Calibrating a Distributed Hydrological Model for Streamflow Simulation. Water 2019, 11, 666. [Google Scholar] [CrossRef]
- Reichle, R.G.; De Lannoy, R.D.; Koster, W.T.; Crow, J.S.; Liu, Q.; Bechtold, M. SMAP L4 Global 9 Km EASE-Grid Surface and Root Zone Soil Moisture Land Model Constants, Version 7. NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2022; Available online: https://nsidc.org/data/spl4smlm/versions/7 (accessed on 30 January 2024).
- European Space Agency SMOS L2 SM V700, Version 700. Available online: https://earth.esa.int/eogateway/catalog/smos-science-products (accessed on 30 January 2024).
- Loizu, J.; Massari, C.; Álvarez-Mozos, J.; Tarpanelli, A.; Brocca, L.; Casalí, J. On the Assimilation Set-up of ASCAT Soil Moisture Data for Improving Streamflow Catchment Simulation. Adv. Water Resour. 2018, 111, 86–104. [Google Scholar] [CrossRef]
- DHI MIKE SHE. User Guide and Reference Manual; DHI MIKE SHE: Hørsholm, Denmark, 2024. [Google Scholar]
- Beven, K.; Freer, J. A Dynamic TOPMODEL. Hydrol. Process 2001, 15, 1993–2011. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil & Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Scharffenberg, B.; Bartles, M.; Brauer, M.; Fleming, M.; Karlovitas, G. Hydrological Modeling System HEC-HMS, User’s Manual; Hydrologic Engineering Center: Davis, CA, USA, 2018. [Google Scholar]
- Thomas, H.A., Jr.; Harvard Water Resources Group. Improved Methods for National Water Assessment, Water Resources Contract: WR15249270; Harvard Water Resources Group: Cambridge, MA, USA, 1981. [Google Scholar]
- Bergström, S. The HBV Model: Its Structure and Applications; SMHI: Norrköping, Sweden, 1992. [Google Scholar]
- Lee, J.W.; Chegal, S.D.; Lee, S.O. A Review of Tank Model and Its Applicability to Various Korean Catchment Conditions. Water 2020, 12, 3588. [Google Scholar] [CrossRef]
- Sugawara, M. On the Analysis of Runoff Structure of Several Japanese Rivers. Jpn. J. Geophys. 1961, 2, 45411395. [Google Scholar]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments; University of Lund: Lund, Sweden, 1976. [Google Scholar]
- Okiria, E.; Okazawa, H.; Noda, K.; Kobayashi, Y.; Suzuki, S.; Yamazaki, Y. A Comparative Evaluation of Lumped and Semi-Distributed Conceptual Hydrological Models: Does Model Complexity Enhance Hydrograph Prediction? Hydrology 2022, 9, 89. [Google Scholar] [CrossRef]
- Abeysekera, A.B.; Punyawardena, B.V.R.; Premalal, K.H.M.S. Recent Trends of Extreme Positive Rainfall Anomalies in the Dry Zone of Sri Lanka. Trop. Agric. 2015, 163, 1–23. [Google Scholar]
- Punyawardena, B.V.R. Climate of the Dry Zone of Sri Lanka. Soil Sci. Soc. Sri Lanka Spec. Pub. 2010, 7, 9–26. [Google Scholar]
- Li, K.; Liu, Y.; Li, Z.; Yang, Y.; Feng, L.; Khokiattiwong, S.; Yu, W.; Liu, S. Impacts of ENSO on the Bay of Bengal Summer Monsoon Onset via Modulating the Intraseasonal Oscillation. Geophys. Res. Lett. 2018, 45, 5220–5228. [Google Scholar] [CrossRef]
- Zubair, L.; Siriwardhana, M.; Chandimala, J.; Yahiya, Z. Predictability of Sri Lankan Rainfall Based on ENSO. Int. J. Climatol. 2008, 28, 91–101. [Google Scholar] [CrossRef]
- Zubair, L. El Niño–Southern Oscillation Influences on Rice Production in Sri Lanka. Int. J. Climatol. 2002, 22, 249–260. [Google Scholar] [CrossRef]
- Prasanna, R.P.I.R. Economic Costs of Drought and Farmers’ Adaptation Strategies: Evidence from Sri Lanka. Sri Lanka J. Econ. Res. 2018, 5, 61–79. [Google Scholar] [CrossRef]
- Dissanayaka, K.D.C.R.; Rajapakse, R.L.H.L. Long-Term Precipitation Trends and Climate Extremes in the Kelani River Basin, Sri Lanka, and Their Impact on Streamflow Variability under Climate Change. Paddy Water Environ. 2019, 17, 281–289. [Google Scholar] [CrossRef]
- Alahacoon, N.; Edirisinghe, M. Spatial Variability of Rainfall Trends in Sri Lanka from 1989 to 2019 as an Indication of Climate Change. ISPRS Int. J. Geoinf. 2021, 10, 84. [Google Scholar] [CrossRef]
- Sirisena, T.A.J.G.; Maskey, S.; Bamunawala, J.; Coppola, E.; Ranasinghe, R. Projected Streamflow and Sediment Supply under Changing Climate to the Coast of the Kalu River Basin in Tropical Sri Lanka over the 21st Century. Water 2021, 13, 3031. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Climate Change 2023: Synthesis Report; Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; pp. 1–34. [Google Scholar]
- Ranasinghe, R.D.U.A.; Dayawansa, N.D.K.; De Silva, R.P. Rainfall and Streamflow Trends in the Upper Maduru Oya Sub-Watershed in Sri Lanka: A Comparative Study Using Different Statistical Methods. Trop. Agric. Res. 2023, 34, 8623. [Google Scholar] [CrossRef]
- Imbulana, K.A.U.S.; Wijesekara, N.T.S.; Neupane, B.R. (Eds.) Sri Lanka National Water Development Report; MAI&MD, UN-WWAP, UNESCO and University of Moratuwa Katubedda: Sri Lanka; Paris, France; New Delhi, India, 2006. [Google Scholar]
- Jayawardane, S.S.B.D.G.; Weerasena, L.A. Crop Diversification in Sri Lanka. In Proceedings of the Crop Diversification in the Asia-Pacific Region; Papademetriou, M., Dent, F., Eds.; FAO Regional Office for Asia and the Pacific: Bangkok, Thailand, 2000. [Google Scholar]
- Irrigation Department. Hydrological Annual of Sri Lanka, 2019/2020; Irrigation Department: Colombo, Sri Lanka, 2021.
- Bennett, D.A. How Can I Deal with Missing Data in My Study? Aust. N. Z. J. Public Health 2001, 25, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Shiri, J.; Sadraddini, A.A.; Nazemi, A.H.; Marti, P.; Fakheri Fard, A.; Kisi, O.; Landeras, G. Independent Testing for Assessing the Calibration of the Hargreaves–Samani Equation: New Heuristic Alternatives for Iran. Comput. Electron. Agric. 2015, 117, 70–80. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Suryoputro, N.; Suhardjono; Soetopo, W.; Suhartanto, E. Calibration of Infiltration Parameters on Hydrological Tank Model Using Runoff Coefficient of Rational Method. AIP Conf. Proc. 2017, 1887, 020056. [Google Scholar] [CrossRef]
- Sugawara, M.; Ozaki, E.; Watanabe, I.; Katsuyama, Y. On a Method of Forecasting the Daily Discharge of the Mae Chao Phraya and Its Tributaries at Several Points by Means of Tank Model; Research Notes of the National Research Center for Disaster Prevention, No. 24; National Research Center for Disaster Prevention: Tokyo, Japan, 1976. [Google Scholar]
- Gunawardhana, L.N.; Kazama, S. A Water Availability and Low-Flow Analysis of the Tagliamento River Discharge in Italy under Changing Climate Conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1033–1045. [Google Scholar] [CrossRef]
- Yokoo, Y.; Kazama, S.; Sawamoto, M.; Nishimura, H. Regionalization of Lumped Water Balance Model Parameters Based on Multiple Regression. J. Hydrol. 2001, 246, 209–222. [Google Scholar] [CrossRef]
- Goodarzi, M.; Jabbarian Amiri, B.; Azarneyvand, H.; Khazaee, M.; Mahdianzadeh, N. Assessing the Performance of a Hydrological Tank Model at Various Spatial Scales. J. Water Manag. Model. 2020, 28, C472. [Google Scholar] [CrossRef]
- Kuok, K.K.; Harun, S.; Shamsuddin, S.M. Tank Model’s Parameters Optimization Using Particle Swarm Optimization (PSO) Technique and Shuffle Complex Evolution (SCE) Technique. In Proceedings of the Curtin University of Technology Science and Engineering International Conference (CUTSE’08), Miri, Malaysia, 28 November 2008. [Google Scholar]
- Basri, H. Development of Rainfall-Runoff Modeling Using a Tank Model: Problems and Challenges in Province of Aceh, Indonesia. Aceh Int. J. Sci. Technol. 2013, 2, 26–37. [Google Scholar] [CrossRef]
- Phuong, H.T.; Tien, N.X.; Chikamori, H.; Okubo, K. A Hydrological Tank Model Assessing Historical Runoff Variation in the Hieu River Basin. Asian J. Water Environ. Pollut. 2018, 15, 75–86. [Google Scholar] [CrossRef]
- Musiake, K.; Wijesekera, N.T.S. Streamflow Modelling of Sri Lankan Catchments (1)-Mahaweli River Catchment at Peradeniya. Seisan Kenkyu 1990, 42, 28–31. [Google Scholar]
- Phien, H.N.; Pradhan, P.S. The Tank Model in Rainfall-Runoff Modelling. Water SA 1983, 9, 93–102. [Google Scholar]
- Kuok, K.K.; Harun, S.; Chiu, P.-C. Investigation Best Number of Tanks for Hydrological Tank Model for Rural Catchment in Humid Region. J. Inst. Eng. Malays. 2011, 72, 1–11. [Google Scholar]
- Sugawara, M. Automatic Calibration of the Tank Model/L’étalonnage Automatique d’un Modèle à Cisterne. Hydrol. Sci. Bull. 1979, 24, 375–388. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koutsoyiannis, D. One Decade of Multi-Objective Calibration Approaches in Hydrological Modelling: A Review. Hydrol. Sci. J. 2010, 55, 58–78. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Jackson, B.; Mcintyre, N.; Wheater, H.S. Catchment Scale Hydrological Modelling: A Review of Model Types, Calibration Approaches and Uncertainty Analysis Methods in the Context of Recent Developments in Technology and Applications. Glob. NEST J. 2013, 13, 193–214. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance Evaluation of Hydrological Models: Statistical Significance for Reducing Subjectivity in Goodness-of-Fit Assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Jackson, E.K.; Roberts, W.; Nelsen, B.; Williams, G.P.; Nelson, E.J.; Ames, D.P. Introductory Overview: Error Metrics for Hydrologic Modelling—A Review of Common Practices and an Open-Source Library to Facilitate Use and Adoption. Environ. Model. Softw. 2019, 119, 32–48. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H. On Typical Range, Sensitivity, and Normalization of Mean Squared Error and Nash-Sutcliffe Efficiency Type Metrics. Water Resour. Res. 2011, 47, WR010962. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and Testing of a Generalized Reduced Gradient Code for Nonlinear Programming. ACM Trans. Math. Softw. 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Barati, R. Application of Excel Solver for Parameter Estimation of the Nonlinear Muskingum Models. KSCE J. Civil Eng. 2013, 17, 1139–1148. [Google Scholar] [CrossRef]
- Housh, M. Optimization of Multi-Quality Water Networks: Can Simple Optimization Heuristics Compete with Nonlinear Solvers? Water 2021, 13, 2209. [Google Scholar] [CrossRef]
- Vishwakarma, D.K.; Kuriqi, A.; Abed, S.A.; Kishore, G.; Al-Ansari, N.; Pandey, K.; Kumar, P.; Kushwaha, N.L.; Jewel, A. Forecasting of Stage-Discharge in a Non-Perennial River Using Machine Learning with Gamma Test. Heliyon 2023, 9, e16290. [Google Scholar] [CrossRef] [PubMed]
- Pfanzagl, J.; Sheynin, O. Studies in the History of Probability and Statistics XLIV A Forerunner of the T-Distribution. Biometrika 1996, 83, 891–898. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Gunasekara, K.; Gunawardhana, L.; Rajapakse, R.L.H.L. The Potential Use of Remotely Sensed Soil Moisture Estimates in Hydrological Modelling. In Proceedings of the 2023 Moratuwa Engineering Research Conference (MERCon), Katubedda, Sri Lanka, 9–11 November 2023; pp. 580–585. [Google Scholar]
- Eini, M.R.; Massari, C.; Piniewski, M. Satellite-Based Soil Moisture Enhances the Reliability of Agro-Hydrological Modeling in Large Transboundary River Basins. Sci. Total Environ. 2023, 873, 162396. [Google Scholar] [CrossRef] [PubMed]
- Chawanda, C.J.; George, C.; Thiery, W.; van Griensven, A.; Tech, J.; Arnold, J.; Srinivasan, R. User-Friendly Workflows for Catchment Modelling: Towards Reproducible SWAT+ Model Studies. Environ. Model. Softw. 2020, 134, 104812. [Google Scholar] [CrossRef]
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.G.; Booij, M.J.; Bhatti, H.A. Multi-Variable Calibration of a Semi-Distributed Hydrological Model Using Streamflow Data and Satellite-Based Evapotranspiration. J. Hydrol. 2013, 505, 276–290. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration, Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
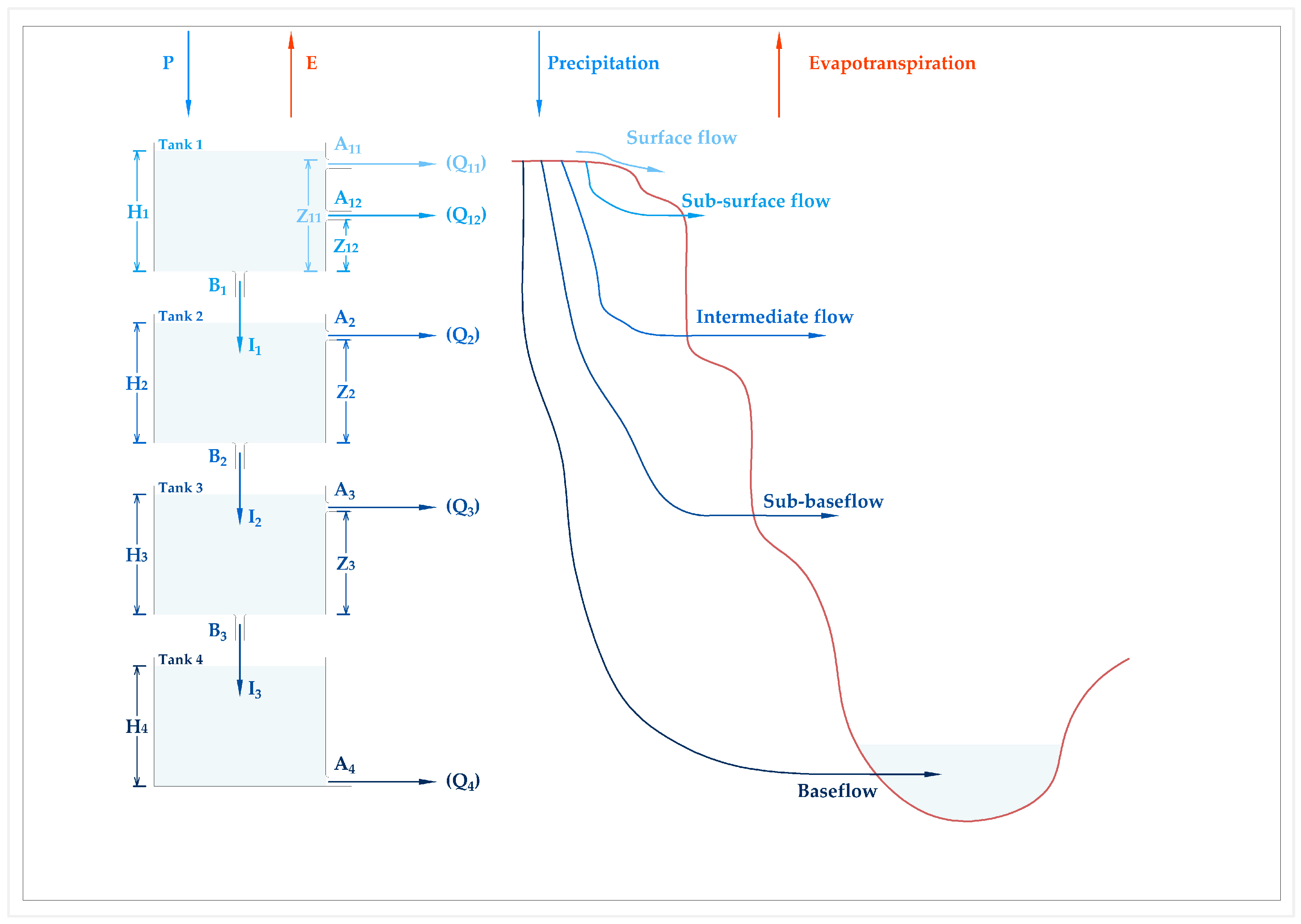
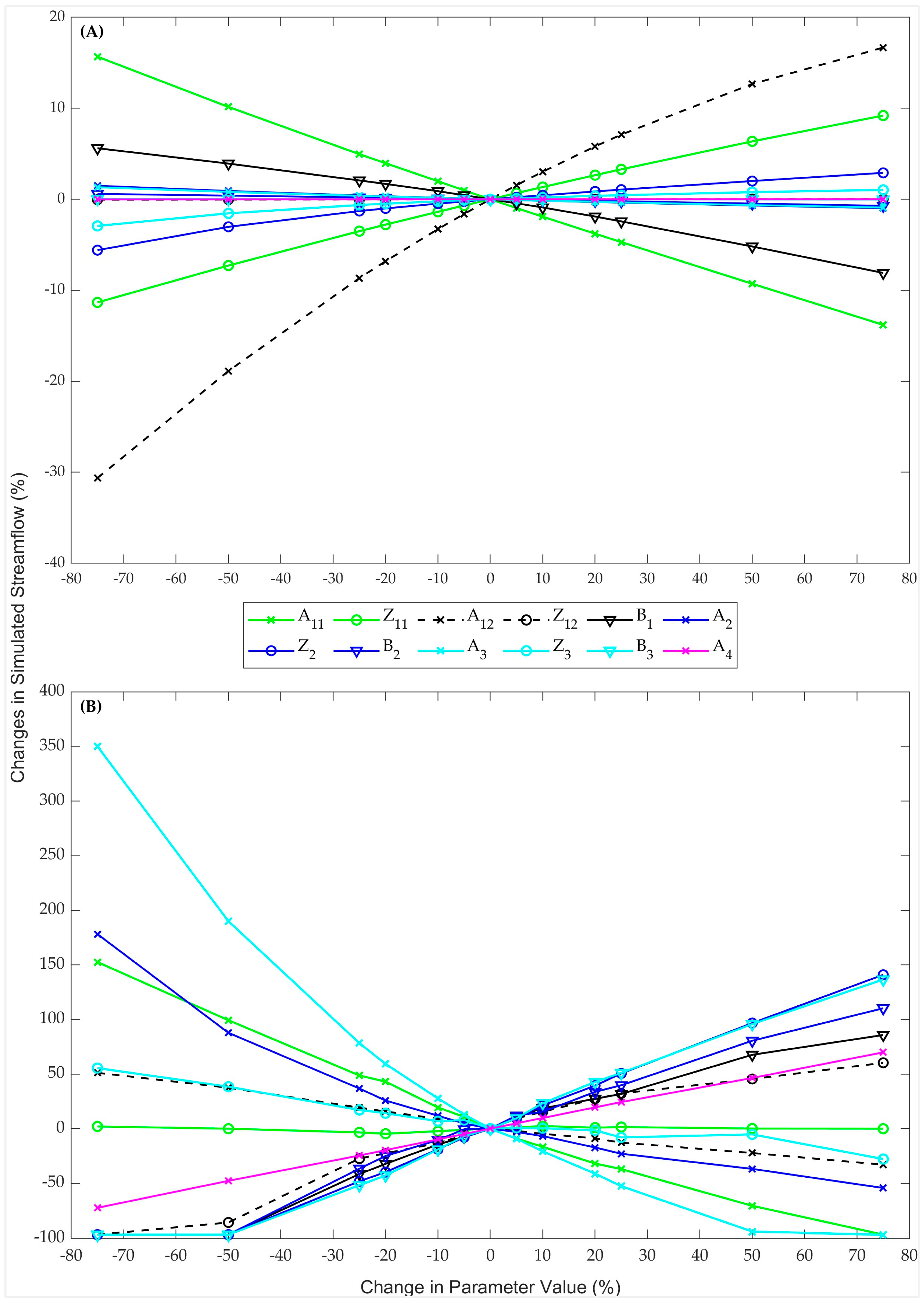

| Tank No. | Model Parameter | Unit | Initial Value (Range) |
|---|---|---|---|
| 1 | B1: infiltration coefficient of the first tank | 1/day | 0.23 (0–1) |
| A11: runoff coefficient to estimate surface flow | 1/day | 0.09 (0–1) | |
| A12: runoff coefficient to estimate sub-surface flow | 1/day | 0.24 (0–1) | |
| Z11: runoff hole depth to estimate surface flow | mm | 2.89 (5–15) | |
| Z12: runoff hole depth to estimate sub-surface flow | mm | 38.77 (25–60) | |
| 2 | B2: infiltration coefficient of the second tank | 1/day | 0.02 (0–1) |
| A2: runoff coefficient to estimate intermediate flow | 1/day | 0.04 (0–1) | |
| Z2: runoff hole depth to estimate intermediate flow | mm | 78.38 (0–30) | |
| 3 | B3: infiltration coefficient of the third tank | 1/day | 0.01 (0–1) |
| A3: runoff coefficient to estimate sub-base flow | 1/day | 0.03 (0–1) | |
| Z3: runoff hole depth to estimate sub-base flow | mm | 1.89 (0–60) | |
| 4 | A4: runoff coefficient to estimate base flow | 1/day | 0.0001 (0–1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pabasara, K.; Gunawardhana, L.; Bamunawala, J.; Sirisena, J.; Rajapakse, L. Significance of Multi-Variable Model Calibration in Hydrological Simulations within Data-Scarce River Basins: A Case Study in the Dry-Zone of Sri Lanka. Hydrology 2024, 11, 116. https://doi.org/10.3390/hydrology11080116
Pabasara K, Gunawardhana L, Bamunawala J, Sirisena J, Rajapakse L. Significance of Multi-Variable Model Calibration in Hydrological Simulations within Data-Scarce River Basins: A Case Study in the Dry-Zone of Sri Lanka. Hydrology. 2024; 11(8):116. https://doi.org/10.3390/hydrology11080116
Chicago/Turabian StylePabasara, Kavini, Luminda Gunawardhana, Janaka Bamunawala, Jeewanthi Sirisena, and Lalith Rajapakse. 2024. "Significance of Multi-Variable Model Calibration in Hydrological Simulations within Data-Scarce River Basins: A Case Study in the Dry-Zone of Sri Lanka" Hydrology 11, no. 8: 116. https://doi.org/10.3390/hydrology11080116
APA StylePabasara, K., Gunawardhana, L., Bamunawala, J., Sirisena, J., & Rajapakse, L. (2024). Significance of Multi-Variable Model Calibration in Hydrological Simulations within Data-Scarce River Basins: A Case Study in the Dry-Zone of Sri Lanka. Hydrology, 11(8), 116. https://doi.org/10.3390/hydrology11080116








