Abstract
Mitigating nonpoint source pollution from stormwater runoff demands effective strategies for treating the first flush depth. Whether through off-stream storage or pass-through treatment devices, designing diversion structures and filtering materials is critical. This study proposes a streamlined procedure for determining first flush design flow rates, employing the modified rational method and rainfall intensity–duration equations applicable to any U.S. location. The dimensionless solution, which is presented as an equation requiring an iterative calculation for the desired flow rates, is complemented by precision graphs. Examples from the semi-arid Southwestern United States illustrate the methodology’s utility.
1. Introduction
The “first flush” is a concept familiar to designers of stormwater treatment systems and refers to the initial surface runoff of a rainstorm [1,2,3]. During this phase, water pollution entering storm drains in areas with high proportions of impervious surfaces is typically more concentrated than that from the rest of the storm. Experimental evidence underscores the substantial pollutant loads associated with initial stormwater wash-off, particularly in catchments dominated by impervious surfaces and rapid runoff conveyance [4]. Regulatory measures often target the treatment of the first flush depth, emphasizing detention or filtration [5,6]. While definitions of a first flush event vary, its significance in pollutant transport is widely acknowledged [2,7,8,9,10,11].
The occurrence and the need to treat the initial cleansing or the first flush effect of contaminants from urban catchments was recognized more than a century ago by Metcalf and Eddy [12]. The urgency to remedy these high concentrations of stormwater pollutants continues worldwide as urbanization intensifies (see, for example [13,14,15]). It is impractical to treat all the runoff from a large storm. However, pass-through filtering and off-stream storage of the first flush from these storms, as well as the entire runoff volume of smaller, more frequent storms, can reduce the long-term nonpoint pollutant loads from stormwater significantly [16].
Treating the first flush depth of runoff, either by storing it until it can be treated and released or passing it through a filtering device that discharges it immediately into the downstream drainage system, is one way of mitigating nonpoint source pollution from stormwater. A diversion structure must be installed that redirects runoff until the desired capture volume fills if off-stream storage is used. The filtering material must be specified if a pass-through treatment device is employed. In either case, a flow rate corresponding to the first flush runoff depth must be determined.
This study presents a straightforward procedure for calculating first flush design flow rates based on the modified rational method and rainfall intensity–duration equations that can be easily determined for any location in the United States [17]. However, the approach can be applied anywhere rainfall data are available to fit an intensity–duration equation like that used in this study. The solution is made dimensionless by grouping parameters and takes the form of an equation that must be solved iteratively for the rainfall duration that produces the desired flow rate. However, graphs that provide solutions of sufficient precision can be created quickly. Examples of such graphs are presented for the semi-arid Southwestern United States, where a single set of rainfall intensity–duration coefficients applies to all the average recurrence intervals.
2. Treating the First Flush of Stormwater Runoff
Experimental studies in catchments where a substantial portion of the land is covered by impervious surfaces and where artificial drainage channels quickly transport runoff to the outlet confirm the comparatively large pollutant loads from the initial wash-off [4,14]. For this reason, regulations for mitigating nonpoint source pollution from small catchments often require treating the first flush depth of the runoff (that is, an initial amount of runoff from a catchment) either by detaining the stormwater until it can be treated and released [5] or by passing it through a filtering device [6]. Saget et al. [7,8] consider the first flush when 80% of the pollutant mass is transported in the initial 30% of the runoff volume, a definition also adopted by Bertrand-Krajewski et al. (1998) [9]. However, other definitions of a first flush runoff event have been proposed [2,10,11].
When first flush runoff is held in a storage area that is not connected directly to a drainage channel (an off-stream storage area), it must be diverted from the contributing stream until the desired volume is captured [18,19]. Where topographic and other conditions permit it, horizontal weirs, whose crests are at about the same elevation as the maximum water level in an adjacent detention area, are often used to redirect first flush runoff from the main channel and allow most of the following flow to bypass the off-stream storage. If such a diversion method is not feasible, controls like the Contech Engineered Solutions StormGate® (Contech 2018) [20] are designed to send initial runoff into storage until the first flush design flow is reached. Most discharge above this set value then avoids being channeled off-line.
Pass-through treatment devices typically house rechargeable, media-filled cartridges that trap particulates and adsorb pollutants such as total suspended solids, hydrocarbons, nutrients, and metals. The number of filter media must be determined based on the first flush design discharge to provide sufficient treatment capacity [21,22]. For example, to size Contech’s StormFilter® [23,24], the design flow rate is divided through the StormFilter’s cartridge treatment flow rate to determine the number of cartridges required. Depending on the targeted pollutants, the cartridge flow rate may vary from 0.125 to 1.0 L per second (2 to 15 gallons per minute). The structure housing the filters can then be sized to accommodate the required number of cartridges.
Ahlfeld and Minihane (2004) [25] developed a probabilistic method to find the first flush design discharge using the rational method to relate flow and rainfall intensity. However, most often, a straightforward approach is taken by summing the accumulated runoff obtained from a calculated hydrograph, in which flow rates increase monotonically until the peak flow rate is reached, to establish the time and the discharge at which the required runoff volume has accumulated [21,26,27]. Following this approach, Froehlich (2009a) [28] developed an uncomplicated graphical procedure for calculating the first flush flow rates from small catchments based on Natural Resources Conservation Service (NRCS) hydrologic methods.
Building on the rationale of Froehlich (2009a) [28], a method is presented for calculating the first flush design flow rate based on runoff hydrographs developed from an extension of the rational formula using a technique known as the modified rational method or MRM [29,30,31,32,33]. Applied with short-duration rainfall intensity–duration equations whose parameters can be obtained without difficulty for most of the United States [34], the MRM provides closed-form expressions for flow rates corresponding to specified first flush runoff volumes. Dimensionless parameters streamline the analysis, thereby providing a comprehensive and practical tool for stormwater management.
3. MRM Hydrology
The rational formula or rational method [35], which is used widely to determine the needed flow capacities of minor drainage structures, gives the peak discharge of stormwater runoff from a catchment as
where C = the runoff coefficient representing the fraction of the incident precipitation that appears as surface runoff, Ac = the contributing catchment area, the average rainfall intensity for a storm of duration td with depth units of rainfall per hour, and ku = a conversion factor that depends on the units of Qp, Ac, and (for example, ku = 0.02778 for Qp = m3/s, Ac = ha, and = cm/h; or ku = 1.008 for Qp = ft3/sec, Ac = ac, and = in/h). Theoretically, C can range from nearly zero to one depending on land use, cover conditions, soil characteristics, watershed slope, and rainfall intensity. However, in practice , where the upper limit represents highly impervious surfaces such as roofs and pavements. When used for a design based on annual exceedance probability, Qp is considered to possess the same average annual exceedance probability as , and C expresses the rate of proportionality between and Qp.
Because average rainfall intensity decreases as rainfall duration increases, Qp, which is given in Equation (1), usually reaches its maximum value when td = tc where tc = the time-of-concentration of the catchment. In an ideal sense, tc is the time needed for water to flow from the most remote point of a catchment to its outlet, where remoteness relates to the time of travel rather than the length of the flow path. However, situations may exist where a portion of a catchment drains to the outlet much faster than the rest in which case the peak discharge may occur when td < tc and only part of the watershed contributes to the outflow. Although such circumstances may not be rare, the limited size of the catchments considered in this analysis precludes the frequent occurrence of this condition.
The original idea behind the rational method is that if rainfall of intensity begins instantaneously and continues indefinitely, the rate of runoff increases until the time of concentration when all of the watershed contributes to the flow at the outlet [36]. When viewed this way, the rational formula is a process-based model of catchment runoff in which C accounts for all rainfall losses (interception, depression storage, and infiltration). However, the relation can also be regarded as a statistical correlation between Qp and the product of the independent variables and Ac where C plays the role of a proportionality coefficient [37,38,39]. No matter the interpretation, the rational formula has been used in the United States for over a century [40] and continues to be applied worldwide for designing minor drainage structures [41].
Perhaps the most favorable aspects of the rational formula are that it is comparatively easy to apply, rainfall intensity–duration relations are usually available, and the information needed to evaluate the catchment time-of-concentration and the runoff coefficient can be obtained without difficulty [42]. Despite several deficiencies and limitations (see American Public Works Association (APWA), 1981; Walesh, 1989; and Westphal, 2001, for thorough assessments) [33,43,44], the rational formula is suitable for calculating the stormwater runoff from small catchments, particularly in urban areas where a large percentage of the land surface is impervious.
The MRM, an American Society of Civil Engineers (ASCE) standard practice for designing urban stormwater systems ([45] ASCE 2006, Section 4.1.8), which also is applied worldwide [46,47], relies on the same assumptions as those of the rational formula and the notion that the runoff coefficient C is constant with respect to time and rainfall intensity during a storm. For td = tc, runoff hydrographs are constructed by considering discharge to increase at a linear rate from the start of rainfall over a period tc and then decrease at a linear rate over a time tc. When td > tc, the entire catchment area A contributes to the flow at the outlet, and discharge remains constant at the peak rate Qp for the period. The discharge then decreases at a linear rate over tc. When td < tc, the flow increases linearly to reach Qp at time td and then remains constant until t = tc. The flow rate then drops at a linear rate over a period td. The total duration of runoff equals tc + td under all circumstances. Finally, based on MRM reasoning, the fraction of the catchment draining to the outlet when td < tc equals the ratio td/tc, which gives
To illustrate the idea, several MRM runoff hydrographs developed for a small catchment for which tc = 30 min are shown in Figure 1, where dimensionless discharge is graphed against dimensionless time for several values of td, the peak discharge from the catchment for td = tc, and t = the time since the start of rainfall. All the runoff hydrographs are equally likely to occur based on MRM reasoning. Dimensionless peak discharge produced by runoff hydrographs from a catchment for several tc values is graphed against in Figure 2. The relations form continuous curves that reach a maximum when (that is, when td = tc). However, the rising portion of the dimensionless hydrograph for is of particular interest to the following analysis.
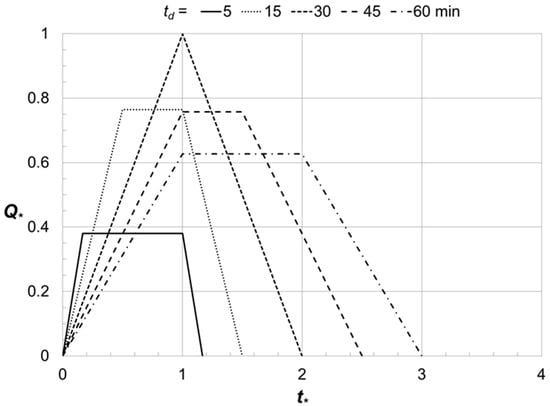
Figure 1.
Runoff hydrographs from a small catchment given through the modified rational method show the effect of storm duration on peak flow rates and hydrograph shape.
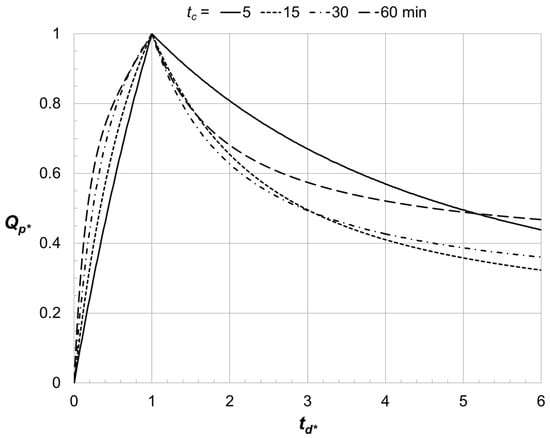
Figure 2.
Normalized peak runoff rate as a function of normalized storm duration for several values of time of concentration.
The maximum size of catchments to which the MRM can be applied is often limited. For example, the Iowa Statewide Urban Design and Specifications Manual (Iowa Center for Transportation Research and Education, 2007, page 2C-9-6) [48] and the Virginia Stormwater Management Handbook (Virginia Department of Conservation and Recreation, 1999, page 4–17) [49] restrict the use of the MRM to drainage areas of 8 ha (20 ac) or less, while the Georgia Stormwater Management Manual (Atlanta Regional Commission, 2001, page 2.1-8) [50] suggests an upper limit of 2 ha (5 ac). Chow et al. [32] recommend the application of the MRM to catchments with areas no larger than 12 ha (30 ac). Based on these customary practices, the writer concludes that the MRM applies best to small catchment draining areas of 12 ha (30 ac) or less.
4. Rainfall Intensity–Duration Relation
Average rainfall intensity for a specified storm duration td is obtained from an equation of the following form:
where ip = the peak rainfall intensity (depth units per hour), io = a constant rainfall intensity (depth units per hour), m = a coefficient that describes the nonuniformity of rainfall intensity during the storm (units of h−1), and td = the rainfall duration (hours). Froehlich (2010) [34] presents an uncomplicated procedure for determining the coefficients in Equation (3) for locations in the United States covered by NOAA Atlas 14, Volumes 1, 2, 3, and 4 [51,52,53,54]. The coefficients were developed from rainfall data for durations ranging from five minutes to one hour. For this reason, the formula should be used for storm durations of no longer than one hour.
For the semi-arid Southwestern United States covered by NOAA Atlas 14, Volume 1 (Arizona, Southeast California, Nevada, New Mexico, and Utah), , , and where , , , and the average 60 min rainfall intensity in rainfall depth per hour [34]. The coefficients apply to all the average recurrence interval (ARI) rainfall in the region.
5. Calculating the First Flush Design Flow Rate
The amount of contaminants in the total annual runoff from a catchment removed by treating the first flush varies depending on the treatment practice’s effectiveness and the geographical region’s rainfall characteristics. Because comparatively small, frequently occurring storms account for most of the rainfall that generates stormwater runoff, the same storms also account for most annual pollutant loadings. For this reason, reducing harmful water quality impacts is possible by managing all runoff from frequently occurring small storms and a portion of the runoff from more significant events [55,56].
The quantity of the initial runoff that needs to be treated, often called the water quality volume, is usually defined as a depth of rainfall excess draining from the catchment, which is denoted here by Df and referred to as the water quality or first flush capture depth [57]. The volume of first flush runoff that needs to be stored or filtered is . Regulations specify Df directly, often 6.35 or 12.7 mm (0.25 or 0.50 in), or they require that Df equals the total runoff from a storm with a specified rainfall depth or ARI.
The flow rate Qf corresponding to a specified first flush runoff volume is obtained in the following analysis from appropriate MRM hydrographs such as those shown in Figure 1. As explained, if a specified first flush volume fills before the hydrograph peak discharge is reached, the volume corresponds to a unique flow rate used to design a control measure. However, suppose the peak discharge occurs before capturing the first flush runoff volume. In that case, the diversion structure or filtering device must be sized based on the maximum peak discharge from the catchment, which occurs when td = tc. One can determine quickly if the specified capture volume fills before the peak discharge is reached by comparing it to the runoff volume under the rising side of the triangular hydrograph produced when td = tc. If then ; otherwise, and does not need to be determined based on MRM runoff hydrographs for which
The capture volume is normalized to simplify the calculation of the first flush design discharge as follows:
If the specified volume does not fill until t > tc and the control devices must be designed for a flow rate equal to . When , the appropriate hydrograph that generates a runoff volume of Vf at its peak (that is, when t = td) must be determined to obtain the corresponding value of , which defines the normalized first flush design flow rate .
For conditions where is equated to the volume under the rising side of the MRM hydrograph as follows:
where tdf = the storm duration producing the first flush capture volume. Dividing through Equation (5) using provides the following expression:
where . With Qp given in Equation (1), Ac by Equation (2), and by Equation (3):
where the runoff coefficient C is considered constant. The expression given in Equation (7) can be solved iteratively for in terms of and the other specified parameters (that is, ). The value of is then used in Equation (6) to recover . The required calculations can be carried out rapidly using commonly available spreadsheet software.
Graphical solutions can also be prepared to provide rapid assessments of and of sufficient precision for designing first flush runoff controls. For example, the graphs shown in Figure 3 and Figure 4 were created using the coefficients given previously for the semi-arid Southwestern United States covered by NOAA Atlas 14, Volume 1 51. The graphs give and for any ARI rainfall within the region.
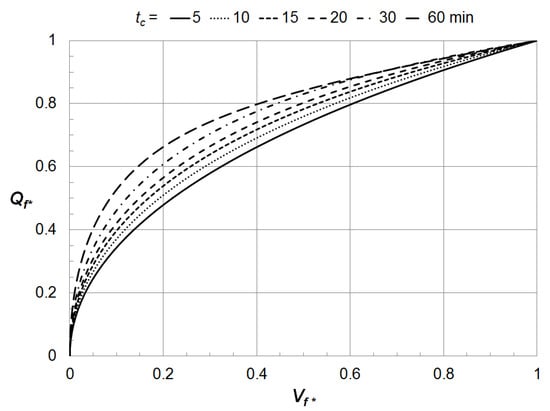
Figure 3.
Normalized first flush design flow rate as a function of normalized first flush capture volume for several values of time of concentration for the semi-arid Southwestern United States covered by NOAA Atlas 14, Volume 1.
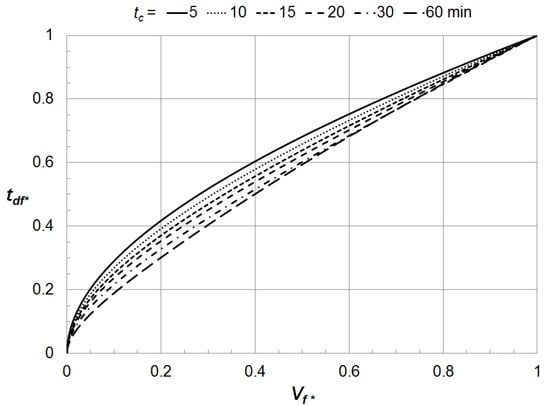
Figure 4.
Normalized first flush storm duration as a function of normalized first flush capture volume for several values of time of concentration for the semi-arid Southwestern United States covered by NOAA Atlas 14, Volume 1.
Graphical relations for presented in Figure 3 are approximated closely through numerical expressions of the form
where a, b, c = coefficients that are functions of tc. Optimal values of a, b, and c for tc ranging from 1 min to 60 min are given in Table 1 and are plotted in Figure 5. Relations for a, b, and c shown in Figure 5 are matched closely through the following expressions:
where tc is in hours and coefficients of determination (r2), which are based on fits to the tabulated data, are given in the right-hand sides of Equations (9)–(11). The expression for given in Equation (8) can be used most effectively in spreadsheet calculations to avoid iterative solutions. Graphical relations for and , like those presented in Figure 3 and Figure 4, and relations similar to Equations (8)–(11) can be developed for other regions of the United States for which rainfall intensity–duration equation coefficients are given by Froehlich (2010) [34].

Table 1.
Coefficients a a, b, and c for values of tc ranging from 1 min to 60 min.
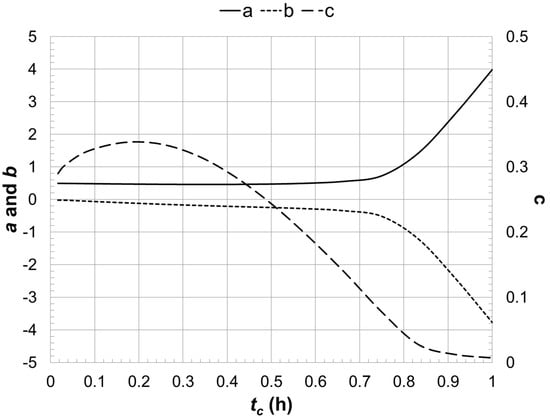
Figure 5.
Coefficients a, b, and c as a function of tc.
6. Application Procedure
Steps taken to apply the procedure developed in this paper to calculate the peak discharge that corresponds to a specified first flush capture volume from a small catchment are as follows:
- Step 1.
- With specified values of , calculate using Equations (1)–(3) and then .
- Step 2.
- Calculate from Equation (4).
- Step 3.
- If ; otherwise, proceed to Step 4.
- Step 4.
- Step 5.
- Calculate and the corresponding rainfall duration .
7. Example Applications
Two examples illustrate applying the procedure described in this paper to calculate first flush flow rates from small catchments in the United States. The first application is to a small multi-family residential development in the country’s southeastern region, and the second example describes the calculation of the first flush design flow for an industrial site located in the semi-arid southwest.
7.1. Example A
A first flush runoff depth Df = 6.35 mm (0.25 in) resulting from a 10-year ARI rainfall on a small multi-family development project in Raleigh, North Carolina, a region of the United States covered by NOAA Atlas 14, Volume 2 [51], is to be treated through a stormwater filtering device before discharge into the primary storm drain system. Parameters that apply to the site are as follows: C = 0.79, A = 2.43 ha, tc = 12 min = 0.200 h = 720 s, (for 10-year ARI rainfall). The rainfall intensity–duration equation parameters only apply to 10-year ARI storms.
The solution for the first flush design discharge is obtained from Equations (6) and (7) as follows:
- Step 1.
- With td = tc = 0.200 h, , , Equation (3) gives.With Ac = A = 2.43 ha, from Equation (1), which gives
- Step 2.
- From Equation (4), .
- Step 3.
- Because , proceed to Step 4.
- Step 4.
- The iterative solution of Equation (7) gives tdf* = 0.733, which gives Qf* = 0.811 from Equation (6).
- Step 5.
- The first flush design discharge and the corresponding rainfall duration
Graphs for Qf* and tdf* for this particular site where tc = 12 min and the first flush design flow rate that is based on 10-year ARI rainfall are shown in Figure 6 and Figure 7, respectively.
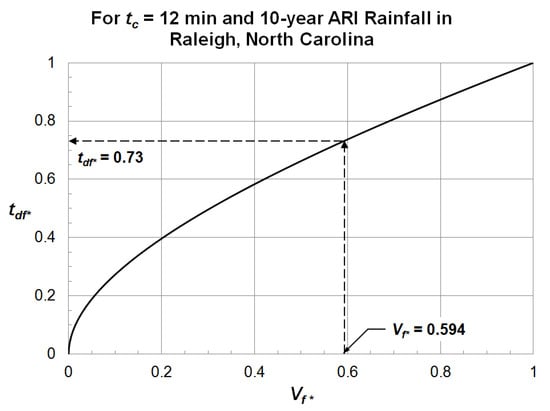
Figure 6.
Graphical solution of tdf* for a catchment with tc = 12 min in Raleigh, North Carolina.
7.2. Example B
The flow rate corresponding to a specified first flush runoff depth of 6.35 mm (0.25 in) from a 10-year ARI storm is found for a small industrial site in Albuquerque, New Mexico, in the semi-arid Southwestern United States. Parameters that apply to the catchment are as follows: C = 0.92, A = 3.24 ha, tc = 15 min = 0.25 h = 900 s, ip* = 4.639, io* = 0.362, m* = 6.676, and . With A in hectares and in mm/h, the unit conversion coefficient is ku = 0.00278. The following solution for the first flush design discharge uses graphs in Figure 3 and Figure 4, which apply to all ARI rainfall in the arid Southwestern United States covered by NOAA Atlas 14, Volume 1 [51].
- Step 1.
- With td = tc = 0.250 h, and , Equation (3) then gives.With Ac = A = 3.24 ha, from Equation (1), which gives
- Step 2.
- From Equation (4), .
- Step 3.
- Because , proceed to Step 4.
- Step 4.
- Step 5.
- The first flush design discharge and the corresponding storm duration
More precise solutions were found by solving Equations (6) and (7) giving tdf = 12.7 min and Qf = 0.540 m3/s.
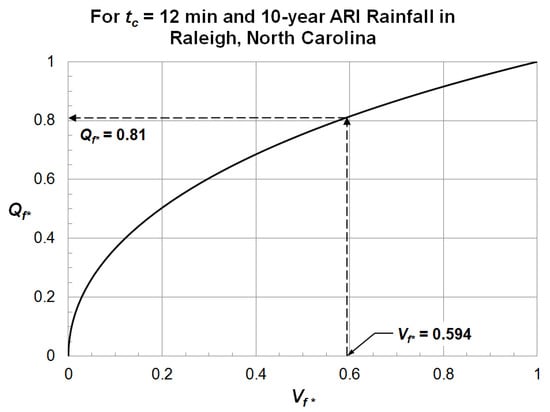
Figure 7.
Graphical solution of Qf* for a catchment with tc = 12 min in Raleigh, North Carolina.
8. Summary and Conclusions
Stormwater first flush runoff held in a storage area not connected directly to a drainage channel (an off-stream storage area) must be diverted from the main channel streamflow until the desired volume is captured. Contaminants, mostly floating debris and suspended solids may also be removed from the first runoff by directing the stormwater through a treatment device. In either case, the structural measure provided for water quality control must be designed or selected to accommodate a specific flow rate corresponding to the first flush runoff volume.
A straightforward procedure for calculating first flush design flow rates is presented based on the MRM and intensity–duration–frequency equations that can be determined readily for locations in the United States covered by NOAA Atlas 14, Volumes 1 through 4. However, the same approach can be used wherever rainfall intensity–duration formulas like Equation (3) can be prepared. The solution uses dimensionless parameters, reducing the number of variables involved in the calculations. The resulting expression for the dimensionless storm duration that provides the desired flow rate requires an iterative solution. Graphs that provide sufficiently precise solutions for the intended purpose can be created to simplify the solution. However, application of the MRM is limited to catchments with drainage areas that are less than 12 ha (30 ac). For this reason, the procedure described in this investigation is restricted to small catchments.
Two examples are presented to show how first flush flow rates can be found where Df = 6.35 mm (that is, where the first 6.35 mm or 0.25 in of runoff is to be treated), one in the Eastern United States (Raleigh, North Carolina) covered by NOAA Atlas 14, Volume 2 [52], and the other one in the arid Southwestern United States (Albuquerque, New Mexico) covered by NOAA Atlas 14, Volume 1 [51]. The method helps us to design first flush treatment facilities for small catchments, which are usually much less than 12 ha in size, where more complicated approaches are unnecessary. These examples illustrate the practical applicability of the method, which can be extended or adapted to different geographic locations, for designing first flush treatment facilities where more complicated approaches are unnecessary.
Funding
This research received no external funding.
Data Availability Statement
No new data were created for this study.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Lee, J.H.; Bang, K.W.; Ketcham, L.H., Jr.; Choe, J.S.C.; Yu, M.J. First flush analysis of urban storm runoff. Sci. Total Environ. 2002, 293, 163–175. [Google Scholar] [CrossRef] [PubMed]
- Bach, P.M.; McCarthy, D.T.; Deletic, A. Redefining the stormwater first flush phenomenon. Water Res. 2010, 44, 2487–2498. [Google Scholar] [CrossRef]
- Perera, T.; McGree, J.; Egodawatta, P.; Jinadas, K.; Goonetilleke, A. Catchment-based estimation of pollutant event mean concentration (EMC) and implications for first flush assessment. J. Environ. Manag. 2021, 279, 111737. [Google Scholar] [CrossRef]
- Barrett, M.E.; Irish, L.B., Jr.; Malina, J.F., Jr.; Charbeneau, R.J. Characterization of highway runoff in Austin, Texas, area. J. Environ. Eng. 1998, 124, 131–137. [Google Scholar] [CrossRef]
- Birch, G.; Matthai, C.; Fazeli, M. Efficiency of a retention/detention basin to remove contaminants from urban stormwater. Urban Water J. 2006, 3, 69–77. [Google Scholar] [CrossRef]
- Lenhart, J.H.; Calvert, P.P. Mass loading and mass load design of stormwater filtration systems. In Proceedings of the World Environmental and Water Resources Congress 2007 Proceedings, Tampa, FL, USA, 15–19 May 2007; American Society of Civil Engineers: Reston, VA, USA, 2007; pp. 243–255. [Google Scholar]
- Saget, A.; Chebbo, G.; Desbordes, M. Urban discharges during wet weather: What volumes have to be treated? Water Sci. Technol. 1995, 32, 225–232. [Google Scholar] [CrossRef]
- Saget, A.; Chebbo, G.; Bertrand-Krajewski, J.L. The first flush in sewer systems. Water Sci. Technol. 1996, 33, 101–108. [Google Scholar] [CrossRef]
- Bertrand-Krajewski, J.; Chebbo, G.; Saget, A. Distribution of pollutant mass vs. volume in stormwater discharges and the first flush phenomenon. Water Resour. 1998, 32, 2341–2356. [Google Scholar] [CrossRef]
- Hager, M.C. Evaluating first-flush runoff. Stormwater 2001, 2, 23–29. [Google Scholar]
- Taebi, A.; Droste, R.L. First flush pollution load of urban stormwater runoff. J. Environ. Eng. Sci. 2004, 3, 301–309. [Google Scholar] [CrossRef]
- Metcalf, L.; Eddy, H.P. American Sewerage Practice—Volume—I—Design of Sewers; McGraw-Hill: New York, NY, USA, 1914. [Google Scholar]
- Mamoon, A.; Jahan, S.; Jahan He, X.; Joergensen, N.E.; Rahma, A. First flush analysis using a rainfall simulator on a micro catchment in an arid climate. Sci. Total Environ. 2019, 693, 133552. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Zhang, Q.; Li, J.; Wang, Y.; Dzakpasu, M.; Wang, X.C. First flush stormwater pollution in urban catchments: A review of its characterization and quantification towards optimization of control measures. J. Environ. Manag. 2023, 340, 117976. [Google Scholar] [CrossRef]
- Mastouri, R.; Pourfallah, H.; Khaledian, M. The first flush analysis of stormwater runoff in a humid climate. J. Environ. Eng. Landsc. Manag. 2023, 31, 82–91. [Google Scholar] [CrossRef]
- Wang, S.; Feng, L.; Min, F. Optimizing first flush diverter for urban stormwater pollution load reduction by most efficiently utilizing first flush phenomena. J. Environ. Manag. 2023, 33, 117563. [Google Scholar] [CrossRef]
- Froehlich, D.C. Graphical calculation of first-flush flow rates for stormwater quality control. J. Irrig. Drain. Eng. 2009, 135, 68–75. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Zhu, J. Design of a diversion system to manage the first flush. J. Am. Water Resour. Assoc. 1989, 25, 517–525. [Google Scholar] [CrossRef]
- Guo, J.C.Y. Design of off-line detention systems. In Stormwater Collection Systems Design Handbook; Mays, L.W., Ed.; McGraw-Hill: New York, NY, USA, 2001; Chapter 8. [Google Scholar]
- Contech. StormGate design guide. In Engineering Guidelines; Contech Engineered Solutions LLC: West Chester, OH, USA, 2018. [Google Scholar]
- Lenhart, J.H. Methods of sizing water quality facilities. Stormwater 2004, 5, 4–7. [Google Scholar]
- Lenhart, J.H. Evaluation of stormwater filtration systems. C.E. News 2007, 1. PDH 1–7. [Google Scholar]
- Contech. StormFilter configuration guide. In Engineering Guidelines RS-0040; Contech Engineered Solutions LLC: West Chester, OH, USA, 2015. [Google Scholar]
- Contech. Sizing methodologies for the stormwater management StormFilter. In Engineering Guidelines RS-0041; Contech Engineered Solutions LLC: West Chester, OH, USA, 2015. [Google Scholar]
- Ahlfeld, D.P.; Minihane, M. Storm flow from first-flush precipitation in stormwater design. J. Irrig. Drain. Eng. 2004, 130, 269–276. [Google Scholar] [CrossRef]
- Adams, T.R. Storm water facility design: Calculating the first flush. Pollut. Eng. 1998, 30, 44–48. [Google Scholar]
- Ogintz, J.B. Sizing stormwater BMPs. Chem. Eng. News 2005, 17, 34–39. [Google Scholar]
- Froehlich, D.C. Graphical Sizing of Small Single-Outlet Detention Basins in the Semi-arid Southwest. J. Irrig. Drain. Eng. 2009, 135, 779–790. [Google Scholar] [CrossRef]
- Baker, W.R. Stormwater detention basin design for small drainage areas. Public Work. 1977, 17, 75–79. [Google Scholar]
- Wanielista, M.P. Stormwater Management-Quantity and Quality; Ann Arbor Science: Ann Arbor, MI, USA, 1978. [Google Scholar]
- Tourbier, J.T.; Westmacott, R. Water Resources Protection Technology; The Urban Land Institute: Washington, DC, USA, 1981. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Walesh, S.G. Urban Surface Water Management; John Wiley: New York, NY, USA, 1989. [Google Scholar]
- Froehlich, D.C. Short-duration rainfall-intensity equations for urban drainage design. J. Irrig. Drain. Eng. 2010, 136, 519–526. [Google Scholar] [CrossRef]
- American Society of Civil Engineers. Design and construction of urban stormwater management systems. In ASCE Manuals and Reports of Engineering Practice No. 77; American Society of Civil Engineers: New York, NY, USA, 1992. [Google Scholar]
- Mulvaney, T.J. On the use of self-registering rain and flood gauges in making observations of the relations of rainfall and flood discharges in a given catchment. In Transactions and Minutes of Proceedings; Institution of Civil Engineers of Ireland: Dublin, Ireland, 1851; Volume 4, Session 1850-1. [Google Scholar]
- Horner, W.W.; Flynt, F.L. Relation between rainfall and runoff from small urban areas. Trans. Am. Soc. Civ. Eng. 1936, 101, 140–206. [Google Scholar]
- Schaake, J.G.; Geyer, J.C.; Knapp, J.W. Experimental examination of the rational method. J. Hydraul. Div. ASCE 1967, 93, 353–370. [Google Scholar] [CrossRef]
- Dooge, J.C.I. Linear theory of hydrologic systems. In Technical Bulletin 1468; Agricultural Research Service, U.S. Department of Agriculture: Washington, DC, USA, 1973. [Google Scholar]
- Kuichling, E. The relation between the rainfall and the discharge of sewers in populous districts. Trans. ASCE 1889, 20, 1–56. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Cordery, I. Flood runoff. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1992; Chapter 9. [Google Scholar]
- Hotchkiss, R.H.; McCallum, B.E. Peak discharge for small agricultural watersheds. J. Hydraul. Eng. 1995, 121, 36–48. [Google Scholar] [CrossRef]
- American Public Works Association. Urban stormwater management. In Special Report No. 49; National Academies Press: Chicago, IL, USA, 1981. [Google Scholar]
- Westphal, J.A. Hydrology for drainage system design and analysis. In Stormwater Collection Systems Design Handbook; Mays, L.W., Ed.; McGraw-Hill: New York, NY, USA, 2001; Chapter 4. [Google Scholar]
- ASCE/EWRI 45-05; Standard guidelines for the design of urban stormwater systems. American Society of Civil Engineers: Reston, VA, USA, 2006.
- Wang, S.; Wang, H. Extending the rational method for assessing and developing sustainable urban drainage systems. Water Res. 2018, 144, 112–125. [Google Scholar] [CrossRef]
- Drumond, P.P.; Moura, P.M.; Coelho, M.M.L.P. Improving the understanding of on-site stormwater detention performances. Urban Water J. 2023, 20, 1271–1289. [Google Scholar] [CrossRef]
- Iowa Center for Transportation Research and Education. Statewide Urban Design and Specifications (SUDAS), Design Manual, Chapter 2, Stormwater; Iowa State University: Ames, Iowa, 2007; 2C-9-6. [Google Scholar]
- Virginia Department of Conservation and Recreation. Virginia Stormwater Management Handbook; Division of Soil and Water Conservation: Richmond, VA, USA, 1981. [Google Scholar]
- Atlanta Regional Commission. Georgia Stormwater Management Manual–Vol. 2: Technical Handbook; Atlanta Regional Commission: Atlanta, GA, USA, 2001. [Google Scholar]
- Bonnin, G.M.; Martin, D.; Lin, B.; Parzybok, T.; Yekta, M.; Riley, D. Precipitation-frequency atlas of the United States, volume 1, version 4: Semi-arid Southwest (Arizona, Southeast California, Nevada, New Mexico, Utah). In NOAA Atlas 14; Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service: Silver Spring, MD, USA, 2006; Volume 1. [Google Scholar]
- Bonnin, G.M.; Martin, D.; Lin, B.; Parzybok, T.; Yekta, M.; Riley, D. Precipitation-frequency atlas of the United States, volume 2, version 3: Delaware, District of Columbia, Illinois, Indiana, Kentucky, Maryland, New Jersey, North Carolina, Ohio, Pennsylvania, South Carolina, Tennessee, Virginia, West Virginia. In NOAA Atlas 14; Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service: Silver Spring, MD, USA, 2006; Volume 2. [Google Scholar]
- Bonnin, G.M.; Martin, D.; Parzybok, T.; Lin, B.; Riley, D.; Yekta, M. Precipitation-frequency atlas of the United States, volume 3, version 3, Puerto Rico and the U.S. Virgin Islands. In NOAA Atlas 14; Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service: Silver Spring, MD, USA, 2006; Volume 3. [Google Scholar]
- Perica, S.; Martin, D.; Lin, B.; Parzybok, T.; Riley, D.; Yekta, M.; Hiner, L.; Chen, L.; Brewer, D.; Yan, F.; et al. Precipitation frequency atlas of the United States, volume 4, version 2, Hawaiian Islands. In NOAA Atlas 14; Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service: Silver Spring, MD, USA, 2009; Volume 4. [Google Scholar]
- Guo, J.C.Y.; Urbonas, R.B. Maximized detention volume determined by runoff capture rate. J. Water Resour. Plan. Manag. 1996, 22, 123–456. [Google Scholar]
- Guo, J.C.Y.; Urbonas, R.B. Runoff capture and delivery curves for storm water quality control designs. J. Water Resour. Plan. Manag. 2002, 128, 123–456. [Google Scholar] [CrossRef]
- Davis, A.P.; McCuen, R.H. Stormwater Management for Smart Growth; Springer: New York, NY, USA, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).