Assessing the Efficiency of Rainstorm Drainage Networks Using Different Arrangements of Grate Inlets
Abstract
1. Introduction
2. Materials and Methods
2.1. Dimensional Analysis
| hI: Water depth at inlets upstream. | Ho: relative flume water height = hd/hu, |
| hd: water depth at flume downstream | Lo: relative grate length = LI/L, |
| I1, I2, I3, I4, I5, I6: refer to the inlet’s number | E: efficiency of discharge = qi/Q. |
| WI: the water spread width beside every inlet | g: gravitational acceleration |
| LI: the distance of each inlet’s position, measured from the start of the flume | W: the channel width, |
| L: the length of the flume | Wo: relative inlet length = WI/W, |
| a I: area of inlet’s cross section | HI: relative inlet water height = hI/hu, |
| Q: the total flume discharge | af: area of flume |
| qi: flow intercepted by inlets | Ao: relative inlet area = aI/af, |
| hu: water depth at flume upstream. | nI: number of inlets |
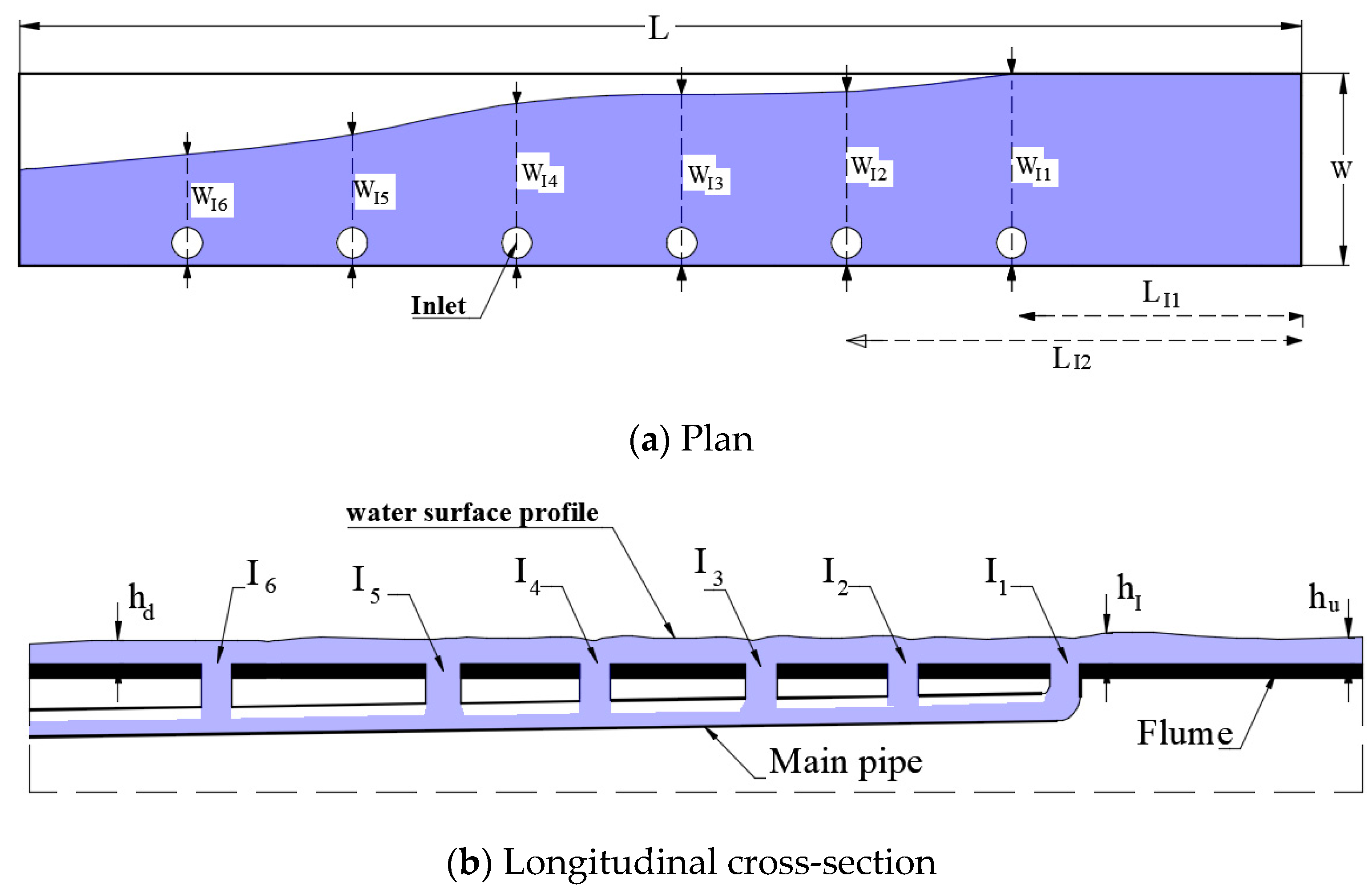
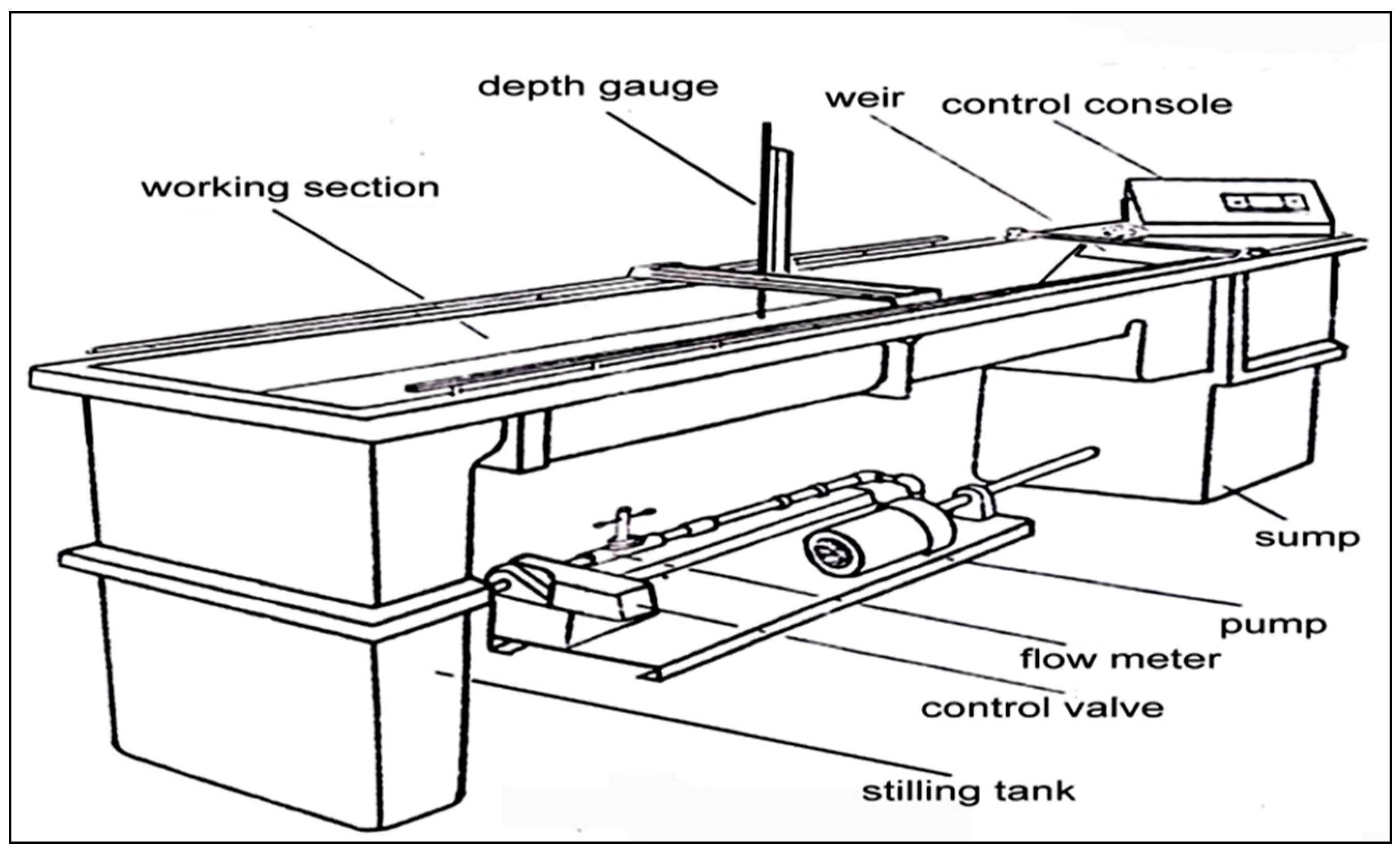
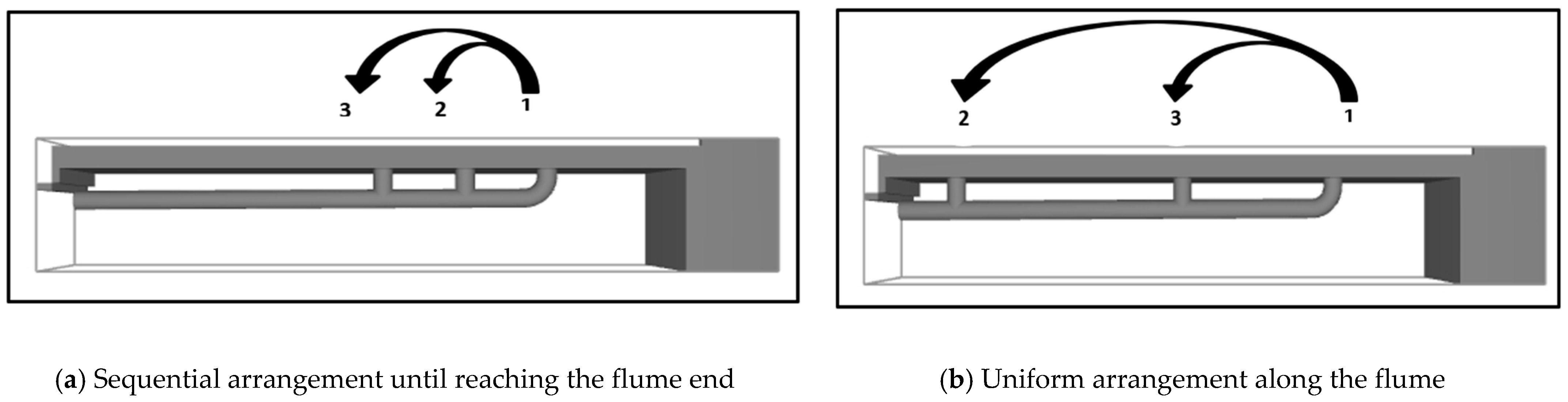
2.2. Experimental Model
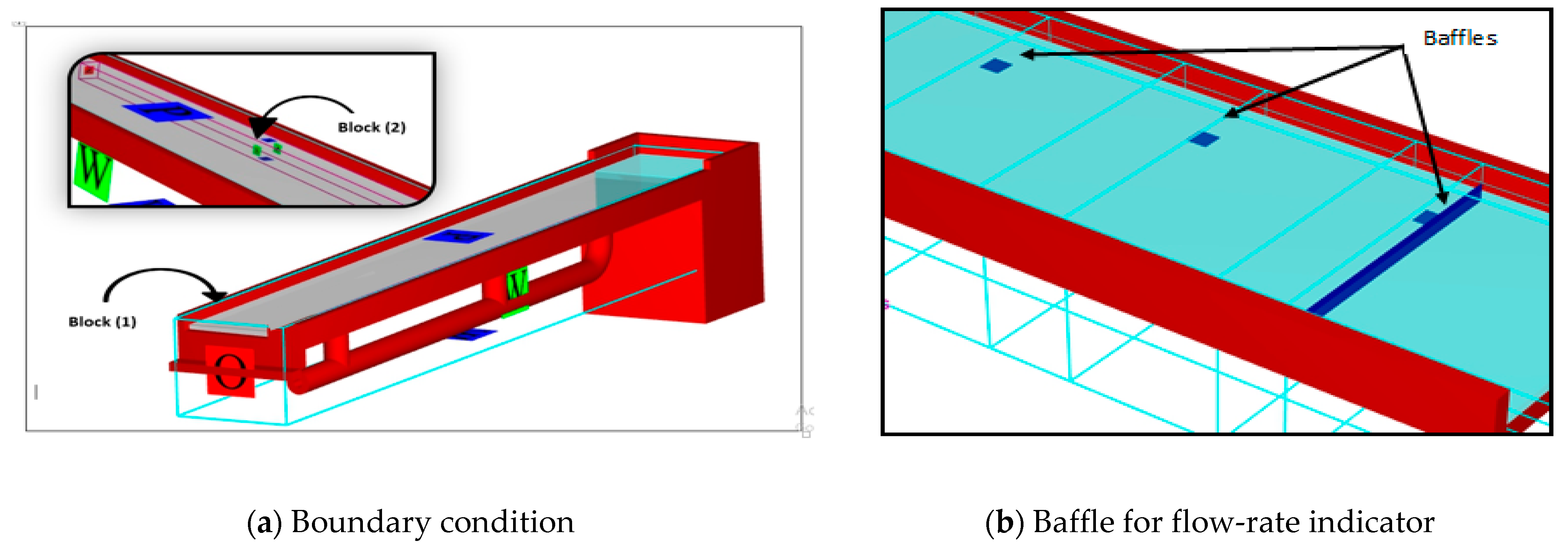
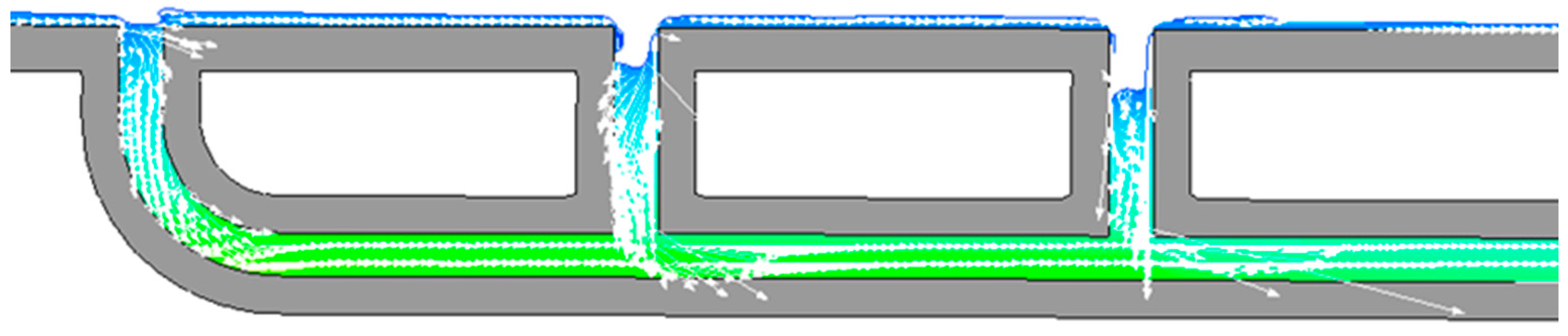
2.3. Numerical Model (FLOW-3D)
3. Results and Discussion
3.1. Experimental Results
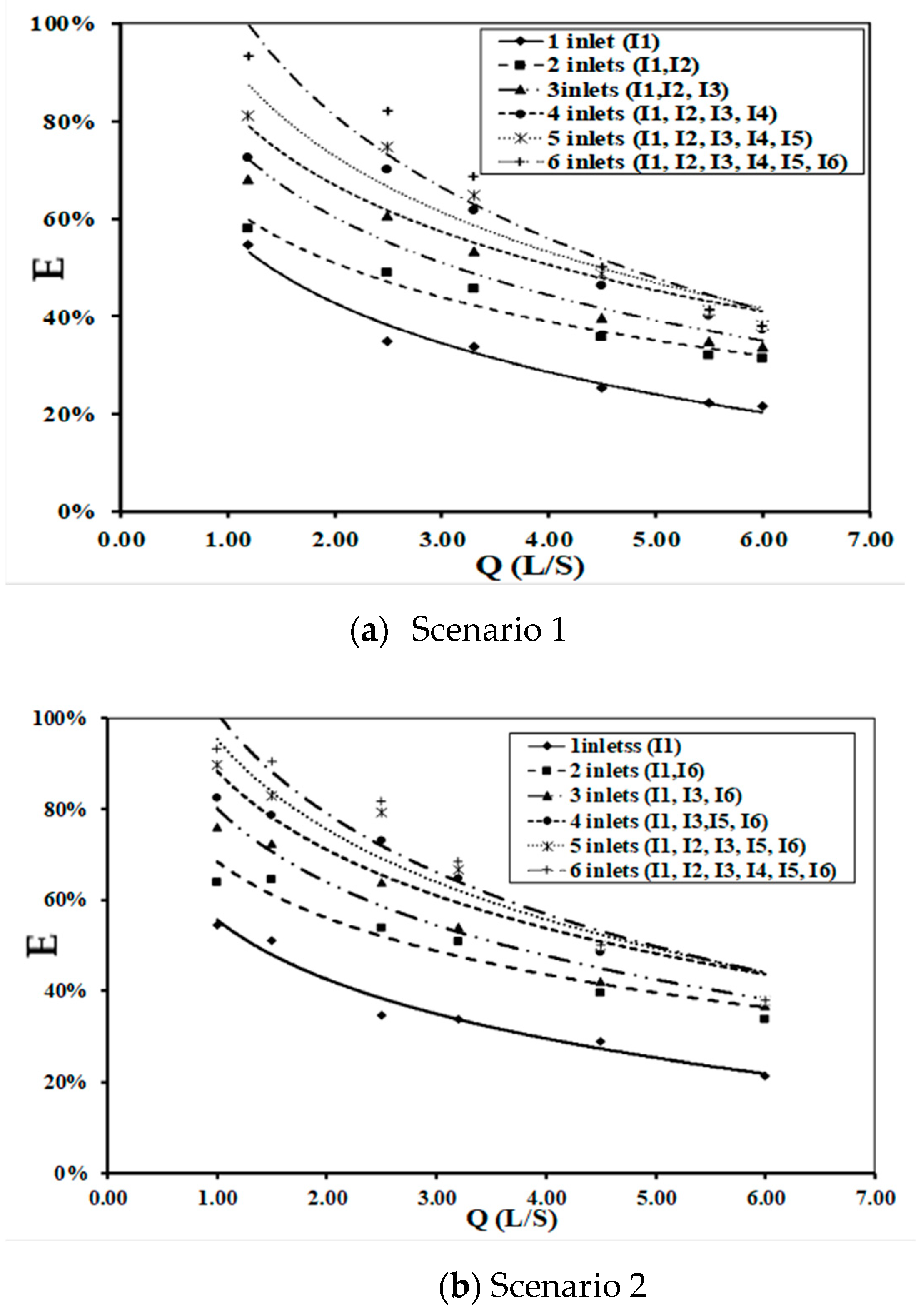
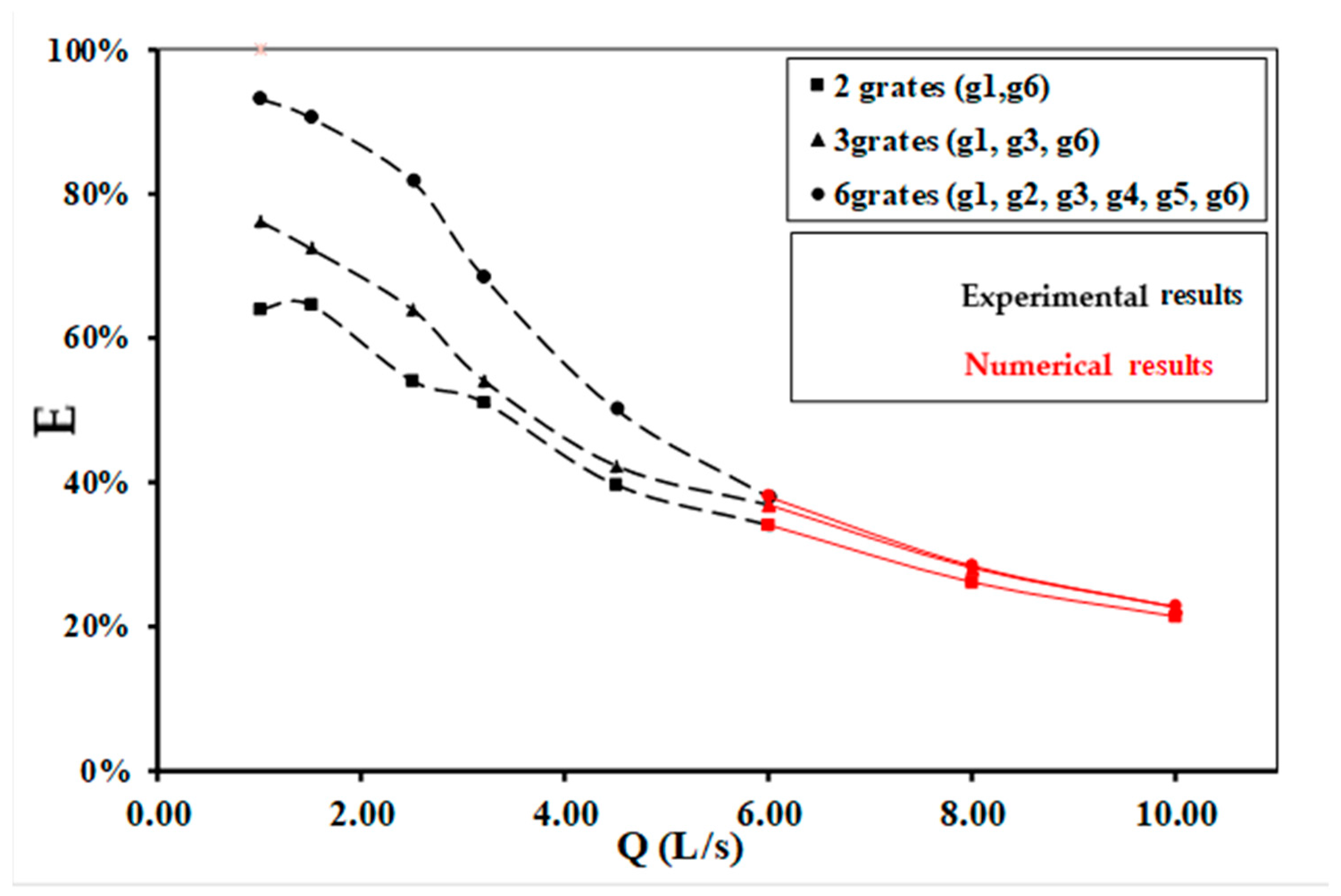
3.1.1. Efficiency of the System
3.1.2. Effect of Inlet Arrangements on Water Surface Profile
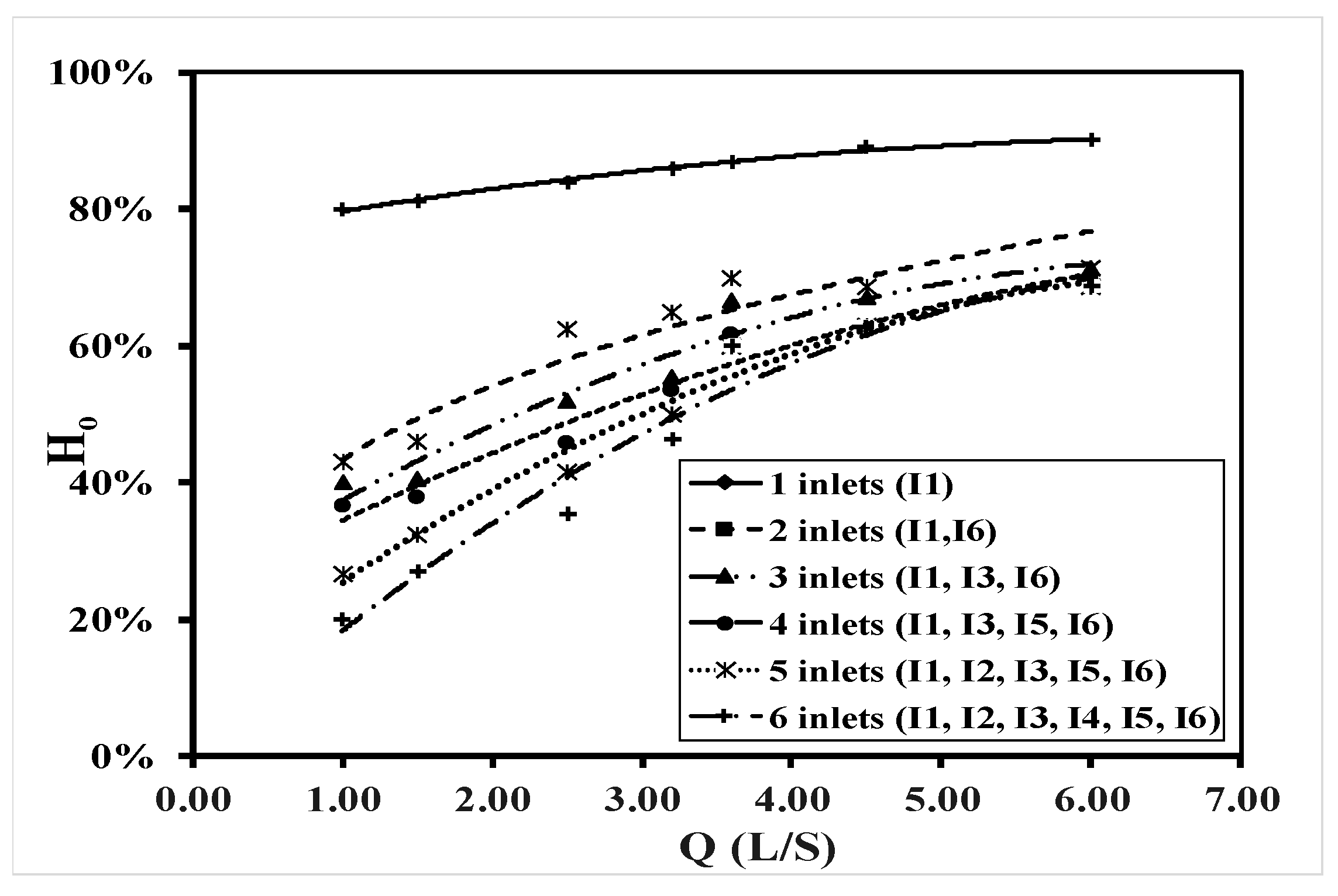
Relative Water Depth
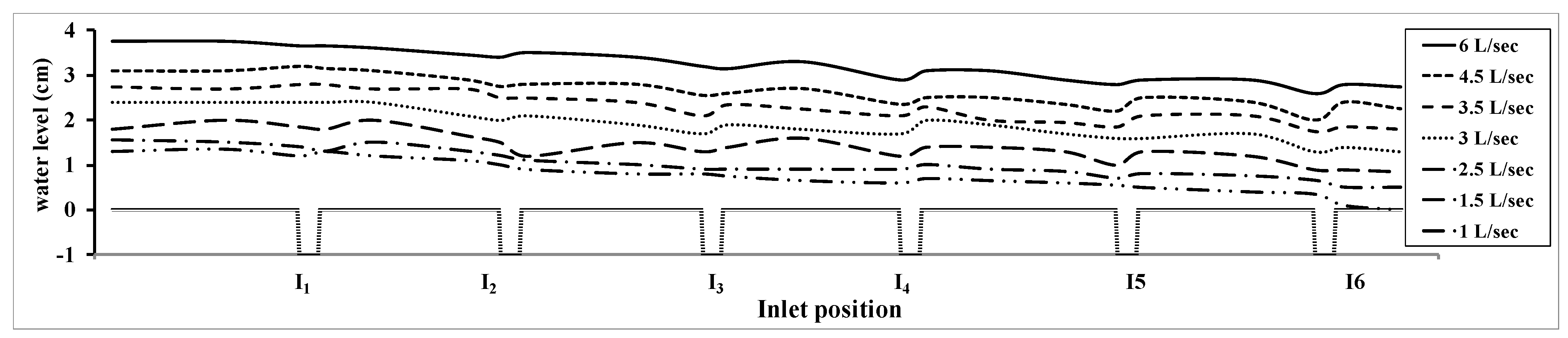
Water Surface Profile (WSP)
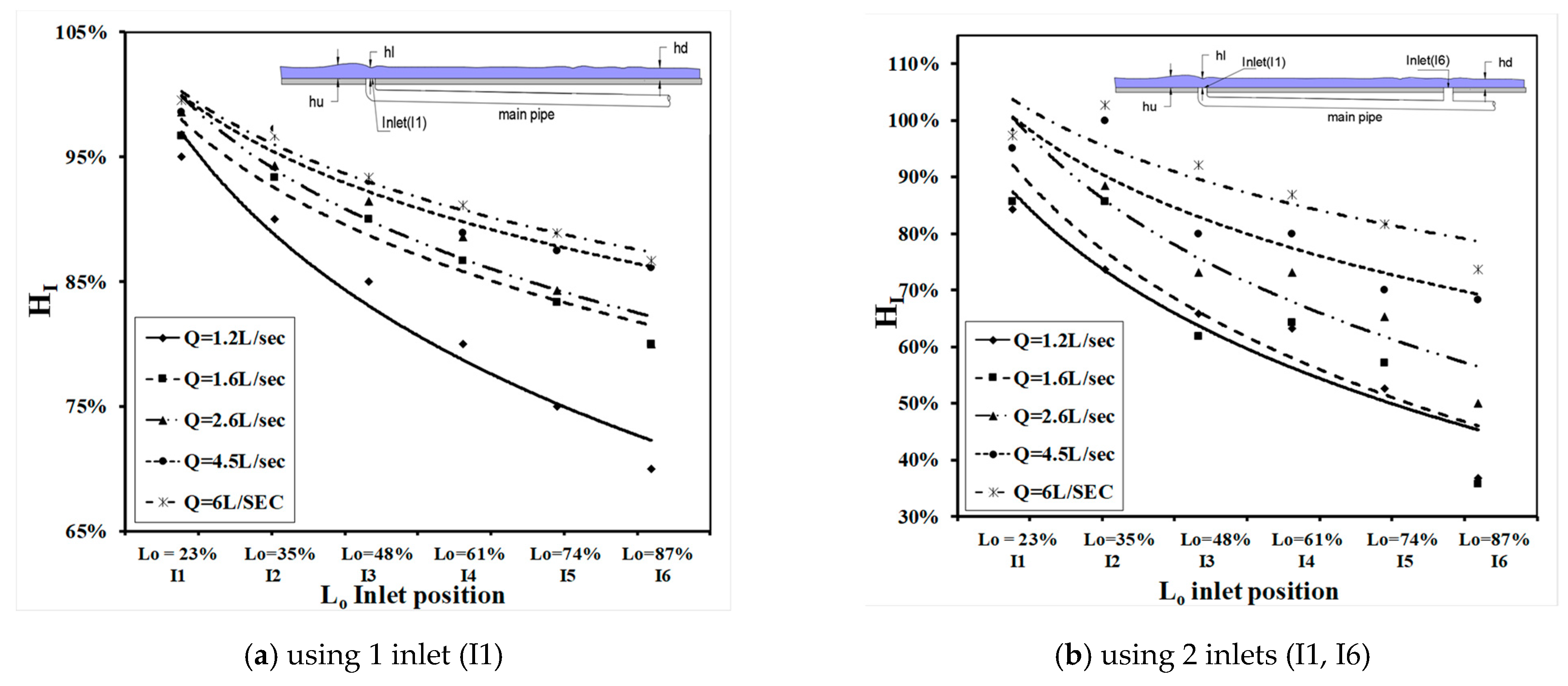
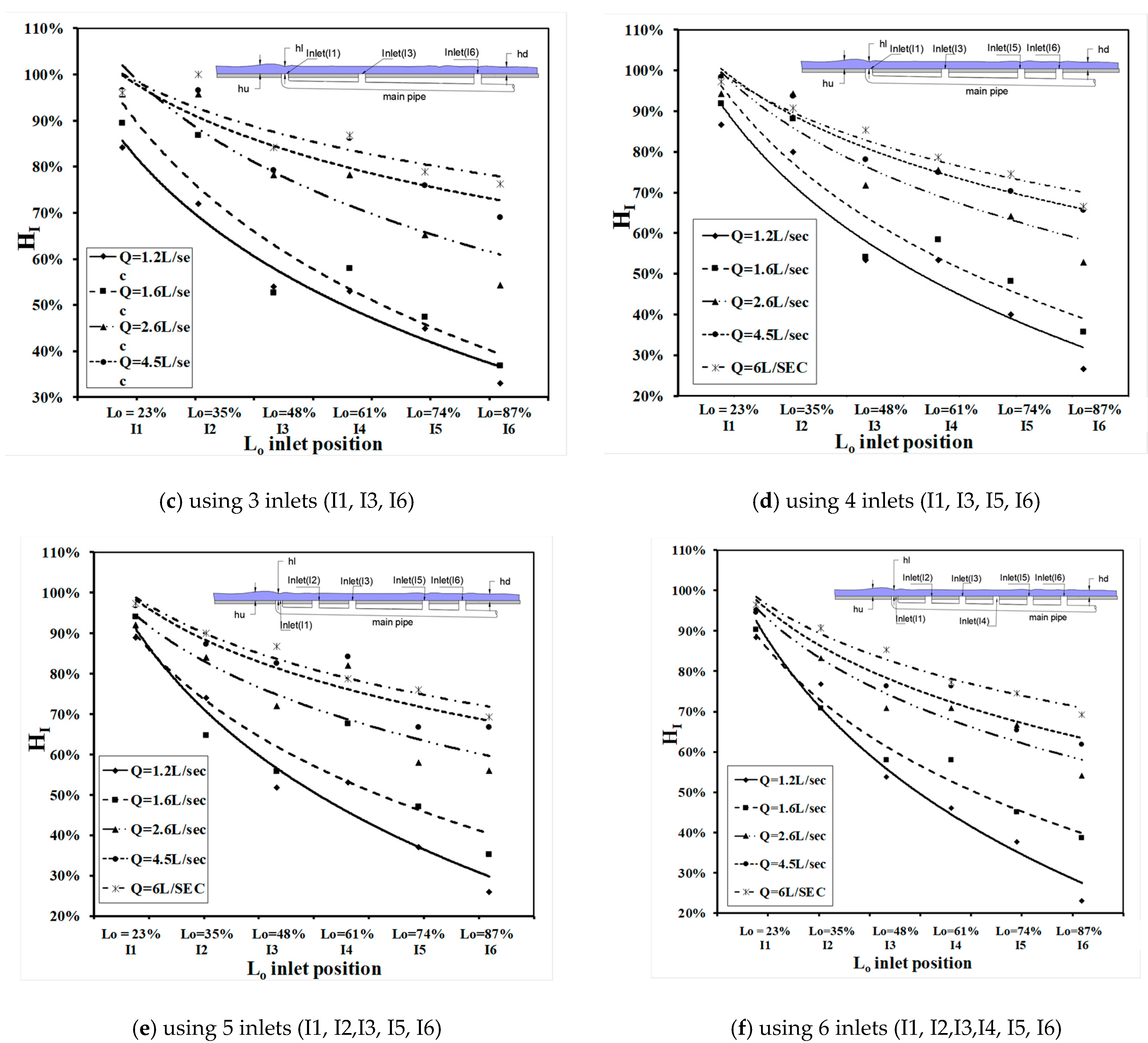
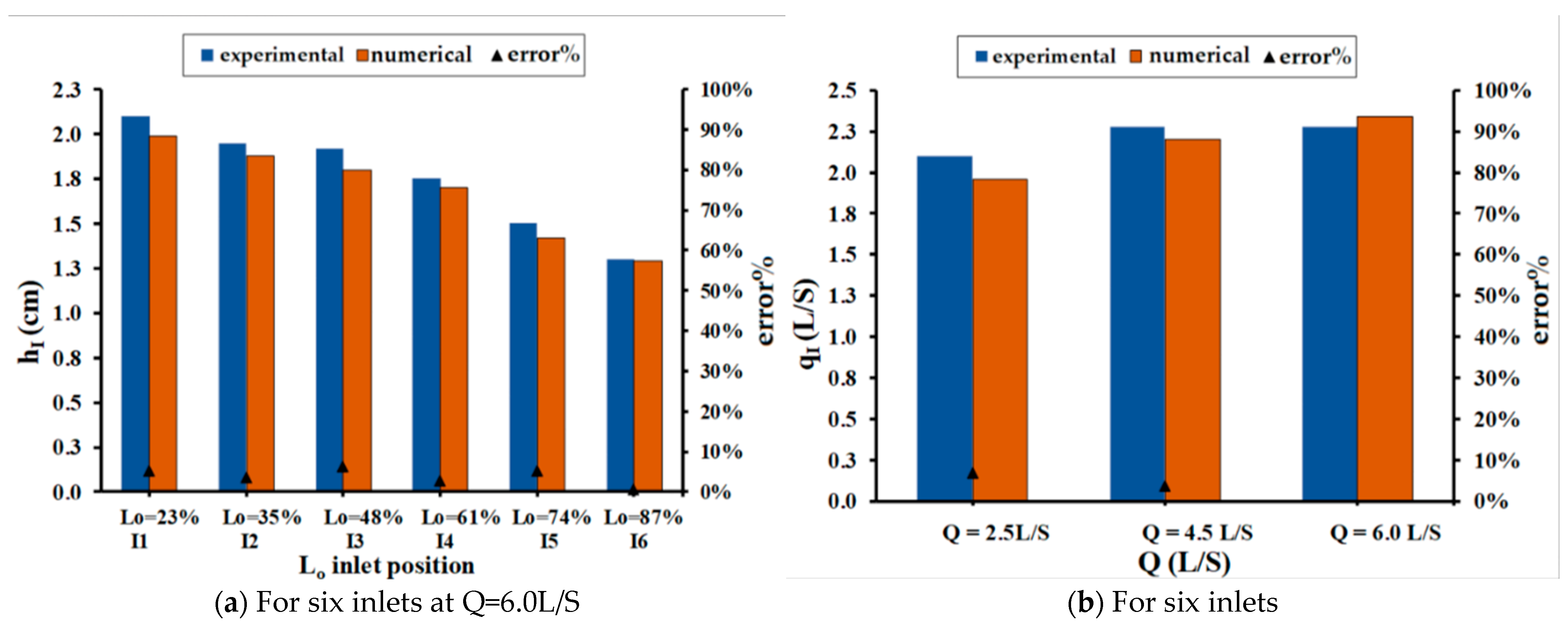
Relative Inlet Water Height
- As Q increases, HI increased for all cases with different numbers of inlets.
- HI decreased along the flume for different numbers of inlets (one, two, three, four, five, and six inlets) by 19%, 39%, 42.2%, 44.6%, 45%, and 45.2%, respectively.
- For the small value of Q, increasing the number of inlets from one to six had a tangible impact on HI, which decreased by 49%.
- For a large value of Q, increasing the number of inlets from one to six inlets HI by 26%; furthermore, when using four, five, and six inlets, the results of HI were similar.
- For the shape of the inlet at high discharge (high water level) and when the distance between inlets is bigger than 1.00 m, the inlet will become submerged and the inlet flow will behave as an orifice.
- For the shape of the inlet at high discharge and when the distance between inlets is less than 1.00 m, the inlet will become submerged, and the flow will have a small spiral. This is because of the presence of air bubbles.
- For the shape of the inlet at low discharge (shallow water depth), the flow will behave as a sharp crested weir.
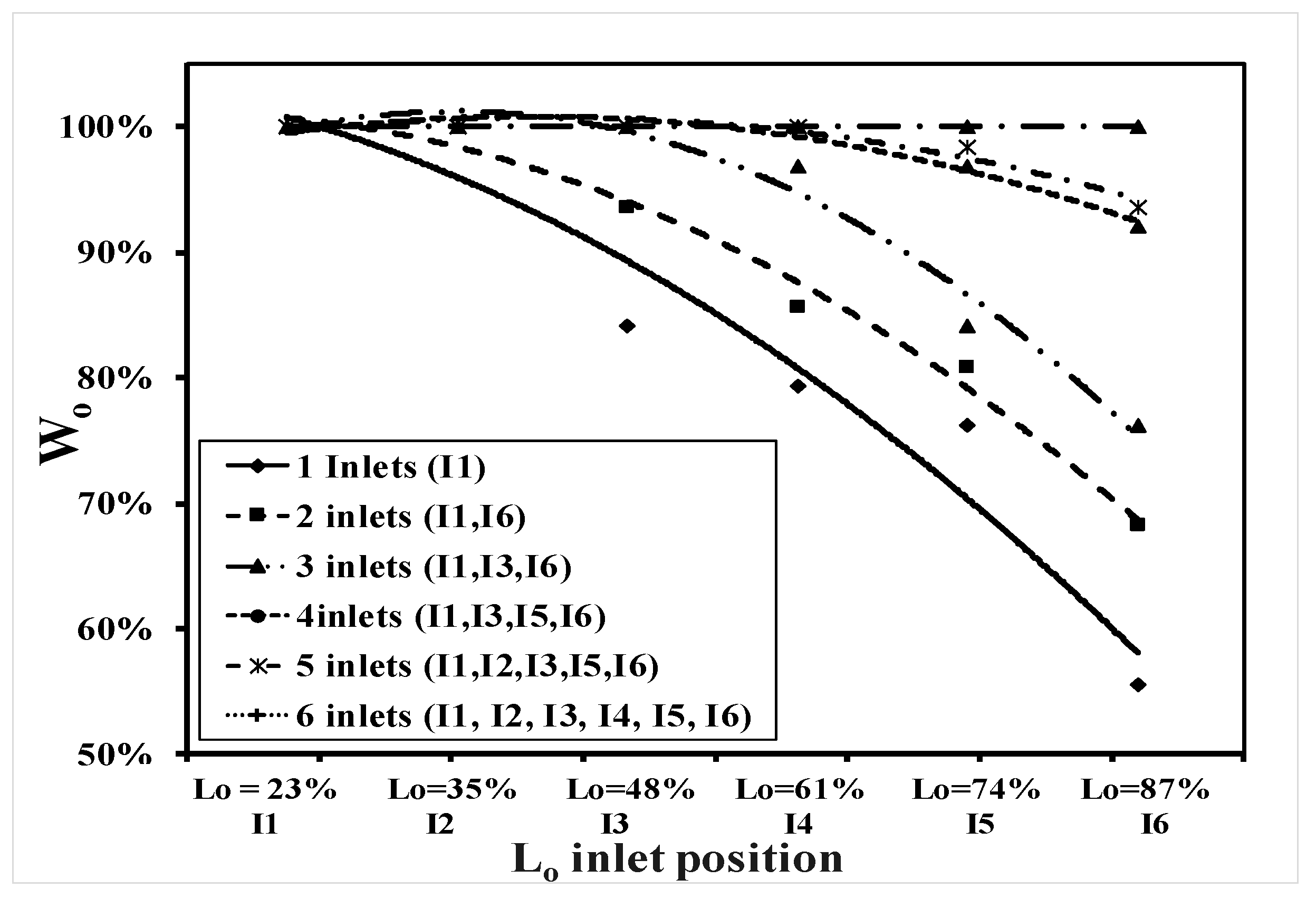
Relative Inlet Water Spread Width
3.2. Numerical Simulation
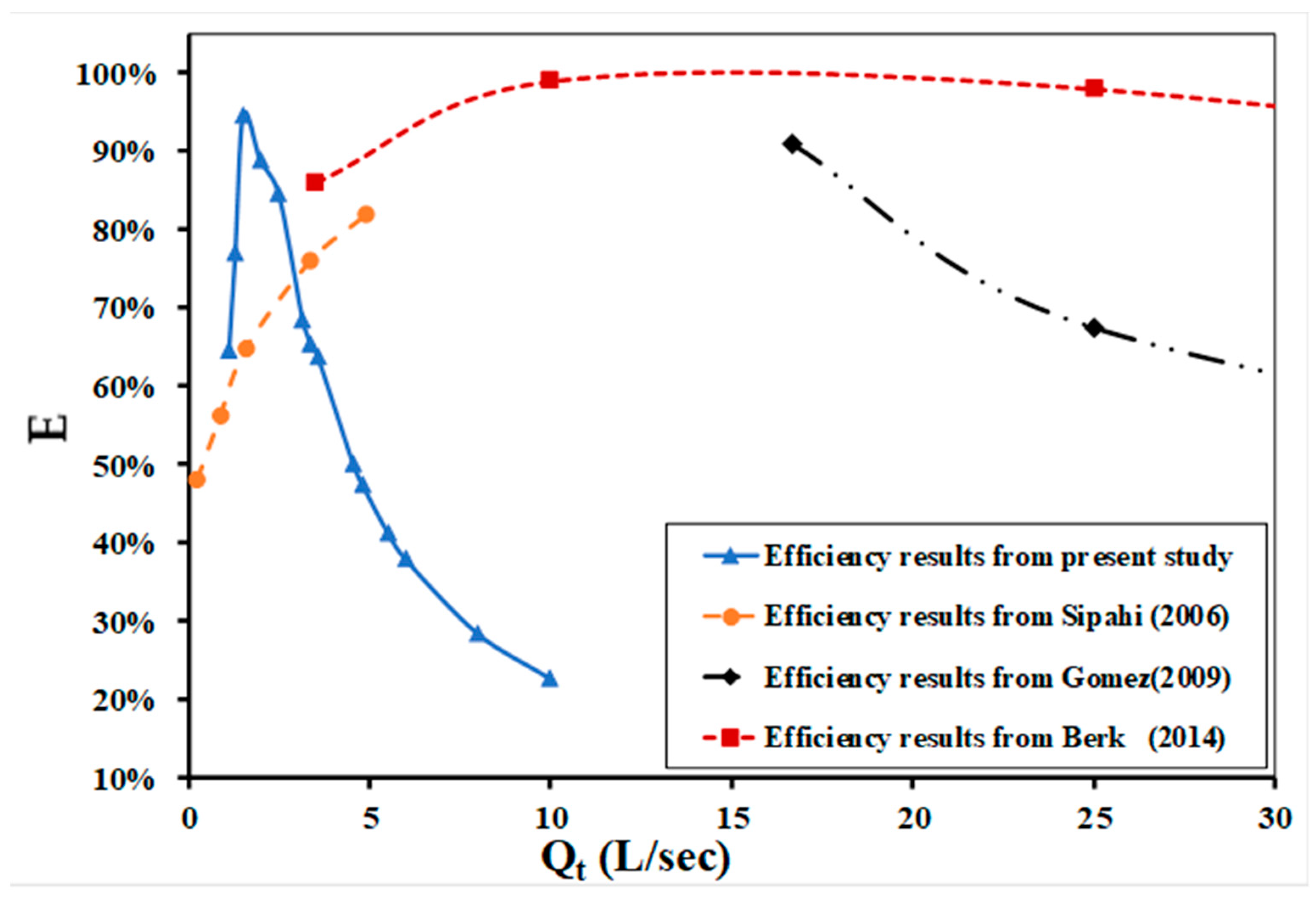
4. Comparison between the Current Study and Previous Studies
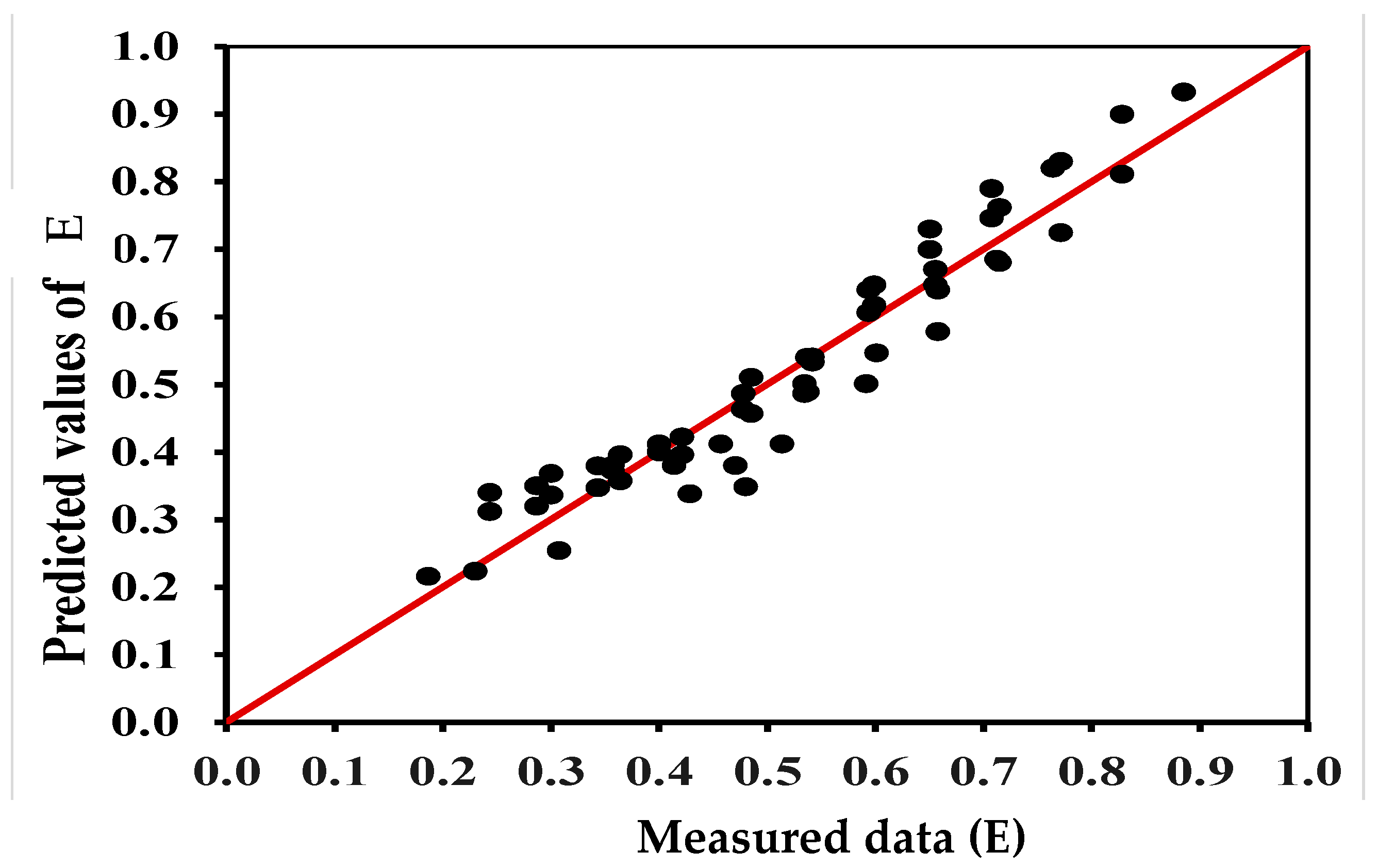
5. Prediction of Efficiency
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Larson, C.L. Experiments on Flow Through Inlet Gratings for Street Gutters; Research Report No. 6-B; Highway Research Board: Washington, DC, USA, 1948; pp. 17–26. [Google Scholar]
- Bob, M.; Gallaway, E.; Schiller, J.; Jerry, G. The Effects of Rainfall Intensity, Pavement Cross Slope, Surface Texture, and Drainage Length on Pavement Water Depths; Research Report Number 138-5; Vehicle-Pavement Interaction Research Study Number 28-69-138; Texas Transportation Institute, University College Station: Houston, TX, USA, 1971. [Google Scholar]
- Govindaraju, R.S.; Kavvas, M.L. Approximate analytical solutions for overland flows. Water Resour. Res. 1990, 26, 2903–2912. [Google Scholar] [CrossRef]
- Jiang, S. Numerical Simulations of Shallow Flow through Curb-Opening Inlets at Various Longitudinal and Cross Slopes. Ph.D. Thesis, Lamar University, Beaumont, TX, USA, 2007. [Google Scholar]
- Fang, X.; Jiang, S.; Alam, R. Numerical simulations of efficiency of curb opening inlets. J. Hydraul. Eng. 2010, 136, 62–66. [Google Scholar] [CrossRef]
- Kurel, S.; Watanabe, A.; Akabane, Y.; Yamada, T. Field Observations of Discharge and Runoff Characteristics in Urban Catchments Area. In Proceedings of the 11th International Conference on Urban Drainage, Edinburgh, Scotland, UK, 31 August–5 September 2008. [Google Scholar]
- Abd-Elhamid, H.; Zelenakova, M.; Vranayova, Z.; Fathy, I. Evaluating the impact of urban growth on the design of storm water drainage system. Water 2020, 12, 1572. [Google Scholar] [CrossRef]
- Gómez, M.; Macchione, F.; Russo, B. Methodologies to study the surface hydraulic behaviour of urban catchments during storm events. Water Sci. Technol. 2010, 63, 2666–2673. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rubinato, M.; Shucksmith, J.; Saul, A.J. Hydraulic performance of a scale model facility and optimization through the use of real time sensors. In Proceedings of the12th International Conference on Urban Drainage, Porto Alegre, Brazil, 11–16 September 2011; pp. 11–16. [Google Scholar]
- Rokade, S.; Agarwal, K.; Shrivastava, R. Study on Drainage Related Performance of Flexible Highway Pavements. Int. J. Adv. Eng. Technol. 2012, 3, 334–337. [Google Scholar]
- Hsieh, P.-C.; Chen, Y.-C. Surface water flow over a pervious pavement. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1095–1105. [Google Scholar] [CrossRef]
- Haghighi, A. Loop-by-loop cutting algorithm to generate layouts for urban drainage systems. J. Water Resour. Plan. Manag. 2013, 139, 693–703. [Google Scholar] [CrossRef]
- Dipanjan, M. Highway Surface Drainage System & Problems of Water Logging in Road Section. Int. J. Eng. Sci. (IJES) 2014, 3, 44–45. [Google Scholar]
- Getachew, W.; Tamene, D. Assessment of the Effect of Urban Road Surface Drainage, A Case Study at Ginjo Guduru Kebele of Jimma Town. Int. J. Sci. Technol. Soc. 2015, 3, 164–173. [Google Scholar]
- Magdi, E. Investigating Surface Drainage Problem of Roads in Khartoum State. Int. J. Civ. Eng. Technol. (IJCIET) 2016, 7, 91–103. [Google Scholar]
- Tu, M.-C.; Traver, R. Clogging Impacts on Distribution Pipe Delivery of Street Runoff to an Infiltration Bed. Water 2018, 10, 1045. [Google Scholar] [CrossRef]
- Yakhot, V.; Orsza, A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Yakhot, V.; Smith, M. The renormalization group, the expansion and derivation of turbulence models. J. Sci. Comput. 1992, 7, 35–61. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Department of Transport and Main Roads (DTMR). (Road Surface and Subsurface Drainage Design), Road Drainage Manual; State of Queensland: Brisbane, Australia, 2015. [Google Scholar]
- Sipahi, O. Calibration of a Grate on a Sloping Channel. Master’s Thesis, Department of Civil Engineering, Middle East Technical University, Ankara, Turkey, 2006. [Google Scholar]
- Gómez, M.; Russo, B. Hydraulic Efficiency of Continuous Transverse Grates for Paved Areas. J. Irrig. Drain. Eng. 2009, 135, 225–230. [Google Scholar] [CrossRef]
- Sezenöz, B. Numerical Modeling of Continuous Transverse Grates for Hydraulic Efficiency. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2014. [Google Scholar]

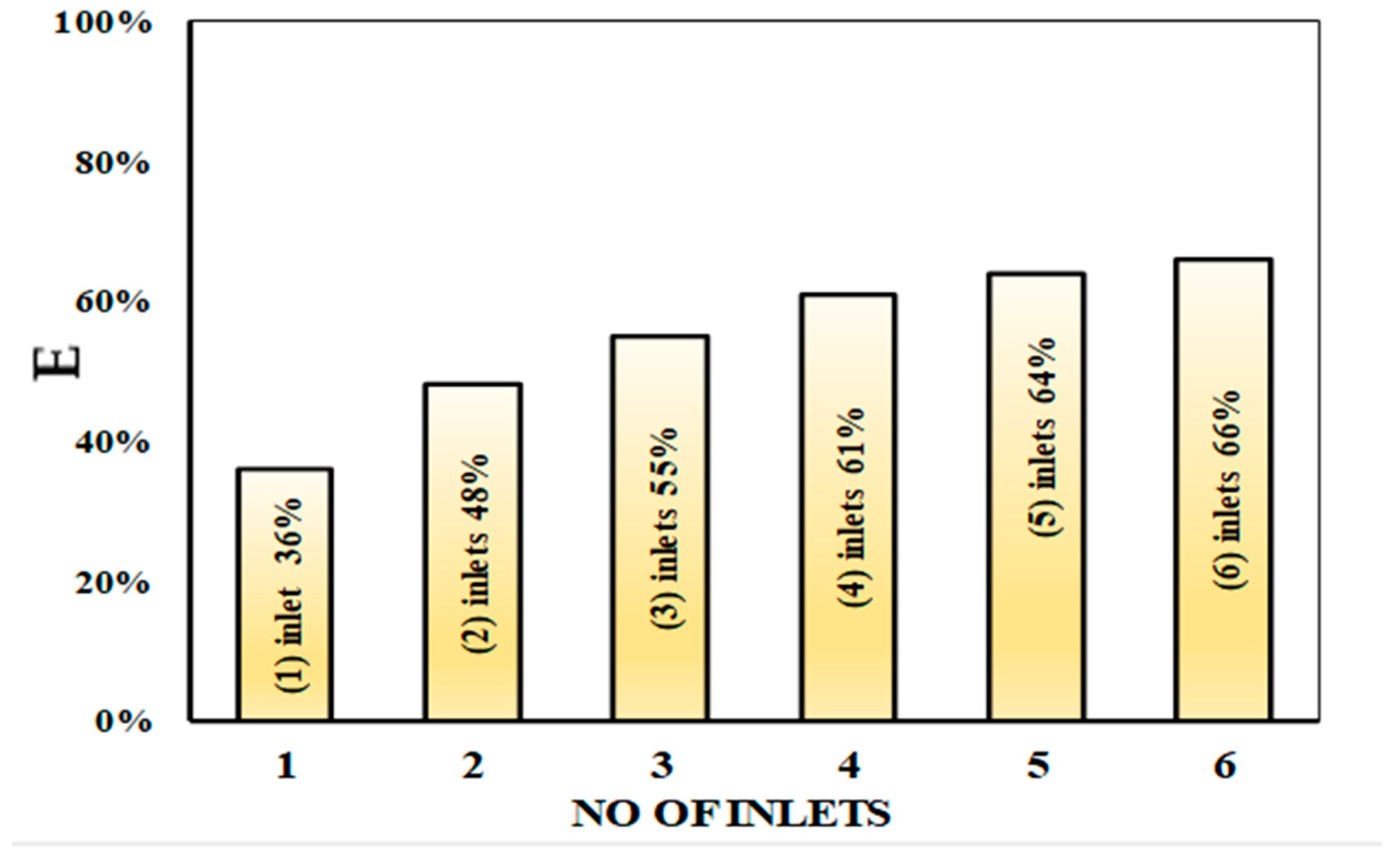


| No of Grates | Average Different Efficiency |
|---|---|
| 1 inlet, 2 inlets | 12% |
| 2 inlets, 3 inlets | 7% |
| 3 inlets, 4 inlets | 6% |
| 4 inlets, 5inlets | 3% |
| 5 inlets, 6 inlets | 2% |
| Items | [21] | [22] | [23] | Present Study |
|---|---|---|---|---|
| Q (L/S) | 0.25–4.91 | 0–100 | 4–500 | 1–10 |
| Number of inlets | 3 | 1 | 1 | 6 |
| Area of flume (aF) m2 | 12 | 8.25 | 8.25 | 2.65 |
| Area of inlets (aI) m2 | 0.20 | 0.3 | 0.07 | 0.012 |
| AO = aI/aF | 1.67% | 3.6% | 0.85% | 0.45% |
| AO/Q | 0.34 | 0.036 | 0.002 | 0.045 |
| Efficiency (E) | 0.48:0.82% | 0.275:0.91% | 0.17:0.99% | 0.93% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathy, I.; Abdel-Aal, G.M.; Fahmy, M.R.; Fathy, A.; Zelenakova, M.; Abd-ElHamid, H.F.; Raček, J.; Moussa, A.M.A. Assessing the Efficiency of Rainstorm Drainage Networks Using Different Arrangements of Grate Inlets. Hydrology 2024, 11, 18. https://doi.org/10.3390/hydrology11020018
Fathy I, Abdel-Aal GM, Fahmy MR, Fathy A, Zelenakova M, Abd-ElHamid HF, Raček J, Moussa AMA. Assessing the Efficiency of Rainstorm Drainage Networks Using Different Arrangements of Grate Inlets. Hydrology. 2024; 11(2):18. https://doi.org/10.3390/hydrology11020018
Chicago/Turabian StyleFathy, Ismail, Gamal M. Abdel-Aal, Maha Rashad Fahmy, Amira Fathy, Martina Zelenakova, Hany F. Abd-ElHamid, Jakub Raček, and Ahmed Moustafa A. Moussa. 2024. "Assessing the Efficiency of Rainstorm Drainage Networks Using Different Arrangements of Grate Inlets" Hydrology 11, no. 2: 18. https://doi.org/10.3390/hydrology11020018
APA StyleFathy, I., Abdel-Aal, G. M., Fahmy, M. R., Fathy, A., Zelenakova, M., Abd-ElHamid, H. F., Raček, J., & Moussa, A. M. A. (2024). Assessing the Efficiency of Rainstorm Drainage Networks Using Different Arrangements of Grate Inlets. Hydrology, 11(2), 18. https://doi.org/10.3390/hydrology11020018