Simulation of Flood-Control Reservoirs: Comparing Fully 2D and 0D–1D Models

Abstract

Flood-control reservoirs are often used as a structural measure to mitigate fluvial floods, and numerical models are a fundamental tool for assessing their effectiveness. This work aims to analyze the suitability of fully 2D shallow-water models to simulate these systems by adopting internal boundary conditions to describe hydraulic structures (i.e., dams) and by using a parallelized code to reduce the computational burden. The 2D results are also compared with the more established approach of coupling a 1D model for the river and a 0D model for the reservoir. Two test cases, including an in-stream reservoir and an off-stream basin, both located in Italy, are considered. Results show that the fully 2D model can effectively handle the simulation of a complex flood-control system. Moreover, compared with the 0D–1D model, it captures the velocity field and the filling/emptying process of the reservoir more realistically, especially for off-stream reservoirs. Conversely, when the basin is characterized by very limited flood dynamics, the two approaches provide similar results (maximum levels in the reservoir differ by less than 10 cm, and peak discharges by about 5%). Thanks to parallelization and the inclusion of internal boundary conditions, fully 2D models can be applied not only for local hydrodynamic analyses but also for river-scale studies, including flood-control reservoirs, with reasonable computational effort (i.e., ratios of physical to computational times on the order of 30–100).

1. Introduction

Worldwide, floods affect communities, urban areas, infrastructure, economic activities, cultural heritage, and environmental assets, causing huge losses (e.g., [1]). Therefore, the damaging consequences of these disasters must be mitigated by means of effective flood risk management. Although it is recognized that structural measures alone cannot eliminate flood risk, these strategies (e.g., levees) are still widely adopted to provide protection against river floods with a medium-high probability of occurrence. One of the most popular structural measures for mitigation is flood-control reservoirs, in which a fraction of the flood volume can be temporarily stored, thus attenuating the peak discharge downstream (e.g., [2]). Storage areas can be built on-stream or off-stream [3,4], and their filling is sometimes controlled by means of gate operations on dams and spillways [5].

To evaluate the effectiveness of storage areas in reducing flood peaks [5,6,7] and to optimize real-time decisions on gate operations, where applicable (e.g., [8]), numerical models are essential. Selecting a suitable modeling approach is crucial for obtaining reliable predictions with reasonable computational effort. Models for flood-control reservoirs can be classified according to their dimensional complexity [9,10]. The simplest method is level pool routing, which adopts a zero-dimensional (0D) approach to represent the reservoir by solving the continuity equation (e.g., [2,4,11]). The 0D model is then usually coupled with a one-dimensional (1D) model for the river [3,5,10,12,13]. Fully 1D models could be used for simulating flow along on-stream reservoirs (i.e., discretizing the reservoir with cross-sections), although the 0D approach can be as accurate and less computationally expensive when the flow dynamics in the reservoir is very limited [14]. Another common approach is the coupling between the 1D river model and a two-dimensional (2D) model for the off-stream storage area [9,15]. Previous studies analyzed and compared the performances of 1D–0D and 1D–2D models in this context [9,16], showing that the 0D approximation is suitable for studying the discharge reduction in the river [9], for preliminary assessments of different scenarios, and for uncertainty evaluations [16]. Conversely, the 2D representation can provide more detailed results in the case of reservoirs with complex topography and for applications requiring velocity data, such as studying erosion/deposition processes and the associated risk [9] and water quality modeling [16].

More complex and computationally demanding approaches include fully 2D models and three-dimensional (3D) models. While the latter are usually disregarded due to their high computational cost, which remains impractical for most applications to flood hazard studies, the former have recently gained popularity thanks to advances in numerical techniques and code parallelization, which made them feasible even for large-scale domains (e.g., [17]) and/or high-resolution meshes (e.g., [18]). However, fully 2D models were mainly applied to floodplain inundations and levee breach scenarios (e.g., [19,20]) or to river domains where dams/reservoirs are located either at the upstream (e.g., [6]) or at the downstream boundary condition (only for in-stream reservoirs, e.g., [14]), while the use of fully 2D models for simulating flood-control reservoirs inside the domain was hampered due to the difficulty of including spillways and flood-control dams in shallow water models. The recent implementation of internal boundary conditions (IBCs) to represent hydraulic structures in fully 2D models [21] addresses this limitation.

In this work, we apply a fully 2D model with IBCs to simulate flood attenuation in flood-control reservoir systems using a high-resolution mesh. Moreover, the fully 2D simulations are compared with simpler 0D–1D models to highlight and discuss the advantages and limitations of each approach. Two case studies in Italy are considered: the on-stream detention basin on the Parma River and one of the two off-stream basins on the Enza River.

This paper is structured as follows: Section 2 briefly introduces the numerical models, the case studies, and the models’ setup; Section 3 describes the results of simulations, which are then discussed in Section 4; finally, Section 5 summarizes the conclusions.

2. Materials and Methods

2.1. Numerical Models

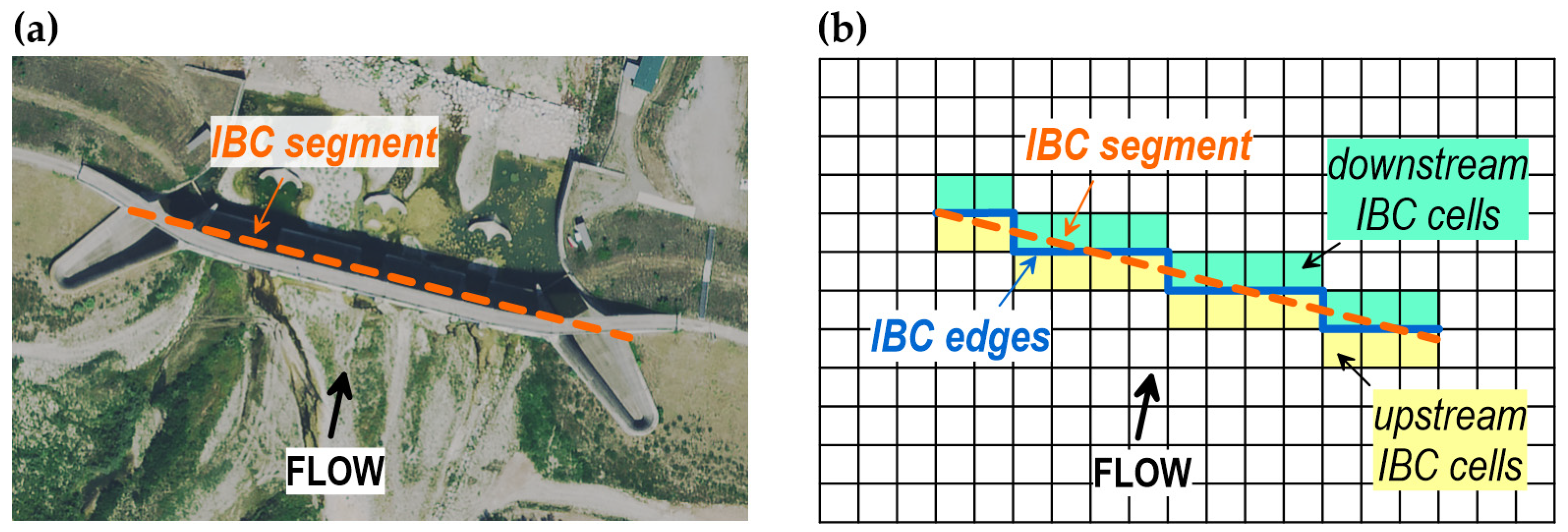
2.1.1. The 0D–1D Model

The 0D–1D model was set up using the HEC-RAS code [22], developed by the United States Army Corps of Engineers (Hydrologic Engineering Center). In its 1D unsteady version, the model solves the full de Saint-Venant equations using an implicit finite difference numerical scheme. The river is discretized by means of a series of cross-sections, and the model also allows including hydraulic structures, such as bridges, culverts, etc. Specifically, flood-control dams can be described by means of inline structures with a prescribed rating curve.

The detention basins are modeled with a 0D approach, i.e., they are described by storage areas with stage-volume curves derived from digital terrain models (DTM). The water surface elevation in the reservoir is assumed to be horizontal, and its temporal variation is computed by means of the continuity equation according to inflow/outflow discharges. For an in-stream reservoir, the storage area can be linked directly to an outflow cross-section just upstream of the flood-control dam, while an off-stream reservoir can be linked to the river by means of lateral structures (weirs). In this latter case, the discharge flowing above the weir is computed according to the following equation:

$$Q=C_{W}L\sqrt{2g}{H}^{3/2},$$

(1)

where Q is the discharge, L is the weir length, g is the acceleration due to gravity, H is the energy head over the weir crest, and C_W is a discharge coefficient (non-dimensional).

2.1.2. The 2D Model

For fully 2D simulations, the PARFLOOD model [23] was herein adopted. PARFLOOD solves the fully dynamic shallow water equations by adopting an explicit finite volume scheme. The domain is discretized with square computational cells. The code is designed to exploit GPU acceleration, which significantly reduces the computational times even when high-resolution grids are adopted.

Including hydraulic structures in 2D models is not straightforward. Here, the recent implementation of internal boundary conditions (IBC) in PARFLOOD [21] is adopted. IBCs are local modifications to the standard numerical scheme near hydraulic structures, which are approximated as zero-width elements (in the horizontal plane) and represented by linear segments (Figure 1a). The adjacent cells in the computational grid are then separated into two groups of IBC cells that are located either “upstream” or “downstream” of the segment itself and separated by IBC edges (Figure 1b). The average water level (assumed approximately horizontal) of upstream IBC cells is first computed, and the global discharge flowing through the structure is interpolated from the rating curve of the hydraulic structure, which must be available from experiments or computed using classical hydraulic principles. The specific discharge (assumed normal to the IBC edge) is then computed and imposed in each upstream IBC cell, and the same values are imposed on the corresponding downstream IBC cells. Fluxes at the edges of IBC cells (blue lines in Figure 1b) are computed in a special way that guarantees mass and momentum conservation [21]. Previous works have confirmed the suitability of IBCs to represent hydraulic structures, such as bridges [24,25]. Here, this strategy is exploited to include flood-control dams in the 2D domain and represent their complex behavior.

Conversely, no special treatment is adopted for lateral structures (weirs), which are assumed to be correctly represented by the local topography when a fine resolution is used. Their functioning is therefore inherently captured by the model, although the hydrostatic pressure assumption underlying the shallow water equations is not strictly valid on these structures. Still, the model is able to reproduce flow contractions and drawdown effects upstream, transcritical flows, hydraulic jumps, or weir submergence downstream.

2.2. Case Studies

In this work, we considered two case studies of flood-control reservoirs near the town of Parma, Italy (Figure 2a). The first case study concerns the on-stream detention reservoir located about 3 km south of Parma, designed to dampen the floods on the Parma River and protect the town [26]. The flood-control structure is a 14.6 m high concrete dam with three openings (equipped with movable gates) at the bottom and an overflow spillway at the top. The reservoir, limited by earthen levees, can store up to 10 Mm³ of water in an area of approximately 1.3 km² (Figure 2b). For the numerical simulations, the 8 km long stretch of the Parma River from just upstream of the reservoir (Vigatto) to the southern borders of the town was considered (Figure 2a), and the domain is about 10 km².

The second case study concerns the flood-control system on the Enza River, located about 8 km southwest of the town of Parma (Figure 2a). Two off-stream reservoirs are available, with maximum storable volumes of about 8 and 4 Mm³ for the first and second one, respectively. Water diversion into each reservoir is regulated by a concrete flow-through dam with five bottom openings (no gates are present) and an overflow spillway, and by a lateral weir on the left (Figure 2c). During floods, the dam generates an increase in the upstream water level, which causes a fraction of the flood discharge to be diverted into the reservoir after overtopping the lateral weir. Just downstream, the reservoir is equipped with an emergency weir with the purpose of releasing the excess volume from the reservoir back into the river, thus preventing the overtopping of the earthen levees. Moreover, a bottom outlet can be opened at the end of the flood event to empty the reservoir. Figure 2c shows a sketch of the first reservoir (upstream), but the second one (downstream) is conceptually similar. In this work, we focus only on the upstream part of the system (reservoir, dam, and weirs), which allows a comparison of how the two modeling approaches predict the system behavior for the same inflow discharge hydrograph. Indeed, the results for the downstream part of the system would be less meaningful, since they are influenced by the differences in the hydrograph attenuated by the first reservoir. The domain (about 16 km²) includes the 8 km long stretch of the Enza River from upstream of the first reservoir (Montecchio) to the railway crossing in Sant’Ilario (Figure 2a).

For both cases, the flood-control system is tested for the flood scenario with a 200-year return period, which is often used in Italy as a standard for hazard mapping and flood-control structure design. Considering that reliable field measurements of real flood events are unavailable for the two case studies and that the purpose here is mainly to compare the two modeling approaches, synthetic flood events are preferred to real events for the simulations, as sometimes carried out in previous works [16].

2.3. Model Setup

For each case study, two numerical models were set up, i.e., a 0D–1D model and a fully 2D one. The topographical data were obtained from available high-resolution DTMs, which were aggregated at 2 m spatial resolution to generate 2D computational grids with uniform square cells for the 2D models. The DTMs were also used to build the 0D–1D models’ geometry by extracting the reservoirs’ stage–volume curves (Figure 3a,b) and the river cross-sections (average distance of 100–150 m, except close to inline structures). Upstream, the discharge hydrograph with a 200-year return period was imposed as the inflow boundary condition, while uniform flow was assumed downstream.

For both case studies, rating curves for the flood-control dams were derived from previous experiments conducted on physical models. For the Parma River test case, the rating curve corresponding to the configuration with gates completely opened (Figure 3a) was used both for the inline structure of the 0D–1D model and for the single IBC imposed in the 2D model. Indeed, gate operations were not considered significant for the purpose of comparing the two modeling approaches.

As regards the Enza River test case, the rating curve for the dam (Figure 3c) was assigned to the corresponding inline structure in the 0D–1D model. Conversely, for the 2D model, preliminary 2D simulations showed that the local flow field is not uniform in the direction parallel to the dam, and therefore, using an average upstream water level might lead to discharge misestimation. For this reason, a separate IBC was assigned to each of the five openings. Since only a global rating curve was available from the scale experiment, it was assumed that, for the same upstream water level, the rating curve of a single opening would provide 1/5 of the discharge that would have flown through the global structure (Figure 3c). This subdivision of the IBC provides more realistic and stable results.

Another crucial issue for the Enza River test is the representation of the weirs that connect the off-stream reservoir and the river. The crest elevation of these elements was directly embedded into the high-resolution DTM used to create the computational mesh of the 2D model. In this way, the possible weir overtopping during a flood simulation is automatically predicted by the 2D model without introducing any IBC. The main advantage is that there is no need to specify any empirical coefficient to represent the weir flow. Conversely, for the 0D–1D model, lateral structures were used to represent the weirs, which requires setting the empirical coefficient in Equation (1). Since the physical model does not provide any guidance about the value of this coefficient and no field data were available for calibration, a sensitivity analysis was conducted adopting the suggested range from [22]. The parameter $C=C_W\sqrt{2g}$ for the inflow weirs and emergency weirs was first set equal to the HEC-RAS default value for lateral weirs (i.e., 1.1 m^1/2s⁻¹); then, additional values of 0.77 and 1.43 m^1/2s⁻¹ (±30% with respect to the default), were analyzed for the inflow weirs, while the default value was maintained for the emergency weirs. Flow contraction effects were also assumed to be incorporated in this global coefficient. Finally, notice that, for both models, the emptying process of the reservoirs is not simulated (i.e., the bottom outlet gate is assumed to be closed).

The calibration of roughness coefficients for the river stretches inside or adjacent to the reservoirs was difficult due to the lack of locally observed data. For this reason, values calibrated in previous studies for the downstream stretches of the same rivers were applied here. As regards the 2D models, for the Parma River, we adopted the Manning coefficient equal to 0.033 m^1/3s⁻¹ as suggested by [18], while for the Enza River, the values 0.04 and 0.06 m^1/3s⁻¹ were set for the channel and vegetated banks, respectively, as suggested by [27]. In the absence of previous calibrations of 1D models, the same values were used for the 0D–1D model. Inside the reservoirs, the roughness had to be set only for the fully 2D models. Considering that previous studies [9] showed that the flow dynamics inside a reservoir are not very sensitive to roughness, a literature value of 0.05 m^1/3s⁻¹ (floodplains with light brush and trees [28]) was assumed for both case studies without further analysis.

3. Results

3.1. On-Stream Reservoir on the Parma River

Figure 4a compares the Parma River reservoir’s inflow and outflow discharge hydrographs. The inflow was set as the upstream boundary condition and is the same for both 0D–1D and 2D approaches, while little differences are present in the outflow discharge extracted just downstream of the flood-control dam. The peak discharge is effectively attenuated by the flood-control system, as the peak value is reduced by about 45% compared with the inflow. The two modeling approaches provide very similar results, except for slight differences near the peak: the maximum outflow discharge is about 25 m³/s larger in the 2D model compared with the 0D–1D model (less than 5% relative to the total discharge).

Figure 4b shows the time series of the water surface elevations in the reservoir: the single available level provided by the 0D model is compared with the results of the fully 2D model, which were extracted at three locations (see Figure 4c), including one just upstream of the flood-control dam (P1), one further upstream along the river channel (P2), and one in an initially dry area on the hydraulic right (P3). These results show that, for this severe flood event, the reservoir is filled completely, and the dam’s overflow spillway is activated between time t ≈ 18 h and t ≈ 24 h. Overall, the maximum water level predicted by the two models differs by less than 10 cm. The 0D levels closely match the 2D results at point P1, which lies in the most depressed area of the reservoir. However, the 2D model provides more insight into the inundation dynamics of the basin, e.g., showing that point P3 is flooded only around t ≈ 13 h, while in-channel point P2 is wet from the beginning of the event despite being located at a higher terrain elevation.

To further analyze the reservoir filling dynamics, Figure 5 reports the water depth maps provided by the 2D model at selected times and compares them to the delineation of the flooded area according to the 0D model (based on the stage–area–volume curve). Moreover, Figure 6 represents the local velocity field at the same times as predicted by the 2D model. At the early stages of the process (Figure 5a,b), some significant differences between the two models can be observed. In particular, the 2D model predicts the flood propagation along the main channel, while the 0D model obviously fills the reservoir statically starting from the most depressed areas, including some areas that are not hydraulically linked to the main channel. During this phase, the 2D model reveals that velocities are not negligible (Figure 6a,b), especially in the main channel (values up to 1–2 m/s). However, as soon as the dam starts to attenuate the outflow more decidedly, thus inducing a strong backwater effect in the reservoir, the two models provide very similar flood extents (Figure 5c,d). Velocities are now negligible, except near the upstream inlet (Figure 6c,d). When the maximum filling is reached, the reservoir acts as a lake at rest with depths up to 10 m in the most depressed areas (Figure 5e) and velocities close to zero everywhere, except near the bottom outlets (Figure 6e). Finally, during the emptying process, some discrepancies between the two models are still visible due to the permanence of small pools in the 2D maps (Figure 5f) and the presence of non-negligible dynamics in the main channel (Figure 6f). In general, we can conclude that, despite the filling/emptying process being reproduced in greater detail by the fully 2D model, the global behavior of the reservoir (specifically, the flood peak attenuation and the maximum reservoir level) is captured well also by the 0D approach.

3.2. Off-Stream Reservoir on the Enza River

3.2.1. General Description of the System Behavior

Before comparing the results of the two modeling approaches, it is worth describing the general behavior of the flood-control system. To this end, the water depth maps and the velocity vectors at selected times extracted from the 2D model in the vicinity of the dam and weirs are shown in Figure 7. At the beginning of the simulation, the discharge is relatively low and flows through the five bottom dam openings without being diverted to the reservoir (Figure 7a). As the discharge increases, the dam limits the discharge that can flow through the openings, and some of the water is diverted into the off-stream reservoir via the lateral weir located on the left of the dam (Figure 7b). As the process continues, part of the discharge that flows on the lateral weir does not actually enter the off-stream reservoir. Instead, it overtops the emergency weir and flows back into the river downstream of the dam due to the terrain configuration and the high velocities and depths near the reservoir entrance (Figure 7c). Thus, the emergency weir acts as an additional overflow spillway, allowing water to bypass the dam and reducing the net inflow into the reservoir, and it is activated well before the water levels in the reservoir exceed the weir crest elevation. Note that this is an unintended mode of operation, which the 2D model highlights and which has also been observed during real events. When the reservoir is almost full, the emergency weir prevents excessive filling (Figure 7d), and it continues to return water downstream into the river as the upstream discharges reduce, while the lateral weir is almost inactive (Figure 7e). At the end of the event, the reservoir remains full, with water levels reaching up to the emergency weir crest elevation (here, it is assumed that the bottom outlet is closed). Meanwhile, the discharge in the river is no longer limited by the dam (Figure 7f). Incidentally, these maps also illustrate how the flow through the dam can be easily incorporated into the 2D model using IBCs.

3.2.2. Comparison of 0D–1D and 2D Results

The results of the 0D–1D and fully 2D models for this case study are shown in Figure 8, focusing on the upstream reservoir. As regards the 0D–1D model, we show here the results obtained adopting the value C = 1.1 m^1/2s⁻¹ for the lateral weir coefficient, while the results of the sensitivity analysis to this parameter are presented in Section 3.2.3. The discharge hydrographs are extracted for two relevant cross-sections along the river (Figure 8a): one upstream of the flood-control system (A) and one in the river stretch downstream of the dam (B). The discharges flowing through the dam and over the lateral and emergency weirs are also investigated. First, the global behavior of the flood-control system can be analyzed by comparing the discharge hydrographs at cross-sections A and B (Figure 8b). The diversion of a portion of the flood volume into the reservoir leads to an attenuation of the peak discharge by about 19–26%, depending on the modeling approach, with the 2D model predicting a slightly more pronounced peak attenuation than the 0D–1D model (Figure 8b).

Despite the overall behavior of the flood-control system being simulated in a similar way by the two models, some significant differences can be observed by looking at the discharge exchange between the river and the reservoir. It is worth recalling that both modeling approaches adopt the same rating curve for the flow-through dam (Figure 3c), while the lateral and emergency weirs are simulated using different approaches (Section 2.3). The 2D model predicts a larger discharge flowing into the reservoir and a lower discharge flowing through the dam compared with the 0D–1D model. However, the most significant difference concerns the activation of the emergency weir, which affects the net inflow into the reservoir. In the 0D–1D model, this weir is activated only after the unique level in the reservoir exceeds the weir crest elevation (t ≈ 36 h). As discussed in Section 3.2.1, in the 2D approach, water flows from the reservoir back into the river through the emergency weir well before the reservoir is full due to the non-negligible flow dynamics close to the weirs. This difference leads to a delayed activation of the emergency weir for the 0D–1D simulation compared with the 2D model. Overall, the combination of higher discharges released through the dam and through the emergency weir for the 0D–1D model leads to a higher peak value in the attenuated hydrograph at cross-section B compared with the 2D model (Figure 8b). It is worth underlining that the complex behavior of water partially bypassing the dam through the emergency weir can only be captured by the 2D model.

The time series of water levels in the reservoir is represented in Figure 8c. The unique level of the 0D–1D model is compared with the values provided by the 2D model extracted at three locations (see Figure 8a): one just downstream of the inflow weirs (E1), one in the most depressed region of the reservoir (E2), and one in the western portion of the reservoir (E3). Overall, both models predict that the reservoirs are filled to a maximum value that exceeds the crest of the emergency weirs, with excess water volume flowing back into the river downstream. Assuming that the bottom outlet is closed, the water level eventually stabilizes at the emergency weir crest elevation. In general, both models predict a similar maximum level, while the timing is slightly different: the 0D–1D model predicts a faster filling of the reservoir compared with the 2D one (Figure 8c). Moreover, the time series of 2D levels show that the flooding dynamics in the reservoir are not negligible.

To better understand the reservoir filling dynamics, the water depth maps at selected times extracted from the 2D model are compared with the delineation of the flooded area according to the 0D–1D model in Figure 9. Moreover, Figure 10 shows the velocity field predicted by the 2D model. The difference in the beginning of the filling process between the two approaches is quite evident (Figure 9a,b). The 0D–1D model assumes that filling starts from the most depressed area of the reservoir, which is located downstream, and that the water level increases from that point. In contrast, the 2D model predicts the propagation of water from the inflow weir into the reservoir according to the topography. As filling progresses, the area becomes completely submerged, and the two models predict a similar behavior, with water levels progressively increasing (Figure 9c,d) up to a maximum (Figure 9e). The slight decrease in water levels towards the end of the event, due to the activation of the emergency weir, is also captured by both models in a similar way, even if the 2D model predicts some pools of water remaining in the southern part of the reservoir (Figure 9f). The 2D simulation also indicates that velocities are non-negligible during the filling process, especially just downstream of the weir (Figure 10b,c) but, once the reservoir is completely filled, it becomes a sort of lake at rest (Figure 10e,f).

3.2.3. Sensitivity to the Lateral Weir Coefficient (0D–1D Model)

In this section, a sensitivity analysis of the weir coefficients adopted with the 0D–1D model is performed. For each simulation, a different value of the weir coefficient was assumed for the lateral weir ($C=C_W\sqrt{2g}$ equal to 0.77, 1.1, and 1.43 m^1/2s⁻¹).

Figure 11 presents the discharge hydrographs and the water levels in the reservoir. As expected, when the coefficient is increased, the discharge flowing into the reservoir increases while the discharge flowing through the dam decreases (Figure 11a). This results in a faster filling of the reservoir (Figure 11b), and higher levels lead to larger discharges through the emergency weir (Figure 11a). As shown in Figure 11a, the weir coefficient significantly affects the flood wave downstream of the flood-control reservoir (at cross-section B), with the peak discharge increasing from around 715 to 800 m³/s as the weir coefficient grows. Clearly, this large difference in the prediction of the flood attenuation would cause significant uncertainties in the flood hazard assessment along the downstream stretch of the river.

If the 0D–1D results are compared with the 2D ones, the best match for the discharge through the dam and over the weirs is with the simulations with C = 1.43 and 1.1. However, for these values, the downstream hydrograph at cross-section B is overestimated compared with the 2D model. In this cross-section, the closest match is obtained with C = 0.77 (Figure 11a): the lower value of the weir coefficient probably compensates for the inaccurate representation of the early emergency weir activation, which can be described only by the 2D model and which reduces the net inflow into the reservoir. Indeed, the results with C = 0.77 also provide the same timing as regards the reservoir filling compared with the 2D simulation, even if the maximum level is slightly underestimated (Figure 11b). Using a reduced value for the lateral weir coefficient in the 0D–1D model (i.e., C = 0.77 instead of 1.1) can serve as a workaround to better match the 2D results. This adjustment compensates for the incorrect estimation of discharge over the emergency weir.

4. Discussion

In this work, we considered two case studies of flood-control reservoirs to compare the performance of two different modeling approaches in simulating this specific type of flood protection measure. The first approach, established and widely adopted in the practice, involves coupling a 0D model for the reservoir with a 1D model for the river. The second approach uses a fully 2D model for both river and reservoir, an option overlooked in previous studies for two main reasons: (i) the difficulty in including hydraulic structures in 2D models and (ii) the high computational demand.

The first issue was addressed here by adopting internal boundary conditions to describe the flow-through dams. IBCs use rating curves to represent the relationship between the water level upstream of the dam and the discharge flowing through it, overcoming the violation of the shallow water equations assumptions (e.g., hydrostatic pressure distribution, negligible vertical acceleration) in the presence of complex flow induced by the presence of bottom openings and overflow spillways. The results of the 2D simulations for both case studies confirm that IBCs can effectively integrate hydraulic structures into 2D domains without inducing numerical instabilities, even for quite complex cases such as the Enza River (Figure 7). One potential disadvantage can be that a relatively high mesh resolution is necessary for this purpose (e.g., it is suggested that at least 5–10 cells be used to discretize the structure with an IBC). However, the main advantage of IBCs is that a single fully 2D simulation can be performed for the whole river reach, avoiding the necessity of coupling separate models for stretches upstream and downstream of flood-control systems.

The issue of the computational burden of 2D simulations was overcome here thanks to the efficient parallelization of the PARFLOOD code for GPU and to High-Performance Computing (HPC) facilities, which can also relieve the increase in simulation time caused by the adoption of a high spatial resolution for the computational grid. For example, in this work, the Parma River simulation (domain of 10 km² at 2 m resolution, i.e., about 2.5 M cells; flood event lasting 48 h; one IBC) takes only about 30 min to run using an NVIDIA A100 GPU. As regards the Enza River case, it takes about 2.6 h to run on the same device because it is characterized by a slightly larger domain (16 km² at 2 m resolution, i.e., about 4M cells), and the simulation focuses on a longer flood event (96 h), in addition to including 10 IBCs. The ratio between physical and simulation time is, therefore, in the range of 37–96, indicating a very good computational performance, which is also suitable for near-real-time forecast models.

The runtimes could have been further reduced if a multi-resolution grid had been adopted (e.g., [25,29]). Just as an example, considering the Enza River case, if the maximum resolution of 2 m is maintained only around the dams and weirs and the rest of the domain is discretized with a larger resolution of 4 m (i.e., about 1.2M cells), the computational time becomes 52 min. Discharges and water levels remain almost the same compared with the ones already shown for the 2 m resolution simulation in Section 3.2.2. This suggests that a careful multi-resolution design of the computational grid can overcome the disadvantage of the high-resolution requirement for cells around IBCs. At the same time, a very high resolution for the basin may not be necessary in practice, unless the flow dynamics inside the reservoir are of particular interest for the specific application. Clearly, in general, the selection of the most appropriate resolution depends on the simulation purpose, on the availability of terrain data (i.e., DTMs), and on the presence of other areas of particular interest (e.g., levees, urban areas, etc., in addition to the structures included by means of IBCs) that require high resolution to be accurately modeled.

As regards the comparison of fully 2D with 0D–1D modeling, in terms of runtimes, it is stressed that 0D–1D simulations can be run in a very short time without requiring dedicated hardware. For the case studies considered here, they take only 10–20 s to run, which makes them very competitive for real-time forecasting and/or probabilistic analyses based on multiple simulations. As regards the accuracy of the results, our comparison shows that, for on-stream reservoirs such as the Parma River case (characterized by limited flow dynamics in the basin), both approaches provide similar results. The largest differences are identified in the early stages of reservoir filling and the last stages of the emptying process (Figure 5), for which the 2D model captures the process in a more realistic way. When the basin is almost full and behaves like a lake at rest, the two models provide almost identical results. The suitability of the 0D approach for in-stream reservoirs with very limited dynamics confirms the outcomes of previous studies [14], although they only compared the 0D results with the fully 1D approach and considered a multi-purpose reservoir (always partially full), so the dynamics of filling/emptying could not be analyzed.

For off-stream basins, the differences between the two modeling approaches can be more pronounced. For the Enza River case, which is characterized by a very complex flow field near the reservoir’s entrance, the 2D model can provide a more realistic representation of the discharge splitting between the flow-through dam and the lateral weir’s overtopping compared with the 0D–1D model. Moreover, only the 2D model can predict the emergency weir’s early activation. Inside the reservoir, the inundation dynamics are better predicted by the 2D model, as expected: the 0D representation of the basin makes flooding start from the depressed areas downstream, whereas the 2D model correctly predicts water entering from the weir. As previously for the on-stream reservoir, the two models show similar results when the reservoir is filled and velocities are close to zero. Despite the differences concerning the water volume exchanges between the river and reservoir for the case of the Enza River, the overall flood attenuation predicted by the 0D–1D model is in line with the predictions of the 2D. Previous studies that compared the 0D or 2D representation of the reservoir also highlighted the suitability of the 0D approach for a global evaluation of the flood attenuation, while the 2D approach provides more comprehensive results for the filling/emptying process of the basin [9,16].

In this work, however, a significant sensitivity of 0D–1D results to the empirical coefficient of the lateral weir equation has been observed (Section 3.2.3). In the absence of calibration data, the results of the 2D model could be used to estimate a more reliable value (or range) for the empirical coefficients of the 0D–1D model, thus improving its accuracy.

Rating curves and/or empirical relations are required by both 2D and 0D–1D to represent the flow through the structures in a reliable way. Obviously, the best option would be to define calibrated coefficients/relationships based on field measurements or physical modeling, but unfortunately, these data are often unavailable. For example, in the case studies presented here, experimental data from physical models were only available for the rating curves of the dams, whose sensitivity was therefore not analyzed here, while for the lateral weirs, only literature values could be used. Moreover, the limited field data from previous flood events were hardly applicable for calibration in these cases because of the large uncertainty of inflow hydrographs (due to the absence of upstream gauge stations). This suggests the importance of equipping flood-control systems with monitoring stations both for operational purposes and for improving the understanding of flood attenuation processes in view of numerical model implementation.

In addition to the specific representation of hydraulic structures, other parameters that may influence the 2D numerical results inside the reservoir are the spatial resolution and the roughness coefficient adopted for the area. The latter parameter was not analyzed here, considering that the outcomes of previous works showed that it has limited influence on the flow dynamics [9]. The same authors [9] also analyzed the sensitivity to the spatial resolution and showed that after increasing the mesh size from 8 m to 25 or 50 m, the results were influenced only at the early stages of the filling process. In this work, simulations conducted for the Enza River case at the resolutions of 2 and 4 m provide very similar results, but a specific analysis for lower resolutions was not performed and is left to future works.

Finally, it should be remarked that the flood attenuation induced by the reservoir may depend on the inflow hydrograph (peak, volume, and shape) [5]. In this work, we focused on a single flood scenario, since the goals were to check the suitability of fully 2D models with IBCs for simulating complex flood-control systems and to compare it with the 0D–1D approach. Further analyses on the influence of the inflow hydrograph and the possible simulation of real flood events are left to future works.

5. Conclusions

In this work, the applicability of a fully 2D SWE model with IBCs to simulate flood-control systems was analyzed. The model was able to capture both the flood attenuation and the filling/emptying process of the reservoir realistically. The fully 2D results were also compared with a simpler 0D–1D model. While for on-stream reservoirs (characterized by very limited flood dynamics) both approaches provide similar results, for off-stream reservoirs, the 2D model is the only one able to capture the local flow field generated in this complex system. The drawback of the higher computational requirement of fully 2D codes compared with the 0D or 1D models can be significantly reduced by resorting to efficient 2D models (e.g., parallelized on GPU), such as the one considered here. Therefore, the 2D approach can be used not only for detailed local hydraulic studies but also for river-scale analyses, including flood-control reservoirs.