MODIS Evapotranspiration Forecasting Using ARIMA and ANN Approach at a Water-Stressed Irrigation Scheme in South Africa
Abstract
1. Introduction
2. Materials and Methods
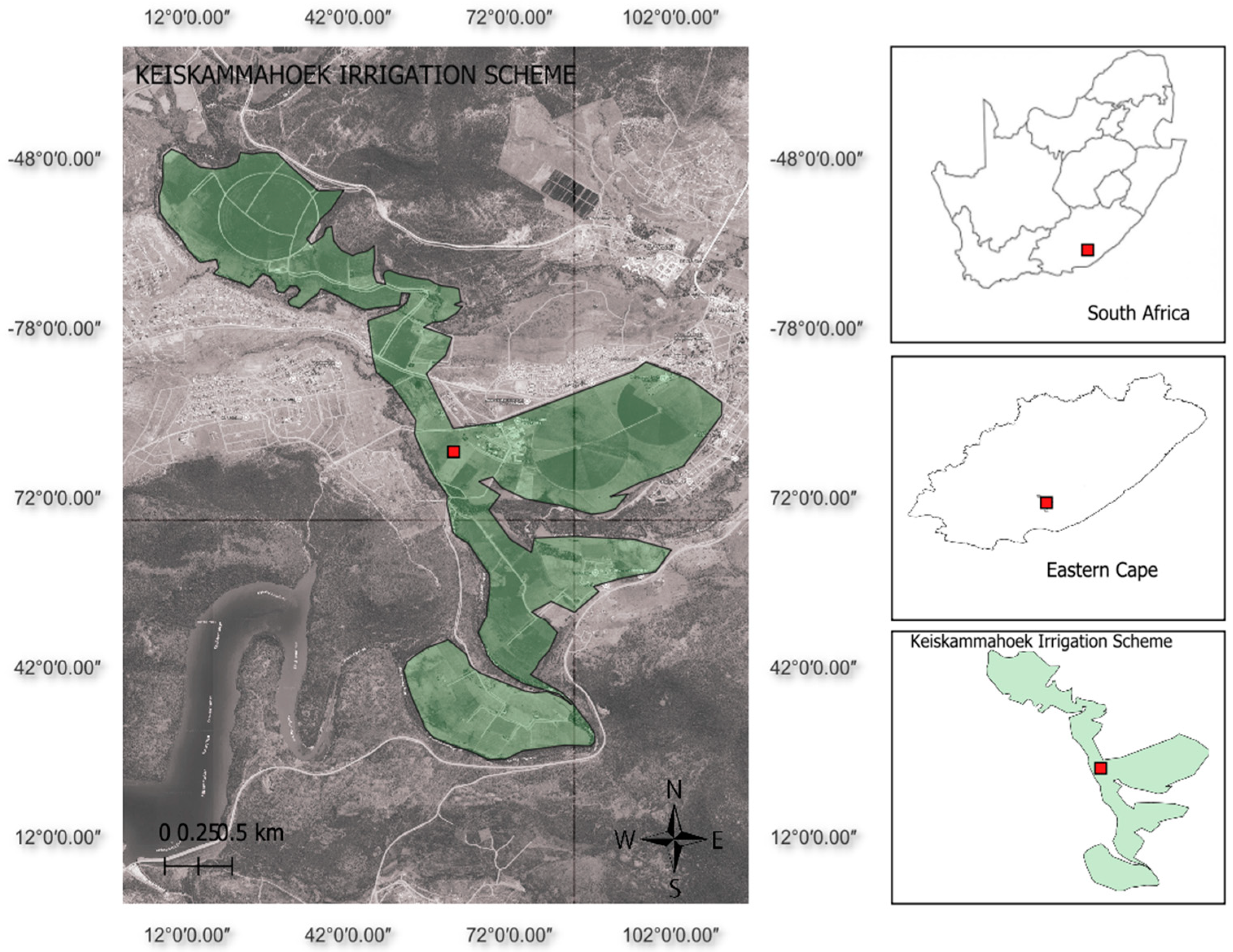
2.1. Study Area
2.2. Data Collection
2.3. Wavelet Analysis
2.4. Wavelet Coherence
2.5. Correlation Statistics
2.6. Theil–Sen’s Estimator
2.7. Mann–Kendall Test (MK)
2.8. Sequential Mann–Kendall (SK-MK) Test
2.9. Multi-Linear Regression (MLR) Model
2.10. Autoregressive Integrated Moving Average (ARIMA) Model
2.11. Artificial Neural Network (ANN) Model
2.12. ANN Training
2.13. Model Statistical Performance Evaluation
2.13.1. Root Mean Square Error (RMSE)
2.13.2. Mean Absolute Percentage Error (MAPE)
2.13.3. Mean Absolute Error
2.13.4. Pearson’s Correlation Coefficient
3. Results and Discussions
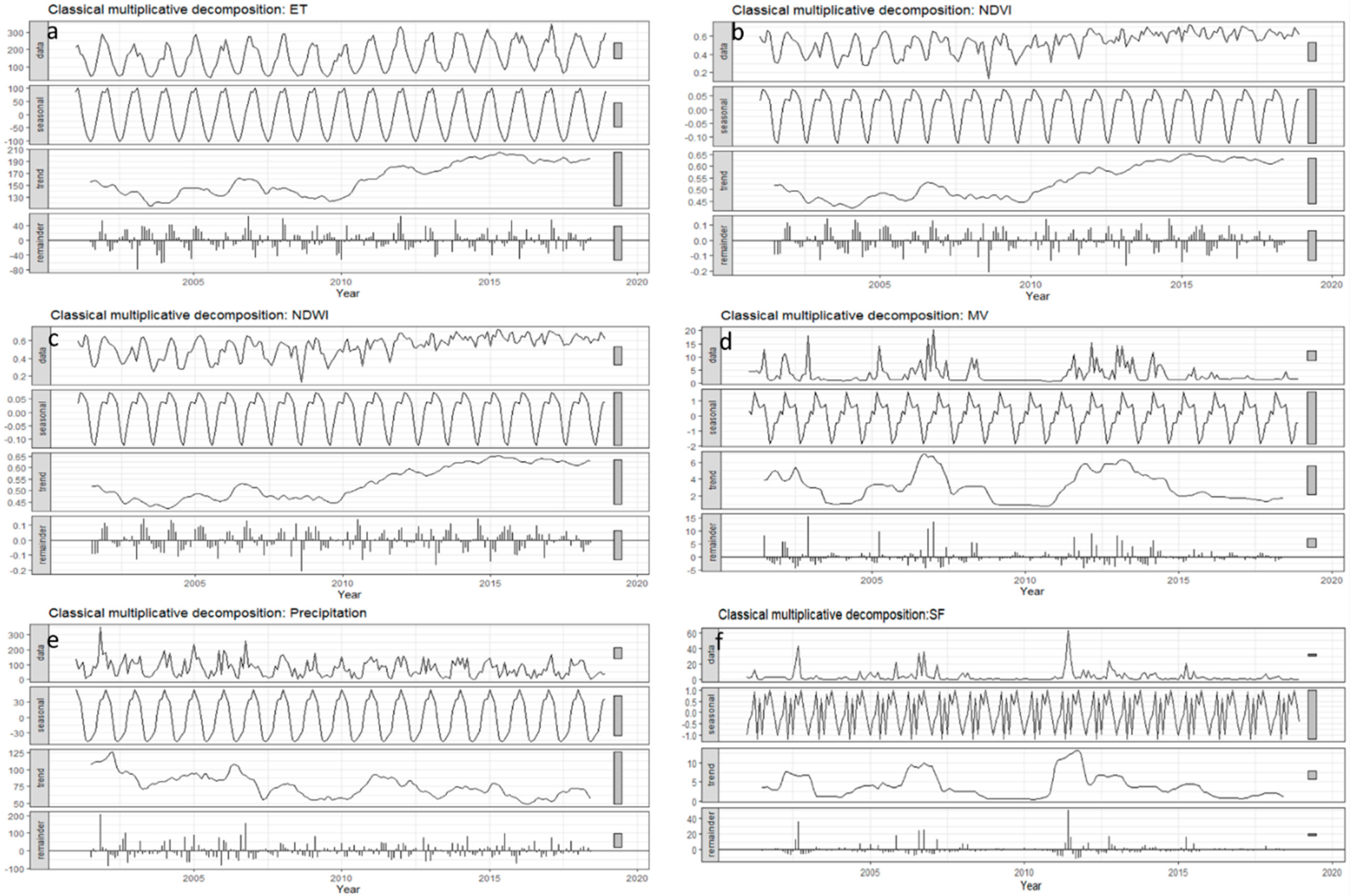
3.1. The Breaks for Additive Seasonal and Trend (BFAST) Analysis
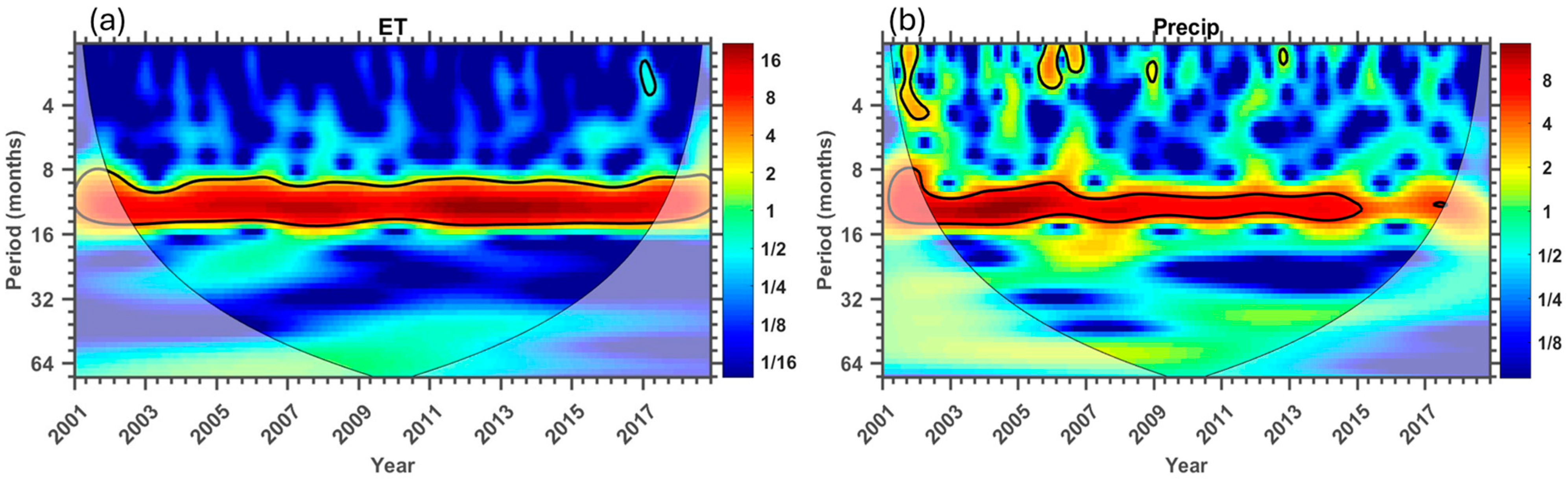
3.2. Wavelength Analysis Results
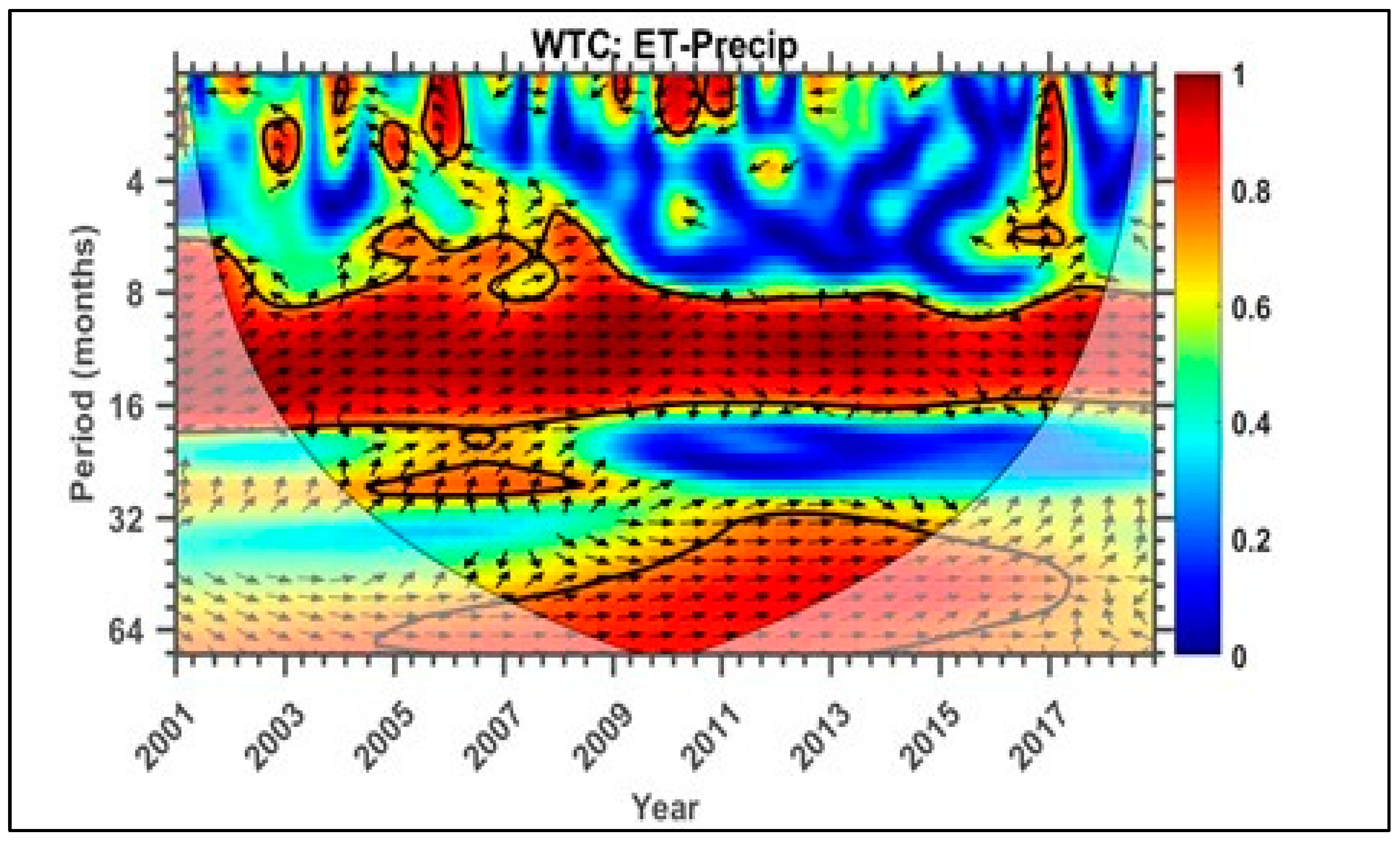
3.3. Wavelet Coherence Results
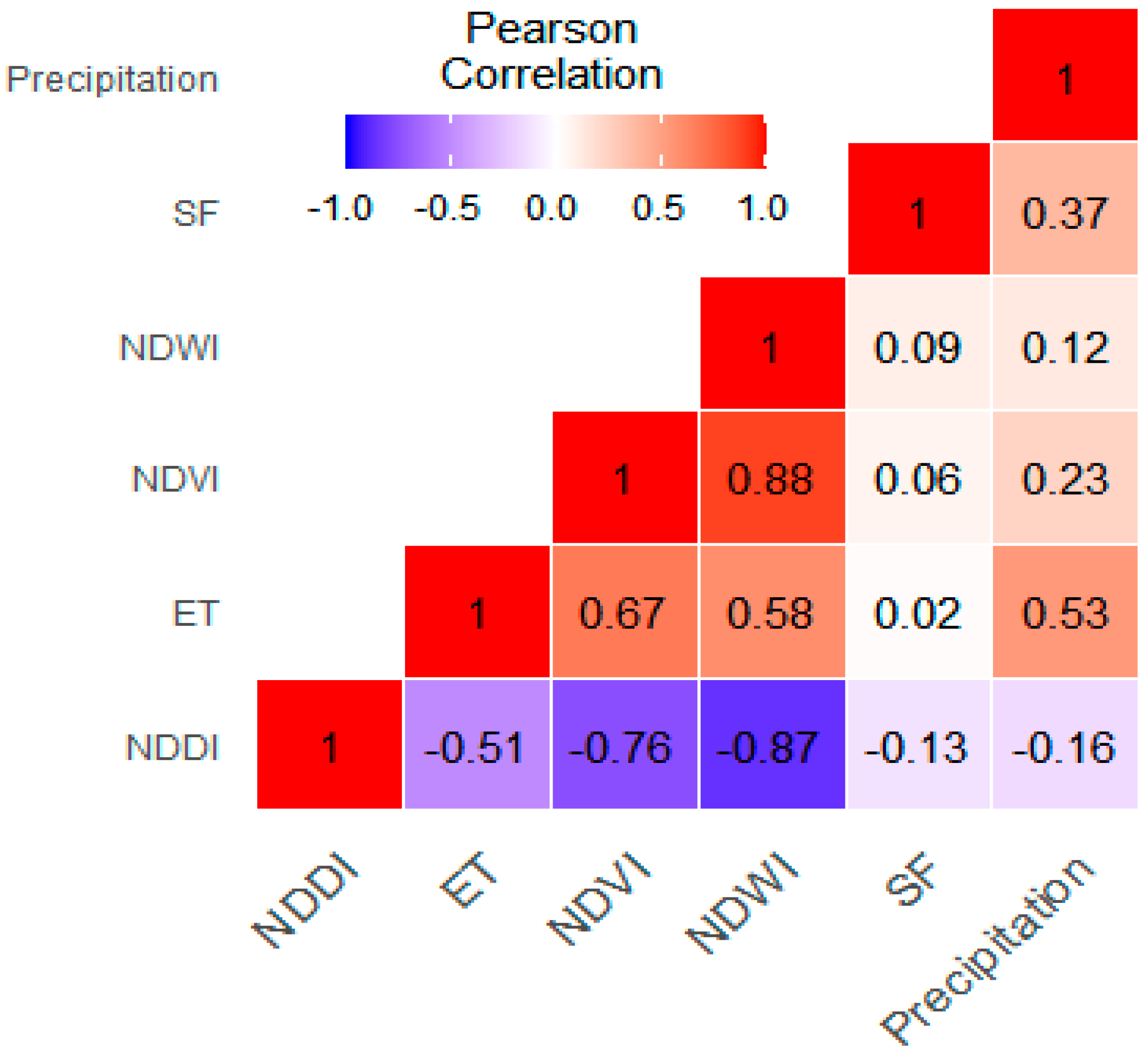
3.4. Correlation Statistics
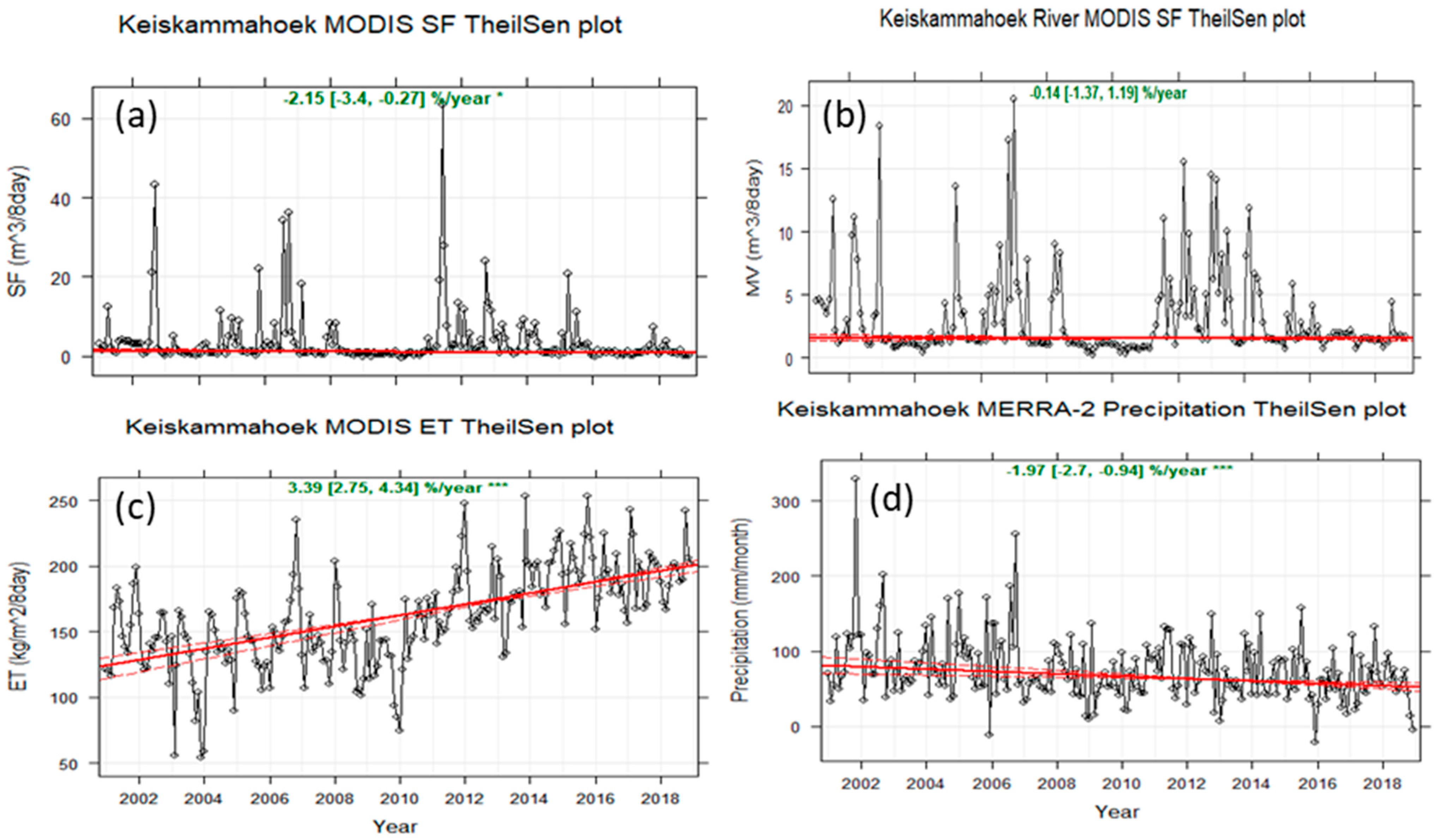
3.5. Theil–Sen Plot
3.6. Mann–Kendall Test (MK)
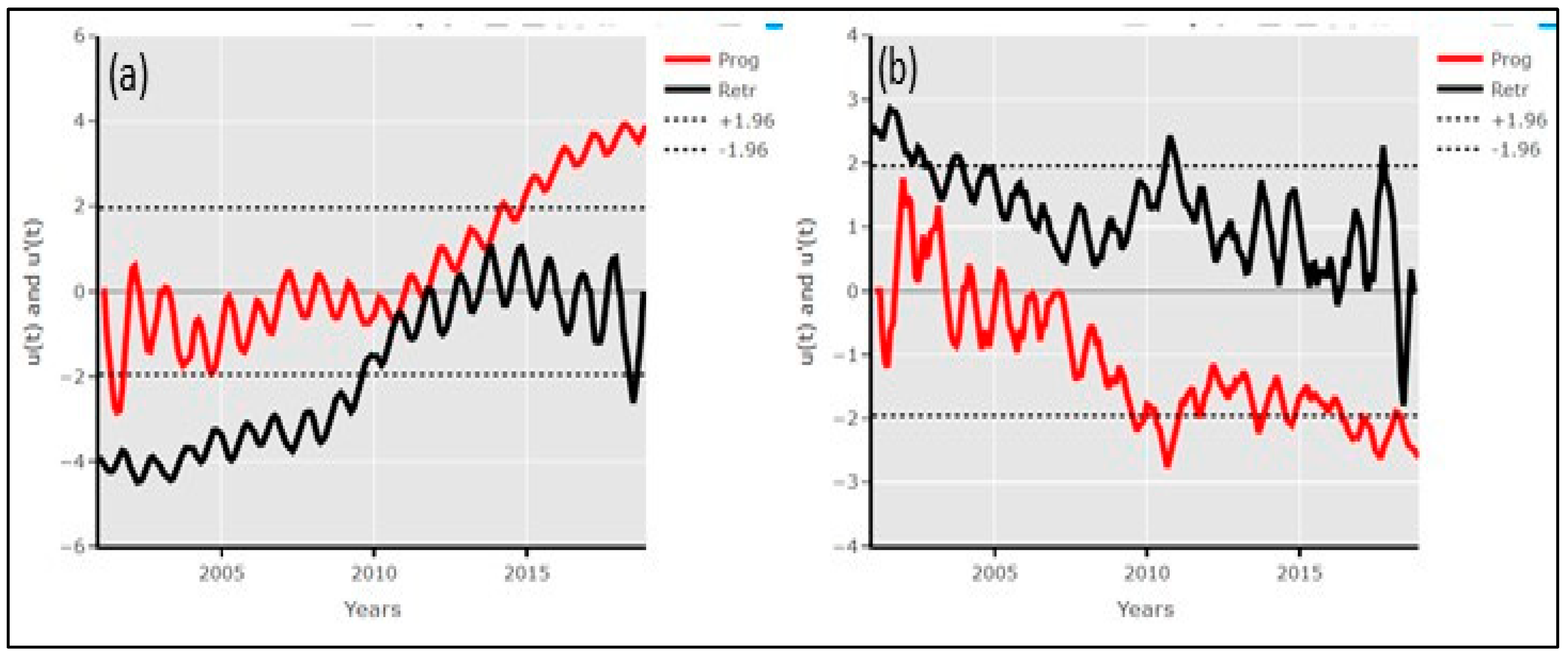
3.7. Sequential Mann–Kendall (SQ-MK)
3.8. Multi-Linear Regression (MLR) Analysis
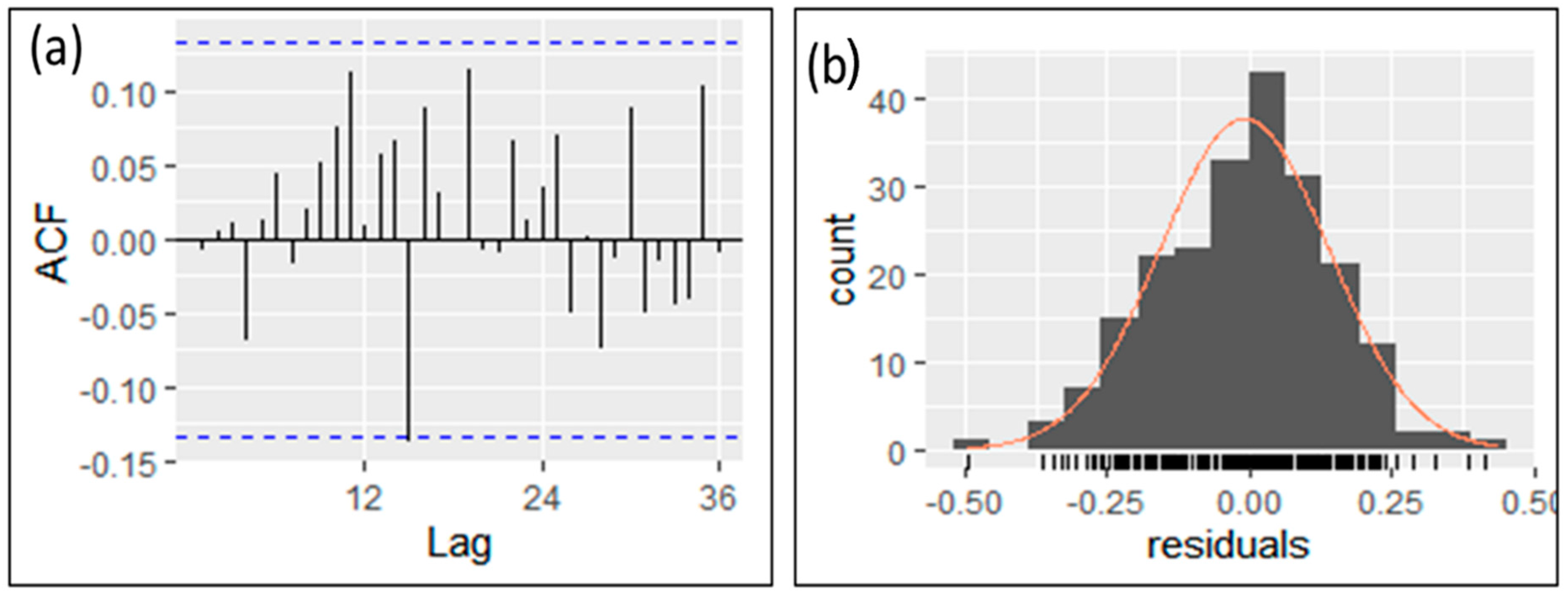
3.9. ARIMA Training and Validation
3.10. ARIMA Forecasting
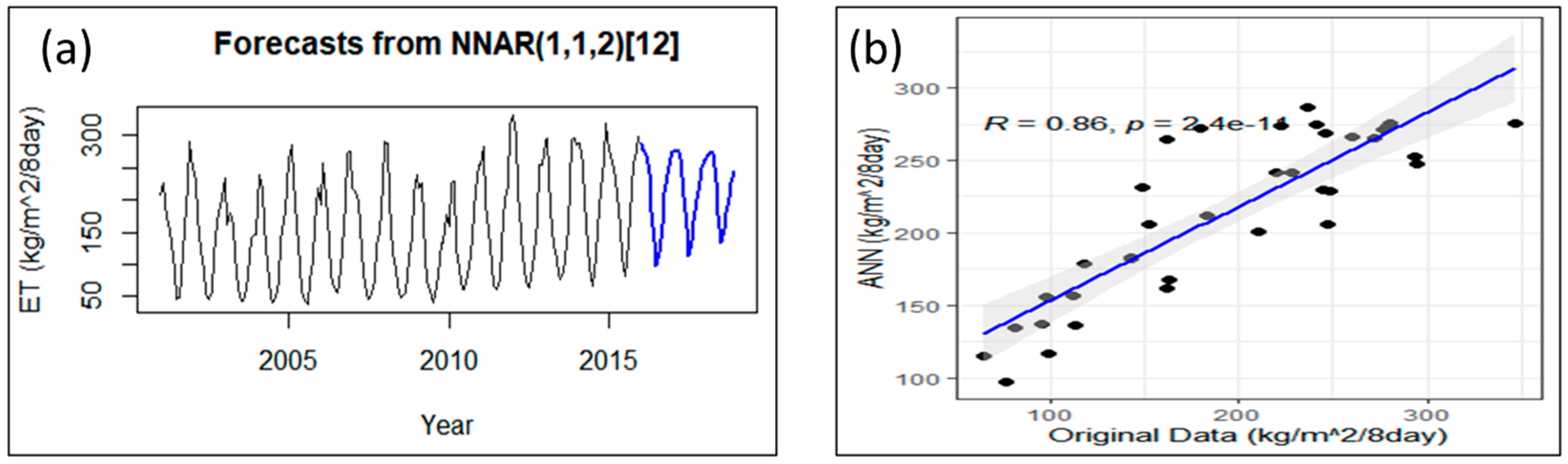
3.11. ANN Modelling
3.12. Model Performance Comparisons
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adebiyi, A.A.; Adewumi, A.O.; Ayo, C.K. Comparison of ARIMA and Artificial Neural Networks Models for Stock Price Prediction. J. Appl. Math. 2015, 2015, 614342. [Google Scholar] [CrossRef]
- Aghelpour, P.; Norooz-Valashedi, R. Predicting daily reference evapotranspiration rates in a humid region, comparison of seven various data-based predictor models. Stoch. Environ. Res. Risk Assess. 2022, 36, 4133–4155. [Google Scholar] [CrossRef]
- Aksoy, S.; Gorucu, O.; Sertel, E. Drought Monitoring using MODIS derived indices and Google Earth Engine Platform. In Proceedings of the 2019 8th International Confrence on Agro geoinformatics, Istanbul, Turkey, 16–19 July 2019. [Google Scholar]
- Albalawi, S. River Water Level Forecasting with Adaptive ARIMA and Extreme Learning Machine Models. Doctoral Dissertation, Flinders University, College of Science and Engineering, Adelaide, Australia, 2023. [Google Scholar]
- Aouissi, J.; Benabdallah, S.; Chabaâne, Z.L.; Cudennec, C. Evaluation of potential evapotranspiration assessment methods for hydrological modelling with SWAT—Application in data-scarce rural Tunisia. Agric. Water Manag. 2016, 174, 39–51. [Google Scholar] [CrossRef]
- Archer, E.; Du Toit, J.; Engelbrecht, C.; Hoffman, M.T.; Landman, W.; Malherbe, J.; Stern, M. The 2015-19 multi year drought in the Eastern Cape, South Africa: It’s evolution and impacts on agriculture. J. Arid Environ. 2022, 196, 104630. [Google Scholar] [CrossRef]
- Bencherif, H.; Toihir, A.M.; Mbatha, N.; Sivakumar, V.; Du Preez, D.J.; Bègue, N.; Coetzee, G. Ozone variability and trend estimates from 20-years of ground-based and satellite observations at Irene Station, South Africa. Atmosphere 2020, 11, 1216. [Google Scholar] [CrossRef]
- Carter, C.; Liang, S. Evaluation of ten machine learning methods for estimating terrestrial evapotranspiration from remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 86–92. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Chen, L.; Lai, X. Comparison between ARIMA and ANN models used in short-term wind speed forecasting. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 March 2011; pp. 1–4. [Google Scholar]
- Cunha, A.; Alvalá, R.C.; Nobre, C.A.; Carvalho, M.A. Monitoring vegetative drought dynamics in the Brazilian semiarid region. Agric. For. Meteorol. 2015, 214, 494–505. [Google Scholar] [CrossRef]
- Dang, X.; Peng, H.; Wang, X.; Zhang, H. Theil-sen estimators in a multiple linear regression model. Olemiss Edu 2008, 2, 1–30. [Google Scholar]
- de Andrade, B.C.C.; de Andrade Pinto, E.J.; Ruhoff, A.; Senay, G.B. Remote sensing-based actual evapotranspiration assessment in a data-scarce area of Brazil: A case study of the Urucuia Aquifer System. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102298. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Dias, S.H.B.; Filgueiras, R.; Fernandes Filho, E.I.; Arcanjo, G.S.; Silva, G.H.d.; Mantovani, E.C.; Cunha, F.F.d. Reference evapotranspiration of Brazil modeled with machine learning techniques and remote sensing. PLoS ONE 2021, 16, e0245834. [Google Scholar] [CrossRef] [PubMed]
- Dile, Y.T.; Ayana, E.K.; Worqlul, A.W.; Xie, H.; Srinivasan, R.; Lefore, N.; You, L.; Clarke, N. Evaluating satellite-based evapotranspiration estimates for hydrological applications in data-scarce regions: A case in Ethiopia. Sci. Total Environ. 2020, 743, 140702. [Google Scholar] [CrossRef] [PubMed]
- Ding, M.; Zhang, Y.; Liu, L.; Zhang, W.; Wang, Z.; Bai, W. The relationship between NDVI and precipitation on the Tibetan Plateau. J. Geogr. Sci. 2007, 17, 259–268. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jhajharia, D.; Fakheri-Fard, A.; Singh, V.P.; Kahya, E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Khabba, S.; Simonneaux, V.; Jarlan, L.; Ouldbba, A.; Rodriguez, J.; Allen, R. Assessment of reference evapotranspiration methods in semi-arid regions: Can weather forecast data be used as alternate of ground meteorological parameters? J. Arid Environ. 2010, 74, 1587–1596. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Meng, E.; Luan, J. Reference evapotranspiration forecasting based on local meteorological and global climate information screened by partial mutual information. J. Hydrol. 2018, 561, 764–779. [Google Scholar] [CrossRef]
- Fashae, O.A.; Olusola, A.O.; Ndubuisi, I.; Udomboso, C.G. Comparing ANN and ARIMA model in predicting the discharge of River Opeki from 2010 to 2020. River Res. Appl. 2019, 35, 169–177. [Google Scholar] [CrossRef]
- Garrote, L. Managing water resources to adapt to climate change: Facing uncertainty and scarcity in a changing context. Water Resour. Manag. 2017, 31, 2951–2963. [Google Scholar] [CrossRef]
- Gautam, R.; Sinha, A.K. Time series analysis of reference crop evapotranspiration for Bokaro District, Jharkhand, India. J. Water Land Dev. 2016, 30, 51. [Google Scholar] [CrossRef]
- Ghauri, S.P.; Ahmed, R.R.; Streimikiene, D.; Streimikis, J. Forecasting exports and imports by using autoregressive (AR) with seasonal dummies and Box-Jenkins approaches: A case of Pakistan. Inžinerinė Ekon. 2020, 31, 291–301. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Gouveia, C.; Bastos, A.; Trigo, R.; DaCamara, C. Drought impacts on vegetation in the pre-and post-fire events over Iberian Peninsula. Nat. Hazards Earth Syst. Sci. 2012, 12, 3123–3137. [Google Scholar] [CrossRef]
- Graw, V.; Ghazaryan, G.; Dall, K.; Delgado Gómez, A.; Abdel-Hamid, A.; Jordaan, A.; Piroska, R.; Post, J.; Szarzynski, J.; Walz, Y. Drought dynamics and vegetation productivity in different land management systems of Eastern Cape, South Africa—A remote sensing perspective. Sustainability 2017, 9, 1728. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Guswa, A.J.; Hamel, P.; Dennedy-Frank, P.J. Potential effects of landscape change on water supplies in the presence of reservoir storage. Water Resour. Res. 2017, 53, 2679–2692. [Google Scholar] [CrossRef]
- Jahromi, M.N.; Zand-Parsa, S.; Razzaghi, F.; Jamshidi, S.; Didari, S.; Doosthosseini, A.; Pourghasemi, H.R. Developing machine learning models for wheat yield prediction using ground-based data, satellite-based actual evapotranspiration and vegetation indices. Eur. J. Agron. 2023, 146, 126820. [Google Scholar] [CrossRef]
- Jha, K.G. Artificial Neural Networks and Its Applications. 2007. Available online: https://www.academia.edu/7575494/ARTIFICIAL_NEURAL_NETWORKS_AND_ITS_APPLICATIONS (accessed on 8 September 2024).
- Ji, Z.; Pan, Y.; Zhu, X.; Zhang, D.; Dai, J. Prediction of corn yield in the USA corn belt using satellite data and machine learning: From an evapotranspiration perspective. Agriculture 2022, 12, 1263. [Google Scholar] [CrossRef]
- Jin, Z.; Guo, L.; Lin, H.; Wang, Y.; Yu, Y.; Chu, G.; Zhang, J. Soil moisture response to rainfall on the Chinese Loess Plateau after a long-term vegetation rehabilitation. Hydrol. Process. 2018, 32, 1738–1754. [Google Scholar] [CrossRef]
- Jovanovic, N.; Mu, Q.; Bugan, R.D.; Zhao, M. Dynamics of MODIS evapotranspiration in South Africa. Water SA 2015, 41, 79–90. [Google Scholar] [CrossRef]
- Kapoi, K.J.; Alabi, O. Agricultural drought severity assessment using land surface temperature and NDVI in Nakuru Region, Kenya. In Proceedings of the Global Geospatial Conference, Addis Ababa, Ethipia, 4–8 November 2013. [Google Scholar]
- Khair, U.; Fahmi, H.; Al Hakim, S.; Rahim, R. Forecasting error calculation with mean absolute deviation and mean absolute percentage error. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; p. 012002. [Google Scholar]
- Khanna, R.; Plyus; Bhalla, P. Study of Artificial Neural Network. Int. J. Res. Inf. Technol. 2014, 930, 271–276. [Google Scholar]
- Kishore, V.; Pushpalatha, M. Forecasting evapotranspiration for irrigation scheduling using neural networks and ARIMA. Int. J. Appl. Eng. Res. 2017, 12, 10841–10847. [Google Scholar]
- Koutroumanidis, T.; Ioannou, K.; Arabatzis, G. Predicting fuelwood prices in Greece with the use of ARIMA models, artificial neural networks and a hybrid ARIMA–ANN model. Energy Policy 2009, 37, 3627–3634. [Google Scholar] [CrossRef]
- Kumar, M.; Thenmozhi, M. Forecasting stock index returns using ARIMA-SVM, ARIMA-ANN, and ARIMA-random forest hybrid models. Int. J. Bank. Account. Financ. 2014, 5, 284–308. [Google Scholar] [CrossRef]
- Lee, S.-J.; Cho, J.; Hong, S.; Ha, K.-J.; Lee, H.; Lee, Y.-W. On the relationships between satellite-based drought index and gross primary production in the North Korean croplands, 2000–2012. Remote Sens. Lett. 2016, 7, 790–799. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Ge, Y.; Li, H.; Han, F.; Hu, X.; Tian, W.; Tian, Y.; Pan, X.; Nian, Y. Hydrological cycle in the Heihe River Basin and its implication for water resource management in endorheic basins. J. Geophys. Res. Atmos. 2018, 123, 890–914. [Google Scholar] [CrossRef]
- Loua, R.T.; Bencherif, H.; Nkanyiso, M.; Begue, N.; Haunchecome, A.; Bamba, Z.; Sivakumar, V. Study on Temporal Variations of Surface Temperatureand Rainfall at Conakry Airport, Guinea: 1960–2016. Climate 2019, 7, 93. [Google Scholar] [CrossRef]
- Ma, Q. Comparison of ARIMA, ANN and LSTM for stock price prediction. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2020. [Google Scholar]
- Machida, F.; Andrzejak, A.; Matias, R.; Vicente, E. On the effectiveness of Mann-Kendall test for detection of software aging. In Proceedings of the 2013 IEEE International Symposium on Software Reliability Engineering Workshops (ISSREW), Pasadena, CA, USA, 4–7 November 2013; pp. 269–274. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Mbatha, N.; Bencherif, H. Time series analysis and forecasting using a novel hybrid LSTM data-driven model based on empirical wavelet transform applied to total column of ozone at buenos aires, argentina (1966–2017). Atmosphere 2020, 11, 457. [Google Scholar] [CrossRef]
- Mbatha, N.; Xulu, S. Time series analysis of MODIS-Derived NDVI for the Hluhluwe-Imfolozi Park, South Africa: Impact of recent intense drought. Climate 2018, 6, 95. [Google Scholar] [CrossRef]
- Morimoto, T.; Ouchi, Y.; Shimizu, M.; Baloch, M.S. Dynamic optimization of watering satsuma mandarin using neaural networks and genetic algorithms. Elsevier 2007, 93, 1–10. [Google Scholar]
- Mujiyo, N.R.; Komariah, S. Agricultural land dryness distribution using the normalized difference drought index (NDDI) algorithm on Landsat 8 imagery in Eromoko, Indonesia. Environ. Nat. Resour. J. 2023, 21, 127–139. [Google Scholar] [CrossRef]
- Mukaka, M.M. A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Ng, E.K.; Chan, J.C. Geophysical applications of partial wavelet coherence and multiple wavelet coherence. J. Atmos. Ocean. Technol. 2012, 29, 1845–1853. [Google Scholar] [CrossRef]
- Obilor, E.I.; Amadi, E.C. Test for significance of Pearson’s correlation coefficient. Int. J. Innov. Math. Stat. Energy Policies 2018, 6, 11–23. [Google Scholar]
- Palacios-Orueta, A.; Khanna, S.; Litago, J.; Whiting, M.L.; Ustin, S.L. Assessment of NDVI and NDWI spectral indices using MODIS time series analysis and development of a new spectral index based on MODIS shortwave infrared bands. In Proceedings of the 1st International Conference of Remote Sensing and Geoinformation Processing, Trier, Germany, 7–9 September 2006; pp. 207–209. Available online: https://blogs.upm.es/dynamicland/wp-content/uploads/sites/294/2019/06/Palacios_etal_2006.pdf (accessed on 5 August 2018).
- Parasuraman, K.; Elshorbagy, A.; Carey, S.K. Modelling the dynamics of the evapotranspiration process using genetic programming. Hydrol. Sci. J. 2007, 52, 563–578. [Google Scholar] [CrossRef]
- Parry, M.L.; Carter, T. An assessment of the effects of climatic change on agriculture. Clim. Chang. 1989, 15, 95–116. [Google Scholar] [CrossRef]
- Phesa, M.; Woyessa, Y.; Mbatha, N. Evapotranspiration Prediction Using ARIMA, ANN and Hybrid Models for Optimum Water Use in Agriculture: A Case Study of Keiskammahoek Irrigation Scheme, Eastern Cape, South Africa. In Proceedings of the 3rd International Symposium on Water, Ecology and Environment—ISWEE; SciTePress: Beijing, China, 2023. [Google Scholar]
- Qi, J.; Du, J.; Siniscalchi, S.M.; Ma, X.; Lee, C.-H. On mean absolute error for deep neural network based vector-to-vector regression. IEEE Signal Process. Lett. 2020, 27, 1485–1489. [Google Scholar] [CrossRef]
- Quilty, J.; Adamowski, J. Addressing the incorrect usage of wavelet-based hydrological and water resources forecasting models for real-world applications with best practices and a new forecasting framework. J. Hydrol. 2018, 563, 336–353. [Google Scholar] [CrossRef]
- Rahman, F.; Devanbu, P. How, and why, process metrics are better. In Proceedings of the 2013 35th International Conference on Software Engineering (ICSE), San Francisco, CA, USA, 18–26 May 2013; pp. 432–441. [Google Scholar]
- Reyes Rojas, L.A.; Moletto-Lobos, I.; Corradini, F.; Mattar, C.; Fuster, R.; Escobar-Avaria, C. Determining actual evapotranspiration based on machine learning and sinusoidal approaches applied to thermal high-resolution remote sensing imagery in a semi-arid ecosystem. Remote Sens. 2021, 13, 4105. [Google Scholar] [CrossRef]
- Reza, A.; Debnath, T. An approach to make comparison of ARIMA and NNAR Models for Forecasting Price of Commodities. Res. Gate 2020. [Google Scholar]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Schultz, A.; Wieland, R.; Lutze, G. Neural networks in agroecological modelling—stylish application or helpful tool? Comput. Electron. Agric. 2000, 29, 73–97. [Google Scholar] [CrossRef]
- Sharma, A.K.; Hubert-Moy, L.; Buvaneshwari, S.; Sekhar, M.; Ruiz, L.; Bandyopadhyay, S.; Corgne, S. Irrigation history estimation using multitemporal landsat satellite images: Application to an intensive groundwater irrigated agricultural watershed in India. Remote Sens. 2018, 10, 893. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S.; Shumway, R.H.; Stoffer, D.S. ARIMA models. In Time Series Analysis and Its Applications, Springer Texts in Statistics; Springer: Cham, Switzerland, 2017; pp. 75–163. [Google Scholar]
- Speer, M.S.; Leslie, L.; MacNamara, S.; Hartigan, J. From the 1990s climate change has decreased cool season catchment precipitation reducing river heights in Australia’s southern Murray-Darling Basin. Sci. Rep. 2021, 11, 16136. [Google Scholar] [CrossRef] [PubMed]
- Tavazohi, E.; Nadoushan, M.A. Assessment of drought in the Zayandehroud basin during 2000-2015 using NDDI and SPI indices. Fresenius Environ. Bull. 2018, 27, 2332–2340. [Google Scholar]
- Tektaş, M. Weather forecasting using ANFIS and ARIMA models. Environ. Res. Eng. Manag. 2010, 51, 5–10. [Google Scholar]
- Torres, A.F.; Walker, W.R.; McKee, M. Forecasting daily potential evapotranspiration using machine learning and limited climatic data. Agric. Water Manag. 2011, 98, 553–562. [Google Scholar] [CrossRef]
- Wanniarachchi, S.; Sarukkalige, R. A review on evapotranspiration estimation in agricultural water management: Past, present, and future. Hydrology 2022, 9, 123. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yuan, X.; Yao, H.; Zhao, Y.; AghaKouchak, A. The interactions between hydrological drought evolution and precipitation-streamflow relationship. J. Hydrol. 2021, 597, 126210. [Google Scholar] [CrossRef]
- Xulu, S.; Peerbhay, K.; Gebreslasie, M.; Ismail, R. Drought influence on forest plantations in Zululand, South Africa, using MODIS time series and climate data. Forests 2018, 9, 528. [Google Scholar] [CrossRef]
- Yang, Y.; Roderick, M.L.; Guo, H.; Miralles, D.G.; Zhang, L.; Fatichi, S.; Luo, X.; Zhang, Y.; McVicar, T.R.; Tu, Z. Evapotranspiration on a greening Earth. Nat. Rev. Earth Environ. 2023, 4, 626–641. [Google Scholar] [CrossRef]
- Yin, J.; Deng, Z.; Ines, A.V.; Wu, J.; Rasu, E. Forecast of short-term daily reference evapotranspiration under limited meteorological variables using a hybrid bi-directional long short-term memory model (Bi-LSTM). Agric. Water Manag. 2020, 242, 106386. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks:: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, G.X.; Li, R.R. Water Quality Analysis and Prediction Using Hybrid Time Series and Neural Network Models. J. Agri. Sci. Tech. 2016, 18, 975–983. [Google Scholar]

| Variables | Z-Score | Kendall’s Tau | S | Var(S) | p-Value |
|---|---|---|---|---|---|
| ET | 3.898 | 1.782946 × 10−1 | 4.140000 × 103 | 1.127460 × 106 | 9.698 × 10−5 |
| Precipitation | −2.6134 | −1.195521 × 10−1 | −2.776000 | 1.127460 × 106 | 0.008964 |
| SF | −1.7508 | −8.016553 × 10−2 | −1.860000 × 103 | 1.127368 × 106 | 0.07997 |
| MV | 0.60747 | 2.785445 × 10−2 | 6.460000 × 102 | 1.127391 × 106 | 0.5435 |
| NDVI | 8.3291 | 3.809626 × 10−1 | 8.845000 × 103 | 1.127455 × 106 | 2.2 × 10−16 |
| NDWI | 10.021 | 4.583118 × 10−1 | 1.061200 × 104 | 1.127460 × 106 | 2.2 × 10−16 |
| NDDI | −9.8859 | −4.521102 × 10−1 | −1.049800 × 104 | 1.127460 × 106 | 2.2 × 10−16 |
| Parameters | Estimate | Std. Error | t Value | Pr-Value | Sig |
|---|---|---|---|---|---|
| ET | 3.4076197 | 0.2009740 | 16.956 | <2 × 10−16 | *** |
| SF | −0.0156514 | 0.0032221 | −4.857 | 2.32 × 10−6 | *** |
| Precipitation | 0.0045486 | 0.0004318 | 10.534 | <2 × 10−16 | *** |
| NDVI | 2.7564601 | 0.4022261 | 6.853 | 7.89 × 10−11 | *** |
| NDWI | −0.3202777 | 0.5270840 | −0.608 | 0.5441 | |
| NDDI | −0.2901542 | 0.1246038 | −2.329 | 0.0208 | * |
| Models | RMSE | MAE | MAPE | R |
|---|---|---|---|---|
| ARIMA | 37.58 | 32.37 | 17.26 | 0.94 |
| ANN | 44.18 | 35.88 | 24.35 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phesa, M.; Mbatha, N.; Ikudayisi, A. MODIS Evapotranspiration Forecasting Using ARIMA and ANN Approach at a Water-Stressed Irrigation Scheme in South Africa. Hydrology 2024, 11, 176. https://doi.org/10.3390/hydrology11100176
Phesa M, Mbatha N, Ikudayisi A. MODIS Evapotranspiration Forecasting Using ARIMA and ANN Approach at a Water-Stressed Irrigation Scheme in South Africa. Hydrology. 2024; 11(10):176. https://doi.org/10.3390/hydrology11100176
Chicago/Turabian StylePhesa, Mbulelo, Nkanyiso Mbatha, and Akinola Ikudayisi. 2024. "MODIS Evapotranspiration Forecasting Using ARIMA and ANN Approach at a Water-Stressed Irrigation Scheme in South Africa" Hydrology 11, no. 10: 176. https://doi.org/10.3390/hydrology11100176
APA StylePhesa, M., Mbatha, N., & Ikudayisi, A. (2024). MODIS Evapotranspiration Forecasting Using ARIMA and ANN Approach at a Water-Stressed Irrigation Scheme in South Africa. Hydrology, 11(10), 176. https://doi.org/10.3390/hydrology11100176






