Next Article in Journal
ARIMA and TFARIMA Analysis of the Main Water Quality Parameters in the Initial Components of a Megacity’s Drinking Water Supply System
Previous Article in Journal
An Integrated Framework to Assess the Environmental and Economic Impact of Fertilizer Restrictions in a Nitrate-Contaminated Aquifer
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrology
Volume 11
Issue 1
10.3390/hydrology11010009
hydrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparison between MODFLOW Groundwater Modeling with Traditional and Distributed Recharge

by
María del Mar Navarro-Farfán
1,
Liliana García-Romero
2,
Marco Antonio Martínez-Cinco
1,
Mario Alberto Hernández-Hernández
3 and
Sonia Tatiana Sánchez-Quispe
2,*
1
Department of Chemical Engineering, Universidad Michoacana de San Nicolás de Hidalgo, Francisco J. Múgica s/n, Morelia 58030, Mexico
2
Department of Hydraulics, Universidad Michoacana de San Nicolás de Hidalgo, Francisco J. Múgica s/n, Morelia 58030, Mexico
3
Institute of Geophysics, Universidad Nacional Autónoma de México, Circuito de la Investigación Científica s/n, Ciudad Universitaria, Ciudad de Mexico 04510, Mexico
*
Author to whom correspondence should be addressed.
Hydrology 2024, 11(1), 9; https://doi.org/10.3390/hydrology11010009
Submission received: 2 November 2023 / Revised: 3 January 2024 / Accepted: 5 January 2024 / Published: 11 January 2024
(This article belongs to the Section Hydrological and Hydrodynamic Processes and Modelling)
Browse Figures
Review Reports Versions Notes

Abstract

Groundwater models serve the function of predicting and analyzing aquifer behavior. They require input information, such as hydrogeological parameters like hydraulic conductivity and storage coefficient, which are used to calibrate the model, and elementary actions that include recharge and extracted volumes. There are cases in which it is insufficient to know the homogeneous recharge entering through the surface basin, referred to as traditional recharge, since, in many instances, the distribution is altered by changes in land use. For this reason, based on the geomorphological characteristics of the basin, weighting is proposed for sites with greater recharge capacity. The present work shows a solution to the recharge distribution using the potential groundwater recharge (PGR) map, which is formed by weighting spatially distributed information: (i) drainage, (ii) precipitation, (iii) land use, (iv) geological faults, (v) soil type, (vi) slope, and (vii) hydrogeology. A comparison is made between groundwater modeling using traditional recharge and PGR recharge. It is noted that the modeling perform similarly for both recharges, and the errors do not exceed 5% absolute error, which validates the model’s reliability. This manuscript demonstrates how to model and calibrate groundwater in aquifers with scarce information and variable recharge, making it reproducible.

1. Introduction

Groundwater models are essential to understand the behavior of aquifers and, therefore, to make decisions in the planning and management of water resources. This significance is especially emphasized in areas with scarce information [1,2,3] and even droughts [4].
Groundwater models are used to obtain information on piezometric levels in aquifers [5,6] and to track variations in the stored volume over time. These models also allow for studying regional flows [7,8] considering possible recharge and discharge zones [9].
Calibration of a groundwater model involves various methods. This includes comparing regional flow processes [8], flow directions in the aquifer [5,7,10], and the similarity between observed and simulated piezometric levels [5,6,11]. A model can also be calibrated by spring volumes [1] and evapotranspiration [11].
The process of calibration involves adjusting hydrogeological parameters that represent the behavior of water in a porous medium; the parameters are hydraulic conductivity, transmissivity, and the storage coefficient. The parameter that most influences the calibration process and limits the variation in piezometric levels is the hydraulic conductivity, ‘k’ [12].
One of the most relevant elements in groundwater modeling is the representation of recharge as an input component to the subsurface model because it varies spatially and temporally [13,14,15,16]. Changes in land use significantly alter recharge patterns associated with the hydrological cycle [17] and are linked to population increase [2].
Traditionally, recharge is obtained as a sheet of water homogeneously distributed along the aquifer [18], which will be referred to as a traditional recharge. Recharge is influenced by the effect of climate change [19], irrigation returns [10], spatial discretization [20], surface basins [21], or even temporal variations in infiltrations patterns [3,10,22].
When there are areas with significant variability between land use and soil type, recharge is not a uniform pattern, which is why using a spatially distributed recharge according to the conditions of the environment has been proposed. This may generate errors or uncertainties in the model [23].
Recharge discretization is applied in Management Aquifer Recharge (MAR) systems. Criteria have been used to describe the weighting of the recharge [24,25], integrating surface and subsurface coverages [26], as well as distinct geological features [27]. Within the recharge processes, the sites with the highest possibility of recharge should be considered, including alluvial fans [28,29,30] and precipitation [31,32].
This work proposes a method for weighted aquifer recharge using the potential groundwater recharge (PGR) map [33,34]. The weighted recharge considers recharge variations spatially depending on the characteristics of the area under study [35], processing and manipulating thematic layers in a geographic information system [30,36,37,38,39]. The PGR map incorporates spatially distributed information: (i) drainage, (ii) precipitation, (iii) land use, (iv) geological faults, (v) soil type, (vi) slope, and (vii) hydrogeology [30,33,34,35,36,37,38,39].
The modeling carried out with the weighted recharge will be compared with the recharge that we have called traditional recharge to verify the reliability of the proposal.
The PGR method allows for a comprehensive consideration of the dynamic nature of land use and soil type in areas characterized by spatial and temporal variability. It is a useful tool for understanding the change that recharge has undergone.
This manuscript explains the case study, detailing the methodology employed, the specific results comparing traditional and weighted recharge, and the overall results.

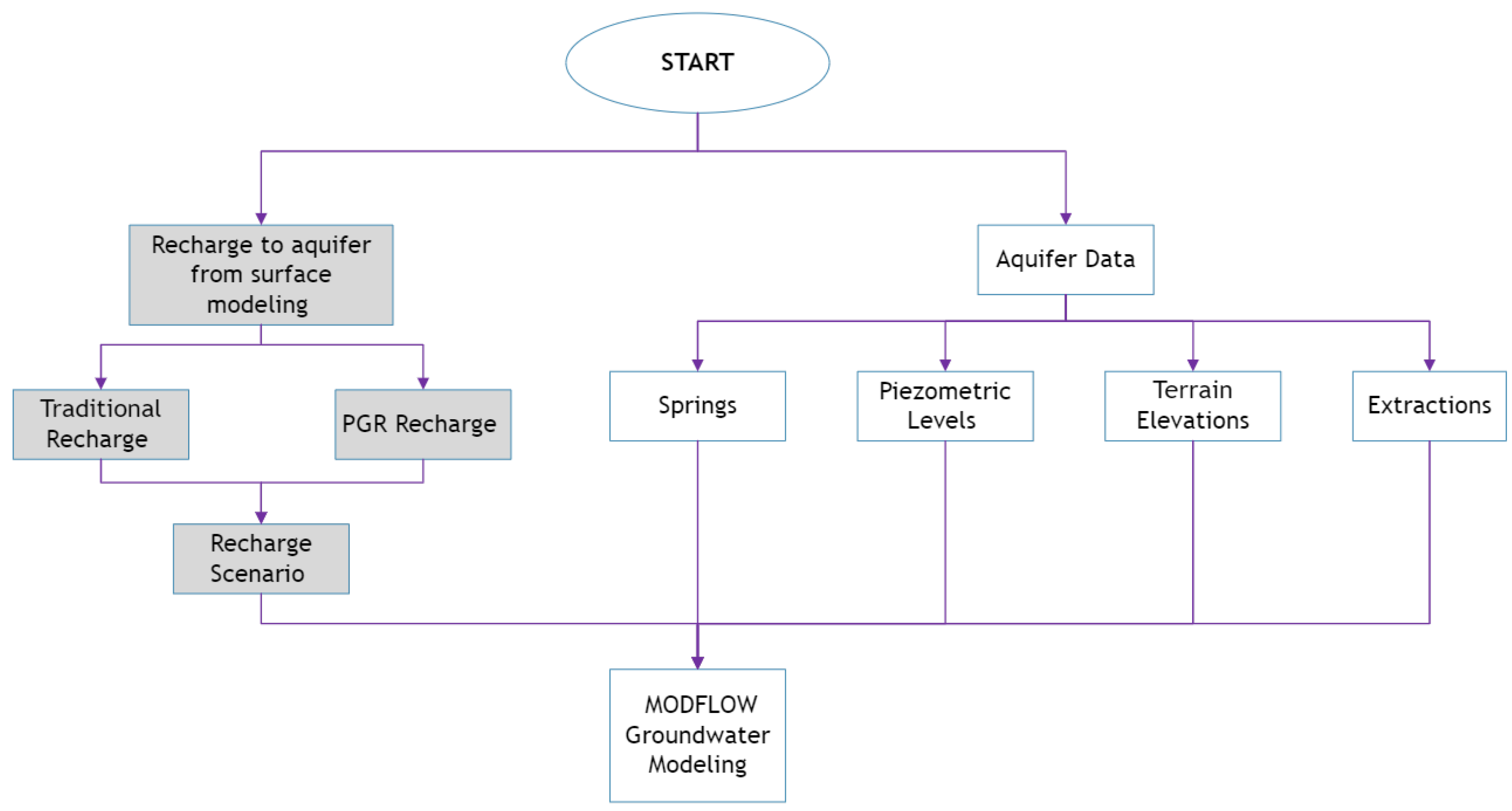
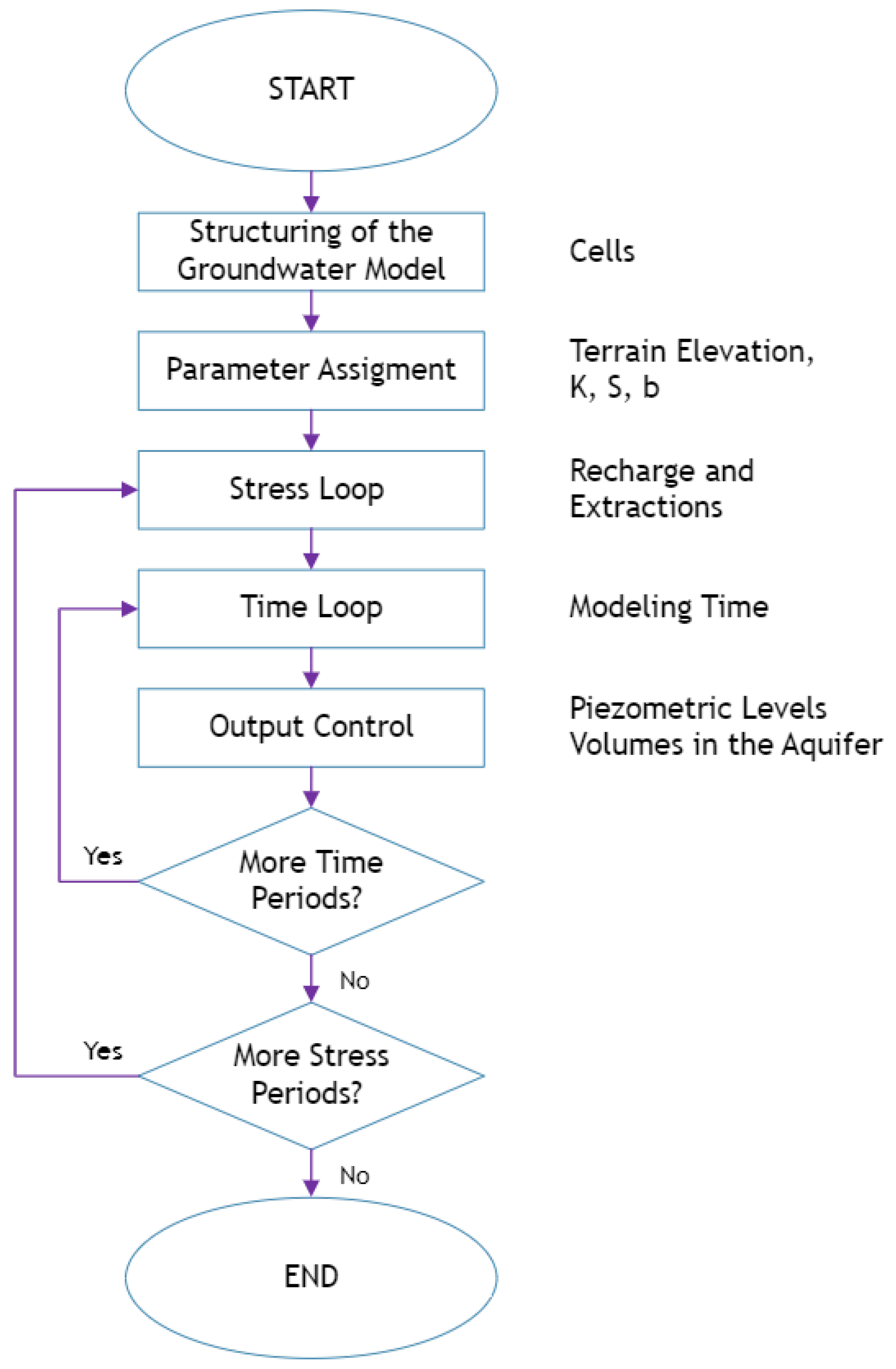
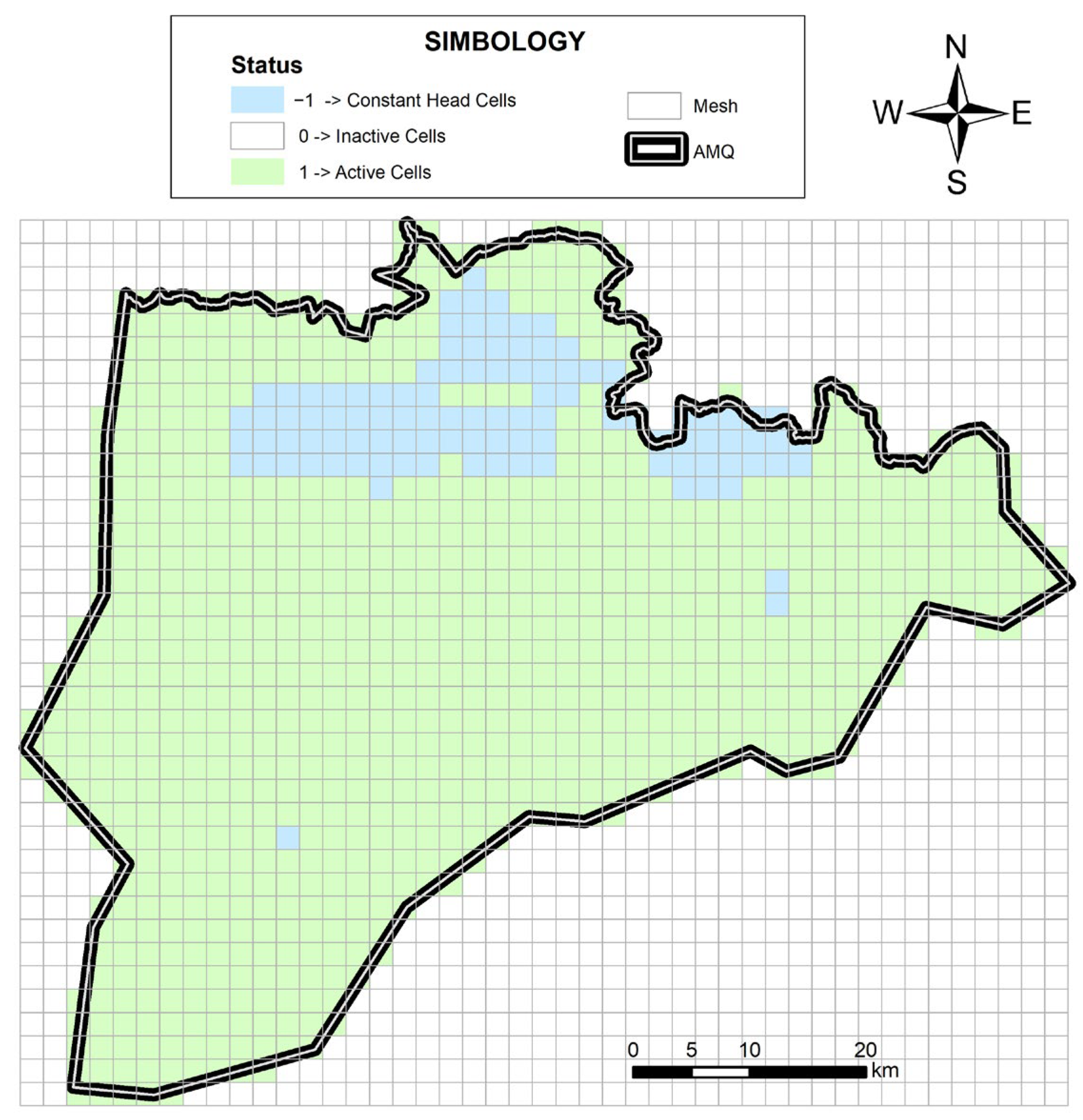
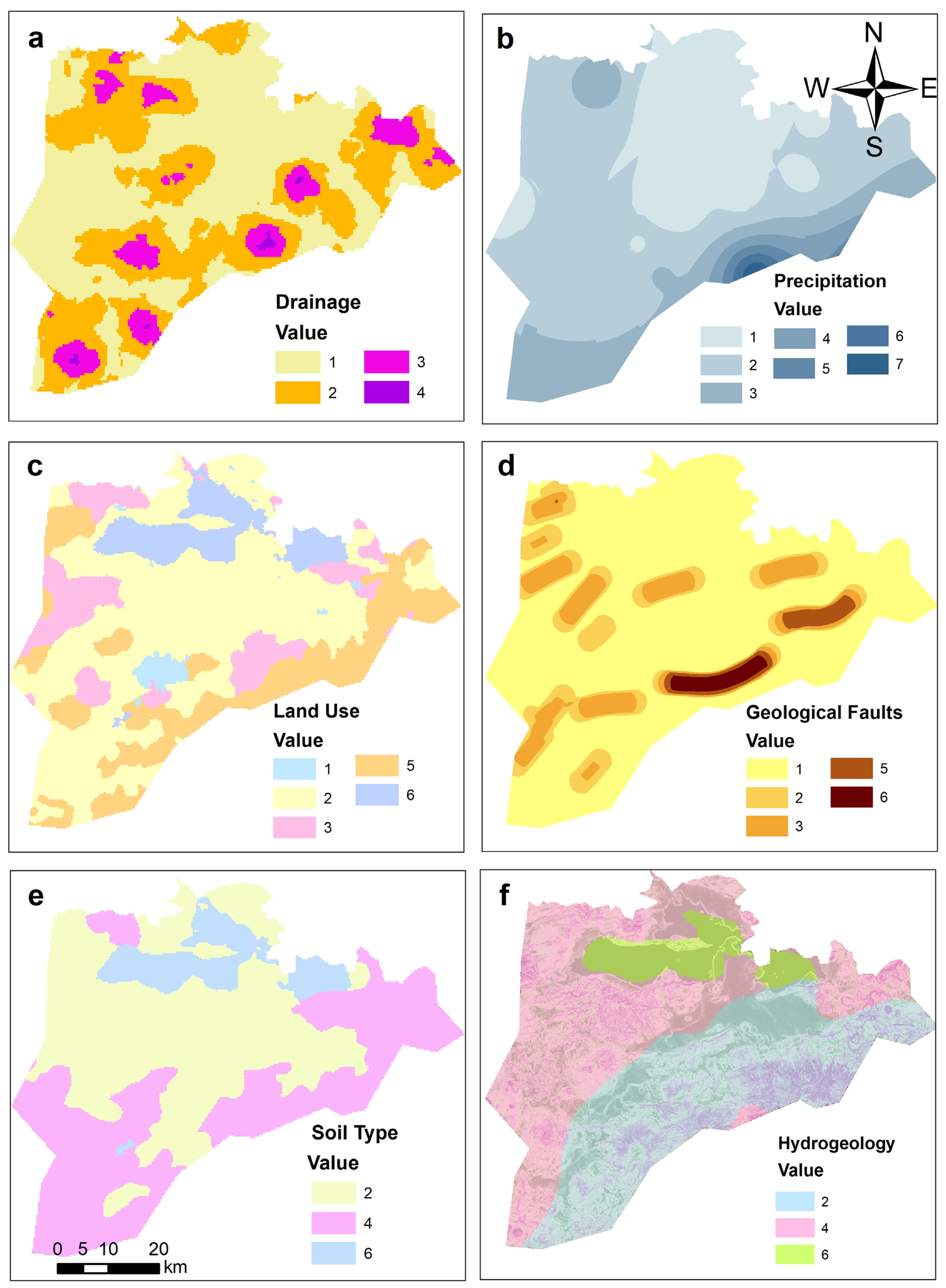
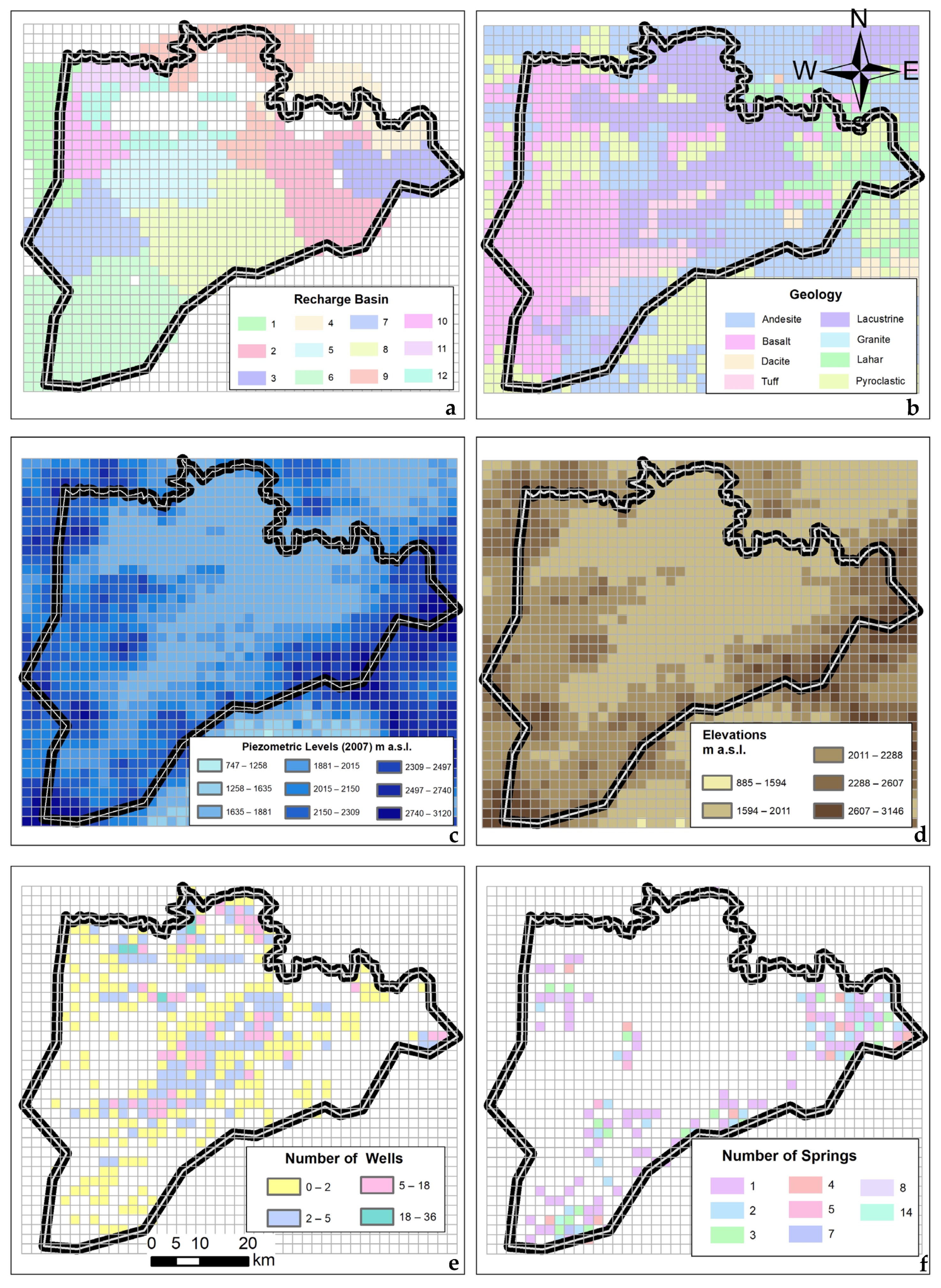
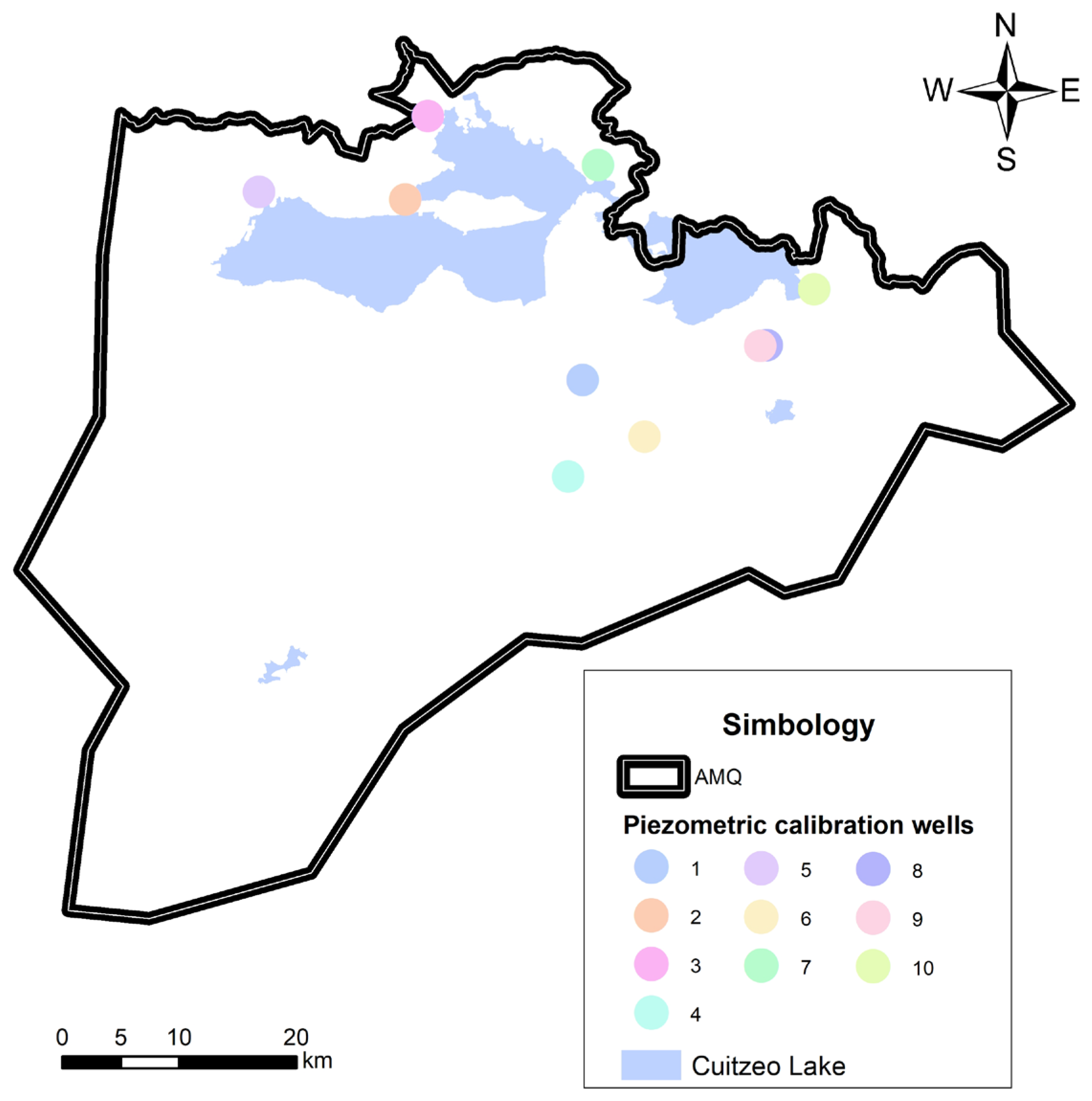
2. Materials and Methods

Groundwater modeling was performed using the PMWIN-MODFLOW software (version 8.0.40) [40] and following the methodology described in Figure 1.
The main motivation for the use of PMWIN-MODFLOW was that it allows for distributed aquifer monitoring and, subsequently, the possibility of carrying out future studies, such as research on the transport of potentially toxic elements [41,42,43]. This model was selected because it fits the needs of the project.
The methodological process employed in the work was carried out employing groundwater modeling using MODFLOW, which requires information on springs, piezometric levels, natural terrain elevations, and groundwater extractions. The modeling was performed using two types of recharge: (i) homogeneous (traditional) recharge and (ii) recharge from the PGR map.
The most important part of the modeling was the focus on the different types of recharge distribution. Recharge was obtained by the soil moisture method, developed in the WEAP (Water Evaluation and Planning System) software (Version: 2019.2134 (Beta)) [44].
The aquifer’s calculated recharge is distributed throughout the study area, which can occur in two ways. The first type is traditional recharge, which is distinguished by a homogeneous distribution of the volume of water throughout the area regardless of the geomorphological characteristics of the basin. The second type is weighted recharge, which discretizes the basin into units of area to establish the percentage of water volume to be recharged depending on the capacity of each zone.
Weighted recharge comes from the map of potential groundwater recharge (PGR map [30,33,34,35,36,37,38,39]. The PGR map is made by weighting thematic layers, where the recharge behavior is interpreted according to the capacity of each layer.
The PGR map was obtained from national databases integrating vector files [45,46]. The precipitation map was made through the interpolation [47] of meteorological information [48] that, together with the drainage map, was processed in a geographic information system.
The groundwater model should be discretized into cells established by rows and columns that completely cover the study area. These should allow the information needed for modeling to be representative in each cell [40].
Groundwater modeling requires data about natural terrain elevation (INEGI, 2023) and aquifer thickness [49]. It also needs information on hydrogeological parameters such as hydraulic conductivity [50] and storage coefficient [51], which depend on the geology [52].
The elementary actions considered in the model are recharge (which may include a percentage of irrigation return) and extracted volumes [53]. The information on piezometric levels was obtained in the field and from official sources [49], from which the flow directions were also acquired.
For the development of groundwater modeling, a model was generated in MODFLOW that solves the finite difference flow equation [40], and Figure 2 illustrates how it works.
Within the diagram shown in Figure 2, the model structuring process refers to the discretization of the study area into cells, which can be of constant height and active and inactive cells; this implies the development and resolution of the flow equation in any part of the model.
The first step is to enter the modeling parameters and the elementary actions that make up the stress loop. Also, the time loop indicates that the model can perform in a steady or transient state. The piezometric levels calculated for each cell and period are obtained in the output control section. The previous step was the model’s point of calibration and validation. If no changes are recorded in the time or stress loops, the modeling process ends. The only requirement for calibration the adjustment of the hydrogeological parameters, looking for values that optimize the model.
In this case, model calibration was performed by comparing piezometric levels measured in different historical periods and the similarity concerning flow directions [5,7,11,54]. The variation between recharges was then calculated to verify whether the model changes when refining the model input data.

3. Study Area

The Morelia–Queréndaro aquifer (AMQ) (Figure 3) provides water to 898 localities in the state of Michoacán. The municipality of Morelia is the state capital and has a population of 849,053 inhabitants [55], of which about 40% are supplied by groundwater.
The Morelia–Queréndaro aquifer records an average annual extraction of 172.65 hm3 [53], which helps supply the city of Morelia, where, as in all of Mexico, approximately 40.3% of the population are supplied by groundwater [56].
The aquifer under study is in deficit, given that more water is withdrawn than recharged [49]. It is fundamental to understand the current behavior to fully comprehend the problem in which the aquifer finds itself.

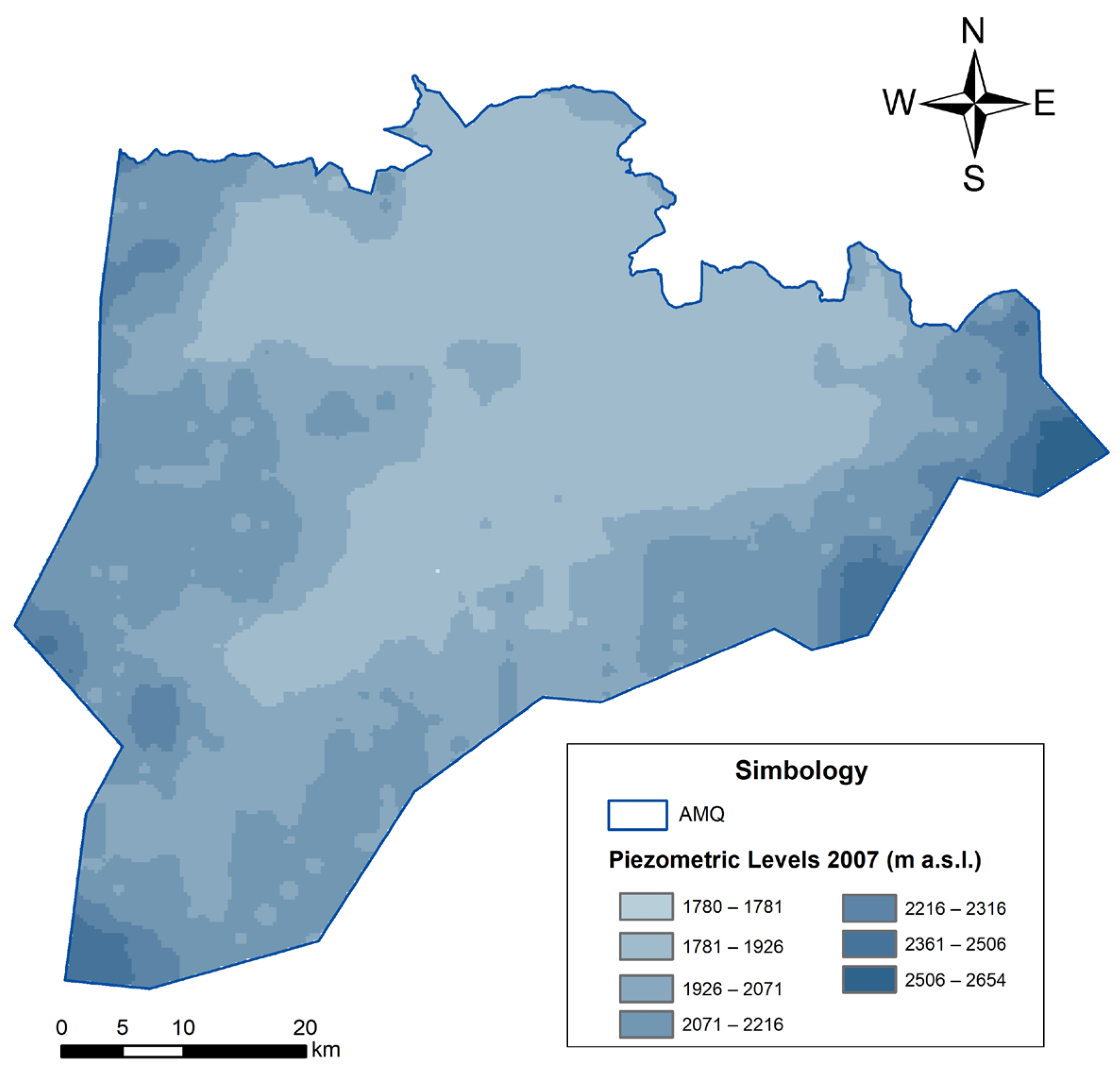
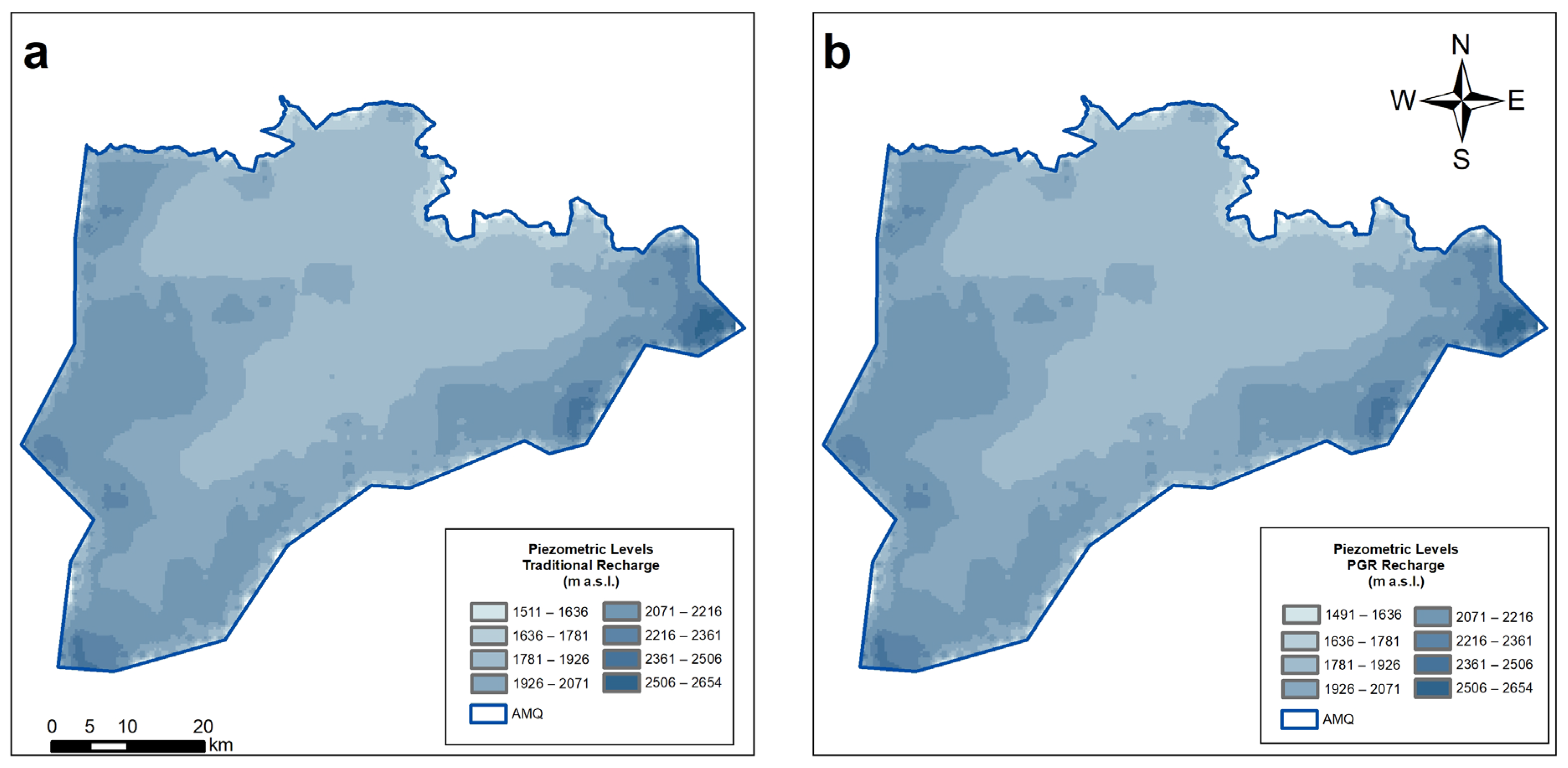
4. Results and Discussion

The Morelia–Queréndaro aquifer was discretized by a 2 km by 2 km grid, divided into 45 columns and 38 rows, of which (Figure 4) there are a total of 973 active cells, 106 constant-height cells, and 867 inactive cells. The constant-height cells correspond to the zones of Lake Cuitzeo, the Cointzio dam, and the Queréndaro dam.
The model works as a semi-confined aquifer, with boundary conditions (constant height) in Lake Cuitzeo. A transient model was made with 192 time periods (October 2006 to September 2022), and three calibration periods are considered: 2008, 2017, and 2022.
Table 1 shows the groundwater balance used for the Morelia–Queréndaro aquifer, which details the inflows and outflows of the aquifer system, as well as the change in storage in the same aquifer, which is known to have an annual deficit of 59,118 ML/year.
Traditional recharge was obtained through calculating the homogeneous distribution of recharge in the basin; this indicates that no sites, regardless of topography, geological faults, or the type of geology itself, influence recharge.
On the other hand, the weighted recharge was obtained using the map of potential recharge zones, which considers the following elements: (a) drainage, (b) precipitation, (c) land use, (d) geological faults, (e) soil type, (f) slope, and hydrogeology (Figure 5).
Table 2 shows the classifications used for the independent maps, considering that value 7 is the one with the greatest recharge capacity and value 1 is considered to have little influence on recharge.
Thus, the reclassified values shown in Table 2 were used to create the thematic layers of the PGR map for Figure 5.
All the thematic layers used for the PGR map were analyzed. The highest drainage density is present in the periphery of the study area, near the hills that border the area. Precipitation values vary from 654 mm/year in the northern zone to 1336 mm/year in the southern zone.
Regarding land use, agriculture has the highest influence on the study site, and the regions of the highest recharge, considering the forest, are in the periphery. The density of faults was obtained utilizing a delimited relationship between the faults’ length and a determined area.
The soil types in the area are fine, medium, and alluvial. The soil that allows the greatest recharge is alluvial soil, such as that found near Lake Cuitzeo. The flatter slopes are in the same area, while the steeper slopes are located on hills bordering the aquifer. Slopes steeper than 10% have no influence on the recharge [57,58].
Concerning the hydrogeological information, there are medium-to-high permeabilities according to existing data at the national level; this recharge is linear and did not undergo post-processing of any kind after obtaining the map.
The map of potential recharge zones (PGR map) is shown in Figure 6, displaying the sites of the highest recharge located on the periphery of the study area, right on the hillslopes that delimit the Lake Cuitzeo basin, of which they form part.
As part of the treatment of the PGR map, a reclassification of the values was conducted, through which a unit recharge in the aquifer was obtained so that the basin recharge could be distributed depending on the recharge in the study area, which was determined to be heterogeneous.
Both traditional and weighted recharge are based on the watersheds that cover the study area, shown in Figure 7a. The watersheds were attained through spatially and temporally extended modeling. Therefore, the necessary information was obtained to carry out the modeling in the period in which data on piezometric levels were available. As already mentioned in the Materials and Methods section, the model requires input information, where the matrices of geology (Figure 7b), piezometric levels (Figure 7c), natural terrain elevations (Figure 7d), extractions (Figure 7e), and springs (Figure 7f) stand out due to the information processing involved.
Figure 7b shows the map containing the geological information of the area, with which the hydrogeological values of hydraulic conductivity and storage coefficient were obtained. These parameters are critical for model calibration.
The calibration was performed using a sensitivity analysis involving the storage coefficient and hydraulic conductivity. Proposals of K and S obtained from the literature were used until the combination that allowed the least variation in levels measured in the calibration was found. Table 3 displays the values used for model calibration: minimum hydraulic conductivity (Kmin) [50] and maximum storage coefficient (Smax) [51].
The map in Figure 8 shows the distribution of the values of the hydraulic conductivity (Figure 8a) and the storage coefficient (Figure 8b). The values were obtained by weighting the value corresponding to the parameter concerning the area of geology present in each cell.
The values of hydraulic conductivity and storage coefficient did not vary in the modeling with traditional recharge or the PGR map because they depend on the geology and the geology does not present any type of variation.
An influential part of the groundwater model is the values of the initial piezometric levels. These were determined by measuring the depths of the piezometric levels in 2007.
The data were processed in a geographic information system that allowed interpolation and provided a distributed file of the depth. The map of piezometric level depths was subtracted from the digital elevation model (topography) employing the map calculator, with which the distributed file of piezometric level elevations was obtained. An analysis was performed to eliminate the values found in the 90th quantile. This allowed the smoothing of the piezometric levels shown in the map presented in Figure 7c, displaying the elevation values of the piezometric level in 2007. Likewise, Figure 7d illustrates the elevations of the natural terrain.
The groundwater modeling was carried out in a transient state for 192 months, in which each month had a recharge matrix (one for each of the recharge types). The extraction series considers a total of 1239 wells, shown in Figure 7e, of which 50% of the water volume is for agricultural use and 26% for domestic use. Groundwater extractions were attained through the concessions granted by the REPDA, which provide the value of the annual volume extracted, presenting an important challenge since monthly distributions must be made. For this purpose, the cropping patterns of the study area were analyzed, indicating whether there are perennial or temporary crops. Likewise, the distribution of the other uses was carried out homogeneously throughout the year.
The springs within the aquifer are considered natural outlets (Figure 7f), and special care is also given to those springs that have a significant discharge volume, such as La Mintzita, San Miguel, Salto La Quemada, and the one in the Vista Bella drinking water treatment plant.
Figure 9 shows the piezometric levels for 2007. They demonstrate that the flow directions of the aquifer are directed towards the north-central region, where Lake Cuitzeo is located, and also coincide with the lowest part of the study area.
The map shown in Figure 10 indicates the piezometric levels obtained with traditional recharge (Figure 10a) and with weighted recharge using the PGR map (Figure 10b). These maps were created from modeling carried out in MODFLOW, where a decrease from the piezometric levels of 2007 can be observed over the next 16 years (Figure 9).
The calibration method of the groundwater model was performed by comparing piezometric levels and flow directions. The flow directions in Figure 9 and Figure 10 are quite similar, proving that this calibration method is valid and works accurately for this particular case.
On the other hand, the groundwater modeling was also calibrated by comparing the piezometric levels in the years 2008, 2017, and 2022. The calibration points are shown in Figure 11, and the ten calibration wells in the northern portion of the Morelia–Queréndaro aquifer are shown.
The graphs in Figure 12 show that the variation between the methods is minimal but exists, and therefore, any method can be applied with the same reliability. The weighted recharge map (Figure 10b) shows an evident homogeneity concerning the intervals of the piezometric levels. In contrast, the map in Figure 10a has a defined heterogeneity that can be seen near the periphery of the aquifer.
Figure 12 displays the values obtained in the calibration years 2008 (Figure 12a), 2017 (Figure 12b), and 2022 (Figure 12c). Figure 10a shows a range of values from 1820 to 1860 m a.s.l., while Figure 12b,c show values from 1825 to 1880 m a.s.l. and from 1820 to 1890 m a.s.l., respectively. This indicates that the aquifer had a recovery of piezometric levels in some wells in the model calibration. However, as shown in Figure 10a,b, there was a generalized decrease in piezometric levels in the study area.
In addition, Figure 12 represents the trend of the observed values in the years 2008, 2017, and 2022, where the piezometric levels had a similar trend between traditional recharge and recharge by PGR; the variation between the values was minimal, which is shown in Table 4.
As part of the MODFLOW calibration, a graphical comparison of the piezometric levels was made. Figure 13 shows that the trends of the piezometric levels measured in the field and calculated in MODFLOW were quite similar.
It can be seen in Figure 13 that the wells that best fit between the measured and simulated wells are located in the northern and northwestern portions of the aquifer. The wells that show the greatest variation are well 3, well 4, well 5, and well 6.
Table 4 shows the values of the static levels measured in the field, as well as the values obtained in the modeling with the traditional method and the variation between PGR and traditional modeling. The largest variation in PGR modeling compared to traditional modeling is 1.827 m in well 3.
Figure 14 shows the variation in piezometric levels considering traditional recharge (Figure 14a) and PGR recharge (Figure 14b); it can be observed that the variations are less clear with PGR recharge, since the eastern portion of the study area has variations ranging from −5 cm to 5 cm, while in traditional recharge, they have variations that reach up to −17 cm.
Table 5 shows the standardization errors as a function of the observed levels. It can be determined from the prior results that the maximum errors obtained in the model were 5% concerning the original value and that these are similar between the two models. The error was obtained with the variation between the simulated value and the value measured in the field.
The map in Figure 15 shows that the distribution of the variations or errors present in the modeling, when comparing the observed values with the simulated values, does not exceed 6%. The variations are distributed in the northern portion of the study area, so they cannot be associated with variations due to boundary conditions. In this case, the PGR map does not influence the variations that occur in the calibration.

5. Conclusions

One of the main problems with model calibration is the scarcity of information, specifically at piezometric levels. In this case, the model was calibrated with only 10% of the cells, and the validation was given using the flow directions.
The flow directions have not changed over time. Therefore, it is possible to understand the regional flows, considering that they are directed towards Lake Cuitzeo, which coincides with the lowest topography in the aquifer.
Traditional recharge is a common and valid practice. However, in areas with relevant changes in the hydrogeological characteristics, such as geological faults or more permeable geologies, it becomes essential to consider these variations, for which the use of the PGR map is proposed.
The PGR map shows recharge potential values between 18% and 61%, indicating that they are within an average range and do not include high recharge values.
The most sensitive calibration parameters are the hydraulic conductivity and storage coefficient, which depend on the geology. Therefore, a range of values must be available with which to perform a sensitivity analysis of the model.
The values of hydraulic conductivity and storage coefficient are the same for both traditional recharge and PGR; the hydrogeological parameters depend on the geology, and this does not change with recharge.
The variability between the observed levels and the models with traditional recharge and PGR recharge is unnoticeable. Consequently, the model offers reliable results and can be considered applicable.
The map of modeling results with PGR recharge is noticeably smoother in general, except for the sites where the abatement cones are punctually represented in response to the variation in recharge and the volumes extracted from the aquifer.
The application of both traditional recharge and PGR recharge is valid, and neither method of recharge distribution is invalidated in this manuscript. However, the use of PGR recharge is recommended when there is significant variability in some of the thematic layers that interfere with the creation of the PGR map.
The wells used for the calibration of the groundwater model are located quite close to Lake Cuitzeo and therefore at constant altitude, so the levels are not sensitive to the other parameters used in the calibration.
The errors in the ground modeling are relatively low, with a maximum error close to 6% regarding the observed level, so the calibration is considered valid. Likewise, the flow directions obtained in 2022 follow the trend marked in 2007 by official sources.
The model shows a recovery in the piezometric levels in the calibration wells. However, the entire aquifer has a general decrease of approximately 20 m in the highest levels found in the periphery of the Morelia–Queréndaro aquifer.

Author Contributions

This manuscript is a result of the doctoral research of M.d.M.N.-F., who received a lot of contributions from the co-authors, as follows: Formal analysis, M.d.M.N.-F.; Investigation, M.d.M.N.-F.; Methodology, M.d.M.N.-F., L.G.-R. and S.T.S.-Q.; Supervision, L.G.-R., S.T.S.-Q., M.A.M.-C. and M.A.H.-H.; Writing—original draft, M.d.M.N.-F.; Writing—review and editing, L.G.-R., S.T.S.-Q., M.A.M.-C. and M.A.H.-H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available as they form part of a doctoral research project that is currently in progress.

Acknowledgments

The authors thank the reviewers for their valuable comments, suggestions, and feedback. The support from the Universidad Michoacana de San Nicolás de Hidalgo, especially from the Department of Chemical Engineering and the Department of Hydraulics, is also gratefully acknowledged. The first author also thanks the Consejo Nacional de Humanidades, Ciencias y Tecnologías de México (CONAHCyT) for the scholarship for her Ph.D. studies.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Uchenna, U.P.; Lancia, M.; Viaroli, S.; Ugbaja, A.N.; Galluzzi, M.; Zheng, C. Groundwater Sustainability in African Metropolises: Case Study from Calabar, Nigeria. J. Hydrol. Reg. Stud. 2023, 45, 101314. [Google Scholar] [CrossRef]
  2. Cook, P.G.; Shanafield, M.; Andersen, M.S.; Bourke, S.; Cartwright, I.; Cleverly, J.; Currell, M.; Doody, T.M.; Hofmann, H.; Hugmann, R.; et al. Sustainable Management of Groundwater Extraction: An Australian Perspective on Current Challenges. J. Hydrol. Reg. Stud. 2022, 44, 101262. [Google Scholar] [CrossRef]
  3. Fotovat, M.; Porhemmat, J.; Sedghi, H.; Babazadeh, H. Evaluation of Weap-Modflow Model as an Integrated Water Resources Management Model for Sustainable Development (a Case Study: Gharesoo at Doab-Merek, Kermanshah, Iran). Civ. Eng. Infrastruct. J. 2019, 52, 167–183. [Google Scholar] [CrossRef]
  4. Alsevavni, I.N.; Almohseen, K.A. Integrated Application of (Modflow) and (Weap) Model in Nineveh Province. J. Univ. Duhok 2017, 20, 680–690. [Google Scholar] [CrossRef]
  5. Khadri, S.F.R.; Pande, C. Groundwater Flow Modeling for Calibrating Steady State Using MODFLOW Software: A Case Study of Mahesh River Basin, India. Model. Earth Syst. Environ. 2016, 2, 39. [Google Scholar] [CrossRef]
  6. Chen, M.; Izady, A.; Abdalla, O.A. An Efficient Surrogate-Based Simulation-Optimization Method for Calibrating a Regional MODFLOW Model. J. Hydrol. 2017, 544, 591–603. [Google Scholar] [CrossRef]
  7. Ochoa-González, G.H.; Carreón-Freyre, D.; Cerca, M.; López-Martínez, M. Assessment of Groundwater Flow in Volcanic Faulted Areas. A Study Case in Queretaro, Mexico. Geofís. Int. 2015, 54, 199–220. [Google Scholar] [CrossRef]
  8. Peñuela Arévalo, L.A.; Carrillo Rivera, J.J. Definición de Zonas de Recarga y Descarga de Agua Subterránea a Partir de Indicadores Superficiales: Centro—Sur de La Mesa Central, México. Investig. Geogr. 2013, 81, 18–32. [Google Scholar] [CrossRef]
  9. Sánchez-San Román, J. Hidrología Superficial y Subterránea, 1st ed.; Universidad de Salamanca: Salamanca, Spain, 2017. [Google Scholar]
  10. El Moneam, M.A. Review of Artificial Recharge Prospects for Augmentation of Groundwater in Egypt: A Case Study of El Bustan Extension Area. Ain Shams Eng. J. 2023, 14, 101995. [Google Scholar] [CrossRef]
  11. Hughes, J.D.; Russcher, M.J.; Langevin, C.D.; Morway, E.D.; McDonald, R.R. The MODFLOW Application Programming Interface for Simulation Control and Software Interoperability. Environ. Model. Softw. 2022, 148, 105257. [Google Scholar] [CrossRef]
  12. Jafari, T.; Kiem, A.S.; Javadi, S.; Nakamura, T.; Nishida, K. Fully Integrated Numerical Simulation of Surface Water-Groundwater Interactions Using SWAT-MODFLOW with an Improved Calibration Tool. J. Hydrol. Reg. Stud. 2021, 35, 100822. [Google Scholar] [CrossRef]
  13. Siddik, M.S.; Tulip, S.S.; Rahman, A.; Islam, M.N.; Haghighi, A.T.; Mustafa, S.M.T. The Impact of Land Use and Land Cover Change on Groundwater Recharge in Northwestern Bangladesh. J. Environ. Manag. 2022, 315, 115130. [Google Scholar] [CrossRef] [PubMed]
  14. Hartmann, A.; Gleeson, T.; Wada, Y.; Wagener, T. Enhanced Groundwater Recharge Rates and Altered Recharge Sensitivity to Climate Variability through Subsurface Heterogeneity. Proc. Natl. Acad. Sci. USA 2017, 114, 2842–2847. [Google Scholar] [CrossRef]
  15. Ayvaz, M.T.; Elçi, A. Groundwater Recharge Rate and Zone Structure Estimation Using PSOLVER Algorithm. Groundwater 2014, 52, 434–447. [Google Scholar] [CrossRef]
  16. Ke, T.; Shu, L.; Chen, X. Modeling the Groundwater Recharge in Karst Aquifers by Using a Reservoir Model. Water Sci. Technol. 2013, 68, 406–412. [Google Scholar] [CrossRef] [PubMed]
  17. Guerrero-Morales, J.; Fonseca, C.R.; Goméz-Albores, M.A.; Sampedro-Rosas, M.L.; Silva-Gómez, S.E. Proportional Variation of Potential Groundwater Recharge as a Result of Climate Change and Land-Use: A Study Case in Mexico. Land 2020, 9, 364. [Google Scholar] [CrossRef]
  18. Ahuanlla Huaccha, J.L.; Díaz Aguilar, R.D.; Vigo Rivera, J.E.; Callate Chura, R.A. Aplicación de Modflow 6 Con Model Mouse 4 Para El Modelamiento Del Flujo Subterráneo de La Microcuenca Macarí, Melgar—Perú. Rev. Investig. Cienc. Tecnol. Desarro. 2022, 7, 1–11. [Google Scholar] [CrossRef]
  19. Abbas, S.A.; Xuan, Y.; Bailey, R.T. Assessing Climate Change Impact on Water Resources in Water Demand Scenarios Using SWAT-MODFLOW-WEAP. Hydrology 2022, 9, 164. [Google Scholar] [CrossRef]
  20. Loukika, K.N.; Venkata Reddy, K.; Durga Rao, K.H.V.; Singh, A. Estimation of Groundwater Recharge Rate Using SWAT MODFLOW Model. In Applications of Geomatics in Civil Engineering, Proceedings of the ICGCE 2018, Phuket, Thailand, 10–12 January 2018; Springer: Singapore, 2020; pp. 143–154. [Google Scholar]
  21. Ware, H.H.; Mengistu, T.D.; Yifru, B.A.; Chang, S.W.; Chung, I.-M. Assessment of Spatiotemporal Groundwater Recharge Distribution Using SWAT-MODFLOW Model and Transient Water Table Fluctuation Method. Water 2023, 15, 2112. [Google Scholar] [CrossRef]
  22. Szymkiewicz, A.; Gumuła-Kawęcka, A.; Šimůnek, J.; Leterme, B.; Beegum, S.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Gorczewska-Langner, W.; Angulo-Jaramillo, R.; Jacques, D. Simulations of Freshwater Lens Recharge and Salt/Freshwater Interfaces Using the HYDRUS and SWI2 Packages for MODFLOW. J. Hydrol. Hydromech. 2018, 66, 246–256. [Google Scholar] [CrossRef]
  23. Noori, R.; Maghrebi, M.; Jessen, S.; Bateni, S.M.; Heggy, E.; Javadi, S.; Noury, M.; Pistre, S.; Abolfathi, S.; AghaKouchak, A. Decline in Iran’s Groundwater Recharge. Nat. Commun. 2023, 14, 6674. [Google Scholar] [CrossRef]
  24. Sallwey, J.; Bonilla Valverde, J.P.; Vásquez López, F.; Junghanns, R.; Stefan, C. Suitability Maps for Managed Aquifer Recharge: A Review of Multi-Criteria Decision Analysis Studies. Environ. Rev. 2019, 27, 138–150. [Google Scholar] [CrossRef]
  25. Niswonger, R.G.; Morway, E.D.; Triana, E.; Huntington, J.L. Managed Aquifer Recharge through Off-season Irrigation in Agricultural Regions. Water Resour. Res. 2017, 53, 6970–6992. [Google Scholar] [CrossRef]
  26. Russo, T.A.; Fisher, A.T.; Lockwood, B.S. Assessment of Managed Aquifer Recharge Site Suitability Using a GIS and Modeling. Groundwater 2015, 53, 389–400. [Google Scholar] [CrossRef]
  27. Maples, S.R.; Fogg, G.E.; Maxwell, R.M. Modeling Managed Aquifer Recharge Processes in a Highly Heterogeneous, Semi-Confined Aquifer System. Hydrogeol. J. 2019, 27, 2869–2888. [Google Scholar] [CrossRef]
  28. López, B.; Rosales, L.; Saavedra, O. Modelación Hidrogeológica en el Valle Central de Cochabamba-Bolivia. Investig. Desarro. 2023, 23, 23–39. [Google Scholar] [CrossRef]
  29. Dar, T.; Rai, N.; Bhat, A. Delineation of Potential Groundwater Recharge Zones Using Analytical Hierarchy Process (AHP). Geol. Ecol. Landsc. 2021, 5, 292–307. [Google Scholar] [CrossRef]
  30. Vasileva, T. An Assessment of Potential Groundwater Recharge Zones in Bulgaria. Geol. Balc. 2019, 48, 43–61. [Google Scholar] [CrossRef]
  31. Andreo, B.; Vías, J.; López-Greta, J.A.; Carrasco, F.; Durán, J.J.; Jiménez, P. Propuesta Metodológica Para La Estimación de La Recarga En Acuíferos Carbonáticos. Bol. Geol. Min. 2004, 115, 177–186. [Google Scholar]
  32. Lara-Vásconez, N.X.; Cushquicullma-Colcha, D.F.; Guaiña-Yungán, J.I.; Espinoza, V.M.; Ati-Cutiupala, G.M. Identificación de Zonas Potenciales de Recarga y Descarga de Agua Subterránea En La Subcuenca Del Río Chambo Mediante Los Sistemas de Información Geográfica y El Análisis Multicriterio. Rev. Cient.-Acad. Multidiscip. 2021, 6, 122–148. [Google Scholar]
  33. Boyás Martínez, E.; Cervantes Victoria, G.I.; González Mora, M.F. Determinación de Sitios Potenciales de Recarga Artificial de Agua Subterránea EN LOS Acuíferos Que Conforman La Subregión Valle de México; Centro de Investigación en Ciencias de Información Geoespacial: México City, Mexico, 2020. [Google Scholar]
  34. Hernández-Juárez, R.A.; Martinez Rivera, L.M.; Peñuela-Arévalo, L.A.; Rivera-Reyes, S. Identificación de Zonas Potenciales de Recarga y Descarga de Agua Subterránea En La Cuenca Del Río Ayuquila-Armería Mediante El Uso de SIG y El Análisis Multicriterio. Investig. Geogr. 2020. [Google Scholar] [CrossRef]
  35. Singh, S.K.; Zeddies, M.; Shankar, U.; Griffiths, G.A. Potential Groundwater Recharge Zones within New Zealand. Geosci. Front. 2019, 10, 1065–1072. [Google Scholar] [CrossRef]
  36. Ardakani, A.H.H.; Shojaei, S.; Shahvaran, A.R.; Kalantari, Z.; Cerdà, A.; Tiefenbacher, J. Selecting Potential Locations for Groundwater Recharge by Means of Remote Sensing and GIS and Weighting Based on Boolean Logic and Analytic Hierarchy Process. Environ. Earth Sci. 2022, 81, 8. [Google Scholar] [CrossRef]
  37. Matus Silva, O.D. Elaboración Participativa de Una Metodología Para La Identificación de Zonas Potenciales de Recarga Hídrica En Subcuencas Hidrográficas, Aplicada a La Subcuenca Del Río Jucuapa, Matagalpa, Nicaragua. Master’s Thesis, CATIE, Turrialba, Costa Rica, 2007. [Google Scholar]
  38. Mussa, K.R.; Mjemah, I.C.; Machunda, R.L. Open-Source Software Application for Hydrogeological Delineation of Potential Groundwater Recharge Zones in the Singida Semi-Arid, Fractured Aquifer, Central Tanzania. Hydrology 2020, 7, 28. [Google Scholar] [CrossRef]
  39. Agarwal, R.; Garg, P.K. Remote Sensing and GIS Based Groundwater Potential Recharge Zones Mapping Using Multi-Criteria Decision-Making Technique. Water Resour. Manag. 2016, 30, 243–260. [Google Scholar] [CrossRef]
  40. Harbaugh, A.W. MODFLOW-2005: The U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005. [Google Scholar]
  41. Chiang, W.-H. 3D-Groundwater Modeling with PMWIN, 2nd ed.; Springer: New York, NY, USA, 2005; ISBN 103-540-27590-8. [Google Scholar]
  42. Bagherzadeh, S.; Nobandegani, A.F.; Rahimi, Z.; Derakhshan, Z.; Rajabi, S.; Shirgahi, F.; Mohammadpour, A. Predicting the Alleviation of Nitrate Contamination in Aquifers by Conducting Management Scenarios Using the PMWIN Software: Application in the Andimeshk Plain, Iran. Groundw. Sustain. Dev. 2023, 20, 100883. [Google Scholar] [CrossRef]
  43. Talebi, S.; Rakhshandehro, G.; ParsiMehr, M.; Rezaei, S. Simulating Quar-Maharlu Aquifer in Fars Province, Iran, and Optimizing Artificial Recharge Using PMWIN Model. J. Adv. Environ. Health Res. 2022, 10, 105–118. [Google Scholar] [CrossRef]
  44. Stockholm Environment Institute. Guía Metodológica. Modelación Hidrológica y de Recursos Hídricos Con El Modelo WEAP; Centro de Cambio Global-Universidad Católica de Chile, Stockholm Environment Institute: Santiago, Chile, 2009. [Google Scholar]
  45. CONABIO. Portal de Geoinformación. 2022. Available online: http://www.conabio.gob.mx/informacion/gis/ (accessed on 19 February 2023).
  46. INEGI. Continuo de Elevaciones Mexicano (CEM). Available online: https://www.inegi.org.mx/app/geo2/elevacionesmex/ (accessed on 22 August 2023).
  47. Arellano-Lara, F.; Escalante-Sandoval, C.A. Multivariate Delineation of Rainfall Homogeneous Regions for Estimating Quantiles of Maximum Daily Rainfall: A Case Study of Northwestern Mexico. Atmosfera 2014, 27, 47–60. [Google Scholar] [CrossRef]
  48. CICESE. Base de Datos Climatológica Nacional (Sistema CLICOM). Available online: http://clicom-mex.cicese.mx/mapa.html (accessed on 19 February 2023).
  49. CONAGUA. Aguas Subterráneas. Available online: https://sigagis.conagua.gob.mx/gas1/sections/Disponibilidad_Acuiferos.html (accessed on 22 August 2023).
  50. Smith, L.; Wheatcraft, S.W. Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; Chapter 6. [Google Scholar]
  51. Villanueva Martínez, M.; Iglesias López, A. Pozos y Acuíferos. Técnicas de Evaluación Mediante Ensayos de Bombeo; Instituto Geológico y Minero de España: Madrid, Spain, 1984; ISBN 84-7474-258-7. [Google Scholar]
  52. Servicio Geológico Mexicano. GeoInfoMEx. Available online: https://www.sgm.gob.mx/GeoInfoMexGobMx/# (accessed on 14 September 2023).
  53. CONAGUA. Base de Datos Del REPDA. Available online: https://app.conagua.gob.mx/consultarepda.aspx (accessed on 22 August 2023).
  54. Chen, F.-W.; Liu, C.-W. Estimation of the Spatial Rainfall Distribution Using Inverse Distance Weighting (IDW) in the Middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
  55. Gobierno de México Data México Morelia. Available online: https://www.economia.gob.mx/datamexico/es/profile/geo/morelia (accessed on 22 August 2023).
  56. CONAGUA. Gerencia de Planificación Hídrica; Sistema Nacional de Información del Agua Numeragua 2022; CONAGUA: Mexico City, Mexico, 2022. [Google Scholar]
  57. Fox, D.M.; Bryan, R.B.; Price, A.G. The Influence of Slope Angle on Final Infiltration Rate for Interrill Conditions. Geoderma 1997, 80, 181–194. [Google Scholar] [CrossRef]
  58. Sharma, K.D.; Singh, H.P.; Pareek, O.P. Rainwater Infiltration into a Bare Loamy Sand. Hydrol. Sci. J. 1983, 28, 417–424. [Google Scholar] [CrossRef]
Hydrology 11 00009 g001
Figure 1. Methodological process of the investigation, including surface modeling and groundwater modeling.
Figure 1. Methodological process of the investigation, including surface modeling and groundwater modeling.
Hydrology 11 00009 g001
Hydrology 11 00009 g002
Figure 2. Diagram of MODFLOW operation.
Figure 2. Diagram of MODFLOW operation.
Hydrology 11 00009 g002
Hydrology 11 00009 g003
Figure 3. Location of the Morelia–Queréndaro aquifer.
Figure 3. Location of the Morelia–Queréndaro aquifer.
Hydrology 11 00009 g003
Hydrology 11 00009 g004
Figure 4. Discretization of the Morelia–Queréndaro aquifer (AMQ).
Figure 4. Discretization of the Morelia–Queréndaro aquifer (AMQ).
Hydrology 11 00009 g004
Hydrology 11 00009 g005
Figure 5. Thematic layers for the PGR map: (a) drainage, (b) precipitation, (c) land use, (d) geological faults, (e) soil type, and (f) slope and hydrogeology.
Figure 5. Thematic layers for the PGR map: (a) drainage, (b) precipitation, (c) land use, (d) geological faults, (e) soil type, and (f) slope and hydrogeology.
Hydrology 11 00009 g005
Hydrology 11 00009 g006
Figure 6. Morelia–Queréndaro aquifer PGR map.
Figure 6. Morelia–Queréndaro aquifer PGR map.
Hydrology 11 00009 g006
Hydrology 11 00009 g007
Figure 7. MODFLOW input information: (a) recharge basins, (b) geology, (c) piezometric levels, (d) elevations, (e) number of wells, and (f) number of springs.
Figure 7. MODFLOW input information: (a) recharge basins, (b) geology, (c) piezometric levels, (d) elevations, (e) number of wells, and (f) number of springs.
Hydrology 11 00009 g007
Hydrology 11 00009 g008
Figure 8. Spatial distribution of the values of (a) hydraulic conductivity, Kmin (m/day), and (b) storage coefficient, Smax (dimensionless).
Figure 8. Spatial distribution of the values of (a) hydraulic conductivity, Kmin (m/day), and (b) storage coefficient, Smax (dimensionless).
Hydrology 11 00009 g008
Hydrology 11 00009 g009
Figure 9. Piezometric levels in the year 2007.
Figure 9. Piezometric levels in the year 2007.
Hydrology 11 00009 g009
Hydrology 11 00009 g010
Figure 10. Piezometric levels for the year 2022: (a) traditional recharge and (b) recharge by PGR.
Figure 10. Piezometric levels for the year 2022: (a) traditional recharge and (b) recharge by PGR.
Hydrology 11 00009 g010
Hydrology 11 00009 g011
Figure 11. Location of the wells used for the calibration of the groundwater model.
Figure 11. Location of the wells used for the calibration of the groundwater model.
Hydrology 11 00009 g011
Hydrology 11 00009 g012
Figure 12. Variations in piezometric levels for the different calibration years (m a.s.l) (a) 2008, (b) 2017, and (c) 2022.
Figure 12. Variations in piezometric levels for the different calibration years (m a.s.l) (a) 2008, (b) 2017, and (c) 2022.
Hydrology 11 00009 g012
Hydrology 11 00009 g013
Figure 13. Calibration graph for the periods (a) 2008, (b) 2017, and (c) 2022. Comparison of historical values between traditional and PGR modeling (m a.s.l.).
Figure 13. Calibration graph for the periods (a) 2008, (b) 2017, and (c) 2022. Comparison of historical values between traditional and PGR modeling (m a.s.l.).
Hydrology 11 00009 g013
Hydrology 11 00009 g014
Figure 14. Variation in piezometric levels in 2017; comparing (a) traditional recharge versus (b) PGR recharge.
Figure 14. Variation in piezometric levels in 2017; comparing (a) traditional recharge versus (b) PGR recharge.
Hydrology 11 00009 g014
Hydrology 11 00009 g015
Figure 15. Variation map of the wells used in the model calibration.
Figure 15. Variation map of the wells used in the model calibration.
Hydrology 11 00009 g015
Table 1. Groundwater balance of the Morelia–Queréndaro aquifer.
Table 1. Groundwater balance of the Morelia–Queréndaro aquifer.
InputsML/YearOutputsML/Year
Vertical Recharge169,672Pumping232,310
Induced Recharge38,500Springs58,780
Lateral Entrance88,000Evapotranspiration64,200
Total296,172Total355,290
Table 2. Reclassification values for the realization of the PGR map.
Table 2. Reclassification values for the realization of the PGR map.
ParameterCharacteristicReclassification Value
HydrogeologyLow–Medium Permeability2
Medium–High Permeability4
High Permeability6
Fault Density Very Low1
Low2
Medium3
High5
Very High6
Soil Type Fine2
Medium4
Alluvial6
Soil Use Agricultural2
Naked3
Urban1
Forest5
Water Body6
Scrub3
Pasture3
Drainage Density Very Low1
Low2
Medium3
Moderate High4
SlopeSmooth (<2%)7
Mild (<6%)6
Inclined (<10%)5
Moderate to Very Steep (>10%)4
PrecipitationVery Low (654–752 mm)1
Low (752–849 mm)2
Medium (849–946 mm)3
Moderate High (946–1044 mm)4
High (1044–1141 mm)5
Very High (1141–1238 mm)6
Too High (1238–1336 mm)7
Table 3. Hydrogeological values used in the aquifer modeling stage.
Table 3. Hydrogeological values used in the aquifer modeling stage.
GeologyKmin
(m/day)		Smax
(Dimensionless
Parameter)
Andesite0.0010.05
Basalt100.05
Dacite0.0010.005
Granite3.30.18
Lacustine3.30.06
Lahar0.00010.005
Limestone0.0010.06
Pyroclastic0.00010.005
Rhyolite0.000010.005
Sandstone–Medium3.30.15
Tuff 0.0010.05
Table 4. Levels and variations in traditional and PGR groundwater modeling.
Table 4. Levels and variations in traditional and PGR groundwater modeling.
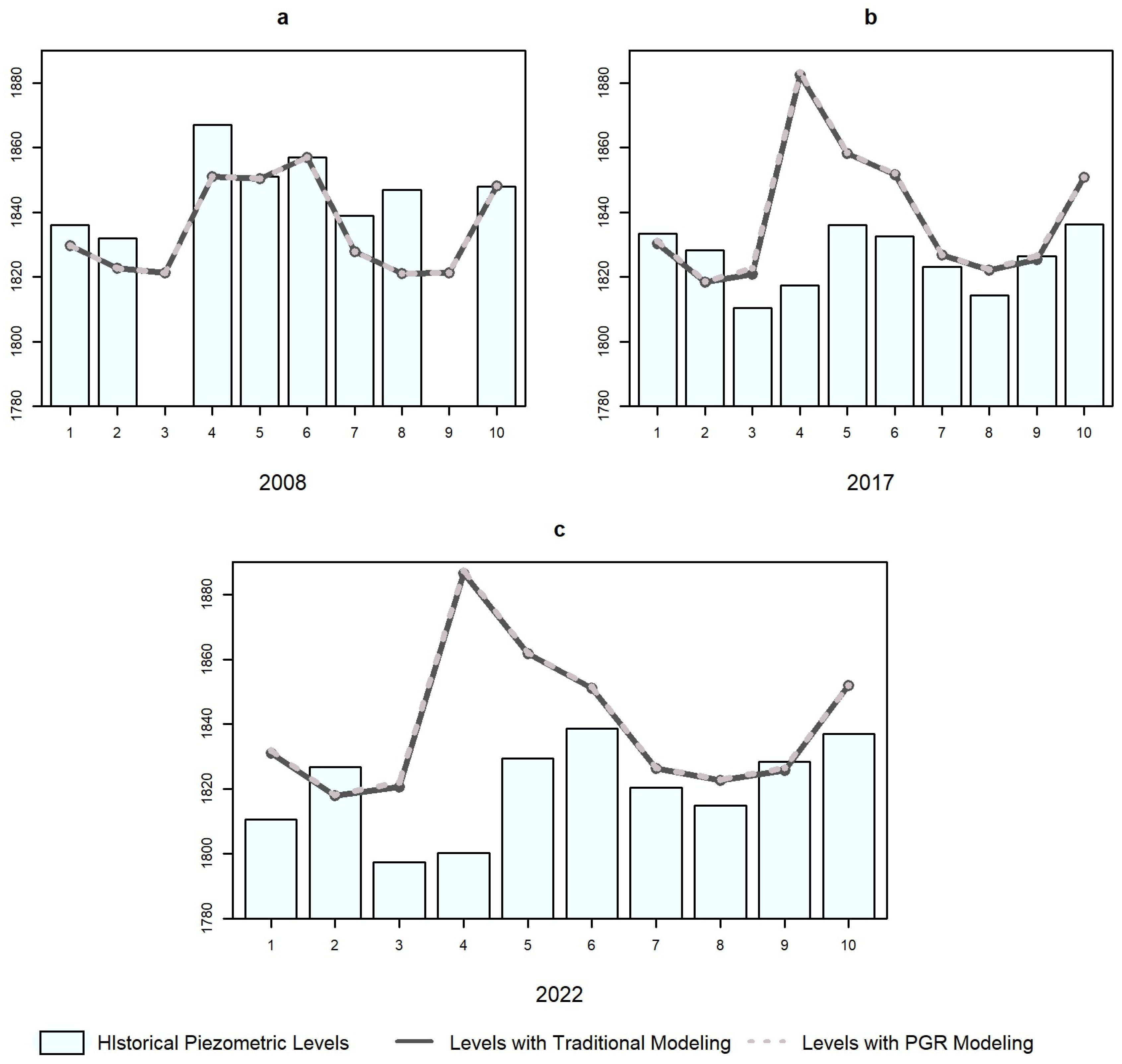
Piezometric Levels
ObservedTraditional ModelingVariation in PGR vs. Traditional
Well200820172022200820172022200820172022
11836.001833.331810.501829.7911830.2341830.950−0.0020.9960.961
21832.001828.191826.651822.6931818.4491817.9280.0030.1150.067
3N/D1810.401797.401821.2541820.9441820.4880.0011.8271.524
41867.001817.451800.131850.9481882.3551886.6430.0010.8550.852
51851.001836.041829.311850.4791858.261861.753−0.0010.1820.163
61856.941832.601838.631857.0791851.6651851.1230.0010.4600.471
71838.891823.231820.441827.8401826.7201826.2950.0020.1380.154
81847.001814.341814.751821.0271822.0721822.530−0.0070.2150.226
9N/D1826.501828.301821.1981825.3461825.665−0.0021.1770.755
101847.941836.341837.001848.2131850.7701851.9270.0000.0110.012
Table 5. Errors in traditional and PGR groundwater modeling.
Table 5. Errors in traditional and PGR groundwater modeling.
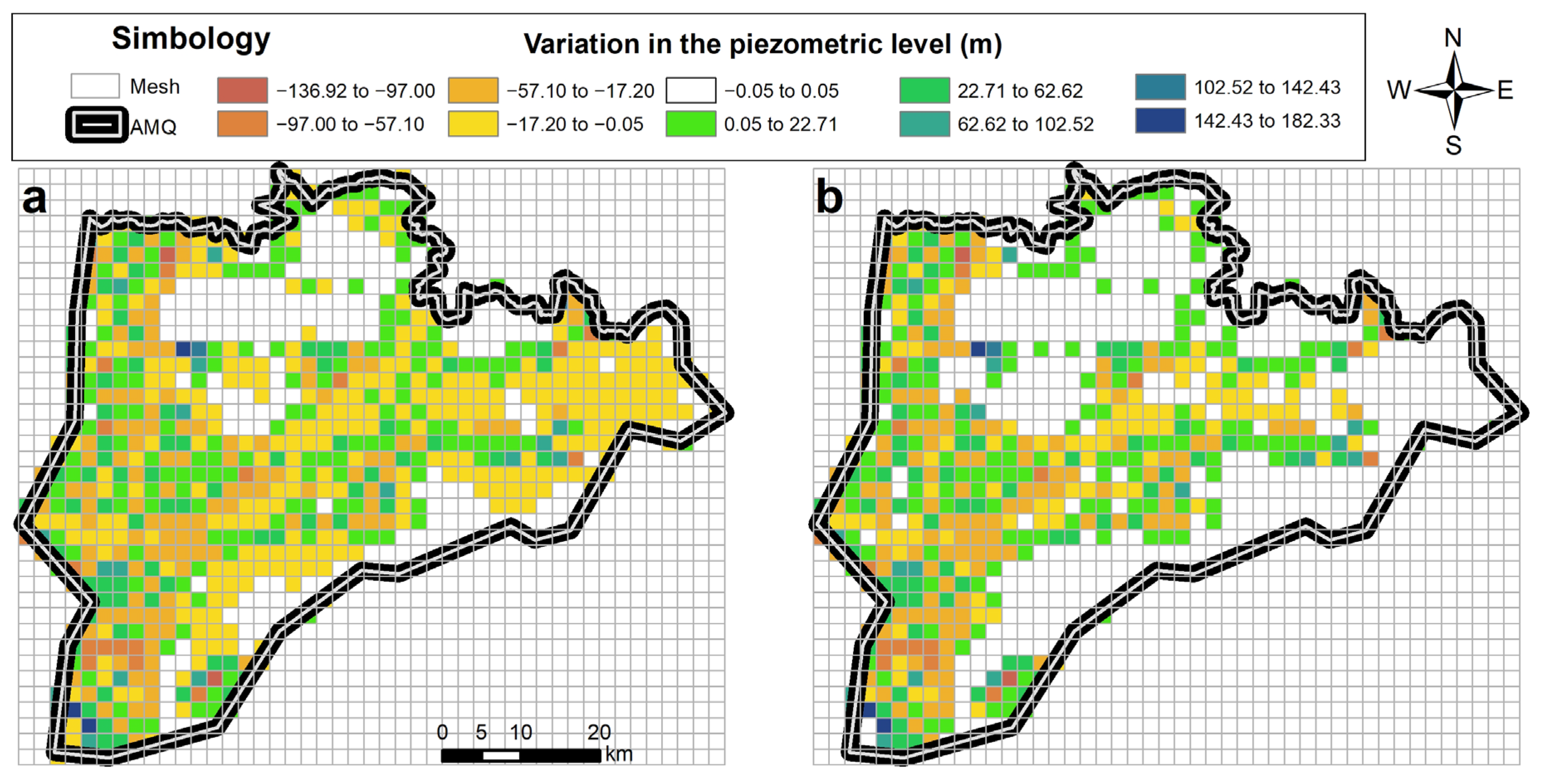
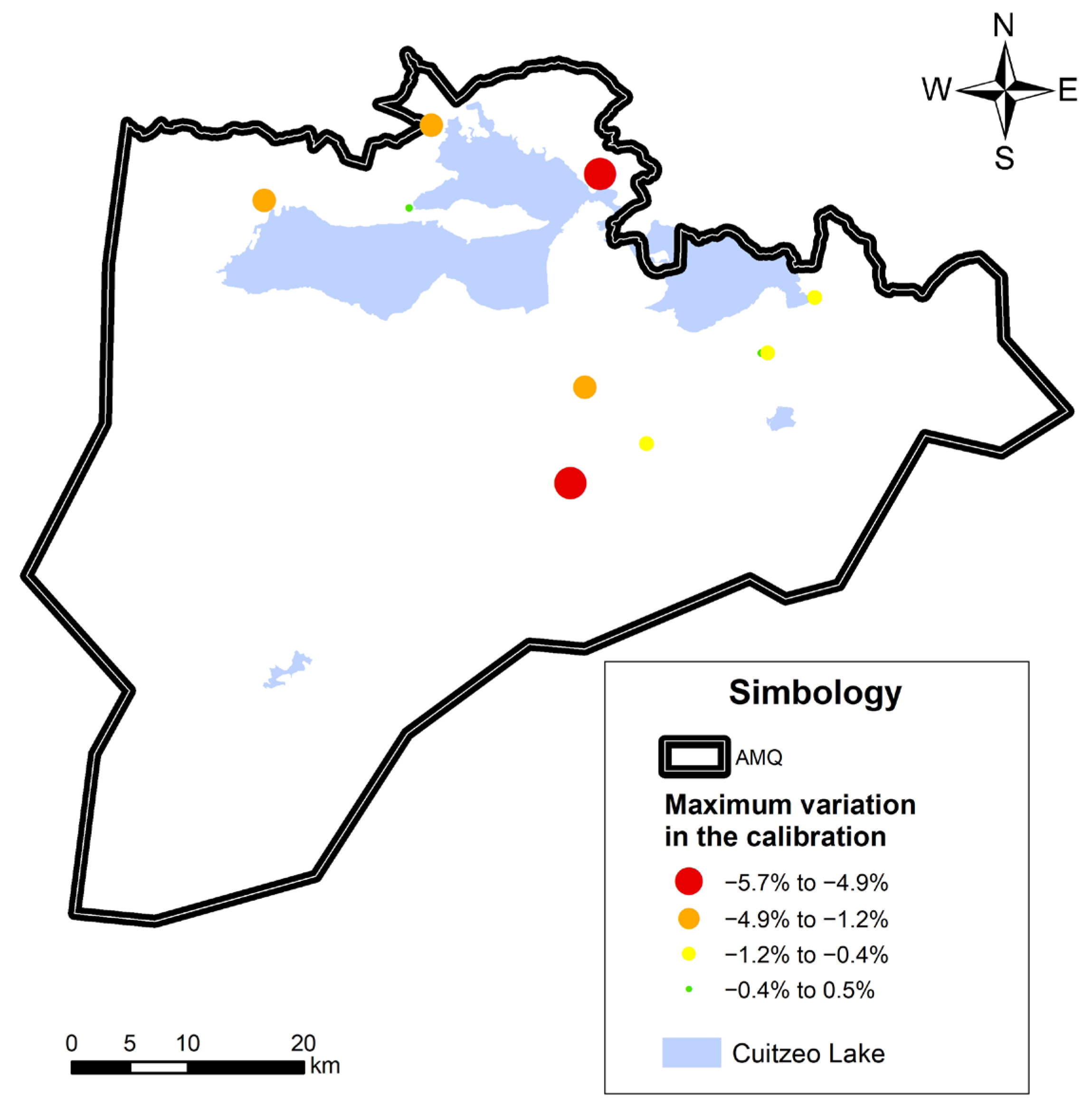
Well
12345678910
Traditional Recharge
20080.3%0.5% 0.9%0.0%0.0%0.6%1.4% 0.0%
20170.2%0.5%−0.6%−3.6%−1.2%−1.0%−5.3%−0.4%0.1%−0.8%
2022−1.1%0.5%−1.3%−4.8%−1.8%−0.7%−5.8%−0.4%0.1%−0.8%
PGR Recharge
20080.3%0.5% 0.9%0.0%0.0%−1.1%1.4% 0.0%
20170.1%0.5%−0.7%−3.6%−1.2%−1.1%−5.3%−0.4%0.0%−0.8%
2022−1.2%0.5%−1.4%−4.9%−1.8%−0.7%−5.7%−0.4%0.1%−0.8%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Navarro-Farfán, M.d.M.; García-Romero, L.; Martínez-Cinco, M.A.; Hernández-Hernández, M.A.; Sánchez-Quispe, S.T. Comparison between MODFLOW Groundwater Modeling with Traditional and Distributed Recharge. Hydrology 2024, 11, 9. https://doi.org/10.3390/hydrology11010009

AMA Style

Navarro-Farfán MdM, García-Romero L, Martínez-Cinco MA, Hernández-Hernández MA, Sánchez-Quispe ST. Comparison between MODFLOW Groundwater Modeling with Traditional and Distributed Recharge. Hydrology. 2024; 11(1):9. https://doi.org/10.3390/hydrology11010009

Chicago/Turabian Style

Navarro-Farfán, María del Mar, Liliana García-Romero, Marco Antonio Martínez-Cinco, Mario Alberto Hernández-Hernández, and Sonia Tatiana Sánchez-Quispe. 2024. "Comparison between MODFLOW Groundwater Modeling with Traditional and Distributed Recharge" Hydrology 11, no. 1: 9. https://doi.org/10.3390/hydrology11010009

APA Style

Navarro-Farfán, M. d. M., García-Romero, L., Martínez-Cinco, M. A., Hernández-Hernández, M. A., & Sánchez-Quispe, S. T. (2024). Comparison between MODFLOW Groundwater Modeling with Traditional and Distributed Recharge. Hydrology, 11(1), 9. https://doi.org/10.3390/hydrology11010009

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop