Abstract
Most of the studies on rainwater harvesting analysis present the outcomes for particular cities, representing a single set of results for a specific city. However, in reality, significant spatial and weather variabilities may exist, due to which presenting only one set of results for a particular city would be misleading. This paper presents the potential weather and spatial variabilities on the expected water savings and supply reliability through the domestic rainwater tank for an inland city. An earlier-developed daily water balance model, eTank, was used for the calculations of annual water savings and reliability. An Australian inland city, Canberra, was selected as a case study and relevant daily rainfall data were collected from the Australian Bureau of Meteorology website. For the analysis of spatial variation, two rain gauge stations within the city of Canberra were selected. For each station, from the historical data, three years were selected as dry, average and wet years. For each weather condition, annual water savings and reliabilities were calculated for different demands with different tank sizes up to 10,000 L connected with different roof sizes. Then, variations in annual water savings and reliabilities among different weather conditions, as well as among different stations, were evaluated. It was found that, with regard to annual water savings, a maximum variation of 68.6% can be expected between dry and wet weather; however, only a 15.4% maximum spatial variation is expected among the selected stations. Regarding reliability, a maximum variation of 123% is expected between dry and wet weather. Whereas, only a 17% spatial variation is expected among the selected stations. Such a study will provide valuable insights for rainwater tank users and stakeholders on potential variabilities due to weather and spatial differences.
1. Introduction
Rainwater harvesting has been in use for many centuries in different parts of the world, where this is the prime source of water for many remote communities as no other suitable source of potable water exists. Recently, even in urban areas where potable water supply exists, authorities have encouraged the implementing of rainwater harvesting for non-potable purposes, which will reduce the tremendous pressure on the current supply systems [1]. The increase in population, as well as other usage, has caused urban water demand to reach a very high level while, in most cases, the existing systems are not designed to cater for such a high demand [2]. Urban water authorities are exploring several options to reduce water demand. Such measures include demand management, water efficient appliances and exploring alternative water sources. Stormwater harvesting and its use for irrigation and toilet flushing has been an attractive option for many urban authorities, as the implementation of rainwater harvesting is easily achievable within existing buildings/house boundaries [3]. As such, for urban areas, there has been a shift in objective; from original objective rainwater tanks (RWT) being a sole source of water supply shifting to be an alternate source of water to augment existing water supplies. In Australia, different government authorities have been promoting water recycling, including stormwater harvesting. In addition to organising different campaigns, they have been offering financial incentives, such as rebates or grants, with the aim of promoting the wider implementations of this sustainable system.
Numerous researchers have studied different aspects of rainwater tanks and most of those have dealt with the potentials of rainwater harvesting, mainly quantifying the expected annual amount of water saving [4,5,6,7]. As in most of the regions, rainfall does not occur uniformly throughout the month/year, there are some periods within a year when the rainwater tank is unable to supply the intended demand and this factor is expressed by a term called ‘reliability’. Some studies mainly focused on the reliability of fulfilling specific demands through specific sizes of rainwater tanks [8,9,10]. Khastagir and Jayasuriya [8] presented a comprehensive analysis of the reliability of rainwater tanks. They have presented the contours of optimum tank sizes needed to have a 90% reliable rainwater supply for seven different uses (toilet only, garden only, laundry only, toilet and laundry, toilet and garden, laundry and garden, toilet, garden and laundry) under varying roof sizes (100~250 m2) for the whole of Melbourne. Imteaz et al. [9] presented detailed reliability charts of rainwater tanks for a single location in the city of Melbourne for different tank sizes (1000~10,000 L) connected with different roof areas (50~300 m2) with varying rainwater demands under three climatic conditions (driest, average and wettest). Preeti and Rahman [10] studied the reliability of rainwater tanks for eight Australian major cities with varying tank sizes (1000~100,000 L) under varying roof areas of 50~300 m2. They have reported that a high reliability (80~100%) is achievable with a large roof area and big tank size for demand catering only to use in toilet and laundry.
As monetary benefit and payback period of initial investments are the main constraints for many users, which is retarding the wide-scale implementation of this sustainable infrastructure, several studies focused on an economic analysis of the RWT benefits, quantifying monetary values of potential water savings [10,11,12,13]. In the study by Preeti and Rahman [10], they found that, only in very few cases, installations of RWTs can yield a benefit–cost ratio value greater than one, which emphasized the need for government support/rebate and/or discount for the installation of RWTs. Imteaz and Moniruzzaman [11] also reported similar findings (i.e., a need for government rebate) through a study in Sydney. They have reported that without government rebate payback period of installations likely to vary 24 to 100 years depending on the locality and associated parameters (i.e., tank size, roof area and demand). However, such long payback periods can be attributed to the regions where installation costs are quite high, while the cost of water is not very high. In regions where installation costs are not high, shorter payback periods are achievable. Karim et al. [12] demonstrated, with a case study of the city of Dhaka (Bangladesh), that payback periods of 3~4 years are achievable for commercial buildings. Matos et al. [13], through a case study of a large commercial building in Portugal, demonstrated that payback periods of 2~6 years are achievable depending on the usage scenario.
The vast majority of the studies on rainwater harvesting are focused on a particular city/locality, delivering a single set of outcomes for a whole city. However, for a large city, single outcomes for water savings or reliability are not realistic. Moreover, within a single location of a city, further variations are expected due to weather variability [14,15,16]. Imteaz and Moniruzzaman [11] presented significant spatial variations of water saving within the large city of Sydney (Australia). Similarly, Imteaz et al. [14] presented significant variations of potential water saving within the city of Adelaide (Australia). Imteaz and Khan [17] presented details of water saving variations within the city of Brisbane (Australia). However, all these mentioned studies on spatial variabilities are based on coastal cities, where spatial variation based on proximity to the coastline is customary. For an inland city, such spatial effects are likely to be different, as the variation of their distance from a coastline become insignificant. However, such spatial variation is yet to be investigated in an inland city. This paper presents the potential spatial and weather variabilities of annual rainwater savings and reliability of supply from RWTs for an Australian inland city, Canberra. Such a study will provide valuable insights on rainwater tank outcomes and related potential variabilities to the end-users, who will be able to make informed decisions on any intended investment for rainwater tanks. Also, the study will be useful for the authorities who will be able to decide a reasonable government rebate (as used to be practiced in Australia) to be given to the end-users for any new installation.
2. Methodology
Potential annual water savings and reliability of fulfilling intended demands from a RWT were estimated using a daily water balance model, eTank, developed by Imteaz et al. [18], which has been widely used in many countries including Australia, Nigeria, Nepal, Bangladesh and Palestine. The input data for the model are daily rainfall for the location of interest, connected roof area (which contributes to the catchment of the RWT), amalgamated losses, tank size and intended rainwater demand. Model calculates annual rainwater used (i.e., potable water savings), annual overflow from tank and reliability of receiving intended demand. As the model was primarily developed to assess effect of weather variability, the prime input data (i.e., daily rainfall) should be provided for three weather conditions (dry, average and wet years). Daily rainfall amount is multiplied with the connected roof area to calculate the runoff generated on the roof. Then, the loss amount is deducted from the generated runoff amount and the remaining amount is assumed to divert to the tank storage. Based on a primary study during the development of the tool and rainwater harvesting analysis, a 10% total loss was applied to account for losses such as first flush, leakage, spilling and evaporation [9]. As the accumulated rainwater in the tank may become full, in every timestep available tank storage (which is successive accumulated runoff minus demand) is compared with the accumulated runoffs. If, at any stage, the accumulated runoff become larger than the available storage, the excess water (accumulated runoff—tank volume) is considered as having overflowed from the system. In every timestep (i.e., day), the daily demand is deducted from the accumulated water in the tank. If demand on a day becomes higher than the remaining amount in the tank, the model calculates the shortfall which is expected to be met by the normal town water supply. The detailed description of the model formulations and logical sequences, as well as the accuracy of the model estimations, are presented in a study by Imteaz et al. [18]. Figure 1 shows the schematic diagram of the operating sequence and functions of the eTank model.
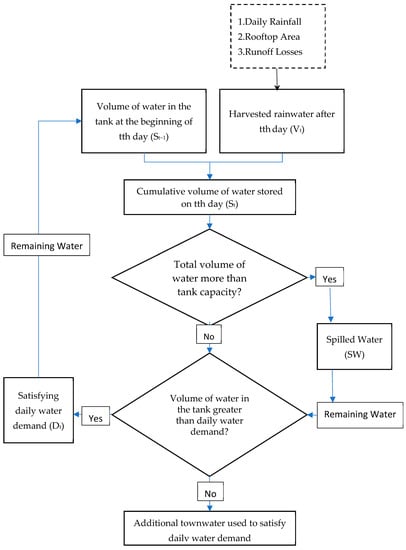
Figure 1.
Flowchart of eTank operations and logical sequences.
The model was used with daily rainfall data from two locations within the city of Canberra. For comparison, apart from daily rainfall data, all other data were kept the same for both the stations. From the model estimations, annual water savings and reliabilities were compared for the selected locations. Reliability was calculated as per the following equation:
where ‘Re’ is the reliability of the tank to be able to supply intended demand (%), ‘U’ is the number of days in a year the tank was unable to meet the demand and ‘N’ is the total number of days in a particular year. The Excel version of the tool was used for this study, which takes a few seconds to compute the output variables for a whole year.
Re = (N − U)/N × 100
The spatial variations in water savings were calculated using the following formula:
where AWS1 and AWS2 are the annual water savings for the station 1 and station 2, respectively (as absolute difference is taken here, any station can be considered as ‘1’ or ‘2’). AWSmin is the minimum of the two values. The same formula was used for the calculation of spatial variation in reliabilities.
For the calculation of weather variabilities for a particular station, the following formula was used:
where AWSwet and AWSdry are the annual water savings in wet and dry years, respectively. The same formula is used for the calculation of weather variabilities in reliability values for a particular station.
3. Study Area and Data
For the current study, the Australian capital Canberra was selected, being an inland city (Figure 2). Being a smaller city compared to other cities (Sydney, Melbourne and Adelaide) where similar studies were conducted previously, two rain gauge stations within the city were selected for the assessment of spatial variability. The stations were selected based on the rainfall data availability for a longer period. One station is located near central Canberra, while the other is located in north Canberra. A brief summary of the selected stations, including their physical features, are provided in Table 1.
Figure 2.
Map of Australia showing location of Canberra.

Table 1.
Location and physical characteristics of the selected stations.
The Australian National Botanic Garden is located near to the city centre and its surrounding is a mixture of plants (i.e., green area), wetland and developed impervious surfaces. Due to the presence of wetland, this area is likely to release more evaporation from water surfaces. The surrounding of ‘Ginninderra CSIRO’ is mostly plants and grass, which is likely to release more evapotranspiration. However, the effects of such localised evaporation and evapotranspiration become diluted when they reach the atmosphere, where such vapour-laden air is often transported by wind speed. The topographic features of the two stations are shown in Figure 3. Figure 4 shows the Google map of the two stations with surrounding areas.
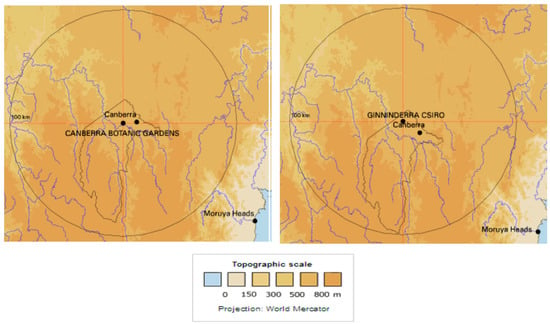
Figure 3.
Topographic features of the selected stations.
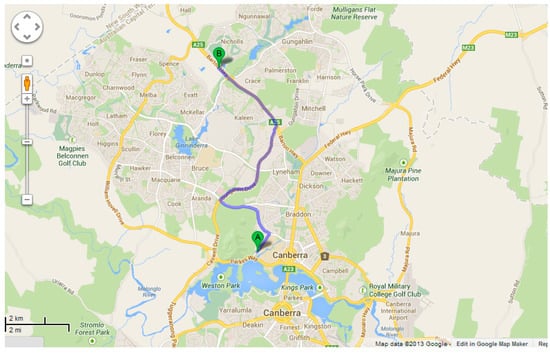
Figure 4.
Google map showing locations and surroundings of the selected stations. (A: Australian National Botanic Garden and B: Ginninderra CSIRO).
Daily rainfall data for both the stations were collected from the Bureau of Meteorology (BoM) website (http://reg.bom.gov.au/climate/data/, accessed on 12 July 2023). Through statistical analysis of the total annual rainfall data for each station, three separate years were selected as dry year, average year and wet year to assess the effect of weather variations on rainwater savings. From historical rainfall data, BoM considers years having annual rainfall amount close to the 10th percentile, 50th percentile and 90th percentiles of the annual rainfall series of the total data period as dry, average and wet years, respectively. For the selected sites, daily rainfall data were available for the period of 1962–2022. For such studies, an analysis of only one year’s worth of data is not justified, as a single year may have an unusual rainfall distribution pattern. To overcome this issue, for each of the dry, average and wet years, a total three years data were considered. For each weather condition, three years were selected in a way that their annual rainfall amounts were very close to the exact values of the 10th, 50th and 90th percentiles. While doing this, one year was selected that had an annual rainfall amount immediately higher and the other year had an annual rainfall amount immediately lower than the rainfall amount of the selected percentile. Table 2 shows all the selected years for different weathers and their corresponding annual rainfall amounts.

Table 2.
Selected years and corresponding annual rainfall for the stations.
A daily water balance model was simulated with the daily rainfall data for the above-mentioned years for several different tank sizes (2500 L, 5000 L, 7500 L and 10,000 L) along with two roof sizes (100 m2 and 200 m2). Regarding demand, two different options were considered; 2 people and 4 people in a household. Conforming with other similar studies in Australia [4,7,9,14,15,16], a non-potable water demand of 150 L/person/day was considered. It is to be noted that most of Australian cities’ total water demand is around 300 L/d/capita, out of which approximately 150 L/d can be from harvested rainwater. Several relationship curves are presented to show the effects of different parameters on annual water saving and on the reliability of rainwater tanks under different weather conditions.
4. Results
The model-simulated results are presented under two categories: (i) effects on annual water saving and (ii) effects on reliability. The following sections elaborate the findings.
4.1. Variability of Annual Water Saving
Figure 5a,b shows the variations of annual water saving with different tank sizes up to 10,000 L under different weather conditions for a higher non-potable water demand scenario (600 L/day, i.e., 4 people) for two roof areas; (i) Figure 5a shows the same for a roof area of 100 m2 and (ii) Figure 5b the same for a roof area of 200 m2.
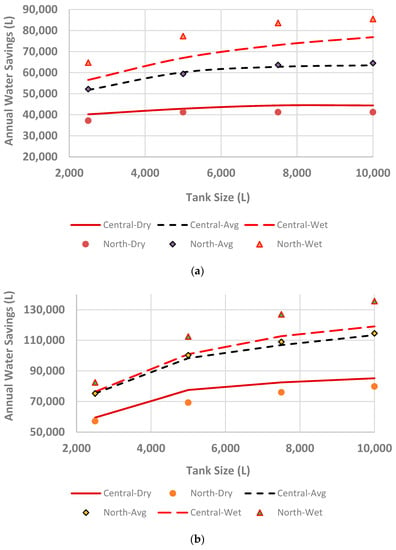
Figure 5.
Variations of annual water savings for a higher water demand (600 L/day); (a) with a roof area of 100 m2 and (b) with a roof area of 200 m2.
From the figures, it is clear that, for both the roof areas in a dry weather scenario, the central region always has a higher water saving level compared to north Canberra, whereas, in an average weather scenario, both the locations’ annual water savings are almost the same. However, in a wet weather scenario, this location-based superiority changes, i.e., north Canberra always has a higher water saving level compared to central Canberra. Such a change in location-based superiority due to weather conditions is an important finding to be noted.
Similar calculations were performed for a low-demand scenario (i.e., rainwater demand of 300 L/day). Figure 6a,b shows the variations in annual water saving with different tank sizes up to 10,000 L under different weather conditions for two roof areas; (i) Figure 6a shows the same for a roof area of 100 m2 and (ii) Figure 6b the same for a roof area of 200 m2.
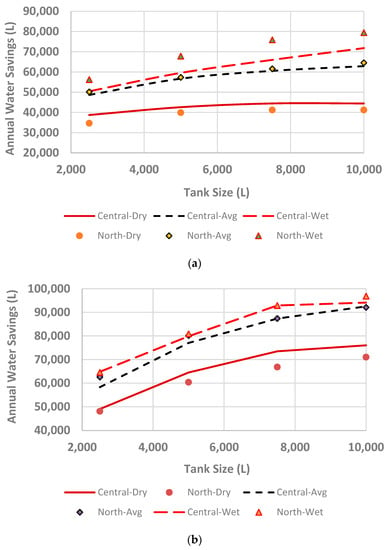
Figure 6.
Variations of annual water savings for a lower water demand (300 L/day); (a) with a roof area of 100 m2 and (b) with a roof area of 200 m2.
Similar trends were observed as with the higher demand scenario, i.e., in a dry year, central Canberra has higher water savings than north Canberra. However, in a wet year, this pattern changes, i.e., north Canberra yields higher water savings than central Canberra. However, for a higher roof area, such differences become insignificant.
In general, variations due to weather variability are quite significant. A height of 68.6% variation within dry and wet years’ water savings was observed for north Canberra with a higher demand scenario. With a lower demand scenario, the maximum variation in annual water savings was 59.2%. However, spatial variations were not very significant. A maximum spatial variability of 10.6% was observed in a dry year, whereas a maximum spatial variability of 15.4% was observed in a wet year. It should be noted that this variability is the potential variation in annual water savings among the two locations considered in this study.
4.2. Variability of Reliability
Figure 7a,b shows the variations of reliability values with different tank sizes up to 10,000 L under different weather conditions for a higher non-potable water demand scenario (600 L/day, i.e., 4 people) for two roof areas; (i) Figure 7a shows the same for a roof area of 100 m2 and (ii) Figure 7b the same for a roof area of 200 m2.
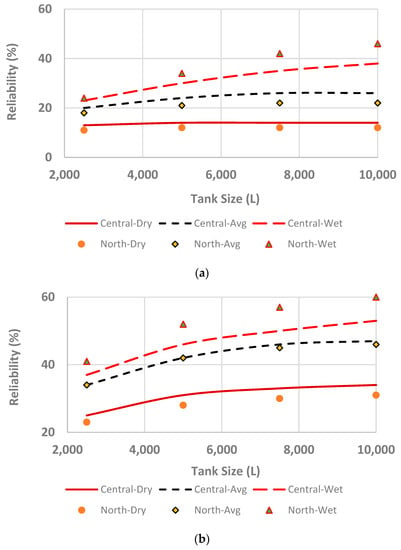
Figure 7.
Variations of reliability for a higher water demand (600 L/day); (a) with a roof area of 100 m2 and (b) with a roof area of 200 m2.
Like the variations in annual water savings, similar trends are also observed for the cases of variations in reliability values. In a dry year, central Canberra has higher reliability compared to north Canberra, whereas the trend changes during a wet year and north Canberra has higher reliability values compared to central Canberra.
With a higher demand scenario in a dry year, a maximum spatial variation of 15.4% is observed in the values of reliabilities between north and central Canberra. Under the same conditions in a wet year, a maximum variation of 17.4% was observed. However, with a lower demand scenario (Figure 8), spatial variations become lessened; in a dry year, a maximum spatial variation of 13.9% was observed whereas, in a wet year, a maximum variation of only 4.6% was observed. Like annual water savings, reliability values exhibit very strong weather variabilities and the magnitude of observed variabilities within dry and wet years’ reliability values are much higher compared to the variabilities in annual water savings. For a higher demand scenario, a maximum variation of 123% was observed between the reliabilities of dry years and wet years. However, for a lower demand scenario, this maximum variation drops down to 70.6%.
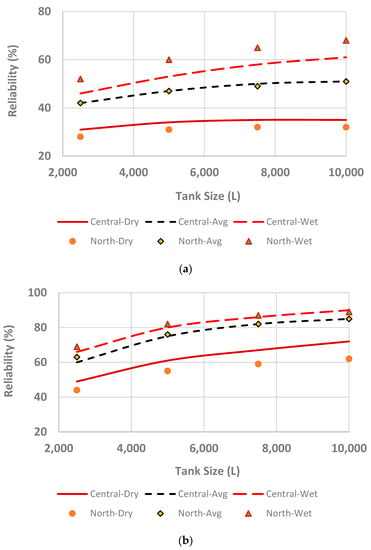
Figure 8.
Variations of reliability for a lower water demand (300 L/day); (a) with a roof area of 100 m2 and (b) with a roof area of 200 m2.
5. Discussion
It is found that a maximum of 68.6% variation in annual water savings between dry and wet years was observed for Canberra. In a similar scenario in the coastal city of Sydney, the maximum weather variation observed was only 31% [14]. In fact, for an inner suburb of Sydney, the maximum weather variation in water savings was much lower (8.7%). For another coastal city, Adelaide, the maximum variation in annual water savings was 57.4% [11]. So, it is clear that, in an inland city, the effect of weather variation on the annual water savings is even more pronounced than in a coastal city. With regard to spatial variation, in the current study, a maximum annual water saving variation of 15.4% was observed whereas, for the coastal city of Adelaide, a maximum variation of 54% was observed for annual water saving. For the coastal city of Sydney, a maximum annual water saving variation of 43% was observed under similar conditions. So, it was found that, for an inland city, the weather variations on annual water savings (through rainwater tanks) are quite significant and more pronounced than the variations observed for a coastal city in Australia. However, the spatial variations are less significant compared to the spatial variations observed in a coastal city in Australia. For an inland city, rainfall is mostly dominated by local factors whereas, for a coastal city, the rainfall is mostly dominated by ocean-atmospheric interactions. As such, in a coastal city, the outcomes of weather variations are somewhat offset by the supply of moisture (and hence rainfall) from the adjacent ocean. As a result, the effects of weather variations are not that prominent compared to the effect of weather variation in an inland city. On the other hand, for a coastal city, the spatial variation is more prominent as the proximity to the ocean has significant effects on the annual water savings of a particular area.
The outcomes of this study would be useful for those end-users who want to install rainwater tanks and are willing to assess the potential benefits of any investment related to the installation and maintenance of rainwater tanks. At present, the end-users make such decisions without any in-depth analysis, solely depending on the tank seller’s verbal information, which is mostly biased. Also, end-users will obtain insights on potential spatial and weather variabilities, which are prominent in the Australian climate. Also, relevant authorities can adopt such study results to derive reasonable government rebates (which has been in practice for many years) to be offered to the end-users. Also, in the past, the same rebates were given to all the installers for a whole city, which is not logical. The findings from this study would help the authorities to decide differential rebates for different parts of the city, depending on the expected amounts of savings to respective area. For such decision making, a more detail economic analysis is recommended.
6. Conclusions
This paper presented potential annual rainwater savings and reliability under different weather conditions for two different regions within the Australian capital city, Canberra. A previously developed daily water balance model (eTank), using daily rainfall and demand data, was employed to calculate the two significant outcomes of a domestic rainwater tank. A different set of graphs was presented depicting relationships between annual water savings and reliability for different standard tank sizes ranging from 2500 L to 10,000 L for three different weather conditions: dry, average and wet. Each graph shows the annual water savings/reliability for two selected locations in Canberra, under three weather conditions. A separate set of graphs was produced for different demand scenarios: high demand (600 L/day) and low demand (300 L/day). From the developed graphs, the stakeholders should be able to envisage the expected variations in rainwater tank outcomes from a certain sized tank under a particular demand scenario.
It was found that significant weather variations in expected annual water savings and reliability are to be expected in both the studied locations. Weather variation is much more prominent for the case of reliability; a maximum variation of 123% is expected between the reliabilities of dry weather and wet weather. In case of annual water savings, the maximum expected variation is 68.6% between the dry year and wet year. Such variations are higher than the expected maximum weather variations (between dry and wet years) for two coastal cities, Sydney and Adelaide, which were revealed in previous studies. However, spatial variabilities among the two selected locations are less significant compared to weather variabilities. Among the two selected locations, a maximum variation of 15.4% is expected with regard to annual water savings, while a maximum variation of 17% is expected with regard to reliability.
From the above findings and observed rainfall data, it can be concluded that reliability (which is directly related to intra-annual rainfall distribution) has significant influence on annual water savings as, among the two selected locations, the annual rainfall amounts do not show significant differences, whereas annual water savings, as well as reliability, show significant differences. Differences in annual water savings are caused by the significant differences in reliabilities, while annual rainfall amounts were not significantly different.
The current study’s results may not be applicable to other geographical areas/cities where rainfall magnitude and/or patterns are different. More studies are recommended with other inland cities in order to be able to derive a generalised pattern. Also, a more detailed economic analysis is recommended for determining the different payback periods of end-users’ investments in rainwater tanks. It is recommended that authorities work out reasonable rebate amounts for different parts of the city. For such economic analysis, the consideration of a mix of dry, average and wet years’ outcomes would provide more realistic results.
It should be noted that the model considers a user-defined rainwater demand, which was kept constant for everyday for the whole year. In reality, the amount of rainwater demand will vary depending on the daily weather conditions. In the current model, it was not possible to consider such variable rainwater demand.
Author Contributions
Project administration, supervision, final paper preparation, M.A.I.; data collection, model setup and analysis, A.G.Y.; conceptualization and final paper checking, C.S.; original draft preparation, writing—review and editing, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
No funding received for the study.
Data Availability Statement
Data are available from the first author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sharma, A.K.; Cook, S.; Gardner, T.; Tjandraatmadja, G. Rainwater tanks in modern cities: A review of current practices and research. J. Water Clim. Chang. 2016, 7, 445–466. [Google Scholar] [CrossRef]
- United Nations. UN World Water Development Report. 2019. Available online: www.unwater.org/publications/un-world-water-development-report-2019 (accessed on 26 June 2023).
- Amos, C.; Rahman, A.; Karim, F.; Gathenya, J. A scoping review of roof harvested rainwater usage in urban agriculture: Australia and Kenya in focus. J. Clean. Prod. 2018, 202, 174–190. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Paudel, U.; Santos, C. Impacts of climate change on weather and spatial variabilities of potential water savings from rainwater tanks. J. Clean. Prod. 2021, 311, 127491. [Google Scholar] [CrossRef]
- Khan, Z.; Alim, M.A.; Rahman, M.M.; Rahman, A. A continental scale evaluation of rainwater harvesting in Australia. Resour. Conserv. Recycl. 2021, 167, 105378. [Google Scholar] [CrossRef]
- Santos, C.; Imteaz, M.A.; Ghisi, E.; Matos, C. The effect of climate change on domestic rainwater harvesting. Sci. Total Environ. 2020, 729, 138967. [Google Scholar] [CrossRef] [PubMed]
- Imteaz, M.A.; Moniruzzaman, M. Potential impacts of climate change on future rainwater tank outcomes: A case study for Sydney. J. Clean. Prod. 2020, 273, 123095. [Google Scholar] [CrossRef]
- Khastagir, A.; Jayasuriya, N. Optimal sizing of rain water tanks for domestic water conservation. J. Hydrol. 2010, 381, 181–188. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Ahsan, A.; Naser, J.; Rahman, A. Reliability analysis of rainwater tanks in Melbourne using daily water balance model. Resour. Conserv. Recycl. 2011, 56, 80–86. [Google Scholar] [CrossRef]
- Preeti, P.; Rahman, A. A case study on reliability, water demand and economic analysis of rainwater harvesting in Australian capital cities. Water 2021, 13, 2606. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Moniruzzaman, M. Spatial variability of reasonablement rebates for rainwater tank installations: A case study for Sydney. Resour. Conserv. Recycl. 2018, 133, 112–119. [Google Scholar] [CrossRef]
- Karim, M.R.; Sakib, B.M.S.; Sakib, S.S.; Imteaz, M.A. Rainwater harvesting potentials in commercial buildings in Dhaka: Reliability and economic analysis. Hydrology 2021, 8, 9. [Google Scholar] [CrossRef]
- Matos, C.; Santos, C.; Bentes, I.; Imteaz, M.A.; Pereira, S. Economic analysis of a rainwater harvesting system in a commercial building. Water Resour. Manag. 2015, 29, 3971–3986. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Paudel, U.; Ahsan, A.; Santos, C. Climatic and spatial variability of potential rainwater savings for a large coastal city. Resour. Conserv. Recycl. 2015, 105, 143–147. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Imteaz, M.A. Generalized equations, climatic and spatial variabilities of potential rainwater savings: A case study for Sydney. Resour. Conserv. Recycl. 2017, 125, 139–156. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Sagar, K.; Santos, C.; Ahsan, A. Climatic and Spatial Variations of Potential Rainwater Savings for Melbourne. Int. J. Hydrol. Sci. Technol. 2016, 6, 45–61. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Khan, M.S. Pioneer attempt of incorporating four variables in generalised equations for predicting water savings through rainwater tanks. Urban Water J. 2022, 19, 714–731. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Karki, R.; Shamseldin, A.; Matos, C. eTank and contemporary online tools for rainwater tank outcomes analysis. Int. J. Comput. Aided Eng. Technol. 2017, 9, 372–384. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).