Sensitivity of the Penman–Monteith Reference Evapotranspiration Equation to Meteorological Variables for Puerto Rico
Abstract
1. Introduction
2. Materials and Methods
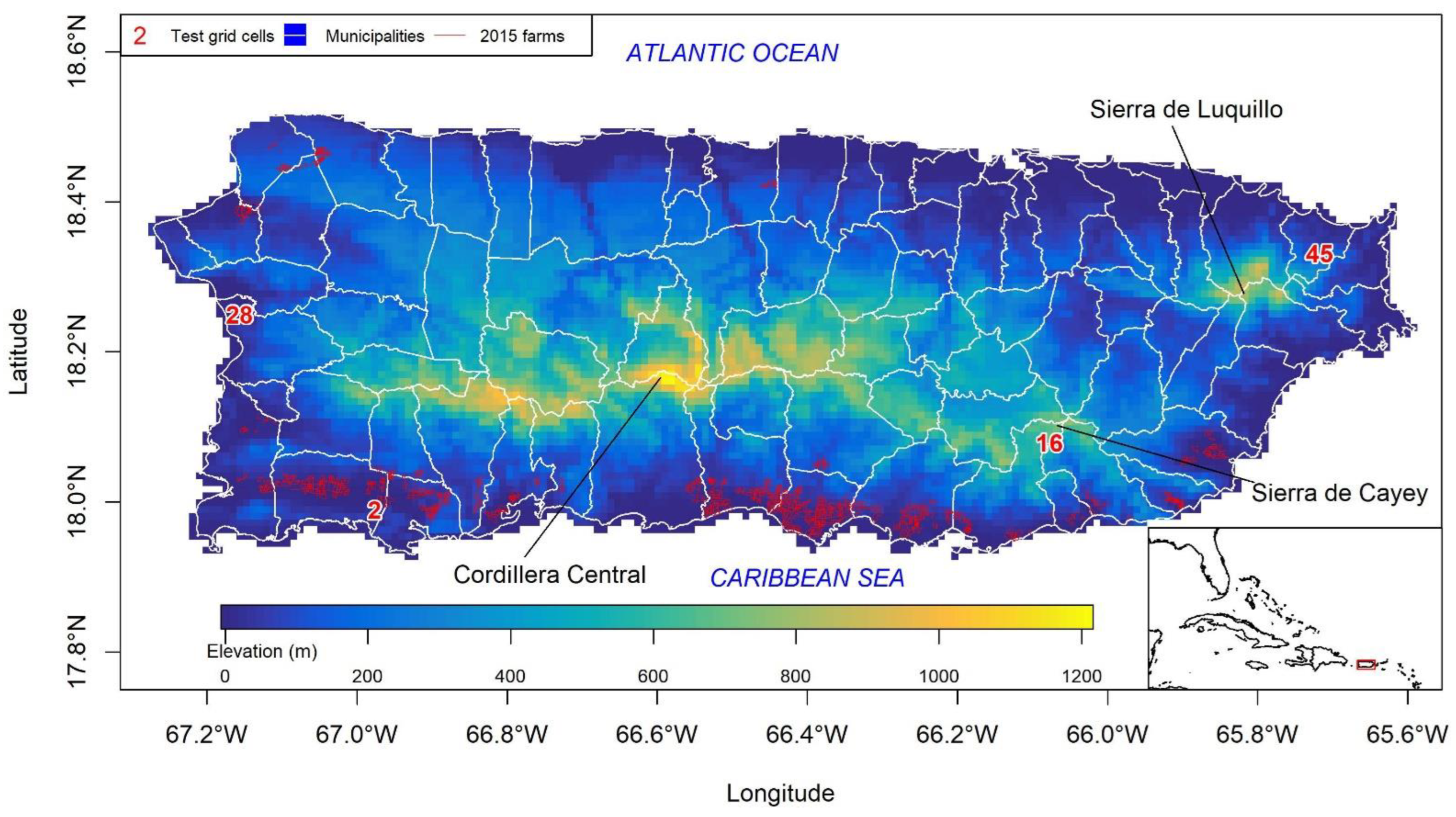
2.1. Study Area
2.2. Data
2.2.1. Gridded Historical Data
2.2.2. WRF Dynamically Downscaled Climate Change Projections
2.3. Methods
3. Results
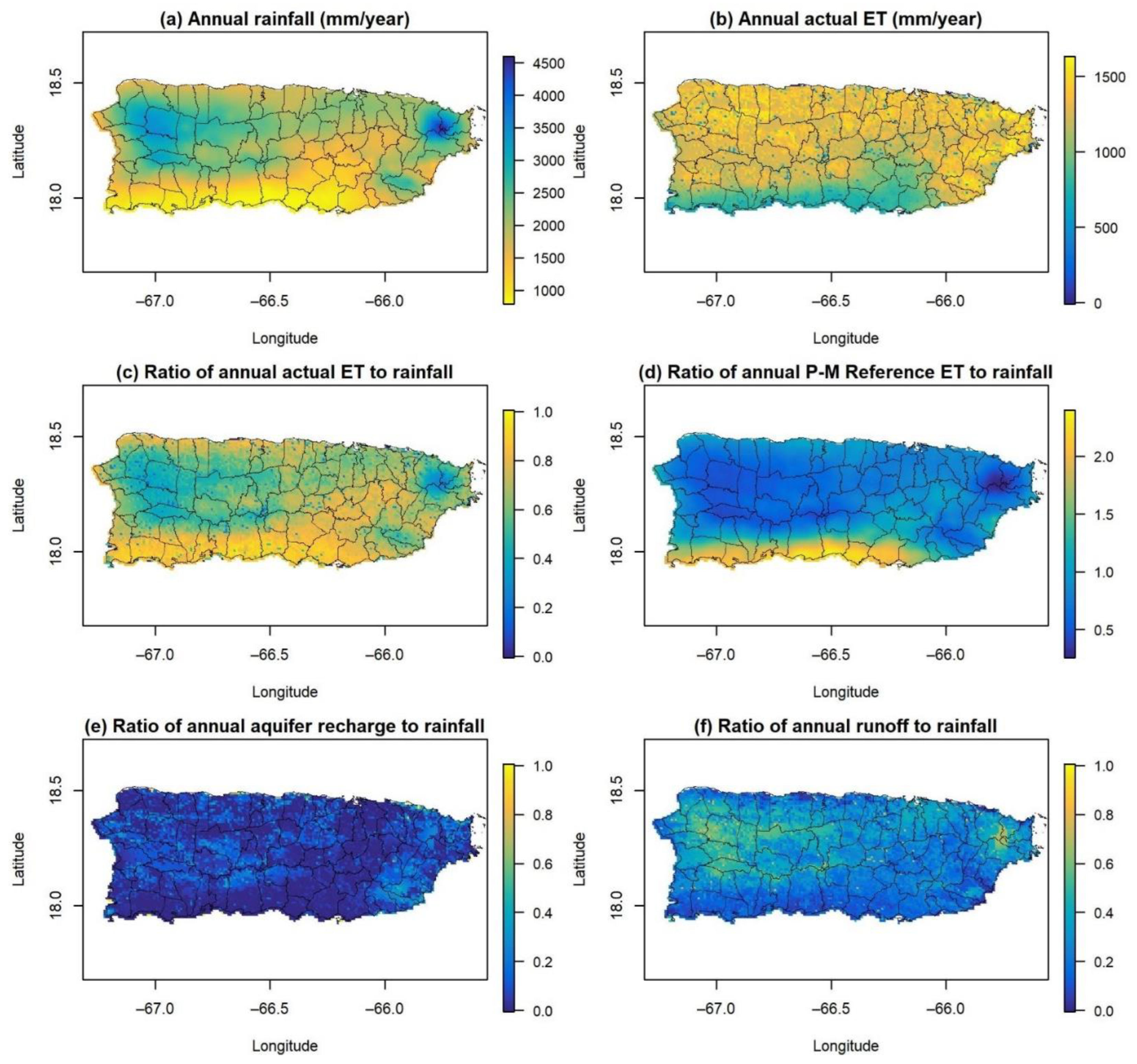
3.1. Spatiotemporal Variations in Rainfall and ET
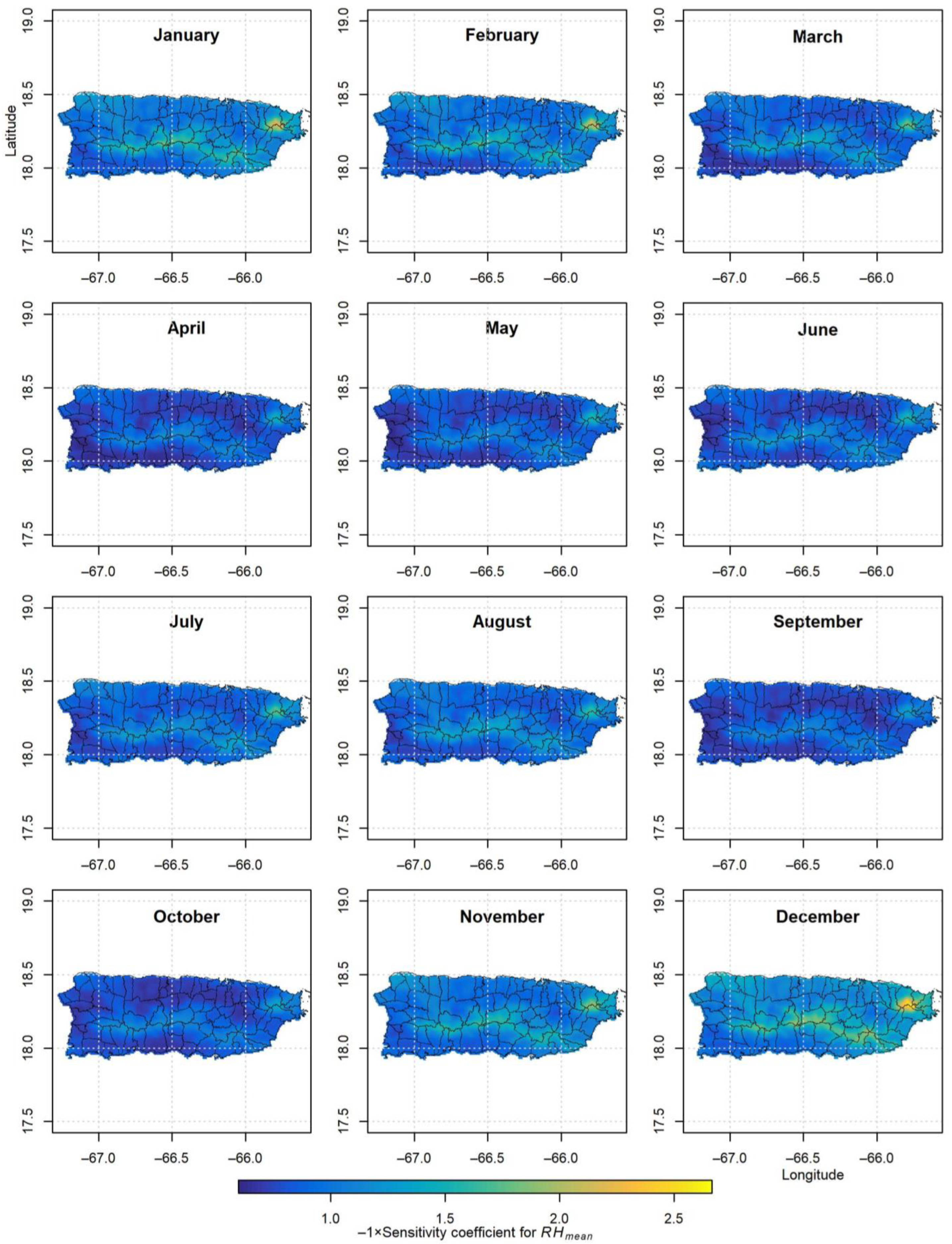
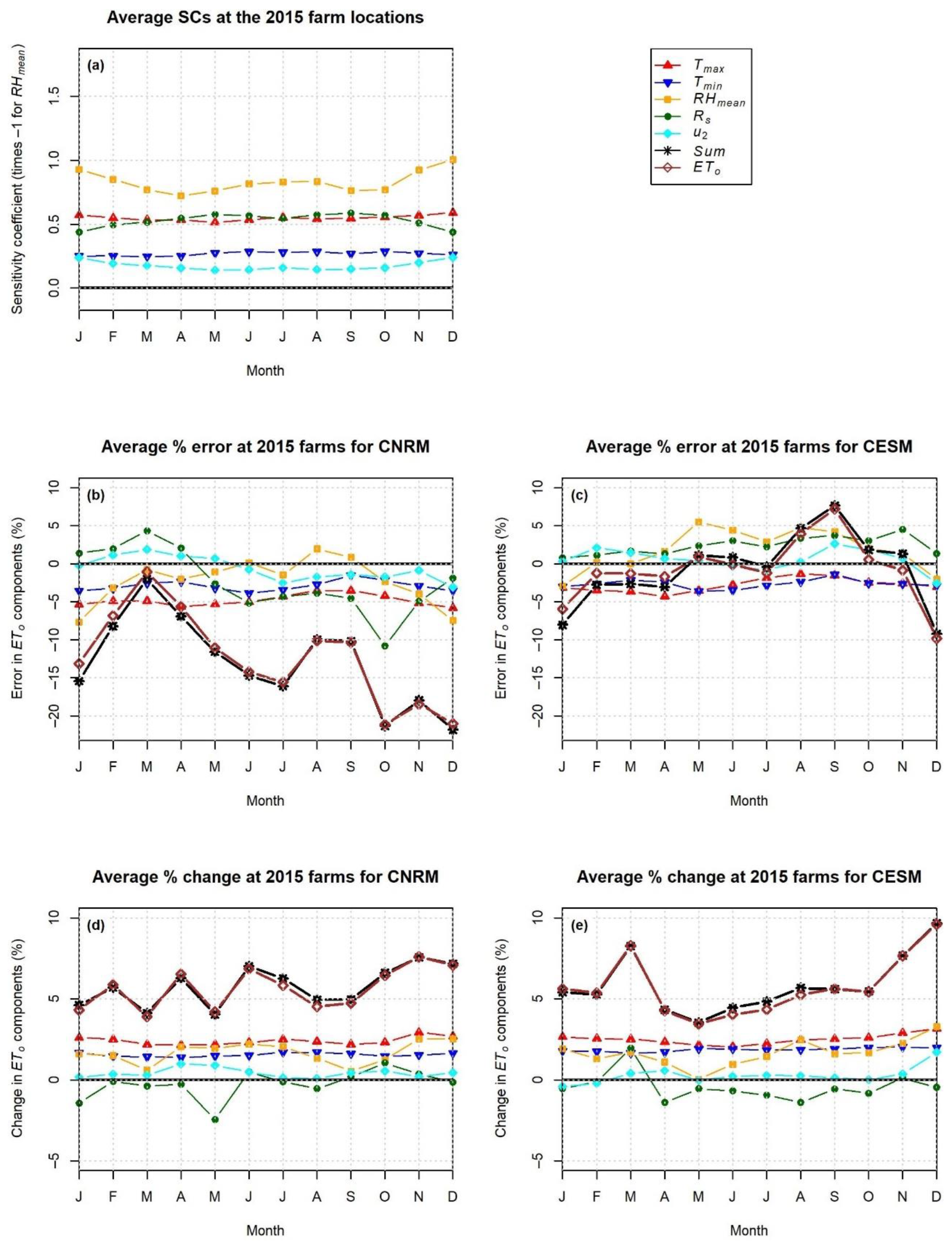
3.2. Sensitivity Coefficients
3.3. Application
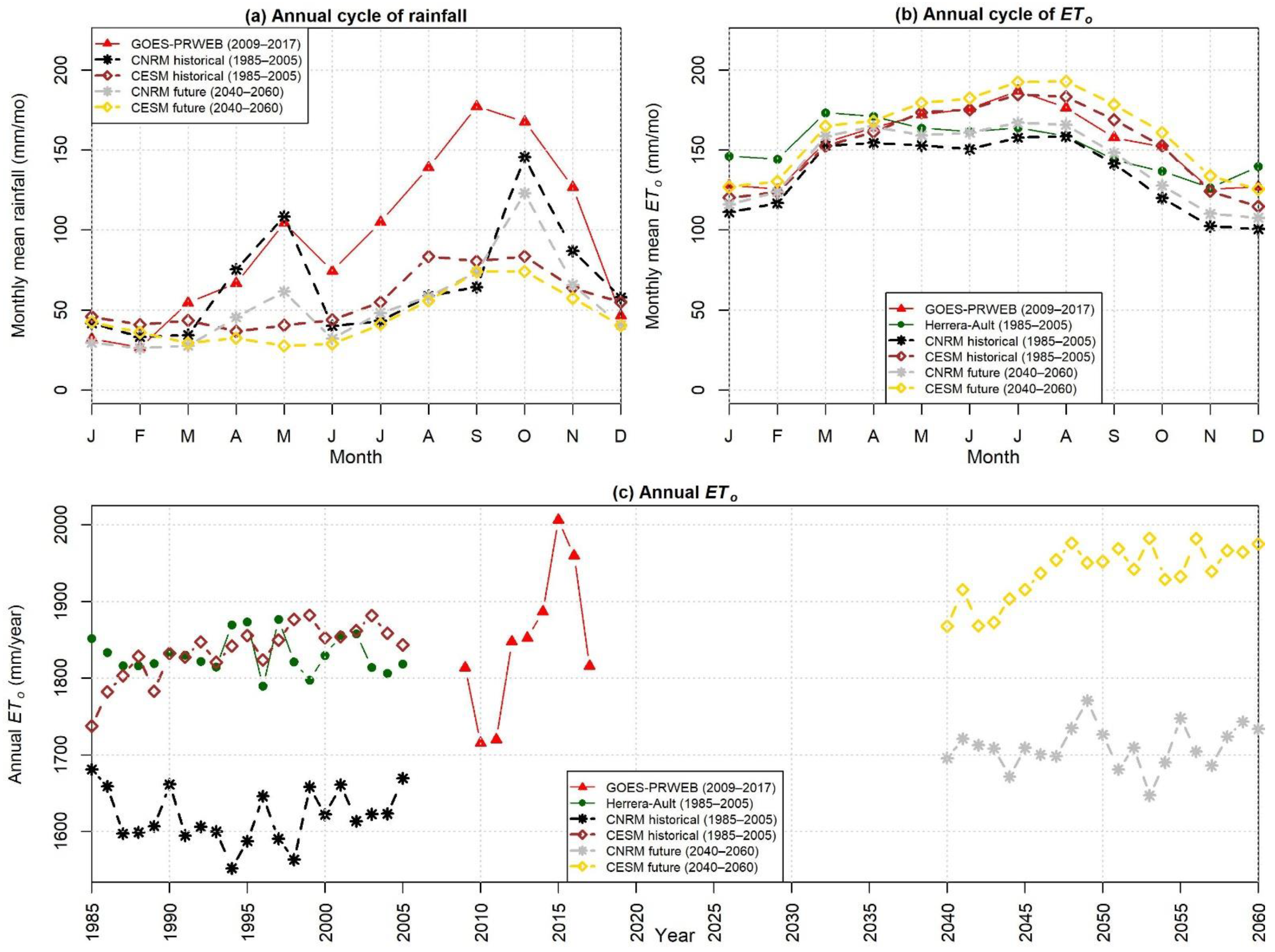
3.3.1. Causes of Errors in Reference ET Estimated from Model Output for 1985–2005
3.3.2. Causes of Changes in Reference ET Estimated from Model Output for 2040–2060
3.4. Limitations
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Puerto Rico Institute of Statistics. Food Security in Puerto Rico, Calendar Year 2015. 2019. Available online: https://estadisticas.pr/files/Comunicados/Seguridad%20Alimentaria%20en%20Puerto%20Rico%20-%20Final%20%28300519%29.pdf (accessed on 20 July 2022).
- Molina-Rivera, W.L.; Irizarry-Ortiz, M.M. Estimated water withdrawals and use in Puerto Rico. U.S. Geol. Surv. Open-File Rep. 2021, 2021-1060, 1–38. [Google Scholar]
- Puerto Rico Planning Board. Memorial of the land use plan, Guide for the Classification of Territories. 2015. Available online: https://www.sciencebase.gov/catalog/item/576bfe89e4b07657d1a26ee5 (accessed on 8 February 2023).
- Puerto Rico Department of Natural and Environmental Resources. Integrated water resources plan for Puerto Rico. 2016. Available online: https://drna.pr.gov/wp-content/uploads/formidable/PIRA-2016.pdf (accessed on 8 February 2023).
- Harmsen, E.W.; Howard-Harmsen, R. Agricultural Water Management and Puerto Rico’s Food Insecurity. Ethos Gubernamental. Special Edition. September 2019. Available online: https://academic.uprm.edu/hdc/HarmsenPapers/Harmsen_and_Harmsen_Ethos.pdf (accessed on 18 July 2022).
- NOAA (National Oceanographic and Atmospheric Administration). National Integrated Drought Information System. Available online: https://www.drought.gov/states/puerto-rico (accessed on 20 July 2022).
- Herrera, D.A.; Ault, T.R.; Fasullo, J.T.; Coats, S.J.; Carrillo, C.M.; Cook, B.I.; Park Williams, A. Exacerbation of the 2013–2016 pan-Caribbean drought by anthropogenic warming. J. Geophys. Res. 2018, 45, 10619–10626. [Google Scholar] [CrossRef] [PubMed]
- Khalyani, A.H.; Gould, W.A.; Harmsen, E.; Terando, A.; Quinones, M.; Collazo, J.A. Climate change implications for tropical islands: Interpolating and interpreting statistically downscaled GCM projections for management and planning. J. Appl. Meteorol. Climatol. 2016, 55, 265–282. [Google Scholar] [CrossRef]
- Bowden, J.; Terando, A.J.; Misra, V.; Wootten, A.; Bhardwaj, A.; Boyles, R.; Gould, W.; Collazo, J.A.; Spero, T.L. High-resolution dynamically downscaled rainfall and temperature projections for ecological life zones within Puerto Rico and for the U.S. Virgin Islands. Int. J. Climatol. 2021, 41, 1305–1327. [Google Scholar] [CrossRef]
- ASCE (American Society of Civil Engineers); EWRI (Environmental and Water Resources Institute). Task Committee on Standardization of Reference Evapotranspiration. The ASCE standardized reference evapotranspiration equation. 2005. Available online: https://ascelibrary.org/doi/book/10.1061/9780784408056 (accessed on 20 April 2023).
- Irmak, S.; Payero, J.O.; Martin, D.L.; Irmak, A.; Howell, T.A. Sensitivity analyses and sensitivity coefficients of standardized daily ASCE Penman–Monteith equation. J. Irrig. Drain Eng. 2006, 132, 564–578. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.-y.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman–Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- McKenney, M.S.; Rosenberg, N.J. Sensitivity of some potential evapotranspiration estimation methods to climate change. Agric. For. Meteorol. 1993, 64, 81–110. [Google Scholar] [CrossRef]
- Debnath, S.; Adamala, S.; Raghuwanshi, N.S. Sensitivity analysis of FAO-56 Penman–Monteith method for different agro-ecological regions of India. Environ. Process. 2015, 2, 689–704. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, Y.; Shi, Y. Climate change effect on hydrological processes over the Yangtze River basin. Quat. Int. 2011, 244, 202–210. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Z.; Cui, B.; Sun, T. The temporal trends of reference evapotranspiration and its sensitivity to key meteorological variables in the Yellow River Basin, China. Hydrol. Process. 2010, 24, 2171–2181. [Google Scholar] [CrossRef]
- Biazar, S.M.; Dinpashoh, Y.; Singh, V.P. Sensitivity analysis of the reference crop evapotranspiration in a humid region. Environ. Sci. Pollut. Res. 2019, 26, 32517–32544. [Google Scholar] [CrossRef] [PubMed]
- Emeka, N.; Ikenna, O.; Okechukwu, M.; Chinenye, A.; Emmanuel, E. Sensitivity of FAO Penman–Monteith reference evapotranspiration (ETo) to climatic variables under different climate types in Nigeria. J. Water Clim. Change 2021, 12, 858–878. [Google Scholar] [CrossRef]
- Hou, L.-g.; Zou, S.-b.; Xiao, H.-l.; Yang, Y.-g. Sensitivity of the reference evapotranspiration to key climatic variables during the growing season in the Ejina oasis northwest China. SpringerPlus 2013, 2 (Suppl. S1), S4. [Google Scholar] [CrossRef]
- Luo, Y.; Gao, P.; Mu, X. Influence of meteorological factors on potential evapotranspiration in Yanhe River Basin, China. Water 2021, 13, 1222. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, J.; Sun, F.; Liu, W. Pan evaporation paradox and evaporative demand from the past to the future over China: A review. WIREs Water 2017, 4, e1207. [Google Scholar] [CrossRef]
- Peterson, T.; Golubev, V.S.; Groisman, P.Y. Evaporation losing its strength. Nature 1995, 377, 687–688. [Google Scholar] [CrossRef]
- Roderick, M.L.; Rotstayn, L.D.; Farquhar, G.D.; Hobbins, M.T. On the attribution of changing pan evaporation. Geophys. Res. Lett. 2007, 34, 251–270. [Google Scholar] [CrossRef]
- USGS (U.S. Geological Survey). Climate of Puerto Rico. 2016. Available online: https://www.usgs.gov/centers/caribbean-florida-water-science-center-%28cfwsc%29/science/climate-puerto-rico (accessed on 20 July 2022).
- Angeles, M.E.; González, J.E.; Ramírez-Beltrán, N.D.; Tepley, C.A.; Comarazamy, D.E. Origins of the Caribbean rainfall bimodal behavior. J. Geophys. Res. 2010, 115, D11106. [Google Scholar] [CrossRef]
- Muñoz, M.M.; Lugo, W.I.; Santiago, C.; Matos, M.; Ríos, S.; Lugo, J. Taxonomic Classification of the Soils of Puerto Rico, 2017. University of Puerto Rico, Mayagüez Campus, College of Agricultural Sciences, Agricultural Experiment Station Bulletin 313. January 2018. Available online: https://www.uprm.edu/tamuk/wp-content/uploads/sites/299/2019/06/Taxonomic_classification_soils_PR_2018_reduced.pdf (accessed on 20 July 2022).
- Dixon, J.F.; Molina-Rivera, W.L.; Irizarry-Ortiz, M.M.; Christesson, K.R. Spatial and Tabular Datasets of Water Withdrawals and Use in Puerto Rico, 2015. U.S. Geological Survey data release 2021. Available online: https://www.sciencebase.gov/catalog/item/600aec34d34e162231fb26d9 (accessed on 9 August 2022).
- Harmsen, E.W.; Mecikalski, J.R.; Reventos, V.J.; Alvarez Perez, E.; Uwakweh, S.S.; Adorno Garcia, C. Water and energy balance model GOES-PRWEB: Development and Validation. Hydrology 2021, 8, 113. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Harmsen, E.W. The use of visible geostationary operational meteorological satellite imagery in mapping the water balance over Puerto Rico for water resource management. In Satellite Information Classification and Interpretation; Rustamov, R.B., Ed.; IntechOpen: London, UK, 2019. [Google Scholar]
- Harmsen, E.W.; Tosado Cruz, P.; Mecikalski, J.R. Calibration of selected pyranometers and satellite derived solar radiation in Puerto Rico. Int. J. Renew. Energy Technol. 2014, 5, 43–54. [Google Scholar] [CrossRef]
- Herrera, D.; Ault, T. Insights from a new high-resolution drought Atlas for the Caribbean spanning 1950–2016. J. Clim. 2017, 30, 7801–7825. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. FAO Irrig. Drain. Paper 1998, 56. Available online: https://www.fao.org/3/x0490e/x0490e00.htm (accessed on 18 July 2022).
- Bowden, J.; Wootten, A.; Terando, A.; Boyles, R. Weather Research and Forecasting (WRF): Puerto Rico and US Virgin Islands Dynamical Downscaled Climate Change Projections. U.S. Geological Survey Data Release 2018. Available online: https://www.sciencebase.gov/catalog/item/5977b95de4b0ec1a4888e493 (accessed on 23 March 2021).
- McCuen, R.H. A sensitivity and error analysis of procedures for estimating evaporation. Water Resour. Bull. 1974, 10, 486–498. [Google Scholar] [CrossRef]
- Harmsen, E.W.; Goyal, M.R.; Torres-Justiniano, S. Estimating evapotranspiration in Puerto Rico. J. Agric. Univ. Puerto Rico 2002, 86, 35–54. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H. Sensitivity of evapotranspiration to climatic change in different climates. Glob. Planet. Change 2014, 115, 16–23. [Google Scholar] [CrossRef]
- Murphy, S.; Stallard, R.F.; Scholl, M.A.; González, G.; Torres-Sánchez, A.J. Reassessing rainfall in the Luquillo Mountains, Puerto Rico: Local and global ecohydrological implications. PLoS ONE 2017, 12, e0180987. [Google Scholar] [CrossRef] [PubMed]
- Koutsoyiannis, D. Revisiting the global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- Ainsworth, E.A.; Long, S.P. 30 years of free-air carbon dioxide enrichment (FACE): What have we learned about future crop productivity and its potential for adaptation? Glob. Change Biol. 2020, 27, 27–49. [Google Scholar] [CrossRef]
- Islam, A.; Ahuja, L.R.; Garcia, L.A.; Ma, L.; Sassendran, A.S. Modeling the effect of elevated CO2 and climate change on reference evapotranspiration in the semi-arid Central Great Plains. Trans. ASABE 2012, 55, 2135–2146. [Google Scholar] [CrossRef]
- Kruijt, B.; Witte, J.-P.M.; Jacobs, C.; Kroon, T. Effects of rising atmospheric CO2 on evapotranspiration and soil moisture: A practical approach for the Netherlands. J. Hydrol. 2008, 349, 257–267. [Google Scholar] [CrossRef]
- Scarpare, F.V.; Rajagopalan, K.; Liu, M.; Nelson, R.L.; Stöckel, C.O. Evapotranspiration of irrigated crops under warming and elevated atmospheric CO2: What is the direction of change? Atmosphere 2022, 13, 163. [Google Scholar] [CrossRef]
- Global Wind Atlas Version 3.0. Available online: https://globalwindatlas.info/en/area/Puerto%20Rico/ (accessed on 30 January 2023).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorolog. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science—An Introductory Survey, 2nd ed.; Elsevier: New York, NY, USA, 2006; p. 483. [Google Scholar]
- American Meteorological Society. Glossary of Meteorology. 2012. Available online: https://glossary.ametsoc.org/wiki/Mixing_ratio (accessed on 8 February 2023).
- CariCOOS (Caribbean Coastal Ocean Observing System). Weather Flow Mesonet Meteorological Station Aggregation Data. Available online: http://52.55.122.42/thredds/caricoos_mesonet_agg.html (accessed on 13 September 2021).
- IOOS (Integrated Ocean Observing System). Environmental Sensor Map. Available online: https://sensors.ioos.us/#map (accessed on 18 November 2021).
- NOAA (National Oceanic and Atmospheric Administration); NCEI (National Centers for Environmental Information). Global Summary of the Day—GSOD. User Engagement and Services Branch. DOC/NOAA/NESDIS/NCDC > National Climatic Data Center, NESDIS, NOAA, U.S. Department of Commerce. Available online: https://www.ncei.noaa.gov/cdo-web/ (accessed on 16 November 2021).
- WRCC (Western Regional Climate Center). National Interagency Fire Center Remote Automatic Weather Stations (RAWS). Available online: https://raws.dri.edu/prF.html (accessed on 10 November 2021).

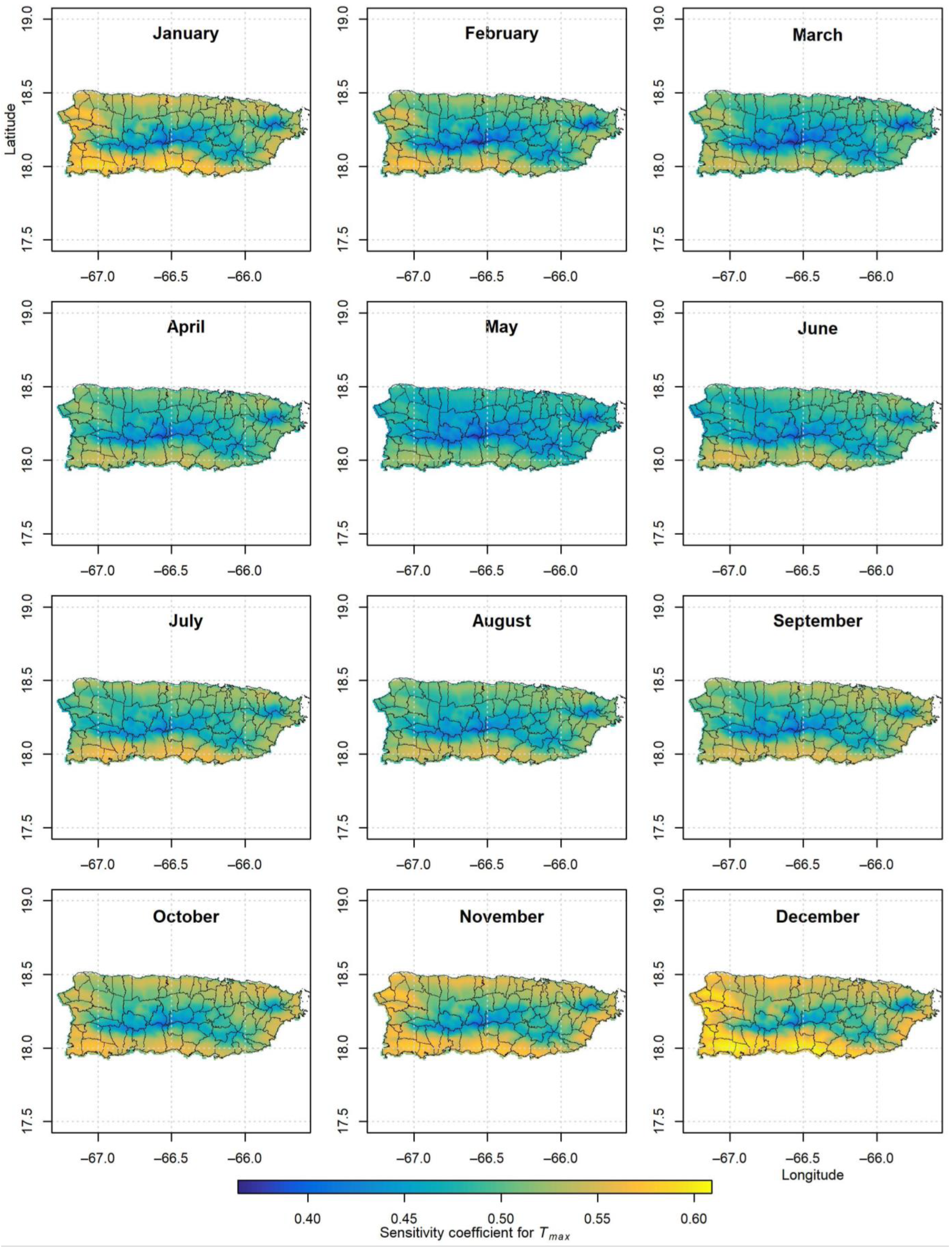
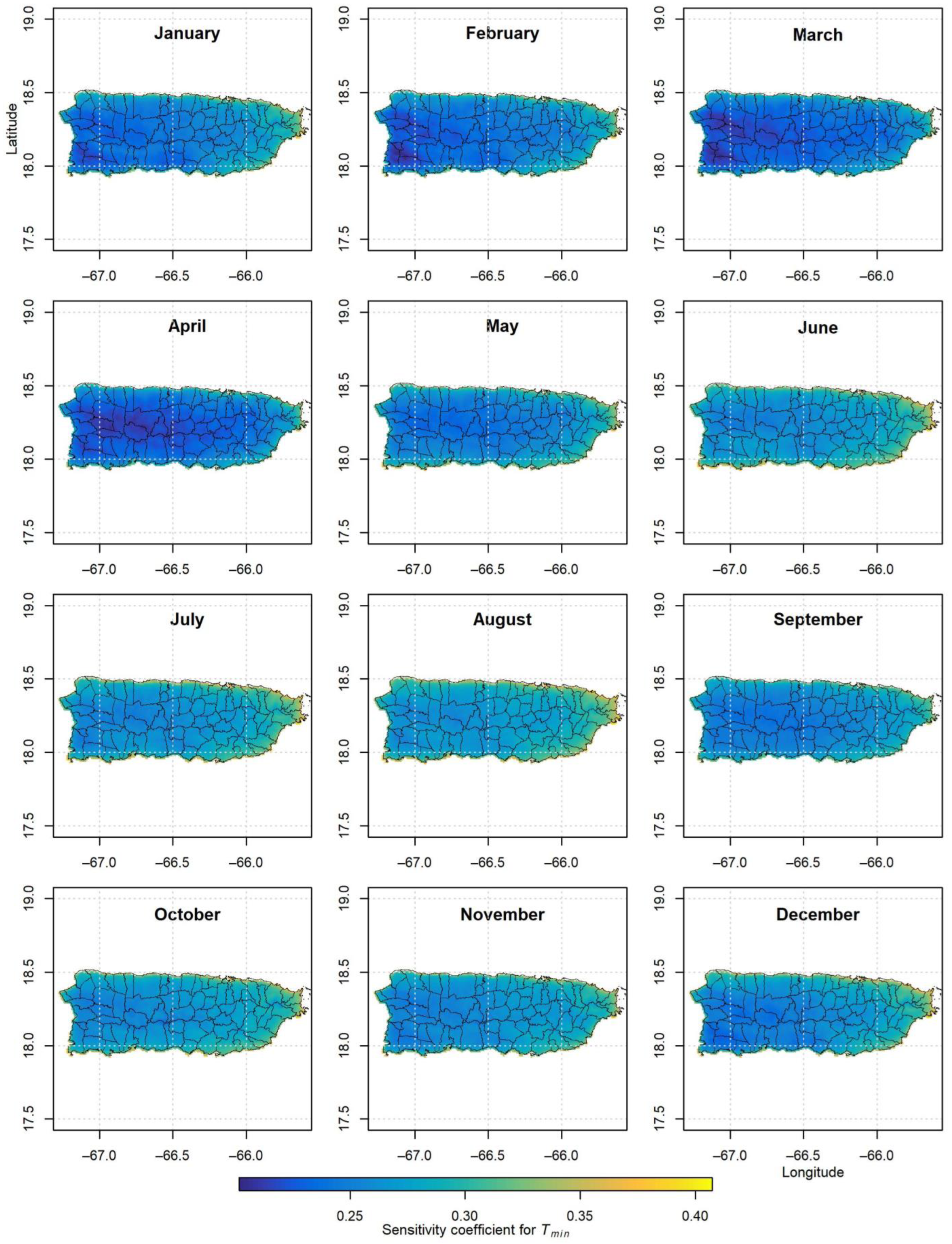
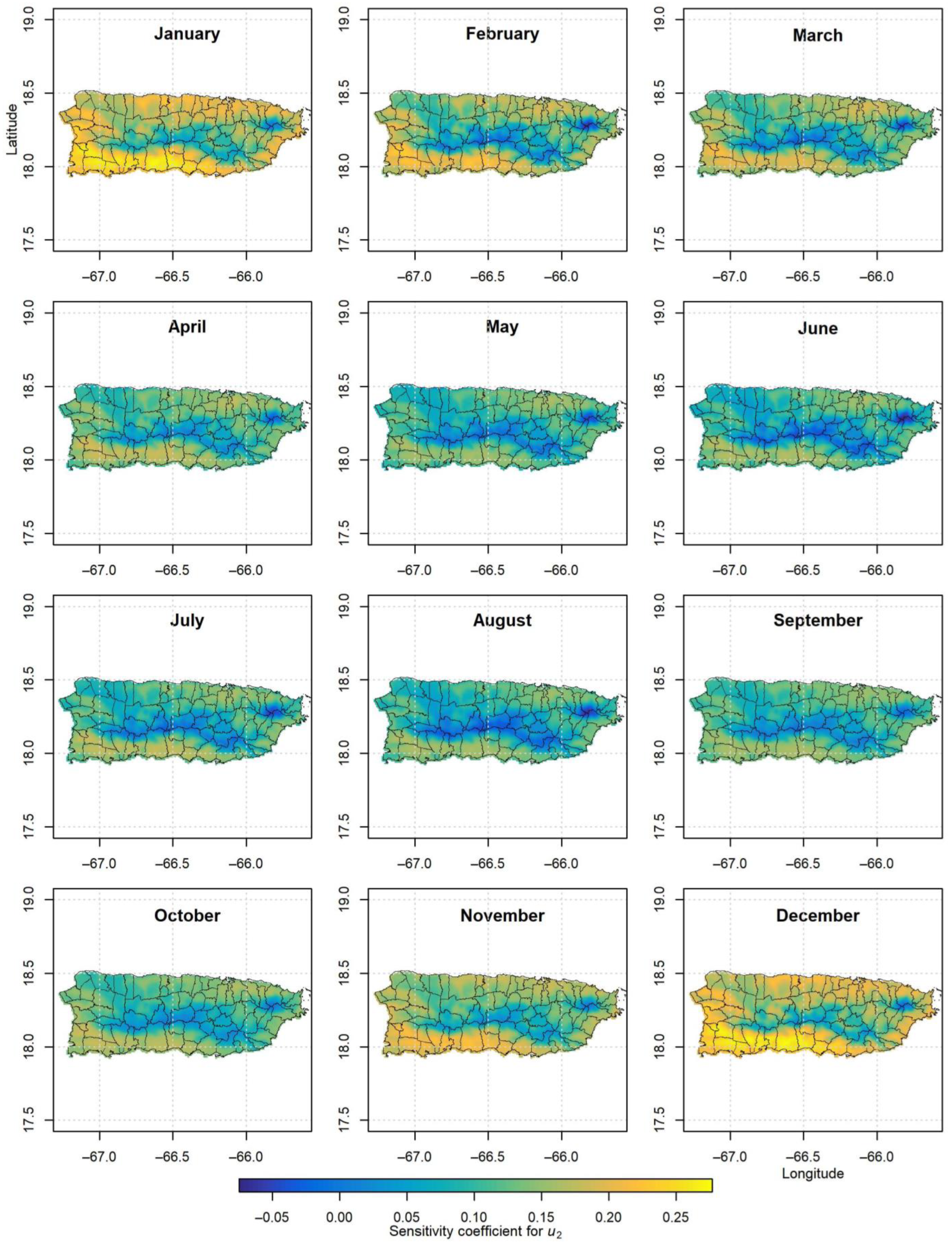

| Variable | RHmean | Rs | Tmax | Tmin | SC RHmean * | SC Rs | SC Tmax | SC Tmin | ||
|---|---|---|---|---|---|---|---|---|---|---|
| RHmean | 1 | −0.29 | −0.72 | −0.49 | −0.02 | −0.73 | 0.47 | −0.69 | 0.07 | −0.80 |
| Rs | −0.29 | 1 | 0.54 | 0.57 | 0.30 | 0.56 | 0.55 | −0.07 | 0.25 | −0.26 |
| Tmax | −0.72 | 0.54 | 1 | 0.88 | 0 | 0.76 | −0.01 | 0.67 | 0.31 | 0.51 |
| Tmin | −0.49 | 0.57 | 0.88 | 1 | 0.22 | 0.51 | 0.06 | 0.49 | 0.70 | 0.33 |
| −0.02 | 0.30 | 0 | 0.22 | 1 | −0.39 | −0.25 | 0.08 | 0.55 | −0.01 | |
| SC RHmean * | −0.73 | 0.56 | 0.76 | 0.51 | −0.39 | 1 | 0.18 | 0.33 | −0.17 | 0.34 |
| SC Rs | 0.47 | 0.55 | −0.01 | 0.06 | −0.25 | 0.18 | 1 | −0.64 | −0.01 | −0.83 |
| SC Tmax | −0.69 | −0.07 | 0.67 | 0.49 | 0.08 | 0.33 | −0.64 | 1 | 0.20 | 0.86 |
| SC Tmin | 0.07 | 0.25 | 0.31 | 0.70 | 0.55 | −0.17 | −0.01 | 0.20 | 1 | 0.04 |
| SC | −0.80 | −0.26 | 0.51 | 0.33 | −0.01 | 0.34 | −0.83 | 0.86 | 0.04 | 1 |
| ETo energ. | −0.30 | 0.96 | 0.65 | 0.65 | 0.10 | 0.66 | 0.62 | −0.05 | 0.23 | −0.23 |
| ETo aero. | −0.86 | 0.48 | 0.72 | 0.67 | 0.49 | 0.49 | −0.44 | 0.67 | 0.31 | 0.66 |
| ETo energ. frac. | 0.68 | 0.24 | −0.30 | −0.23 | −0.39 | −0.04 | 0.94 | −0.77 | −0.16 | −0.90 |
| ETo aero. frac. | −0.68 | −0.24 | 0.30 | 0.23 | 0.39 | 0.04 | −0.94 | 0.77 | 0.16 | 0.90 |
| Rainfall | 0.27 | 0.17 | 0.17 | 0.19 | −0.32 | 0.15 | 0.60 | −0.27 | 0.05 | −0.38 |
| Elevation | 0.78 | −0.65 | −0.92 | −0.92 | −0.10 | −0.66 | 0.68 | −0.85 | −0.47 | −0.84 |
| Variable | ETo energ. | ETo aero. | ETo energ. frac. | ETo aero. frac. | Rainfall | Elevation | ||||
| RHmean | −0.30 | −0.86 | 0.68 | −0.68 | 0.27 | 0.78 | ||||
| Rs | 0.96 | 0.48 | 0.24 | −0.24 | 0.17 | −0.65 | ||||
| Tmax | 0.65 | 0.72 | −0.30 | 0.30 | 0.17 | −0.92 | ||||
| Tmin | 0.65 | 0.67 | −0.23 | 0.23 | 0.19 | −0.92 | ||||
| 0.10 | 0.49 | −0.39 | 0.39 | −0.32 | −0.10 | |||||
| SC RHmean * | 0.66 | 0.49 | −0.04 | 0.04 | 0.15 | −0.66 | ||||
| SC Rs | 0.62 | −0.44 | 0.94 | −0.94 | 0.60 | 0.68 | ||||
| SC Tmax | −0.05 | 0.67 | −0.77 | 0.77 | −0.27 | −0.85 | ||||
| SC Tmin | 0.23 | 0.31 | −0.16 | 0.16 | 0.05 | −0.47 | ||||
| SC | −0.23 | 0.66 | −0.90 | 0.90 | −0.38 | −0.84 | ||||
| ETo energ. | 1 | 0.42 | 0.32 | −0.32 | 0.33 | −0.88 | ||||
| ETo aero. | 0.42 | 1 | −0.72 | 0.72 | −0.32 | −0.80 | ||||
| ETo energ. frac. | 0.32 | −0.72 | 1 | −1 | 0.56 | 0.77 | ||||
| ETo aero. frac. | −0.32 | 0.72 | −1 | 1 | −0.56 | −0.77 | ||||
| Rainfall | 0.33 | −0.32 | 0.56 | −0.56 | 1 | 0.02 | ||||
| Elevation | −0.88 | −0.80 | 0.77 | −0.77 | 0.02 | 1 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irizarry-Ortiz, M.; Harmsen, E.W. Sensitivity of the Penman–Monteith Reference Evapotranspiration Equation to Meteorological Variables for Puerto Rico. Hydrology 2023, 10, 101. https://doi.org/10.3390/hydrology10050101
Irizarry-Ortiz M, Harmsen EW. Sensitivity of the Penman–Monteith Reference Evapotranspiration Equation to Meteorological Variables for Puerto Rico. Hydrology. 2023; 10(5):101. https://doi.org/10.3390/hydrology10050101
Chicago/Turabian StyleIrizarry-Ortiz, Michelle, and Eric W. Harmsen. 2023. "Sensitivity of the Penman–Monteith Reference Evapotranspiration Equation to Meteorological Variables for Puerto Rico" Hydrology 10, no. 5: 101. https://doi.org/10.3390/hydrology10050101
APA StyleIrizarry-Ortiz, M., & Harmsen, E. W. (2023). Sensitivity of the Penman–Monteith Reference Evapotranspiration Equation to Meteorological Variables for Puerto Rico. Hydrology, 10(5), 101. https://doi.org/10.3390/hydrology10050101











