The Role of Water and Weathering Processes in Landslides in Hungarian Loess Sediments

Abstract

Loess-paleosol bluffs can be unstable, but in the course of urbanization, houses may be built in such locations to take advantage of the view. One factor affecting the stability of such bluffs is water, the role of which in mass movements is well established. In this study, the connection of mass movements to meteorological conditions, such as rainfall and subsequent water level changes, was researched using new statistical methods. The periodicity of the water level of the Danube was analyzed using wavelet spectrum analyses, while changepoint analysis was used to determine variations in the quantity of precipitation. These results were compared to the chronology of six mass movements in Kulcs, Hungary. This study also focused on the changes in geochemical properties of loess in different weather conditions (dry periods, wet periods, and flooding). The results showed that only two mass movements were connected to hydrological conditions, and in the other case human activity and geochemical changes may have been factors. The results of geochemical models created using PHREEQC showed calcite and kaolinite precipitation, and albite and dolomite dissolution as the main mineral changes over the course of a year. Albite was found to dissolve only in wet periods, and kaolinite precipitation was significant during flood periods.

1. Introduction

In the course of urbanization, homes have often been built on loess–paleosol bluffs, with panorama and proximity to a river being factors in the choice of location. However, these bluffs are unstable, and mass movements are frequent. One of the reasons for mass movements is the special hydrological properties of these areas [1]. The river water level, the ground water, rain, and the domestic water together affect the physical and chemical properties of the soil in these areas.

Loess-paleosol sequences are frequent worldwide (e.g., China, Central Asia, North America and Central Europe). In Central Europe during the Pleistocene, loess was deposited in the colder climate of the most recent glaciation, and paleosols were deposited in warmer climatic conditions [2]. Loess is unconsolidated sediment containing quartz, feldspar, mica, clay minerals and carbonates [3]. Carbonate minerals are a vulnerable material in water–rock reactions because of their pH sensitivity [4]. Pedogenesis begins when weather conditions are favorable for the formation of organic matter, feldspars and other aluminosilicates, which may then be transformed into clay minerals such as smectite, illite, and chlorite [5]. Bluffs can frequently form where a river crosses a loess–paleosol sequence (e.g., in China [6]).

The stability of loess–paleosol sequences is a well-known problem [7,8,9]. Clayey paleosol can form sliding surfaces, and wet loess can fail. The role of water in mass movements is important and relatively well researched, especially in the case of loess–paleosol series [10,11]. The stability of loess decreases as water content increases, while the degree of chemical weathering increases with water content. Furthermore, rainy weather also increases the water level of the river. In these circumstances, increased pressure on loess stability comes from the backfilling of underground water, which prevents the escape of subsurface springs [12,13]. When the water level decreases, the supporting force disappears and fresh rainfall can trigger landslides [12,14,15]. The use of models may help to demonstrate how precipitation affects slope stability [16]. Earlier studies showed that chemical weathering always precedes mass movements [17]. Clay mineral precipitation is the result of chemical weathering [18], and minerals such as smectite and illite may also decrease stability in loess.

Such loess–paleosol sediments are common in Hungary, particularly on the right bank of the River Danube [19]. Landslides are frequent on these bluffs (Figure 1) [20,21,22]. One well-known bluff is located in Kulcs, a town built on a bluff over the Danube (Figure 1) [23]. According to earlier studies, the hydrogeological properties of Kulcs are influenced by both the water level of the Danube and the amount of rainfall [12,22]. Earlier studies show that a three-year period of rainy weather could cause landslides at the edge of the bluff, the minimum amount of rain required in such a period being 600 mm per year (Average rainfall is ~500 mm/year) [22]. Many holiday homes and family houses were built on the bluff at Kulcs, so any landslides could result in significant economic damage. Moreover, these houses have altered the water balance of the area as well.

This study aimed to examine the relations between mass movements, the water balance of the area, and geochemical changes in the loess, in the interests of better predicting mass movements and preventing them in the future. This is a key issue both from the economic and safety points of view. In this research, the following were studied: (1) the relation between the water level of the Danube (1960–2020), the amount of rainfall (1960–2012), and dates of mass movements from 1960–2014 in Kulcs; (2) changes in the mineral composition of loess and loessy sediments during dry, wet, and flood periods; and (3) human influence on the occurrence of landslides.

2. Materials and Methods

2.1. Study Area

The study area is located in Kulcs, in Central Hungary (Europe) (Figure 1), an area of 16.73 km² with a population of ~3500. In the space of just over a decade, the population of the area increased by 31.3% (2010: 2669; 2021: 3504). The result of this increase was that holiday houses, which had often been built in the slope alluvium of earlier mass movements, were transformed into family houses. The houses use piped water, but a sewage system was not constructed until 2021.

There have been recurring mass movements (1964, 1966, 1977, 2006, 2011, 2013) along the 1800 m river bank of Kulcs, their frequency showing the importance of investigating landslides [13,24]. Four actively moving blocks can be identified in the area (Figure 1). These are ~40 m thick and 290–350 m long [24]. To understand the processes which can take place in a landslide area, it is important to study local hydrological conditions. When the water table level rises in the direction of the Danube, the water can escape at two sites: a mixed water spring and a subaqueous spring (Figure 1). The prevailing direction of regional groundwater flow is west to east [25].

The location of Kulcs makes it a meeting point of the Mezőföld Plateau and River Danube on the right bank of the Danube. The Plateau is a water-catchment area, while the bank of the river is a 20–50 m high bluff. The bluff is built up from Quaternary Formations overlying Upper Miocene and Pliocene clay layers. The Quaternary Formations consist of Pleistocene loess and paleosols. Miocene (Pannonian) sediments, which are clayey and sandy layers, also occur in the area (Rónai & Bartha, 1965) (Figure 1). The 2–3 cm sliding surface is paleosol and red clay sediments overlain by 20–50 m thick loess [19]. The main sliding surface is the Tengelic Red Clay Formation, which originated from aeolian material (Figure 1) [26]. Earlier studies show that weathering processes affected the red clay. For this reason, clay minerals are the most important minerals in this situation [23]. Furthermore, carbonate precipitation is observable at the top of the sliding surface [27].

Because of the morphology and composition of the bluff, rain-induced runoff cannot flow down in the direction of Danube, thus creating potential conditions for a pluvial flood. However, there was no internal water drainage system in Kulcs until construction began in 2018.

Construction of the sewage system was finished in 2021. The houses in the centre of Kulcs can now connect to the system, which is partly a gratification leak system, and the other part is a hardwired system. If a house cannot be connected to the system, they must use a closed sewage reservoir [28].

In the most sensitive area (Figure 1), a construction ban was introduced. Therefore, only lightweight houses can be built there, and care must be taken to ensure rain drainage and sewage treatment. On the other hand, riverbank reinforcement was begun in the southern area of Kulcs, as new residential areas are planned there according to the new settlement development scheme.

Figure 1. The study area in: (a) Europe; and (b) Hungary. The rose colored areas are the loess–paleosol sequences, the red lines show the mass movements areas and the circle indicates the location of the study area, Kulcs [21]; (c) map of Kulcs, where red areas show the four moving blocks, with a picture as an example of a local landslide (modified after [23]); and (d) schematic sequence of the study area with the potential sliding surface, water table, clayey layer, sediment of the river and spring [29].

Figure 1. The study area in: (a) Europe; and (b) Hungary. The rose colored areas are the loess–paleosol sequences, the red lines show the mass movements areas and the circle indicates the location of the study area, Kulcs [21]; (c) map of Kulcs, where red areas show the four moving blocks, with a picture as an example of a local landslide (modified after [23]); and (d) schematic sequence of the study area with the potential sliding surface, water table, clayey layer, sediment of the river and spring [29].

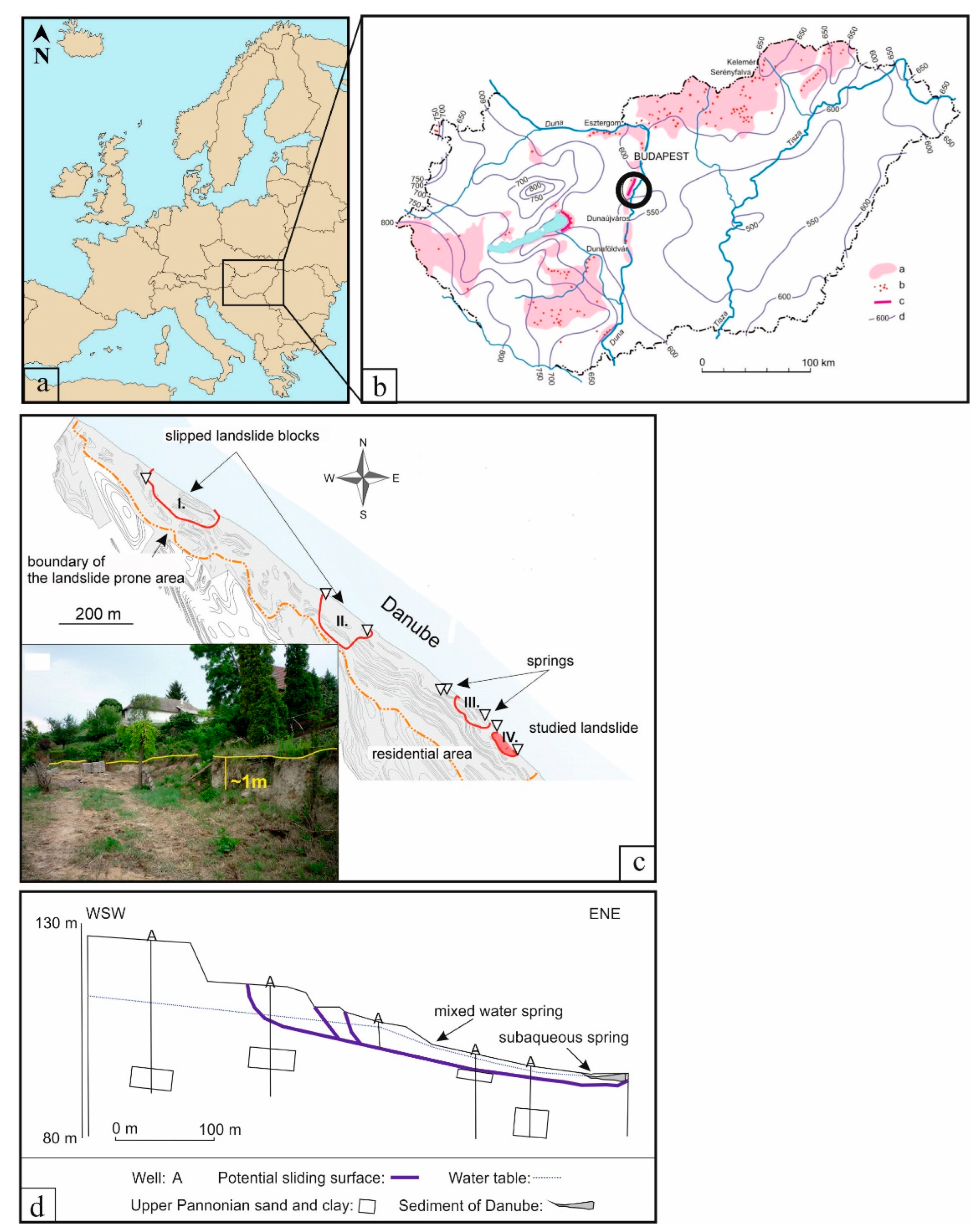
2.2. Data Sources for Statistical Analysis

Precipitation data (Figure 2) were obtained from a global reanalysis database. The mean data from January to December are for the grid closest to 47° N 19° E for the variable precipitation rate (kg/m²/s) on a level surface; these data are available for the years 1960 to 2012. The monthly sum of daily precipitation data (1960–2012) was used for changepoint detection and figures the daily water level (Figure 2) of the Danube (1960–2020) in Budapest (station code: 00106, https://www.hydroinfo.hu/vituki/archivum/bp.htm, accessed on 29 January 2023) were used in the wavelet spectrum analysis.

2.3. Statistical Analyses

In the course of the analysis, the first step was to determine if there were statistically significant changes (p < 0.05) in the time series (e.g., change in trend, amplitude, average amount) that corresponded to the various mass movements. This was done by applying the Bayesian changepoint-detection algorithm (BCPa for short) [30] (Section 2.3.1). Next, wavelet spectrum analysis was employed (Section 2.3.2) to identify the potential lack of annual period(s) in water levels around the time of the provisionally identified changepoints.

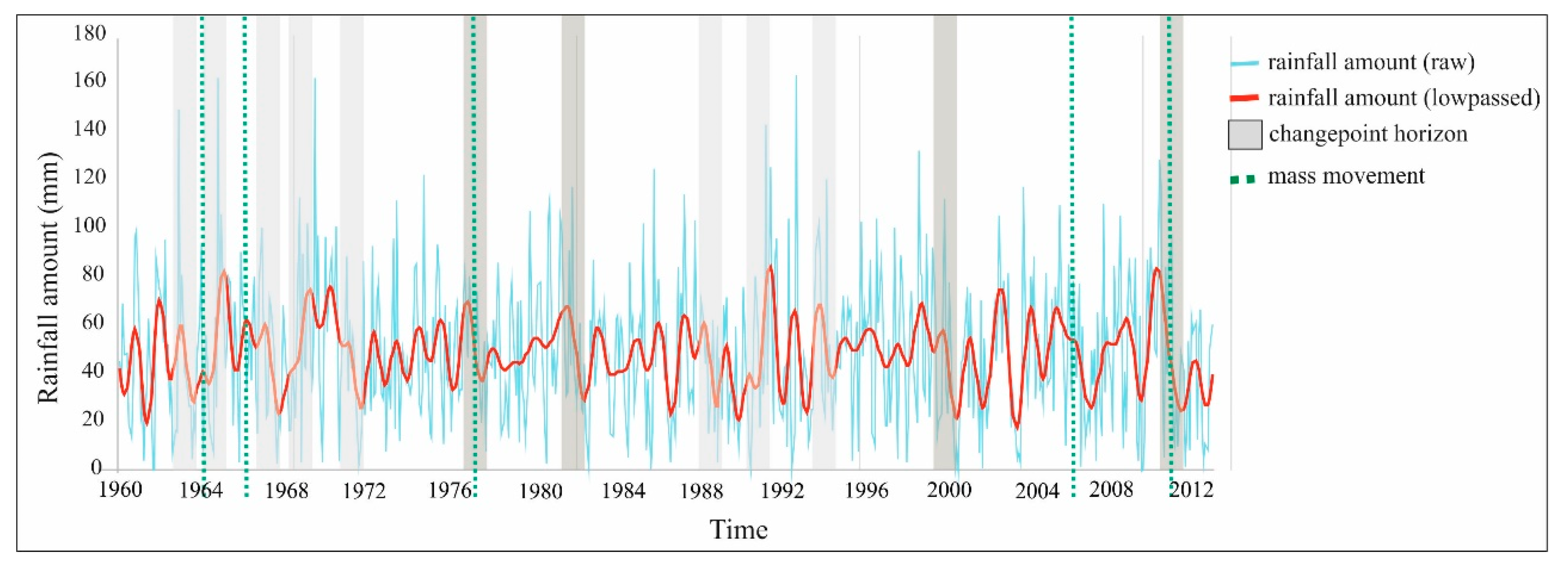
2.3.1. Changepoint Detection

BCPa [30] can generate the posterior distribution on both the number and location of changepoints in a dataset [31]. The procedure assumes that the parameters of the model for any two segments of the data are independent and the error terms are uncorrelated random variables and—besides other results, see [31]—returns the posterior distribution on the number and location of changepoints in the time series, providing probabilistic bounds on their location (if the reader is interested in additional technical derivation of BCPa are referred to in [30] and the SOM of [31]).

In the present case, a 12-month lowpass filter was applied to the monthly sum precipitation record to increase the signal-to-noise ratio relative to the magnitude of the supposed changes, thus aiding the detectability of valid changepoints [32,33]. The 12-month low-passed time series was then centered and fed into the linear model of BCPa using the same parametrization as used by Hatvani et al. [31]. A Bayesian approach to the changepoint problem provides a posterior distribution, that is, uncertainty estimates, concerning the location of changepoints, distinguishing it from many other methods [34]. Next, the changepoint time series thus obtained were passed through a six-month centralized rolling summary function in order to cumulate the probability dispersed between consecutive months. The use of this function assumed that the uncertainty in the location of a changepoint was less than six months. Allowing for a larger window could increase the overall probability of a changepoint (depending on how abrupt and how “obvious” the change is) in a certain region of the data. This cumulative probability is in fact the probability of the changepoint(s) shown later on in the study. Only “practically certain” changepoints with a six-month sum probability >95% were considered, and these are called ‘changepoint horizons’ hereinafter.

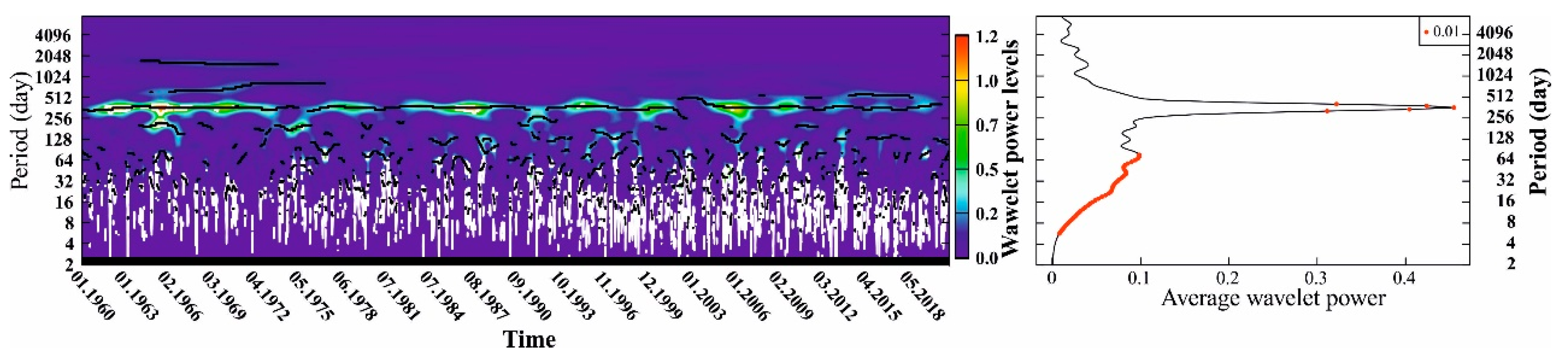
2.3.2. Wavelet Spectrum Analysis

Wavelet spectrum analysis (WSA) can be taken as a function with a zero mean localized in both frequency and time [35], and the convolution of the data and the wavelet function [36] for a time series (Χn, n = 1, …, N) with a ‘Δt’ degree of uniform resolution is (Equation (1)):

$${\Psi }_0\left(\eta \right)={\pi }^{-1/4}{e}^{i{\omega }_0\eta }{e}^{{-\eta }^2/2}$$

(1)

where $\eta$ stands for the length of the time series, ψ₀ is the wavelet function and ω₀ is the nondimensional frequency. In this study, the Morlet mother wavelet was used to generate daughter wavelets [37].

2.3.3. Software Used

The statistical analyses were done in the R statistical environment [38]. Bandpass filtering was performed with the bandpass() function of the astrochron package [39] and changepoint detection was done using the Bayesian changepoint algorithm of Ruggieri [30]. The wavelet spectrum analysis was performed with the WaveletComp package [40].

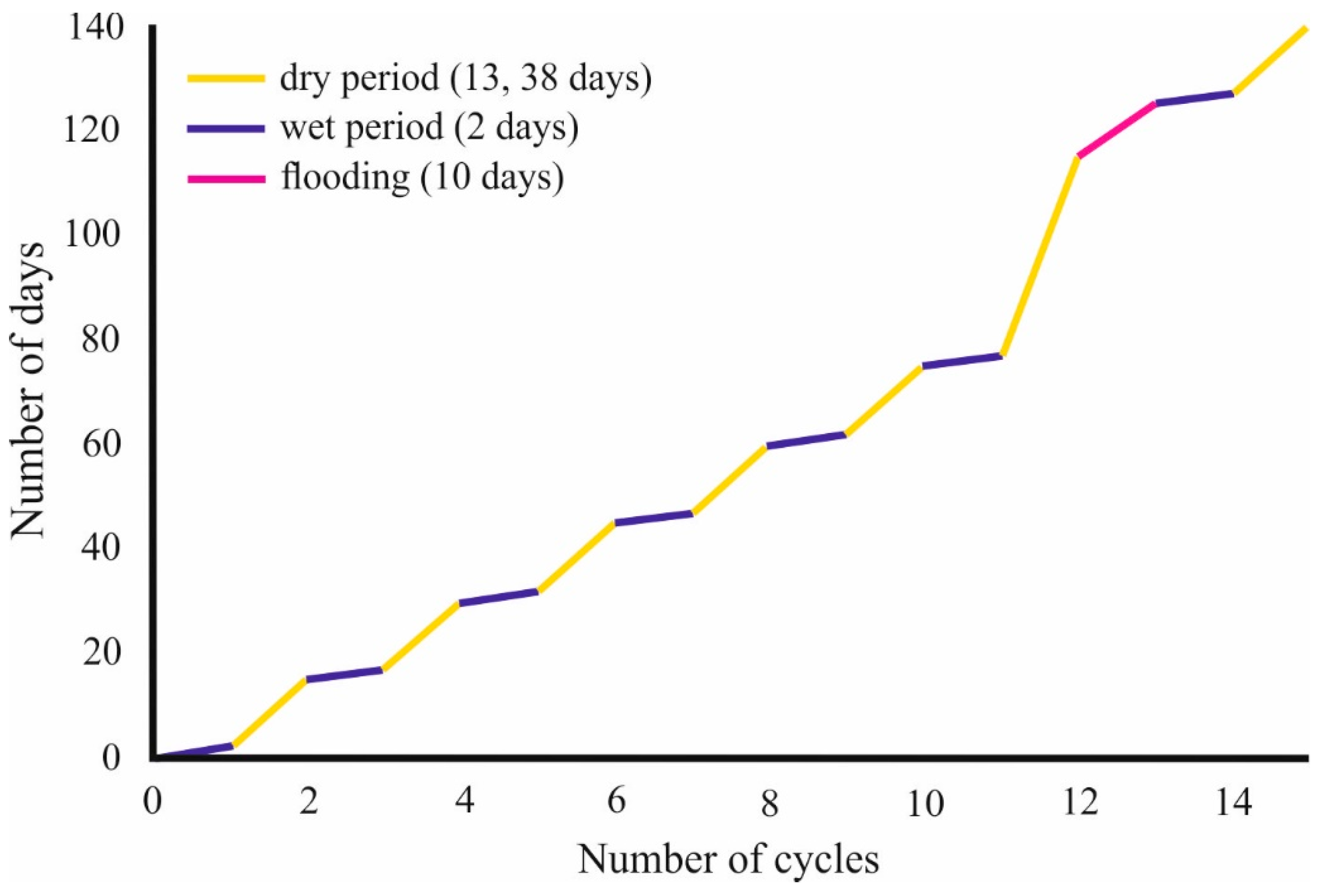
2.4. Geochemical Modeling

Geochemical modeling was used to simulate the effect of water saturation on the mineral changes, which also affect the stability of the loess. PHREEQC 3 geochemical modeling software [41] was used with the PHREEQC.dat database for thermodynamic and kinetic calculations. Kinetic-batch models were run to follow the chemical changes in the water composition and mineral phases over time. The kinetic-batch models were run for one year. The figures were created using R code [38].

The input data were characteristic of the area studied and contained the chemical composition of water (Water data), the loess mineral composition and porosity (Rock data), and the temperature of the water (Temperature data). Water data were represented by spring waters in Kulcs (K_B0502; sampling date: 23 March 2016; 28 July 2016) and the chemical composition of the Danube (MBFH 9/2015) (

Table 1. Input data of water for geochemical modeling.

Name of Parameter in PRHEEQC	Parameter	Danube (mg·L−1)	Spring Water
			Dry Period (mg·L−1)	Wet Period (mg·L−1)
pH	pH	8.17	7.46	7.81
Temperature	temperature (°C)	14.7	11.40	20.9
Oxg	Oxygen saturation	10.57	9.92	8.03
Na	Na+	12.17	37.9	2.85
K	K+	2.22	2.52	6.69
Ca	Ca2+	48.70	68.1	29.7
Mg	Mg2+	12.00	77.8	6.42
Fe	Fe2+	0.05	0.01	0.07
Amm	NH4	0.11	0.05	0.05
Mn	Mn2+	0.01	0.00	0.00
Si	H4SiO4	7.78	26.83	12.025
Cl	Cl−	15.07	35.6	4.6
S	SO42−	24.97	89	17.40
N(+5)	NO3−	6.94	77	2.37
N(+3)	NO2−	0.11	0.05	0.1
P	PO43−	0.16	0.13	0.73
Alkalinity as HCO3	HCO3−	180.33	445	104
OH−	OH−		0.05	0.05
Al	Al3+	0.04	0.01	0.04

). Spring samples from Kulcs were measured by ICP-AES at the Hungarian Supervisory Authority for Regulatory Affairs. The water data of the humid period originated in spring water, which was sampled during rainy weather (23 March 2016). This was essential because the chemical composition of water changes in the course of interactions with loess, e.g., the pH and the amount of CO₃²⁻ in the water increases. The Temperature data were the measured temperatures of the water (Danube, springs of Kulcs; Table 1).

Rock data: The mineral composition of loess from Kulcs was used in the models (

Table 2. Input data of the loess rock composition. SSA: specific surface area.

Minerals	ρ (g·cm−3)	M (mol g−1)	Loess		SSA (m2·g−1)
			vol%	c (mol·kgW−1)
Albite	2.62	262	3.64	0.6835	21.6
Kaolinite	2.6	258	1.28	0.2426	200
Calcite	2.71	100	20.57	10.4624	22
Chlorite(14A)	2.65	554	8.96	0.8042	2.9
Dolomite	2.85	184	7.7	2.2371	2.8
Ca-montmorillonite	2.35	366.27	5.65	0.6805	898
Illite	2.75	383.5	14.19	1.9095	200
K-feldspar	2.56	278	1.5	0.2598	12
Quartz	2.63	60	33.37	27.4497	58
SiO2(a)	2.2	60	1.28	0.8826	0.073

). The input loess composition originated in the average loess mineral composition of the Kulcs area according to Udvardi et al. [27]. The loess samples were measured using XRD at the Hungarian Supervisory Authority for Regulatory Affairs. Smectite was defined as Ca-montmorillonite, muscovite as illite, chlorite as chlorite(14A) and amorphous silica as SiO₂(a) in the models. The following minerals were not allowed to precipitate in the models: albite, dolomite, K-feldspar and quartz. The appropriate thermodynamic data were not available for goethite (FeOOH)—for this reason it was eliminated from the models.

The composition of the loess rock has been converted into mol·kg_W⁻¹ (mol·kg_H2O⁻¹) units using the following equation [42]:

$$c_{mineral}\left[\frac{\mathrm{mol}}{\mathrm{kgW}}\right]=\frac{{10\times \rho }_{mineral}\left[\frac{\mathrm{g}}{{\mathrm{cm}}^3}\right]\times {\mathrm{vol}\mathrm{\%}}_{mineral}\times {\mathrm{vol}\mathrm{\%}}_{rock}}{M_{mineral}\left[\frac{\mathrm{g}}{\mathrm{mol}}\right]\times {\mathrm{vol}\mathrm{\%}}_{water}}$$

(2)

where $c_{mineral}$ is amount of mineral, ${\rho }_{mineral}$ is density of the mineral, ${\mathrm{vol}\mathrm{\%}}_{mineral}$ is amount of mineral, according to the XRD, ${\mathrm{vol}\mathrm{\%}}_{rock}$ is the proportion of rock (100-porosity), $M_{mineral}$ is the molar mass of the minerals and ${\mathrm{vol}\mathrm{\%}}_{water}$ is proportion of the water filled area, which is equal to the porosity. The porosity of loess was 34.76 v/v% [27].

The specific surface area (SSA) used here is the largest available data in the RES’T database (HZDR online). The activation energy of quartz was modified in the case of basic reactions, because it was incorrect in [43]. The reactive surface area was a tenth of the specific surface area, and the velocity of mineral formation was 100 times slower than the velocity of mineral dissolution [44,45].

In the kinetic-batch models, chemical interactions were simulated in the Loess-Danube water system, Loess-spring water in dry periods and Loess-spring water in wet periods over a one-year time interval. According to the weather and hydrological parameters (https://www.hydroinfo.hu/vituki/archivum/bp.htm, accessed on 29 January 2023) of the area, three kinds of water tables with different water chemistry were defined (Table 1). A total of 38 cycles·year⁻¹ were built up in the model which contained dry periods (short period: 13 days·cycle⁻¹ and long period: 38 days·cycle⁻¹), two floodings of the Danube (10 days·cycle⁻¹) and a wet period (2 days·cycle⁻¹) (Figure 3).

3. Results

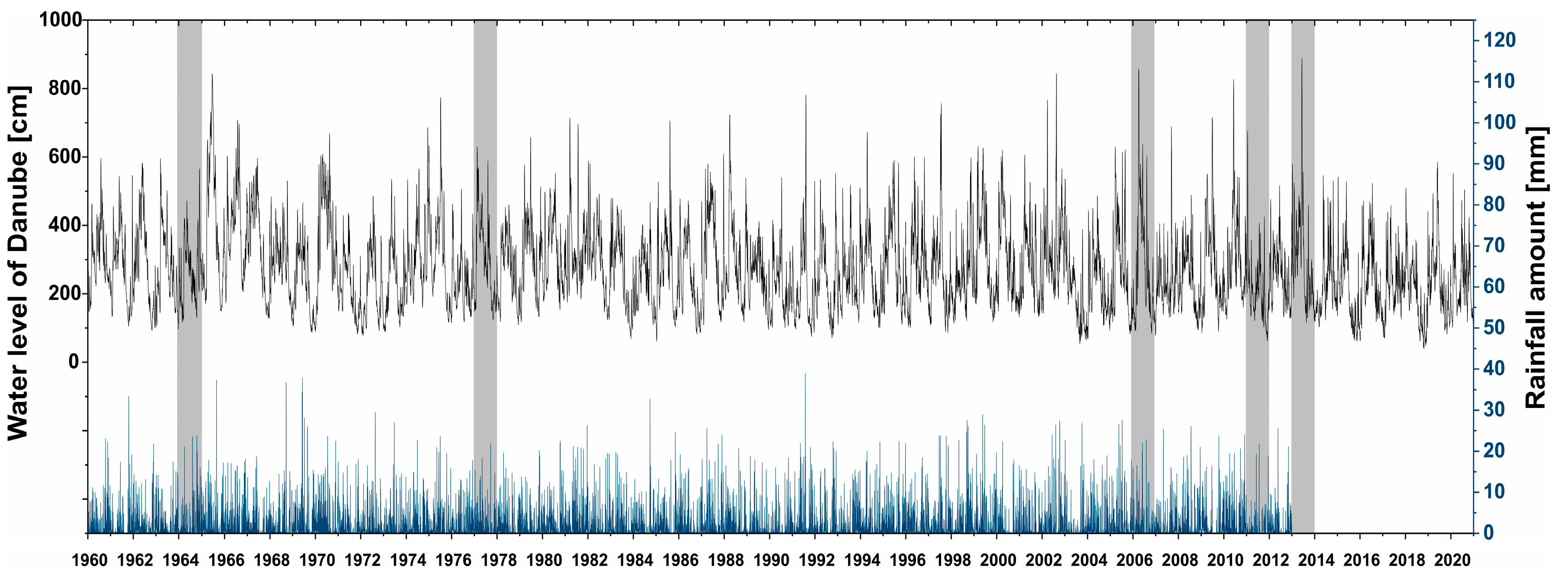
3.1. Changes in the Hydrological Dynamics

Out of the twelve detected changepoint horizons, four were proven to be significant at a = 0.05 in the precipitation time series of the study area (1960–2012), specifically, 1977, 1981, 2000, 2010 (Figure 4). The period between April 1977 and December 1981 can be characterized by higher mean precipitation and a significant increasing trend compared to the previous and next time intervals (January 1960–March 1977; December 1981–January 2000). Two of the above-mentioned events overlap with the time of the mass movements (March 1977, January, and February 2011) if the ±6-month uncertainty of the changepoints’ location is taken into account.

The daily water-level time series of the Danube measured at Budapest between 1960 and 2020 was assessed using wavelet spectrum analysis. The annual (365 days) periodicity was significantly (p < 0.01) present in the investigated time interval except in some short periods in 1976, 1991, 2002–2003 (Figure 5). Of these, 1976 was close to a mass movement in March 1977. Other years without periods could not be connected to the time of mass movements.

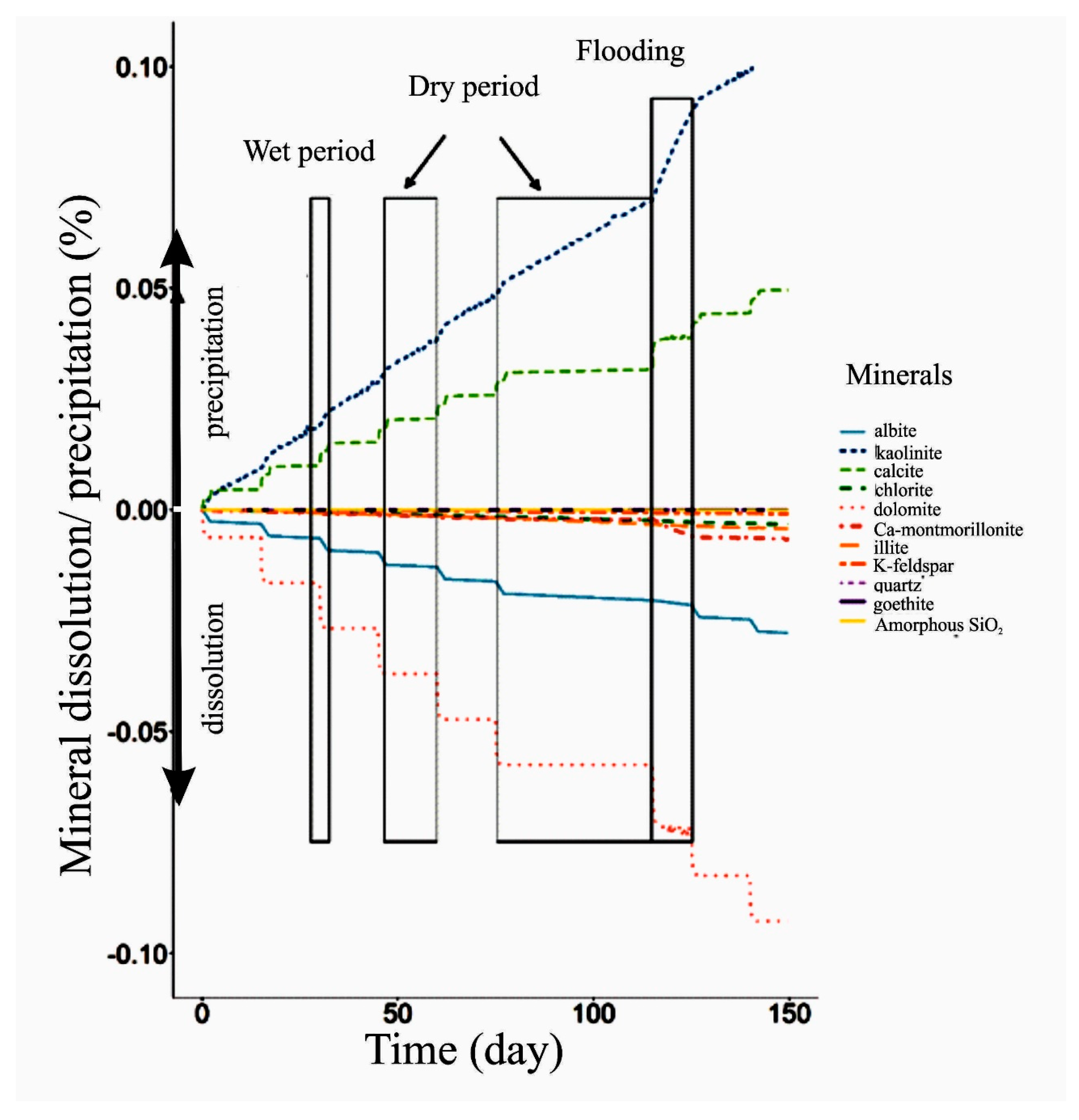
3.2. Results of Geochemical Models

According to the kinetic-batch geochemical models, the main change in the modal composition of loess is the amount of kaolinite (0.1%), calcite (~0.05%), dolomite (~0.1%) and albite (~0.025%) (Figure 6). Kinetic-batch models show that kaolinite was formed mainly from the clay minerals (Ca-montmorillonite, illite and chlorite), albite and K-feldspar. Calcite mainly formed after dolomite dissolution. The intensity of mineral changes was more significant (twice as much so) in the period of flood compared to the dry period. Calcite is not precipitated in dry periods, and albite is dissolved only in wet periods (Figure 6).

4. Discussion

4.1. Relation between the Hydrological Properties and Mass Movements

Whereas earlier studies had suggested that mass movements take place in relation to the water level of Danube and amount of rain [13,20], the present study shows that, taken alone, water levels and the amounts of rain do not provide a clear explanation. For example, the first noted mass movement was in March of 1964, though the water level of the Danube was actually higher in 1965–1967 (Figure 1).

Neither the amount of rain nor the water level was exceptional in March 1977; but the rainfall shows a changepoint after the landslide (April) (Figure 4). If it is accepted that a ±6-month changepoint horizon is more reliable [31], then this changepoint may be connected to the mass movements of 1977. The periodicity analyses also signal that the periodicity was shorter (~200 days) in 1976 (Figure 5). For these reasons, we believe that the mass movement in 1977 may have been the result of the weather. A changepoint was also identified in November 2010, close to the mass movements in February 2011, although the periodicity analyses did not signal any changes. Therefore, this mass movement may also be linked to weather conditions, particularly rainfall. The last mass movement was in 2013, a year not included in the changepoint analyses because of lack of data. However, there was a snowfall (~20 cm) on March 15th, followed by a landslide on April 5th.

Of a total of six mass movements, three might be related to the weather and the Danube’s water level [27]. As one consequence of climate change, extreme rainfall is becoming more common in Hungary [48]. These extreme weather events may also affect the mass movements. The Danube’s water level is higher than the sliding surface [19], so for this reason, any water level changes in the river have a practically immediate effect on loess stability, as the capillary pressure changes instantly, and if the stability of the loess decreases, the risk of mass movement will increase. It should be stressed, however, that the stability of the loess does not depend only on the water balance, but also on geochemical changes in the system [4,10,49].

4.2. Relation between the Geochemical Properties and Water

The results of the geochemical modeling suggested that the wet and flood periods play a crucial role in the chemical reaction between loess and water, causing changes in the mineral composition of the loess. The main mineral changes in these periods are kaolinite precipitation and albite dissolution. These reactions decrease the stability of the loess [10]. Furthermore, the stability of the loess also decreases if the loess gets wet [7]. The models indicate that the number and length of wet and flood periods are important in the mass movements, and this is in agreement with [10]. Weathering processes are inactive in the dry period, and it is interesting to note that the weathering of albite is not observable during floods, a fact which can be explained with reference to the Na⁺ content of Danube (12.17 mg/L) in comparison to the Na⁺ content of spring in the wet period (2.85 mg/L) (Table 1). However, kaolinite precipitation is most intense in this period (Figure 6).

Carbonates are more sensitive to the loess–water interaction than the batch-kinetic models indicate. The carbonate minerals occur in the loess as detrital and diagenetic minerals (mainly dolomite) and as cement (calcite) material. The secondary calcite can occur in different forms, such as in fine-grained (1–10 µm) form, root cells, hypocoating, carbonate coating, needle-fiber calcite and earthworm biospheroids [50]. Loess is more compressible in the absence of the cement material, which causes compaction and therefore increases its density. Taken together, these factors can drive to landslide [4]. For this reason, the question of whether carbonates are dissolved or precipitated can also affect loess stability. Furthermore, where the flow of groundwater slows down, the dissolved carbonates can reprecipitate in the layer of loess, red clay or paleosol. Dolomite dissolution in natural loess systems is rare. However, red clay contains a smaller amount of dolomite than loess [27], and red clay originated from loess-like sediments [26].

The weathering processes depend not only on the amount of water, but also depend on the heterogeneity of the loess (mineral content, porosity, and permeability changes, clayey layers). For this reason, a kinetic reactive transport geochemical model in three dimensions may help to understand this complex system better. In these models, the dynamic processes of calcite dissolution and reprecipitation may also be characterized.

4.3. Anthropogenic Effect in the Area

Furthermore, we must note that human activity also affects the area. Kulcs and the other bluffs, with their panoramic views, are attractive. For this reason, initially, weekend houses were built there, and today, family houses have been built, which are heavier and take a higher water load off the bluff of Kulcs. Building on the landslide area started in 1964 (after the mass movement, during the reclamation). The load and the mass of the houses is too much for the shear strength, increasing the chances of sliding and slippage [10]. For this reason, according to [28], only lightweight houses can now be built in the sensitive area of Kulcs.

In 2013, a reclamation project was begun after the last landslide, under the supervision of Sycons Ltd. (KFI_16-1-2016-0228). In this project, in order to enhance drainage from the loess layer, layers were made more open by the inclusion/incorporation of gravel [24]. Sand layers were opened up for better drainage. The excavation for pipes started in 2018 [28], and where the sewage needs of a particular locality cannot be connected to the system, rain drainage and sewage treatment must be built. As a result, in the future, the anthropogenic effect on the water balance in the area may decrease.

Landslide processes represent a really complex system, and it is not possible within the confines of this article to study all their properties. In this study, for example, several aspects of the problem were not analyzed, namely, the effect of temperature changes, the underground water flow or the biodiversity changes of the area—properties which also affect the stability of the loess–paleosol system.

5. Conclusions and Outline

The role of water and the stability of loess–paleosol bluffs is well established in the literature. According to the literature, landslides are connected to the water balance of loess–paleosol sequences, and the role of weathering is also an important factor. In this study, new methods were tested to understand the effect of the previous two properties, which are summarized as follows.

(1)

Even though the results of earlier studies show that rainfall amount and high-water levels in the river are responsible for the landslides in the paleosol–loess sequences, the present study indicates that the effect of the amount of water in the landslides can only be conclusively demonstrated in two cases. In other cases, it may affect the other studied or unstudied properties;

(2)

One of the studied properties is the effect of the weathering. Geochemical modeling results show that weathering processes depend on the weather conditions (dry period, wet period, flood). Albite only weathers in wet periods, and kaolinite precipitation is faster during floods, while calcite is not precipitated during dry periods;

(3)

The other studied property is the effect of human activity. The results show that it is a complex factor that can facilitate landslides due to the mass of houses, watering, and to the decreasing biodiversity. However, bluff stabilization and building regula19tions can be one of the keys to decrease the anthropogenic effects.

The results in this study indicate that the detected mass movements in the loess–paleosol bluff were connected to hydrological conditions, human activity, and changes in the geochemical conditions of the loess.

As a methodological outlook, the study demonstrated that wavelet spectrum analysis and Bayesian changepoint analysis is capable of aiding the detection of environmental variables fundamentally responsible for the stability of loess–paleosol bluffs. A clear novelty of the research was the combined application of the aforementioned statistical tools and the assessment of changes in geochemical properties of loess in different weather conditions.

The proposed combined methodology can be applied in similar settings to account for the combined effect of environmental circumstances as the geochemical properties of the loess–paleosol buffs. The more areas that are explored with this approach, the more we can understand the role of weathering in landslides with respect to their geochemical properties.