Analysis of Changes in Water Flow after Passing through the Planned Dam Reservoir Using a Mixture Distribution in the Face of Climate Change: A Case Study of the Nysa Kłodzka River, Poland
Abstract
1. Introduction
2. Materials and Methods
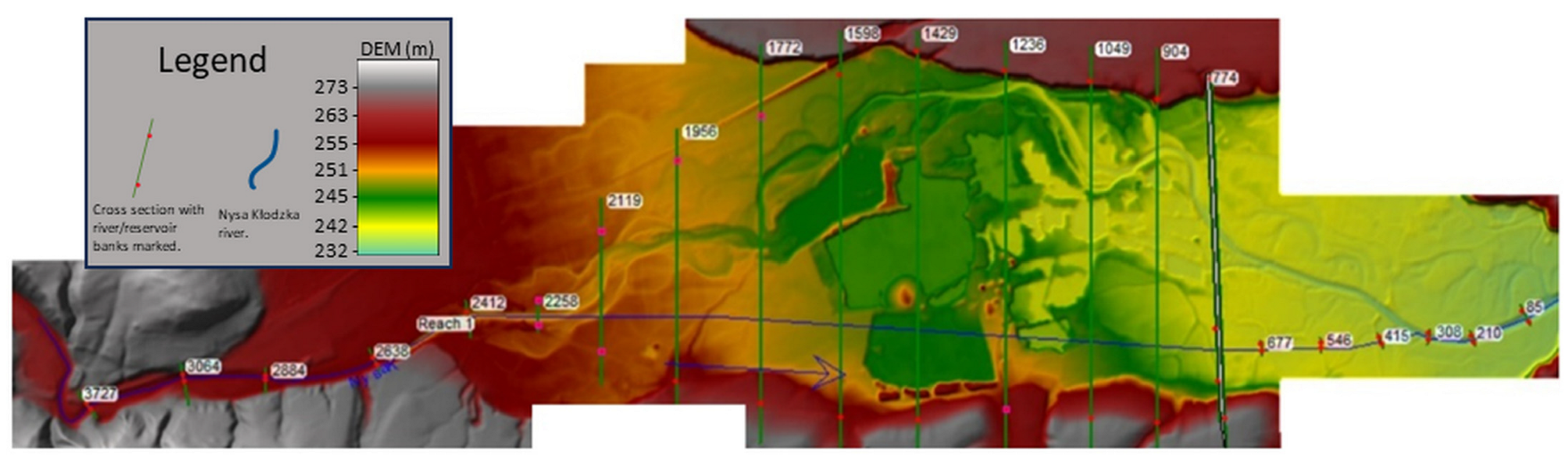
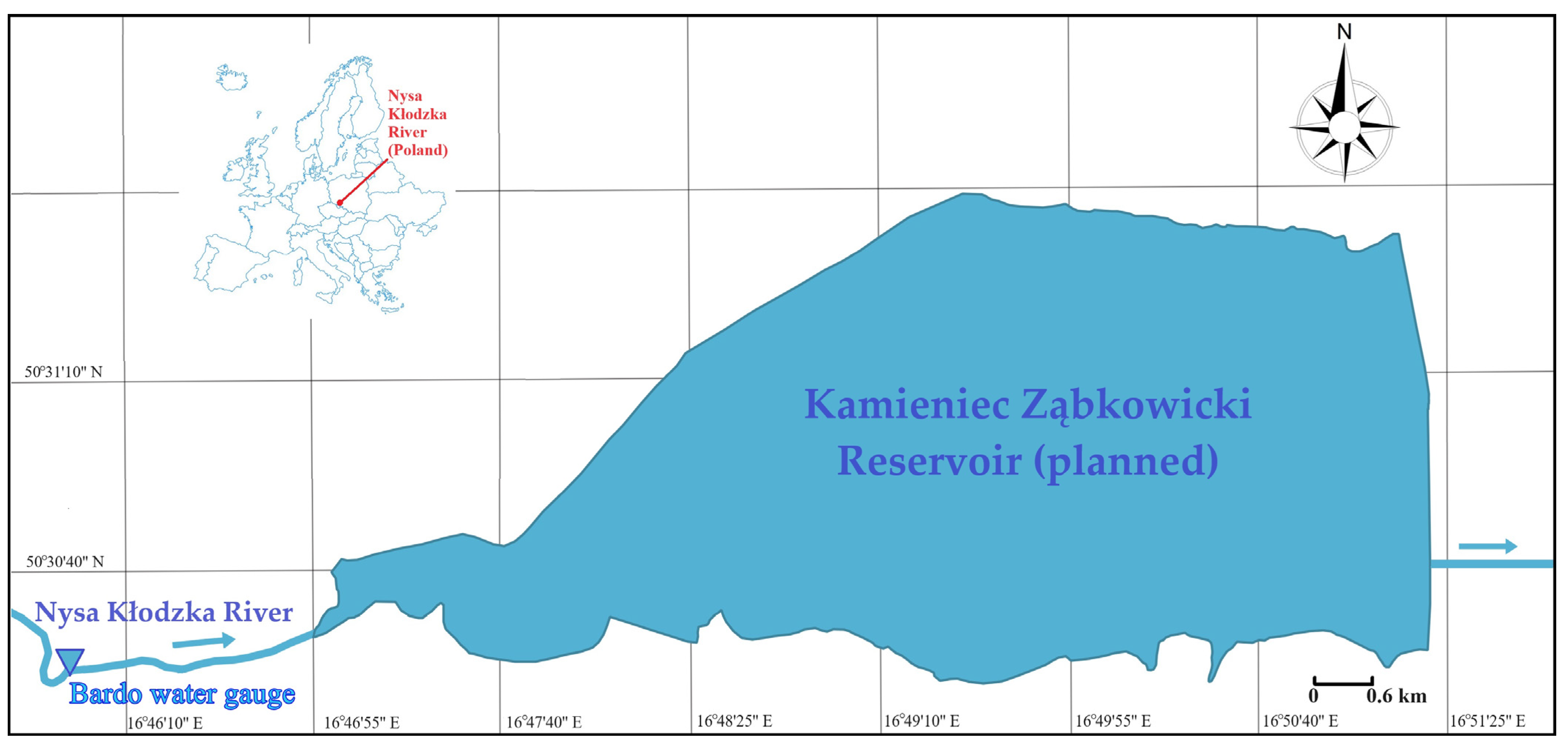
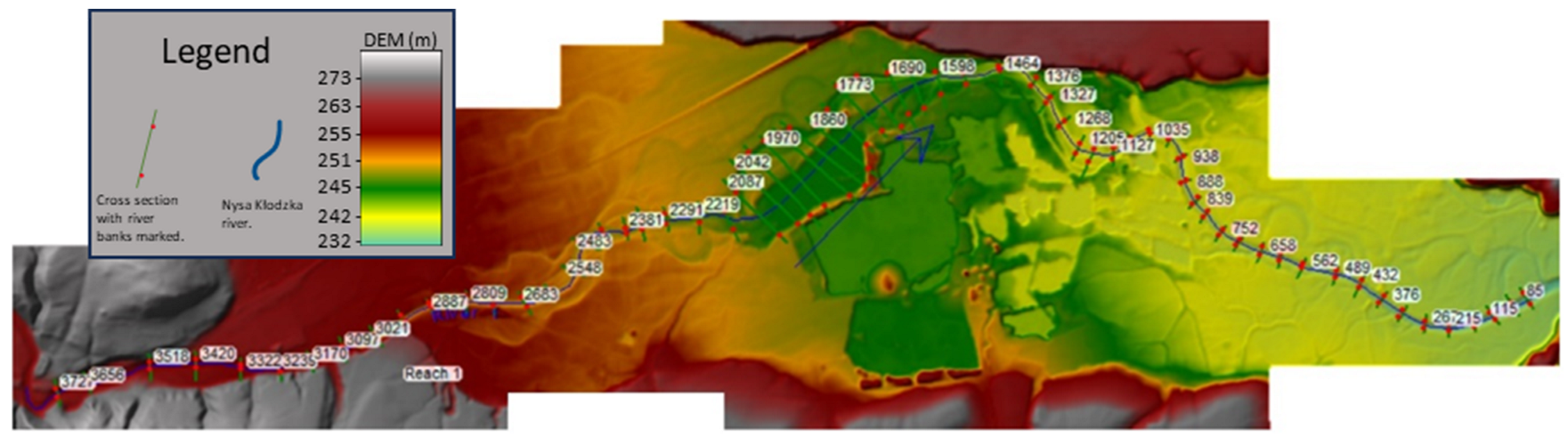
2.1. Study Area
2.2. HEC-RAS Model
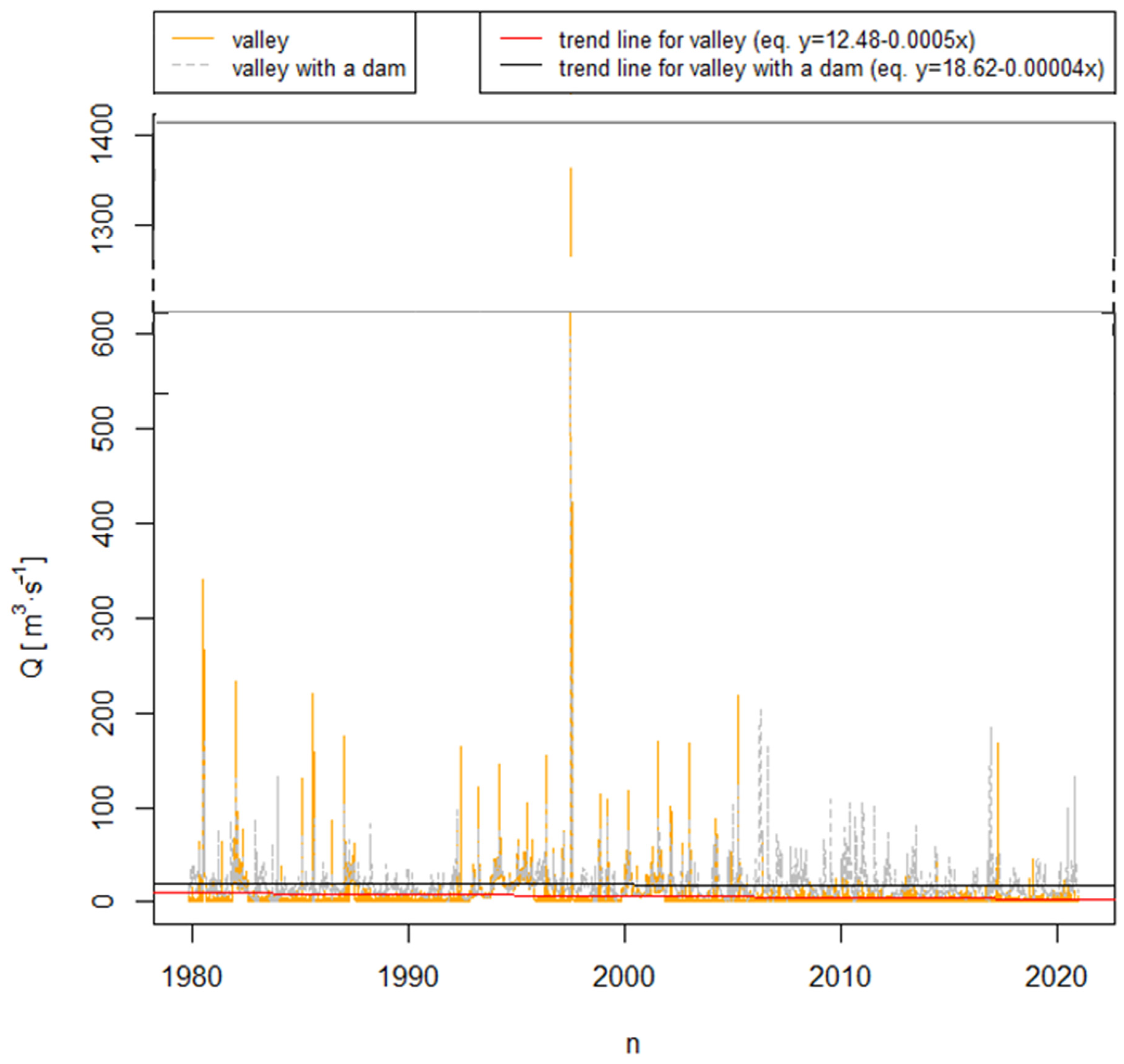
2.3. Hydrological Data Collection and Temporal Trend Analysis
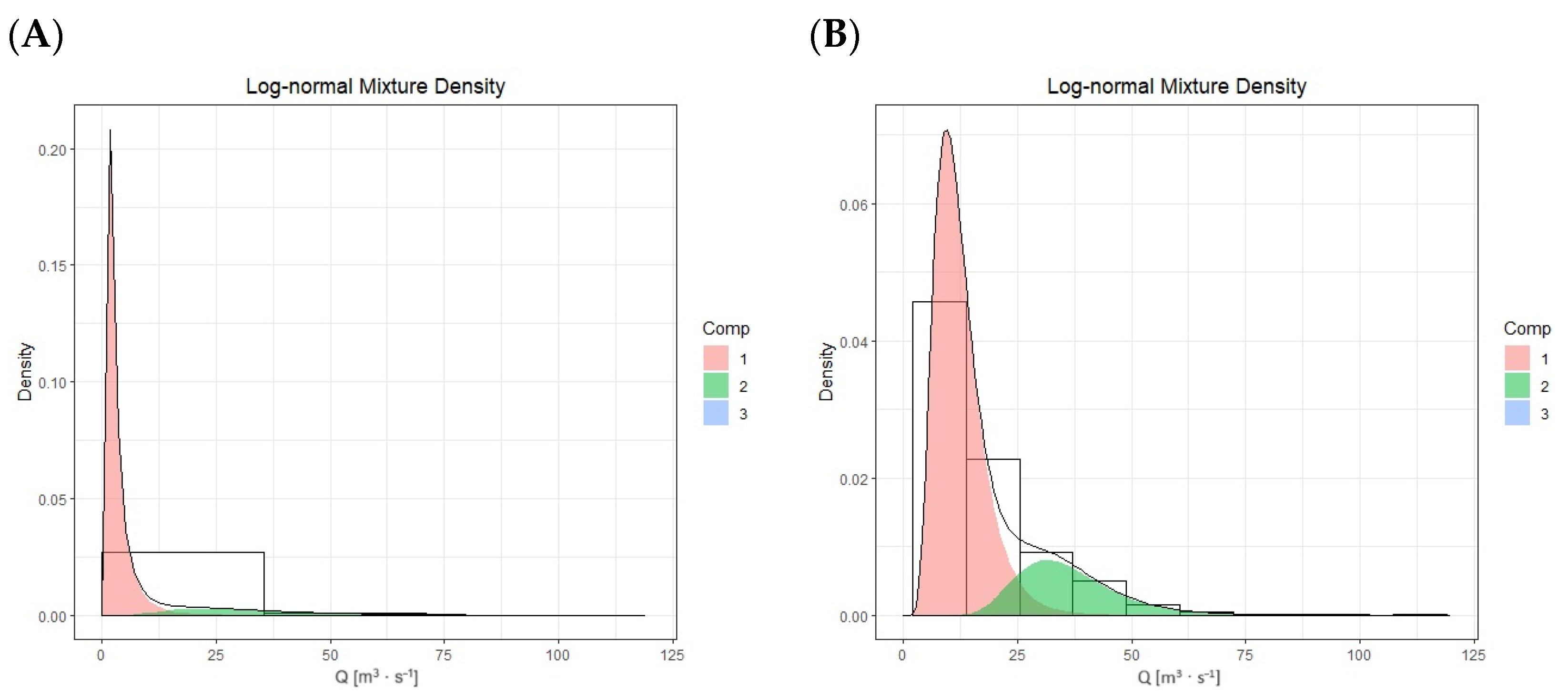
2.4. A Mixture Log-Normal Model
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hunt, K.M.R.; Menon, A. The 2018 Kerala Floods: A Climate Change Perspective. Clim. Dyn. 2020, 54, 2433–2446. [Google Scholar] [CrossRef]
- Rudd, A.C.; Kay, A.L.; Sayers, P.B. Climate Change Impacts on Flood Peaks in Britain for a Range of Global Mean Surface Temperature Changes. J. Flood Risk Manag. 2023, 16, e12863. [Google Scholar] [CrossRef]
- Barbhuiya, S.; Ramadas, M.; Biswal, S.S. Nonstationary Flood Frequency Analysis: Review of Methods and Models. In River, Sediment and Hydrological Extremes: Causes, Impacts and Management; Pandey, M., Gupta, A.K., Oliveto, G., Eds.; Disaster Resilience and Green Growth; Springer Nature Singapore: Singapore, 2023; pp. 271–288. ISBN 978-981-9948-10-9. [Google Scholar]
- Stathi, E.; Kastridis, A.; Myronidis, D. Analysis of Hydrometeorological Characteristics and Water Demand in Semi-Arid Mediterranean Catchments under Water Deficit Conditions. Climate 2023, 11, 137. [Google Scholar] [CrossRef]
- Van Dyck, J.; Willems, P. Probabilistic Flood Risk Assessment over Large Geographical Regions: Probabilistic Flood Risk. Water Resour. Res. 2013, 49, 3330–3344. [Google Scholar] [CrossRef][Green Version]
- Kreibich, H.; Van Loon, A.F.; Schröter, K.; Ward, P.J.; Mazzoleni, M.; Sairam, N.; Abeshu, G.W.; Agafonova, S.; AghaKouchak, A.; Aksoy, H.; et al. The Challenge of Unprecedented Floods and Droughts in Risk Management. Nature 2022, 608, 80–86. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Ng, J.Y.; Galelli, S. Examining Global Electricity Supply Vulnerability to Climate Change Using a High-Fidelity Hydropower Dam Model. Sci. Total Environ. 2017, 590–591, 663–675. [Google Scholar] [CrossRef] [PubMed]
- Park, J.Y.; Kim, S.J. Potential Impacts of Climate Change on the Reliability of Water and Hydropower Supply from a Multipurpose Dam in South Korea. J. Am. Water Resour. Assoc. 2014, 50, 1273–1288. [Google Scholar] [CrossRef]
- Nazari-Sharabian, M.; Taheriyoun, M.; Ahmad, S.; Karakouzian, M.; Ahmadi, A. Water Quality Modeling of Mahabad Dam Watershed–Reservoir System under Climate Change Conditions, Using SWAT and System Dynamics. Water 2019, 11, 394. [Google Scholar] [CrossRef]
- Kang, B.; Lee, S.-J.; Kang, D.-H.; Kim, Y.-O. A Flood Risk Projection for Yongdam Dam against Future Climate Change. J. Hydro-Environ. Res. 2007, 1, 118–125. [Google Scholar] [CrossRef]
- Boulange, J.; Hanasaki, N.; Yamazaki, D.; Pokhrel, Y. Role of Dams in Reducing Global Flood Exposure under Climate Change. Nat. Commun. 2021, 12, 417. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing Climate Both Increases and Decreases European River Floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Rizwan, M.; Li, X.; Chen, Y.; Anjum, L.; Hamid, S.; Yamin, M.; Chauhdary, J.N.; Shahid, M.A.; Mehmood, Q. Simulating Future Flood Risks under Climate Change in the Source Region of the Indus River. J. Flood Risk Manag. 2023, 16, e12857. [Google Scholar] [CrossRef]
- Yun, X.; Tang, Q.; Wang, J.; Liu, X.; Zhang, Y.; Lu, H.; Wang, Y.; Zhang, L.; Chen, D. Impacts of Climate Change and Reservoir Operation on Streamflow and Flood Characteristics in the Lancang-Mekong River Basin. J. Hydrol. 2020, 590, 125472. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, S.; Shi, H. Impacts of Dams and Reservoirs on Local Climate Change: A Global Perspective. Environ. Res. Lett. 2021, 16, 104043. [Google Scholar] [CrossRef]
- Sun, L.; Jaramillo, F.; Cai, Y.; Zhou, Y.; Shi, S.; Zhao, Y.; Wang, W.; Yi, Y.; Yang, W.; Yang, Z.; et al. Exploring the Influence of Reservoir Impoundment on Surrounding Tree Growth. Adv. Water Resour. 2021, 153, 103946. [Google Scholar] [CrossRef]
- Wiatkowski, M. Influence of Słup Dam Reservoir on Flow and Quality of Water in the Nysa Szalona River. Pol. J. Environ. Stud. 2011, 20, 469–478. [Google Scholar]
- Gruss, Ł.; Głowski, R.; Wiatkowski, M. Modeling of Water Flows through a Designed Dry Dam Using the HEC-RAS Program. ITM Web Conf. 2018, 23, 9. [Google Scholar] [CrossRef]
- Arantes, C.C.; Fitzgerald, D.B.; Hoeinghaus, D.J.; Winemiller, K.O. Impacts of Hydroelectric Dams on Fishes and Fisheries in Tropical Rivers through the Lens of Functional Traits. Curr. Opin. Environ. Sustain. 2019, 37, 28–40. [Google Scholar] [CrossRef]
- Ashouri, M.; Piry, Z.; Rezaei Moghaddam, M.H. A Comparison of the Influence of the Sattarkhan Reservoir Dam on the Upstream and Downstream of the Ahar Chai River, NW Iran. Environ. Earth Sci. 2015, 73, 4099–4108. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, J.Y.; An, K.-G. Multivariate Statistical Analysis of Water Quality and Trophic State in an Artificial Dam Reservoir. Water 2021, 13, 186. [Google Scholar] [CrossRef]
- Tomczyk, P.; Gałka, B.; Wiatkowski, M.; Wdowczyk, A.; Gruss, Ł. Toxicity Studies on Sediments near Hydropower Plants on the Ślęza and Bystrzyca Rivers, Poland, to Establish Their Potential for Use for Soil Enrichment. Land. Degrad. Dev. 2022, 33, 756–770. [Google Scholar] [CrossRef]
- Hoque, M.M.; Islam, A.; Ghosh, S. Environmental Flow in the Context of Dams and Development with Special Reference to the Damodar Valley Project, India: A Review. Sustain. Water Resour. Manag. 2022, 8, 62. [Google Scholar] [CrossRef] [PubMed]
- Mezger, G.; González Del Tánago, M.; De Stefano, L. Environmental Flows and the Mitigation of Hydrological Alteration Downstream from Dams: The Spanish Case. J. Hydrol. 2021, 598, 125732. [Google Scholar] [CrossRef]
- Li, Y.; Wen, Z.; Schneidewind, U.; Liu, H.; Krause, S. Effects of a Large-Scale Dam Structure on Upstream and Downstream Lateral Hyporheic Exchange and Residence Time Distributions—The Xinglong Water Conservancy Dam, China. J. Hydrol. 2023, 625, 130073. [Google Scholar] [CrossRef]
- Mailhot, A.; Talbot, G.; Ricard, S.; Turcotte, R.; Guinard, K. Assessing the Potential Impacts of Dam Operation on Daily Flow at Ungauged River Reaches. J. Hydrol. Reg. Stud. 2018, 18, 156–167. [Google Scholar] [CrossRef]
- Amirataee, B.; Montaseri, M. Joint Probability Analysis of Storage Reservoir System Characteristics. J. Hydrol. 2023, 622, 129753. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Galelli, S. Regime-shifting Streamflow Processes: Implications for Water Supply Reservoir Operations. Water Resour. Res. 2016, 52, 3984–4002. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.; Liu, D.; Hu, T.; Xu, C. Frequency Analysis of Nonstationary Annual Maximum Flood Series Using the Time-varying Two-component Mixture Distributions. Hydrol. Process. 2017, 31, 69–89. [Google Scholar] [CrossRef]
- Evin, G.; Merleau, J.; Perreault, L. Two-component Mixtures of Normal, Gamma, and Gumbel Distributions for Hydrological Applications. Water Resour. Res. 2011, 47, 2010WR010266. [Google Scholar] [CrossRef]
- Smith, J.A.; Villarini, G.; Baeck, M.L. Mixture Distributions and the Hydroclimatology of Extreme Rainfall and Flooding in the Eastern United States. J. Hydrometeorol. 2011, 12, 294–309. [Google Scholar] [CrossRef]
- Bowers, M.C.; Tung, W.W.; Gao, J.B. On the Distributions of Seasonal River Flows: Lognormal or Power Law? Water Resour. Res. 2012, 48, 2011WR011308. [Google Scholar] [CrossRef]
- Gruss, Ł.; Wiatkowski, M.; Tomczyk, P.; Pollert, J.; Pollert, J. Comparison of Three-Parameter Distributions in Controlled Catchments for a Stationary and Non-Stationary Data Series. Water 2022, 14, 293. [Google Scholar] [CrossRef]
- Bezak, N.; Brilly, M.; Šraj, M. Comparison between the Peaks-over-Threshold Method and the Annual Maximum Method for Flood Frequency Analysis. Hydrol. Sci. J. 2014, 59, 959–977. [Google Scholar] [CrossRef]
- Gottschalk, L.; Krasovskaia, I.; Yu, K.; Leblois, E.; Xiong, L. Joint Mapping of Statistical Streamflow Descriptors. J. Hydrol. 2013, 478, 15–28. [Google Scholar] [CrossRef]
- Sangal, B.P.; Biswas, A.K. The 3-Parameter Lognormal Distribution and Its Applications in Hydrology. Water Resour. Res. 1970, 6, 505–515. [Google Scholar] [CrossRef]
- Młyński, D.; Wałęga, A.; Ozga-Zielinski, B.; Ciupak, M.; Petroselli, A. New Approach for Determining the Quantiles of Maximum Annual Flows in Ungauged Catchments Using the EBA4SUB Model. J. Hydrol. 2020, 589, 125198. [Google Scholar] [CrossRef]
- Adamson, M.J.; Dixon, P.T. On the Application of Mixtures of Two Log-Normal Distributions to the Analysis of Water Quality Data. Water SA 1983, 9, 1–8. [Google Scholar]
- Gruss, Ł.; Wiatkowski, M.; Buta, B.; Tomczyk, P. Verification of the Methods for Calculating the Probable Maximum Flow in the Widawa River in the Aspect of Water Management in the Michalice Reservoir. Annu. Set. Environ. Prot. 2019, 21, 566–585. [Google Scholar]
- Ma, Q.; Zhang, J.; Xiong, B.; Zhang, Y.; Ji, C.; Zhou, T. Quantifying the Risks That Propagate from the Inflow Forecast Uncertainty to the Reservoir Operations with Coupled Flood and Electricity Curtailment Risks. Water 2021, 13, 173. [Google Scholar] [CrossRef]
- Pirnia, A.; Golshan, M.; Darabi, H.; Adamowski, J.; Rozbeh, S. Using the Mann–Kendall Test and Double Mass Curve Method to Explore Stream Flow Changes in Response to Climate and Human Activities. J. Water Clim. Change 2019, 10, 725–742. [Google Scholar] [CrossRef]
- Talukdar, S.; Pal, S.; Shahfahad; Naikoo, M.W.; Parvez, A.; Rahman, A. Trend Analysis and Forecasting of Streamflow Using Random Forest in the Punarbhaba River Basin. Environ. Monit. Assess. 2023, 195, 153. [Google Scholar] [CrossRef] [PubMed]
- Ali, R.; Kuriqi, A.; Abubaker, S.; Kisi, O. Long-Term Trends and Seasonality Detection of the Observed Flow in Yangtze River Using Mann-Kendall and Sen’s Innovative Trend Method. Water 2019, 11, 1855. [Google Scholar] [CrossRef]
- Fentaw, F.; Melesse, A.M.; Hailu, D.; Nigussie, A. Precipitation and Streamflow Variability in Tekeze River Basin, Ethiopia. In Extreme Hydrology and Climate Variability; Elsevier: Amsterdam, The Netherlands, 2019; pp. 103–121. ISBN 978-0-12-815998-9. [Google Scholar]
- Yaghmaei, H.; Sadeghi, S.H.; Moradi, H.; Gholamalifard, M. Effect of Dam Operation on Monthly and Annual Trends of Flow Discharge in the Qom Rood Watershed, Iran. J. Hydrol. 2018, 557, 254–264. [Google Scholar] [CrossRef]
- Norouzi, N. Climate Change Impacts on the Water Flow to the Reservoir of the Dez Dam Basin. Water Cycle 2020, 1, 113–120. [Google Scholar] [CrossRef]
- Li, F.-F.; Liu, C.-M.; Wu, Z.-G.; Qiu, J. Balancing Ecological Requirements and Power Generation in Reservoir Operation in Fish Spawning Seasons. J. Water Resour. Plann. Manage. 2020, 146, 04020074. [Google Scholar] [CrossRef]
- Brown, C.A.; King, J.M. Implications of Upstream Water Uses on Downstream Ecosystems and Livelihoods. Int. J. Ecol. Environ. Sci. 2006, 32, 99–108. [Google Scholar]
- Unitek Polska Feasibility Study. Kamieniec Ząbkowicki Reservoir on the Nysa Kłodzka River, Implemented as Part of the “Oder Program—2006”. Kamieniec Ząbkowicki Municipality: Bardo Municipality, Poland, 2004; unpublished work.
- Head Office of Geodesy and Cartography Geoportal. Access to Spatial Data Services in Poland on the Website. 2023. Available online: https://www.geoportal.gov.pl/en/ (accessed on 2 October 2023).
- The Institute of Meteorology and Water Management, the National Research Institute in Warsaw. Time Series of Flows of the Nysa Kłodzka River, Bardo Profile (1980–2020). 2023. Available online: https://danepubliczne.imgw.pl (accessed on 10 July 2023).
- Zakwan, M.; Pham, Q.B.; Bonacci, O.; Đurin, B. Application of Revised Innovative Trend Analysis in Lower Drava River. Arab. J. Geosci. 2022, 15, 758. [Google Scholar] [CrossRef]
- Pohlert, T. Non-Parametric Trend Tests and Change-Point Detection 2023. CC BY-ND 2016, 4, 1–18. [Google Scholar]
- Wang, Y.; Xu, Y.; Tabari, H.; Wang, J.; Wang, Q.; Song, S.; Hu, Z. Innovative Trend Analysis of Annual and Seasonal Rainfall in the Yangtze River Delta, Eastern China. Atmos. Res. 2020, 231, 104673. [Google Scholar] [CrossRef]
- Esit, M. Investigation of Innovative Trend Approaches (ITA with Significance Test and IPTA) Comparing to the Classical Trend Method of Monthly and Annual Hydrometeorological Variables: A Case Study of Ankara Region, Turkey. J. Water Clim. Change 2023, 14, 305–329. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Significance Test and Applications. Theor. Appl. Clim. 2017, 127, 939–947. [Google Scholar] [CrossRef]
- Yu, Y. Finite Mixture Modeling for Raw and Binned Data. R Package Version 0.2.0. 2021. Available online: https://cran.r-project.org/web/packages/mixR/index.html (accessed on 20 November 2023).
- Yang, T.; Zhang, Q.; Chen, Y.D.; Tao, X.; Xu, C.; Chen, X. A Spatial Assessment of Hydrologic Alteration Caused by Dam Construction in the Middle and Lower Yellow River, China. Hydrol. Process. 2008, 22, 3829–3843. [Google Scholar] [CrossRef]
- Kędra, M. Dam-Induced Changes in River Flow Dynamics Revealed by RQA. Eur. Phys. J. Spec. Top. 2023, 232, 209–215. [Google Scholar] [CrossRef]
- Perz, A.; Sobkowiak, L.; Wrzesiński, D. Probabilistic Approach to Precipitation-Runoff Relation in a Mountain Catchment: A Case Study of the Kłodzka Valley in Poland. Water 2021, 13, 1229. [Google Scholar] [CrossRef]
- Solari, S.; Losada, M.A. A Unified Statistical Model for Hydrological Variables Including the Selection of Threshold for the Peak over Threshold Method. Water Resour. Res. 2012, 48, 2011WR011475. [Google Scholar] [CrossRef]
- Chalise, D.R.; Sankarasubramanian, A.; Ruhi, A. Dams and Climate Interact to Alter River Flow Regimes Across the United States. Earth’s Future 2021, 9, e2020EF001816. [Google Scholar] [CrossRef]
- Mersin, D.; Tayfur, G.; Vaheddoost, B.; Safari, M.J.S. Historical Trends Associated with Annual Temperature and Precipitation in Aegean Turkey, Where Are We Heading? Sustainability 2022, 14, 13380. [Google Scholar] [CrossRef]

| No. | Parameters | Value |
|---|---|---|
| 1 | Maximum Pool Elevation | 255.50 m a.s.l. |
| 2 | Maximum Pool Capacity | 83 million m3 |
| 3 | Surface Area at Maximum Pool Elevation in the reservoir | 920 ha |
| Method | Parameter | Pre-Dam Period | Post-Dam Period |
|---|---|---|---|
| Mann–Kendall | statistic S | −0.14 | −0.05 |
| Mann–Kendall | p-value | <0.0001 | <0.0001 |
| Sen Slope | slope | −6.486217 × 10−5 | −0.00016 |
| Sen Slope | p-value | <0.0001 | <0.0001 |
| Innovative Trend Analysis | slope | −0.00071 | −0.0001 |
| Innovative Trend Analysis | p-value | <0.0001 | <0.0001 |
| Output Flows from the Model | Pre-Dam Period | Post-Dam Period | ||||
|---|---|---|---|---|---|---|
| Parameter | Component 1 | Component 2 | Component 3 | Component 1 | Component 2 | Component 3 |
| Proportion | 0.893 | 0.106 | 0.0005 | 0.780 | 0.212 | 0.008 |
| Mean | 2.725 | 35.943 | 519.56 | 12.219 | 35.674 | 128.30 |
| Standard deviation | 3.422 | 22.217 | 378.77 | 5.428 | 11.312 | 65.801 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gruss, Ł.; Wiatkowski, M.; Połomski, M.; Szewczyk, Ł.; Tomczyk, P. Analysis of Changes in Water Flow after Passing through the Planned Dam Reservoir Using a Mixture Distribution in the Face of Climate Change: A Case Study of the Nysa Kłodzka River, Poland. Hydrology 2023, 10, 226. https://doi.org/10.3390/hydrology10120226
Gruss Ł, Wiatkowski M, Połomski M, Szewczyk Ł, Tomczyk P. Analysis of Changes in Water Flow after Passing through the Planned Dam Reservoir Using a Mixture Distribution in the Face of Climate Change: A Case Study of the Nysa Kłodzka River, Poland. Hydrology. 2023; 10(12):226. https://doi.org/10.3390/hydrology10120226
Chicago/Turabian StyleGruss, Łukasz, Mirosław Wiatkowski, Maksymilian Połomski, Łukasz Szewczyk, and Paweł Tomczyk. 2023. "Analysis of Changes in Water Flow after Passing through the Planned Dam Reservoir Using a Mixture Distribution in the Face of Climate Change: A Case Study of the Nysa Kłodzka River, Poland" Hydrology 10, no. 12: 226. https://doi.org/10.3390/hydrology10120226
APA StyleGruss, Ł., Wiatkowski, M., Połomski, M., Szewczyk, Ł., & Tomczyk, P. (2023). Analysis of Changes in Water Flow after Passing through the Planned Dam Reservoir Using a Mixture Distribution in the Face of Climate Change: A Case Study of the Nysa Kłodzka River, Poland. Hydrology, 10(12), 226. https://doi.org/10.3390/hydrology10120226