Abstract
The most common method for in situ measurement of saturated hydraulic conductivity (Ksat) of the vadose zone is the constant head well permeameter method. Our general objective is to provide an empirical method for determining volume of water required for measuring Ksat using this procedure. For one-dimensional infiltration, steady state reaches as time (t) → ∞. For three-dimensional water flow from a cylindrical hole under a constant depth of water, however, steady state reaches rather quickly when a saturated bulb forms around the hole. To reach a quasi-steady state for measuring Ksat, we assume an adequate volume of water is needed to form the saturated bulb around the hole and increase the water content outside of the saturated bulb within a bulb-shaped volume of soil, hereafter, referred to as wetted soil volume. We determined the dimensions of the saturated bulb using the Glover model that is used for calculating Ksat. We then used the values to determine the volume of the saturated and wetted bulbs around the hole. The volume of water needed to reach a quasi-steady state depends on the difference between the soil saturated and antecedent water content (Δθ). Based on our analysis, between 2 and 5 L of water is needed to measure Ksat when Δθ varies between 0.1 and 0.4 m3 m−3, respectively.
1. Introduction
Of all the processes that occur in soil, water flow is perhaps the only phenomenon that directly or indirectly affects all other processes. These include, but are not limited to, infiltration and percolation of water in the vadose zone, groundwater flow, transport of dissolved and suspended materials, and evaporation. The Buckingham–Darcy law (generally known and, hereafter, referred to as Darcy’s law) governs water flow through soil under saturated and unsaturated conditions [1]. In Darcy’s law, the flux (v, dimensional unit L/T) is directly related to the soil hydraulic conductivity (K, L/T) and hydraulic gradient, dH/dX (L/L), where H is the total soil hydraulic head (total soil water potential expressed on weight basis), and X is the distance along the flow path. Hydraulic conductivity, defined as a measure of the ability of soil to transmit water [2,3], is a soil property that depends not only on the soil pore size distribution and geometry, but also on the quantity (i.e., soil water content, θ) and quality of water (e.g., solute content, temperature) flowing through the soil [4]. Under saturated conditions, when soil water pressure head (h) = 0, soil water content (θs) is equal to total soil porosity, and the saturated hydraulic conductivity (hereafter, denoted as Ksat) is a constant at any given time or space. The unsaturated hydraulic conductivity (hereafter, denoted as Kunsat), on the other hand, depends on θ and h and is generally written as a function of soil water content, K(θ), or pressure head, K(h).
Both Ksat and Kunsat of the vadose zone can be measured in the field or laboratory using a number of procedures [5,6,7,8,9,10,11,12]. In addition, a number of empirical approaches (e.g., pedotransfer functions) are available for estimating Ksat and Kunsat [13,14,15,16,17,18,19,20,21]. These empirical approaches, however, may require accurate knowledge of other soil properties, therefore, may have limitations for determining K for practical applications [22]. For example, only someone with a great deal of expertise in soil mapping can properly determine soil particle size distribution (which is required by some of the approaches) via feel method in the field. Zhang and Schaap [23] presented a review of pedotransfer functions for estimating soil saturated hydraulic conductivity and offered suggestions for improving their capabilities. Due to difficulties associated with determining Kunsat and analysis of water flow under unsaturated conditions, Ksat is often used as a proxy for a number of environmental and engineering purposes. These include designing large septic systems for wastewater disposal and infiltration galleries for groundwater recharge, storm water management, and bioremediation of contaminated soil and groundwater [24,25,26].
The most widely used method for in situ determination of Ksat from the soil surface to a few meters in depth (e.g., 4 m) in the vadose zone is the constant head well permeameter (also known as shallow well pump-in or borehole permeameter) method [5,27,28,29,30]. In the original method, Ksat was measured using a relatively large hole (e.g., 30 cm dimeter) requiring a large volume of water (e.g., 200 L) [2,31,32]. Based on theoretical and experimental evaluations showing that a steady state is reached rather quickly, for most applications, Ksat can be measured in a hole with a small diameter (e.g., 6 cm) using a few liters of water [30,33,34,35,36].
To measure Ksat, a cylindrical hole of known radius (r) is bored to the desired depth. A constant depth of water (L) is maintained in the hole, and the flow rate of water from the hole to the soil (Q, L3/T) is measured after reaching a quasi-steady state [5,30]. Saturated hydraulic conductivity is calculated using Q, r, and L via the equation
where A is a factor that must be determined by a model using r and L. All the models developed for determining the factor A are based on the idealized assumptions that Darcy’s law is valid and the soil under consideration is homogeneous and isotropic.
Ksat = Q/A
For cases where the distance from the bottom of the hole to a restrictive layer is >2 L, Zangar [37] presented the model developed by R. E. Glover (commonly referred to as the Glover model), in which
where arcsinh is the inverse hyperbolic sine function, and r and L are as defined before. [Note: USBR [32] presents the Glover model by expressing arcsinh (L/r) by (natural log) ln (L/r).] This model was developed based only on the saturated flow from a hole within a cylindrical volume with a limited radius under a dome above the level of water in the hole (see Figure 57 of Zangar [37]). Water that leaves the hole sidewall in the horizontal direction due to hydrostatic pressure inside the hole, however, changes its course due to gravity into vertical flow lines within the saturated cylindrical volume around the hole. Therefore, the model takes into account both pressure head and gravity. Philip [38], Reynolds et al. [39], and Stephens and Neuman [40] developed models for A by considering both saturated and unsaturated flow around the cylindrical hole. These models are based on the assumption that the unsaturated hydraulic conductivity can be described via the exponential function given by [41]
where h, as defined before, is the soil water pressure head, and α (L−1) is an empirical parameter, referred to as the capillary factor or sorptive number. Amoozegar [33] compared the Glover model with the models presented by Philip [38], Reynolds et al. [39], and Stephens and Neuman [40] and showed that the Glover model is the most suitable one for calculating Ksat based on Q, r, and L from field measurements.
A = 2πL2/[arcsinh(L/r) − (1+ r2/L2)1/2 + (r/L)]
K(h) = Ksatexp(αh)
2. Objectives
As stated earlier, based on theoretical evaluations and practical measurements, steady state reaches relatively quickly for three-dimensional water flow from a cylindrical hole, and using a relatively small diameter hole, Ksat can be measured in situ via the constant head well permeameter method using a few liters of water in a few hours. However, to our knowledge, no procedure has been offered to determine the amount of water and the required time for an in situ measurement of Ksat via this method. Our objectives here are (1) to present a simple analysis of water flow from a cylindrical hole within the vadose zone, and (2) to provide a protocol based on a conceptual model for estimating the volume of water required to reach a steady state condition for measuring Ksat via the constant head well permeameter method using the Glover model.
3. Methods
There are major differences between one-dimensional vertical infiltration and three-dimensional water flow from a cylindrical hole. To demonstrate their similarities and differences, we first compare one-dimensional vertical infiltration with three-dimensional flow from a cylindrical hole in a homogeneous, isotropic, and uniformly dry infinitely deep soil.
3.1. One-Dimensional Infiltration under Constant Depth of Ponding
The soil water profile during one-dimensional infiltration in an idealized soil system composed of a homogeneous, uniformly moist, and semi-infinite soil is composed of a saturation zone, saturation front, transmission zone, transmission front, wetting zone, and wetting front (Figure 1A,B). Within the bottom part of the transmission zone and in the wetting zone, water content and pressure head decrease rapidly to the initial soil water content (θi) and pressure head (hi), respectively. As explained by Hillel [4], despite relatively low Kunsat within the wetting zone, due to a rather large hydraulic gradient across the wetting front, the wetting front advances more rapidly than the saturation front, and the flux (v) decreases rapidly to the background level ahead of the wetting front. In addition, the saturation zone grows (i.e., thickness of the saturated zone increases) while the infiltration rate declines with time.
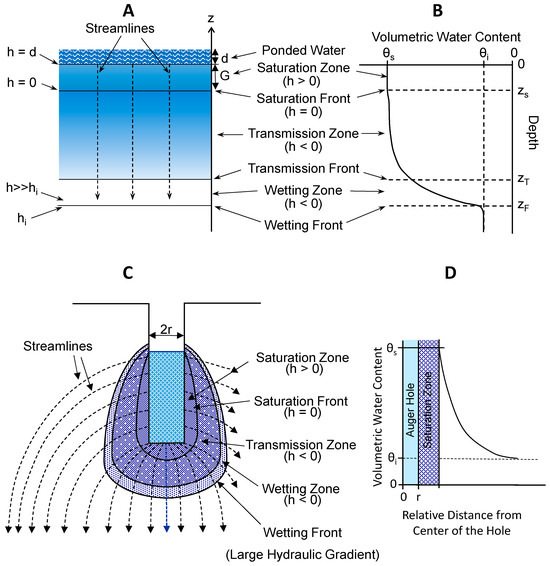
Figure 1.
Idealized schematic diagram of the wetted regions (A) and water content distribution with depth (soil water profile) (B) for vertical infiltration under a constant depth of ponding, and wetted regions (C) and water content distribution as a function of distance (D) around a cylindrical hole under a constant depth (head) of water in the hole.
To assess infiltration rate (i) for a homogeneous, initially uniform moist soil, we take the origin of the Cartesian coordinate system at the soil surface with positive z-axis going upward (see Figure 1A). Within the saturation zone, soil water content is at saturation (a constant, θs), the hydraulic conductivity is equal to Ksat (a constant value), but the pressure head decreases from d at the soil surface to zero at the saturation front. Under a constant depth of ponding (d), pressure head at the soil surface is h(0, t) = d, gravitational head is hz(0, t) = 0, and total hydraulic head is H(0, t) = d. At the saturation front, where the depth zs = −G(t) (see Figure 1), the pressure head is h(G, t) = 0, gravitational head is hz(G, t) = −G(t), and total hydraulic head is H(G, t) = −G(t). According to Darcy’s law, the flux at the soil surface (i.e., infiltration rate i) can be estimated by
or
v(0, t) = i = −Ksat[H(G, t) − H(0, t)]/G(t) = Ksat[d + G(t)]/G(t)
i = Ksat + Ksat[d/G(t)]
For one-dimensional infiltration under a constant depth of ponding, steady state will be reached only as t → ∞ (see Philip [42]) when d/G(t) → zero (i.e., when G(t) >> d). Therefore, according to Equation (4b), infiltration rate decreases asymptotically, reaching a final value that is often taken as the Ksat of the soil [5].
3.2. Three-Dimensional Infiltration from a Cylindrical Hole under a Constant Depth of Water
Similar to one-dimensional infiltration, we consider water flow from a cylindrical hole of radius r under a constant depth of water (L) in an idealized, unsaturated, homogeneous, and isotropic soil system. Under a constant depth of ponding, the soil water regime around the hole is composed of a saturation zone (h > 0), saturation front (h = 0), transmission and wetting zones (h < 0), and wetting front (h < < 0) (Figure 1C). Unlike one-dimensional infiltration, however, water that leaves the sidewall of the hole in the horizontal direction moves along curvilinear streamlines that diverge both radially and vertically due to gravity (see Figure 1C). These streamlines form paraboloid surfaces (hereafter, referred to as streamline surfaces) that expand with time. Since water flow from a cylindrical hole is three-dimensional, as infiltration continues, the surface area of flow bounded by any two neighboring streamline surfaces increases with distance from the hole, resulting in a rapid drop in soil water content (Figure 1D), Kunsat, and flux. Therefore, the quantity of water that enters the soil through the sidewall and bottom of the hole cannot fill all the air-filled pores beyond a relatively short distance from the wall or bottom of the hole, and the saturation zone stops growing. Stephens [43] and Stephens and Neuman [40] recognized that a tear-shaped saturation zone (referred to as saturated bulb) of limited size forms around the hole once steady state is reached. While, for one-dimensional vertical infiltration, both saturation zone and transmission zone grow indefinitely, and steady state reaches as t → ∞, for three-dimensional flow, the rate of water flow into the soil from a cylindrical hole reaches steady state when the saturated bulb is formed while the transmission zone and wetting front continue to advance.
Considering a reference elevation at the bottom of the hole, the total hydraulic head H (i.e., h + hz) at any point on the sidewall and bottom of the hole is equal to L, as shown in Figure 2 (4, 33, 43). Following water application to the hole, the rate of water entry into the soil and the rate of advance of the saturation front and wetting front are controlled by the hydrostatic pressure head on the hole sidewall and bottom and the matric potential in the transmission zone and across the wetting front. At steady state, the gradient at any point on the wetted wall or bottom of the cylindrical hole is greater than 1, therefore, the flux at any point on the wetted wall and bottom is numerically greater than Ksat but decreases continuously along any streamline surface in the saturated zone, while the hydraulic conductivity remains the same (i.e., Ksat). As discussed above, outside of the saturated bulb, both the flux and Kunsat decrease rapidly because the soil water content decreases exponentially due to the three-dimensional nature of the flow. Moving on any streamline surface starting from the hole wall, there is a point at which the flux is numerically equal to Ksat. These points on the streamline surfaces form a surface area that bounds a soil volume around the hole that is similar in shape to the saturated bulb. Amoozegar [33] presented a rather simple analysis of water flow from a cylindrical auger hole under a constant depth of water and stated that the volume of the saturated bulb is independent of the initial soil water content and soil texture. In addition, he showed that the surface where the flux is numerically equal to Ksat lies directly over the surface of the saturated bulb. After reaching steady state, the flow rate of water infiltrating from the hole to the soil (i.e., Q) is the same as the flow rate of water passing through the surface area of the saturated bulb (SSB). Therefore, we can write
where vSB is the flux through the saturated bulb surface. Considering that at the surface of the saturated bulb vSB = Ksat, and comparing Equations (1) and (5), we determine that SSB is numerically equal to the factor A determined by the models for calculating Ksat.
Q = SSB × vSB
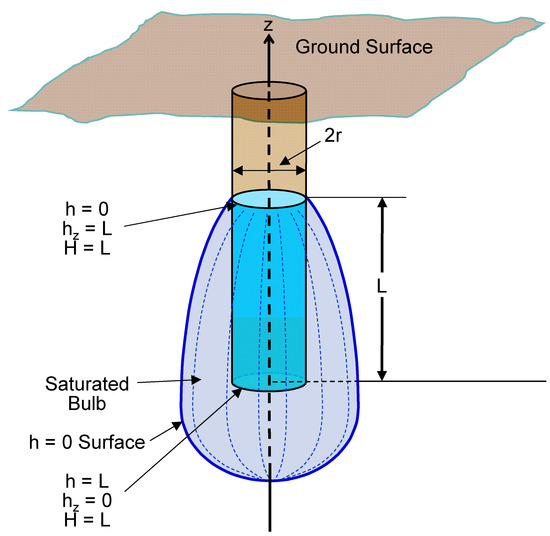
Figure 2.
Schematic diagram of the three-dimensional representation of the saturated bulb around a cylindrical hole of radius r showing the pressure head (h), gravitational head (hz), and total hydraulic head (H) on the sidewall and bottom of the hole under a constant depth of water (L). Adapted from Amoozegar [33].
Outside the saturated bulb, the pressure head and soil water content decrease in tandem reaching the background (initial condition) levels away from the hole. The points for any constant pressure head (hereafter, referred to as the equipressure head surfaces) form a bulb-shaped volume, as shown by Amoozegar [33] and represented in Figure 3.
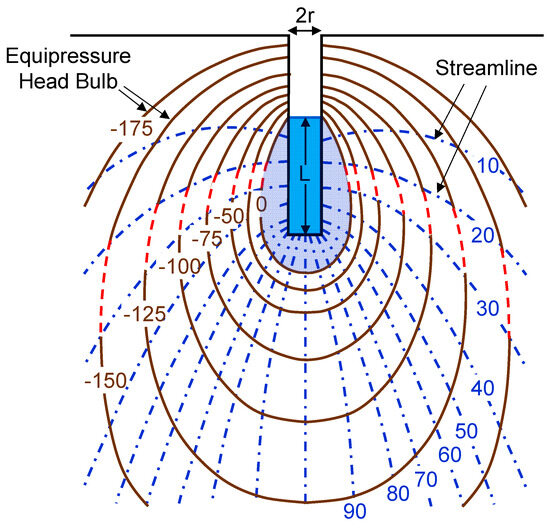
Figure 3.
Cross-sectional area of the saturated bulb surrounded by bulb-shaped equipressure head surfaces (adapted from Stephens [43], as presented by Amoozegar [33]).
4. Water Requirements to Reach Steady State for Measuring Ksat
At an initial water content of θi, the smaller pores contain water while the larger pores contain air. As water moves from the hole to the soil, the large pores conduct water at a faster rate than the small pores, but water in the small pores also moves outward as water from the hole enters the soil. In addition, as described by Hillel [4] for one-dimensional flow, the relatively high rate of infiltration after application of water to the soil depends on θi. The volume of water required to reach steady state and determine Ksat at a given site depends on the soil total porosity (taken to be saturated water content, θs) and the initial soil water content, θi. The time to make a measurement depends on this volume, initial infiltration of water into soil, and Ksat of the soil.
To estimate the required volume of water that is needed to determine Ksat for practical applications, we consider that the rate of water entry from the cylindrical hole to the soil is measured after reaching a quasi-steady state condition. To reach a quasi-steady state condition, we assume an adequate volume of water is needed to form the saturated bulb and increase the water content outside of the saturated bulb within a bulb-shaped volume of soil (hereafter, referred to as wetted soil volume) where the water content at the corresponding equipressure head surface nearly reaches the background (i.e., initial) soil water content. Furthermore, we assume the water content in the wetted soil volume (θwv) can be estimated using the average water content between saturation and background soil water content, i.e., θwv = (θs − θi)/2. This is a reasonable assumption when considering the soil water content decreases exponentially with distance from the cylindrical hole (see Figure 1D). To measure the flow rate (i.e., Q) for calculating Ksat, we increase this volume by a minimum of 100 to 400 cm3, depending on the quasi-steady state rate of water flow into the soil (i.e., depending on Ksat).
4.1. Surface Area and Volume of the Saturated Bulb
As presented by Amoozegar [33], we recognize that the saturated bulb resembles the shape of an egg. We then use one of the techniques used for determining the surface area and volume of an egg in the poultry industry [44] to determine the volume of water needed to reach a quasi-steady state.
Inspecting the shape of the saturated bulb and wetted soil volume, we visualize that each can be divided into two half-spheroids (also known as ellipsoid of revolution) where they meet at the middle sharing their axes that are equal (Figure 4). Due to the requirement of H/r ≥ 5 suggested for using the Glover model by Amoozegar [45], we postulate that the upper spheroid is a prolate for both bulb volumes. For the bottom half, we can choose a prolate or oblate spheroid for one or both volumes.
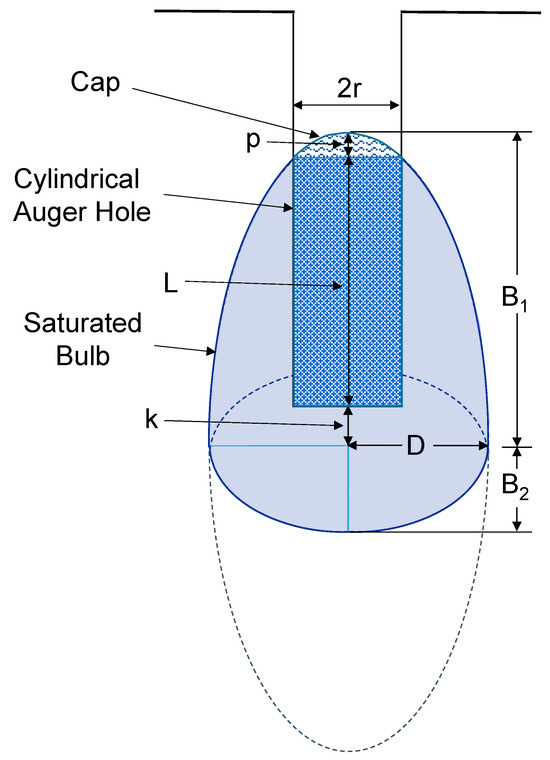
Figure 4.
Schematic diagram of the saturated bulb composed of two half-spheroids forming around a cylindrical hole under a constant depth of water after reaching steady state flow rate. Adapted from Amoozegar [33].
For the saturated bulb, following Amoozegar [33], we set the upper half prolate spheroid with axes B1 and D in such a way that it touches the perimeter of the surface of the water in the hole (Figure 2 and Figure 4). We then set the distance from the water level in the hole to the top of the crown (upper vertex) of the spheroid as p and set the distance from the centers of the two spheroids to the bottom of the hole as k, as shown in Figure 4. Under this setup, we have
B1 = L + k + p
We chose the lower half to be an oblate spheroid, with axes B2 and D, and selected the length of B2 such that the ratio of (B2 + k)/D < 1.0. This ratio is in agreement with the analysis conducted by Stephens [43]. The surface area of the saturated bulb is the sum of the surface areas of the upper and lower half-spheroids minus the surface area of the cap above the water level in the hole.
There are a number of analytical equations for determining the surface area of prolate and oblate spheroids. For our analysis, we used the equations presented by Tee [46] for determining the one-half of the surface areas of the upper prolate and lower oblate spheroids to determine the surface area of the saturated bulb via
where e = 1 − D2/B12 for the upper prolate and f = D2/B22 −1 for the lower oblate spheroid. As an alternative, the surface area of the saturated bulb can be determined using the general empirical equation for ellipsoid S = 4π[(anbn+ ancn +bncn)/3]1/n where a, b, and c are half the length of the principal axes of the ellipsoid and the constant n = 1.6075 [47]. For surface areas of the two one-half spheroids, two of the axes are the same and the surface area of the saturated bulb can be estimated using
SSB = πD[2D + B1arcsin(e1/2)/e1/2 + B2arcsinh(f1/2)/f1/2] − π(r2 + p2)
SSB = 2π{[2(B1D)1.6075/3 + D3.215/3]1/1.6075 + [(2(B2D)1.6075/3 + D3.215/3]1/1.6075} − π(r2 + p2)
The volume of the saturated bulb is the sum of the volumes of the two half-spheroids minus the volume of cap and volume of water in the hole, as determined by the equation
V = (2/3)πD2(B1 + B2) − πr2L − (πp/6)[3r2 + p2]
As stated earlier, the surface area of the saturated bulb is numerically equal to factor A in Equation (1). By selecting values for k, p, B1, B2, and D through the trial and error method, we can exactly match the surface area of the saturated bulb to be equal to factor A. We then use the values of B1, B2, and D to calculate the volume of the saturated bulb. We conducted our analysis for measuring Ksat using 15 cm depth of water in a 6 cm diameter hole, as recommended for practical applications. Values for k, p, B1, B2, and D for matching the surface area of the saturated bulb with factor A in the Glover model, Equation (2), are presented in Table 1.

Table 1.
Dimensions, volume, and surface area of the saturated bulb and wetted volume after reaching a quasi-steady state for water flow from a cylindrical hole with r = 3 cm and L = 15 cm. Factor A is from the Glover model presented by Equation (2).
4.2. Volume of the Wetted Bulb
To reach a quasi-steady state, we assumed distances k, B2 + k, and D − r for the saturated bulb (see Figure 4) to increase by a factor of three for the wetted bulb, as presented in Table 1 and Figure 5. This is a reasonable assumption when we consider that the volume of equipressure head bulbs (see Figure 3) increases approximately with R3, where R is the horizontal distance from the center of the bulb. Consequently, the average water content near the equipressure head surfaces is also inversely related to R3. Based on the above assumptions, the volume of the wetted bulb is composed of one-half prolate and one-half oblate spheroids. We adjusted the length p so the surface of the wetted bulb touches the perimeter of the surface of the water in the hole to obtain the major axis of the upper prolate spheroid (see Table 1). We followed a similar method as used for the saturated bulb and determined the surface area and volume of the wetted bulb around the saturated bulb using Equations (7) and (9), and the results are presented in Table 1.
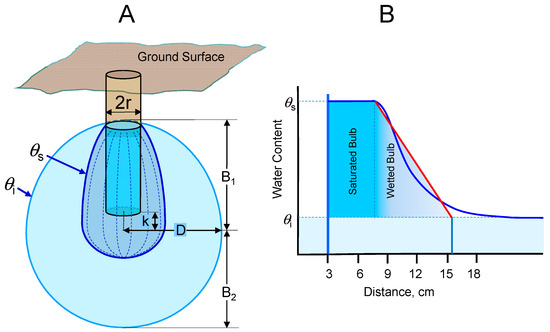
Figure 5.
Schematic diagram of the saturated and wetted bulbs (A), and the soil water content distribution with distance from the center of the bulbs (B).
4.3. Example Calculation
Here, we present example calculations for determining Ksat in a 6 cm diameter cylindrical hole under 15 cm of depth (head) of water (the most common type of Ksat measurements for using the Glover model). For these calculations, the volume of the saturated bulb is 2256 cm3, and the volume of the wetted bulb associated with D = 16.5 cm is 19,386 cm3. As stated earlier, the quasi-steady state flow rate should be determined three or four times while applying 100–400 cm3 of water to the soil depending on the flow rate into the soil. The volume of water needed for measuring Ksat is
- Volume of water to fill the hole to 15 cm depth, π × 9 × 15 cm3;
- Volume of water to increase the water content within the saturated bulb from θi to θs, 2256 × (θs − θi) cm3;
- Volume of water to increase the water content of the wetted volume outside of the saturated bulb, (19,386 – 2256) × (θs − θi)/2 cm3;
- Volume of water to reach the quasi-steady state is the sum of the three values determined above, and volume of water to be applied to soil to measure the quasi-steady state rate, Q, is 100–400 cm3.
Based on the example values, we estimated the volume of water that must be applied to the soil to reach a quasi-steady state and measure Ksat for four θs − θi scenarios (Table 2). We should note that the quasi-steady state flow rates for different Ksat values were determined using the Glover model (Equations (1) and (2)). The values in Table 2 can be used to estimate the volume of water for in situ measurement of Ksat for various porosity (θs) and initial water content (θi) combinations.

Table 2.
Estimated volume of water needed to reach a quasi-steady state flow rate (Q) and make measurements for different Ksat values measured in a 6 cm diameter cylindrical hole under 15 cm depth (head) of water in a soil with saturated water content θs and initial soil water content θi. Volume of water to fill the cylindrical hole to 15 cm depth is 424 cm3.
We should note that due to the soil micro variability and other factors (e.g., presence of air entrapped in soil pores), the initial rate of water flow into the soil as well as the steady state rate do not follow a smooth declining curve. Often, the rate of water flow after reaching a quasi-steady state fluctuates slightly around an average value. Also, considering soil spatial variability, particularly with respect to soil hydraulic conductivity [48], reaching a quasi-steady state condition is adequate for measuring Ksat for most practical applications.
Since the quasi-steady state flow rate of water from a cylindrical home to the soil depends on Ksat, a pre-determined set of time periods or volumes of water entering the soil cannot be prescribed for making Ksat measurements for all cases. Instead, the individual making measurements must allow enough time for the flow to reach a quasi-steady state condition and obtain accurate measurements for determination of the quasi-steady state rate of water flow for calculating Ksat. To determine if a quasi-steady state has been reached, the individual making measurements must either plot the rate of water infiltration into the soil or make an adequate number of measurements to confirm that required quasi-steady state has been reached. In general, for most practical applications, measurements must be continued until 3–5 consecutive rates of water entry into the soil are not on a continuous declining trend, but instead vary within a reasonably small range of their average value. The analysis presented in this paper provides general guidelines for determining reasonable bounds on the volume of water that should be used to measure these nearly constant flow rates.
5. Summary and Conclusions
The constant head well permeameter method is used around the world to measure soil saturated hydraulic conductivity (Ksat) in the vadose zone. Since water flow from a cylindrical hole in this method is three-dimensional, steady state reaches quickly when a saturated bulb forms around the hole. Although it has been reported that Ksat can be measured in a relatively short time using a few liters of water, no analysis has been performed to estimate the volume of water needed to make measurements. At steady state, the rate of water flow from the hole to the soil depends on Ksat, height of water in the hole (L), and radius of the hole (r). For a given r and L, the minimum volume of water required to reach a quasi-steady state depends on the volume of the saturated bulb, soil total porosity, and antecedent (i.e., initial) soil water content. Using an innovative approach, a protocol is developed to estimate the volume of water required to reach a quasi-steady state condition for measuring Ksat for practical applications. In this approach, the volumes of the saturated bulb and wetted volume of the soil around it are determined using the Glover model for calculating Ksat based on r, L, and quasi-steady rate of water flow into the soil (Q). The time of measurement and volume of water required to infiltrate the soil for measuring Q depends on Ksat. Based on our analysis, using a 6 cm diameter hole and 15 cm depth of water in the hole, for most practical applications, Ksat of the vadose zone can be measured via the constant head well permeameter method using 2 to 5 L of water.
Author Contributions
Aziz Amoozegar: Conceptualization; Formal analysis; Investigation; Methodology; Project administration; Validation; Visualization; Writing—original draft; Writing—review & editing. Joshua L. Heitman: Conceptualization; Investigation; Methodology; Writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in parts by USDA-NIFA Multi-State Project 4188 and by the North Carolina Agricultural Research Service (NCARS), NC State University.
Data Availability Statement
No data were collected in this study. Additional relevant information about methodology will be provided upon request.
Conflicts of Interest
The authors have no conflicts of interest regarding this research.
References
- Jury, W.A.; Horton, T. Soil Physics, 6th ed.; John Wiley and Son: Hoboken, NJ, USA, 2004; p. 384. [Google Scholar]
- Amoozegar, A.; Warrick, A.W. Hydraulic conductivity of saturated soils: Field methods. In Methods of Soil Analysis, Part 1. Physical and Mineralogical Methods, 2nd ed.; Agron. Monograph No. 9; Klute, A., Ed.; Soil Science Society of America: Madison, WI, USA, 1986; pp. 735–770. [Google Scholar]
- SSSA. Glossary of Soil Science Terms; Soil Science Society of America: Madison, WI, USA, 2023; Available online: https://www.soils.org/publications/soils-glossary/ (accessed on 10 May 2023).
- Hillel, D. Introduction to Environmental Soil Physics; Elsevier Academic Press: San Diego, CA, USA, 2004; p. 494. [Google Scholar]
- Amoozegar, A.; Wilson, G.V. Methods for measuring hydraulic conductivity and drainable porosity. In Agricultural Drainage; Monograph No. 38; Skaggs, R.W., van Schilfgaarde, J., Eds.; American Society of Agronomy, Inc.: Madison, WI, USA; Crop Science Society of America, Inc.: Madison, WI, USA; Soil Science Society of America, Inc.: Madison, WI, USA, 1999; pp. 1149–1205. [Google Scholar]
- ASTM. Standard method for measurement of hydraulic conductivity of saturated porous materials using a flexible wall permeameter, D5084-16a. In Annual Book of ASTM Standards; Section 4 Construction; ASTM International: West Conshohocken, PA, USA, 2020; Volume 04.08, pp. 1089–1112. [Google Scholar]
- ASTM. Standard guide for comparison of field methods for determining hydraulic conductivity in vadose zone. D5126-16. In Annual Book of ASTM Standards, Section 4 Construction; ASTM International: West Conshohocken, PA, USA, 2020; Volume 04.08, pp. 1156–1167. [Google Scholar]
- Booltink, H.W.G.; Bouma, J. Suction crust infiltrometer. In Methods of Soil Analysis, Part 4. Physical Methods; SSSA Book Series No. 5; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 926–930. [Google Scholar]
- Clothier, B.; Scotter, D. Unsaturated water transmission parameters obtained from infiltration. In Methods of Soil Analysis, Part 4. Physical Methods; SSSA Book Series No. 5; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 879–898. [Google Scholar]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Govindaraju, R.S. In situ measurements of soil saturated hydraulic conductivity: Assessment of reliability through rainfall–runoff experiments. Hydrol. Process. 2017, 31, 3084–3094. [Google Scholar] [CrossRef]
- Sakellariou-Makrantonaki, M.; Angelaki, A.; Evangelides, C.; Bota, V.; Tsianou, E.; Floros, N. Experimental determination of hydraulic conductivity at unsaturated soil column. Procedia Eng. 2016, 162, 83–90. [Google Scholar] [CrossRef]
- Vachaud, G.; Dane, J.H. Instantaneous profile. In Methods of Soil Analysis, Part 4. Physical Methods; SSSA Book Series No. 5; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 937–962. [Google Scholar]
- Ahuja, L.R.; Rawls, W.J.; Nielsen, D.R.; Williams, R.D. Determining soil hydraulic properties and their field variability from simpler measurements. In Agricultural Drainage; Monograph No. 38; Skaggs, R.W., van Schilfgaarde, J., Eds.; American Society of Agronomy, Inc.: Madison, WI, USA; Crop Science Society of America, Inc.: Madison, WI, USA; Soil Science Society of America, Inc.: Madison, WI, USA, 1999; pp. 1207–1233. [Google Scholar]
- Granata, F.; Di Nunno, F.; Modoni, G. Hybrid machine learning models for soil saturated conductivity prediction. Water 2022, 14, 1729. [Google Scholar] [CrossRef]
- Kosugi, K.; Hopman, J.W.; Dane, J.H. Parametric models. In Methods of Soil Analysis, Part 4. Physical Methods; SSSA Book Series No. 5; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 739–757. [Google Scholar]
- Ottoni, M.V.; Filho, T.B.O.; Lopes-Assad, M.R.C.; Filho, O.C.R. Pedotransfer functions for saturated hydraulic conductivity using a database with temperate and tropical climate soils. J. Hydrol. 2019, 575, 1345–1358. [Google Scholar] [CrossRef]
- Peters, A.; Hohenbrink, T.L.; Iden, S.C.; van Genuchten, M.T.; Durner, W. Prediction of the absolute hydraulic conductivity function from soil water retention data. Hydrol. Earth Syst. Sci. 2023, 27, 1565–1582. [Google Scholar] [CrossRef]
- Tian, Z.; Kool, D.; Ren, T.; Horton, R.; Heitman, J.L. Approaches for estimating unsaturated soil hydraulic conductivities at various bulk densities with the extended Mualem-van Genuchten model. J. Hydrol. 2019, 572, 719–731. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of the unsaturated soil. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Williams, W.G.; Ojuri, O.O. Predictive modelling of soils’ hydraulic conductivity using artificial neural network and multiple linear regression. SN Appl. Sci. 2021, 3, 152. [Google Scholar] [CrossRef]
- Zuo, Y.; He, K. Evaluation and development of pedo-transfer functions for predicting soil saturated hydraulic conductivity in the Alpine Frigid Hilly region of Qinghai Province. Agronomy 2021, 11, 1581. [Google Scholar] [CrossRef]
- Shuster, W.D.; Schifman, L.; Kelleher, C.; Golden, H.E.; Bhaskar, A.S.; Parolari, A.J.; Stewart, R.D.; Herrmann, D.L. K in an urban world: New contexts for hydraulic conductivity. J. Am. Water Resour. Assoc. 2021, 57, 493–504. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Estimation of saturated hydraulic conductivity with pedotransfer functions: A review. J. Hydrol. 2019, 575, 1011–1030. [Google Scholar] [CrossRef]
- Bekele, E.; Toze, S.; Patterson, B.; Fegg, W.; Shackleton, M.; Higginson, S. Evaluating two infiltration gallery design for managed aquifer recharge using secondary treated wastewater. J. Environ. Manag. 2013, 117, 115–120. [Google Scholar] [CrossRef]
- Hawkins, G.; Brown, J.T.T.; Radcliffe, D.E.; Freshly, P. Measuring Soil Saturated Hydraulic Conductivity for On-Site Wastewater Treatment Systems. University of Georgia Cooperative Extension Bulletin 1535. 2022. Available online: https://secure.caes.uga.edu/extension/publications/files/pdf/B%201535_1.PDF (accessed on 10 May 2023).
- Sims, J.L.; Suflita, J.M.; Russell, H.H. In-situ bioremediation of contaminated ground water. In Ground Water Issue; EPA/540/S-92/003; US Environmental Protection Agency, Robert S. Kerr Environmental Research Laboratory: Ada, OK, USA, 1992. [Google Scholar]
- Braud, I.; Desprats, J.-F.; Ayral, P.-A.; Bouvier, C.; Vandervaere, J.-P. Mapping topsoil; field-saturated hydraulic conductivity from point measurements using different methods. J. Hydrol. Hydromech. 2017, 65, 264–275. [Google Scholar] [CrossRef]
- Hangen, E.; Vieten, F. A comparison of five different techniques to determine hydraulic conductivity of a riparian soil; in North Bavaria, Germany. Pedosphere 2018, 28, 443–450. [Google Scholar] [CrossRef]
- Libohova, Z.; Schoeneberger, P.; Bowling, L.C.; Owens, P.R.; Wysoki, D.; Wills, S.; Williams, C.O.; Seybold, C. Soil systems for upscaling saturated hydraulic conductivity of hydrological modeling in the critical zone. Vadose Zone J. 2018, 17, 170051. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E. Constant head well permeameter (vadose zone). In Methods of Soil Analysis, Part 4. Physical Methods; SSSA Book Series No. 5; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 844–858. [Google Scholar]
- Stephens, D.B.; Lambert, K.; Watson, D. Regression models for hydraulic conductivity and field test of the borehole permeameter. Water Resour. Res. 1987, 23, 2207–2214. [Google Scholar] [CrossRef]
- USBR. Procedure for performing field permeability testing by the well permeameter method. In Earth Manual, Part 2, Water Resources Technical Publication, 3rd ed.; USBR 7300-89; The Bureau of Reclamation, US Department of the Interior: Denver, CO, USA, 1990; pp. 1227–1236. Available online: https://www.usbr.gov/tsc/techreferences/mands/mands-pdfs/earth2.pdf (accessed on 10 May 2023).
- Amoozegar, A. Examination of models for determining saturated hydraulic conductivity by the constant head well permeameter method. Soil Tillage Res. 2020, 200, 104572. [Google Scholar] [CrossRef]
- Schoeneberger, P.J.; Amoozegar, A.; Buol, S.W. Variation of physical properties of a soil and saprolite continuum at three geomorphic positions. Soil Sci. Soc. Am. J. 1995, 59, 1389–1397. [Google Scholar] [CrossRef]
- Talsma, T. Some aspects of three-dimensional infiltration. Aust. J. Soil Res. 1970, 8, 179–184. [Google Scholar] [CrossRef]
- Talsma, T.; Hallam, P.M. Hydraulic conductivity measurement of forest catchments. Aust. J. Soil Res. 1980, 30, 139–148. [Google Scholar] [CrossRef]
- Zangar, C.N. Theory and Problems of Water Percolation; Engin. Monograph No. 8; The Bureau of Reclamation, US Department of the Interior: Denver, CO, USA, 1953; p. 78. [Google Scholar]
- Philip, J.R. Approximate analysis of the borehole permeameter in unsaturated soil. Water Resour. Res. 1985, 21, 1025–1033. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E.; Clotheir, B.E. The constant head well permeameter: Effect of unsaturated flow. Soil Sci. 1985, 139, 172–180. [Google Scholar] [CrossRef]
- Stephens, D.B.; Neuman, S.P. Vadose zone permeability tests: Steady state results. J. Hydraul. Div. ASCE 1982, 108, 640–659. [Google Scholar] [CrossRef]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Philip, J.R. The theory of infiltration: 2. The profile of infinity. Soil Sci. 1957, 83, 435–448. [Google Scholar] [CrossRef]
- Stephens, D.B. Analysis of Constant Head Borehole Infiltration Tests in the Vadose Zone. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1979. [Google Scholar]
- Narushin, V.G.; Romanov, M.N.; Griffin, D.K. Non-destructive measurement of chicken egg characteristics: Improved formulae for calculating egg volume and surface area. Biosys. Eng. 2021, 201, 42–49. [Google Scholar] [CrossRef]
- Amoozegar, A. A compact constant-head permeameter for measuring saturated hydraulic conductivity of the vadose zone. Soil Sci. Soc. Am. J. 1989, 53, 1356–1361. [Google Scholar] [CrossRef]
- Tee, G.J. Surface Area of Ellipsoid Segment; Department of Mathematics, University of Auckland: Auckland, New Zealand, 2005; Available online: https://www.math.auckland.ac.nz/Research/Reports/Series/539.pdf (accessed on 10 May 2023).
- Wikipedia. Ellipsoid. 2023. Available online: https://en.wikipedia.org/wiki/Ellipsoid (accessed on 10 May 2023).
- Warrick, A.W.; Nielsen, D.R. Spatial variability of soil physical properties in the field. In Applications of Soil Physics; Hillel, D., Ed.; Academic Press: New York, NY, USA, 1980; pp. 319–344. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).