Experimental Investigation of the Two-Phase Loop Thermosyphon Working with Low-GWP Mixtures for Heat Reclaim
Abstract
1. Introduction
2. Experimental Setup and Method
- Single refrigerants: R32 and R600a;
- Mixture of R32/R600a.
- Inlet water temperatures of 25 °C and 32 °C;
- Heater powers of 225, 150, 100, and 50 Watts.
3. Results and Discussion
3.1. Experimental Setup Verification
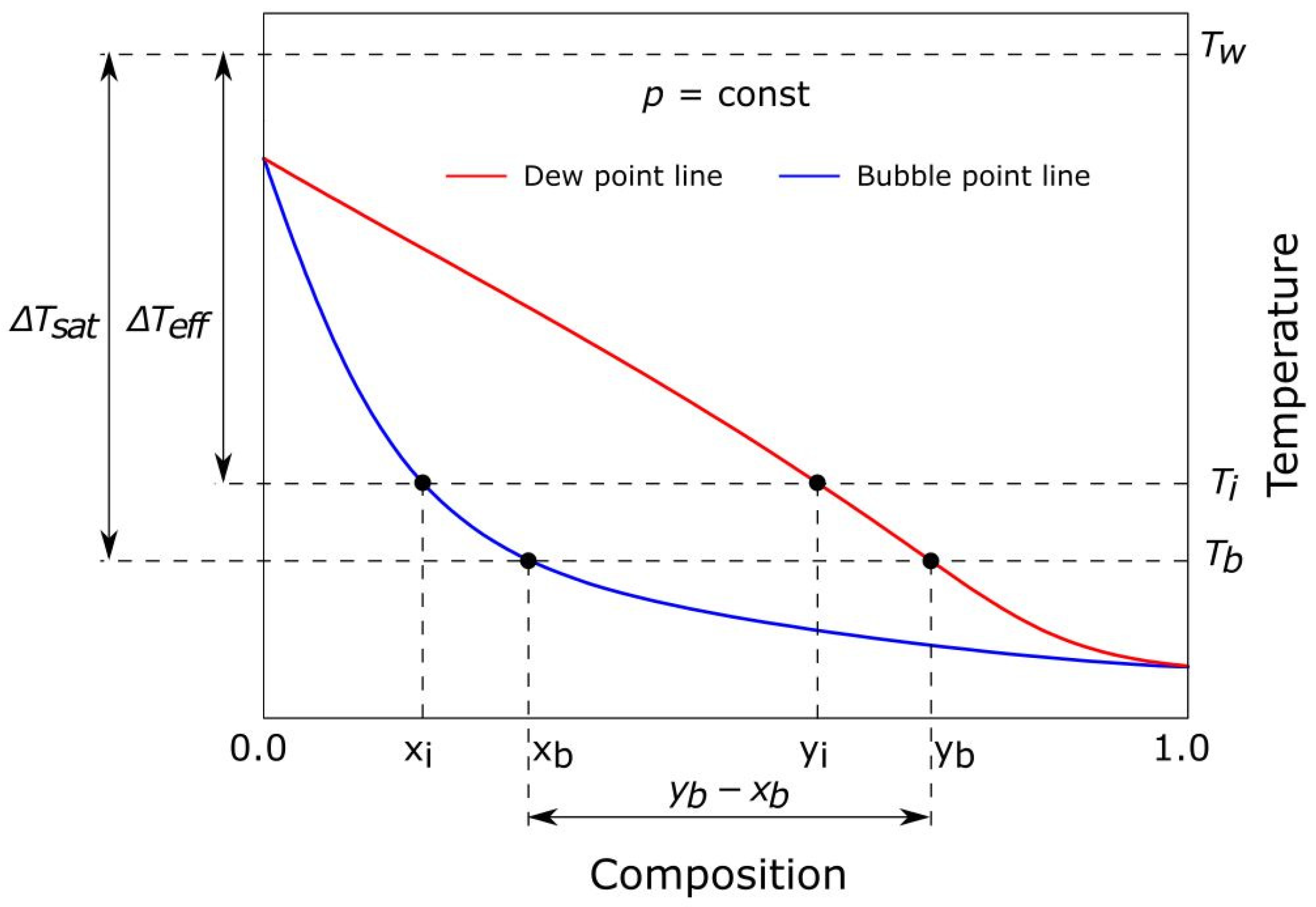
3.2. Working Conditions of the TPTL Operating with Zeotropic Mixture
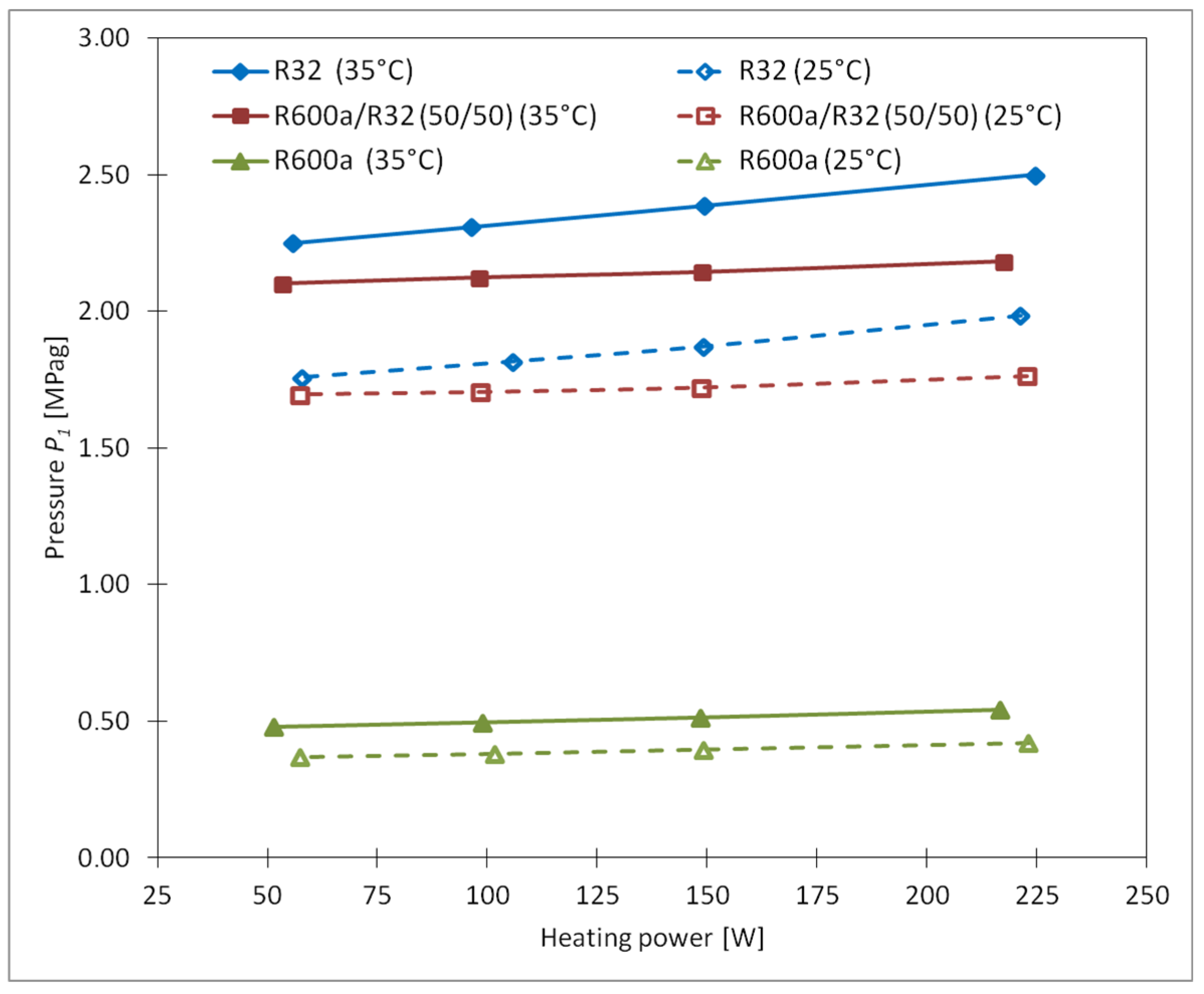
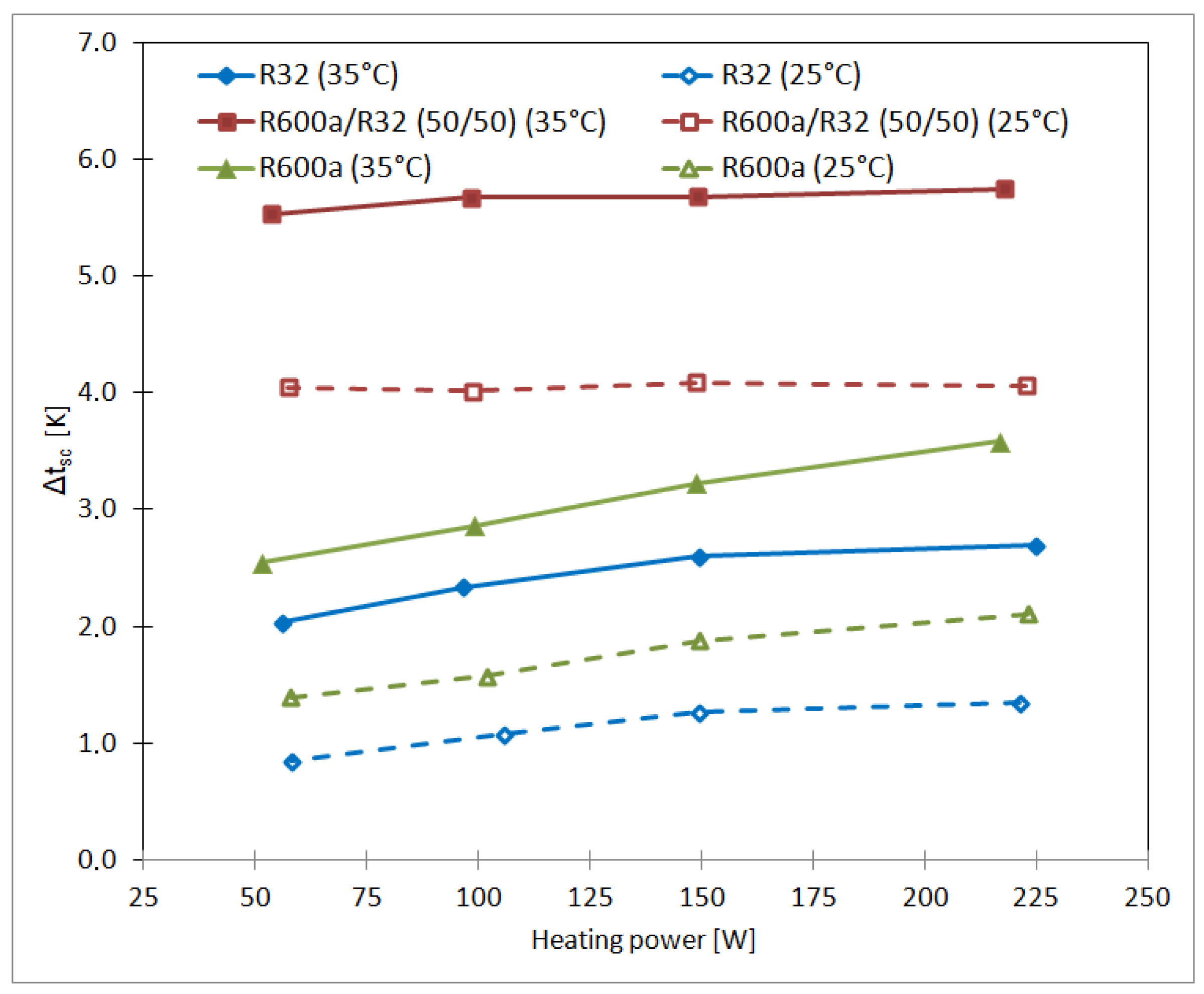
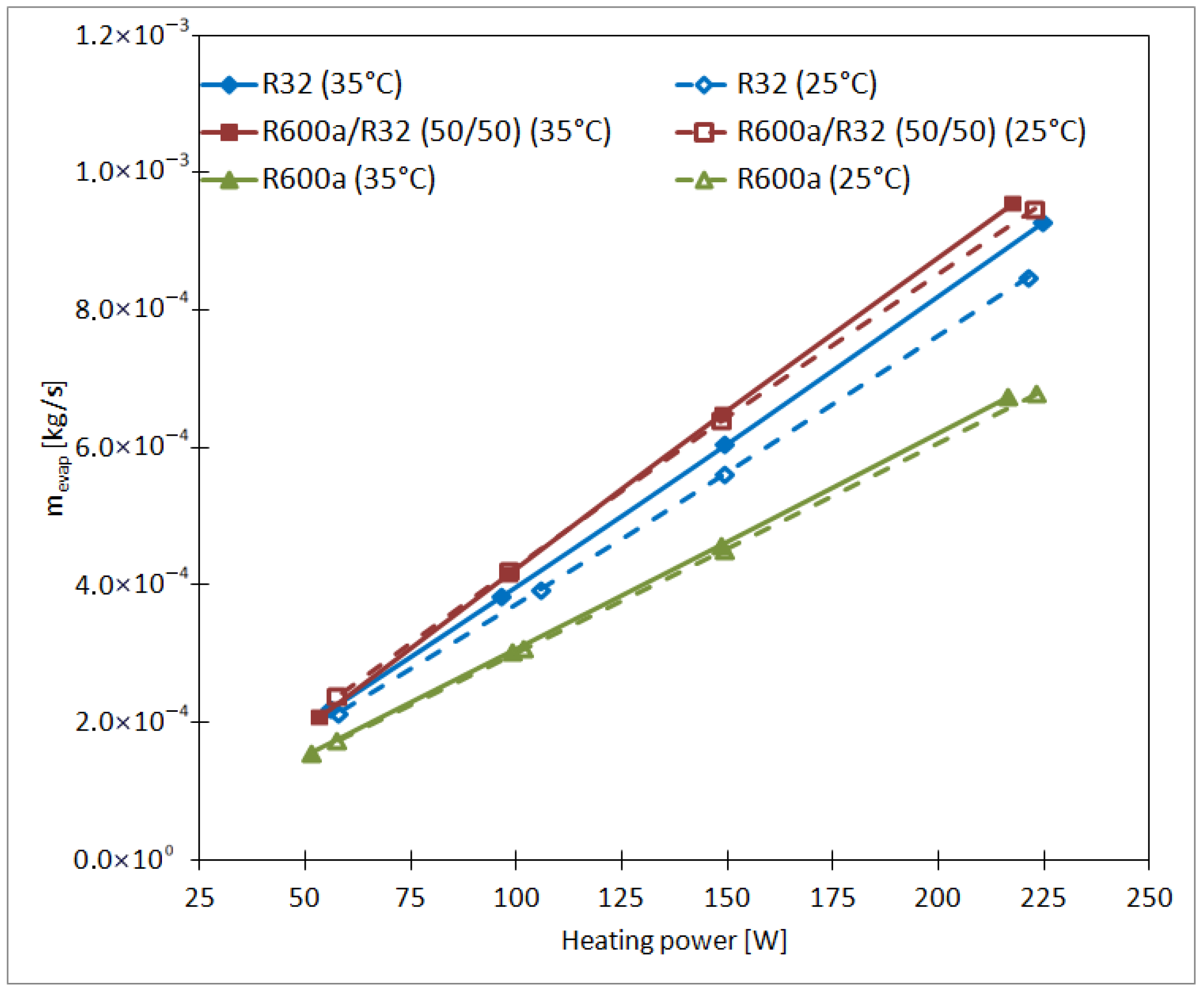
3.3. Thermal Performance Under Varying Heat Loads and Condensing Temperatures
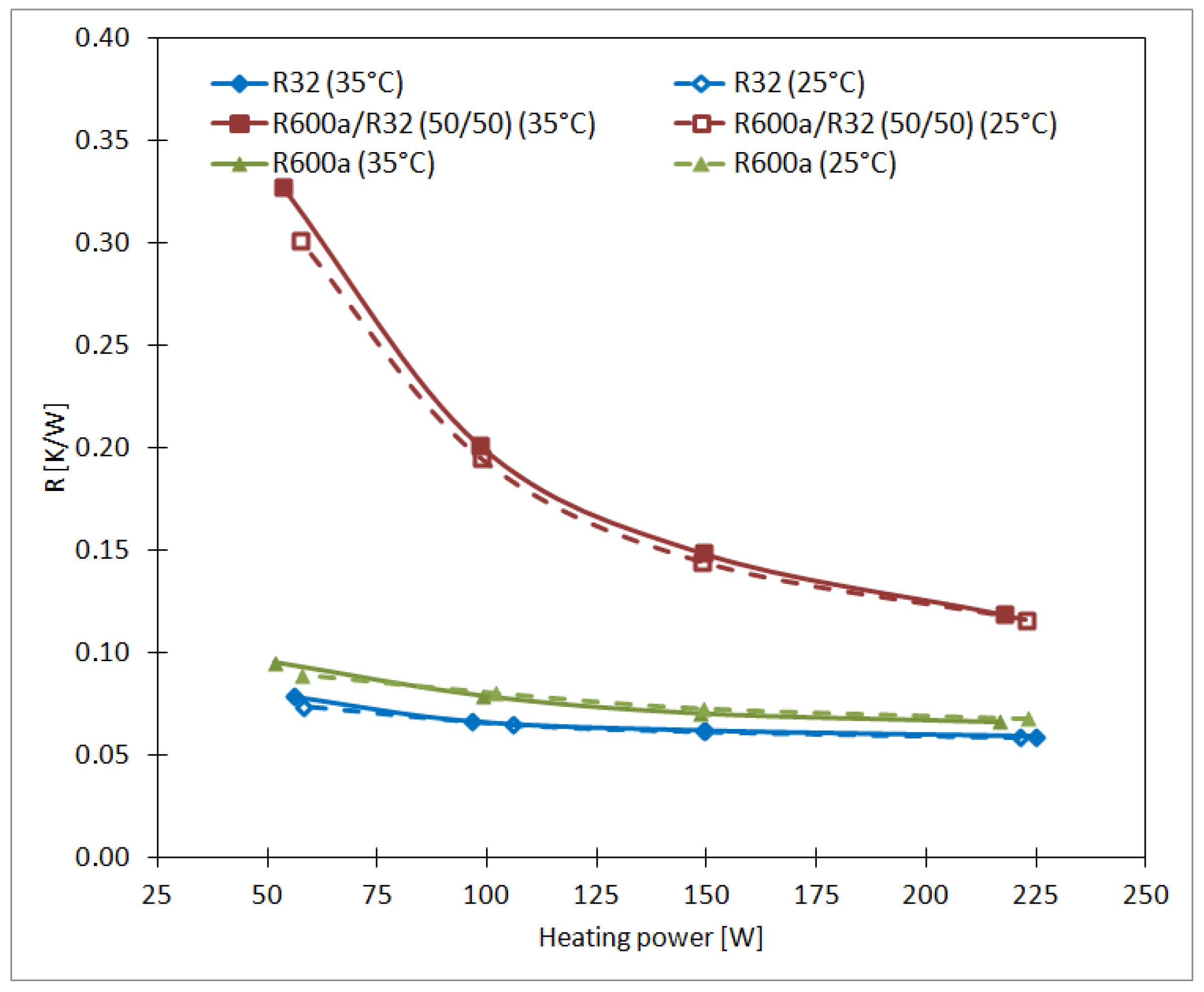
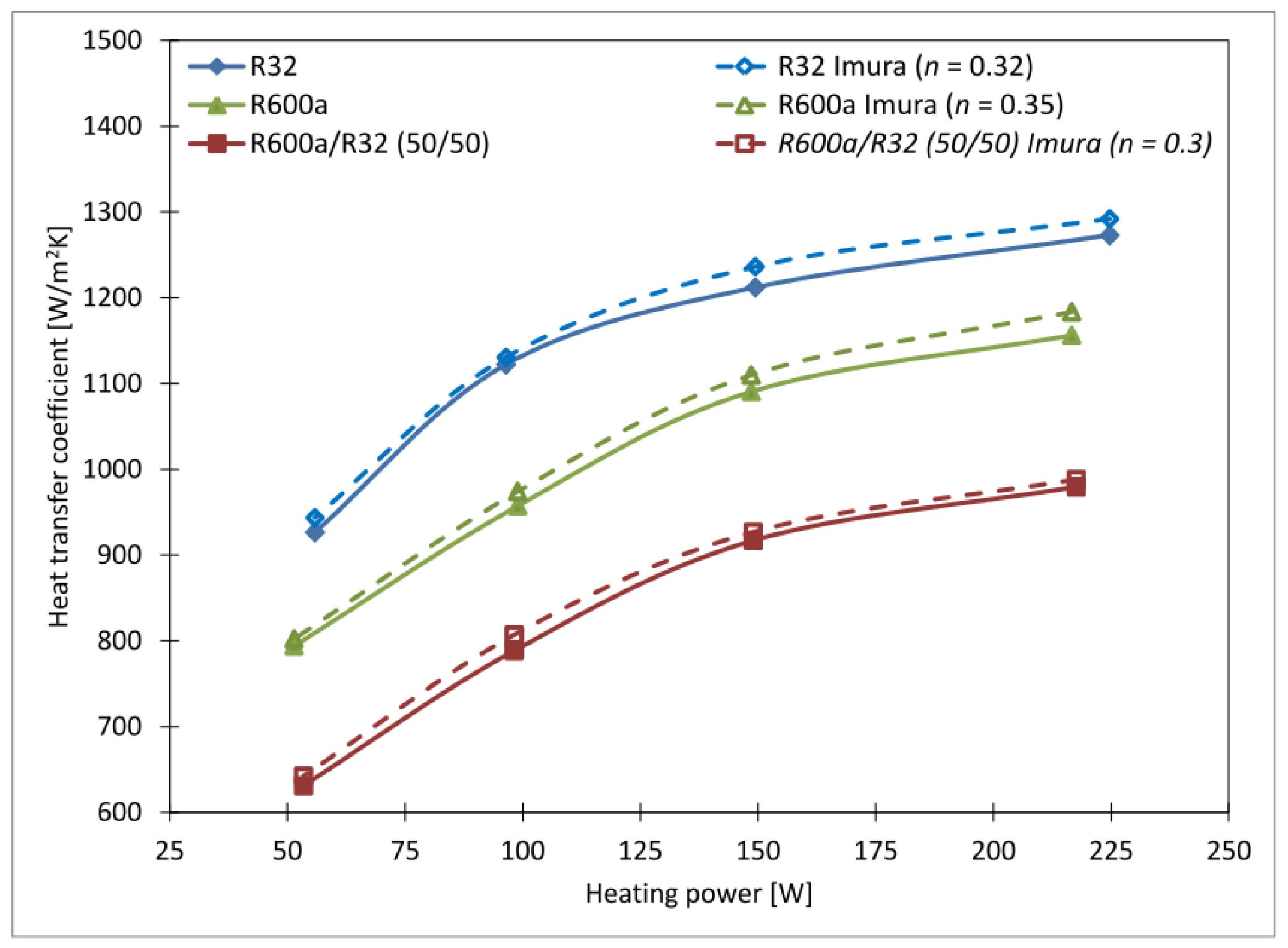
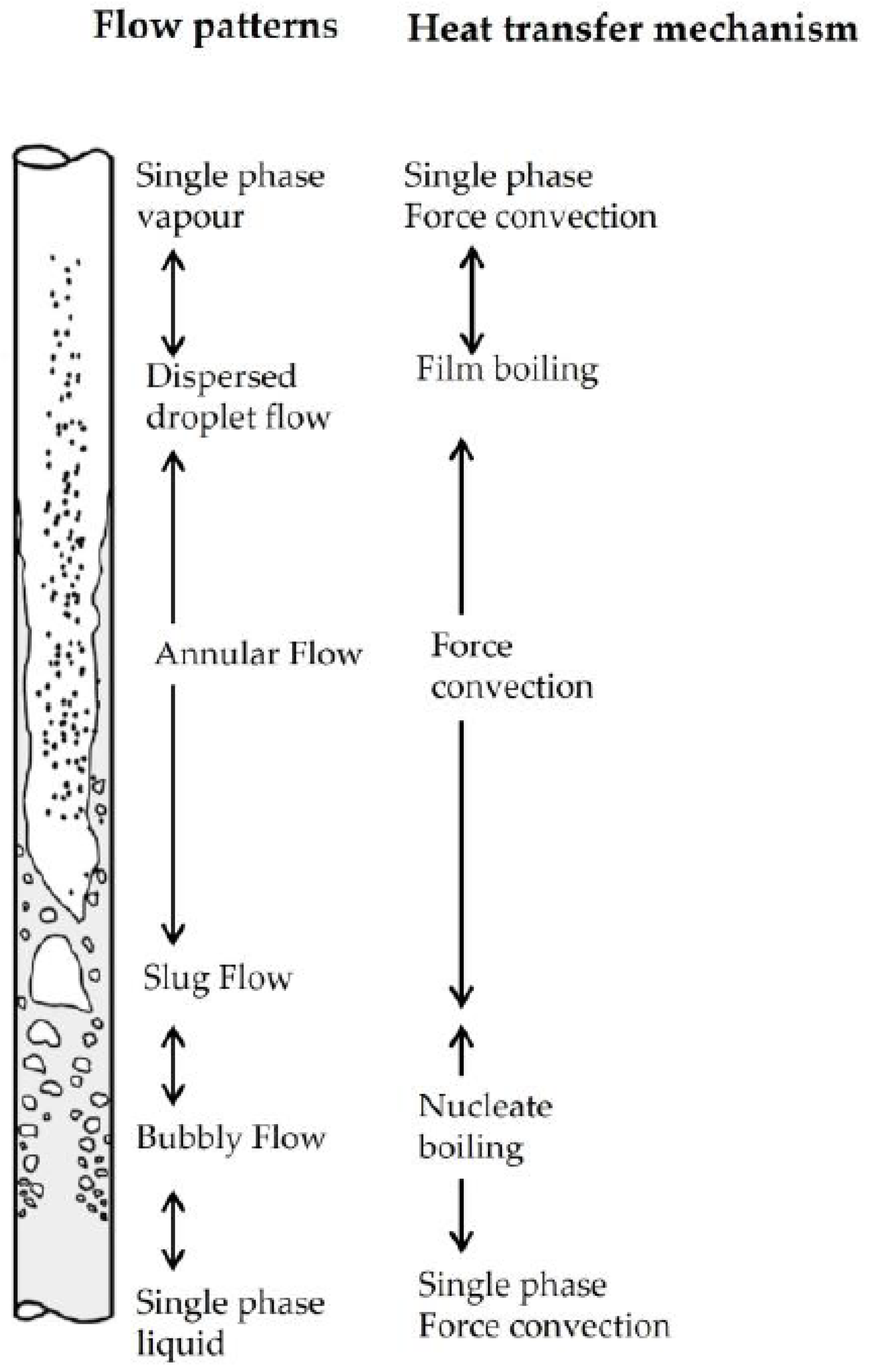
3.4. Boiling-Heat Transfer Coefficient
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ding, T.; He, Z.G.; Hao, T.; Li, Z. Application of separated heat pipe system in data center cooling. Appl. Therm. Eng. 2016, 109, 207–216. [Google Scholar] [CrossRef]
- Yang, S.; Guo, X.; Xu, H.; Tang, F.; Zhang, B.; Zhang, Y. Experimental studies on the heat transfer characteristics and instability of a loop thermosyphon with a vertical flat evaporator for IGBT heat dissipation. Appl. Therm. Eng. 2025, 264, 125524. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, B.; Wu, W.; Shi, W.; Li, X. Heat recovery from internet data centers for space heating based on an integrated air conditioner with thermosyphon. Renew. Energy 2015, 80, 396–406. [Google Scholar] [CrossRef]
- Ding, T.; Wen Cao, H.; Guang He, Z.; Li, Z. Boiling heat transfer characteristics of the R744 coolant in the evaporator of the separated heat pipe system. Int. J. Heat. Mass. Transf. 2017, 113, 1254–1264. [Google Scholar] [CrossRef]
- Ding, T.; Cao, H.W.; He, Z.G.; Li, Z. Visualization experiment on boiling heat transfer and flow characteristics in separated heat pipe system. Exp. Therm. Fluid. Sci. 2018, 91, 423–431. [Google Scholar] [CrossRef]
- Zou, S.; Zhang, Q.; Yue, C.; Wang, J.; Du, S. Study on the performance and free cooling potential of a R32 loop thermosyphon system used in data center. Energy Build. 2022, 256, 111682. [Google Scholar] [CrossRef]
- Tong, Z.; Ding, T.; Li, Z.; Liu, X.H. An experimental investigation of an R744 two-phase thermosyphon loop used to cool a data center. Appl. Therm. Eng. 2015, 90, 362–365. [Google Scholar] [CrossRef]
- Başaran, A. Experimental investigation of R600a as a low GWP substitute to R134a in the closed-loop two-phase thermosyphon of the mini thermoelectric refrigerator. Appl. Therm. Eng. 2022, 211, 118501. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M. NIST Reference Fluid Thermodynamic and Transport Properties—REFPROP; Version 8.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007.
- Calm, J.; Hourahan, G. Refrigerant data update. HPAC Eng. 2007, 79, 50–64. Available online: http://www.hourahan.com/wp/wp-content/uploads/2010/08/2007-Refrig-Update.pdf (accessed on 26 August 2025).
- Gil, B.; Fijałkowska, B. Experimental study of nucleate boiling of flammable, environmentally friendly refrigerants. Energies 2019, 13, 160. [Google Scholar] [CrossRef]
- Tong, Z.; Liu, X.H.; Li, Z.; Jiang, Y. Experimental study on the effect of fill ratio on an R744 two-phase thermosyphon loop. Appl. Therm. Eng. 2016, 99, 302–312. [Google Scholar] [CrossRef]
- Tong, Z.; Liu, X.H.; Jiang, Y. Experimental study of the self-regulating performance of an R744 two-phase thermosyphon loop. Appl. Energy 2017, 186, 1–12. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Li, Y.; Jiang, Y.; Tang, D. Heat transfer and instability characteristics of a loop thermosyphon with wide range of filling ratios. Appl. Therm. Eng. 2019, 151, 262–271. [Google Scholar] [CrossRef]
- Das, K.M.; Guha, A.; Ramgopal, M. Quantitative assessment of various low-GWP zeotropic mixtures of CO2 as the working fluid in two-phase natural circulation loops. Appl. Therm. Eng. 2025, 266, 125512. [Google Scholar] [CrossRef]
- Wang, H.; Bao, Y.; Zhu, S.; Liu, M.; Rao, Z. Experimental research on heat transfer performance of CO2 low temperature heat pipe. Int. J. Heat. Mass. Transf. 2021, 170, 120987. [Google Scholar] [CrossRef]
- Tong, Z.; Wang, W.; Wang, P.; Han, Z.; Yu, H.; Hu, S. Effect of valve regulation on the operating state of a CO2 two-phase thermosyphon loop. Case Stud. Therm. Eng. 2025, 69, 106055. [Google Scholar] [CrossRef]
- Tong, Z.; Zhu, Z.; Wang, W.; Han, Z. Impact of flow resistance on the operational stability of two-phase thermosyphon loop with different working fluids. Therm. Sci. Eng. Prog. 2025, 60, 103463. [Google Scholar] [CrossRef]
- Hu, J.; He, Y.; Wang, X.; Liu, J.; Liu, B.; Liu, L. Experimental study on the loop thermosyphon cooling system for IGBT in high-speed trains. Appl. Therm. Eng. 2025, 274, 126613. [Google Scholar] [CrossRef]
- Qu, J.; Zhao, Y.; Hua, Y.; Yang, W.; Gao, S. Comparative study of operational characteristics for two-phase loop thermosyphons with and without pump assistant: Heat transfer performance and high-speed visualization observation. Appl. Therm. Eng. 2025, 271, 126382. [Google Scholar] [CrossRef]
- Corigliano, O.; Algieri, A.; Fragiacomo, P. Turning Data Center Waste Heat into Energy: A Guide to Organic Rankine Cycle System Design and Performance Evaluation. Appl. Sci. 2024, 14, 6046. [Google Scholar] [CrossRef]
- Zhao, S.C.; Zhang, Z.; Zhao, R.; Wu, T.; Zhang, X.; Liu, Z.C.; Liu, W. An R1234ze(E) loop heat pipe with flat-plate evaporator for cooling electronic devices. Therm. Sci. Eng. Prog. 2023, 42, 101935. [Google Scholar] [CrossRef]
- Marcinichen, J.B.; Olivier, J.A.; Thome, J.R. On-chip two-phase cooling of datacenters: Cooling system and energy recovery evaluation. Appl. Therm. Eng. 2012, 41, 36–51. [Google Scholar] [CrossRef]
- Brendel, L.P.M.; Bernal, S.N.; Widmaier, P.; Roskosch, D.; Arpagaus, C.; Bardow, A.; Bertsch, S.S. High-glide refrigerant blends in high-temperature heat pumps: Part 1—Coefficient of performance. Int. J. Refrig. 2024, 165, 84–96. [Google Scholar] [CrossRef]
- Chen, X.; Ding, T.; Wang, X.; Li, Z. Research on energy saving potentials using pure and zeotropic refrigerants in data center cooling systems. Case Stud. Therm. Eng. 2024, 57, 104324. [Google Scholar] [CrossRef]
- Naresh, Y.; Balaji, C. Experimental investigations of heat transfer from an internally finned two phase closed thermosyphon. Appl. Therm. Eng. 2017, 112, 1658–1666. [Google Scholar] [CrossRef]
- Long, Z.Q.; Zhang, P. Heat transfer characteristics of thermosyphon with N2-Ar binary mixture working fluid. Int. J. Heat. Mass. Transf. 2013, 63, 204–215. [Google Scholar] [CrossRef]
- Guichet, V.; Almahmoud, S.; Jouhara, H. Nucleate pool boiling heat transfer in wickless heat pipes (two-phase closed thermosyphons): A critical review of correlations. Therm. Sci. Eng. Prog. 2019, 13, 100384. [Google Scholar] [CrossRef]
- Liu, Z.; Winterton, R.H.S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation. Int. J. Heat. Mass. Transf. 1991, 34, 2759–2766. [Google Scholar] [CrossRef]
- Imura, H.; Kusuda, H.; Ogata, J.-I.; Miyazaki, T.; Sakamoto, N. Heat Transfer in Two-Phase Closed-Type Thermosyphons. Heat. Transf. Jpn. Res. 1979, 45, 712–722. [Google Scholar]
- Louahlia-Gualous, H.; Le Masson, S.; Chahed, A. An experimental study of evaporation and condensation heat transfer coefficients for looped thermosyphon. Appl. Therm. Eng. 2017, 110, 931–940. [Google Scholar] [CrossRef]
- Arora, C.P. Refrigeration and Air Conditioning; McGraw Hill Education: Noida, India, 2009. [Google Scholar]
- Ding, T.; Cao, H.W.; He, Z.G.; Li, Z. Experiment research on influence factors of the separated heat pipe system, especially the filling ratio and Freon types. Appl. Therm. Eng. 2017, 118, 357–364. [Google Scholar] [CrossRef]
- Ling, L.; Zhang, Q.; Yu, Y.; Liao, S.; Sha, Z. Experimental study on the thermal characteristics of micro channel separate heat pipe respect to different filling ratio. Appl. Therm. Eng. 2016, 102, 375–382. [Google Scholar] [CrossRef]
- Ma, L.; Shang, L.; Zhong, D.; Ji, Z. Experimental investigation of a two-phase closed thermosyphon charged with hydrocarbon and Freon refrigerants. Appl. Energy 2017, 207, 665–673. [Google Scholar] [CrossRef]
- Park, K.J.; Jung, D. Nucleate boiling heat transfer coefficients of mixtures containing propane, isobutane and HFC134a. J. Mech. Sci. Technol. 2006, 20, 399–408. [Google Scholar] [CrossRef]
- Hernaiz, M.; Elexpe, I.; Aranzabe, E.; Aguayo, A.T. Flow Boiling Heat Transfer; Experimental Study of Hydrocarbon Based Nanorefrigerant in a Vertical Tube. Nanomaterials 2023, 13, 2230. [Google Scholar] [CrossRef] [PubMed]
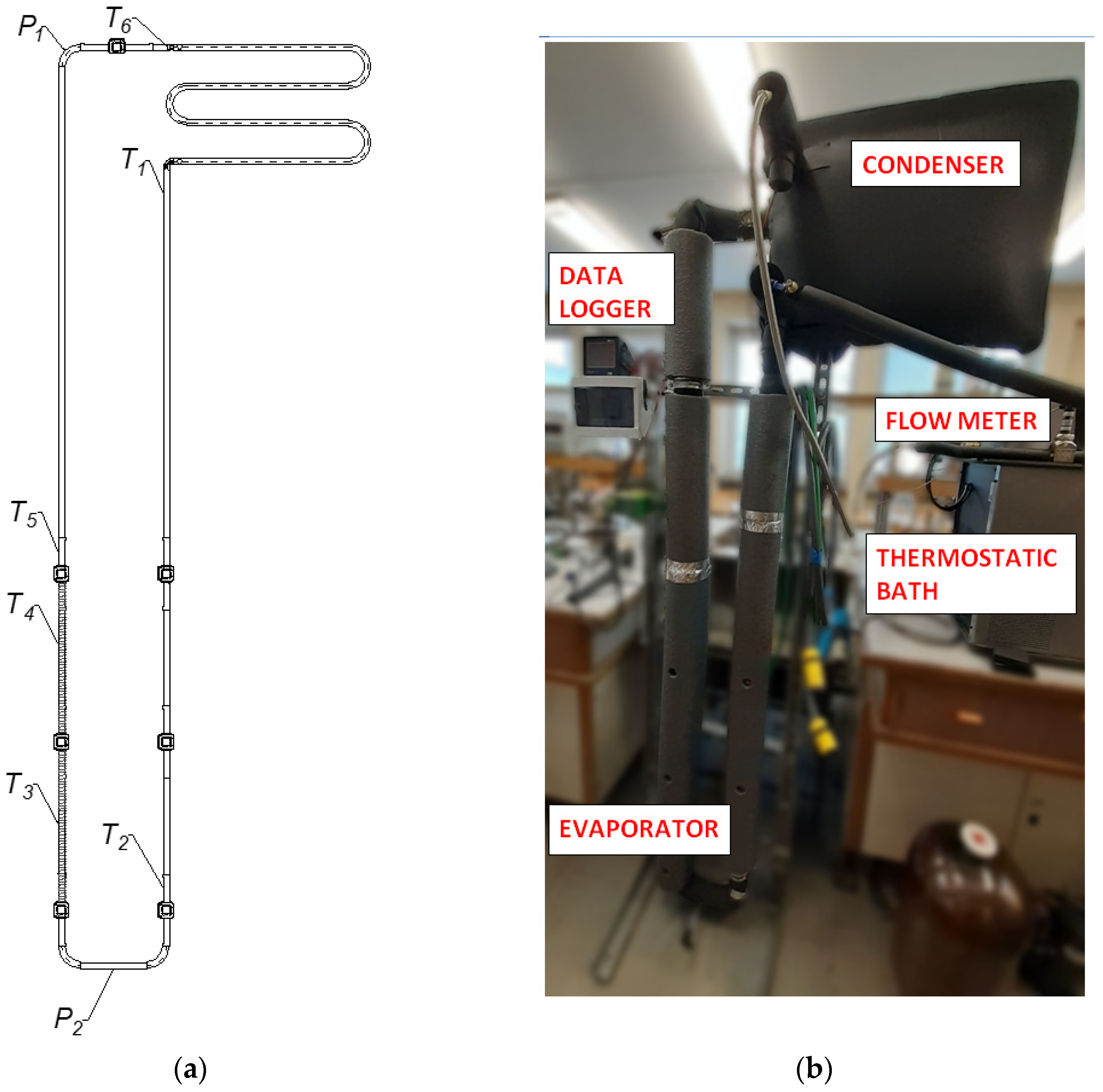
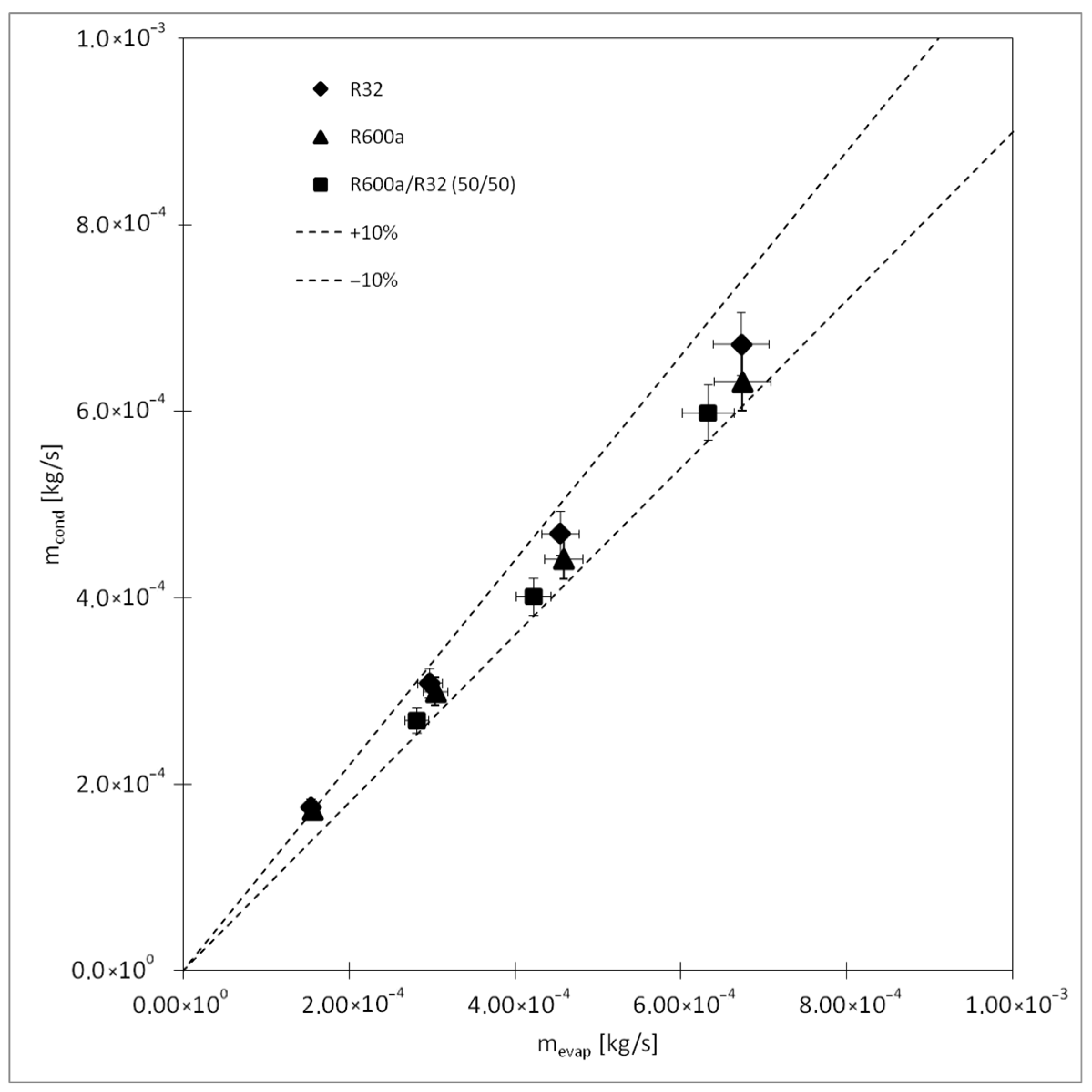
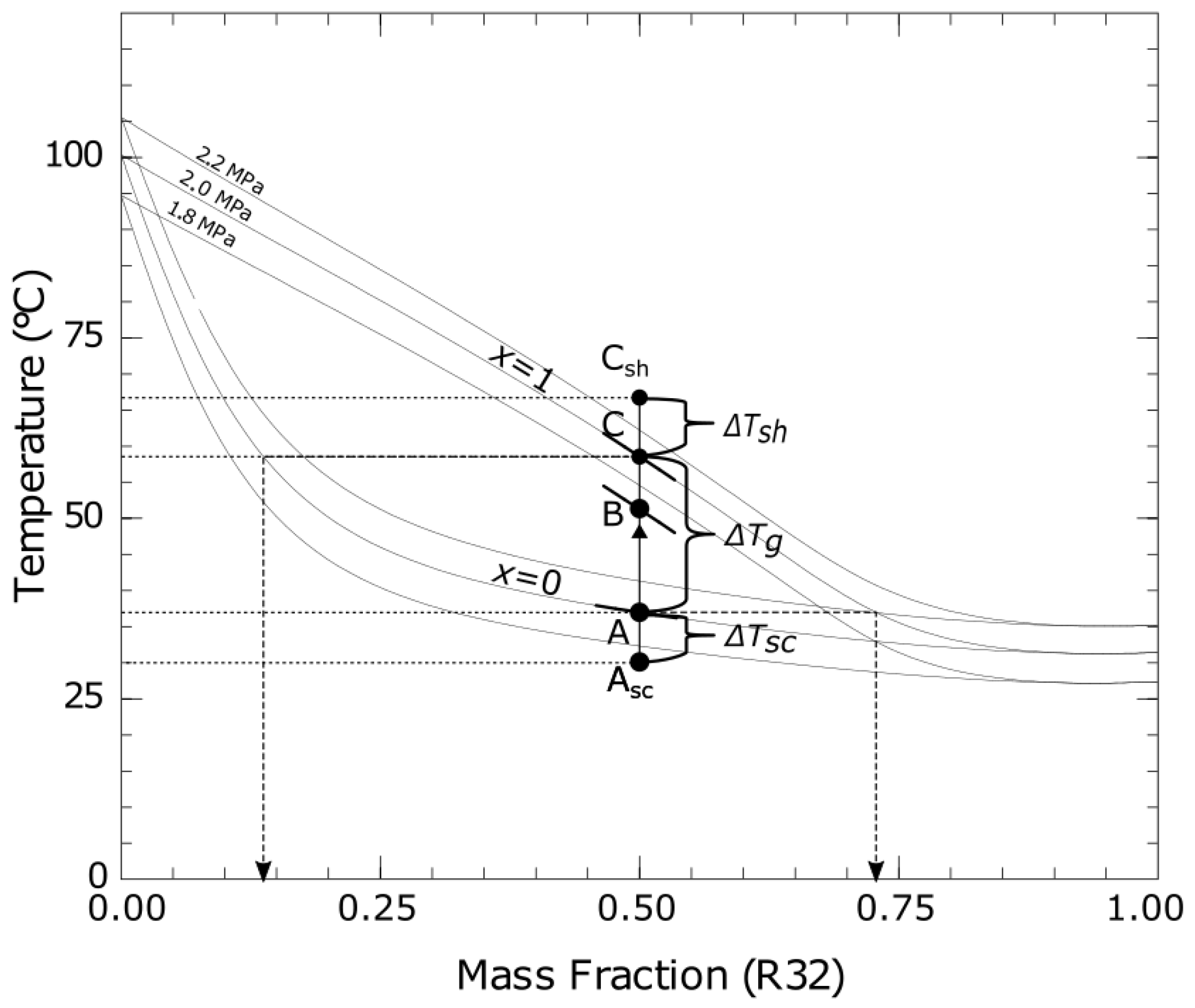
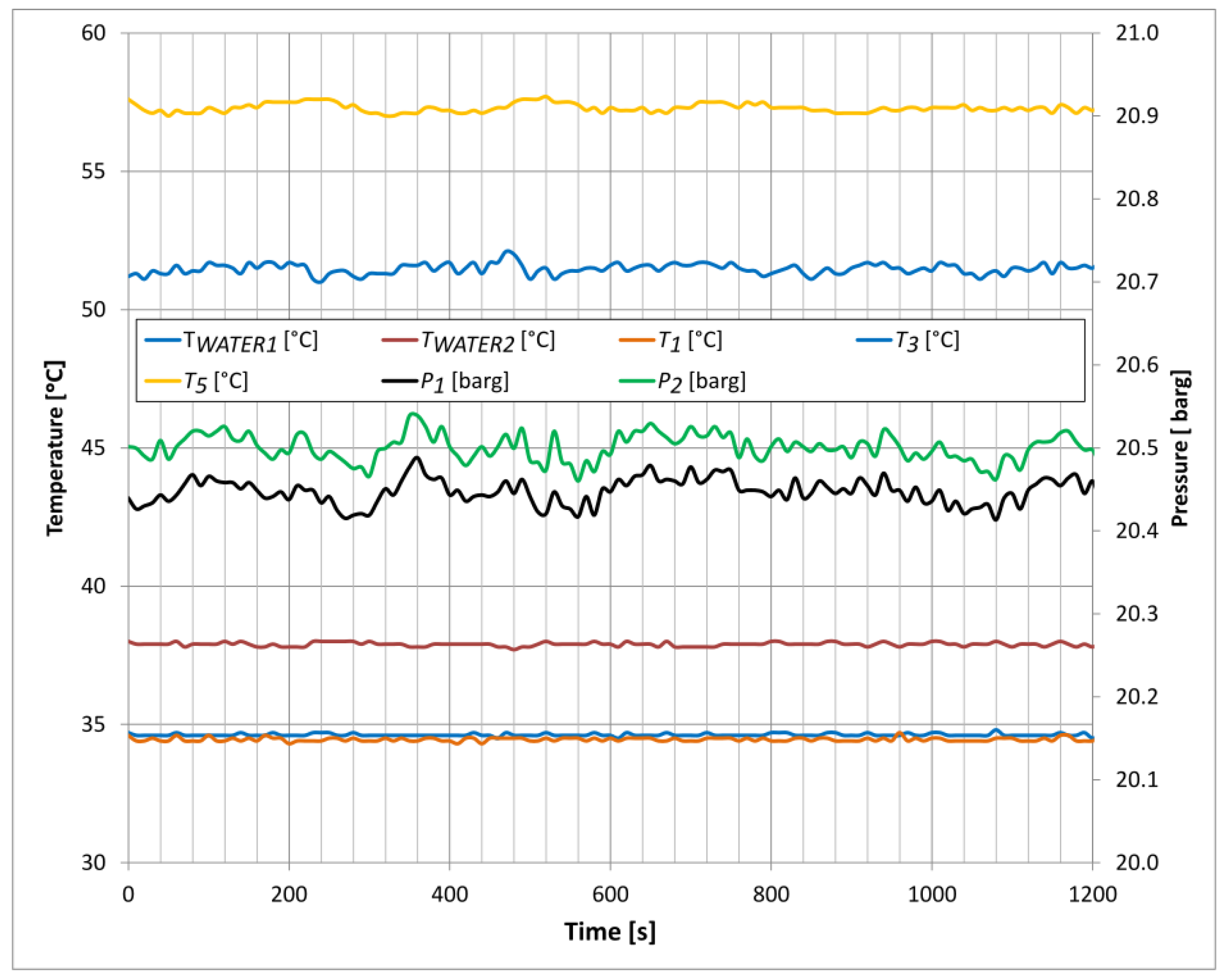

| Parameter | Instrument | Uncertainty |
|---|---|---|
| Temperature | Pt100 M222 A class resistor (Heraeus, Hanau, Germany) | ±0.1 K |
| Pressure | 0–3 MPa pressure transducer (Sanhua, Shaoxing, China) | ±0.015 MPa |
| Power | F&F LE-01MR power transducer (F&F, Pabianice, Poland) | ±2 W |
| Refrigerant | Mass [kg] | Density [kg/m3] | Volume [m3] | FR |
|---|---|---|---|---|
| R32 | 0.15 | 981.4 | 0.000153 | 1.01 |
| R600a | 0.0858 | 556.9 | 0.000154 | 1.02 |
| R600a/R32 (50/50) | 0.1024 | 657.1 | 0.000156 | 1.03 |
| - | T5 | x | d0 | T5 | x | d0 | T5 | ΔTsh | d0 |
|---|---|---|---|---|---|---|---|---|---|
| - | R600a | R600a/R32 | R32 | ||||||
| 225 | 40.6 | 1.0 | 1.28 | 58.0 | 0.87 | 0.83 | 40.2 | 0 | 0.74 |
| 150 | 38.5 | 1.0 | 1.29 | 57.2 | 0.87 | 0.83 | 38.1 | 0 | 0.76 |
| 100 | 37.1 | 1.0 | 1.30 | 57.5 | 0.89 | 0.84 | 46.5 | 9.3 | 0.77 |
| 55 | 35.8 | 1.0 | 1.31 | 59.5 | 0.97 | 0.93 | 50.6 | 14.4 | 0.78 |
| - | MAD | RMS | MAD | RMS | MAD | RMS |
|---|---|---|---|---|---|---|
| Refrigerant | R600a | R32 | R600a/R32 | |||
| Imura | 1.014 | 1.172 | 2.914 | 3.102 | 1.389 | 1.394 |
| Imura n | 0.017 | 0.018 | 0.015 | 0.016 | 0.015 | 0.016 |
| Cooper | 1.317 | 1.417 | 2.860 | 3.034 | 4.276 | 4.396 |
| Arora | 0.282 | 0.331 | 0.547 | 0.714 | 0.702 | 0.889 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobieraj, M.; Ksionek, D.; Kamiński, M.; Karczmarczyk, F. Experimental Investigation of the Two-Phase Loop Thermosyphon Working with Low-GWP Mixtures for Heat Reclaim. ChemEngineering 2025, 9, 131. https://doi.org/10.3390/chemengineering9060131
Sobieraj M, Ksionek D, Kamiński M, Karczmarczyk F. Experimental Investigation of the Two-Phase Loop Thermosyphon Working with Low-GWP Mixtures for Heat Reclaim. ChemEngineering. 2025; 9(6):131. https://doi.org/10.3390/chemengineering9060131
Chicago/Turabian StyleSobieraj, Michał, Dariusz Ksionek, Michał Kamiński, and Filip Karczmarczyk. 2025. "Experimental Investigation of the Two-Phase Loop Thermosyphon Working with Low-GWP Mixtures for Heat Reclaim" ChemEngineering 9, no. 6: 131. https://doi.org/10.3390/chemengineering9060131
APA StyleSobieraj, M., Ksionek, D., Kamiński, M., & Karczmarczyk, F. (2025). Experimental Investigation of the Two-Phase Loop Thermosyphon Working with Low-GWP Mixtures for Heat Reclaim. ChemEngineering, 9(6), 131. https://doi.org/10.3390/chemengineering9060131





