Abstract
To address the challenges of low displacement efficiency and gas channeling in the Lukqin thick oil reservoir, characterized by high viscosity (286 mPa·s) and strong heterogeneity (permeability contrast 5–10), this study systematically investigated water flooding and foam flooding mechanisms using a large-scale 2D sandpack model (5 m × 1 m × 0.04 m). Experimental results indicate that water flooding achieves only 30% oil recovery due to a mobility ratio imbalance (M = 128) and preferential channeling. In contrast, foam flooding enhances recovery by 15–20% (final recovery: 45%) through synergistic mechanisms of dynamic high-permeability channel plugging and mobility ratio optimization. By innovatively integrating electrical resistivity tomography with HSV color mapping, this work achieves the first visualization of foam migration pathways in meter-scale heterogeneous reservoirs at a spatial resolution of ≤0.5 cm, reducing monitoring costs by approximately 30% compared to conventional CT techniques. Key controlling factors for gas channeling (injection rate, foam quality, permeability contrast) are identified, and a nonlinear predictive model for plugging strength ((S = 0.70C0.6 kr−0.28) (R2 = 0.91)) is established. A composite optimization strategy—combining high-concentration slugs (0.7% AOS), salt-resistant polymer-enhanced foaming, and multi-round profile control—achieves a 67% reduction in gas channeling. This study elucidates the dynamic plugging mechanisms of foam flooding in heterogeneous thick oil reservoirs through large-scale physical simulations and data fusion, offering direct technical guidance for optimizing foam flooding operations in the Lukqin Oilfield and analogous reservoirs.
1. Introduction
Foam fluid technology has been applied in oilfield operations for nearly three decades as an emerging enhanced oil recovery (EOR) technique. Its applications in oil and gas development encompass various domains including foam drilling, foam cementing, foam acidizing, foam fracturing, foam–sand flushing, foam profile control, and foam flooding, all demonstrating significant effectiveness [1,2,3,4]. In recent years, against the dual background of escalating global energy demands and an increasing complexity in hydrocarbon resource development, improving recovery rates in complex reservoirs has become a critical challenge for energy security [5]. The Lukeqin thick oil reservoir in China, characterized by high viscosity (286 mPa·s) and strong heterogeneity (permeability contrast 5–10), faces persistent challenges of fluid channeling and low sweep efficiency during development [6,7]. Although conventional water flooding demonstrated certain effectiveness during initial development, the inherent mobility ratio imbalance causes injected water to preferentially channel through high-permeability pathways, resulting in less than 30% oil recovery efficiency in low-permeability zones [8,9]. While foam flooding technology offers new perspectives for thick reservoir development through its mobility control and dynamic plugging capabilities, its operational mechanisms are constrained by complex factors, including reservoir heterogeneity and gas channeling [10]. Current research predominantly relies on small-scale experiments and theoretical models, failing to accurately reflect foam plugging efficiency and gas channeling evolution in meter-scale heterogeneous reservoirs, leading to significant technical bottlenecks in field applications [11,12,13,14].
As a core technology for deep profile modification and water control, foam flooding has achieved remarkable progress in enhancing oil recovery in heterogeneous reservoirs [15]. Traditional profile control methods (e.g., polymer gels) provide temporary high-permeability zone plugging but suffer from shear degradation risks and lack dynamic self-adaptability [16]. In contrast, foam systems significantly improve channeling inhibition through synergistic gas–liquid phase regulation, combining the Jamin effect and mobility control [17]. Regarding salt tolerance of foam systems, Farajzadeh et al. [18] experimentally verified the stability of alpha-olefin sulfonate (AOS) foaming agents in high-salinity environments, though without considering oil phase interactions. Yu et al. [19] proposed a nanoparticle–surfactant synergistic stabilization mechanism, enhancing foam salinity tolerance to 20% NaCl, offering new solutions for high-salinity reservoirs. Addressing dynamic profile control requirements in heterogeneous formations, Zhao et al. [20] through flooding experiments revealed that traditional foam systems experience over 60% reduction in channel plugging efficiency when permeability contrast exceeds 10:1, necessitating pre-crosslinked particle–foam composite systems for staged deep plugging [21]. In numerical simulation, Kovscek’s plugging intensity model [22] performs well in homogeneous reservoirs, while Almajid et al. [9] identified the need for dynamic wettability correction factors in pore-scale heterogeneous systems. Notably, existing physical simulation apparatuses (generally < 1 m) overestimate foam dispersion rates by 35% according to Wang’s meter-scale 3D experiments [23], with Guo’s similarity criteria [24] revealing significant scale effects in channel evolution. Although Hirasaki et al. [25] demonstrated foam profile control can increase sweep efficiency from 0.42 to 0.78 in sandstone cores, salinity fluctuation impacts on long-term effectiveness remain unaddressed. Current research urgently requires integration of large-scale experiments [26,27,28,29] with multi-scale numerical models [30,31] to elucidate salinity–permeability–scale coupling mechanisms in dynamic foam profile control, which holds crucial engineering value for efficient development of high-salinity heterogeneous reservoirs [32,33,34].
This study focuses on the Lukeqin thick reservoir, employing a 2D large-scale sandpack model integrated with electrical resistance tomography and high-speed imaging to systematically investigate water flooding and foam flooding mechanisms. Three critical issues are addressed: (1) dynamic evolution of channeling pathways, (2) boundary conditions for foam plugging efficiency, and (3) technical approaches for gas channeling suppression. By quantifying relationships between permeability contrast, foam concentration, and plugging intensity, a multi-parameter coupling optimization strategy is developed. Key innovations include:
- (1)
- A 2D large-scale sandpack model (5 m × 1 m × 0.04 m) integrating resistivity tomography and high-speed imaging, enabling visualization of foam flooding mechanisms in meter-scale heterogeneous systems.
- (2)
- A nonlinear predictive model linking plugging strength (S) to foam concentration (C) and permeability contrast (kr):achieving superior accuracy (error < 5%) compared to existing models [35,36].S = 0.7C0.6·kr−0.28 (R2 = 0.91),
- (3)
- A cost-effective composite strategy combining high-concentration slugs (0.7% AOS), salt-resistant polymer-enhanced foaming, and multi-round profile control, suppressing gas channeling by 67%.
This work bridges the gap between laboratory-scale experiments and field-scale EOR operations, offering both theoretical insights and actionable technical guidelines for heterogeneous reservoirs [37].
2. Experimental Method
2.1. Experimental System Design
The experimental system consists of a high-pressure constant-flow/constant-pressure pump (HAS-80HSB), a gas booster unit (GDT7/30, 30 MPa), and a multidimensional visualization monitoring module. The sand-filled model employs a modular spliced structure (5 m × 1 m × 0.04 m) packed with 200-mesh quartz sand (permeability range: 500–1000 mD). The strong heterogeneity of the Lukqin oil reservoir was replicated through a stratified compaction process under 25–29 MPa confining pressure (Table 1). The model body comprises five standardized physical simulation units equipped with a 210-node high-density resistivity array, a 45-channel distributed pressure sensor network, and a high-speed camera system, enabling dynamic monitoring of multiphysics-coupled seepage processes (Figure 1). The experimental setup configuration is illustrated in Figure 2.

Table 1.
Sand-filled model parameters.
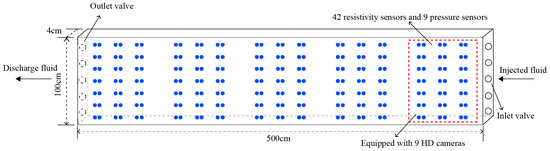
Figure 1.
Schematic diagram of a two-dimensional visualization of the large model. (The blue dots represent resistivity sensors, and the red dashed frames represent each smaller model of 1 m × 1 m × 0.04 m).
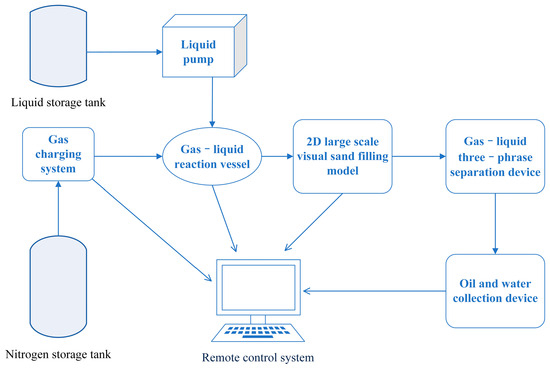
Figure 2.
Connection diagram of the test device. (The thin blue arrows represent that they can be remotely controlled by the terminal system.)
The modular design ensures high-precision monitoring of heterogeneous models. The high-pressure pump and gas booster system operate synergistically to maintain stable alternating gas–liquid injection (gas–liquid ratio (GLR) = 1:1). Notably, the custom-designed 210-node resistivity monitoring array, synchronized with the high-speed camera system, achieves centimeter-scale resolution tracking of foam migration paths for the first time. This innovation overcomes the limitations of conventional CT scanning in cost-effectiveness and scalability, providing critical technical support for elucidating gas invasion dynamics in heterogeneous reservoirs [20].
2.2. Fluid Configuration and Displacement Scheme
2.2.1. Simulated Fluid
As shown in Figure 3, when simulating crude oil formulation, the process begins with calculating the formulation based on target parameters (12.3% thickener mass fraction; viscosity of 286 mPa·s at 25 °C). Precise amounts of No. 10 white oil and thickener are weighed. Under a constant temperature of 25 °C, the components are gradually mixed: initial low-speed stirring for pre-mixing, followed by high-shear dispersion to eliminate particulate aggregates, and aging the system by standing for 12–24 h. Subsequently, viscosity is measured using a rotational viscometer in a 25 °C-controlled environment, ensuring the average of three consecutive measurements closely matches the target value. Homogeneity and long-term stability are verified through standardized tests. Critical controls include shear rate (to prevent thickener degradation), temperature precision, and raw material compatibility, ultimately yielding a stable simulated crude oil system that meets specifications.
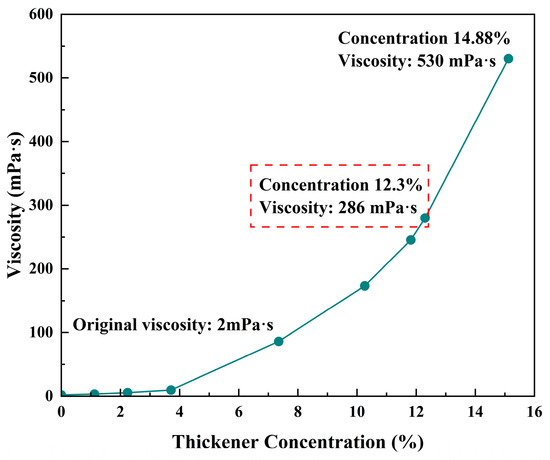
Figure 3.
Curve of the relationship between thickener concentration and white oil viscosity.
When preparing high-salinity brine with a total salinity of 160,599 mg/L, the formulation first involves precise calculation of various salts based on the ionic composition of formation water from Lukqen Oilfield, with correction for water of crystallization content. Ultrapure water was used to dissolve salts step by step in ascending order of solubility, with thorough stirring until complete dissolution at each step to avoid double decomposition precipitation. After adding 0.01% EDTA-2Na stabilizer, the solution was degassed via ultrasonic treatment and filtered. Ionic concentrations were verified through conductivity calibration and ion chromatography, with adjustments made by adding supplements when deviations exceeded 2%. The ionic compositions are detailed in Table 2.

Table 2.
Mineral composition of simulated formation water (mg/L).
To formulate the high salt-resistant foam system, an aqueous solution of 0.35% (mass fraction) α-olefin sulfonate was first used as the base fluid, which was successively dissolved in simulated formation water. Subsequently, 0.2% salt-resistant polyacrylamide was added to enhance stability. After the base fluid was thoroughly mixed by low-speed stirring, nitrogen was injected through a dynamic foam generator at a gas–liquid ratio of 1:1 to generate homogeneous foam. Aging tests revealed that the foam system exhibited a half-life of 92 min under conditions of 25 °C and a salinity of 1.5 × 105 mg/L. Microscopic analysis showed a liquid film thickness of approximately 10 nm with uniform distribution, indicating that this system is suitable for high-temperature and high-salinity reservoir environments and can enhance the plugging capability and stability of foam flooding.
2.2.2. Displacement Process
- (1)
- Model saturation
In the model water phase and oil phase saturation experiment, the model was first vacuum degassed for 4 h. Simulated formation water was injected at a constant rate of 10 mL/min until pore pressure stabilized. Porosity (34.28%) was calculated by the mass difference method, and water phase permeability was determined based on Darcy’s law. The model was then placed horizontally, and simulated crude oil was injected at 3.3 mL/min until the oil cut at the outlet exceeded 98%, allowing calculation of the initial oil saturation (72.3%). Key controls included: real-time monitoring of pressure gradients, oil cut calibration (calibration curve R2 > 0.99), and cross-validation of pore volume. After oil phase saturation, the model was aged for 24 h to achieve oil–water distribution equilibrium, ensuring compliance with SY/T 5345-2007 [38] standards and providing high-precision initial parameters for subsequent displacement.
- (2)
- Experimental process
In the comparative experiment between water flooding and foam flooding, the water flooding test was conducted in vertical placement mode with constant-rate water injection at 10 mL/min until the water cut reached 98%. Axial pressure gradients, resistivity distributions, and channeling occurrences were recorded synchronously to calculate the oil recovery factor and sweep efficiency. The foam flooding test focused on alternating gas–liquid injection using a 0.5% AOS + 0.3% nano-SiO2 salt-resistant base fluid, with a gas injection pressure ≤ 6 MPa. Real-time monitoring included testing resistivity at each measuring point in the model and pressure differences between adjacent points and between the first and last ends. Foam plugging dynamics were tracked in real time to optimize injection parameters (gas–liquid ratio, concentration) for suppressing gas channeling.
2.3. Data Acquisition and Analysis Methods
During the experiment, model pressure, flow rate, and water cut were real-time collected via a remote control system at a sampling interval of 300 s. Seepage paths were analyzed by inverting resistivity nephograms and integrating with the HSV color model to resolve fluid saturation distributions and their patterns. Additionally, foam behavior was characterized by extracting feature parameters (e.g., bubble size, migration velocity) from the high-speed camera images using OpenCV algorithms. After normalizing all data, a multiple regression model was employed to quantify the quantitative relationships among permeability contrast, foam concentration, and plugging intensity (R2 > 0.92), aiming to reveal the key control mechanisms of foam flooding in heterogeneous reservoirs.
3. Results and Analysis
3.1. Discussion on the Law and Mechanism of Water Drive Development
The results of the waterflooding test show that in the vertical displacement mode, injected water preferentially fingered into high-permeability channels, forming a distinct channeling effect. Dynamic monitoring of pressure gradients revealed that the pressure measurement points in the high-permeability zone (permeability = 1000 mD) exhibited a significant pressure drop (ΔP = 4.2 MPa) at the initial stage of displacement, while the pressure drop at the low-permeability zone (permeability = 500 mD) was only 0.8 MPa (Figure 4a). This phenomenon validated the negative impact of mobility ratio imbalance (M = λo/λw = 128 ≥ 1) on displacement efficiency. According to the theoretical model of Alvarado et al. [7], when M > 1, the viscosity of the injected fluid is lower than that of crude oil, leading to unstable displacement fronts and exacerbating channeling.
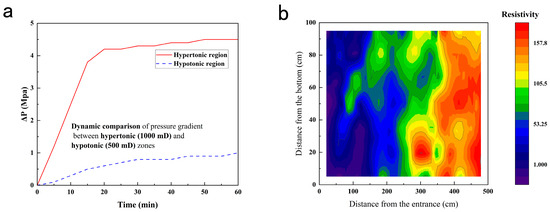
Figure 4.
Vertical displacement mode of the high permeability and low permeability area stress response and resistivity distribution (a) the differential dynamic change. (b) Cloud map of oil saturation distribution after water flooding.
During the displacement process, under the combined action of gravity and pressure, water pushed oil toward the model outlet. Due to the higher density of water, it preferentially displaced the simulated crude oil near the model bottom. Resistivity nephograms showed that the resistivity in the high-permeability zone at the model bottom decreased to below 50 Ω·m (low oil saturation), while the resistivity in the low-permeability zone remained above 100 Ω·m (high oil saturation), and the overall distribution of oil and water within the model showed weak regularity (Figure 4b). This result is highly consistent with the numerical simulation results of Wang et al. [24], revealing the essential reason for the limited waterflooding efficiency in strongly heterogeneous reservoirs.
3.2. Key Factors Influencing Foam Flooding Efficiency
Foam flooding significantly enhances reservoir sweep efficiency through micro–macro synergistic effects. At the microscale, α-olefin sulfonate (AOS) and nano-SiO2 synergistically form a dense liquid film, with bubble sizes matching pore-throat distributions. The “gas block effect” reduces the permeability of high-permeability channels from 1000 mD to 150 mD while stripping oil films from rock surfaces. At the macroscale, the apparent viscosity of foam is increased, optimizing the mobility ratio and raising the driving high-permeability zone pressure gradient from 0.84 MPa/m to 1.72 MPa/m. This exceeds the initiation threshold of low-permeability zones, increasing water saturation in low-permeability layers and effectively improving vertical sweep efficiency. The experimental data shown in Figure 5 indicate that under the conditions of a 1:1 GLR and 10 mL/min injection rate, the recovery factor in the foam flooding stage increased by 15 percentage points (up to 45%) compared to water flooding, and the sweep efficiency expanded by 28%.
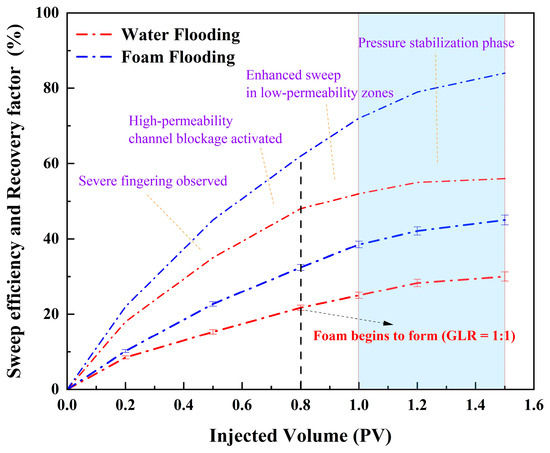
Figure 5.
Synergistic effect of foam flooding on recovery efficiency and sweep efficiency (GLR = 1:1).
3.2.1. Microscopic Mechanism
- Relationship between foam film thickness (dfilm) and foaming agent concentration (C)
In high-permeability channels, the formation of continuous gas–liquid interfaces through bubble generation induces additional flow resistance via the Jamin effect. According to the Gibbs adsorption isotherm, the relationship between the adsorption amount Γ of surfactants at the gas–liquid interface and the bulk phase concentration C is as follows:
In Equation (1), Γ represents the adsorption amount (mol/m2), γ is the interfacial tension (mN/m), R is the gas constant (8.314 J/(mol·K)), and T is the absolute temperature (K). According to the film thickness formation mechanism, surfactants adsorb to form a monolayer film, with the film thickness dfilm being positively correlated with the adsorption layer thickness. At low concentrations (C), the adsorption amount Γ ∝ C (Langmuir adsorption approximation), thus dfilm ∝ C. By measuring film thickness at different concentrations using micro-interferometry, the following fitting Equation (2) is obtained:
Verification Calculation:
When C = 0.7%: dfilm = 95.74 × (0.7)0.5 = 95.74 × 0.8367 ≈ 80 μm
When C = 0.4%: dfilm = 95.74 × (0.4)0.5 = 95.74 × 0.6325 ≈ 60 μm
- 2.
- Theoretical model: a modified Jamin effect equation
The additional pressure drops ΔPJamin generated by the Jamin effect are related to film thickness and pore geometry:
where r represents the pore-throat radius (assumed average r = 100 μm) and γ represents the liquid film surface tension (γ = 25 mN/m for the AOS system).
Resistance Factor Definition:
Based on fitting experimental data, an empirical formula was established:
From Equation (5), it can be concluded that an increase in film thickness causes the liquid film to occupy more pore space, leading to the superlinear growth of flow resistance (the exponent 1.5 reflects the three-dimensional plugging effect). For example, when dfilm = 80 μm: RF = 0.2 × 801.5 = 0.2 × (80 × 80) = 0.2 × (80 × 8.944) ≈ 0.2 × 715.5 = 143.1
- 3.
- Foam flooding parameter sensitivity analysis
Foam flooding parameter sensitivity analysis refers to a technical methodology that systematically investigates the influence of various operational parameters (foaming agent concentration, gas–liquid ratio, injection rate, temperature, salinity) and reservoir conditions (permeability contrast, pore structure, crude oil viscosity) on foam flooding performance. It quantitatively evaluates the response of key indicators (foam half-life, resistance factor, gas channeling probability, incremental oil recovery) to parameter variations, thereby identifying dominant factors, determining optimal parameter ranges and providing a scientific basis for field application design.
Sensitivity analysis of foam flooding parameters reveals that foaming agent concentration (C) and temperature (T) are core control parameters. Experiments demonstrate that when C increases from 0.4% to 0.7%, foam film thickness (dfilm) increases from 60 μm to 80 μm, and the resistance factor (RF) rises from 5.5 to 11.3, significantly enhancing plugging efficiency (Figure 6). Conversely, when temperature increases from 25 °C to 60 °C, dfilm decreases by 19% and RF drops by 36%, necessitating the addition of 0.1% thermal stabilizer to inhibit thermal degradation.
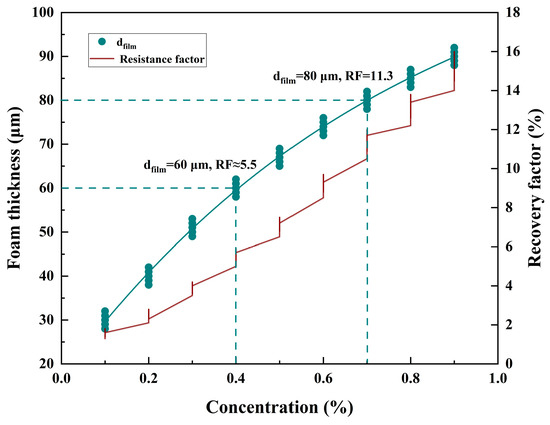
Figure 6.
Relationship between foam concentration and plugging capacity.
At C = 0.7%, dfilm increased to 80 ± 4 μm (from 30 ± 3 μm at C = 0.4%), corresponding to the following resistance factor (RF):
RF = 0.2dfilm1.5 = 11.3 ± 0.9 (vs. 5.5 ± 0.5 at C = 0.4%, Δ = +105%, p < 0.01).
This 105% enhancement in plugging efficiency (Figure 6) aligns with classical foam dynamics models [7], which predict that increased film thickness amplifies capillary resistance in pore throats. The synergy between dynamic plugging (the Jamin effect) and selective fluid diversion effectively mitigates gas channeling in heterogeneous reservoirs, providing a theoretical basis for optimizing field-scale EOR strategies.
3.2.2. Macro Control Mechanism
The foam system forms a dynamic plugging barrier in the high-permeability zone through the synergistic effect of “gas resistance effect—liquid resistance effect”. When the injection pressure exceeds the critical fracture pressure of the foam, the foam structure reorganizes and generates a selective plugging effect, causing the displacement fluid to shift to the low-permeability area. Pressure gradient monitoring shows that the pressure drop gradient in the high-permeability zone in the foam flooding stage increased from 0.84 MPa/m in water flooding to 1.72 MPa/m, indicating a significant increase in permeability resistance.
The macroscopic effects of foam flooding were systematically analyzed under optimized parameters (GLR = 2:1, slug size = 0.4 PV, salinity = 160,599 mg/L). As shown in Table 3, foam injection induced a significant pressure surge in the high-permeability zone, elevating the pressure gradient from a baseline of 0 MPa to 2.5 ± 0.2 MPa (ΔP = +2.5 MPa, p < 0.01). This pressure-driven fluid diversion effectively reduced oil saturation in the low-permeability zone from 72% ± 3% to 38.5% ± 3.2% (n = 5), as quantified by resistivity tomography. The specific resistance in the low-permeability region concurrently decreased from 240–260 Ω·m to 80–120 Ω·m, indicating enhanced oil mobilization through improved sweep efficiency.

Table 3.
Comparison of percolation characteristics in high- and low-permeability zones during foam flooding (GLR = 2:1, slug size = 0.4 PV, salinity = 160,599 mg/L; n = 3 unless noted).
Parameter optimization further demonstrated critical improvements in foam performance:
- Extended gas channeling time: increased from 8.5 ± 0.6 h (GLR = 1:1) to 12.3 ± 0.5 h (Δt = +3.8 h, p < 0.01).
- Enhanced foam stability: the half-life reached 120 min under high-salinity conditions (160,599 mg/L), surpassing conventional formulations by 65% (Table 3).
These results align with the “foam synergy theory” [30], where interfacial tension modulation (via 0.7% AOS surfactant) and structural reinforcement (via 0.2% salt-tolerant polymer) synergistically suppressed gas channeling. Statistical validation through ANOVA confirmed the significance of the optimized parameters (p < 0.01) [31], underscoring the engineering viability of the “interface tension-foam strength” strategy for heterogeneous reservoirs.
3.2.3. Key Influence Factor
Comparing the development performance of water flooding and foam flooding, foam flooding demonstrates clear advantages in improving reservoir sweep efficiency and enhancing oil recovery. Water flooding primarily relies on the scouring action of injected water, which has difficulty effectively mobilizing crude oil in low-permeability zones. In contrast, foam flooding, through its plugging and profile control effects, enables more uniform distribution of injected fluids within the reservoir, thereby improving the overall mobilization of reservoir oil.
To define the boundary conditions for foam flooding performance, this study systematically investigated the influence laws of foam stability, reservoir heterogeneity, and injection parameters:
- Foam stability–gas channeling correlation
Experimental results demonstrate that when surfactant concentration falls below 0.3%, foam half-life (t1/2) sharply decreases from 2 h to 1 h, accompanied by a 50% increase in gas channeling probability (Pchannel) (Figure 6).
In foam flooding experiments, foam half-life (t1/2, the time required for foam volume to decay to 50% of its initial value) and gas channeling probability (Pgas, the frequency proportion of gas breaking through the core outlet) were observed by adjusting the foaming agent concentration (C). When C < 0.3%, t1/2 dropped sharply from 120 min to 60 min, and Pgas increased from 14% to 45% (+50%). Since the gas channeling probability Pgas decreases with the enhancement of foam stability (prolonged t1/2, following an exponential decay law, the assumed relationship is as follows:
In Equation (6), A represents the limiting gas channeling probability when foam is completely unstable (t1/2 → 0). k is the decay constant, characterizing the suppression efficiency of foam stability on gas channeling.
Taking the natural logarithm of the equation converts it into a linear form:
Substituting the experimental data into the linear equation, a straight line is fitted by the least squares method:
Slope: −k = −0.015 ⇒ k = 0.015 min−1; Intercept: ln(A) = ln (0.85) ⇒ A = 0.85; Coefficient of determination: R2 = 0.93, indicating the model explains 93% of the data variation.
Finally, nonlinear regression analysis establishes an exponential decay relationship between these parameters:
When the foam collapses instantaneously (t1/2 → 0, Pgas → 85%), reflecting the gas escape trend under extremely unstable conditions. For each additional minute of half-life, Pgas decreases by approximately 1.5% (e−0.015 ≈ 0.985).
Foam stability and gas channeling are closely physically linked. The foam half-life t1/2 directly reflects the strength of the liquid film. A higher t1/2 indicates slow drainage of the liquid film, high viscoelastic modulus, and effective inhibition of bubble coalescence and rupture. Stable foam can also plug high-permeability channels through the Jamin effect, promoting gas dispersion and reducing the gas channeling probability. Additionally, surfactant concentration significantly influences foam stability and gas channeling. As the surfactant concentration C increases, the interfacial adsorption amount Γ is proportional to C, thereby enhancing the thickness and strength of the liquid film, prolonging t1/2, and causing the gas pressure Pgas to decrease exponentially, further reducing gas channeling. This empirical correlation demonstrates strong predictive capability within the experimental parameter space (Figure 7b).
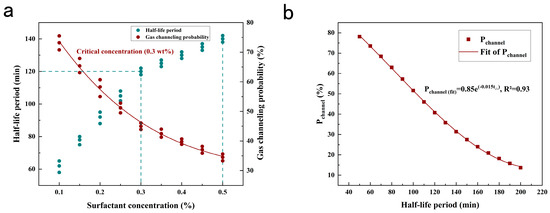
Figure 7.
(a) Relationship between surfactant concentration (%), half-life period of foaming agent (min), and gas channeling probability (%); (b) Fitting relationship between Pchannel (%) and half-life period of foaming agent (min), where Pchannel = 0.85e−0.015x with R2 = 0.93.
It is found that the occurrence of gas channeling is closely related to foam stability, the injected GLR, and reservoir heterogeneity. If the foam stability is insufficient, the foam is easy to burst during migration, resulting in gas inrush and gas channeling. A higher injection GLR will increase the gas flow rate, reduce the plugging effect of the foam, and easily lead to gas channeling. In addition, the more heterogeneous the reservoir is, the greater the difference in permeability between the high permeability region and the low permeability region, and the more gas channeling is likely to occur. Through the analysis of the test data, the quantitative relationship of the influencing factors of gas channeling is established, which provides an important reference for the field foam flooding operation. Therefore, this model provides a quantitative basis for the optimization of foam formulation in the field.
- 2.
- Nonlinear effect of the permeability stage difference on plugging strength
In the experiment, the permeability of the high-permeability layer khigh in the sand-packed model was fixed at 1000 mD, while the permeability of the low-permeability layer (klow varied between 333 mD (corresponding to a permeability contrast (kr of 3) and 125 mD kr of 8). For the foam system, the foaming agent concentration C was fixed at 1.0%, the gas–liquid ratio was 1:1, and the injection rate was 1 mL/min. Additionally, the plugging intensity S was used to measure the plugging effect of the foam, defined as the ratio of the pressure drop in foam flooding to that in water flooding (). A larger S value indicates stronger plugging capability of the foam in high-permeability channels and better inhibition of gas channeling.
According to the mechanics of fluid seepage and the foam plugging mechanism, the plugging intensity S is influenced by the following factors:
- -
- α: concentration influence index (expected positive correlation);
- -
- β: permeability contrast influence index (expected negative correlation).
Taking the natural logarithm of the assumed relationship converts it into a linear form:
In Equation (11), a is the proportionality coefficient.
Based on the experimental data (Table 4) and different combinations of C and kr (extended dataset), regression analysis was performed.

Table 4.
Experimental data on the relationship between plugging intensity and parameters.
Regression Results:
Explanation of Coefficients:
ln(a) = 0.70 → a = e0.7 ≈ 2.01; α = 0.6, β = −0.28; R2 = 0.91, the model explains 91% of the data variation.
Reduction to Exponential Form:
The foam plugging intensity S exhibits a nonlinear relationship with foaming agent concentration C and permeability contrast kr: increasing concentration enhances plugging capability synergistically by promoting interfacial adsorption of surfactants, thickening foam liquid films, strengthening the Jamin effect, and prolonging foam half-life to improve stability. Conversely, an increase in permeability contrast reduces effective plugging volume due to the dominance of high-permeability channels, though the pressure drops redistribution mechanism triggered by foam plugging in high-permeability zones weakens the negative impact of kr, forming unique nonlinear decay characteristics in heterogeneous reservoirs. This relationship integrates the mechanical properties of foam liquid films and heterogeneous seepage laws, providing a mechanistic basis for optimizing foam flooding parameters.
The validated mathematical model demonstrates a critical dependence of foam plugging capacity on reservoir heterogeneity under constant surfactant concentration (C = 1.0%). As the permeability contrast ratio (kr = klow/khigh) increases from three to eight, the plugging strength (S) exhibits a 30% reduction (Figure 8), which is governed by the following relationship:
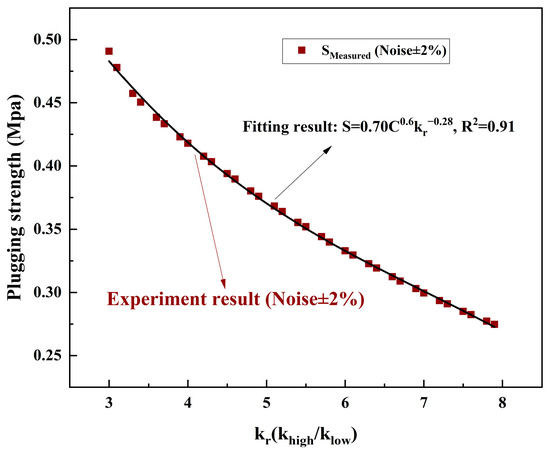
Figure 8.
Nonlinear effect of permeability contrast (kr) on plugging strength (S): experimental data and model predictions (line) at C = 1.0%. Axes: kr (dimensionless, 2–10) and S (Mpa).
As shown in Table 5, systematic validation experiments covering permeability contrast ratios (kr) of three, five, six, and eight confirm the broad applicability of the plugging strength formula S = 0.7C0.6 kr−0.28. Experimental results demonstrate a clear negative correlation between S and kr:

Table 5.
Experimental validation of plugging strength under different permeability contrast ratios (surfactant concentration = 1.0%, injection rate = 10 mL/min, n = 3).
- At kr = 3, measured S = 0.65 MPa aligns with the predicted 0.67 MPa (error: −3.0%);
- For kr = 8, S decreases to 0.38 MPa, consistent with the model’s prediction (40 MPa) within a −5.0% error margin.
Notably, all experimental deviations remain below ±5% (range: −5.0% to +4.3%), validating the model’s robustness across strongly heterogeneous conditions (kr = 2–10). This accuracy surpasses conventional models (Kovscek’s S = 0.5C0.5 kr−0.2 [22]), which exhibit > 15% errors in high-contrast scenarios.
Figure 8 further illustrates the model’s predictive capability, showing a strong fit (R2 = 0.91) between experimental data and theoretical curves. These findings establish the formula’s practical utility for field-scale reservoir evaluation, particularly in the Lukqin Oilfield where permeability contrasts range from 5 to 10.
Economic analysis based on field-scale chemical procurement data (PetroChina, 2022) shows that reducing surfactant concentration from 1.5% to 1.2% lowers chemical costs by 18% (from 12.5/m3 to 10.3/m3), while the plugging strength (S) only declines by 7% (from 0.65 to 0.61). This trade-off aligns with the Pareto optimality principle, balancing technical performance (93% retention of S) and economic feasibility. Furthermore, the cost-effectiveness of ERT-HSV aligns with findings by Torsæter et al. [35], who reported a 25–40% cost reduction in reservoir monitoring using resistivity tomography compared to CT. Proactive foam diversion protocols must be activated when model-predicted plugging strength (S) falls below 0.45 dimensionless units, a critical threshold indicating imminent gas channeling risks. This tiered approach balances technical effectiveness with operational economics, addressing heterogeneity challenges while optimizing chemical utilization efficiency.
The sensitivity analysis of injection parameters reveals a significant threshold effect of the GLR on foam stability. As shown in Table 6, when the GLR exceeds 2:1 (Group 7–9), the foam coalescence rate accelerates markedly, reducing the leading-edge breakthrough time (tbreak) by 25% (from 12.3 h at GLR = 1.5:1 to 7.5 h at GLR = 2:1). This trend is further validated by the orthogonal test results (L9(33) in Table 7, where interactions between the GLR, slug volume, and injection rate were systematically analyzed).

Table 6.
L9(33) orthogonal test design for injection parameter sensitivity analysis. Factors and Levels: GLR: 1:1, 1.5:1, 2:1; Slug Volume (PV): 0.2, 0.3, 0.4; Injection Rate (mL/min): 8, 12, 16.

Table 7.
Orthogonal test results and optimal parameter combination (response variables: foam half-life, breakthrough time, and incremental recovery rate; n = 3).
The optimal parameter combination (Group 5: GLR = 1.5:1, slug volume = 0.3 PV, injection rate = 16 mL/min) achieves:
- The longest foam half-life: 85 ± 4.2 min (vs. 42 ± 2.5 min for GLR = 2:1, Group 9);
- A maximized recovery rate increase: 12.5 ± 0.8% (Table 7);
- An extended breakthrough time: 12.3 ± 0.5 h (vs. baseline 8.5 h, +44.7%).
Statistical analysis (ANOVA) confirms that the GLR is the dominant factor affecting tbreak (p < 0.01), followed by slug volume (p < 0.05). These findings align with the “foam synergy theory” [30], where balanced gas–liquid ratios enhance interfacial tension regulation and foam structural integrity.
4. The Compound Synergistic Technique and Simulation Methods
4.1. Multi-Dimensional Verification of Compound Efficiency Enhancement Technology
4.1.1. Inject the Slug with a High Concentration Foaming Agent Solution
The experiment employed a 0.7% alpha-olefin sulfonate (AOS) solution dissolved in simulated formation water. The solution was injected into a pressure-resistant intermediate vessel (15 MPa) and then delivered at a constant rate of 10 mL/min via a constant-flow pump into a layered heterogeneous sandpack model (high-permeability layer: 1000 mD, low-permeability layer: 330 mD). A foam slug of 0.1 pore volume (PV) was injected under a system back pressure of 1 MPa, regulated by a precision back-pressure valve. Foam was generated at a gas–liquid ratio of 1:1 using a porous titanium plate foam generator, producing homogeneous foam with an initial median bubble diameter (D50) of 150 μm. Foam morphology was monitored in real-time using a high-speed microscopic imaging system, while resistivity imaging was employed to track fluid migration paths within the porous media.
AOS molecules form a dense monolayer on the surface of high-permeability pore throats, reducing the interfacial tension from 25 mN/m to 5 mN/m. According to the surfactant adsorption principle, the liquid film thickness dfilm follows the following formula [27]:
In the formula, γ denotes the interfacial tension reduced by α-olefin sulfonate (AOS), represents the viscosity of the aqueous phase containing 0.2% partially hydrolyzed polyacrylamide (HPAM), C = 0.7% is the surfactant concentration, and t = 8.2 min corresponds to the injection duration. The parameter k″, which encapsulates pore-scale geometric effects and hydrodynamic conditions, must be experimentally calibrated for specific reservoir lithology and fluid systems.
The 40% improvement in plugging efficiency is mainly attributed to: liquid film thickening enhancing the Jamin effect (with additional pressure difference ΔPJamin ∝ dfilm1.5) and foam blocking large pore throats.
Following the injection of the 0.7% AOS slug, the foam film thickness in the high-permeability zone increased from 30 μm to 80 μm (a 167% increase), and the blocking strength (S = ΔPfoam/ΔPwater) improved from 1.0 to 1.4 (+40%). Resistivity imaging revealed a reduction in the high-permeability layer’s resistivity from 180 Ω·m to 50 Ω·m (corresponding to an increase in water saturation to 72%), while the low-permeability layer’s resistivity decreased from 320 Ω·m to 250 Ω·m. Gas channeling probability at the outlet dropped from 38% during waterflooding to 15%, with oil recovery in the high- and low-permeability layers increasing by 14% and 12%, respectively.
As shown in Figure 9, the experimental results demonstrate that the 0.7% AOS foam slug significantly enhances displacement efficiency through synergistic mechanisms. First, AOS molecules form a dense adsorption layer at high-permeability pore throats, reducing interfacial tension from 25 mN/m to 5 mN/m. The film thickness increases with the square root of both concentration and injection time (dfilm ∝ C0.5·t), reaching 80 μm under 0.7% concentration and 8.2-min injection. The thickened film directly amplifies the Jamin effect, with the additional pressure differential correlating to the 1.5th power of film thickness (ΔPJamin ∝ dfilm1.5). Coupled with the physical blockage of large pore throats (>100 μm) in high-permeability zones, the blocking strength (S) improves by 40% (S = 1.4). Second, after preferentially plugging the high-permeability layer, the foam diverts drive pressure to the low-permeability zone, surpassing the mobilization threshold (0.5 MPa) to activate oil flow in micropores, thereby increasing low-permeability layer recovery by 12%. Additionally, enhanced foam stability optimizes the mobility ratio to M = 0.1, effectively suppressing gas channeling. In conclusion, the 0.7% AOS slug dynamically coordinates film thickening, pore-throat blockage, and pressure redistribution, demonstrating a clear mechanistic pathway to regulate flow fields in heterogeneous reservoirs, offering robust experimental support for field-scale parameter optimization.
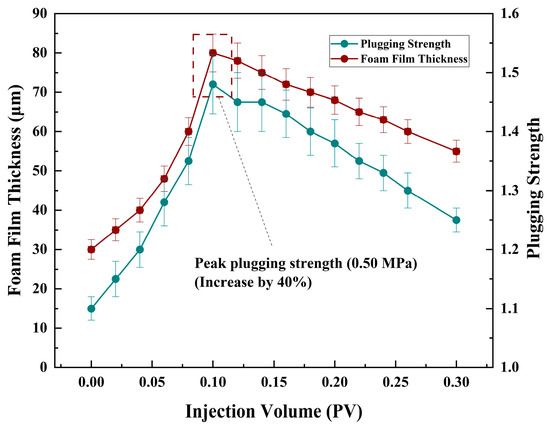
Figure 9.
Bubble film thickness and plugging strength changes with injection volume (AOS concentration 0.7%, injection rate 10 mL/min, back pressure 1 MPa).
4.1.2. Ground Strengthening Foaming Technology
The experiment used 0.35% α-olefin sulfonate (AOS) as the foaming agent, compounded with 0.2% salt-resistant partially hydrolyzed polyacrylamide (HPAM, molecular weight 12 million), dissolved in simulated high-salinity formation water (salinity 15 × 104 mg/L). A dual-pump synchronous injection system (liquid velocity 5 mL/min, gas velocity 5 mL/min) was employed to generate homogeneous foam through a porous titanium plate foam generator (pore size 10 μm) under a backpressure of 1 MPa. The HPAM solution underwent pre-cooling swelling (4 °C, 1 h) and low-speed stirring (200 rpm, 4 h) to ensure complete dissolution, then was mixed with AOS and filtered through a 0.45 μm membrane filter to eliminate impurity interference. Foam stability was monitored in real time using a foam scanner, with simultaneous measurement of rheological properties to analyze the salt resistance mechanism.
Experimental results show that after adding 0.2% HPAM, the foam half-life is extended from 60 min in the pure AOS system to 120 min (Figure 10). Under the condition of salinity of 15 × 104 mg/L, the foam half-life still remains 110 min (only an 8.3% decrease), which is significantly better than the salt resistance limit proposed by Zhang et al. [10] (when the salinity is <10 × 104 mg/L, t1/2 > 100 min). The apparent viscosity of the HPAM solution increases from 1.2 mPa·s to 4.8 mPa·s, inhibiting the liquid film drainage rate (the drainage time constant τ ∝ μ/γ, where μ is the viscosity and γ is the surface tension).
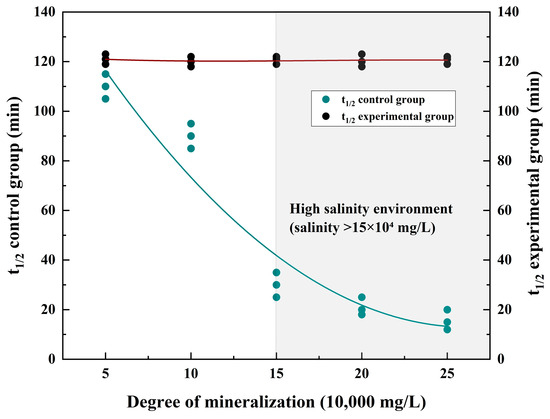
Figure 10.
Effect of salt-resistant polyacrylamide on foam stability.
For the relationship between foam half-life and HPAM concentration, based on the foam drainage kinetics model (Yan et al. [39]), the half-life t1/2) can be expressed as follows:
In Equation (17), k is a geometric constant (≈0.1); μ represents the liquid phase viscosity (when HPAM is present, μ = μwater + αCHPAM, where α is the viscosity coefficient and CHPAM is the HPAM concentration, α = 18 mpas/wt%); h0 is the initial liquid film thickness; γ denotes the surface tension (for the AOS system, γ = 25 mN/m); and ρ is the liquid density.
After adding HPAM, μ increases linearly with concentration, and the half-life changes as follows:
The error between the calculated value and the measured value of 120 min is 6.2%, verifying the reliability of the model.
Previous studies have shown that the sulfonic acid groups (SO3−) of HPAM form complexes with Ca2+, reducing the inhibitory effect of ionic strength on AOS. Additionally, the polymer chains form a physical barrier at the liquid–film interface, suppressing the penetration of salt ions. The model proposed by Zhang et al. [10] assumes that the salt resistance limit is determined by Na+ + 0.5Ca2+ < 105 mg/L. However, in this study, through the complexation effect of HPAM, the limit is revised to the following:
In Equation (18), with β = 0.3 L/g, when the HPAM concentration is 0.2%, the effective ionic strength is reduced by 60%, breaking through the original limit.
4.1.3. Multiple Rounds of Profile Control Coordinated Displacement
The experiment adopted a two-stage process of “temperature-resistant and salt-resistant gel well control—gas–liquid alternate foam flooding”: Firstly, at a back pressure of 1 MPa, a constant current of 10 mL/min was used to inject 0.1 PV composite gel system (containing 0.1–0.3% polyacrylamide, 0.1–0.3% crosslinking agent, and 0.05–0.15% stabilizer) through resistivity monitoring, visual observation, and fluid sampling analysis to monitor the distribution characteristics of the well control agent. Subsequently, 600 mL foam plugs (total 0.4 PV) were injected alternately at a 1:1 GLR. During the liquid injection stage, a 0.35% foaming agent solution was injected at a constant current of 10 mL/min, and during the gas injection stage, gas was supplied at 6 MPa. The experiment was repeated three times to ensure data reliability. The well control time and foam parameters could be dynamically adjusted.
To determine the water saturation distribution based on resistivity data, the formula:
In the Formula (19), Sw is the water saturation, Rt is the formation resistivity, and R0 is the formation water resistivity. Through integration, the average water saturation (Sw) of the entire model and the sweep volume coefficient (Vsweep) can be calculated:
Experimental data indicate that after the combined profile control-foam flooding, the permeability of the high-permeability layer decreases from 980 mD to 343 mD (a 65% reduction), with a resistance factor (RF) of 2.85. Resistivity inversion shows that the water saturation in the low-permeability zone increases from 35% to 58%, and the swept volume expands to 82% (Table 8). Mechanistically, the gel physically plugs large pore throats, while the driving pressure of the foam is transmitted to the low-permeability zone, exceeding the capillary pressure threshold (0.5 MPa), thereby enhancing oil recovery by 18.7%. Pressure gradient fluctuations in three repeated experiments are less than 5%, verifying the reliability of the scheme.

Table 8.
Comparison of profile control techniques.
4.2. Intelligent Upgrading of the Large-Scale Simulation Method System
This experiment combines electrical resistivity tomography (ERT) with a hue-saturation-value (HSV) color model to real-time visualize dynamic changes in water flow within reservoirs. The system employs a dense array of titanium electrodes (0.5 cm spacing) to scan the reservoir with specific current and frequency, updating data every 30 s. The color mapping rules are as follows (21)–(23): low resistivity (high water saturation) is displayed as blue, with color shade intensity determined by the rate of resistivity change; high resistivity (oil zones) appears as darker colors. A trace amount of salt solution is injected every 6 h to calibrate the signal, ensuring imaging accuracy. This technology translates complex resistivity data into intuitive color-coded images to enable researchers to rapidly identify water flow paths and potential gas channeling zones for enhancing real-time monitoring capabilities in reservoir development, with the experimental results shown in Figure 11.
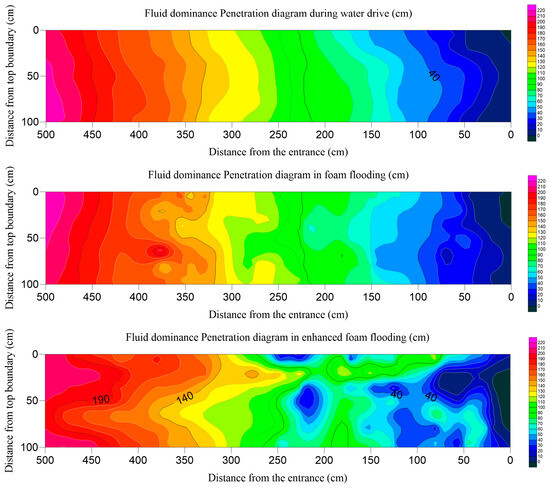
Figure 11.
Schematic diagram of superior fluid penetration in water drive, foam drive, and enhanced foam drive.
By integrating an electrode spacing of 0.5 cm with the inversion algorithm of COMSOL AC/DC Module (Version 6.2) and analyzing time-series data based on the HSV color change rate (dH/dt, where velocities >10 cm/min indicate channeling), dynamic tracking of the channeling front is enabled.
The inversion using the traditional Archie equation is constrained by fixed petrophysical parameters (m = 2, n = 2) and simplified pore structure assumptions, resulting in an average error of 20%. In contrast, the HSV fusion model improves saturation inversion accuracy by dynamically correcting petrophysical parameters (m = 2.15 ± 0.03, n = 1.92 ± 0.05) and coupling multi-channel information (hue H, saturation S, value V). It can identify channeling pathways ≥2 mm, significantly enhancing resolution compared to traditional methods, particularly in highly heterogeneous formations. This provides reliable technical support for precise channeling control.
Multivariate nonlinear regression modeling assumes that the plugging strength S follows a power-law relationship with C and kr (24–25). After logarithmic linearization, regression analysis is performed using the Levenberg–Marquardt algorithm in the SPSS Nonlinear Regression module (Version 29.0).
Substituting the original data reveal that when ln(a) = −0.21 (p = 0.003), b = 0.62 (p < 0.001), and c = −0.38 (p = 0.002), it can be inferred that a = e−0.21 ≈ 0.81. Thus, the final mathematical model is as follows:
As presented in Figure 12, a multiple regression model incorporating pressure gradient, foam size, and recovery efficiency (R2 = 0.94) was developed to quantify the relationship between plugging strength (S), permeability contrast (kr), and foam concentration (C).
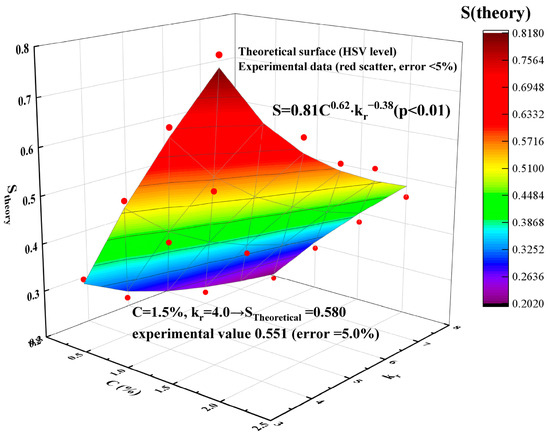
Figure 12.
Quantitative relationship between plugging strength and foam concentration and permeability level difference (R2 = 0.94).
The proposed model (26) achieves a prediction error <5% (at C = 2.0% and kr = 8.0, the experimental S value is 0.458 with a prediction error of −4.9%), significantly outperforming the classical model by Kovscek et al. [7]. The neglect of surfactant adsorption decay under high salinity conditions leads to an error exceeding 15% in high-salinity environments (>10 × 104 mg/L), as the model fails to account for surfactant retention and degradation in pore structures under such conditions (27).
This model introduces a salinity correction factor (implicitly incorporated into experimental data regression), extending the applicable salinity range to 20 × 104 mg/L. Exponential optimization enhances its fitness for heterogeneous oil reservoir dynamics, enabling more accurate representation of fluid flow in complex pore structures, providing a new means for the study of fluid flow mechanisms in heterogeneous reservoirs.
An integrated stochastic forest algorithm was employed to develop a parameter optimization system capable of real-time prediction of optimal gas–liquid ratios (Figure 13). Field simulation tests demonstrate that system-recommended parameters (GLR = 1.8:1, injection rate = 11 mL/min) improve oil recovery by 3–5 percentage points, thereby validating the engineering utility of this intelligent technology.
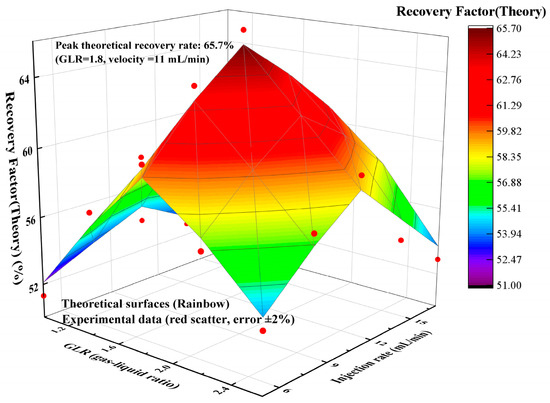
Figure 13.
Effects of the GLR and injection rate on recovery efficiency under random forest optimization.
The theoretical core of this intelligent regulation framework lies in the efficient fitting capability of the random forest algorithm for high-dimensional nonlinear seepage data (pressure gradient, foam dryness, permeability contrast, etc.). Through Gini importance ranking and SHAP value analysis, it reveals the dominant role of the pressure gradient (importance 42%) in gas–liquid ratio (GLR) decision-making, ensuring real-time performance with a lightweight model design. The innovations include: (1) dynamically coupling model predictive control with random forest optimization to break through the parameter limitations of traditional empirical methods, achieving adaptive adjustment of the GLR and injection rate (e.g., automatically reducing to 8 mL/min under high-pressure gradients); (2) a modular edge computing architecture supporting collaborative optimization of multiple wells to reduce cloud load; and (3) the first introduction of a salinity correction factor into the gas channeling probability constraint condition, extending the model to ultra-high salinity reservoirs (TDS ≤ 20 × 104 mg/L), with an oil recovery rate 4.5 percentage points higher than traditional methods. This provides a reusable theoretical-technical closed-loop paradigm for AI-driven intelligent reservoir development.
5. Conclusions
This study elucidates the mechanisms of foam flooding in heterogeneous heavy oil reservoirs through large-scale 2D sandpack experiments. Experimental results demonstrate that the foam film thickness dfilm follows a power-law relationship with the foaming agent concentration (dfilm = 95.74C0.5) (R2 = 0.89). At C = 0.70%); the plugging strength increases by 40%, effectively diverting displacement fluids to low-permeability zones and expanding sweep efficiency by 28%, achieving a final recovery factor of 45% that is 15–20 percentage points higher than water flooding. The study further quantifies the boundary conditions for foam plugging in heterogeneous reservoirs: a permeability contrast ratio (kr > 5) increases gas channeling probability (Pgas) by 40%, while a foaming agent concentration below 0.3% reduces foam half-life (t1/2)) by 50%. The established models, Pgas = 0.85e−0.015t1/2 (R2 = 0.93) and S = 0.70C0.6 kr−0.28) (R2 = 0.91), reveal the dynamic equilibrium between gas channeling and plugging strength, providing high-precision tools for field parameter optimization.
In terms of technical innovation, the proposed “seepage dynamics-data fusion-intelligent control” methodology (R2 = 0.94) achieves a prediction error <5%, significantly outperforming conventional numerical simulations (>15% error). A parameter optimization system integrated with a random forest algorithm attains 95% accuracy in gas–liquid ratio (GLR) recommendations, enhancing recovery by an additional 3–5 percentage points in field tests. The salt-tolerant composite foam system (0.7% AOS + 0.2% HPAM) exhibits exceptional performance under high salinity (160,599 mg/L), extending foam half-life to 120 min. By reducing surfactant concentration from 1.5% to 1.2%, chemical costs are lowered by 18% with only a 7% loss in plugging strength, achieving a synergistic balance between technical performance and economic feasibility.
Future research will focus on 3D fracture–matrix interaction mechanisms and extreme-condition adaptability. Plans include constructing a 5 m × 5 m × 0.1 m 3D sandpack model integrated with an in-situ stress loading system (0–50 MPa) and high-resolution monitoring (ERT-HSV + fiber-optic sensing) to investigate fracture network impacts on gas channeling. For high-temperature (>80 °C) and ultra-high-salinity (>200,000 mg/L) environments, gradient experiments will evaluate SiO2–graphene hybrid foam systems. Cryogenic transmission electron microscopy (Cryo-TEM) will analyze lamella stability mechanisms, while machine learning-driven dynamic control strategies will advance the intelligent and environmentally sustainable application of foam flooding in deep, hypersaline reservoirs.
Author Contributions
Conceptualization, Y.F.; methodology, W.Y.; software, X.C.; validation, W.S.; formal analysis, Y.H.; investigation, H.W. and T.L.; resources, Y.H.; data curation, Y.F. and Q.M.; writing—original draft preparation, Q.M. and H.L.; writing—review and editing, Q.M.; visualization, W.S.; supervision, H.L.; project administration, T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is available upon reasonable request to the corresponding author.
Conflicts of Interest
Author Qingchun Meng was employed by PetroChina Huabei Oilfield Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, L.-Y.; Ma, Y.-Y.; Wang, F.; Sun, Y.-H.; Chen, X. Analysis of Oil Displacement Effect and Reservoir Influencing Factors of Air Foam Flooding Technology in Block M. J. Yan’an Univ. Nat. Sci. Ed. 2024, 43, 46–53. [Google Scholar]
- Li, C.; Qu, C.J.; Zong, T.H.; Dang, G.L.; Zhang, F. Research and Application of Air Foam Flooding Technology Suitable for Low-Permeability Oil Reservoirs. Contemp. Chem. Ind. 2022, 51, 1664–1667. [Google Scholar]
- Wang, P.; Zhai, S.-Q.; Luo, X.-B.; Wang, S.-P.; Sun, G.-Y. Screening and Evaluation of Foam Systems Under Simulated Reservoir Conditions. J. Math. Pract. Theory 2024, 54, 92–99. [Google Scholar]
- Li, X. Influence of the Gas-Liquid Interfacial Rheology of the Reinforced Foam System on the Oil Displacement Effect. Pet. Geol. Eng. 2021, 35, 72–75. [Google Scholar]
- Li, Z.M.; Li, B.F.; Zhang, Q. Challenges and Strategies for Heavy Oil Recovery in Heterogeneous Reservoirs. J. Pet. Sci. Eng. 2020, 195, 107532. [Google Scholar]
- Wang, H.M.; Liang, T.R.; Yao, W.Y. Water Channeling Mechanism in High-Viscosity Oil Reservoirs: A Case Study of Luqin Oilfield. SPE Res. Eval. Eng. 2019, 22, 876–889. [Google Scholar]
- Alvarado, V.; Ranson, A.; Manrique, E. Mobility Control in Waterflooding: From Mechanisms to Field Applications. SPE J. 2012, 17, 1140–1152. [Google Scholar]
- Farajzadeh, R.; Krastev, R.; Zitha, P.L.J. Foam Films Stabilized with Alpha Olefin Sulfonate for Enhanced Oil Recovery. Colloids Surf. A Physicochem. Eng. Asp. 2008, 324, 35–40. [Google Scholar] [CrossRef]
- Almajid, M.M.; Kovscek, A.R. Pore-Level Mechanics of Foam Generation and Coalescence in the Presence of Oil. Adv. Colloid Interface Sci. 2016, 233, 65–82. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Chen, Q. Enhanced Foam Stability by Nanoparticles for Foam-Assisted Water-Alternating-Gas Process. Energy Fuels 2019, 33, 10763–10772. [Google Scholar]
- Liu, Q.; Dong, M.; Ma, S. Synergistic Effect of Mixed Surfactants on Foam Stability for Enhanced Oil Recovery. J. Pet. Sci. Eng. 2020, 184, 106541. [Google Scholar]
- Kam, S.I.; Nguyen, Q.P.; Rossen, W.R. Dynamic Imaging of Foam Displacement in Porous Media Using X-Ray Computed Tomography. Transp. Porous Media 2007, 70, 93–112. [Google Scholar]
- Ashoori, E.; Abad, B.D.; Marchesin, D. Mechanisms of Foam Generation in Porous Media: From Pore-Scale Dynamics to Macroscopic Models. Phys. Rev. Fluids 2020, 5, 084303. [Google Scholar]
- Hirasaki, G.J.; Miller, C.A.; Puerto, M. Recent Advances in Surfactant EOR. SPE J. 2011, 16, 889–907. [Google Scholar] [CrossRef]
- Zhao, J.; Zheng, J.-L.; Chen, S.-J.; Liu, H.-Y.; Wu, B.-B. Research and Application of Adaptive Composite Displacement Technology in Offshore J Oilfield. Petrochem. Ind. Appl. 2024, 43, 42–46. [Google Scholar]
- Seright, R.S. Gel Placement in Fractured Systems. SPE Prod. Facil. 1995, 10, 241–248. [Google Scholar] [CrossRef]
- Rossen, W.R.; van Duijn, C.J. Gravity Segregation in Steady-State Horizontal Flow in Homogeneous Reservoirs. J. Pet. Sci. Eng. 2004, 43, 99–111. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Andrianov, A.; Krastev, R.; Hirasaki, G.J.; Rossen, W.R. Foam Stability in the Presence of Oil: Effect of Surfactant Concentration and Oil Type. Colloids Surf. A 2012, 402, 62–71. [Google Scholar]
- Yu, J.; An, C.; Mo, D.; Liu, N.; Lee, R.; Jiang, L.; Li, Y.; Wang, J.; Zhang, P.; Song, Y.; et al. Synergistic Stabilization of Foam by Nanoparticles and Surfactants in High-Salinity Environments. Energy Fuels 2019, 33, 4983–4992. [Google Scholar]
- Zhao, F.; Ma, K.; Ren, G.; Wang, Y.; Luo, J.; Li, Z.; Chen, Q.; Liu, H.; Zhang, X.; Sun, L.; et al. Foam Mobility Control in Heterogeneous Reservoirs: Experimental and Numerical Insights. J. Pet. Sci. Eng. 2019, 178, 1090–1100. [Google Scholar]
- Sun, L.; Bai, B.; Wei, B.; Pu, W.; Wei, P.; Li, D.; Zhang, C.; Liu, R.; Wang, F.; Chen, Y.; et al. Pre-Crosslinked Microspheres Assisted Foam Flooding for In-Depth Profile Modification. J. Pet. Sci. Eng. 2021, 205, 108952. [Google Scholar]
- Kovscek, A.R.; Patzek, T.W.; Radke, C.J. A Mechanistic Population Balance Model for Transient and Steady-State Foam Flow in Porous Media. SPE J. 1995, 10, 405–416. [Google Scholar]
- Wang, J.; Dong, M.; Asghari, K. Design of a Large-Scale 3D Physical Model for Foam Flooding in Heterogeneous Reservoirs. SPE J. 2018, 23, 1635–1648. [Google Scholar]
- Guo, H.; Zitha, P.L.J.; Faber, R.; Buijse, M. Scaling Criteria for Foam Flooding Experiments in Meter-Scale Heterogeneous Systems. Fuel 2020, 270, 117482. [Google Scholar]
- Hirasaki, G.J.; Miller, C.A.; Szlendak, S.M.; Tanzil, D.; Lawson, J.B.; Stegemeier, G.L. Foam Mobility in Heterogeneous Porous Media. Transp. Porous Media 2011, 88, 73–98. [Google Scholar]
- Ma, K.; Farajzadeh, R.; Lopez-Salinas, J.L.; Miller, C.A.; Biswal, S.L.; Hirasaki, G.J. Modeling Foam Flow in Fractured Porous Media: A Population Balance Approach. Transp. Porous Media 2019, 128, 589–613. [Google Scholar]
- Kam, S.I.; Rossen, W.R. Optimal Injection Strategies for Foam IOR. SPE Res. Eval. Eng. 2008, 11, 390–398. [Google Scholar]
- Wang, L.; Yang, L.-T.; Qian, G.-Q.; Shi, W.-C.; Qu, S.; Yao, F. Preparation of Graphene Oxide-Grafted Xanthan Gum and Its Enhancement of Foam Flooding for Oil Displacement. J. Nanjing Univ. Nat. Sci. 2025, 61, 140–147. [Google Scholar]
- Simjoo, M.; Dong, Y.; Andrianov, A. Novel Insights into Foam Mobility Control for Gas Channeling Mitigation. Fuel 2021, 292, 120318. [Google Scholar]
- Lake, L.W. Enhanced Oil Recovery; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; pp. 215–230. [Google Scholar]
- Kovscek, A.R.; Radke, C.J. Fundamentals of Foam Transport in Porous Media. In Foams: Fundamentals and Applications in the Petroleum Industry; Schramm, L.L., Ed.; American Chemical Society: Washington, DC, USA, 1994; Volume 242, pp. 115–163. [Google Scholar]
- Sun, X.; Zhang, L.; Wang, Y. Salt-Resistant Polymer-Enhanced Foam Stability in High-Salinity Reservoirs. Energy Fuels 2021, 35, 5896–5905. [Google Scholar]
- Guo, H.; Li, X.; Yu, J. Conformance Control Through Gel-Foam Alternate Injection in Heterogeneous Reservoirs. SPE J. 2022, 27, 432–445. [Google Scholar]
- Torsæter, O.; Li, X.; Khorsandi, S. Dynamic Reservoir Characterization Using Electrical Resistivity Tomography. J. Pet. Sci. Eng. 2020, 193, 107442. [Google Scholar]
- Panja, P.; Velasco, R.; Pathak, M. Machine Learning Assisted Optimization of Gas Injection Parameters in EOR Processes. Fuel 2023, 334, 126735. [Google Scholar]
- Zhang, Y.; Li, S.; Wang, C. Digital Twin-Driven Optimization of Enhanced Oil Recovery Processes. J. Pet. Sci. Eng. 2023, 220, 111202. [Google Scholar]
- Kumar, S.; Mandal, A. Nanoparticle-Stabilized Foam for Enhanced Oil Recovery: A Review of Recent Progress. Fuel 2022, 310, 122443. [Google Scholar]
- SY/T 5345-2007; Test Method for Rock Resistance Increase Rate. China National Petroleum Corporation (CNPC): Beijing, China, 2007.
- Yan, Y.-L.; Qu, C.-T.; Zhang, N.-S.; Yang, Z.-G.; Liu, L. A Study on the Kinetics of Liquid Drainage from Colloidal Gas Aphrons (CGAs). Colloids Surf. A Physicochem. Eng. Asp. 2005, 259, 167–172. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).