An Upgraded FOS/TAC Titration Model Integrating Phosphate Effects for Accurate Assessments of Volatile Fatty Acids and Alkalinity in Anaerobic Media
Abstract
1. Introduction
2. Materials and Methods
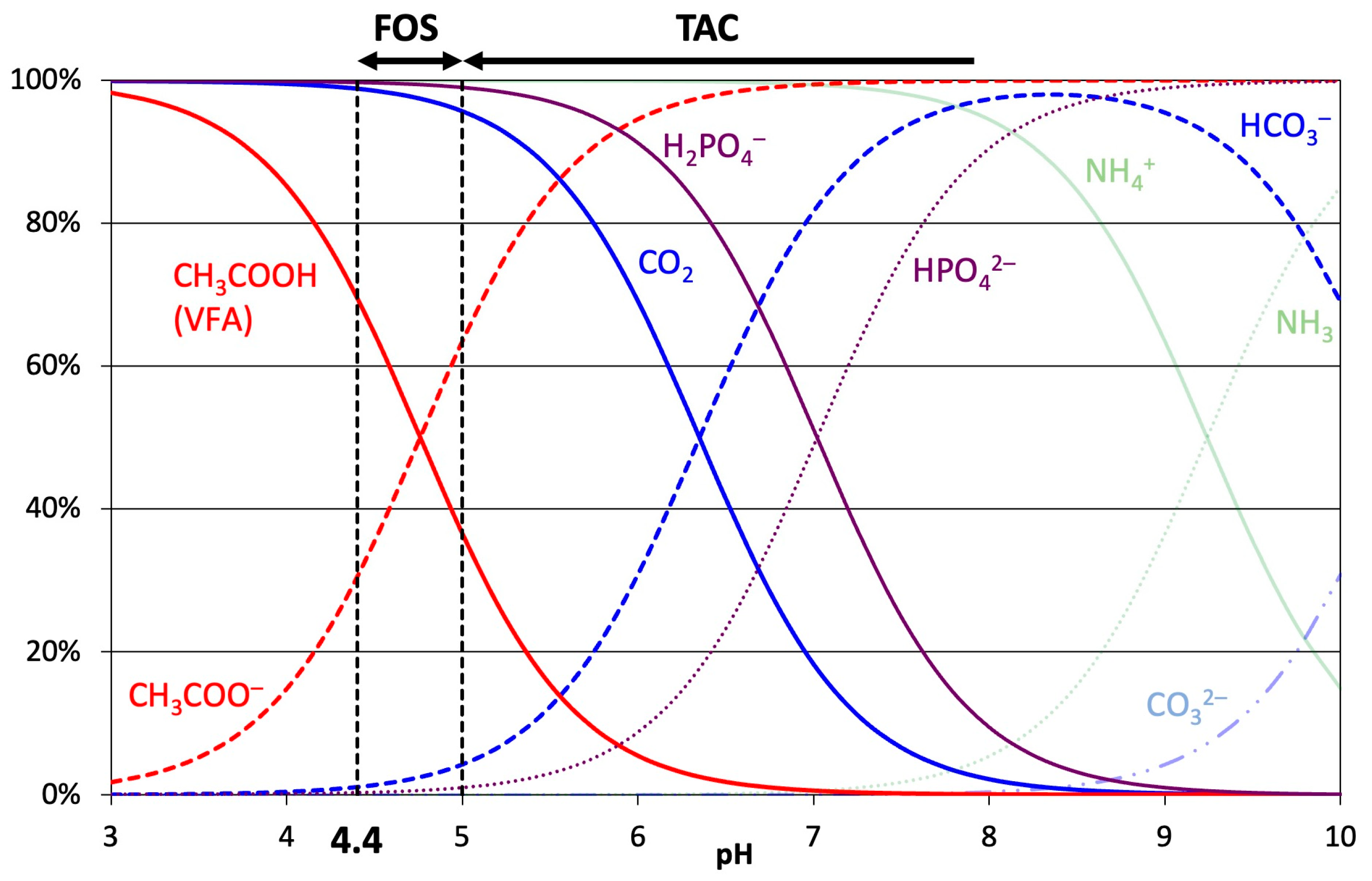
2.1. FOS/TAC Titration
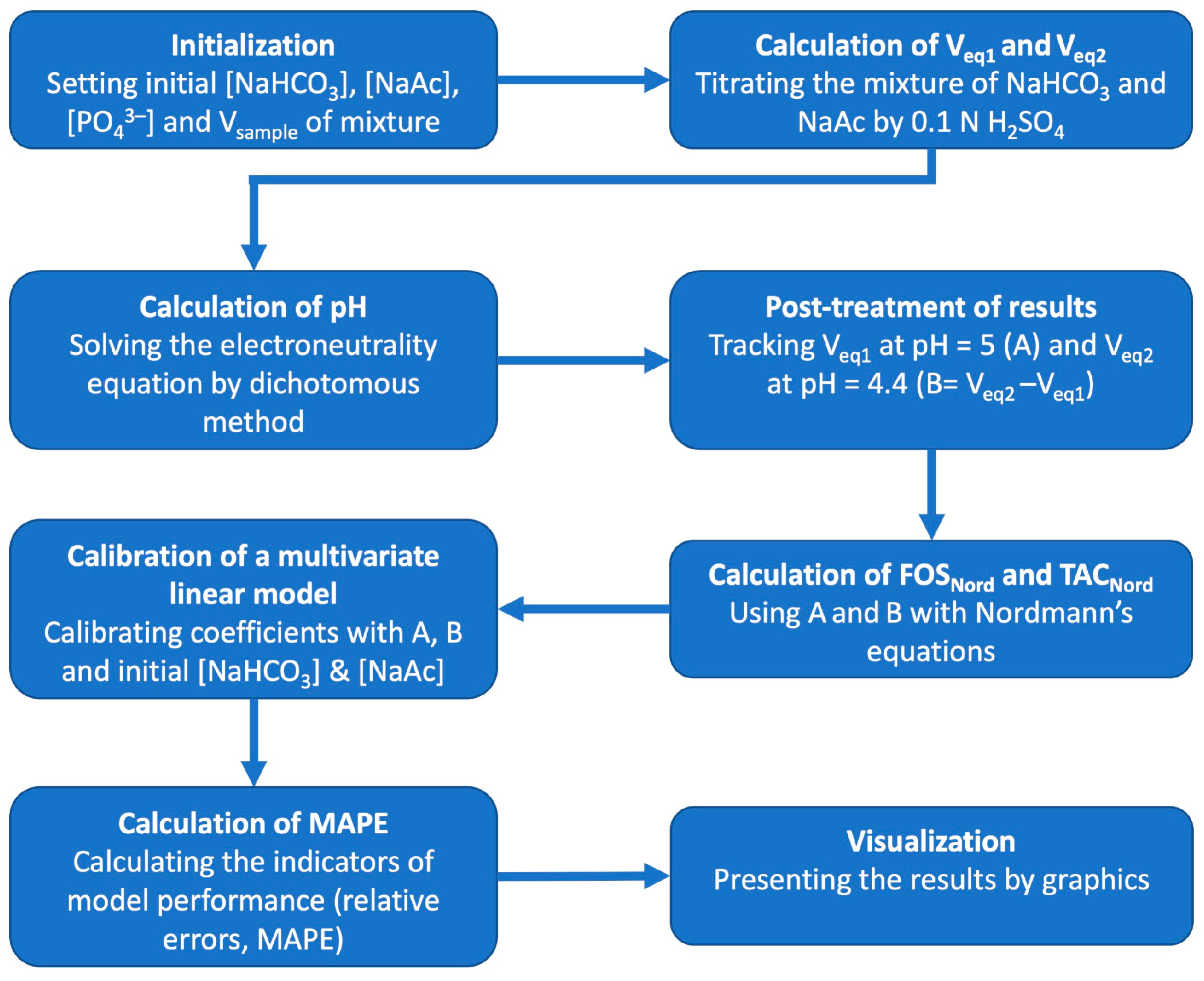
2.2. Numerical Simulation of FOS/TAC Titration by Scilab
3. Results
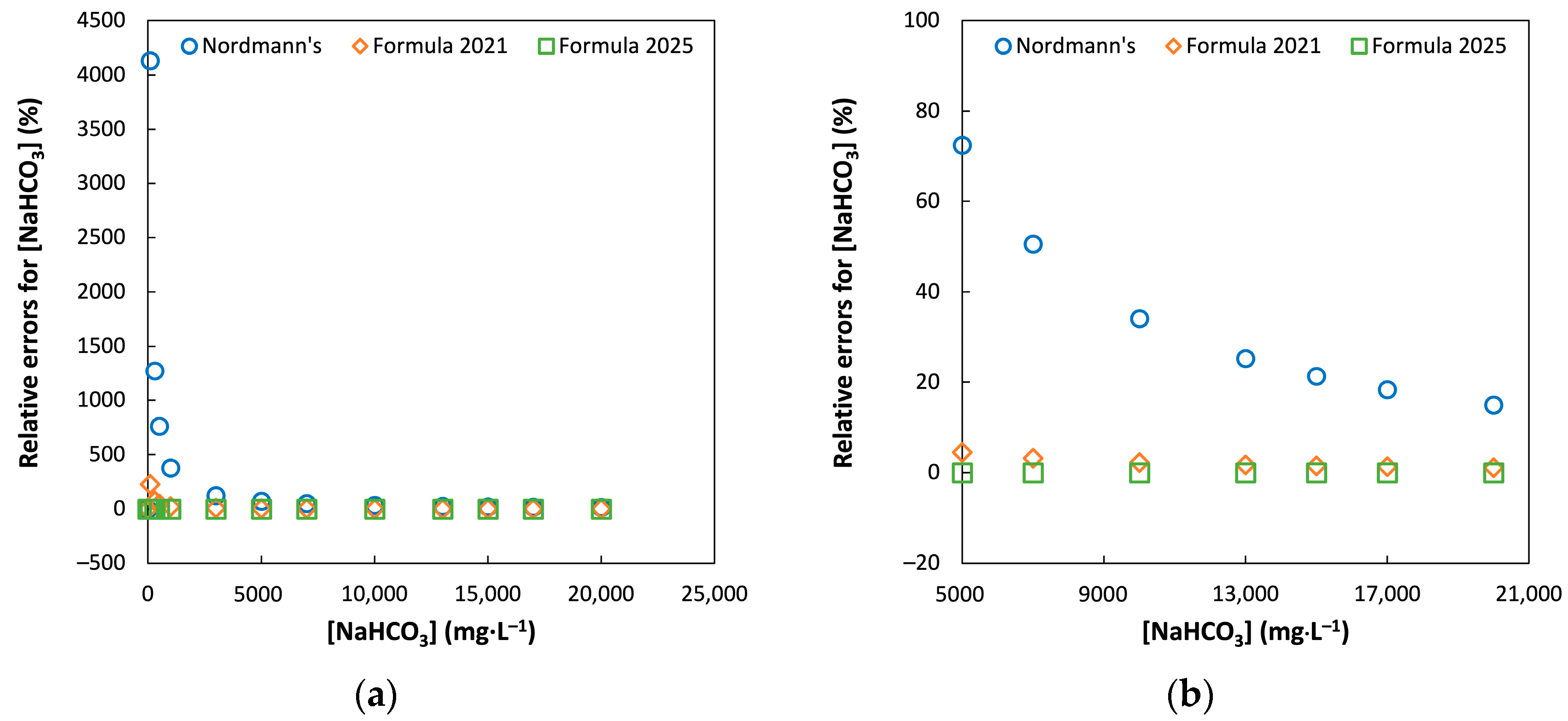
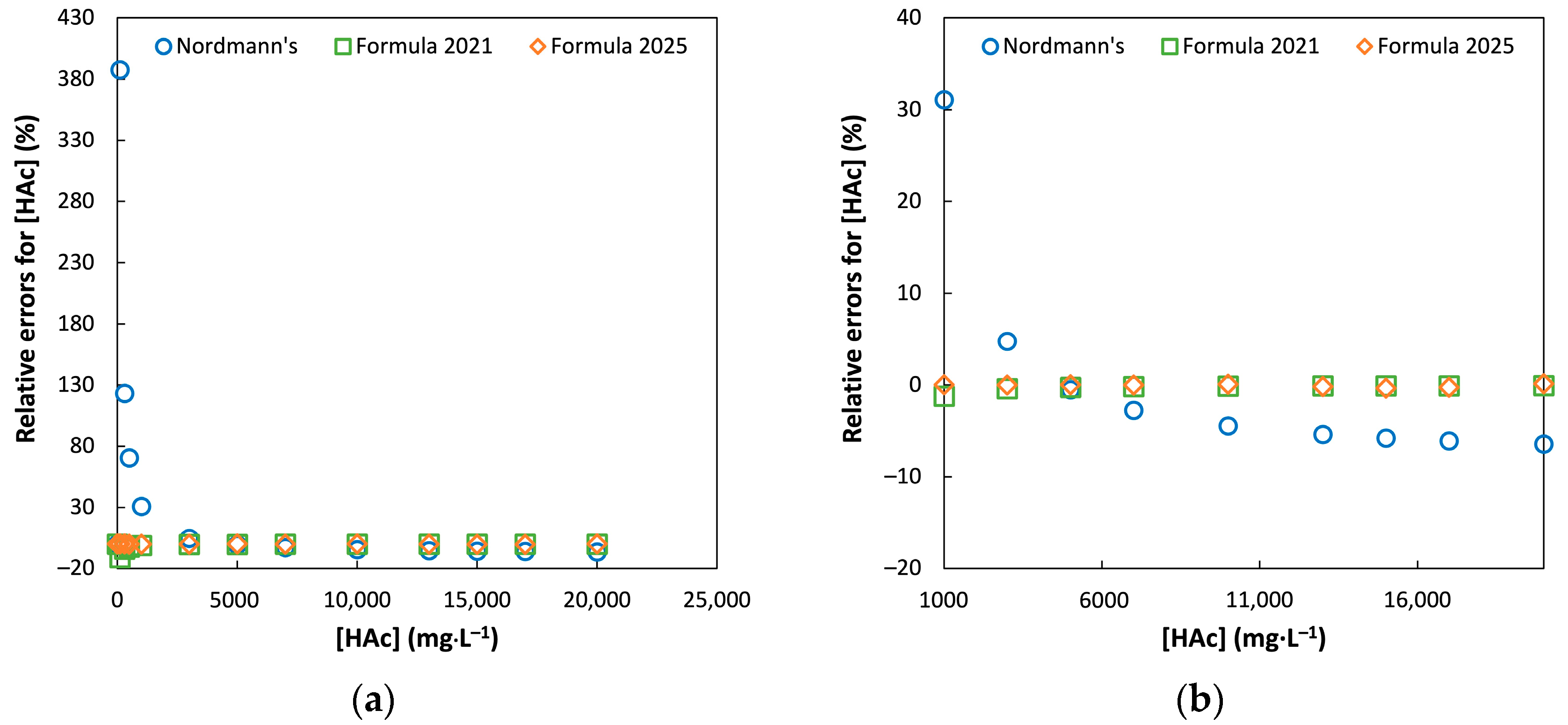
3.1. Comparison of Model Accuracy
3.2. Model Parameter Variation with Calibration Ranges
3.3. Effect of Total Phosphate Level on the Modeling Parameters
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Acid/Base Couple | Dissociation Reaction | pKa (−) |
|---|---|---|
| Volatile fatty acid | ||
| Acetic acid | 4.76 | |
| Propionic acid | 4.87 | |
| Butyric acid | 4.82 | |
| Valeric acid | 4.82 | |
| Alkalinity | ||
| H2CO3/HCO3− | 6.35 | |
| HCO3−/CO32− | 10.35 | |
| H3PO4/H2PO4− | 2.15 | |
| H2PO4−/HPO42− | 7.20 | |
| HPO42−/PO43− | 12.4 | |
| NH4+/NH3 | 9.24 |
| [HAc]max | 100 | 300 | 500 | 1000 | 3000 | 5000 | 7000 | 10,000 | 13,000 | 15,000 | 17,000 | 20,000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [NaHCO3]max | |||||||||||||
| 100 | |||||||||||||
| 300 | |||||||||||||
| 500 | |||||||||||||
| 1000 | |||||||||||||
| 3000 | |||||||||||||
| 5000 | 1822 * | ||||||||||||
| 7000 | |||||||||||||
| 10,000 | |||||||||||||
| 13,000 | |||||||||||||
| 15,000 | |||||||||||||
| 17,000 | |||||||||||||
| 20,000 | |||||||||||||
| [HAc]max | 100 | 300 | 500 | 1000 | 3000 | 5000 | 7000 | 10,000 | 13,000 | 15,000 | 17,000 | 20,000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [NaHCO3]max | |||||||||||||
| 100 | −1996 | −2002 | −2003 | −2027 | −2013 | ||||||||
| 300 | |||||||||||||
| 500 | |||||||||||||
| 1000 | |||||||||||||
| 3000 | |||||||||||||
| 5000 | −2011 * | ||||||||||||
| 7000 | |||||||||||||
| 10,000 | −2050 | −2016 | |||||||||||
| 13,000 | −1948 | −2000 | |||||||||||
| 15,000 | −2096 | −2033 | |||||||||||
| 17,000 | −2031 | −2014 | |||||||||||
| 20,000 | −2033 | −2031 | |||||||||||
| [HAc]max | 100 | 300 | 500 | 1000 | 3000 | 5000 | 7000 | 10,000 | 13,000 | 15,000 | 17,000 | 20,000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [NaHCO3]max | |||||||||||||
| 100 | |||||||||||||
| 300 | |||||||||||||
| 500 | |||||||||||||
| 1000 | |||||||||||||
| 3000 | |||||||||||||
| 5000 | −219 * | ||||||||||||
| 7000 | |||||||||||||
| 10,000 | |||||||||||||
| 13,000 | |||||||||||||
| 15,000 | |||||||||||||
| 17,000 | |||||||||||||
| 20,000 | |||||||||||||
| [HAc]max | 100 | 300 | 500 | 1000 | 3000 | 5000 | 7000 | 10,000 | 13,000 | 15,000 | 17,000 | 20,000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [NaHCO3]max | |||||||||||||
| 100 | −131 | −120 | −114 | −118 | −123 | −153 | −133 | ||||||
| 300 | −134 | −131 | −133 | −125 | |||||||||
| 500 | −134 | −135 | |||||||||||
| 1000 | |||||||||||||
| 3000 | |||||||||||||
| 5000 | −126 * | ||||||||||||
| 7000 | |||||||||||||
| 10,000 | |||||||||||||
| 13,000 | |||||||||||||
| 15,000 | |||||||||||||
| 17,000 | |||||||||||||
| 20,000 | |||||||||||||
| [HAc]max | 100 | 300 | 500 | 1000 | 3000 | 5000 | 7000 | 10,000 | 13,000 | 15,000 | 17,000 | 20,000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [NaHCO3]max | |||||||||||||
| 100 | 3794 | 3770 | |||||||||||
| 300 | 3770 | 3761 | |||||||||||
| 500 | 3771 | 3774 | |||||||||||
| 1000 | |||||||||||||
| 3000 | |||||||||||||
| 5000 | 3763 * | ||||||||||||
| 7000 | |||||||||||||
| 10,000 | 3805 | ||||||||||||
| 13,000 | 3696 | ||||||||||||
| 15,000 | 3873 | 3792 | 3780 | 3774 | |||||||||
| 17,000 | |||||||||||||
| 20,000 | 3775 | 3789 | 3773 | 3776 | |||||||||
| [HAc]max | 100 | 300 | 500 | 1000 | 3000 | 5000 | 7000 | 10,000 | 13,000 | 15,000 | 17,000 | 20,000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [NaHCO3]max | |||||||||||||
| 100 | |||||||||||||
| 300 | |||||||||||||
| 500 | |||||||||||||
| 1000 | |||||||||||||
| 3000 | |||||||||||||
| 5000 | −11.1 * | ||||||||||||
| 7000 | |||||||||||||
| 10,000 | |||||||||||||
| 13,000 | |||||||||||||
| 15,000 | |||||||||||||
| 17,000 | |||||||||||||
| 20,000 | |||||||||||||
References
- IEA. Renewables 2023; IEA: Paris, France, 2024.
- Sun, H.; Wu, S.; Dong, R. Monitoring Volatile Fatty Acids and Carbonate Alkalinity in Anaerobic Digestion: Titration Methodologies. Chem. Eng. Technol. 2016, 39, 599–610. [Google Scholar] [CrossRef]
- Nordmann, W. Die Überwachung Der Schlammfaulung. KA-Informationen Für Das Betriebspersonal Beil. Zur Korresp. Abwasser 1977, 3, 77. [Google Scholar]
- McGhee, T.J. A Method for Approximation of the Volatile Acid Concentrations in Anaerobic Digesters. Water Sew. Work. 1968, 165, e166. [Google Scholar]
- Nkuna, R.; Roopnarain, A.; Rashama, C.; Adeleke, R. Insights into Organic Loading Rates of Anaerobic Digestion for Biogas Production: A Review. Crit. Rev. Biotechnol. 2022, 42, 487–507. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Guo, J.; Wu, S.; Liu, F.; Dong, R. Development and Validation of a Simplified Titration Method for Monitoring Volatile Fatty Acids in Anaerobic Digestion. Waste Manag. 2017, 67, 43–50. [Google Scholar] [CrossRef]
- Nativ, P.; Gräber, Y.; Aviezer, Y.; Lahav, O. A Simple and Accurate Approach for Determining the VFA Concentration in Anaerobic Digestion Liquors, Relying on Two Titration Points and an External Inorganic Carbon Analysis. ChemEngineering 2021, 5, 15. [Google Scholar] [CrossRef]
- Jenkins, S.R.; Morgan, J.M.; Sawyer, C.L. Measuring Anaerobic Sludge Digestion and Growth by a Simple Alkalimetric Titration. J. Water Pollut. Control Fed. 1983, 55, 448–453. [Google Scholar]
- Kapp, H. Schlammfaulung Mit Hohem Feststoffgehalt. In Stuttgarter Berichte Zur Siedlungswasserwirtschaft; Oldenbourg Verlag: Munich, Germany, 1984; p. 300. [Google Scholar]
- Moosbrugger, R.E.; Wentzel, M.C.; Ekama, G.A.; Marais, G.v.R. A 5 pH Point Titration Method for Determining the Carbonate and SCFA Weak Acid/Bases in Anaerobic Systems. Water Sci. Technol. 1993, 28, 237–245. [Google Scholar] [CrossRef]
- Lahav, O.; Shlafman, E.; Morgan, B.E.; Loewenthal, R.E.; Tarre, S. Accurate On-Site Volatile Fatty Acids (VFA) Measurement in Anaerobic Digestion—Verification of a New Titrative Method. Acad. Edu J. 2002, 9, 118–125. [Google Scholar]
- Lahav, O.; Morgan, B.E.; Loewenthal, R.E. Rapid, Simple, and Accurate Method for Measurement of VFA and Carbonate Alkalinity in Anaerobic Reactors. Environ. Sci. Technol. 2002, 36, 2736–2741. [Google Scholar] [CrossRef]
- DiLallo, R.; Albertson, O.E. Volatile Acids by Direct Titration. J. Water Pollut. Control Fed. 1961, 33, 356–365. [Google Scholar]
- O’Brien, J.E.; Donlan, R.J. Direct Method for Differentiating Bicarbonate and Acetate in Digester Control. In Abstracts of Papers of the American Chemical Society; American Chemical Society: Washington, DC, USA, 1977; Volume 173, p. 121. [Google Scholar]
- Pauss, A.; Roza, A.; Ledrut, M.-J.; Naveau, H.; Nyns, E.-J. Bicarbonate Determination in Complex Acid-Base Solutions by a Back-titration Method. Environ. Technol. 1990, 11, 469–476. [Google Scholar] [CrossRef]
- Zan, F.; Zeng, Q.; Chi, K.; Hao, T.; Ekama, G.A. A Novel Approach for Rapidly Measuring Volatile Fatty Acids in Anaerobic Process. Water Res. 2020, 182, 115960. [Google Scholar] [CrossRef]
- Scherer, P.; Pydde, M.; Antonczyk, S.; Krakat, N. The FOS/TAC (VFA/TIC) Value Put to the Test; German Biogas Association: Freising, Germany, 2021. [Google Scholar]
- Chatterjee, B.; Radhakrishnan, L.; Mazumder, D. New Approach for Determination of Volatile Fatty Acid in Anaerobic Digester Sample. Environ. Eng. Sci. 2018, 35, 333–351. [Google Scholar] [CrossRef]
- Lin, Q.; Yuan, Y.; Zan, F.; Lu, H.; Wang, Z.; Guo, G. A Novel Online Analyzer for Accurate and Rapid Measurement of Volatile Fatty Acids in Anaerobic Wastewater Treatment. J. Environ. Sci. 2022, 122, 72–82. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.; Sun, Y.; Chen, S.; Miao, X. Fast Detection of Volatile Fatty Acids in Biogas Slurry Using NIR Spectroscopy Combined with Feature Wavelength Selection. Sci. Total Environ. 2023, 857, 159282. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Kim, G.-B.; Pandey, A.K.; Park, J.-H.; Kim, S.-H. Prediction of Total Organic Acids Concentration Based on FOS/TAC Titration in Continuous Anaerobic Digester Fed with Food Waste Using a Deep Neural Network Model. Biomass Bioenergy 2024, 190, 107411. [Google Scholar] [CrossRef]
- Mu, Z.-X.; He, C.-S.; Jiang, J.-K.; Zhang, J.; Yang, H.-Y.; Mu, Y. A Modified Two-Point Titration Method for the Determination of Volatile Fatty Acids in Anaerobic Systems. Chemosphere 2018, 204, 251–256. [Google Scholar] [CrossRef]
- Münch, E.V.; Greenfield, P.F. Estimating VFA Concentrations in Prefermenters by Measuring pH. Water Res. 1998, 32, 2431–2441. [Google Scholar] [CrossRef]
- Liu, X.; André, L.; Mercier-Huat, M.; Grosmaître, J.-M.; Pauss, A.; Ribeiro, T. Accurate Estimation of Bicarbonate and Acetic Acid Concentrations with Wider Ranges in Anaerobic Media Using Classical FOS/TAC Titration Method. Appl. Sci. 2021, 11, 11843. [Google Scholar] [CrossRef]
- Buchauer, K. A Comparison of Two Simple Titration Procedures to Determine Volatile Fatty Acids in Influents to Waste-Water and Sludge Treatment Processes. Water SA 1998, 24, 49–56. [Google Scholar]
- Lili, M.; Biró, G.; Sulyok, E.; Petis, M.; Borbély, J.; Tamás, J. Novel Approach on the Basis of FOS/TAC Method. In Proceedings of the Analele Universităţ ii din Oradea, Fascicula Protecţia Mediului, Oradea, Romania, 4–5 November 2011; Volume 17, pp. 713–718. [Google Scholar]
- Jobling Purser, B.J.; Thai, S.-M.; Fritz, T.; Esteves, S.R.; Dinsdale, R.M.; Guwy, A.J. An Improved Titration Model Reducing over Estimation of Total Volatile Fatty Acids in Anaerobic Digestion of Energy Crop, Animal Slurry and Food Waste. Water Res. 2014, 61, 162–170. [Google Scholar] [CrossRef] [PubMed]
- Lahav, O.; Morgan, B. Titration Methodologies for Monitoring of Anaerobic Digestion in Developing Countries? A Review. J. Chem. Technol. Biotechnol. 2004, 79, 1331–1341. [Google Scholar] [CrossRef]
- Vannecke, T.P.W.; Lampens, D.R.A.; Ekama, G.A.; Volcke, E.I.P. Evaluation of the 5 and 8 pH Point Titration Methods for Monitoring Anaerobic Digesters Treating Solid Waste. Environ. Technol. 2015, 36, 861–869. [Google Scholar] [CrossRef]
- Mazzini, S.; Borgonovo, G.; Scaglioni, L.; Bedussi, F.; D’Imporzano, G.; Tambone, F.; Adani, F. Phosphorus Speciation during Anaerobic Digestion and Subsequent Solid/Liquid Separation. Sci. Total Environ. 2020, 734, 139284. [Google Scholar] [CrossRef]

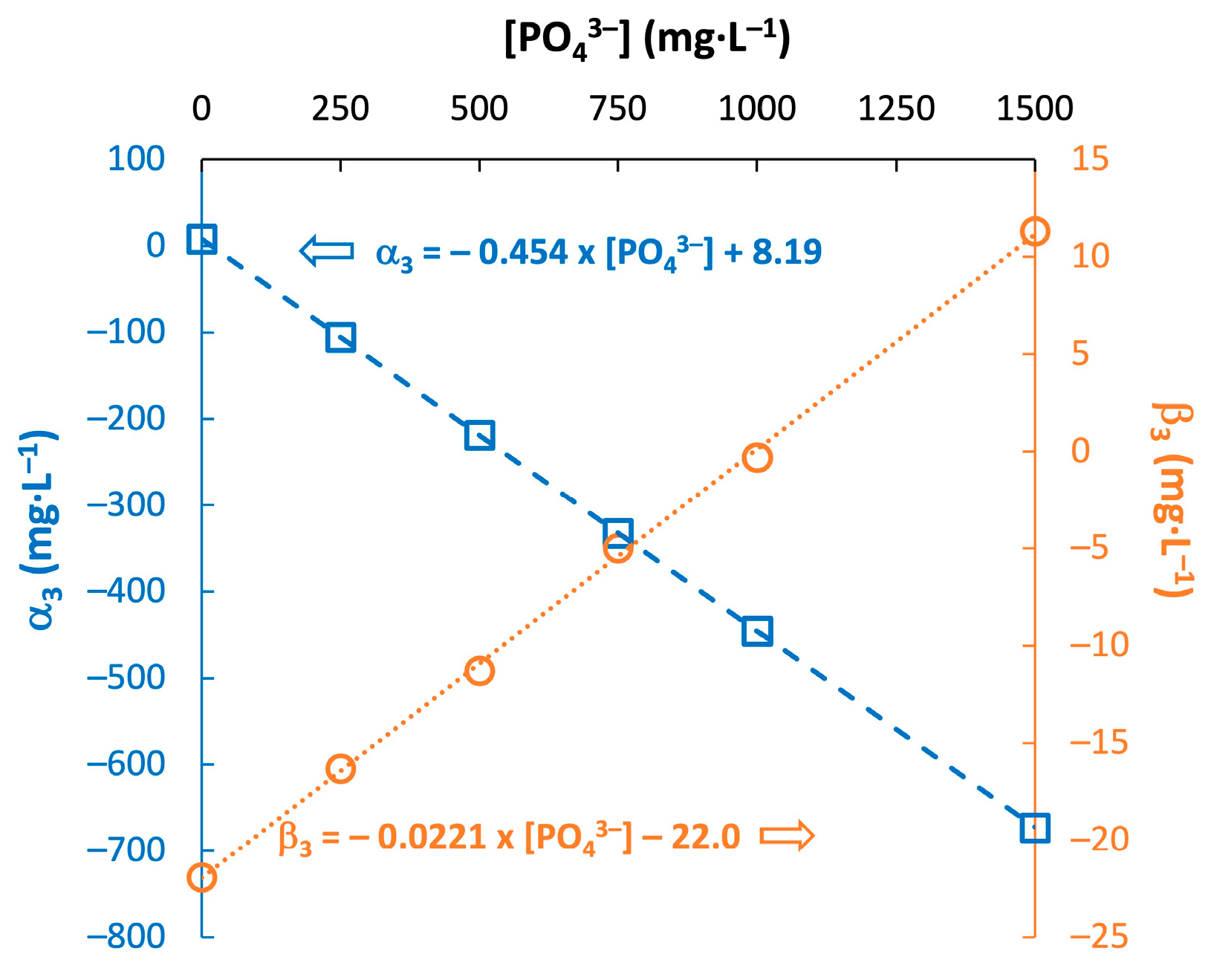
| [PO43−] (mg·L−1) | (mg·L−1) | (mg·L−1) | MAPE for [NaHCO3] (%) | MAPE for [HAc] (%) | ||||
|---|---|---|---|---|---|---|---|---|
| Nordmann’s | Formula 2021 | Formula 2025 | Nordmann’s | Formula 2021 | Formula 2025 | |||
| 0 | 8.06 | −21.9 | 525 | 0.139 | 0.151 | 60.9 | 0.117 | 0.118 |
| 250 | −105 | −16.3 | 539 | 16.4 | 0.151 | 61.0 | 0.880 | 0.135 |
| 500 | −218 | −11.3 | 555 | 33.0 | 0.145 | 61.1 | 1.68 | 0.153 |
| 750 | −333 | −4.99 | 570 | 49.6 | 0.176 | 61.2 | 2.50 | 0.141 |
| 1000 | −445 | −0.290 | 585 | 66.1 | 0.123 | 61.3 | 3.30 | 0.156 |
| 1500 | −673 | 11.3 | 616 | 99.1 | 0.180 | 61.4 | 4.99 | 0.129 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Pauss, A.; André, L.; Ribeiro, T. An Upgraded FOS/TAC Titration Model Integrating Phosphate Effects for Accurate Assessments of Volatile Fatty Acids and Alkalinity in Anaerobic Media. ChemEngineering 2025, 9, 53. https://doi.org/10.3390/chemengineering9030053
Liu X, Pauss A, André L, Ribeiro T. An Upgraded FOS/TAC Titration Model Integrating Phosphate Effects for Accurate Assessments of Volatile Fatty Acids and Alkalinity in Anaerobic Media. ChemEngineering. 2025; 9(3):53. https://doi.org/10.3390/chemengineering9030053
Chicago/Turabian StyleLiu, Xiaojun, André Pauss, Laura André, and Thierry Ribeiro. 2025. "An Upgraded FOS/TAC Titration Model Integrating Phosphate Effects for Accurate Assessments of Volatile Fatty Acids and Alkalinity in Anaerobic Media" ChemEngineering 9, no. 3: 53. https://doi.org/10.3390/chemengineering9030053
APA StyleLiu, X., Pauss, A., André, L., & Ribeiro, T. (2025). An Upgraded FOS/TAC Titration Model Integrating Phosphate Effects for Accurate Assessments of Volatile Fatty Acids and Alkalinity in Anaerobic Media. ChemEngineering, 9(3), 53. https://doi.org/10.3390/chemengineering9030053









