Abstract
Aging is a natural process that is also influenced by some factors like the food someone eats, lifestyle decisions, and impacts on general health. Despite the recognized role of nutrition in modulating the molecular and cellular mechanisms underlying aging, there is a lack of comprehensive exploration into potential interventions that can effectively mitigate these effects. In this study, we investigated the potential anti-aging properties of vitamin D by examining its interactions with key molecular targets involved in aging-related pathways. By using molecular docking and dynamics techniques, we evaluate the interactions and stability of vitamins D2 and D3 with key proteins involved in aging pathways, such as SIRT1, mTOR, AMPK, Klotho, AhR, and MAPK. Our results reveal promising binding affinities between vitamin D and SIRT1 forms, with energy values of −48.33 kJ/mol and −45.94 kJ/mol for vitamins D2 and D3, respectively, in aqueous environments. Moreover, molecular dynamics simulations revealed that the vitamin D3–SIRT1 complex exhibited greater stability compared with the vitamin D2–SIRT1 complex. The study calculated the solvation free energy to compare the solubility of vitamins D2 and D3 in water and various organic solvents. Despite their strong interactions with water, both vitamins exhibited low solubility, primarily due to the high energy cost associated with cavity formation in the aqueous environment. Compared with other solvents, water demonstrated particularly low solubility for both vitamins. This suggested that vitamins D2 and D3 preferred binding to aging receptors over dissolving in bulk aqueous environments, supporting their strong therapeutic interactions with these receptors. These findings shed light on the molecular mechanisms underlying vitamin D’s potential anti-aging effects and lay the groundwork for developing nutraceuticals targeting aging and associated diseases. Understanding these mechanisms holds promise for future interventions aimed at promoting healthy aging and enhancing overall well-being.
1. Introduction
Aging is a multifactorial process marked by a progressive loss of physiological integrity, leading to a decline in tissues’ and organs’ homeostatic and regenerative capacities. This deterioration results in impaired function and increased vulnerability to disease and death [1,2]. Aging is the primary risk factor for major human pathologies, including neurodegenerative and cerebrovascular disorders, cancer, diabetes, and other diseases, which are among the leading causes of mortality in the African region [3,4]. The contributing mechanisms include genomic instability, telomere attrition, epigenetic alterations, loss of proteostasis, deregulated nutrient-sensing, mitochondrial dysfunction, cellular senescence, stem cell exhaustion, and altered intercellular communication [5,6]. These markers are typically associated with increased production of reactive oxidant species and free radicals, which result from a wide range of physiological processes [7,8,9]. That is why the isolation and characterization of compounds that may delay the onset of aging are of utmost importance.
The evidence strongly suggests that interventions targeting aging can delay and prevent the onset of numerous chronic diseases, potentially extending the healthy lifespan in both adults and older individuals [10,11]. Recent advancements in modern medicine have led to interventions that address the underlying mechanisms of aging, thereby promoting longevity [2,12]. These interventions can be broadly categorized into lifestyle changes and pharmaceutical/genetic regulation. Lifestyle changes encompass practices such as caloric restriction and regular physical exercise. In contrast, pharmaceutical/genetic regulation includes a diverse range of chemically unrelated molecules, from natural products and endogenous substances to approved drugs and synthetic compounds. Notable examples include metformin, rapamycin, resveratrol, astaxanthin, curcumin, nordihydroguaiaretic acid, tambulin, and vitamin D, all of which have garnered significant attention for their potential to enhance longevity [7,10,13].
Among numerous factors, vitamin D (Figure 1) emerges as a significant player in slowing the aging process at the cellular and molecular levels, exhibiting a wide range of actions [14]. As a fat-soluble essential nutrient, vitamin D is crucial for cellular processes such as differentiation, proliferation, and apoptosis [15,16]. The elevation of calcitriol [1,25(OH)2D], the active form of vitamin D, stimulates vitamin D nuclear receptors (VDR) throughout the body, triggering the activation of gene transcription [17,18]. The interaction between [1,25(OH)2D] and VDR in various sites produces a multitude of biological actions that impact the potential development of various diseases [18,19]. These biological actions encompass calcium and phosphorus in the intestines and bones (osteoporosis), insulin sensitivity and secretion (diabetes), cellular growth and angiogenesis (immune regulation and cancer), expression of renin, inhibition of vascular smooth muscle proliferation (hypertension and cardiovascular disease), and modulation of inflammation and amyloid plaque formation in the brain (cognitive decline and Alzheimer’s disease) [20,21,22].

Figure 1.
The 2D structure of vitamin D: (A) vitamin D2 and (B) vitamin D3.
The six proteins selected for this study were chosen for their roles in vitamin D metabolism and involvement in key aging-related signaling pathways. Aging is influenced by a network of energy-sensing molecular pathways, and modulating certain components of this network can slow down the aging process and mitigate related disorders [23]. Vitamin D metabolism involves vitamin D receptor (VDR) [24]; vitamin D binding protein (DBP) [25]; and enzymes such as CYP2R1, CYP27B1, and CYP24A1 [26]. VDR regulates gene expression related to calcium and phosphate balance and is present in the nuclei of cells in various tissues including the intestines, kidneys, and bones [27]. DBP, abundant in the serum, transports vitamin D metabolites to target tissues. Enzymes like CYP2R1 and CYP27B1, located in the liver and kidneys, respectively, activate vitamin D, while CYP24A1, found in various tissues, catabolizes it to maintain and regulate its levels [26,27,28].
The examined proteins included Sirtuin1 (PDB: 4ZZI), Mammalian target of rapamycin (PDB: 3FAP), Activated mammalian protein kinase (PDB: 5EZV), Klotho (PDB: 5W21), Mitogen-activated protein kinase (PDB: 1KV2), and Aryl hydrocarbon receptor (PDB: 5NJ8). These proteins’ cellular localization (mainly in the nucleus and cytoplasm) influences their interactions with vitamin D, which affect their role in aging pathways. Understanding these interactions is crucial for elucidating how these proteins contribute to vitamin D homeostasis and its biological effects across key pathways related to cellular repair, metabolism, and stress responses. The in silico approach aimed to provide precise atomistic details of vitamin D’s interaction with aging proteins. Molecular dynamics and electronic structure calculations complemented this by predicting the solvation free energy of vitamin D in water and a range of polar protic, polar aprotic, and non-polar organic solvents to characterize the interactions of vitamin D in bulk aqueous solution compared with an inbound state.
2. Computational Methodologies
2.1. Molecular Docking Calculations
2.1.1. Ligand Preparation
The structures of vitamin D2 (Ergocalciferol, CAS: 50-14-6) and D3 (Cholecalciferol, CAS: 67-97-0) were obtained from the PubChem database [29] with CIDs 5280793 and 5280795, respectively. Ligands were energy minimized using an MMFF94 force field [30] in Open Babel [31], and hydrogen atoms (at a pH of 7.4) with Gasteiger atomic charges were added using AutoDock tools [32]. Finally, structures were converted to pdbqt format, as required by AutoDock Vina v1.1.2 [32] for docking simulations.
2.1.2. Protein Preparation
The crystallographic structures of anti-aging proteins were obtained from the research collaborative for structural biology (RCSB) Protein Data Bank (PDB) [33]. The proteins included in the study were Sirtuin 1 (PDB: 4ZZI), Mammalian target of rapamycin (PDB: 3FAP), Activated mammalian protein kinase (PDB: 5EZV), Klotho (PDB: 5W21), Mitogen-activated protein kinase (PDB: 1KV2), and Aryl hydrocarbon receptor (PDB: 5NJ8).
Proteins were prepared by removing crystallographic water, ions, and co-crystallized ligands. Missing side chain residues, Gasteiger charges [34], and polar hydrogen were added using the AutoDock tool to reflect a physiological pH of 7.4 [32]. Both blind and grid docking simulations were performed, where in the former, proteins were set as the whole receptor, allowing ligands to self-recognize binding pockets. For grid-based molecular docking, binding pockets were identified using a co-crystallized ligand, and the grid box for each protein was specified. The two grid docking simulations were performed, with and without water molecules at the binding site, which followed a well-established protocol by [35]. After molecular docking, the complex with the highest binding affinity was subjected to a relaxed complex scheme (RCS) to accommodate protein flexibility. A molecular dynamics simulation was conducted, and a total of 20 snapshots were extracted at every 5 ns. These structures were prepared and subjected to molecular docking. The results were recorded and compared with single-protein structures.
2.2. Molecular Dynamic (MD) Simulation
To investigate the structural dynamics and stability of protein–ligand complexes, molecular dynamics (MD) simulation was conducted using Gromacs version 2018 (https://manual.gromacs.org/2018/download.html, accessed on 1 July 2024) [30]. The simulation was performed to compare SIRT1 with the vitamin D complex (holo) and the non-bonded Sirt1 (apo). Sirtuin 1 protein was selected based on its overall high binding affinity obtained in the molecular docking simulation. The protein topology was generated using the OPLS-AA force field [36], and ligand topologies were generated using the LigPerGen tool [37,38]. The systems were immersed in a cubic simulation box of 10.0 nm, 10.0 nm, and 10.0 nm dimensions with a distance of 1 nm from the edge of the box on both sides, solvated with the TIP4P water model [39], followed by the addition of 5 sodium counter ions at a concentration of 0.15 M for neutralization [40]. The systems were energy minimized using the steepest descent algorithm to avoid artifacts with a convergence criterion of maximum force not greater than 1000 kJ/mol (fmax ≤ 1000 kJ/mol). Subsequently, the systems were equilibrated in a constant number of particles, volume, and temperature (NVT), followed by a constant number of particles, pressure, and temperature (NPT) both for 0.5 ns and a production run for 100 ns. During equilibration and production, a v-rescale thermostat [41] was used for temperature coupling at 300 K and a Parrinello–Rahman barostat [42] for pressure coupling at 1 bar. The particle mesh Ewald (PME) [43,44] was used to treat long-range electrostatic interactions, with a cutoff distance of 12 Å for electrostatic and van der Waals interactions. Covalent bonds were constrained by LINCS [45]. During the simulation, periodic boundary conditions (PBC) [46] were applied in all directions, and an integration time step of 2 fs was used throughout the production using the Leap-frog integration algorithm [47]. The stability of the complex was assessed using metrics such as root mean square deviation (RMSD), radius of gyration (Rg), pose RMSD, and center of mass distance.
After production, the MD trajectory of the apoprotein was utilized to generate 20 snapshots, extracted at 5 ns intervals. These snapshots were then used in the relaxed complex scheme (RCS) docking calculations.
2.3. Binding Free Energy Calculated by Molecular Mechanics–Poisson–Boltzmann and Surface Area (MM-PBSA)
Free energy governs all cellular biochemical processes [48]. Although molecular mechanics-based scoring functions used in ligand docking are computationally efficient and cost-effective, they are less accurate [49]. End-point methods like MM-PBSA offer a favorable balance between the higher computational demands of alchemical methods and the simplicity of molecular docking scoring functions [50].
The study utilized the endpoint free energy method based on MM-PBSA to evaluate the binding affinity of vitamin D. The binding free energy calculation (∆Gbind) was performed on the complexes of vitamins D2 and D3, obtained from the MD run. The g_mmpbsa tool integrated within Gromacs [51] was used to estimate the solvation free energy (∆Gsolv) by combining polar and non-polar components. A total of 200 frames were evenly sampled at a predetermined time of 500 ps and subjected to MM-PBSA calculations. In MM-PBSA, the standard MM energy terms from bonded (bond, angle, and dihedral), electrostatic, and van der Waals ∆EMM were calculated in the gas phase. The polar component (∆GPB) was evaluated by solving the Poisson–Boltzmann equation linearly, employing a grid spacing of 0.5 Å. The solvent dielectric constant (ε) was set to 80, while the solute’s dielectric constant was set to 2. The non-polar component (∆GSASA) was calculated based on the solvent-accessible surface area (SASA), utilizing the constants for the non-polar solvation energy gamma (γ) value of 0.0226 kJ/(mol Å−2) and b = 3.84928 kJ/mol [51]. In the g_mmpbsa tool, all energy terms were calculated individually and then combined to assess the contribution of each residue to the overall binding energy.
2.4. Solvation Free Energy Calculations
The solvation free energy of vitamins D2 and D3 was predicted in bulk solvents using molecular dynamics and electronic structure calculations with the uESE (universal Easy Solvation Estimation) continuum solvation model [52,53,54]. The molecular dynamics solvation free energy calculations followed exactly our previous work [55], except here we used geometric mixing rules for Lennard–Jones cross interactions consistent with the OPLS-AA force field. Molecular simulations were performed for vitamins D2 and D3 in the organic solvents’ ethanol, butanone, and cyclohexane. The organic solvents were modeled using OPLS-AA with force fields generated using the LigPerGen tool. Water was modeled using TIP4P. In summary, we first equilibrated simulation boxes containing a single solute molecule (vitamin D2 or D3) in solution. The number of solvent molecules was chosen to obtain a cubic box with an edge length of approximately 4.6 nm. The initial structures were generated using Packmol [56], and then we subsequently performed 3000 steps of steepest descent minimization to remove any bad contacts. We then performed a total of 14 ns of equilibration in the NPT ensemble. The minimization and all molecular dynamics calculations were performed using GROMACS version 2020.2 (https://manual.gromacs.org/2020.2/download.html, accessed on 1 July 2024).
The equilibrated structures were then used as the initial structures for the free energy calculations. The solvation free energy was computed using the multi-state Bennett’s acceptance ratio method (MBAR) [57]. The solute–solvent intermolecular interactions were coupled/decoupled using 15 total stages, where an independent 22 ns NPT simulation was performed for each stage. In the first stage (m = 0), the solute–solvent interactions were turned off, corresponding to the solute in a non-interacting ideal gas state. From stages m = 1 to 10, the solute–solvent electrostatic interactions remained off, while the solute–solvent intermolecular Lennard–Jones interactions were gradually turned on using a “soft-core” potential [57]. Then from states m = 10 to 14, the Lennard–Jones interactions were at full strength, while the solute–solvent electrostatic interactions were gradually turned on. The change in free energy in going from m = 0 (non-interacting) to m = 14 (fully interacting) corresponded to the solvation free energy. We termed the Lennard–Jones contribution the change in going from m = 0 to m = 10 (full Lennard–Jones interactions and no electrostatic interactions). And the change in going from m = 10 to m = 14 we termed the electrostatic contribution.
Compared with the molecular dynamics simulation, using electronic structure calculations with uESE was computationally less expensive and allowed for the solvation free energy to readily be computed in a range of 91 organic solvents and water. For these calculations, the first 3D structures of vitamins D2 and D3 were generated from SMILES using open Babel 3.0.0 [31,58,59]. The structures were generated by performing a conformational search with geometry optimization (--gen3d --best) using the General Amber Force Field (GAFF) with Electronegativity Equalization Method (EEM) atomic partial charges (--ff gaff –partial charge eem2015ba). Subsequently, a single-point energy calculation was performed with the B3LYP/def2-TZVP theory/basis set to obtain CM5 atomic charges using Gaussian 16 Revision C.01 [60,61]. The structure and CM5 atomic charges were then used to predict the solvation free energy with uESE, using freely available software provided by the uESE developers [62]. Free energy calculations were made in all 92 solvents (including water) for which uESE was parameterized.
3. Results and Discussion
3.1. Molecular Interactions of Vitamin D with Key Aging-Related Proteins
Our investigation into vitamin D’s anti-aging potential started with evaluating its binding affinity with several key aging proteins. To elucidate how vitamin D modulated aging effects, we selected six aging receptors known as molecular targets in aging research. Three distinct docking simulations were conducted: docking with a grid, blind docking (without a grid), and hydrated docking. Both vitamin D2 and vitamin D3 were docked to each protein, with ten independent docking calculations performed for each.
When assessing the docking results of vitamins D2 and D3 with grid settings, only SIRT1 (4ZZI) exhibited a favorable binding affinity compared with the other receptors. Notably, when moving from grid to blind docking, we observed a decreased binding affinity, indicating reduced self-recognition and binding ability of vitamin D to the six aging receptors investigated in this work. Interestingly, upon hydrating the receptors, an improvement in affinity was observed (Figure 2). It is crucial to highlight that among all aging receptors, SIRT1 (4ZZI) and Mitogen-activated protein kinase, MAPK, (1KV2) consistently demonstrated superior docking affinity across all simulations. This finding suggests that vitamin D’s anti-aging potential may stem from its ability to target these two proteins, effectively activating their functions. The binding distribution for all proteins is illustrated in Figures S2–S4 with SIRT1 consistently exhibiting higher rankings.
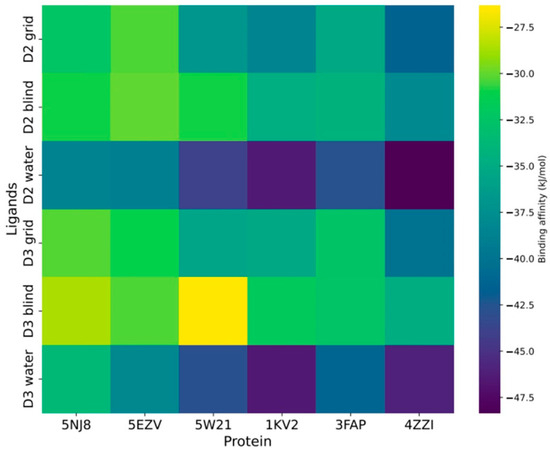
Figure 2.
Proteomic binding landscape of vitamin D (D2 and D3) across the aging receptors.
Further investigation into the origin of the difference in binding affinity led us to focus on SIRT1 (4ZZI), which displayed favorable binding affinities of −37.99 and −34.85 kJ/mol for vitamins D2 and D3, respectively. As depicted in Figure 3, a double bond in the alkyl group of D2 contributed to its increased activity and stronger binding affinity compared with its saturated counterpart, D3. The documented effect of double bonds in the alkyl group enhancing molecule reactivity and binding affinity further supports this observation [25]. Figure 3A highlights that the double bonds in D2 facilitated interactions with residues Try280, Ile347, and Phe273. Although D3 also exhibited similar interactions with these residues, the absence of interaction with Try280 (Figure 3B) may explain its lower binding affinity compared with D2. Both grid and blind docking resulted in vitamins D2 and D3 binding to the active site in a similar manner (Figure 3C,D). However, the reduced activity observed in blind docking simulations may stem from the inherent conformations of vitamin D when attempting to accommodate it into the active site.
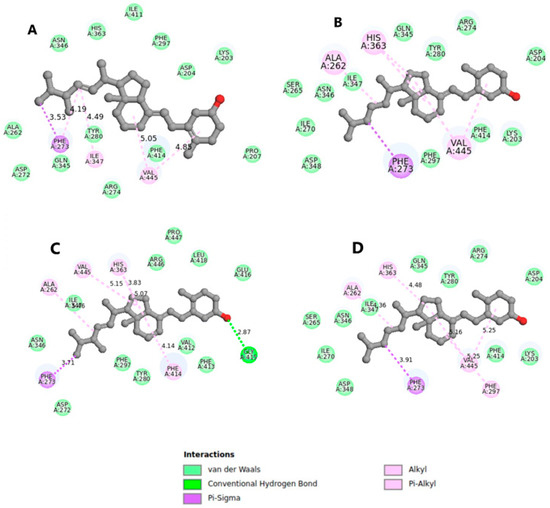
Figure 3.
Binding orientation for the blind (A,B) and grid (C,D) when SIRT1 docked with vitamins D2 and D3, respectively, with explicit hydrogen removed for clarity.
Water molecules played a crucial role in protein–ligand interactions by stabilizing protein structures, shaping protein conformations, enhancing binding free energy, and mediating intermolecular interactions [63,64,65]. Hydrating the proteins led to an increase in binding affinity, particularly evident in SIRT1 (4ZZI), where vitamin D2 exhibited the strongest affinity of −48.33 kJ/mol compared with vitamin D3 with a binding affinity of −45.94 kJ/mol. These findings suggest that water molecules could significantly influence the design of anti-aging molecules, with the interaction of SIRT1 with vitamin D2 favored by water molecules in the active site.
Accommodating Receptor Flexibility: The Relaxed Complex Scheme (RCS)
To account for receptor flexibility, we employed a relaxed complex scheme (RCS) to enhance the sensitivity of ligand docking to the receptor. Our results, as depicted in Figure 4, revealed the docking scores of both crystal structures and an ensemble structure of SIRT1. Notably, the average binding affinities of the ensemble structure with vitamins D2 and D3 were −32.79 kJ/mol and −31.12 kJ/mol, respectively. In contrast, the crystal structure from blind docking exhibited higher average binding affinities of −37.99 kJ/mol for D2 and −34.85 kJ/mol for D3. Similarly, grid-based docking demonstrated even greater average binding affinities of −41.38 kJ/mol for D2 and −40.08 kJ/mol for D3. Our findings suggest that both blind and grid docking outperformed the ensemble docking approach, likely due to the rigidity of the receptor in blind and grid docking, resulting in minimal variations in binding affinity compared with ensemble docking. This indicated a higher likelihood of a specific receptor conformation extracted from snapshots matching those used in grid and blind docking. Overall, our study underscores the importance of considering receptor flexibility in molecular docking studies and highlights the utility of the relaxed complex scheme in elucidating the influence of receptor dynamics on ligand binding affinity.
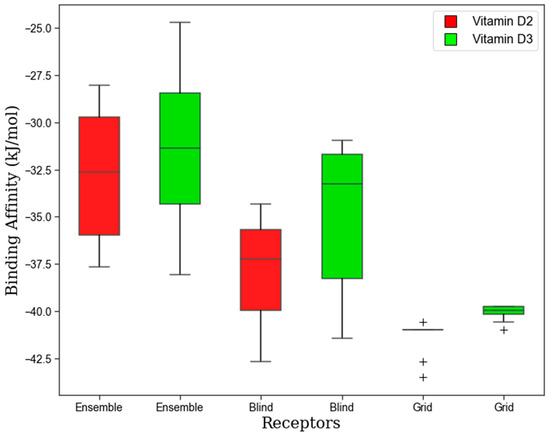
Figure 4.
The binding affinity for vitamins D2 and D3 with SIRT1 receptor from ensemble structure and crystal structure.
3.2. Molecular Dynamics Simulation
3.2.1. Structural Stability and Compactness
The reliability of the docking results can be compromised due to inherent limitations of the docking algorithm, particularly in fully incorporating protein hydration and global flexibility. To further elucidate the observed binding affinity of vitamin D with aging receptors, we conducted molecular dynamics (MD) simulations. Sirtuin 1, consistently ranking high in all docking simulations, was chosen as a model to study complex stability over time. Two reaction coordinates, root mean square deviation (RMSD) and radius of gyration (Rg), were employed to assess the complex stability. While RMSD measured structural deviation over time relative to the initial configuration, the Rg provided insights into SIRT1–vitamin D complex compactness.
The time-dependent values for RMSD and Rg (Figures S5–S7) revealed an increased RMSD and Rg for the vitamin D2 complex compared with the apo structure. In Figure 5A, the 2D free energy surface illustrated two energy minima with RMSD values of 0.3 and 0.5 nm and Rg values of 2.10 and 2.14 nm. An RMSD value of 0.5 nm coupled with an increased Rg value of 2.14 nm suggested reduced stability and compatibility of the complex. Conversely, the complex formed by vitamin D3 exhibited a single free energy minimum at an RMSD value of 0.35 nm and an Rg value of 2.06 nm as shown in Figure 5B. The free energy surface indicated a strong complex formation between vitamin D3 and the SIRT1 receptor. These observations contrasted with the docking results, which suggested a good affinity for vitamin D2.
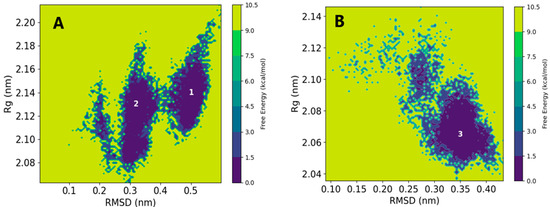
Figure 5.
The 2D free energy surface as a function of RMSD and Rg for SIRT1: (A) vitamin D2 and (B) vitamin D3.
Overall, the structural stability analysis suggests that vitamin D3 forms a more stable complex and does not induce conformational fluctuations in the SIRT1 receptor. These findings highlight the importance of employing MD simulations to complement docking studies and provide a more comprehensive understanding of ligand–receptor interactions.
3.2.2. Vitamin D Fluctuation within Sirtuin 1 Receptor
In computational drug design, the efficacy of a drug can be assessed by its residence time or by exploring its fluctuations within its binding pocket. In the latter case, higher fluctuations of a drug molecule may indicate increased entropy, resulting in weaker affinity and potentially rendering it ineffective. To investigate this phenomenon, we analyzed two reaction coordinates that provided insights into ligand fluctuations: pose RMSD, which measured changes in the drug’s orientation over time, and the center of mass distance (dCOM) between selected residues in the pocket and the drug molecule.
The time-dependent pose RMSD (Figure S7) revealed that both D2 and D3 exhibited minimal changes in the active site. Notably, D3 displayed a slight increase in pose RMSD, possibly due to internal rearrangements in the active site, while D2 showed minimal changes, suggesting good efficacy. Pose RMSD values ≤ 0.4 nm indicated minimal alterations in the binding mode, implying strong activity.
The 1D free energy for dCOM demonstrated a flat, deep energy minimum for D3 at distances ranging from 0.15 to 0.2 nm (Figure 6C). However, D2 exhibited a deep energy minimum at a distance of 0.35 nm. The observed increase in distance from 0.2 to 0.35 nm suggested some weak interaction for D2 in a complex. In Figure 6A,B, we present the 2D FES as a function of the two reaction coordinates. D2 displayed a stable minimum with distance fluctuations ranging from 0.2 to 0.45 nm, accompanied by minor changes in its binding pose (Figure 6A). Conversely, D3 exhibited a smaller distance with a slight increase in pose RMSD to 0.35 nm (Figure 6B). Visual analysis suggests that both D2 and D3 interacted within the SIRT1 pocket, albeit with fluctuations. Internal fluctuations indicated that although both D2 and D3 interacted similarly, D3 was somehow favored, demonstrating good efficacy. To confirm this observation, we conducted end-point free energy calculations based on MM-PBSA, as described in the next subsection.
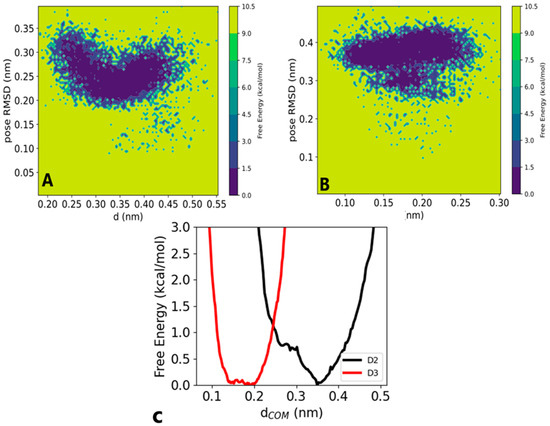
Figure 6.
The 2D free energy surface (FES) as a function of pose RMSD and distance for (A) vitamin D2 at (0.35, 0.24) nm and (B) vitamin D3 at (0.15, 0.38) nm. (C) The 1D free energy for the center of mass distance, D3 ranging from 0.15 nm to 0.2 nm and D2 at 0.35 nm.
3.3. MM-PBSA Binding Free Energy Calculation
The MM-PBSA calculations offered quantitative insights into protein–ligand binding energetics, complementing docking, and MD simulation results. Table 1 presents binding free energy values, with the vitamin D3–SIRT1 complex exhibiting a higher binding free energy compared with the vitamin D2–SIRT1 complex. The MD results showed vitamin D3’s stability and burial in the SIRT1 pocket aligned with the high contribution of electrostatic interactions to complex stabilization. Non-polar interactions also stabilized the vitamin D3–SIRT1 complex when compared with the vitamin D2–SIRT1 complex. However, the higher polar interaction in vitamin D3–SIRT1 led to a decrease in other forms of interaction. Importantly, MM-PBSA binding free energy values suggested that vitamin D3 was more stable than vitamin D2 as shown by their binding energies.

Table 1.
The binding free energy (kJ/mol) of vitamin D–SIRT1 complexes calculated using the MM-PBSA approach.
The energy contributions to protein–ligand binding were further analyzed to highlight disparities in the binding free energy between vitamin D2 and vitamin D3. Figure 7 displays energy contributions from various residues, with both vitamins adopting distinct orientations and interacting with different amino acids within the binding pocket. Interactions with residues His363, Phe414, Phe273, and Ile316 were consistently observed across all complexes, albeit with varying energetic contributions.
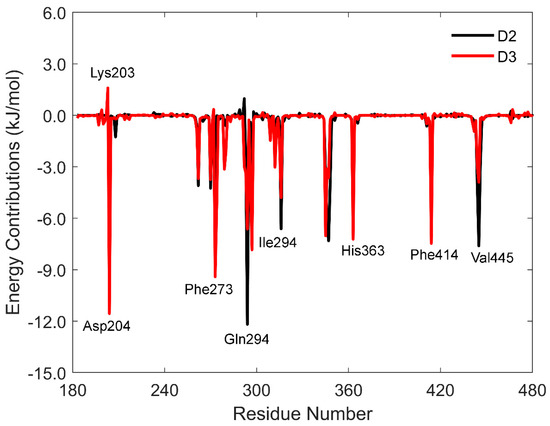
Figure 7.
The MM-PBSA binding free energy calculations showing energy contribution per residue for vitamin D.
An interesting distinction was observed between the vitamin D2 complex and the vitamin D3 complex. In the vitamin D2 complex, residues Asp292 (0.97 kJ/mol) and Lys203 (1.59 kJ/mol) contributed unfavorably to the total binding free energy, while Gln294 played a significant role. In contrast, the vitamin D3 complex was influenced by Asp204 as a major contributor (Figure 7). Both Gln294 and Asp203 formed conventional hydrogen bonds with the hydroxyl groups of vitamin D, highlighting their roles in complex stability.
3.4. Solvation Free Energy Calculations
In Table 2 and Table 3 we summarize the molecular dynamics solvation free energy calculations of vitamins D2 and D3, respectively, in water and a representative polar protic (ethanol), polar aprotic (butanone), and non-polar (cyclohexane) solvent. As described earlier, the total solvation free energy (non-interacting to fully interacting solute), ΔGsolv, is written as a sum of an electrostatic contribution resulting from solute–solvent intermolecular electrostatic interactions (full Lennard–Jones and no electrostatic to full electrostatic) and a Lennard–Jones (LJ) contribution (non-interacting to full Lennard–Jones and no electrostatic interactions). The electrostatic contribution captured association and long-range interactions between the solute and solvent, while the LJ contribution accounted for cavity formation and short-range dispersion and repulsion interactions. In our discussion of solvation free energy, remember that the solvation free energy corresponded to the transfer of the solute from a non-interacting ideal gas state to a solution at the same molar density. Therefore, the lower the solvation free energy, the greater the affinity of the solute for the solution.

Table 2.
The total solvation free energy of vitamin D2 (kJ/mol) in water and a representative polar protic (ethanol), polar aprotic (butanone), and non-polar (cyclohexane) solvent. The solvation free energy is broken down into a contribution from solute–solvent electrostatic intermolecular interactions (“electrostatic”) and Lennard–Jones intermolecular interactions (“LJ”).

Table 3.
The total solvation free energy of vitamin D3 (kJ/mol) in water and a representative polar protic (ethanol), polar aprotic (butanone), and non-polar (cyclohexane) solvent. The solvation free energy is broken down into a contribution from solute–solvent electrostatic intermolecular interactions (“electrostatic”) and Lennard–Jones intermolecular interactions (“LJ”).
In Table 4 and Table 5 we summarize the solvation free energy calculations with the uESE of vitamins D2 and D3, respectively, in the same solvents considered using molecular dynamics simulations. Within uESE, the total solvation free energy, ΔGsolv, is likewise written as a sum of an electrostatic contribution resulting from solute–solvent intermolecular electrostatic interactions and a second “correction” term that accounts for cavity formation and dispersion and repulsion interactions.

Table 4.
The total solvation free energy of vitamin D2 (kJ/mol) in water and a representative polar protic (ethanol), polar aprotic (butanone), and non-polar (cyclohexane) solvent. The solvation free energy is broken down into a contribution from solute–solvent electrostatic intermolecular interactions (“electrostatic”) and a second term accounting for all other effects (“correction”).

Table 5.
The total solvation free energy of vitamin D3 (kJ/mol) in water and a representative polar protic (ethanol), polar aprotic (butanone), and non-polar (cyclohexane) solvent. The solvation free energy is broken down into a contribution from solute–solvent electrostatic intermolecular interactions (“electrostatic”) and a second term accounting for all other effects (“correction”).
Considering the electrostatic contribution, for both vitamins D2 and D3, we found that water < ethanol < butanone < cyclohexane. Vitamins D2 and D3 contain a single hydroxyl (OH) group capable of donating and accepting a hydrogen bond, so this trend was not unexpected. Both molecular dynamics and uESE predicted the same qualitative trend. We do note, however, that the numerical values were different. As compared with the molecular dynamics predictions, uESE predicted that the electrostatic contributions in water, ethanol, and butanone did not vary significantly.
Next, considering the LJ contribution from the molecular dynamics calculations, we found that water > ethanol > butanone > cyclohexane. Moreover, in general, the change in LJ contribution was much greater than the change in the electrostatic contribution, thus dictating the trend in the total solvation free energy that water > ethanol > butanone > cyclohexane. For the case of vitamin D2, while the electrostatic contribution was 11.53 kJ/mol lower in water than in ethanol, the LJ contribution was 62.20 kJ/mol greater in water than in ethanol. This led to a total solvation free energy that was 50.67 kJ/mol greater in water than in ethanol.
Considering the correction term for the uESE calculations, we likewise found that water > methanol > butanone, and while butanone < cyclohexane, the difference was small as compared with water and the polar solvents. For water and the polar solvents, we found that the change in the correction term was much greater than the change in the electrostatic term and dictated the trend in the total solvation free energy that water > ethanol > butanone. As compared with the molecular dynamics results, uESE did predict butanone < cyclohexane; nonetheless, the difference between cyclohexane and water was comparable.
PubChem reports that both vitamins D2 and D3 are insoluble in water (PubChem—Cholecalciferol, 2024; PubChem—Ergocalciferol, 2024). The results here suggest that while vitamins D2 and D3 can hydrogen bond favorably with water, the cavity formation is highly unfavorable, and that is a reason for the poor aqueous solubility. The difference in the total solvation free energy between two solvents is equivalent to the transfer-free energy and is directly related to the log partition coefficient or log relative solubility. Using the uESE results, comparing water and ethanol, the results suggest the solubility is 1011 and 108 times larger in methanol for vitamins D2 and D3, respectively. Comparing water and cyclohexane, the results suggest the solubility is 1014 and 1010 times larger in cyclohexane methanol for vitamins D2 and D3, respectively.
The results corroborate our finding that the binding affinity of vitamins D2 and D3 increased (or the binding free energy decreased) in an aqueous environment. Given the unfavorable cavity formation of vitamins D2 and D3 in water leading to poor aqueous solubility, it was preferable for vitamins D2 and D3 to be bound to the protein as compared with being solvated in bulk water.
While there were differences between the molecular dynamics and the uESE results presented in the manuscript, both led to the same result that vitamins D2 and D3 had a relatively poor aqueous solubility as a result of the unfavorable process of carving a cavity in solution. For the case of water, this would involve disrupting water’s hydrogen bond network, which includes overcoming favorable water–water hydrogen bonds. The advantage of using uESE was we could readily perform calculations in water and 91 organic solvents with significantly less computational cost. In the Supporting Information accompanying the electronic version of this manuscript, we tabulated the total solvation free energy and its contributions for vitamins D2 and D3 in all 92 solvents computed using uESE.
4. Conclusions
The current study offers insights into the potential mechanisms of vitamin D as an anti-aging agent, focusing specifically on its interaction with various protein targets, notably Sirtuin 1 (SIRT1). Utilizing molecular docking techniques, the research analyzed binding affinity values, revealing that SIRT1 displayed a significant binding affinity with both forms of vitamin D. This led to further exploration of its stability through molecular dynamics simulations.
The results from molecular docking, RCS, and classical MD simulations suggest that vitamin D may serve as an activator of Sirtuin 1 (SIRT1) [66]. Upon activation, SIRT1 plays a crucial role in regulating cellular longevity and metabolism by deacetylating proteins that control gene expression, including those involved in aging processes [67]. Since SIRT1 is primarily localized in the nucleus, it can interact with transcription factors that work alongside the Vitamin D Receptor (VDR). This interaction enhances VDR activity by promoting deacetylation, thereby modulating vitamin D’s effects on gene expression related to hallmarks of aging such as inflammation and stress resistance [68].
The solvation free energy calculation compared the solubility of vitamins D2 and D3 in water relative to other organic solvents. It was observed that even though both vitamins D2 and D3 strongly interacted with water, the overall solubility was low due to a higher correction contribution, which was highly attributed by unfavorable higher cavity formation in water. Even when compared with other solvents, water scored a low solubility; these findings verified that vitamins D2 and D3 preferred to interact with SIRT1 than in a bulk aqueous environment strongly.
Our study provides insights into the interactions, stability, and solubility of vitamin D and anti-aging proteins. While these findings suggest that vitamin D may support healthy aging, particularly through its interactions with proteins, further research is necessary to establish a direct link between these molecular interactions and the management of specific human pathologies. Although it is well documented that adequate vitamin D levels contribute to overall health, our results do not directly confirm that vitamin D alone can mitigate human diseases. Therefore, we recommend continued exploration of vitamin D’s therapeutic potential, combining experimental studies with clinical trials to better understand its role in disease prevention and health promotion.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/chemengineering8050104/s1: Figure S1: Conformational changes of different conformers indicating their RMSD for (A) 2ZC9 (B) 2ZDA (C) 2ZFP (D) 2ZGB (E) 2ZHQ (F) 2ZIQ. Figure S2: Binding affinity of vitamin D2 and D3 across anti-aging receptors in blind docking. Figure S3: Binding affinity of vitamin D2 and D3 against anti-aging receptors for grid-based docking. Figure S4: The binding affinity of vitamin D2 and D3 against anti-aging receptors in a hydrated system. Figure S5: Time-dependent RMSD values for apo and holo of Sirt1 with vitamin D. Figure S6: Time-dependent Rg values for apo and holo proteins of Sirt1 with vitamin D. Figure S7: Time-dependent pose RMSD values of vitamin D to the Sirt1 pocket’s residues. The Supplementary Materials also includes: “a spreadsheet containing the results of all of the uESE solvation free energy calculations for Vitamin D2 and D3 in water and 92 solvents”.
Author Contributions
Conceptualization, J.R., E.T. and D.M.S.; methodology, D.M.S., L.P. and E.T.; validation, L.P., J.R., D.M.S., A.S.P. and M.C.; formal analysis, E.T., L.P., D.M.S. and A.S.P.; investigation, E.T., L.P., D.M.S. and A.S.P.; resources, L.P., D.M.S. and A.S.P.; data curation, D.M.S.; writing—original draft preparation, E.T., L.P., J.R., D.M.S., A.S.P. and M.C.; writing—review and editing, E.T., L.P., J.R., D.M.S., A.S.P. and M.C.; visualization, E.T., L.P., D.M.S. and A.S.P.; supervision, L.P., J.R., D.M.S., A.S.P. and M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article or Supplementary Materials.
Acknowledgments
Computational resources for the solvation free energy calculations (molecular dynamics and electronic structure calculations) were provided by the Ohio Supercomputer Center (Ohio Supercomputer Center, 1987); all calculations were performed on the Owens Cluster. Also, we are grateful to NM-AIST for providing a conducive environment for this work. DMS acknowledges the AGNES junior research grant award. We are humbled to submit this manuscript in honor of William Acree, Jr. Acree’s work is inspirational in that he not only has developed efficient methods to predict phase behavior, but his use of simple physical descriptors related to intermolecular interactions can be used to provide invaluable insight for design applications. On a personal note, one of us (ASP) is grateful for the encouragement and friendship he has received from Acree while a junior faculty. I (ASP) have since strived to emulate this positive behavior and will always be grateful for the impact Acree has had on me.
Conflicts of Interest
The authors confirm that there are no conflicts of interest.
References
- Rando, T.A. Stem cells, ageing and the quest for immortality. Nature 2006, 441, 1080–1086. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, K.L. Stem cell aging. Mech. Ageing Dev. 2021, 193, 111394. [Google Scholar] [CrossRef]
- Coughlan, K.A.; Valentine, R.J.; Ruderman, N.B.; Saha, A.K. AMPK activation: A therapeutic target for type 2 diabetes? Diabetes Metab. Syndr. Obes. 2014, 7, 241–253. [Google Scholar] [CrossRef]
- López-Otín, C.; Kroemer, G. Hallmarks of Health. Cell 2021, 184, 33–63. [Google Scholar] [CrossRef]
- López-Otín, C.; Blasco, M.A.; Partridge, L.; Serrano, M.; Kroemer, G. The Hallmarks of Aging. Cell 2013, 153, 1194–1217. [Google Scholar] [CrossRef]
- Mittelbrunn, M.; Kroemer, G. Hallmarks of T cell aging. Nat. Immunol. 2021, 22, 687–698. [Google Scholar] [CrossRef] [PubMed]
- De Sousa Lages, A.; Lopes, V.; Horta, J.; Espregueira-Mendes, J.; Andrade, R.; Rebelo-Marques, A. Therapeutics That Can Potentially Replicate or Augment the Anti-Aging Effects of Physical Exercise. Int. J. Mol. Sci. 2022, 23, 9957. [Google Scholar] [CrossRef] [PubMed]
- Paredes-López, O.; Cervantes-Ceja, M.L.; Vigna-Pérez, M.; Hernández-Pérez, T. Berries: Improving Human Health and Healthy Aging, and Promoting Quality Life—A Review. Plant Foods Hum. Nutr. 2010, 65, 299–308. [Google Scholar] [CrossRef]
- Tosato, M.; Zamboni, V.; Ferrini, A.; Cesari, M. The aging process and potential interventions to extend life expectancy. Clin. Interv. Aging 2007, 2, 401–412. [Google Scholar]
- Grabowska, W.; Sikora, E.; Bielak-Zmijewska, A. Sirtuins, a promising target in slowing down the ageing process. Biogerontology 2017, 18, 447–476. [Google Scholar] [CrossRef]
- Russo, G.L.; Spagnuolo, C.; Russo, M.; Tedesco, I.; Moccia, S.; Cervellera, C. Mechanisms of aging and potential role of selected polyphenols in extending healthspan. Biochem. Pharmacol. 2020, 173, 113719. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.; Lee, Y.D.; Wagers, A.J. Stem cell aging: Mechanisms, regulators and therapeutic opportunities. Nat. Med. 2014, 20, 870–880. [Google Scholar] [CrossRef]
- Pignatti, C.; D’Adamo, S.; Stefanelli, C.; Flamigni, F.; Cetrullo, S. Nutrients and Pathways that Regulate Health Span and Life Span. Geriatrics 2020, 5, 95. [Google Scholar] [CrossRef]
- Fantini, C.; Corinaldesi, C.; Lenzi, A.; Migliaccio, S.; Crescioli, C. Vitamin D as a Shield against Aging. Int. J. Mol. Sci. 2023, 24, 4546. [Google Scholar] [CrossRef]
- Sosa-Díaz, E.; Hernández-Cruz, E.Y.; Pedraza-Chaverri, J. The role of vitamin D on redox regulation and cellular senescence. Free Radic. Biol. Med. 2022, 193, 253–273. [Google Scholar] [CrossRef] [PubMed]
- Żmijewski, M.A. Nongenomic Activities of Vitamin D. Nutrients 2022, 14, 5104. [Google Scholar] [CrossRef]
- Ekimoto, T.; Kudo, T.; Yamane, T.; Ikeguchi, M. Mechanism of Vitamin D Receptor Ligand-Binding Domain Regulation Studied by gREST Simulations. J. Chem. Inf. Model. 2021, 61, 3625–3637. [Google Scholar] [CrossRef] [PubMed]
- Hill, T.R.; Granic, A.; Aspray, T.J. Vitamin D and Ageing. In Biochemistry and Cell Biology of Ageing: Part I Biomedical Science; Harris, J.R., Korolchuk, V.I., Eds.; Springer: Singapore, 2018; pp. 191–220. [Google Scholar] [CrossRef]
- Berridge, M.J. Vitamin D deficiency accelerates ageing and age-related diseases: A novel hypothesis. J. Physiol. 2017, 595, 6825–6836. [Google Scholar] [CrossRef]
- Gallagher, J.C. Vitamin D and Aging. Endocrinol. Metab. Clin. 2013, 42, 319–332. [Google Scholar] [CrossRef]
- Hossein-nezhad, A.; Holick, M.F. Vitamin D for Health: A Global Perspective. Mayo Clin. Proc. 2013, 88, 720–755. [Google Scholar] [CrossRef]
- Meehan, M.; Penckofer, S. The Role of Vitamin D in the Aging Adult. J. Aging Gerontol. 2014, 2, 60–71. [Google Scholar] [CrossRef] [PubMed]
- Salekeen, R.; Ahmed, A.; Islam, M.E.; Billah, M.M.; Rahman, H.; Islam, K.M.D. In-silico screening of bioactive phytopeptides for novel anti-ageing therapeutics. J. Biomol. Struct. Dyn. 2022, 40, 4475–4487. [Google Scholar] [CrossRef] [PubMed]
- Voltan, G.; Cannito, M.; Ferrarese, M.; Ceccato, F.; Camozzi, V. Vitamin D: An Overview of Gene Regulation, Ranging from Metabolism to Genomic Effects. Genes 2023, 14, 1691. [Google Scholar] [CrossRef]
- Bikle, D.D. Vitamin D Metabolism, Mechanism of Action, and Clinical Applications. Chem. Biol. 2014, 21, 319–329. [Google Scholar] [CrossRef]
- Bergadà, L.; Pallares, J.; Arcidiacono, M.V.; Cardus, A.; Santacana, M.; Valls, J.; Cao, G.; Fernàndez, E.; Dolcet, X.; Dusso, A.S.; et al. Role of local bioactivation of vitamin D by CYP27A1 and CYP2R1 in the control of cell growth in normal endometrium and endometrial carcinoma. Lab. Investig. 2014, 94, 608–622. [Google Scholar] [CrossRef]
- Fetahu, I.S.; Höbaus, J.; Kállay, E. Vitamin D and the epigenome. Front. Physiol. 2014, 5, 164. [Google Scholar] [CrossRef] [PubMed]
- Dastani, Z.; Li, R.; Richards, B. Genetic Regulation of Vitamin D Levels. Calcif. Tissue Int. 2013, 92, 106–117. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, J.; Suzek, T.O.; Zhang, J.; Wang, J.; Bryant, S.H. PubChem: A public information system for analyzing bioactivities of small molecules. Nucleic Acids Res. 2009, 37 (Suppl. S2), W623–W633. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminformatics 2011, 3, 33. [Google Scholar] [CrossRef]
- Morris, G.M.; Huey, R.; Olson, A.J. Using AutoDock for Ligand-Receptor Docking. Curr. Protoc. Bioinform. 2008, 24, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Burley, S.K.; Berman, H.M.; Bhikadiya, C.; Bi, C.; Chen, L.; Di Costanzo, L.; Christie, C.; Dalenberg, K.; Duarte, J.M.; Dutta, S.; et al. RCSB Protein Data Bank: Biological macromolecular structures enabling research and education in fundamental biology, biomedicine, biotechnology and energy. Nucleic Acids Res. 2018, 47, D464–D474. [Google Scholar] [CrossRef] [PubMed]
- Gasteiger, J.; Marsili, M. Iterative partial equalization of orbital electronegativity—A rapid access to atomic charges. Tetrahedron 1980, 36, 3219–3228. [Google Scholar] [CrossRef]
- Roberts, B.C.; Mancera, R.L. Ligand–Protein Docking with Water Molecules. J. Chem. Inf. Model. 2008, 48, 397–408. [Google Scholar] [CrossRef] [PubMed]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef]
- Dodda, L.S.; Cabeza de Vaca, I.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Horn, H.W.; Swope, W.C.; Pitera, J.W.; Madura, J.D.; Dick, T.J.; Hura, G.L.; Head-Gordon, T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. [Google Scholar] [CrossRef] [PubMed]
- Baum, B.; Mohamed, M.; Zayed, M.; Gerlach, C.; Heine, A.; Hangauer, D.; Klebe, G. More than a Simple Lipophilic Contact: A Detailed Thermodynamic Analysis of Nonbasic Residues in the S1 Pocket of Thrombin. J. Mol. Biol. 2009, 390, 56–69. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Cheatham, T.E., III; Miller, J.L.; Fox, T.; Darden, T.A.; Kollman, P.A. Molecular Dynamics Simulations on Solvated Biomolecular Systems: The Particle Mesh Ewald Method Leads to Stable Trajectories of DNA, RNA, and Proteins. J. Am. Chem. Soc. 1995, 117, 4193–4194. [Google Scholar] [CrossRef]
- Darden, T.; Perera, L.; Li, L.; Pedersen, L. New tricks for modelers from the crystallography toolkit: The particle mesh Ewald algorithm and its use in nucleic acid simulations. Structure 1999, 7, R55–R60. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- White, J.A.; Román, F.L.; González, A.; Velasco, S. Periodic boundary conditions and the correct molecular-dynamics ensemble. Phys. A Stat. Mech. Its Appl. 2008, 387, 6705–6711. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Dill, K.; Bromberg, S.; Stigter, D. Polymer Solutions; Garland Science: New York, NY, USA, 2010; Volume 3, pp. 643–657. [Google Scholar]
- Guedes, I.A.; Pereira, F.S.S.; Dardenne, L.E. Empirical Scoring Functions for Structure-Based Virtual Screening: Applications, Critical Aspects, and Challenges. Front. Pharmacol. 2018, 9, 1089. [Google Scholar] [CrossRef] [PubMed]
- Mey, A.; Allen, B.K.; Macdonald, H.E.B.; Chodera, J.D.; Hahn, D.F.; Kuhn, M.; Michel, J.; Mobley, D.L.; Naden, L.N.; Prasad, S.; et al. Best Practices for Alchemical Free Energy Calculations [Article v1.0]. Living J. Comput. Mol. Sci. 2020, 2, 18378. [Google Scholar] [CrossRef]
- Kumari, R.; Kumar, R.; Lynn, A. g_mmpbsa—A GROMACS Tool for High-Throughput MM-PBSA Calculations. J. Chem. Inf. Model. 2014, 54, 1951–1962. [Google Scholar] [CrossRef]
- Voityuk, A.A.; Vyboishchikov, S.F. A simple COSMO-based method for calculation of hydration energies of neutral molecules. Phys. Chem. Chem. Phys. 2019, 21, 18706–18713. [Google Scholar] [CrossRef]
- Voityuk, A.A.; Vyboishchikov, S.F. Fast and accurate calculation of hydration energies of molecules and ions. Phys. Chem. Chem. Phys. 2020, 22, 14591–14598. [Google Scholar] [CrossRef] [PubMed]
- Vyboishchikov, S.F.; Voityuk, A.A. Fast non-iterative calculation of solvation energies for water and non-aqueous solvents. J. Comput. Chem. 2021, 42, 1184–1194. [Google Scholar] [CrossRef]
- Paul, L.; Namba-Nzanguim, C.T.; Telesphory, A.; Oppong Mensah, J.; Mteremko, D.; Costa, R.; Katundu, S.M.; Kwiyukwa, L.P.; Kambaine, N.D.; Juvenary, J.; et al. Investigation of the structure, stability, and relative solubility of psilocybin in water and pure organic solvents: A molecular simulation study. J. Mol. Liq. 2023, 392, 123479. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R.; Chodera, J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef]
- Geidl, S.; Bouchal, T.; Raček, T.; Svobodová Vařeková, R.; Hejret, V.; Křenek, A.; Abagyan, R.; Koča, J. High-quality and universal empirical atomic charges for chemoinformatics applications. J. Cheminformatics 2015, 7, 59. [Google Scholar] [CrossRef]
- Yoshikawa, N.; Hutchison, G.R. Fast, efficient fragment-based coordinate generation for Open Babel. J. Cheminformatics 2019, 11, 49. [Google Scholar] [CrossRef]
- Marenich, A.V.; Jerome, S.V.; Cramer, C.J.; Truhlar, D.G. Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases. J. Chem. Theory Comput. 2012, 8, 527–541. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Vyboishchikov, S.F. A quick solvation energy estimator based on electronegativity equalization. J. Comput. Chem. 2023, 44, 307–318. [Google Scholar] [CrossRef]
- Bellissent-Funel, M.-C.; Hassanali, A.; Havenith, M.; Henchman, R.; Pohl, P.; Sterpone, F.; van der Spoel, D.; Xu, Y.; Garcia, A.E. Water Determines the Structure and Dynamics of Proteins. Chem. Rev. 2016, 116, 7673–7697. [Google Scholar] [CrossRef] [PubMed]
- Levy, Y.; Onuchic, J.N. Water and proteins: A love–hate relationship. Proc. Natl. Acad. Sci. USA 2004, 101, 3325–3326. [Google Scholar] [CrossRef]
- Schiebel, J.; Gaspari, R.; Wulsdorf, T.; Ngo, K.; Sohn, C.; Schrader, T.E.; Cavalli, A.; Ostermann, A.; Heine, A.; Klebe, G. Intriguing role of water in protein-ligand binding studied by neutron crystallography on trypsin complexes. Nat. Commun. 2018, 9, 3559. [Google Scholar] [CrossRef] [PubMed]
- Nemeth, Z.; Patonai, A.; Simon-Szabó, L.; Takács, I. Interplay of Vitamin D and SIRT1 in Tissue-Specific Metabolism—Potential Roles in Prevention and Treatment of Non-Communicable Diseases Including Cancer. Int. J. Mol. Sci. 2023, 24, 6154. [Google Scholar] [CrossRef] [PubMed]
- Piwpong, R. Systematic Review on Anti-Aging Health Care. Naresuan Univ. J. Sci. Technol. (NUJST) 2018, 26, 98–112. [Google Scholar] [CrossRef]
- Feldman, J.L.; Dittenhafer-Reed, K.E.; Denu, J.M. Sirtuin Catalysis and Regulation. J. Biol. Chem. 2012, 287, 42419–42427. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).