Antisolvent Effects of C1–C4 Primary Alcohols on Solid-Liquid Equilibria of Potassium Dihydrogen Phosphate in Aqueous Solutions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
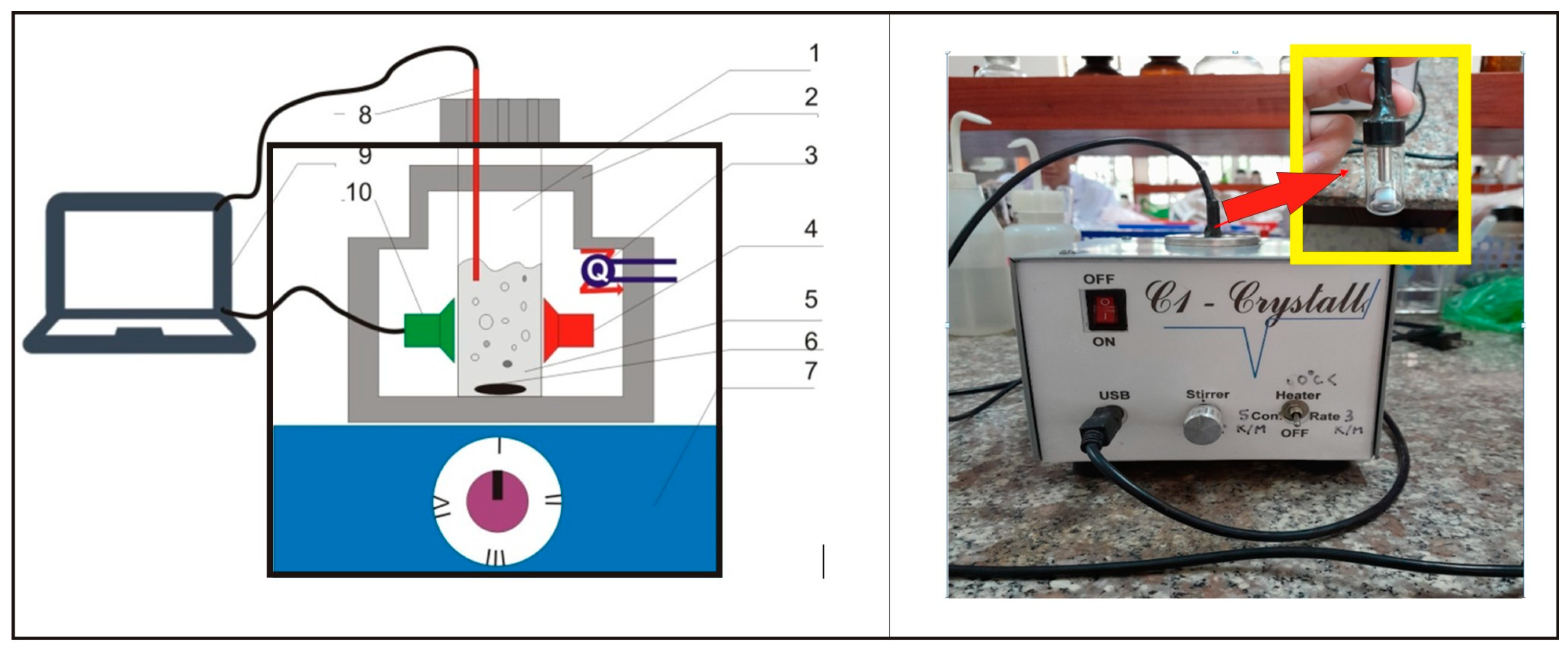
2.2. Polythermal Solubility Determination
2.3. The Isothermal Method
2.4. SLE Thermodynamic Description for Electrolyte KDP in Single and Mixed Solvents
2.5. Parameter Estimation
3. Results
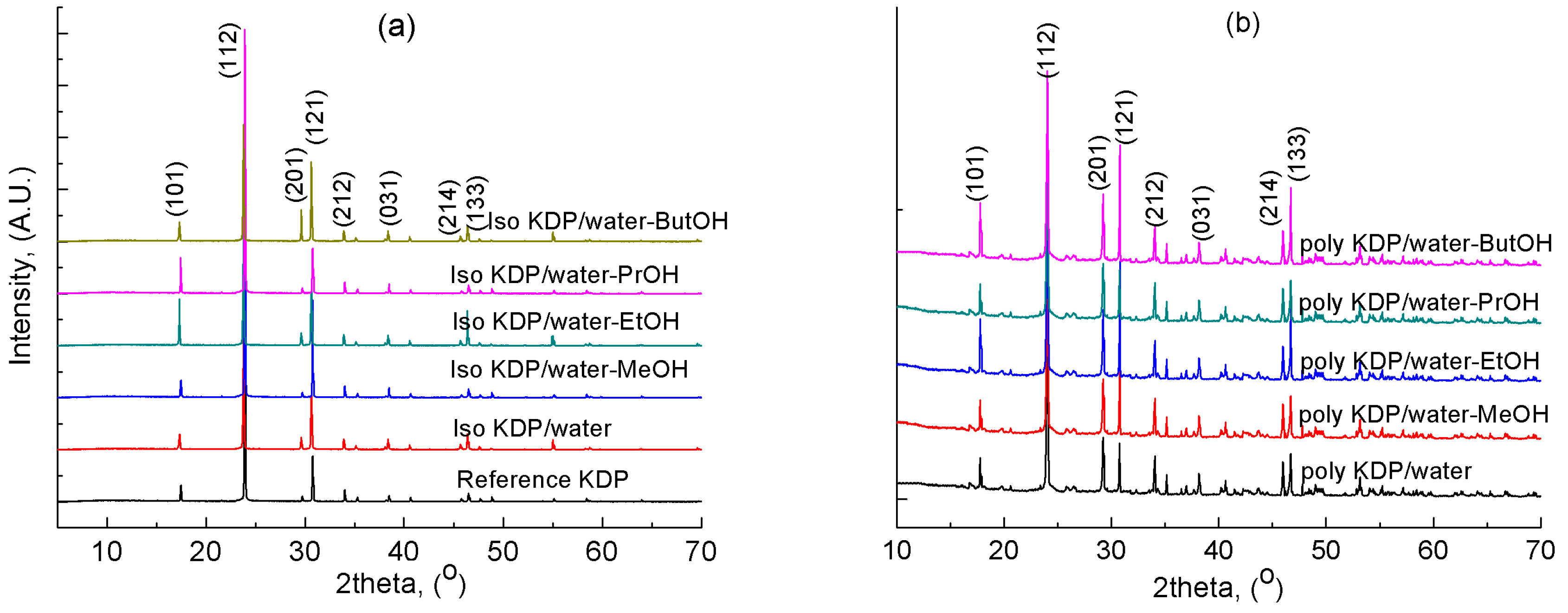
3.1. Solid Phase Analysis
3.2. SLE Determination
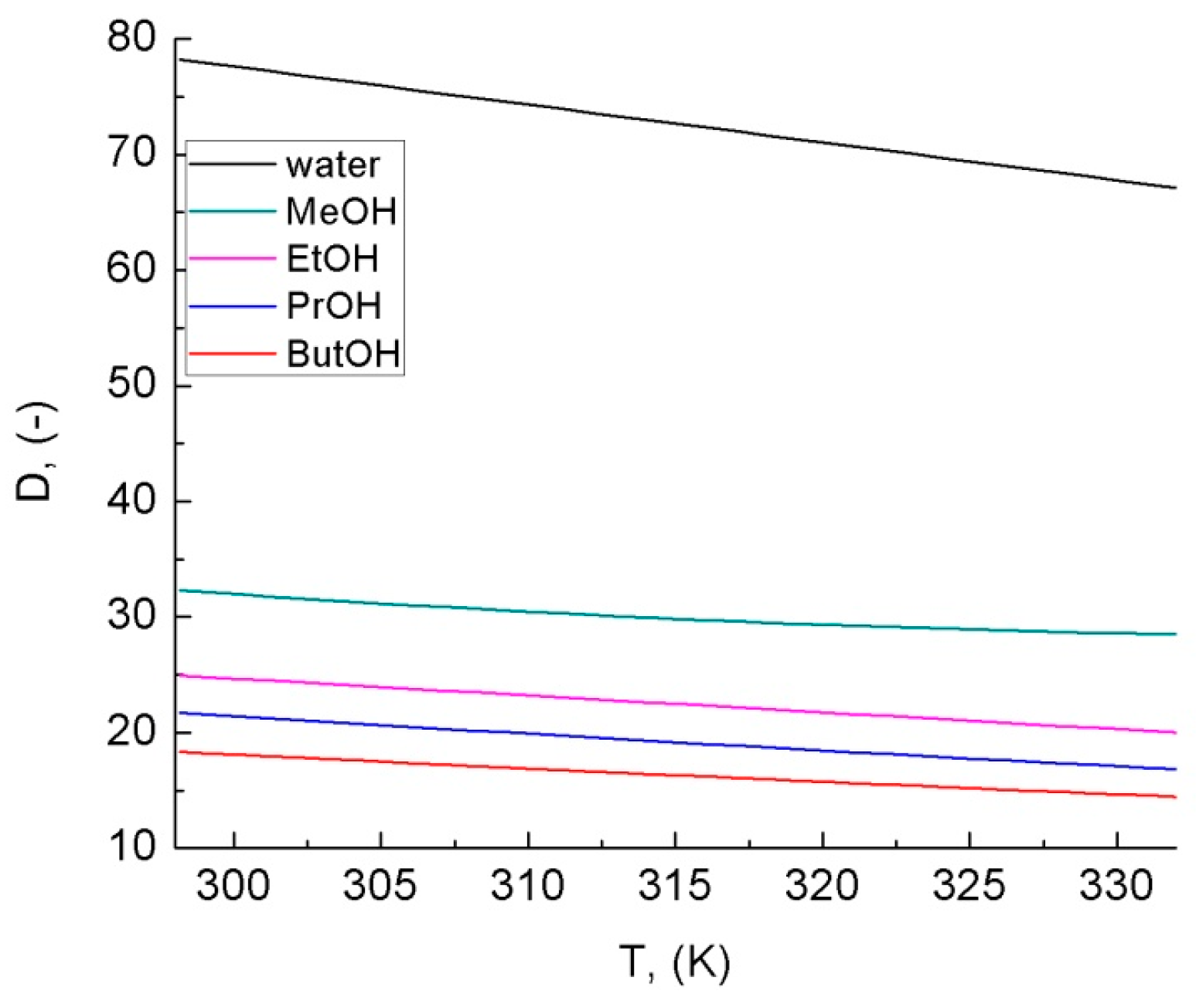
3.3. Antisolvent Effects of C1–C4 Primary Alcohols for KDP Solution
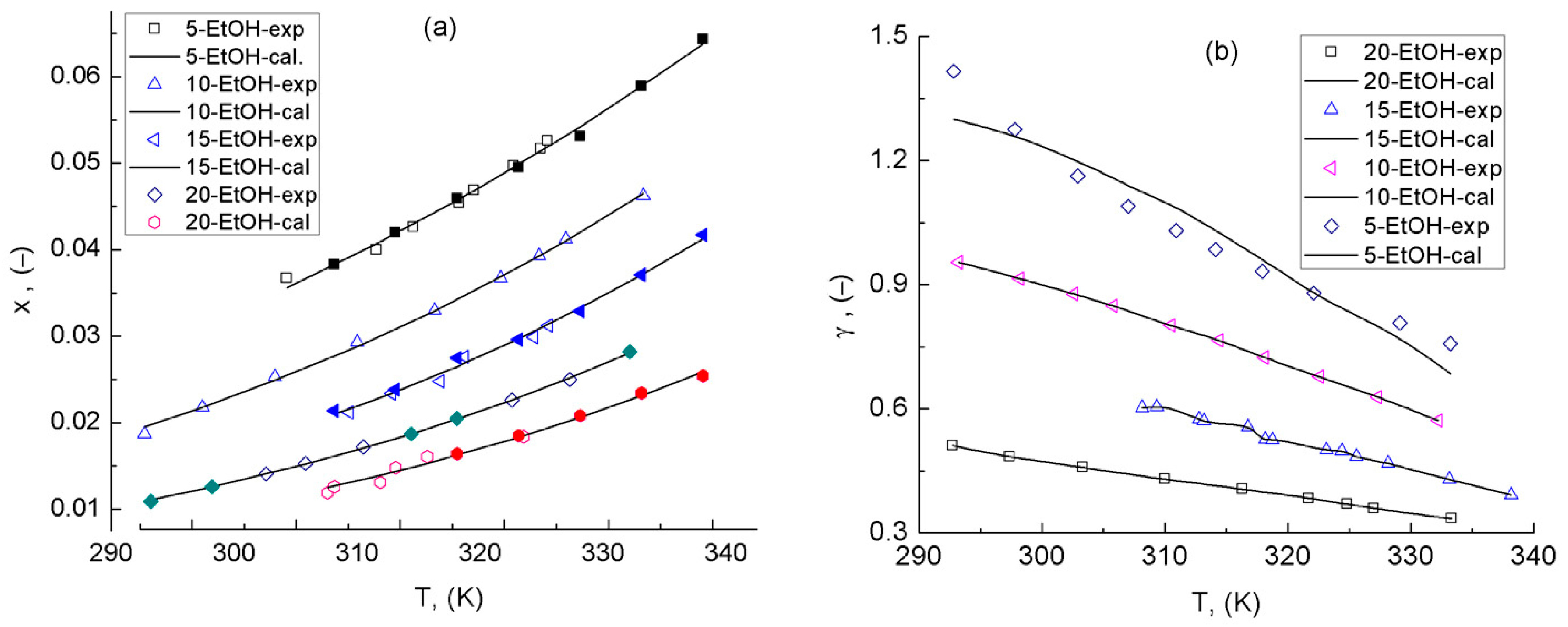
3.4. eNRTL Model Characterization
3.5. Validation of the Obtained eNRTL for Quaternary System
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Aϕ | Debye-Hückel constant |
| a | anion |
| D | dielectric constant |
| c | cation |
| l | liquid |
| m | molality |
| Ix | Ionic strength |
| s | solid |
| x | mole fraction |
| NA | Avogadro constant |
| kB | Boltzmann constant |
| μ | chemical potential |
| υ | stoichiometry |
| γ | activity coefficient |
| γ± | mean ionic activity coefficient |
| π | pi constant |
| gij, gji | interaction parameters |
| αij | non-randomness factor |
| Bromley’s parameter | |
| The modified Apelblat’s parameter |
References
- Qiu, J.; Albrecht, J.; Janey, J. Solubility Behaviors and Correlations of Common Solvent–Antisolvent Systems. Org. Process Res. Dev. 2020, 24, 2722–2727. [Google Scholar] [CrossRef]
- Franco, P.; Marco, I. Supercritical Antisolvent Process for Pharmaceutical Applications: A Review. Processes 2020, 8, 938. [Google Scholar] [CrossRef]
- Bjelobrk, Z.; Rajagopalan, A.K.; Mendels, D.; Karmakar, T.; Parrinello, M.; Mazzotti, M. Solubility of Organic Salts in Solvent–Antisolvent Mixtures: A Combined Experimental and Molecular Dynamics Simulations Approach. J. Chem. Theory Comput. 2022, 18, 4952–4959. [Google Scholar] [CrossRef]
- Wu, M.; Feng, Z.; Deng, Y.; Zhong, C.; Liu, Y.; Liu, J.; Zhao, X.; Fu, Y. Liquid antisolvent precipitation: An effective method for ocular targeting of lutein esters. Int. J. Nanomed. 2019, 14, 2667–2681. [Google Scholar] [CrossRef] [PubMed]
- Zai-Qun, Y.; Reginald, B.H.T. Anti-Solvent Crystallization. Crystals 2020, 10, 748. [Google Scholar]
- Jia, S.; Yang, P.; Gao, Z.; Li, Z.; Fang, C.; Gong, J. Recent progress in antisolvent crystallization. Cryst. Eng. Comm. 2022, 24, 3122–3135. [Google Scholar] [CrossRef]
- Thorat, A.A.; Dalvi, S.V. Liquid antisolvent precipitation and stabilization of nanoparticles of poorly water soluble drugs in aqueous suspensions: Recent developments and future perspective. Chem. Eng. J. 2012, 181–182, 1–34. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Reed Educational and Professional Publishing Ltd.: Oxford, UK, 2001. [Google Scholar]
- Lewis, E.A.; Seckler, M.; Kramer, H.; Rosmalen, G. Industrial Crystallization Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Van Hook, A. Crystallization: Theory and Practice; Reinhold Publishing Corporation: Hoboken, NJ, USA, 1961. [Google Scholar]
- Ulrich, J.; Frohberg, B. Problems, potentials and future of industrial crystallization. Front. Chem. Sci. Eng. 2013, 7, 1–8. [Google Scholar] [CrossRef]
- Barbir, F.; Veziroǧlu, T.N.; Plass, H.J. Environmental damage due to fossil fuels use. Int. J. Hydrog. Energy 1990, 15, 739–749. [Google Scholar] [CrossRef]
- Lonare, A.A.; Patel, S.R. Antisolvent Crystallization of Poorly Water Soluble Drugs. Int. J. Chem. Eng. Appl. 2013, 4, 337–341. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Zeng, Z. The antisolvent coprecipitation method for enhanced bioavailability of poorly water-soluble drugs. Int. J. Pharm. 2022, 626, 122043. [Google Scholar] [CrossRef]
- Jančaitienė, K.; Šlinkšienė, R.; Žvirdauskienė, R. Properties of potassium dihydrogen phosphate and its effects on plants and soil. Open Agric. 2023, 8, 20220167. [Google Scholar] [CrossRef]
- Hu, W.; Wang, J.; Deng, Q.; Liang, D.; Xia, H.; Lin, L.; Lv, X. Effects of Different Types of Potassium Fertilizers on Nutrient Uptake by Grapevine. Horticulturae 2023, 9, 470. [Google Scholar] [CrossRef]
- Pritula, I.; Gayvoronsky, V.; Gromov, Y.; Kopylovsky, M.; Kolybaeva, M.; Puzikov, V.; Kosinova, A.; Savvin, Y.; Velikhov, Y.; Levchenko, A. Linear and nonlinear optical properties of dye-doped KDP crystals: Effect of thermal treatment. Opt. Commun. 2009, 282, 1141–1147. [Google Scholar] [CrossRef]
- Priyadharshini, R.S.; Saravanan, M. Doped potassium dihydrogen phosphate single crystals with enhanced second-harmonic generation efficiency: An investigation of phase purity, nonlinear, piezoelectric, optical, and crystalline qualities. Phys. Scr. 2023, 98, 025801. [Google Scholar] [CrossRef]
- Deng, L.; Duan, J.; Zeng, X.; Yang, H.; Huang, S. A study on dual laser beam separation technology of KDP crystal. Int. J. Mach. Tools Manuf. 2013, 72, 1–10. [Google Scholar] [CrossRef]
- Lee, S.; Wi, H.S.; Jo, W.; Cho, J.Y. Multiple pathways of crystal nucleation in an extremely supersaturated aqueous potassium dihydrogen phosphate (KDP) solution droplet. Proc. Natl. Acad. Sci. USA 2016, 113, 13618–13623. [Google Scholar] [CrossRef]
- Raja, R.; Vedhavalli, D.; Kurinji Nathan, P.; Kanimozhi, R. Growth and Characterization of KDP doped single crystal. Int. J. Mater. Sci. 2017, 12, 273–281. [Google Scholar]
- Rastogi, R.P.; Rama Varma, K.T. Solid-Liquid Equilibria in Mixtures of Non-electrolytes. J. Phys. Chem. 1958, 62, 641–644. [Google Scholar] [CrossRef]
- Rocha, S.A.; da Silva, L.K.; Boros, L.A.D.; Krahenbuhl, M.A.; Guirardello, R. Solid-Liquid Equilibrium Calculation and Parameters Determination in Thermodynamic Models for Binary and Ternary Fatty Mixtures. Chem. Eng. Trans. 2014, 37, 535–540. [Google Scholar]
- Pereira, C.G. Thermodynamics of Phase Equilibria in Food Engineering; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- McCabe, W.L.; Smith, J.; Harriott, P. Unit Operation of Chemical Engineering, 5th ed.; McGraw-Hill Inc.: New York, NY, USA, 1993. [Google Scholar]
- Lafitte, T.; Papaioannou, V.; Dufal, S.; Pantelides, C.C. A general framework for solid-liquid equilibria in pharmaceutical systems. In Chemical Engineering in the Pharmaceutical Industry: Active Pharmaceutical Ingredients, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Rogowska, R. Surface free energy of thin-layer coatings deposited by means of the arc-vacuum method. Maint. Probl. 2006, 2, 193–204. [Google Scholar]
- Nývlt, J.; Söhnel, O.; Matachová, M.; Broul, M. The Kinetics of Industrial Crystallization; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Le Minh, T.; Langermann, J.; Lorenz, H.; Seidel-Morgenstern, A. Enantiomeric 3-chloromandelic acid system: Binary melting point phase diagram, ternary solubility phase diagrams and polymorphism. J. Pharm. Sci. 2010, 99, 4084–4095. [Google Scholar] [CrossRef] [PubMed]
- Le Minh, T.; Phan Thanh, T.; Nguyen Thi Hong, N.; Phan Minh, V. A Simple Population Balance Model for Crystallization of L-Lactide in a Mixture of n-Hexane and Tetrahydrofuran. Crystals 2022, 12, 221. [Google Scholar] [CrossRef]
- Kowalska, T. Chromatographic Determination of the Solubility of Low Soluble Substances-A Practical Possibility. MonatsheftefuerChemie 1987, 118, 879–882. [Google Scholar] [CrossRef]
- Tam, L.; Phan, T.; Nguyen, N.; Duong, D. Application of the polythermal method in constructing a quick solid-liquid equilibrium determination of l-lactide in a solvent mixture of 40% mass percentage of n-hexane in tetrahydrofuran. VNUHCM J. Nat. Sci. 2021, 5, 1474–1481. [Google Scholar]
- Kwok, K.S.; Chan, H.C.; Chan, C.K.; Ng, K.M. Experimental Determination of Solid-Liquid Equilibrium Phase Diagrams for Crystallization-Based Process Synthesis. Ind. Eng. Chem. Res. 2005, 44, 3788–3798. [Google Scholar] [CrossRef]
- Zemaitis, J.F., Jr.; Clark, D.M.; Rafal, M.; Noel, C. Handbook of Aqueous Electrolyte Thermodynamics: Theory and Application; American Institute of Chemical Engineers (AIChE): New York, NY, USA, 1986. [Google Scholar]
- Spitzer, J.J. Ionic Radii and the Distance of Closest Approach in the Debye-Htickel Theory of Electrolytes. J. Solut. Chem. 1978, 7, 669–673. [Google Scholar] [CrossRef]
- Malmberg, C.G. Dielectric constant of water from 0° to 100 °C. J. Reseach Natl. Bur. Stand. 1956, 56, 2641. [Google Scholar] [CrossRef]
- Chaudgari, A.; More, N.M.; Mehrotra, S.C. Static Dielectric Constant and Relaxation Time for the Binary Mixture of Water, Ethanol, N. N-Dimethylformamide, Dimethylsulphoxide, and N,M-Dimethylacetamide with 20Hethoxyethanol. Bull. Korean Chem. Soc. 2001, 22, 357–361. [Google Scholar]
- Mohsen-Nia, M.; Amiri, H.; Jazi, B. Dielectric Constants of Water, Methanol, Ethanol, Butanol and Acetone: Measurement and Computational Study. J. Solut. Chem. 2010, 39, 701–708. [Google Scholar] [CrossRef]
- Méndez-Bermúdez, J.G.; Dominguez, H.; Pusztai, L.; Guba, S.; Horváth, B.; Szalai, I. Composition and temperature dependence of the dielectric constant of 1-propanol/water mixtures: Experiment and molecular dynamics simulations. J. Mol. Liq. 2016, 219, 354–358. [Google Scholar] [CrossRef]
- Zuber, A.; Cardozo-Filho, L.; Ferreira, V.; Ricardo, C.; Checoni, F.; Castier, M. An Empirical Equation for the Dielectric Constant in Aqueous and Nonaqueous Electrolyte Mixtures. Fluid Phase Equilibria 2014, 376, 116–123. [Google Scholar] [CrossRef]
- Chen, C.C.; Nritt, H.I.; Boston, J.F.; Evans, L.B. Local Composition Model for Excess Gibbs Energy of Electrolyte Systems. AlChE J. 1982, 28, 588–596. [Google Scholar] [CrossRef]
- Kurihara, K.; Minoura, T.; Takeda, K.; Kojim, K. Isothermal Vapor-Liquid Equilibria for Methanol + Ethanol + Water, Methanol + Water, and Ethanol + Water. J. Chem. Eng. Data 1996, 40, 679–684. [Google Scholar] [CrossRef]
- Valverde, J.L.; Ferro, V.R.; Giroir-Fendler, A. Application of the e-NRTL model to electrolytes in mixed solvents methanol-, ethanol- water, and PEG-water. Fluid Phase Equilibria 2022, 560, 113516. [Google Scholar] [CrossRef]
- Gabaldon, C.; Marzal, P.; Monton, J.B.; Rodrigo, M.A. Isobaric Vapor-Liquid Equilibria for Binary and Ternary Systems Composed of Water, 1-Propanol, and 2-Propanol at 100 kPa. Chem. Eng. Data 1996, 41, 1379–1382. [Google Scholar] [CrossRef]
- Mandhane, J.M.; Heidemann, R.A. NRTL parameters for the ternary system n-butanol, n-butyl acetate and water. Can. J. Chem. Eng. 1973, 51, 381–385. [Google Scholar] [CrossRef]
- Apelblat, A.; Manzurola, E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic, and p-toluic acid, and magnesium-DL-aspartate in water from T = (278 to 348) K. J. Chem. Thermodyn. 1999, 31, 85–91. [Google Scholar] [CrossRef]
- Apelblat, A.; Manzurola, E. Solubilities of L-aspartic, DL-aspartic,DL-glutamic, p-hydroxybenzoic, o-anistic, p-anisic, and itaconic acids in water fromT = 278 K to T = 345 K. J. Chem. Thermodyn. 1997, 29, 1527–1533. [Google Scholar] [CrossRef]
- Grant, D.J.W.; Mehdizadeh, M.; Chow, A.L.; Fairbrother, J.E. Non-linear van’t Hoff solubility-temperature and their pharmaceutical interpretation. Int. J. Pharm. 1984, 18, 25–38. [Google Scholar] [CrossRef]
- Bromley, L.A. Thermodynamic properties of strong electrolyte in aqueous solutions. AIChE J. 1973, 19, 313–320. [Google Scholar] [CrossRef]
- Barata, P.A.; Serrano, M.L. Thermodynamic representation of the solubility for potassium dihydrogen phosphate (KDP) + water + alcohols systems. Fluid Phase Equilibria 1997, 141, 247–263. [Google Scholar] [CrossRef]
- Manov, G.G.; Bates, R.G.; Hamer, W.J.; Acree, S.F. Values of the Constants in the Debye-Hiickel Equation for Activity Coefficients. J. Am. Chem. Soc. 1943, 65, 1765–1767. [Google Scholar] [CrossRef]
- Ji, P.; Zou, J.; Feng, W. Effect of alcohol on the solubility of amino acid in water. J. Mol. Catal. B Enzym. 2009, 56, 185–188. [Google Scholar] [CrossRef]
- Han, C.; Gao, J.; Sun, W.; Han, C.; Li, F.; Li, B. Structure study of water in alcohol-water binary system based on Raman spectroscopy. J. Phys. Conf. Ser. 2022, 2282, 012021. [Google Scholar] [CrossRef]
- Neklyudov, V.; Khafizov, N.; Ayrat, I.; Dimiev, M. New Insights to Solubility of Graphene Oxide in Water and Alcohols. Phys. Chem. Chem. Phys. 2017, 19, 17000–17008. [Google Scholar] [CrossRef]
| SLE Set | Solvent | Apelblat’s Parameter | Bromley’s Parameter | |||
|---|---|---|---|---|---|---|
| , [J/mol] | ||||||
| 1st | Water | −6862.38 | 23.44 | 127.89 | 0.67 (48) | −0.05 (31) |
| 2nd | 5%EtOH | −6937.20 | 33.25 | 2978.07 | 0.21 (98) | −0.05 (18) |
| 3rd | 10%EtOH | −6980.43 | 39.07 | 4670.01 | 0.19 (88) | −0.06 (12) |
| 4th | 15%EtOH | −6986.25 | 39.40 | 4763.34 | 0.18 (14) | −0.08 (82) |
| 5th | 20%EtOH | −6980.43 | 39.07 | 4670.01 | 1.01 (52) | −0.02 (61) |
| 6th | 5%MeOH | −6900.62 | 28.35 | 1552.15 | 0.21 (97) | −0.05 (18) |
| 7th | 10%MeOH | −6979.60 | 39.07 | 4670.84 | 0.22 (89) | −0.06 (12) |
| 8th | 15%MeOH | −6945.52 | 33.92 | 3168.06 | 0.21 (17) | −0.08 (83) |
| 9th | 5%PrOH | −6869.03 | 24.11 | 319.54 | 0.22 (01) | −0.05 (18) |
| 10th | 10%PrOH | −6947.18 | 34.66 | 3389.49 | 0.21 (94) | −0.05 (18) |
| 11th | 15%PrOH | −6936.37 | 32.75 | 2830.17 | 0.21 (94) | −0.05 (17) |
| 12th | 5%ButOH | −6861.54 | 23.94 | 277.45 | 0.21 (84) | −0.05 (17) |
| 13th | 10%ButOH | −6934.71 | 33.08 | 2930.99 | 0.22 (07) | −0.05 (18) |
| 14th | 15%ButOH | −6965.47 | 36.99 | 4065.27 | 0.22 (07) | −0.05 (18) |
| 15th | 2.5%:2.5% MeOH + EtOH | −6936.37 | 32.75 | 2830.17 | 0.21 (97) | −0.05 (18) |
| 16th | 5.0%:5.0% MeOH + EtOH | −6992.07 | 40.82 | 5178.92 | 0.21 (98) | −0.05 (18) |
| 17th | 7.5%:7.5% MeOH + EtOH | −6886.49 | 26.35 | 971.37 | 0.21 (97) | −0.05 (18) |
| SLE | Solvent | eNRTL | τij | τji | |||
|---|---|---|---|---|---|---|---|
| αij | gij | gji | |||||
| 1st | Water | 0.36 (2) | −1705. (7) | 1097 (3) | −0.68 | 4.42 | 5.1 |
| 2nd | 5%EtOH | 0.12 (6) | −5236. (3) | 3636 (8) | −2.11 | 14.65 | 16.76 |
| 3rd | 10%EtOH | 0.12 (3) | −4211. (7) | 2325 (7) | −1.69 | 9.38 | 11.07 |
| 4th | 15%EtOH | 0.10 (1) | −4911. (6) | 2448 (6) | −1.98 | 9.88 | 11.86 |
| 6th | 5%MeOH | 0.16 (2) | −1397. (9) | 3041 (7) | −5.64 | 12.27 | 17.91 |
| 7th | 10%MeOH | 0.19 (3) | −2049. (5) | 2340 (6) | −8.27 | 9.44 | 17.71 |
| 8th | 15%MeOH | 0.20 (5) | −2055. (2) | 2344 (3) | −8.29 | 9.46 | 17.75 |
| 9th | 5%PrOH | 0.06 (9) | −2481. (2) | 5869 (9) | −1.00 | 23.69 | 24.69 |
| 10th | 10%PrOH | 0.08 (9) | −7715. (3) | 5565 (4) | −3.11 | 22.46 | 25.57 |
| 11th | 15%PrOH | 0.05 (1) | −2101. (3) | 3995 (6) | −8.48 | 16.12 | 24.6 |
| 12th | 5%ButOH | 0.03 (1) | −7497. (8) | 5751 (0) | −3.02 | 23.21 | 26.23 |
| 13th | 10%ButOH | 0.06 (9) | −2481. (4) | 5869 (9) | −1.00 | 23.69 | 24.69 |
| 14th | 15%ButOH | 0.29 (8) | 5743. (2) | 7838 (5) | 2.31 | 31.63 | 29.32 |
| 15th | 2.5%:2.5% MeOH + EtOH | 0.02 (9) | −89,526. (5) | −504,241. (2) | −36.23 | −203.73 | 167.50 |
| 16th | 5.0%:5.0% MeOH + EtOH | 0.01 (2) | 4025. (8) | 2413 (3) | 1.63 | 9.74 | 8.22 |
| 17th | 7.5%:7.5% MeOH + EtOH | 0.01 (1) | 4006. (7) | 1394 (5) | 1.62 | 5.63 | 4.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.M.; Nguyen, T.D.; Nguyen, G.T.; Tran, N.T. Antisolvent Effects of C1–C4 Primary Alcohols on Solid-Liquid Equilibria of Potassium Dihydrogen Phosphate in Aqueous Solutions. ChemEngineering 2023, 7, 99. https://doi.org/10.3390/chemengineering7050099
Le TM, Nguyen TD, Nguyen GT, Tran NT. Antisolvent Effects of C1–C4 Primary Alcohols on Solid-Liquid Equilibria of Potassium Dihydrogen Phosphate in Aqueous Solutions. ChemEngineering. 2023; 7(5):99. https://doi.org/10.3390/chemengineering7050099
Chicago/Turabian StyleLe, Tam Minh, Tan Dzung Nguyen, Giang Tien Nguyen, and Nhung Thi Tran. 2023. "Antisolvent Effects of C1–C4 Primary Alcohols on Solid-Liquid Equilibria of Potassium Dihydrogen Phosphate in Aqueous Solutions" ChemEngineering 7, no. 5: 99. https://doi.org/10.3390/chemengineering7050099
APA StyleLe, T. M., Nguyen, T. D., Nguyen, G. T., & Tran, N. T. (2023). Antisolvent Effects of C1–C4 Primary Alcohols on Solid-Liquid Equilibria of Potassium Dihydrogen Phosphate in Aqueous Solutions. ChemEngineering, 7(5), 99. https://doi.org/10.3390/chemengineering7050099





