Raman Calibration Models for Chemical Species Determination in CO2-Loaded Aqueous MEA Solutions Using PLS and ANN Techniques
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
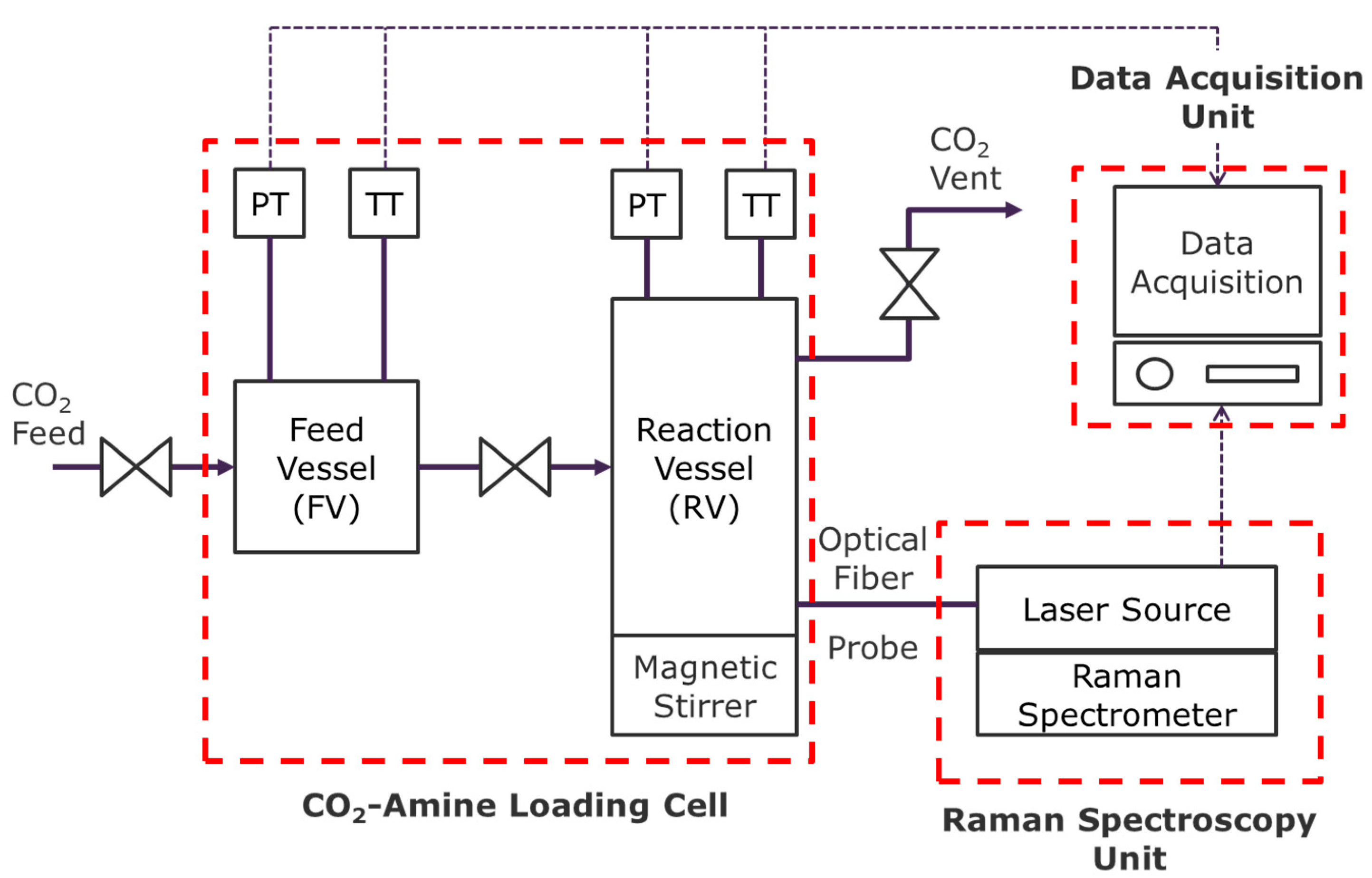
2.2. Experimental Setup and Method
2.3. Thermodynamic Framework and Kent–Eisenberg Model
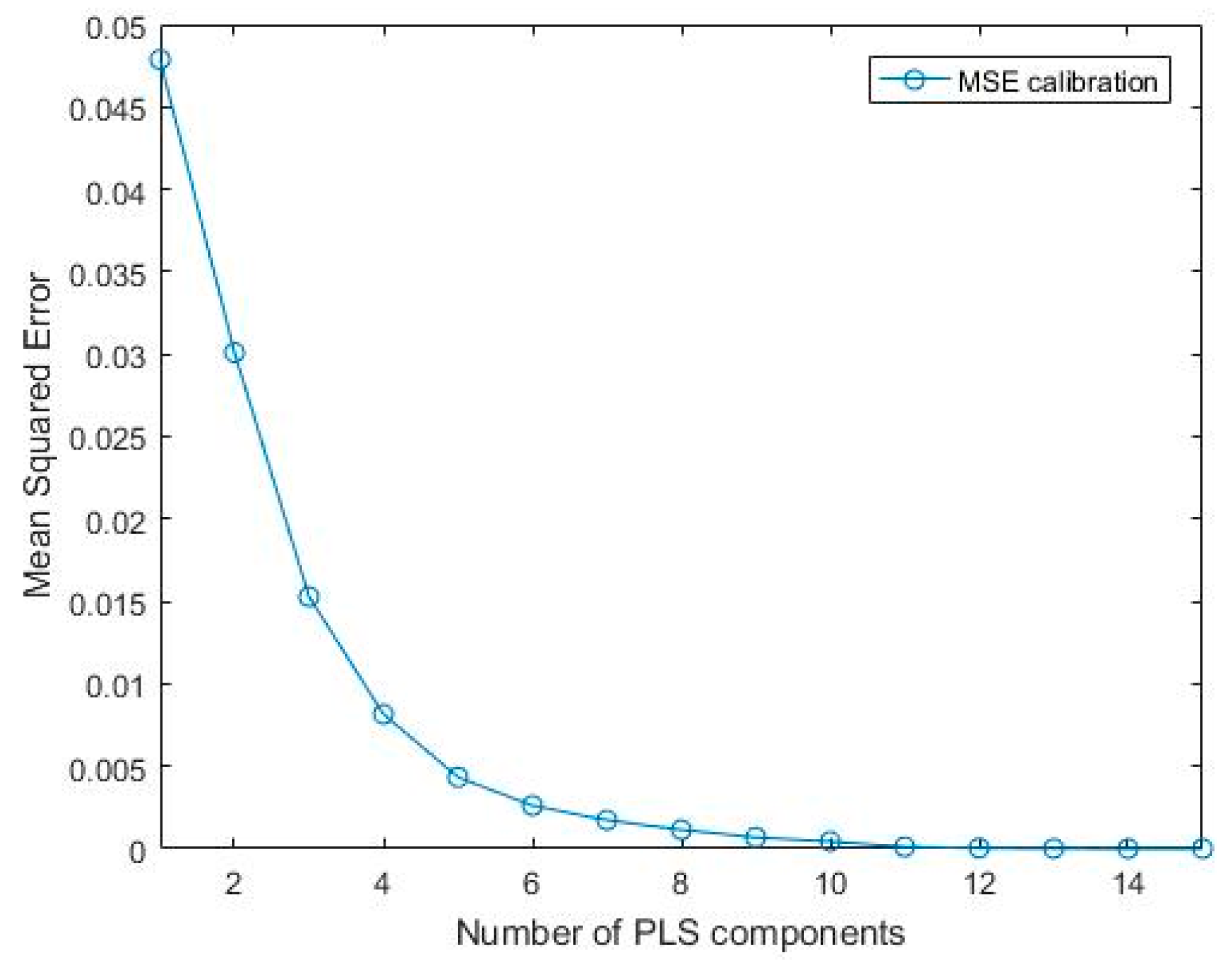
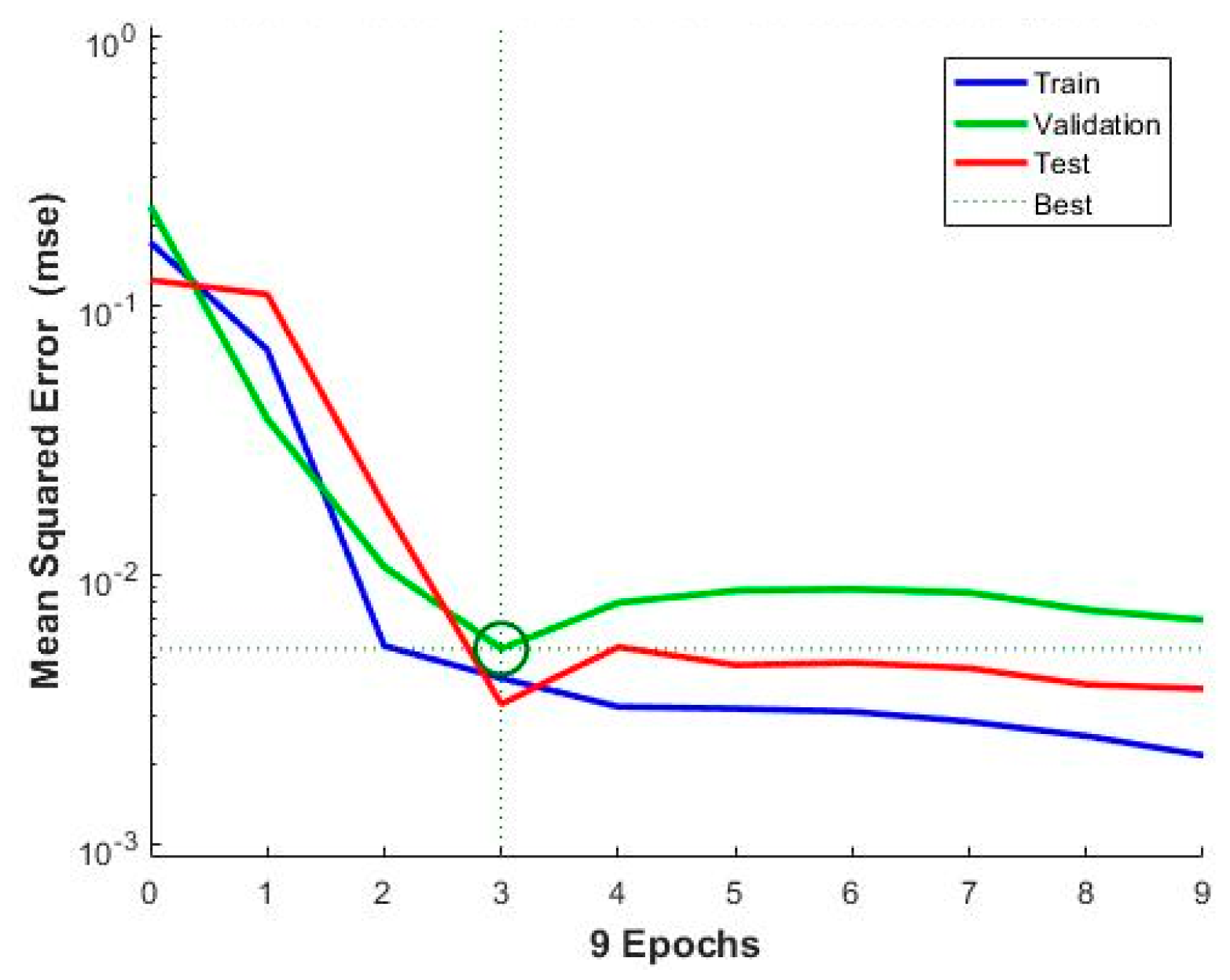
2.4. Calibration Models Development and Evaluation
3. Results and Discussion
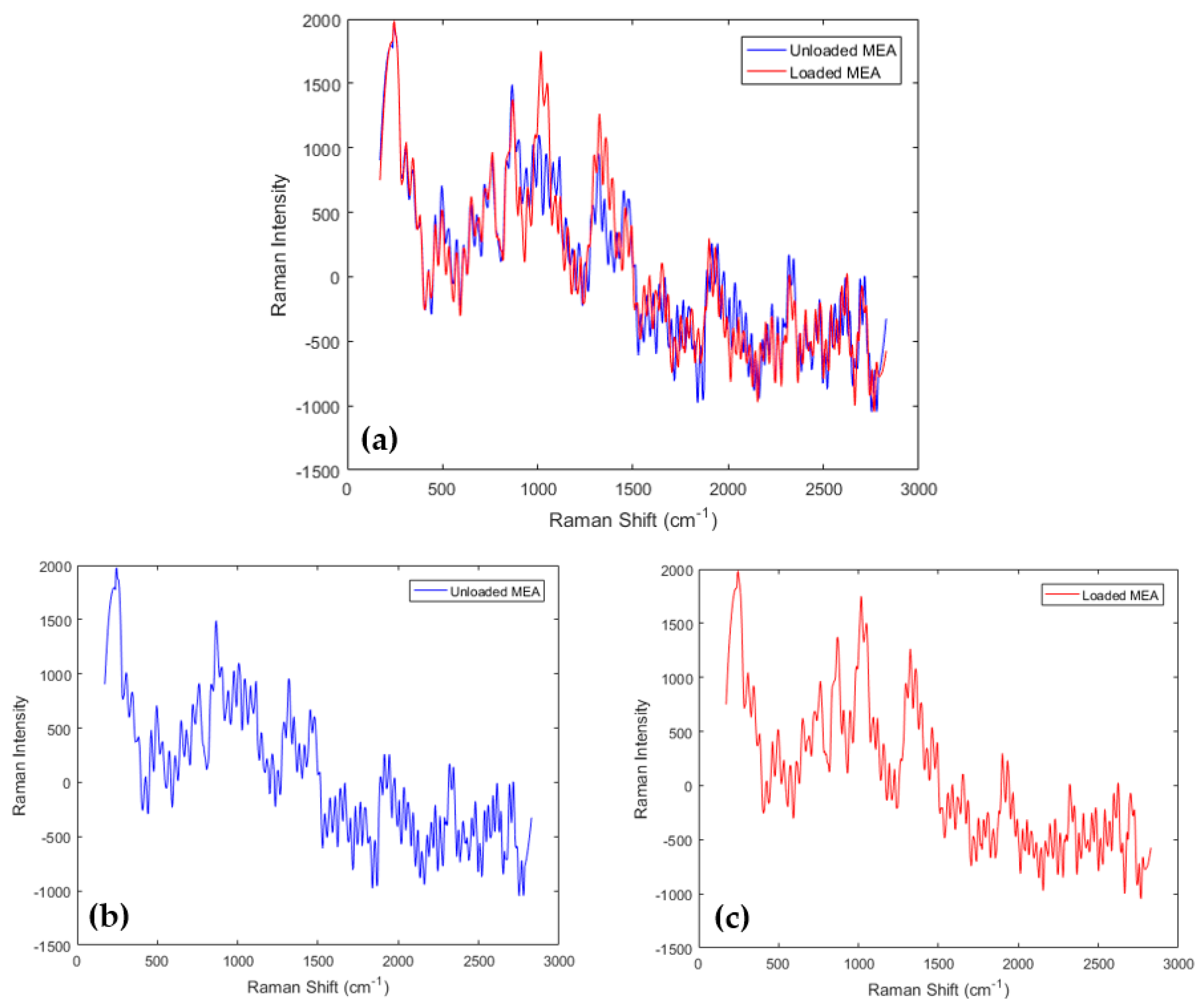
3.1. Characteristic Bands of Chemical Species in CO2-Loaded Aqueous Monoethanolamine (MEA) System
3.2. Evaluation of the Raman Species Calibration Models
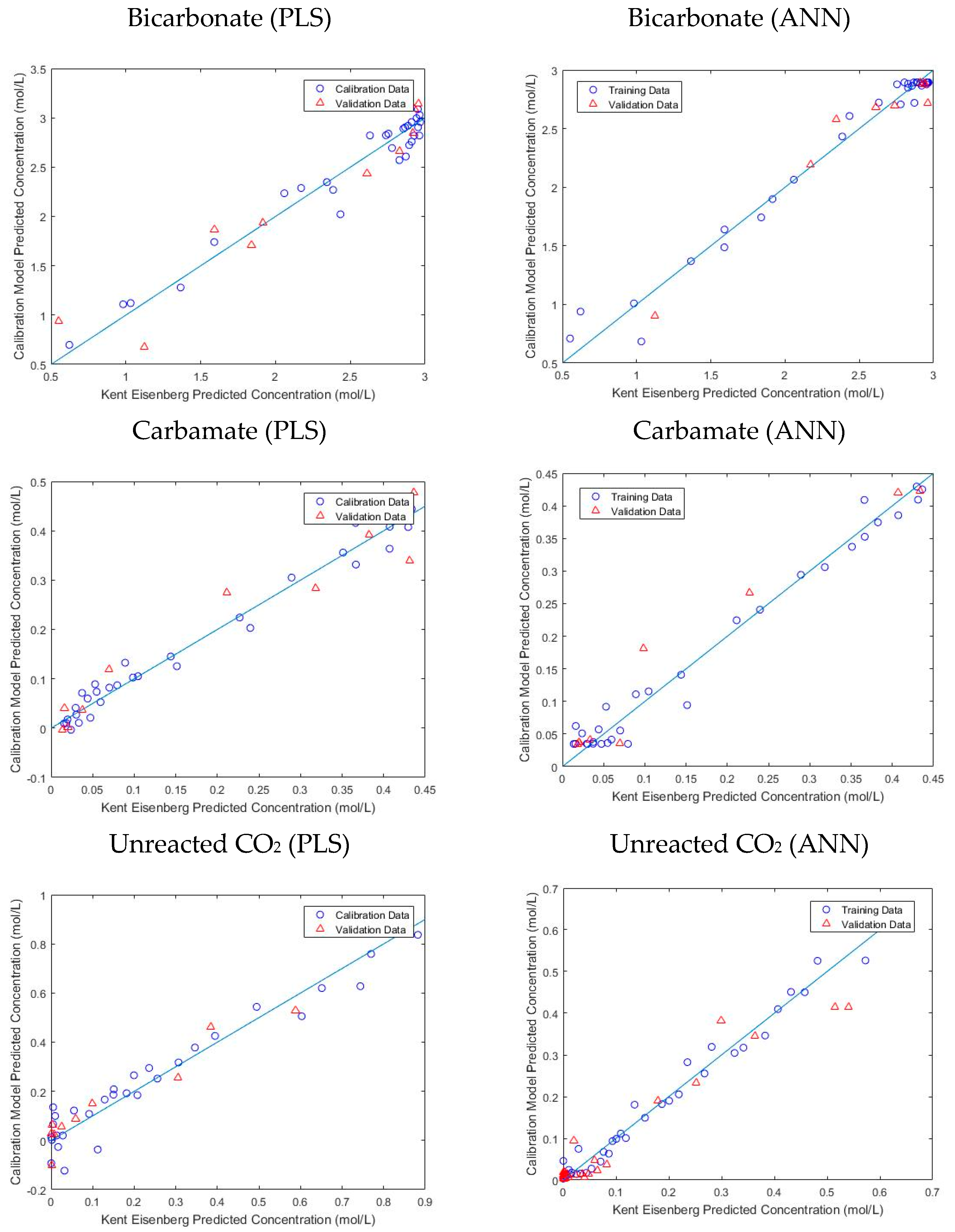
3.3. Comparative Analysis between Partial Least Squares (PLS) and Artificial Neural Network (ANN) Technique for the Development of Raman Calibration Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Luis, P. Use of monoethanolamine (MEA) for CO2 capture in a global scenario: Consequences and alternatives. Desalination 2016, 380, 93–99. [Google Scholar] [CrossRef] [Green Version]
- Fan, G.J.; Wee, A.G.H.; Idem, R.; Tontiwachwuthikul, P. NMR studies of amine species in MEA-CO2-H2O system: Modification of the model of vapor-liquid equilibrium (VLE). Ind. Eng. Chem. Res. 2009, 48, 2717–2720. [Google Scholar] [CrossRef]
- Rogelj, J.; Shindell, D.; Jiang, K.; Fifita, S. Mitigation Pathways Compatible with 1.5 °C in the Context of Sustainable Development. In Global Warming of 1.5 °C; An IPCC Special Report; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- Kachko, A.; van der Ham, L.V.; Bardow, A.; Vlugt, T.J.H.; Goetheer, E.L.V. Comparison of Raman, NIR, and ATR FTIR spectroscopy as analytical tools for in-line monitoring of CO2 concentration in an amine gas treating process. Int. J. Greenh. Gas Control 2016, 47, 17–24. [Google Scholar] [CrossRef]
- Cole, I.S.; Corrigan, P.; Sim, S.; Birbilis, N. Corrosion of pipelines used for CO2 transport in CCS: Is it a real problem? Int. J. Greenh. Gas Control. 2011, 5, 749–756. [Google Scholar] [CrossRef]
- Wong, M.K.; Bustam, M.A.; Shariff, A.M. Chemical speciation of CO2 absorption in aqueous monoethanolamine investigated by in situ Raman spectroscopy. Int. J. Greenh. Gas Control 2015, 39, 139–147. [Google Scholar] [CrossRef]
- Rochelle, G.T. Amine Scrubbing for CO2 Capture. Science 2009, 325, 1652–1654. [Google Scholar] [CrossRef] [PubMed]
- Puxty, G.; Maeder, M. The fundamentals of post-combustion capture. In Absorption-Based Post-Combustion Capture of Carbon Dioxide; Woodhead Publishing: Sawston, UK, 2016; pp. 13–33. ISBN 9780081005156. [Google Scholar]
- Böttinger, W.; Maiwald, M.; Hasse, H. Online NMR spectroscopic study of species distribution in MEA-H2O-CO2 and DEA-H2O-CO2. Fluid Phase Equilib. 2008, 263, 131–143. [Google Scholar] [CrossRef]
- Kontogeorgis, G.M.; Folas, G.K. Thermodynamic Models for Industrial Applications: From Classical and Advanced Mixing Rules to Association Theories; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 9780470747537. [Google Scholar]
- Rinker, E.B.; Ashour, S.S.; Sandall, O.C. Kinetics and Modeling of Carbon Dioxide Absorption into Aqueous Solutions of Diethanolamine. Ind. Eng. Chem. Res. 1996, 35, 1107–1114. [Google Scholar] [CrossRef]
- Souchon, V.; Aleixo, M.D.O.; Delpoux, O.; Sagnard, C.; Mougin, P.; Wender, A.; Raynal, L. In situ determination of species distribution in alkanolamine-H2O-CO2 systems by Raman spectroscopy. Energy Procedia 2011, 4, 554–561. [Google Scholar] [CrossRef] [Green Version]
- Beumers, P.; Brands, T.; Koss, H.J.; Bardow, A. Model-free calibration of Raman measurements of reactive systems: Application to monoethanolamine/water/CO2. Fluid Phase Equilib. 2016, 424, 52–57. [Google Scholar] [CrossRef]
- Smith, E.; Dent, G. Modern Raman Spectroscopy—A Practical Approach; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 9780471497943. [Google Scholar]
- Vogt, M.; Pasel, C.; Bathen, D. Characterisation of CO2 absorption in various solvents for PCC applications by Raman spectroscopy. Energy Procedia 2011, 4, 1520–1525. [Google Scholar] [CrossRef] [Green Version]
- Samarakoon, P.A.G.L.; Andersen, N.H.; Perinu, C.; Jens, K.J. Equilibria of MEA, DEA and AMP with bicarbonate and carbamate: A Raman study. Energy Procedia 2013, 37, 2002–2010. [Google Scholar] [CrossRef] [Green Version]
- Swinehart, D.F. The Beer-Lambert Law. J. Chem. Educ. 1962, 39, 333. [Google Scholar] [CrossRef]
- Matin, N.S.; Remias, J.E.; Neathery, J.K.; Liu, K. Facile method for determination of amine speciation in CO2 capture solutions. Ind. Eng. Chem. Res. 2012, 51, 6613–6618. [Google Scholar] [CrossRef]
- Kent, R.L.; Elsenberg, B. Better Data for Amine Treating. Hydrocarb. Process. 1976, 55, 87–90. [Google Scholar]
- Haji-Sulaiman, M.Z.; Aroua, M.K.; Benamor, A. Analysis of equilibrium data of CO2 in aqueous solutions of DEA, MDEA and their mixtures using the modified Kent Eisenberg Model. Trans. Chem. E 1998, 76, 1–8. [Google Scholar] [CrossRef]
- Suleman, H.; Maulud, A.S.; Man, Z. Carbon Dioxide Solubility in Aqueous Potassium Lysinate Solutions: High Pressure Data and Thermodynamic Modeling. Procedia Eng. 2016, 148, 1303–1311. [Google Scholar] [CrossRef] [Green Version]
- Suleman, H.; Maulud, A.S.; Man, Z. Review and selection criteria of classical thermodynamic models for acid gas absorption in aqueous alkanolamines. Rev. Chem. Eng. 2015, 31, 599–639. [Google Scholar] [CrossRef]
- Sartori, G.; Savage, D.W. Sterically hindered amines for carbon dioxide removal from gases. Ind. Eng. Chem. Fundam. 1983, 22, 239–249. [Google Scholar] [CrossRef]
- Haji-Sulaiman, M.Z.; Aroua, M.K.; Pervez, M.I. Equilibrium concentration profiles of species in CO2—alkanolamine—water systems. Gas Sep. Purif. 1996, 10, 13–18. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality Reduction: A Comparative Review. J. Mach. Learn. Res. 2009, 10, 66–71. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933. [Google Scholar] [CrossRef]
- Varmuza, K.; Filzmoser, P. Introduction to Multivariate Statistical Analysis in Chemometrics; CRC Press: Boca Raton, FL, USA, 2009; ISBN 9781420059472. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Marini, F.; Bucci, R.; Magri, A.L.; Magri, A.D. Artificial Neural Networks in Chemometrics: History, Examples and Perspectives. Microchem. J. 2008, 88, 178–185. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Kuang, B.; Tekin, Y.; Mouazen, A.M. Comparison between artificial neural network and partial least squares for on-line visible and near infrared spectroscopy measurement of soil organic carbon, pH and clay content. Soil Tillage Res. 2015, 146, 243–252. [Google Scholar] [CrossRef]
- Ramadan, Z.; Hopke, P.K.; Johnson, M.J.; Scow, K.M. Application of PLS and Back-Propagation Neural Networks for the estimation of soil properties. Chemom. Intell. Lab. Syst. 2005, 75, 23–30. [Google Scholar] [CrossRef]
- Jinadasa, M.H.W.N.; Chandra, K.A.; Halstensen, M. System Development for On-line Monitoring using Raman Spectroscopy for CO2 Absorption by MEA. In Proceedings of the 59th Conference on Simulation and Modelling (SIMS 59), 26–28 September 2018; Oslo Metropolitan University: Oslo, Norway, 2018. [Google Scholar]
- Jinadasa, M.H.W.N.; Jens, K.; Øi, L.E.; Halstensen, M. Raman Spectroscopy as an Online Monitoring Tool for CO2 Capture Process: Demonstration Using a Laboratory Rig. Energy Procedia 2017, 114, 1179–1194. [Google Scholar] [CrossRef]
- Shahid, M.Z.; Maulud, A.S.; Bustam, M.A. Non-invasive monitoring of CO2concentration in aqueous diethanolamine (DEA), methyldiethanolamine (MDEA) and their blends in high CO2loading region using Raman spectroscopy and partial least square regression (PLSR). Int. J. Greenh. Gas Control 2018, 68, 42–48. [Google Scholar] [CrossRef]
- Shahid, M.Z.; Suleman, H.; Maulud, A.S.; Khalil, M.A.B.; Man, Z. Monitoring of Chemical Speciation of DEA-CO2-Water System by Raman Spectroscopy. Adv. Mater. Res. 2015, 1113, 358–363. [Google Scholar] [CrossRef]
- Edwards, T.J.; Maurer, G.; Newman, J.; Prausnitz, J.M. Vapor-liquid equilibria in multicomponent aqueous solutions of volatile weak electrolytes. AIChE J. 1978, 24, 966–976. [Google Scholar] [CrossRef]
- Aroua, M.K.; Salleh, R.M. Solubility of CO2 in aqueous piperazine and its modeling using the Kent-Eisenberg approach. Chem. Eng. Technol. 2004, 27, 65–70. [Google Scholar] [CrossRef]
- Vasques, G.M.; Grunwald, S.; Sickman, J.O. Comparison of multivariate methods for inferential modeling of soil carbon using visible/near-infrared spectra. Geoderma 2008, 146, 14–25. [Google Scholar] [CrossRef]
- Silva, M.A.M.; Ferreira, M.H.; Braga, J.W.B.; Sena, M.M. Development and analytical validation of a multivariate calibration method for determination of amoxicillin in suspension formulations by near infrared spectroscopy. Talanta 2012, 89, 342–351. [Google Scholar] [CrossRef] [PubMed]
- Uysal, R.S.; Boyaci, I.H.; Genis, H.E.; Tamer, U. Determination of butter adulteration with margarine using Raman spectroscopy. Food Chem. 2013, 141, 4397–4403. [Google Scholar] [CrossRef] [PubMed]
- de Jong, S. SIMPLS: An alternative approach to partial least squares regression. Chemom. Intell. Lab. Syst. 1993, 18, 251–263. [Google Scholar] [CrossRef]
- Smits, J.R.M.; Melssen, W.J.; Buydens, L.M.C.; Kateman, G. Using artificial neural networks for solving chemical problems. Part I. Multi-layer feed-forward networks. Chemom. Intell. Lab. Syst. 1994, 22, 165–189. [Google Scholar] [CrossRef] [Green Version]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Svozil, D.; Kvasnička, V.; Pospíchal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Janik, L.J.; Cozzolino, D.; Dambergs, R.; Cynkar, W.; Gishen, M. The prediction of total anthocyanin concentration in red-grape homogenates using visible-near-infrared spectroscopy and artificial neural networks. Anal. Chim. Acta 2007, 594, 107–118. [Google Scholar] [CrossRef] [PubMed]
- Despagne, F.; Massart, D.L. Neural networks in multivariate calibration. Analyst 1998, 123, 157R–178R. [Google Scholar] [CrossRef] [PubMed]
- Williams, K. Near-infrared technology in the agricultural and food industries. In Near-Infrared Technology in the Agricultural and Food Industries; American Association of Cereal Chemists, Inc.: Saint Paul, MI, USA, 2001; ISBN 1-891127-24-1. [Google Scholar]
- Batista de Carvalho, L.A.E. Raman spectra, conformational stability and normal coordinate analysis of ethylmethylamine. J. Raman Spectrosc. 1995, 26, 653–661. [Google Scholar] [CrossRef]
- Larkin, P. IR and Raman Spectra-Structure Correlations. In Infrared and Raman Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 9780128041628. [Google Scholar]
- Salciccioli, J.D.; Crutain, Y.; Komorowski, M.; Marshall, D.C. Sensitivity analysis and model validation. In Secondary Analysis of Electronic Health Records; Spring: Berlin/Heidelberg, Germany, 2016; ISBN 9783319437422. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA, 2014; ISBN 0262325748. [Google Scholar]
- Posada, D.; Buckley, T.R. Model selection and model averaging in phylogenetics: Advantages of akaike information criterion and bayesian approaches over likelihood ratio tests. Syst. Biol. 2004, 53, 793–808. [Google Scholar] [CrossRef]
- Bakeev, K.A. Process Analytical Technology: Spectroscopic Tools and Implementation Strategies for the Chemical and Pharmaceutical Industries: Second Edition; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 9780470722077. [Google Scholar]
- Davis, A.R.; Oliver, B.G. A vibrational-spectroscopic study of the species present in the CO2-H2O system. J. Solut. Chem. 1972, 1, 329–339. [Google Scholar] [CrossRef]
- Wen, N.; Brooker, M.H. Ammonium carbonate, ammonium bicarbonate, and ammonium carbamate equilibria: A raman study. J. Phys. Chem. 1995, 99, 359–368. [Google Scholar] [CrossRef]
- Axrup, L.; Markides, K.; Nilsson, T. Using miniature diode array NIR spectrometers for analysing wood chips and bark samples in motion. J. Chemom. 2000, 14, 561–572. [Google Scholar] [CrossRef]
- Xu, F.; Wang, D. Rapid determination of sugar content in corn stover hydrolysates using near infrared spectroscopy. Bioresour. Technol. 2013, 147, 293–298. [Google Scholar] [CrossRef]
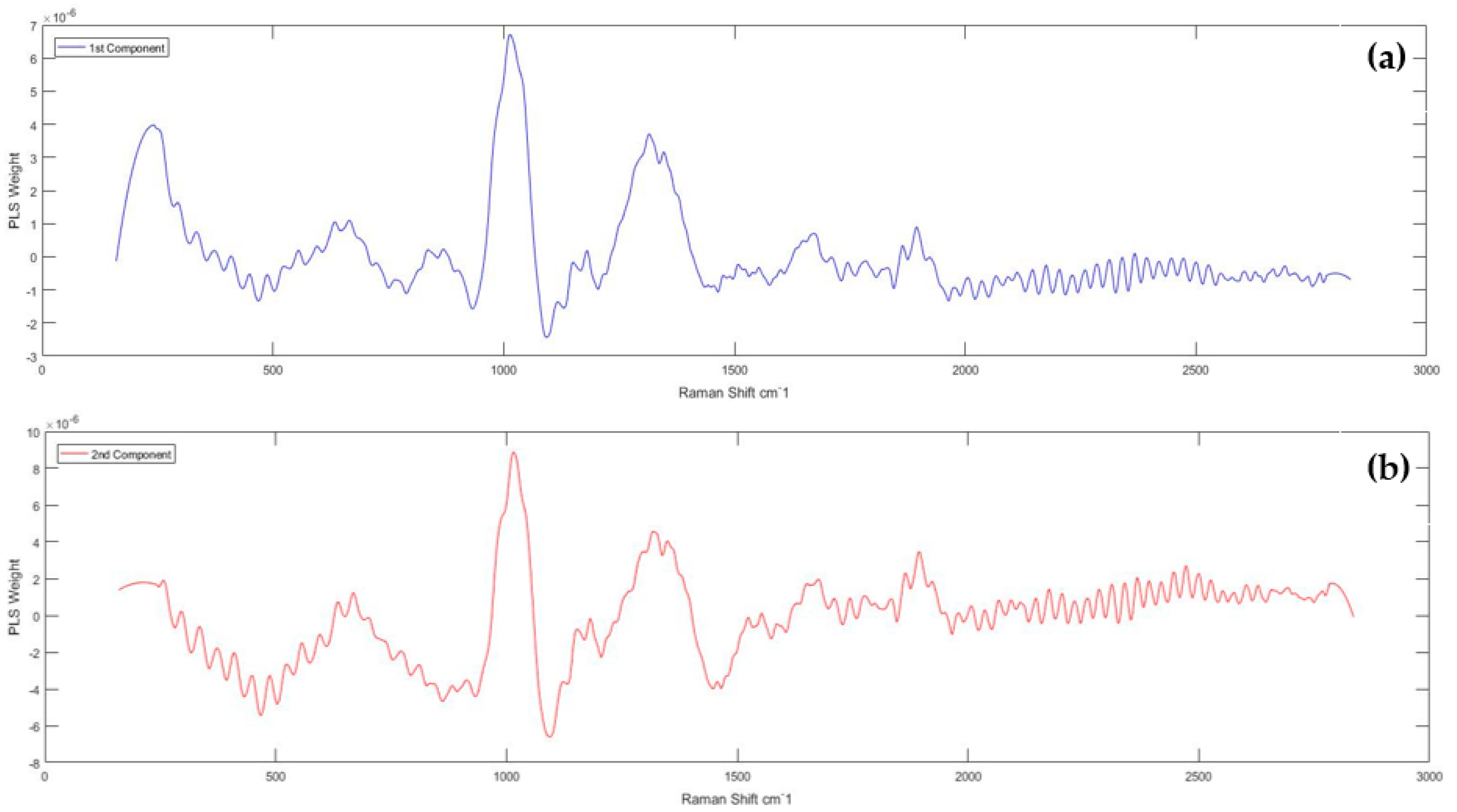
| Materials | Abbreviation | CAS No. | Purity |
|---|---|---|---|
| Monoethanolamine | MEA | 141-43-5 | 0.995 (mass fraction) |
| Carbon dioxide | CO2 | 124-38-9 | 0.9990 (volume fraction) |
| Water | H2O | 7732-18-5 | ~1.000 (mass fraction) |
| MEA Concentration (Molar) | Number of Datapoints | CO2 Loading Range (Moles of CO2/Moles of MEA) |
|---|---|---|
| 3 | 40 | 0.2593–1.2838 |
| 4 | 67 | 0.0261–1.0418 |
| 5 | 66 | 0.1754–1.0232 |
| Species/CO2 Loading | Amine Concentration (mol/L) | Number of LV Components | R2 Calibration | R2 Validation | RMSE Calibration | RMSE Validation |
|---|---|---|---|---|---|---|
| CO2 Loading | 3 | 6 | 0.9636 | 0.9319 | 0.0510 | 0.0762 |
| 4 | 6 | 0.9438 | 0.9075 | 0.0771 | 0.0790 | |
| 5 | 6 | 0.9562 | 0.9092 | 0.0652 | 0.0758 | |
| MEAH+ | 3 | 6 | 0.9437 | 0.9122 | 0.1497 | 0.2110 |
| 4 | 6 | 0.9400 | 0.9031 | 0.2653 | 0.3564 | |
| 5 | 6 | 0.9460 | 0.9137 | 0.3256 | 0.3655 | |
| HCO3− | 3 | 5 | 0.9466 | 0.9139 | 0.1539 | 0.2381 |
| 4 | 6 | 0.9421 | 0.9027 | 0.2727 | 0.3407 | |
| 5 | 5 | 0.9485 | 0.9039 | 0.3181 | 0.4228 | |
| CO32− | 3 | 6 | 0.9614 | 0.9133 | 0.0067 | 0.0072 |
| 4 | 6 | 0.9361 | 0.9031 | 0.0027 | 0.0035 | |
| 5 | 6 | 0.9321 | 0.9254 | 0.0052 | 0.0059 | |
| MEA | 3 | 6 | 0.9571 | 0.9201 | 0.1136 | 0.1095 |
| 4 | 7 | 0.9304 | 0.9074 | 0.2820 | 0.3163 | |
| 5 | 6 | 0.9211 | 0.9017 | 0.3736 | 0.3963 | |
| MEACOO− | 3 | 6 | 0.9755 | 0.9361 | 0.0224 | 0.0436 |
| 4 | 9 | 0.9497 | 0.9082 | 0.0364 | 0.0518 | |
| 5 | 8 | 0.9282 | 0.9003 | 0.0565 | 0.0661 | |
| CO2 | 3 | 6 | 0.9396 | 0.9383 | 0.0616 | 0.0548 |
| 4 | 6 | 0.9358 | 0.9147 | 0.0439 | 0.0580 | |
| 5 | 6 | 0.9311 | 0.9050 | 0.0497 | 0.0460 |
| Species/CO2 Loading | Amine Concentration (mol/L) | Number of Principal Components | Number of Hidden Nodes | R2 Calibration | R2 Validation | RMSE Calibration | RMSE Validation |
|---|---|---|---|---|---|---|---|
| CO2 Loading | 3 | 2 | 2 | 0.9527 | 0.9582 | 0.0469 | 0.0616 |
| 4 | 2 | 2 | 0.9305 | 0.9377 | 0.0600 | 0.0938 | |
| 5 | 2 | 2 | 0.9589 | 0.9069 | 0.0539 | 0.0592 | |
| MEAH+ | 3 | 1 | 1 | 0.9758 | 0.9584 | 0.1072 | 0.1439 |
| 4 | 1 | 1 | 0.9225 | 0.9250 | 0.2956 | 0.3038 | |
| 5 | 2 | 2 | 0.9521 | 0.9543 | 0.2377 | 0.2421 | |
| HCO3− | 3 | 1 | 1 | 0.9779 | 0.9528 | 0.1105 | 0.1425 |
| 4 | 2 | 2 | 0.9453 | 0.9476 | 0.2352 | 0.2975 | |
| 5 | 3 | 3 | 0.9232 | 0.9010 | 0.1559 | 0.2124 | |
| CO32− | 3 | 3 | 3 | 0.9788 | 0.9796 | 0.0035 | 0.0042 |
| 4 | 2 | 2 | 0.9397 | 0.9032 | 0.0023 | 0.0028 | |
| 5 | 3 | 3 | 0.9833 | 0.9490 | 0.0024 | 0.0038 | |
| MEA | 3 | 1 | 1 | 0.9215 | 0.9041 | 0.1315 | 0.1712 |
| 4 | 2 | 2 | 0.9363 | 0.9062 | 0.1881 | 0.2715 | |
| 5 | 2 | 2 | 0.9517 | 0.9574 | 0.2191 | 0.2900 | |
| MEACOO− | 3 | 2 | 2 | 0.9783 | 0.9400 | 0.0111 | 0.0238 |
| 4 | 3 | 3 | 0.9421 | 0.9394 | 0.0265 | 0.0616 | |
| 5 | 3 | 3 | 0.8835 | 0.8621 | 0.0424 | 0.0693 | |
| CO2 | 3 | 2 | 2 | 0.9652 | 0.9423 | 0.0412 | 0.0574 |
| 4 | 2 | 2 | 0.9612 | 0.9516 | 0.0332 | 0.0387 | |
| 5 | 2 | 2 | 0.9803 | 0.9692 | 0.0220 | 0.0223 |
| Species/CO2 Loading | PLS R2 Validation | ANN R2 Validation | PLS RMSE Validation | ANN RMSE Validation |
|---|---|---|---|---|
| CO2 Loading | 0.9162 | 0.9343 | 0.0770 | 0.0715 |
| MEAH+ | 0.9097 | 0.9459 | 0.3110 | 0.2299 |
| HCO3− | 0.9068 | 0.9338 | 0.3339 | 0.2175 |
| CO32− | 0.9139 | 0.9439 | 0.0055 | 0.0036 |
| MEA | 0.9097 | 0.9226 | 0.2740 | 0.2442 |
| MEACOO− | 0.9149 | 0.9138 | 0.0538 | 0.0516 |
| CO2 | 0.9193 | 0.9544 | 0.0564 | 0.0395 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanafiah, A.S.; Maulud, A.S.; Shahid, M.Z.; Suleman, H.; Buang, A. Raman Calibration Models for Chemical Species Determination in CO2-Loaded Aqueous MEA Solutions Using PLS and ANN Techniques. ChemEngineering 2021, 5, 87. https://doi.org/10.3390/chemengineering5040087
Hanafiah AS, Maulud AS, Shahid MZ, Suleman H, Buang A. Raman Calibration Models for Chemical Species Determination in CO2-Loaded Aqueous MEA Solutions Using PLS and ANN Techniques. ChemEngineering. 2021; 5(4):87. https://doi.org/10.3390/chemengineering5040087
Chicago/Turabian StyleHanafiah, Ahmad Syukri, Abdulhalim Shah Maulud, Muhammad Zubair Shahid, Humbul Suleman, and Azizul Buang. 2021. "Raman Calibration Models for Chemical Species Determination in CO2-Loaded Aqueous MEA Solutions Using PLS and ANN Techniques" ChemEngineering 5, no. 4: 87. https://doi.org/10.3390/chemengineering5040087
APA StyleHanafiah, A. S., Maulud, A. S., Shahid, M. Z., Suleman, H., & Buang, A. (2021). Raman Calibration Models for Chemical Species Determination in CO2-Loaded Aqueous MEA Solutions Using PLS and ANN Techniques. ChemEngineering, 5(4), 87. https://doi.org/10.3390/chemengineering5040087







