Abstract
It has been suggested that the energy-efficient production of microalgae biomass can be more easily obtained in short light path photobioreactors that can be operated at high biomass concentration. On the downside, however, high biomass concentrations also require an efficient gas exchange rate to avoid metabolic growth limitation or inhibition. A cascade photobioreactor featuring a thin liquid layer flowing down a sloping, wavy-bottomed surface can be operated at a biomass concentration that is much higher compared to most usual open-type equipment. Liquid flow, upon investigation, proved to exhibit peculiar “local recirculation” hydrodynamics, potentially conducive to the mixing of superficial and deep zones of the photobioreactor. Mass transfer coefficient represents a useful parameter to optimize the performance of a microalgal photobioreactor and its scale-up. The aim of the present article is to discuss the experimental mass transfer features of this novel type of photobioreactor and highlight expected opportunities and issues entailed by different ways of installing and operating such novel types of photobioreactors.
1. Introduction
Microalgae are currently used as food and sources of food fractions and are touted to be a potential feedstock for green biochemicals and biofuels. Even though microalgae are the fastest-growing biomass on Earth, their real-life deployment in low added-value production scenarios is unfeasible at current production prices.
Several hindrances prevent the adoption of microalgae as a low-value feedstock, among which are the scarce scalability of both open (ponds) and closed photobioreactors (PBRs), the significant cost (both capital and operational) to run them, plus a downstream processing cost that is generally higher than that affecting traditional storage biomass [1]. All these hindrances are being actively scavenged to make large-scale production and deployment of microalgal biomass possible at a lower cost and to make microalgal biomass a viable alternative to other biomass sources beyond current niche high value markets.
Scalability issues are multifaceted and interweaving. An adequate CO2 supply is required to avoid biomass growth limitation, but a symmetric buildup of waste and toxic O2 should also be avoided; if inorganic carbon is supplied as bicarbonate, an efficient escape path for O2 waste must be ensured. While uniform levels of (high) CO2 and (low) O2 ensure a uniformly high growth rate throughout the photobioreactor volume, the uniform and constant lighting at optimal levels is unfeasible, since light is not a “soluble substrate” and must diffuse through the culture from its source. Ensuring an optimal illumination at every point of the photobioreactor implies that the culture is very dilute, which is undesired for both downstream processing and productivity. Otherwise, ensuring an optimal irradiance at some point of the photobioreactor either implies that the harmful effect (photoinhibition, photodamage) of excessive illumination is experienced and/or that the equally harmful effect of limiting illumination or even the complete darkness (biomass decay) is experienced at other points. In this respect, high-rate alternation of light and dark has been found to warrant a high productivity. Creating an appropriate light–dark cycle for the cells in photobioreactors requires a good balance of hydrodynamics (conducive to long-range mixing) and biomass concentration (attenuating the irradiance over the optical thickness of the photobioreactor). Provisions that are effective toward mixing are usually energetically costly and produce a short-range mixing, again deleterious because hydrodynamic stress effects reduce biomass growth.
Mass transfer from the gas phase to the liquid phase has been identified as an important rate-limiting step in many chemical and biochemical processes. The rate of mass transfer is expressed by the overall volumetric mass transfer coefficient, which is expressed as the product of the interfacial area times the liquid phase mass transfer coefficient. Several models have been proposed in the literature for determining the volumetric mass transfer coefficient, also known as kLa. Most of the models proposed are based on the concept of a rigid interface or an interface where surface renewal occurs through the displacement of liquid at the interface or a combination of these concepts [2]. The kLa of photobioreactors is dependent on various factors such as mixing rate, the type of sparger, surfactants/antifoam agents, and temperature.
Mass transfer coefficients are often, although not routinely, measured by photobioreactor developers [3,4,5,6,7,8,9]. Knowing mass transfer capabilities is essential information for judging the potential of a photobioreactor’s geometry to scale its performance when other bottlenecks are removed. Ideally, for optimal deployment of a microalgal culture, the limiting biomass growth performance should be intrinsic to the species, and not determined by suboptimal external conditions. Inasmuch as irradiance can be defective or excessive, both being deleterious, an insufficient CO2 supply reduces the potential productivity as that of any other essential nutrient. When CO2 is fixed, it is consumed at the theoretical rate of 1.83 kg per kg of new dry biomass, but more will be required in practice to account for losses, open cultures departing most from the previous figure because of dispersion effects [10]. When inorganic carbon is supplied as CO2, waste oxygen will be eliminated through the same route at a comparatively similar efficiency. However, this may not be true when inorganic carbon is supplied as bicarbonate, because in this latter case, it can be dosed and dispersed as efficiently as other soluble nutrients are, while waste oxygen needs to escape through the gas–liquid interface, and this can lead to high oxygen supersaturation values at low values of the gas–liquid mass transfer coefficient.
The overall gas mass transfer being the product of the mass transfer coefficient times the driving force, mass transfer benefits from a large surface gas–liquid contact surface per unit culture volume, because the large surface-to-volume ratio directly translates into a favorable mass transfer coefficient. While enclosed photobioreactors need gas insufflation to create such a surface, open ones both expose the free liquid surface to the contact of air and can be insufflated.
Thin layer photobioreactors represent a special class of photobioreactors that feature a large contact surface with the upper gas phase, generally represented by atmosphere, with respect to their liquid holdup volume. Thin layer photobioreactors date back to the 1960s [11] and aim at cultivating microalgae at much higher concentrations (up to 30 g/L) than allowed by photobioreactors characterized by higher optical length. They have evolved over time in different incarnations including medium-scale implementations in the industry (A4F, Portugal [12]), extremely thin versions actively developed in the academia such as the AlgoFilm photobioreactor, and shaped-bottom versions such as the wavy-bottomed cascade photobioreactor proposed in [13]. As the AlgoFilm inventors showed, although thin-layer photobioreactors were conceived as units open to the atmosphere, they can be enclosed thus allowing protection from airborne contaminants, control of the gas phase composition, and recycling of any CO2 escaped from the surface.
The Torzillo et al. [13] prototype was aimed at inducing fast light/dark cycles and improving mass transfer without special turbulence enhancing devices and only resorting to gravity for liquid motion. This system was characterized both experimentally and computationally [14,15] and, for some operating conditions, it was found to be characterized by a particular fluid dynamics structure conducive to a flashing light regime for the circulated microalgae due to the fast and long-range ordered circulation of the microalgal suspension [14].
The current work reports a specific experimental and modeling analysis aimed at characterizing the mass transfer performance of the inclined, thin-layer, wavy-bottomed cascade photobioreactor that will be adopted as the case study because of its ordered local recirculation streams that warrants a continuous renewal of the liquid surface layer and a (perceived) pulsing of light of adjustable frequency.
2. Materials and Methods
The experimental activity at the core of this analysis was carried out independently on two prototypes sharing the same base shape and geometry (wavy bottom with equal pitch between ridges and cavities), different in total surface (0.4 and 5 m2 respectively). Although made from different materials and finishing (fiberglass/glass vs. painted metal), they exhibited comparable superficial smoothness. Installation and operating conditions were varied in each unit to investigate regions of the operating window of possible interest of the research group owning the unit with a partial overlap. The adopted conduit for the experimental runs was slightly different in the two units, mainly as a consequence of the relevant equipment arrangement, size, and location, thus requiring a different modeling to derive the relevant mass transfer parameters.
2.1. Experimental Setup
Two different units were used to carry out the experimental mass transfer coefficient experiments, which required using different procedures. Both units were characterized during operation entailing water flowing on the cascade. Cascades are characterized by the specific flow rate (L m−1 s−1), that is the flow rate flowing on the cascade per unit width of the cascade in the direction perpendicular to water flow. In the following, a specific flow rate was always used because it permitted the aggregation of the results obtained from the two units which had a different width. Measurement runs were carried out with a once-through flow of water for the smaller unit (hence, no recirculation: during the test runs, water flowed through the photobioreactor and was then stored away), while measurement runs were carried out in recirculated flow for the larger unit.
The smaller photobioreactor was 120 cm long and 15 cm wide and was installed at an inclination of 6° and 9° with respect to a horizontal plane, with 10 cm high side rims, as described in [15]. Tests were carried out at 1.11 and 1.67 L m−1 s−1 flow rates. The larger photobioreactor was 5 m long and 1 m wide and was installed at an inclination of 3° and 6° with respect to a horizontal plane that consisted of a wavy-bottomed iron surface 5 m long and 1 m wide, provided with 10 cm high side rims. The tested flow rates were: 1.45 L m−1 s−1, 2.00 L m−1 s−1, and 2.90 L m−1 s−1. The two installations are denoted in the following as the “small” and “large” instances of the wavy photobioreactor, respectively.
Mass transfer experiments in the small photobioreactor unit consisted of feeding the wavy channel with an assigned flow rate of previously deoxygenated water and recording the return to saturation exhibited by the down flowing liquid as a function of the linear abscissa along the photobioreactor, after the oxygen concentration profile on the wavy cascade had reached steady state. Specifically, tap water collected in a stirred tank (Figure 1a) and oxygen by sparging nitrogen until oxygen concentration in the tank was below 1.5 ppm. Nitrogen was sparged in the stripping tank by a large porous stone and measurement of the prevailing dissolved oxygen concentration was carried out in a location inside the tank that was not disturbed by the rising nitrogen bubbles. Then, pumping was started and the measurements in the adopted locations of the photobioreactor (vanes 1 and 13) were started. Oxygen measurements were carried out with a recording instrument fitted with a chemiluminescent probe (HACH 440d, Hach-Lange, Loveland, CO, USA). The temperature was approximately 25 °C during the tests.
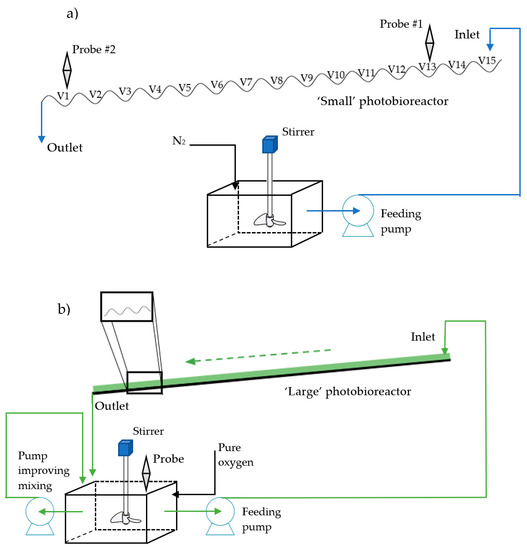
Figure 1.
(a) Schematic illustration of the experimental setup of the “small” wavy photobioreactor unit; (b) schematic illustration of the experimental setup of the “large” wavy photobioreactor unit.
The large photobioreactor unit (see picture in Figure 1b) could not be tested with the technique adopted for the small unit because of practical limitations deriving from its larger size and locally available facilities and instrumentation. Notably, testing the “large” unit with the strategy used for the small unit would have required a comparatively larger storage tank and gas availability. Therefore, a testing strategy was devised that allowed to perform measuring the time evolution of the oxygen concentration in one single spot of the photobioreactor during its operation. The experiments consisted of preparing a uniformly oxygen-supersaturated batch of distilled water in the feed tank before starting the run. Supersaturation was obtained by sparging pure oxygen and oxygen concentration was measured by an amperometric probe (Hamilton Oxysens 120, Bonaduz, Switzerland) and oxygen concentration data were recorded as a function of time by a dissolved oxygen and temperature analyzer-controller (Chemitec µACP4082, Scandicci, Italy,). The temperature was approximately 27 °C during the tests. After preparing the feed batch, the circulation pump was started at an assigned flow rate and the water was pumped to the inlet rim of the photobioreactor where from it flowed along the wavy surface, eventually returning to the feed tank located just below the lower end of the cascade. After starting the recirculation pump, a note was made of the time required for water to fully cover the photobioreactor surface and returning into the feed tank. To ensure thorough mixing of the water tank, it was equipped with a rotary stirrer installed in the neighborhood of the probe and with an auxiliary recirculation pump which improved bottom-to-top mixing (Figure 1b).
2.2. Mathematical Modeling
For the smaller unit that was tested at steady state, a simple model was written considering that the wavy profile can be considered uniform, so that an infinitely small element of its volume (), which exchanges oxygen with the atmosphere by the mass exchange coefficient () during its downward flow along the sloping photobioreactor surface, could also be considered. We will also define as the recirculation flow rate, as the local oxygen concentration, as the inlet oxygen concentration, as the outlet oxygen concentration, as the saturation oxygen concentration, and as the entire photobioreactor volume. The oxygen balance for this infinitely small volume element can thus be written as:
By integrating it over the whole photobioreactor volume, :
the equation that was used to calculate the prevailing mass transfer coefficient from the experiments carried out in the smaller photobioreactor was obtained.
Since the larger equipment included a hopper (the feed tank) located right under the photobioreactor outlet and water got mixed with the feed water after the cascade holdup reached the steady-state value, a simple data analysis approach could not be used to derive the mass transfer coefficient relevant to the open photobioreactor surface only. A dynamic model considering the whole loop was thus created to consider the open photobioreactor surface and the storage tank.
For the purpose of calculating the relevant mass transfer coefficient, the “large” photobioreactor was modeled as shown in Figure 2.
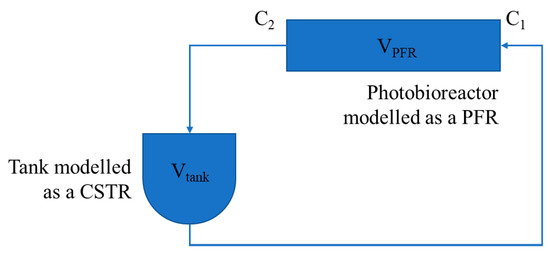
Figure 2.
Compartmental dynamic model of the “large” wavy photobioreactor loop.
The model considers the photobioreactor as a plug-flow reactor (PFR), which has an outlet section that discharges water into the feed tank where from the latter is pumped back to the inlet section. The feed tank is well mixed and was modeled as a continuous, stirred-tank reactor (CSTR), while the recirculation piping volume, and that of the centrifugal pump itself, was deemed negligible. Therefore, separate models were written for the photobioreactor and for the feed tank to relate the relevant inlet and outlet oxygen concentrations and considering their holdup volumes and the circulating feed flow rate. In this model, represents the inlet concentration to the photobioreactor as well as the uniform concentration of the tank, that is, the measured quantity. Then, these models were coupled by considering that the inlet stream to the PFR was the outlet stream from the CSTR and vice versa, thus obtaining the overall model, where the feed tank concentration was expressed as a function of three characteristic times, namely, the residence time in the PFR (), the residence time in the CSTR (), and the mass transfer characteristic time (), which is the inverse of the mass transfer coefficient (), the quantity that should be determined.
The part of the overall model considering the photobioreactor volume is essentially identical to that reported for the smaller test unit and will not be repeated here.
Let us denote:
Hence:
For the receiving tank, modeled as a CSTR, it is:
For the entire looping process, by substituting , we obtain:
Let us denote:
Thus, the expression can be simplified as:
By integrating we obtain:
β can be obtained from the slope of vs. t.
To obtain the mass transfer coefficient, the model requires the average residence time of the photobioreactor cascade and in the feed tank as input data. These parameters were determined from holdup measurements in the feed tank before the beginning of each run and at the steady state during the run itself. Figure 3 shows an example of application of this modeling to the estimation of the photobioreactor mass transfer coefficient.
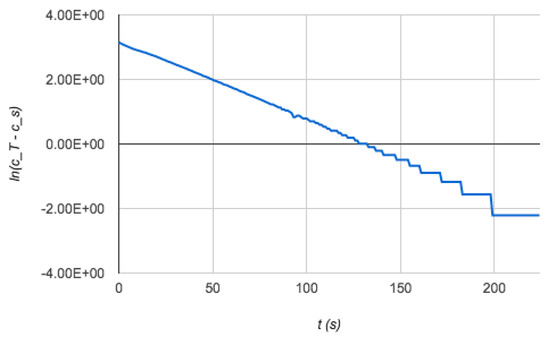
Figure 3.
Plot of measured feed tank concentration from the “large” bench scale photobioreactor which had a slope that yielded the mass transfer coefficient based on the overall dynamic model.
3. Results
The results of the experiments carried out on the small and the large units are collectively reported in Table 1.

Table 1.
Aggregate view of mass transfer measurement results.
Interesting features can be observed regarding the changes exhibited by the mass transfer coefficient with operating conditions. This can be readily appreciated by plotting these data in a bubble chart (Figure 4).
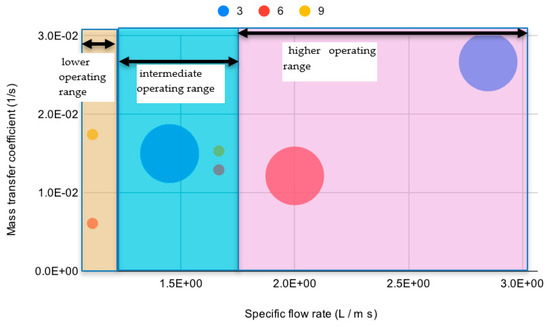
Figure 4.
Dependence of the mass transfer coefficient as a function of the circulating flow rate (abscissa), cascade inclination (color), and unit adopted for the test (large dots = large unit, small dots = small unit).
Figure 4 shows the dependence of the mass transfer coefficient on the specific flow rate on the cascade, highlighting both the dependence on inclination and on the unit size. Indeed, most measured coefficients range from 0.01 to 0.02 s−1, with only one operating condition producing a coefficient below 0.01, and one larger than 0.02 s−1. At a closer look into Figure 4 it can be observed that the plot can be divided in three sections, defined by the specific flow rate adopted: the lower operating range, where the mass transfer coefficient appears to depend on the installation inclination, the intermediate range, where the mass transfer coefficient appears scarcely sensitive to changes of inclination, and even of flow rate itself, and the higher range, where the highest mass transfer coefficient is obtained at the lowest inclination.
4. Discussion
The variation in the mass transfer coefficient can possibly be related with the observed macroscopic hydrodynamic features of the wavy-bottomed photobioreactor geometry. Indeed, the local recirculation frequency relevant to the very same photobioreactor geometry published in [15,16] could explain the behavior of mass transfer coefficients obtained by the smaller test unit and could provide hints about those obtained with the larger one. Indeed, by inspecting the measured recirculation frequency data reported by both our previous papers and plotting them (Figure 5a) the liquid flowing down on the cascade recirculates locally (i.e., in each cavity) at a frequency which is linearly dependent upon the flow rate up to an inclination of 6°, while such a frequency becomes independent of the flow rate for steeper inclinations. It should also be recalled that when the cascade inclination was 3°, the position of the recirculating core was below the transport stream, while when the cascade was installed at 6° or above, it was above the transport stream (Figure 5b).
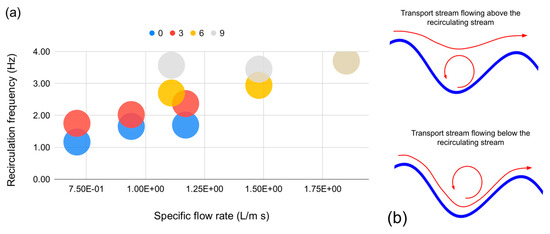
Figure 5.
(a) Relation between the specific flow rate and the measured recirculation frequency measured in the smaller test unit; (b) relative position of the recirculation and transport stream in each photobioreactor cavity.
The apparent linear behavior of frequency with flow rate that was ascertained experimentally in [15,16] was then used in this work to obtain simple linear models of frequency vs. specific flow rate which were used to calculate a first approximation estimate of the recirculation frequency for all experiments for which experimental values were not available, regardless of the test units they had been carried on. Table 2 collectively presents results from Table 1 above and these estimates.

Table 2.
Relationship of the mass transfer coefficient with the measured recirculation frequencies within cavities obtained in [15,16]. * Estimated from original data by linear models obtained from the data shown in Figure 5.
Indeed, the relationship between mass transfer coefficients at 6° and 9° can be very well observed and is shown in Figure 6. The change in installation angle and specific operating flow rate is reflected by the recirculation frequency, and this latter translates into a proportionate change of the mass transfer coefficient.
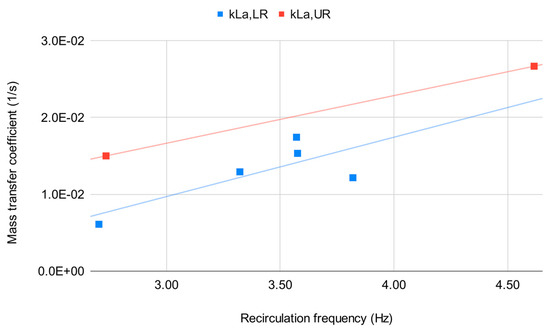
Figure 6.
Relationship between recirculation frequency and mass transfer coefficient values obtained from the smaller test unit.
From Figure 6 the frequency estimates suggest that both installation slope and local hydrodynamic “structure” (i.e., whether the local recirculation macro-vortex stays above or below the transport stream) play a role in determining the value of the mass transfer coefficient of the wavy-bottomed photobioreactor.
Low inclination angles seem to be favorable in that they award a linear increase in the local recirculation frequency which, in turn, translates into a higher mass transfer coefficient. However, the upper locations of the transport stream with respect to the recirculation stream awards a higher mass transfer coefficient. It should also be noted that by staying above the recirculation vortex, the transport stream shows as a continuous layer, always staying in contact with the upper gas phase.
The location of the transport stream may have implications on the practical deployment of the wavy-bottomed cascade photobioreactor by considering that the maximum practical length of a cascade unit is dictated by the maximum accepted height of the inlet with respect to the outlet. With this height being roughly proportional to the angle for small values of the installation angle (), by adopting a smaller angle (e.g., 3° instead of 6°), one can deploy a cascade that is twice as long, which ultimately means that a smaller numbers of pumps and external recirculation pipes are required for a given total installed area.
Before stating that low installation angles are a win–win choice to deploy wavy-bottomed cascades, other aspects should be taken in consideration. The wavy-bottomed cascade photobioreactor, indeed, seems to exhibit interesting flashing light features due to the local (i.e., internal to each cavity) recirculation, and the effect of the prevailing hydrodynamics on the effective light–darkness alternation experienced by microalgae has been characterized in [14]. The authors of [14] show that the long-range recirculation (in the order of centimeters) is more effective in producing a powerful alternation frequency compared with other major photobioreactors such as the bubble column and the flat plane. However, Moroni adopted for said study a 6° installation angle where the transport stream flows below, and it would not be fair to conclude that, even at the same tumbling frequency, in the case of an upper-flowing transport stream, the frequency spectrum of perceived light flashing maintains the same level of sustained frequency excitation found for the bottom-flowing transport stream.
Based on the results obtained in this study, the wavy-bottomed photobioreactor investigated seemed to exhibit equivalent or better gas transfer performances than other widely adopted geometries as shown in Table 3. In particular, it apparently also exhibited a higher performance with respect to the flat-bottomed, thin-layer photobioreactor discussed in [4], although it should be noted that the two units were characterized using a different approach.

Table 3.
Comparison of volumetric mass transfer coefficient among different photobioreactor configurations.
In this work, only the contribution to mass transfer coming from the section of the circuit exposed to light was characterized so that variations of the mass transfer coefficient along the channel length were not expected upon scale-up. The local recirculation photobioreactor must be completed with a circulation device, which may well impact not only on the mass transfer coefficient but also the hydrodynamic stress. An air-lift device would boost mass transfer, while a centrifugal pump may not only be neutral from the point of view of gas transfer but could even be deleterious as a consequence of a greater hydrodynamic stress [17].
Some of the considerations reported in this discussion clearly and greatly extend the scope of the studies required to fully characterize the wavy-bottomed cascade photobioreactor. Indeed, the wavy-bottomed cascade photobioreactor has been comparatively much less studied than most mainstream configurations and studies considering multiple converging sides, including its actual biomass production performance and an analysis of its improvement potential would be most welcome to make firm statements about its actual deployment potential.
5. Conclusions
The present article provides a core study concerning the mass transfer features of the wavy-bottomed cascade photobioreactor based on data obtained from experiments carried out on two test units of different sizes that were analyzed in light of previously published hydrodynamic studies concerning the tumbling frequency of big recirculation vortices that establish in the cavities. The preliminary results reported in this study suggest that the mass transfer coefficient depends upon the prevailing specific flow rate and the installation slope. In conclusion, installing the cascade at a slope less than 6° appears to be beneficial for the mass transfer coefficient compared to 6° or more. Whatever the angle, increasing the specific flow rate apparently roughly translates into a linear increase of the mass transfer coefficient.
Author Contributions
Conceptualization, M.B., M.M. and A.C.; methodology, A.C., G.S. and G.T.; software, M.B. and M.M.; validation, M.B. and A.C.; formal analysis, B.M. and N.V.; investigation, M.M., A.C. and G.S.; resources, M.B. and G.T.; data curation, M.B., A.C. and G.S.; writing—original draft preparation, M.M. and M.B.; visualization, M.M.; supervision, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request.
Acknowledgments
The authors wish to thank Edoardo Pinzani for the valuable technical assistance during the measurements performed outdoors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tenorio, A.T.; Kyriakopoulou, K.E.; Suarez-Garcia, E.; van den Berg, C.; van der Goot, A.J. Understanding differences in protein fractionation from conventional crops, and herbaceous and aquatic biomass-consequences for industrial use. Trends Food Sci. Technol. 2018, 71, 235–245. [Google Scholar] [CrossRef]
- Ranganathan, P.; Sivaraman, S. Investigations on hydrodynamic and mass transfer in gas–liquid stirred reactor using computational fluid dynamics. Chem. Eng. Sci. 2011, 66, 3108–3124. [Google Scholar] [CrossRef]
- Merchuk, J.C.; Rosenblat, Y.; Berzin, I. Fluid flow and mass transfer in a counter-current gas–liquid inclined tubes photo-bioreactor. Chem. Eng. Sci. 2007, 62, 7414–7425. [Google Scholar] [CrossRef]
- Doucha, J.; Lívanský, K. Productivity, CO2/O2 exchange and hydraulics in outdoor open high density microalgal (Chlorella sp.) photobioreactors operated in a Middle and Southern European climate. J. Appl. Phycol. 2006, 18, 811–826. [Google Scholar] [CrossRef]
- Ye, Q.; Cheng, J.; Guo, W.; Xu, J.; Li, K.; Zhou, J. Serial lantern-shaped draft tube enhanced flashing light effect for improving CO2 fixation with microalgae in a gas-lift circumflux column photobioreactor. Bioresour. Technol. 2018, 255, 156–162. [Google Scholar] [CrossRef]
- Huang, J.; Feng, F.; Wan, M.; Ying, J.; Li, Y.; Qu, X.; Pan, R.; Shen, G.; Li, W. Improving performance of flat-plate photobioreactors by installation of novel internal mixers optimized with computational fluid dynamics. Bioresour. Technol. 2015, 182, 151–159. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, J.; Xu, X.; Zhou, J.; Cen, K. Enhanced solution velocity between dark and light areas with horizontal tubes and triangular prism baffles to improve microalgal growth in a flat-panel photo-bioreactor. Bioresour. Technol. 2016, 211, 519–526. [Google Scholar] [CrossRef] [PubMed]
- Pirouzi, A.; Nosrati, M.; Shojaosadati, S.A.; Shakhesi, S. Improvement of mixing time, mass transfer, and power consumption in an external loop airlift photobioreactor for microalgae cultures. Biochem. Eng. J. 2014, 87, 25–32. [Google Scholar] [CrossRef]
- Kubar, A.A.; Cheng, J.; Kumar, S.; Liu, S.; Chen, S.; Tian, J. Strengthening mass transfer with the Tesla-valve baffles to increase the biomass yield of Arthrospira platensis in a column photobioreactor. Bioresour. Technol. 2021, 320, 124337. [Google Scholar] [CrossRef]
- Le Gouic, B.; Marec, H.; Pruvost, J.; Cornet, J.F. Investigation of growth limitation by CO2 mass transfer and inorganic carbon source for the microalga Chlorella vulgaris in a dedicated photobioreactor. Chem. Eng. Sci. 2021, 233, 116388. [Google Scholar] [CrossRef]
- Setlik, I.; Veladimir, S.; Malek, I. Dual purpose open circulation units for large scale culture of algae in temperate zones. I. Basic design considerations and scheme of pilot plant. Algol. Stud. 1970, 1, 11. [Google Scholar]
- Available online: https://a4f.pt/en/tecnologic-plataforms# (accessed on 10 July 2021).
- Torzillo, G.; Giannelli, L.; Martinez-Roldan, S.J.; Verdone, N.; De Filippis, P.; Scarsella, M.; Bravi, M. Microalgae culturing in thin-layer photobioreactors. Chem. Eng. Trans. 2010, 20, 265–270. [Google Scholar]
- Olivieri, G.; Moroni, M.; Janssen, M.; Piersanti, L.; Mezza, D.; Bravi, M. Model-based prediction of perceived light flashing in Recirculated inclined wavy-bottomed photobioreactors. Processes 2021, 9, 1158. [Google Scholar] [CrossRef]
- Moroni, M.; Cicci, A.; Bravi, M. Experimental Investigation of a Local Recirculation Photobioreactor for Mass Cultures of Photosynthetic Microorganisms. Water Res. 2014, 52, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Moroni, M.; Lorino, S.; Cicci, A.; Bravi, M. Design and Bench-Scale Hydrodynamic Testing of Thin-Layer Wavy Photobioreactors. Water 2019, 11, 1521. [Google Scholar] [CrossRef] [Green Version]
- Scarsella, M.; Torzillo, G.; Cicci, A.; Belotti, G.; De Filippis, P.; Bravi, M. Mechanical stress tolerance of two microalgae. Process Biochem. 2012, 47, 1603–1611. [Google Scholar] [CrossRef]
- Sánchez-Mirón, A.; García-Camacho, F.; Contreras-Gómez, A.; Molina-Grima, E.; Chisti, Y. Bubble-column and airlift photobioreactors for algal culture. AIChE J. 2000, 46, 1872–1887. [Google Scholar] [CrossRef]
- Sierra, E.; Acién, F.G.; Fernández, J.M.; García, J.L.; González, C.; Molina, E. Characterization of a flat plate photobioreactor for the production of microalgae. Chem. Eng. J. 2008, 138, 136–147. [Google Scholar] [CrossRef]
- Siegel, M.H.; Merchuk, J.C. Mass transfer in a rectangular air lift reactor: Effects of geometry and gas recirculation. Biotechnol. Bioeng. 1988, 32, 1128–1137. [Google Scholar] [CrossRef] [PubMed]
- Reyna-Velarde, R.; Cristiani-Urbina, E.; Hernández-Melchor, D.J.; Thalasso, F.; Cañizares-Villanueva, R.O. Hydrodynamic and mass transfer characterization of a flat-panel airlift photobioreactor with high light path. Chem. Eng. Process. Process Intensif. 2010, 49, 97–103. [Google Scholar] [CrossRef]
- Contreras, A.; Garcia, F.; Molina, E.; Merchuk, J.C. Interaction between CO2-mass transfer, light availability, and hydrodynamic stress in the growth of Phaeodactylum tricornutum in a concentric tube airlift photobioreactor. Biotechnol. Bioeng. 1998, 60, 317–325. [Google Scholar] [CrossRef]
- Miyamoto, K.; Wable, O.; Benemann, J.R. Vertical tubular reactor for microalgae cultivation. Biotechnol. Lett. 1988, 10, 703–708. [Google Scholar] [CrossRef]
- Zhang, K.; Kurano, N.; Miyachi, S. Optimized aeration by carbon dioxide gas for microalgal production and mass transfer characterization in a vertical flat-plate photobioreactor. Bioprocess. Biosyst. Eng. 2002, 25, 97–101. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).