Abstract
In this paper we analyse static properties of mass spring models (MSMs) with the focus of modelling non crystalline materials, and explore basic improvements, which can be made to MSMs with disordered point placement. Presented techniques address the problem of high variance of MSM properties which occur due to randomised nature of point distribution. The focus is placed on tuning spring parameters in a way which would compensate for local non-uniformity of point and spring density. We demonstrate that a simple force balancing algorithm can improve properties of the MSM on a global scale, while a more detailed stress distribution analysis is needed to achieve local scale improvements. Considered MSMs are three dimensional.
1. Introduction
Mass spring models are used for the purpose of simulating elastic objects in various fields. Their potential applications include computer games, animations, virtual reality environments as well as engineering of structures or materials in which deformation under stress is considered, crack propagation studies or human tissue simulations. Related fields range from ultramicroscopy to astrophysics [1,2,3,4,5,6]. Specific needs of specific application may vary, but the general theory of how mass spring models (MSM) deform concerns all of them.
We distinguish two broad classes of mass-spring networks—crystal (lattice) based and disordered. In crystal based networks, mass points are placed on a periodic lattice and mechanical properties of such networks can be expressed with analytical formulas. This allows for more precise analysis and description of their behaviour. In disordered networks, on the other hand, the mass placement rules are relaxed and do not have to follow any regular order (Figure 1). The downside of such models is reduced accuracy and increased difficulty of estimating their mechanical properties [7]. Consequently, lattice based networks are usually preferred over disordered ones and are even used to model materials, which are known not to be crystals.

Figure 1.
Cubic lattice and disordered mass placement.
For numerous applications this is not a problem, however, there is a danger that in certain situations the material may inherit some unexpected properties of the periodic network and exhibit unintended behaviours. An example is the crack propagation problem, where geometry of the network may influence the observed crack patterns considerably. If the numerical model has a regular, lattice-like topology which determines the potential crack placement, it creates “easy propagation planes” for cracks (whether it is based on MSM or FEM, or some other modelling technique). In such models cracks tend to form and propagate along lattice dependent directions and resulting patterns may reflect lattice properties instead of material ones (Figure 2). In such cases it is difficult to asses, if the obtained results follow from the mathematical model, or if they are only artefacts of the numerical representation. For example, in a model with cubic lattice topology a curved crack may appear as two straight segments approaching each other at 45 degrees, or worse, the crack may not bend at all, if breaking of subsequent segments influences tensions within the system.
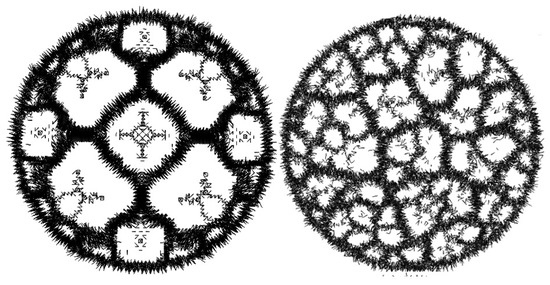
Figure 2.
Example crack patterns observed on cubic lattice and disordered networks.
Some attempts have been made to address these problems, such as Chen et al. [8], where introduction of non-local interactions into the model is shown to reduce negative effects of a lattice topology. Such solutions may mitigate most apparent artefacts in certain situations, however they do not eliminate the problem completely. A class of conditions for which such methods are unlikely to work involves situations where cracking is induced by a shrinkage front progressing through a material, such as in the case of drying or cooling materials [9,10,11,12,13]. For example if a cooling front is advancing through solidifying lava in presence of water, the problem has a translational symmetry. Cracks which appear at the top, allow for the water to be in contact with the top of the front, keeping the temperature at 100 °C, while the bottom of the front is in contact with non-solidified lava at an approximately constant temperature . The front itself is expected to have a linear gradient of temperature between these two values [14]. Modelling such process with lattice-based networks will result with exactly the same conditions at each cracking step, and since the tip of the crack can follow only discretised paths, it may never turn if the incentive to turn is too weak.
In such situations it may be beneficial to use disordered MSMs instead of lattice-based ones. As mentioned, the downside of such models is the reduced accuracy when compared to lattice-based MSMs, which in turn may cause discrepancies between modelled and theoretical properties of the material e.g., such as reported in [15]. In this work we place focus on disordered MSMs.
Mass spring models studied in this work are based on [7,16] and the reader is encouraged to refer to these papers for a more detailed introduction. We achieve varying values of Poisson’s ratio in our models, by introducing a force dissipation mechanism. This technique offers a considerable simplicity in terms of implementation as well as low conceptual and computational complexity, when compared to alternative methods capable of achieving full spectrum of . A comprehensive review of other MSM-like techniques can be found in [17].
In the following sections we show how to formalise the force dissipation mechanism proposed in [16], with a focus on ease of implementation. We introduce a new pair of elastic constants for the material, which translate into simple properties of springs and nodes of the network. We also demonstrate how to mitigate the accuracy problems of disordered MSMs by adjusting stiffness coefficients of the springs. Presented techniques allow to improve both global and local behaviour of disordered mass-spring networks.
It should be noted, that we investigate only the static properties of MSMs. We do not address here the question of how these systems evolve over time or what are the most efficient numerical schemes to track their dynamics. Efficient ways of simulating the dynamics can be found e.g., in [18,19].
2. Elastic Moduli
In linear elasticity, the relation between tensions and deformations of a continuous medium is linear. This can be expressed in general form by:
where denotes the stress and the strain tensor; is a tensor of elastic constants. Components of are tied together by various relations which follow from symmetry of and . In this paper we discuss homogeneous isotropic media, which further restricts the values of .
In a medium which behaves like fluid or gas, in an equilibrium state, all the “tensions” are distributed equally in all directions, that is , where p denotes pressure (for fluids or gasses we should not be using quantities like stress or strain, however the purpose here is only to highlight analogies in the description of various media, in situations, where it is applicable to do so; same comment applies to E and below). More precisely if we consider a small deformation from a reference configuration, so that:
where K is a bulk modulus, V volume and N is the number of dimensions of the space. In this case Lamé parameters are equal , , Young’s modulus and Poisson’s ratio . One realisation of such a medium is a disordered collection of particles, which collide with each other, bouncing off randomly, so that there is no way to induce a momentum flow/surface pressure higher in one direction than in others. We will say, that the interactions which lead to such relations, are of a completely dispersive nature.
Let us now take our ensemble of particles and impose fixed relative positions on them, so that deformations are properly expressed by the strain tensor. We will assume here, that a change in the distance r between a pair of particles gives rise to a force (acting between them) which can be represented by a central potential . In such setup there is no way to displace a chosen particle and induce tension in only one given direction. If we move a particle by along x axis, y components of the distances to its neighbours will be affected as well. This is a geometrical property of euclidian space and it gives rise to the elastic moduli tensor of the from [7,17,20]:
There is, similarly as in the case of gas/fluid, only one elastic constant here, however, this time bulk modulus depends on the connectivity, which follows from the dimensionality (the higher the dimension, the more particles are present in the immediate neighbourhood). It is given by . Similarly and . We also have . This one elastic constant corresponds to direct interactions.
There exist materials with these properties, an example of which is a diamond, however this model is too simplistic to properly describe elastic solids in general, as it results in only one degree of freedom, corresponding to a single elastic constant, while real materials are characterised by two.
Possible solutions, which allow to achieve two degrees of freedom, include introduction of angular springs or beams into the model, usage of non central forces or introduction of a volume change component into the potential energy [17,21,22,23,24,25] (some of them limited to very specific lattice topologies). However, a particularly simple way of extending this model, which works both with lattice based networks as well as disordered ones, is to allow for the force to be partially dispersed, so that all the interactions become superpositions between direct and dispersive forces [16].
where denotes the direct, and dispersive component of the force. The resulting elastic body then becomes a superposition between fluid and diamond like materials [16,17,26].
The reasoning behind this is, that direct interactions are in essence interactions by means of idealised classical Newtonian force, which acts across time and space, instantly, without accounting for relative velocities or other possible characteristics of the bodies involved in the problem, such as their shape, which could potentially influence the net effect of one body acting on another from a distance (There is plenty of evidence suggesting that the real character of the interaction on a distance depends on factors other than just relative position of the bodies in question, the prime example of which is electrodynamics, where the presence of relative velocity gives rise to a magnetic force).
If we take:
then Q denotes the ratio between dissipative forces and the direct ones, with its values spanning from to infinity. , and . Other elastic constants become:
In practice, when implementing a mass spring model for the representation of an elastic material, it may be more convenient to introduce yet another pair of constants.
C now can be interpreted as the total amount of interaction potential (e.g., a density of interaction carriers between two particles). The dissipative part is given by , and the direct one by . D is the dispersion fraction with values between −0.5 and 1. With this description we avoid the singularity in Q around the point and allow for expressing possible dynamic differences between media with , but varying C (the aspects of MSMs not explicitly addressed in this work). Other elastic constants become:
A few examples of the decomposition of the interactions into dissipative and direct parts are illustrated in the Figure 3 (with ). The first extreme, , corresponds to , where almost all the forces are dispersed, making the material fluid-like ( in means no change in volume under unidirectional compression; the limit value of is unstable). The second extreme, has ( once again is an unstable limit), which means that half of the compressing force acts in a dispersive manner, but with a “reversed sign”. In such regime and the material can be uniformly compressed without changing its elastic energy. As we can see, the unidirectional compression gives rise to considerably high forces, both direct and dispersive, which cancel out each other almost perfectly in the resulting concave shape. The has no dispersive forces at all and for , we have .

Figure 3.
A cube compressed in x direction by (x-borders frozen). First row , second , third , fourth . First column: total force on springs, second: direct component, third: dispersive component. Red colour indicates expansive force, blue compressive.
3. Mass Spring Models
Mass spring models represent elastic solids with discrete points connected by springs. As mentioned in Section 1, we distinguish two broad classes here—a regular crystal-like models and disordered ones [7]. In both cases, elastic constants of the material follow from spring coefficients. As elucidated in the previous section, if classical, direct force springs are used, the value of Poisson’s ratio for three dimensional isotropic and homogeneous models is fixed and equal to . The relation between bulk modulus K and spring parameters is given by:
where and denote the length of i-th spring and its stiffness coefficient. V is the volume of the object and the sum is taken over all springs inside this volume.
In order to model materials with other values of Poisson’s ratio, we can introduce the force dissipation mechanism discussed in previous sections with the C modulus obeying:
where the classical stiffness coefficient of a spring is now . And the force propagation follows the algorithm [16]:
For each node:
- Compute forces from springs .
- Apply as a regular force
- Additionally accumulate as .
In the second pass:
- Redistribute the accumulated force asto all the springs connected with the node (by applying it on both nodes the spring connects), where b denotes the number of these springs.
4. Accuracy of Random MSM Models
In this study we consider MSM networks with randomly generated points connected by springs with their nearest neighbours. The network topology is characterised by two parameters—first, , gives a minimal allowed distance between any pair of MSM nodes; second, , is the range within which spring connections are formed (any two nodes which are less than apart get connected by a spring) [7]. Please note, that the random point generation mechanism described in [7] is flawed. The article suggests a performance improvement for the implementation, which advocates a usage of a small spherical brush-like window traveling through the material in order to fill it with random points. The performance improvement for point collision calculation is real, however the “window” should be moved after each point addition, in contrast to a procedure which fills the window region fully first, before advancing to the next region of the material. The latter may introduce a non-homogeneity at the window borders. This was not stated clearly in the original article.
For such MSMs, our previous experiments show, that as long as the average number of springs attached to one node is sufficiently high, Equations (12) and (14) give the elastic properties of the network in bulk with a reasonable accuracy. The values of Poisson’s ratio for such models are very close to theoretical predictions (observed discrepancies were in many cases of magnitude of measurement errors) and the values of E diverge from theoretical by no more than [7,16]. Such accuracy may be satisfactory for many applications, but there is certainly a room for improvement.
Currently we will focus not only on bulk properties, but also investigate how MSMs behave locally, on a scale of internode distances. We perform a simple test, in which we consider a model of a cube , that undergoes compression (expansion) uniformly in all directions and observe how the MSM reacts. The following setup was used for this test. The elastic constants of the material were set to and (this means , which makes the theoretical analysis simpler. Materials with are expected to inherit the same properties here, which was confirmed by additional tests afterwards). The material was modelled with a random MSM with and , which gives around 6700 nodes, 55,000 springs and approximately springs connected to one node inside of the material. All springs were assigned the same spring constant calculated with Equation (14). The cube was expanded uniformly in all directions by (We will use expansion and compression interchangeably in the rest of the article when discussing the phenomenon analysed in this experiment; for technical reasons expansion is easier to perform). In such setup the values of diagonal components of the strain tensor should be equal to and corresponding diagonal elements of the stress tensor should be equal to (with being the unit of length and the unit of force).
In our numerical experiments we measure the stress inside of MSM according to the procedure proposed by Hardy [27,28]. It estimates the stress by measuring the tension inside a probe sphere placed in the point of interest. The tension in each spring in the surroundings of the point is weighted by a bond function. If only a fraction of the spring is contained within the probe sphere, the corresponding fraction of the tension is taken into account:
where:
- —distance between nodes and
- —force acting through the spring
- —bond value
In order to calculate the bond value, we associate an influence sphere with each spring—the center of the sphere is placed in the middle of the spring, and its radius is equal to half of the length of the spring. Then the bond value is calculated as a fraction of the volume of that sphere, intersecting with a probing region. This is a slight modification to the original method, which measured intersections between raw springs and a probing region. Our experiments shown that calculating intersections with three dimensional spheres surrounding the springs reduces noice and allows for more localised measurements (smaller probe regions).
Experiments presented in this article are using spherical probing region with the radius , where denotes the average length of a spring in MSM.
The test consists of two steps. First we scale the cube uniformly, mimicking the perfect uniform deformation, then we let the MSM relax (holding only borders in place). In both stages we measure stress and strain present inside of the cube. In a perfect model the relaxation phase should not lead to any additional displacements.
As an example the strain tensor component and the stress tensor component measured in this experiment are presented on Figure 4 and Figure 5. The character of discrepancies in other tensor components is similar. The measurements were taken along the line in X direction in the middle of the cube, with regions in close proximity to the border omitted (to avoid various problems with stress measurements near the border). Standard deviation from theoretical value of the final (relaxed) stress is denoted by , and the standard deviation from the average value by . Standard deviation between the stress in compressed (scaled) state and the stress in relaxed state is denoted by .
where A denotes measured, average and theoretical value of a strain or stress component; M is a number of measurements.
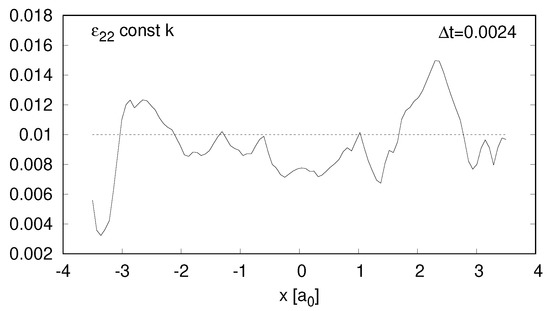
Figure 4.
The strain component in a uniformly compressed solid modeled with mass spring models (MSM) with constant k, same for all springs. Dotted lines represent theoretical values. Solid lines indicate the strain after material has relaxed to the equilibrium compressed state.
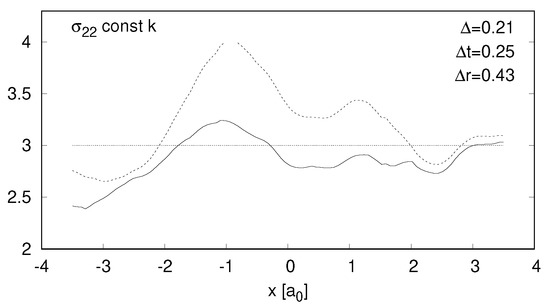
Figure 5.
Same as Figure 4, but for . Dotted lines represent stress in uniformly compressed material. Solid lines indicate stress after the material has relaxed to its new equilibrium state.
As we can see, the plotted tensor components average out to match theoretical predictions reasonably well. Local divergences, however, are high. The root cause of this behaviour is that the random MSM achieves isotropy statistically in bulk, but is not isotropic on singular nodes. To understand what exactly we mean by that, let us look at a simplified, one dimensional example from Figure 6. In disordered MSMs lengths of the springs are not equal. In uniform compression and if all the springs have the same k, the force acting on a spring is , and as a result springs do not compress by the same degree under a constant pressure. If they did, the red coloured node from Figure 6 would experience non-zero net force and would move. In 3D networks, additionally, the number of springs facing each direction may differ, which further influences local isotropy.

Figure 6.
An MSM node with springs of different lengths connected to it.
These are the reasons for local discrepancies in deformation as well as for stress in the material from Figure 4 and Figure 5. Forces on the nodes do not balance to zero when the springs get compressed by the same degree. This also affects the estimation of C (and consequently K and E) from Equations (14) and (15). These equations measure the energy needed to compress material uniformly, but in this case the energy is lower, and the corresponding K is lower as well. The values of average to the desired when the MSM is scaled uniformly (indicated by dotted line on the Figure 5), however after the relaxation this value drops to around .
5. MSM Tuning
Our goal is to adjust stiffness coefficients for springs in such way, that in an MSM subjected to uniform compression (realized by simple scaling):
- (a)
- forces acting on inner MSM nodes sum to zero,
- (b)
- stress is isotropic.
Achieving (a) would reduce both, the variations of strain, and the change in stress which occurs when a scaled model relaxes (), and in consequence would allow for a better estimation of the actual K in bulk. Achieving (b) would reduce the variations of stress. It should be noted, that condition (a) does not apply to the nodes which lie on the border of the MSM, where forces will sum to a value that counteracts the outside pressure. To distinguish which nodes are “inner”, and which lie on the border, for each node, we measure the intersection between modelled object and a sphere centered on the node, with a radius equal to . If the whole sphere intersects we treat the node as inner. Otherwise we assume it lies on the border.
To give some notion about how well (a) holds for a chosen MSM, we introduce the following measure, which we call kL-score:
where the inner sums indexed by b are taken over all springs connected to a node n. Outer sum is taken over all the nodes, the total number of nodes is N, and is the vector between nodes connected by a spring b; is the length of a vector . The lower the value of is, the closer to zero is the sum of forces acting on an MSM node (the lower the better). Such inner kl-score of the model from Figure 4 and Figure 5 is equal .
5.1. Constant kL
Since we have identified that in uniform compression the force exerted by a spring equals , our first attempt at improving accuracy of random MSMs could be by setting the stiffness coefficients of the springs in such way that . This would certainly help in 1-d case from Figure 6, however for three dimensional MSMs effects of such modification should be rather limited. In 3D the number of springs facing each direction is of bigger importance than differences in their lengths.
Setting does however improve the MSM slightly with dropping to and divergences from Figure 4 and Figure 5 becoming: , .
This actually results, right away, in improvement for the estimation of the bulk value of K by a few percent (more results in following sections).
5.2. kL-Tuning
As described in previous sections, the source of divergences in strain within MSM are unbalanced forces which appear during uniform compression. They cause the nodes to move and springs relax to new equilibrium lengths.
Our first goal is to construct an MSM in which the unbalanced forces do not appear. It can be achieved in a number of ways, one of which is simply by solving as a set of linear equations for stiffness coefficients . As the number of springs is an order of magnitude larger than the number of nodes, this may turn out to be problematic (but not impossible) for large systems, unless we have a whole computational cluster at our disposal. An alternative way, is to use the original MSM (with either or ) and follow the same relaxation path which our MSM from Figure 5 traveled when reaching the equilibrium state. If we consider a simple time integrator (e.g., Euler or Verlet scheme) its basic steps are:
- compute forces
- update velocities
- update positions
the “update positions” step will result in changes in lengths of springs and consequently in changes of forces exerted by these springs. We can achieve the same change in forces by changing stiffness coefficients of the springs instead of moving the nodes. Such algorithm (with damping) will find an MSM with .
This is the approach we use, however in our case we skip the “update velocities” step and modify spring coefficients directly, increasing or decreasing their value depending on the magnitude of the projection of the force vector onto the direction of the spring. This is analogous to a simulation of an overdamped movement and basically is a variation of steepest descent minimisation procedure. The tuning procedure starts by artificially changing natural lengths of all springs by the same degree and then following with a number of minimisation steps. In our implementation we use . Additionally appropriate border conditions need to be set, similarly as it was done in compression/expansion experiment, where borders were frozen in place. This basically means that the relaxation should only be applied to inner nodes. Nodes that lie near the border have by definition non-isotropic spring connections and achieving is not even possible for them.
Each iteration of the algorithm reduces and increases the MSM quality. We stop when a certain value of is reached (), or the progress becomes too slow (max relative change of k smaller than ).
Additionally, we place a restriction on the maximal allowed change of k for each spring to of its original value. This way we explore only the set of solutions close to our original choice of k, and avoid degenerate solutions with negative k. In the last step we restore natural lengths of springs to their original values.
The values of and for the resulting MSM of the cube test are presented on Figure 7 and Figure 8. The divergence in strain is now practically zero and is two orders of magnitude smaller than for . The profile of stress in this case is exactly the same as the relaxed profile from k-const model (Figure 5), but shifted towards desired value of . This means that we have managed to improve the estimate of bulk K, however local divergences did not change.
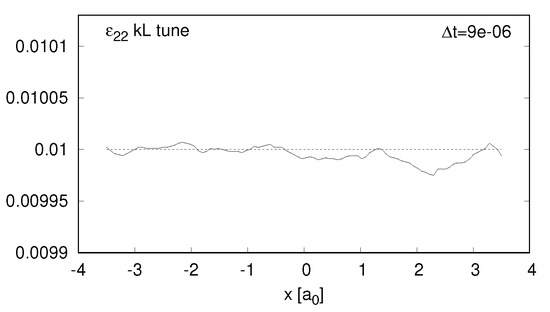
Figure 7.
Same as Figure 4, but for kl–tune MSM.
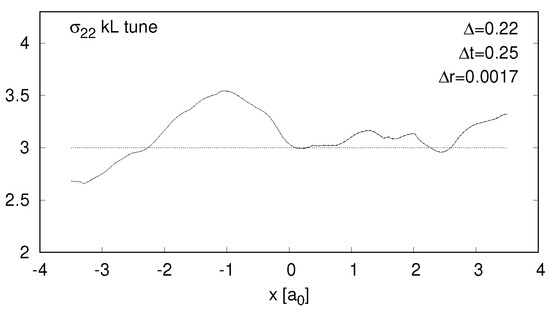
Figure 8.
Same as Figure 5, but for kl–tune MSM.
5.3. ikL-Tuning
Figure 8 shows, that does not necessary translate into isotropy on a node basis. To further improve MSM representations we need to make sure, that not only forces on singular nodes sum up to zero, but also that their magnitude is approximately the same in all directions. Figure 9 illustrates an MSM node for which this is not the case; in this example forces do sum to zero, but their magnitude is different in X and Y directions.
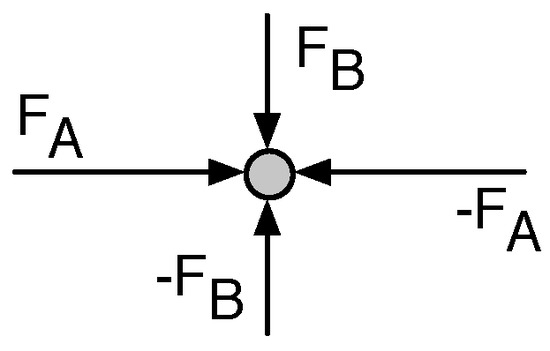
Figure 9.
An MSM node for which forces balance to zero but are not isotropic.
In kL-tuning at each step of the algorithm we modified based on the current value of the force acting on each node. In the improved procedure, instead of calculating the force, we will calculate the stress tensor at the point where the node is placed and see how much it diverges from the expected tensor:
where is the Kronecker’s delta.
The contribution of each spring to can be expressed as:
where is the relative length change of the spring, L the current length and the neutral length. V is the volume of the region in which we are measuring the stress and B is a bond between this region and the spring. The bond can be calculated in a number of ways [27,28]; in our case we use the percentage of the overlap between probing region, which is a sphere and another sphere placed in the middle of the spring with radius equal . As we remember is artificially changed in the first step of the tuning procedure.
We project the spring influence onto the and compute the for each spring as:
where , and t is step size for the steepest descent algorithm (, where b is the number of springs connected to a node). The stress tensor tuning is run in addition to kL-tuning, and it also has a limit for the relative change of k on each spring to prevent degenerate solutions in which k becomes negative. After this procedure the strain tensor is as close to theoretical as it was in Figure 7. This time however we observe an improvement in stress tensor. The component is presented on Figure 10. The divergence dropped to 0.067, and is about three times smaller than it was for kL-tune.
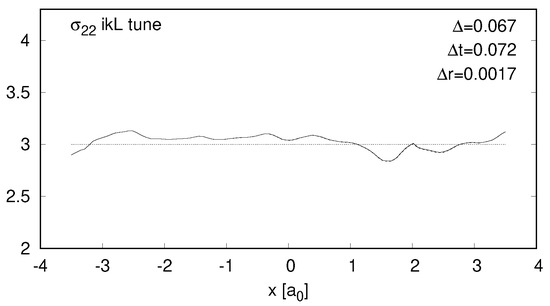
Figure 10.
Same as Figure 5, but for ikl–tune MSM.
Comparison of the four presented algorithms is terms of divergences , and observed in the cube compression test is presented on Figure 11, Figure 12 and Figure 13. As we can see kL-tune procedure eliminates divergencies , , which are caused by internal relaxation of unbalanced forces. The ikL-tune additionally reduces local variations in stress and reduces divergencies between stress present in the deformed body and its theoretical value.
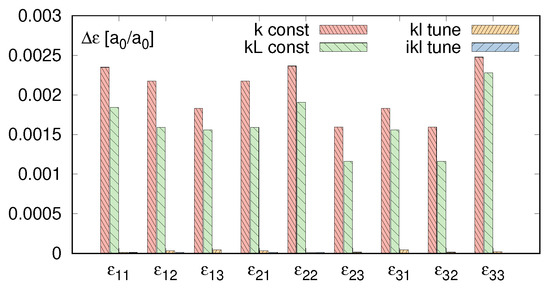
Figure 11.
Comparison of for four variants of random MSM.
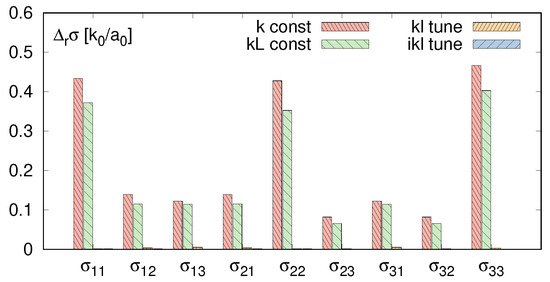
Figure 12.
Comparison of for four variants of random MSM.
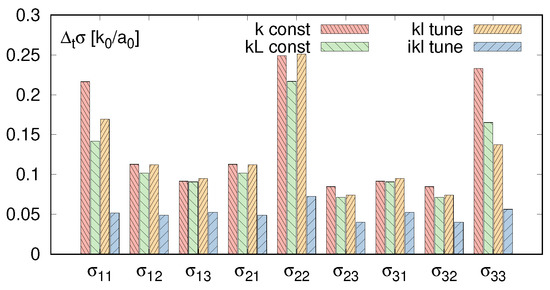
Figure 13.
Comparison of for four variants of random MSM.
6. Effects on Young’s Modulus
Next we investigate what are the effects of tuning, on global material properties and how reduced variations of local stress and strain translate into the value of Young’s modulus E.
We measure the value of E by performing a numerical experiment similar to the one described in [7]. We apply a static displacement to a block of material with dimensions , so that it gets compressed along X axis and we estimate E by measuring forces present in the material. In [7] we have measured the force passing through plane in the middle of the system, following the equation:
where F is the reaction force, A the cross-sectional area of the block (in plane), and is the deformation of the block along x direction.
This equation however does not account for the possibility of non-zero stress in directions other than X in the system. As we have seen in previous section such stress may be present even for stress components which theoretically should be equal zero. A more accurate equation gives E as:
This time we measure not only a force through plane, but also and planes. After applying this correction to the measurement procedure, the resulting estimates of E become smaller by 2–5%, showing that the E calculated this way may diverge from theoretical value by a higher degree than our original estimates.
The results for the four variants of random MSM are presented in the Figure 14. First we notice that simple setting instead of does improve the value of E noticeably. Introduction of kL-tune gives further improvement, however ikL-tune does not. For high it is as good as kL-tune, however for lower values it is worse. The curve seems however more stable with lower variations around its trend value.
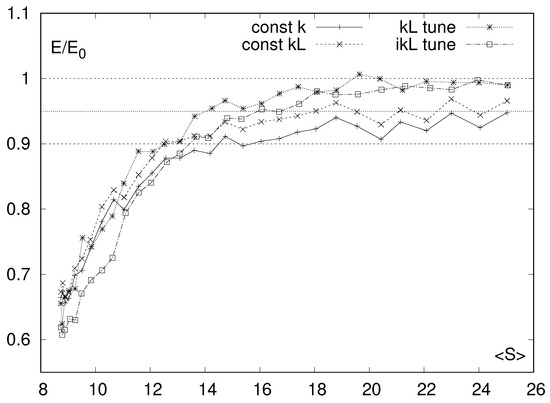
Figure 14.
Values of Young’s modulus relative to theoretical value for four variants of random MSM.
In all the cases the lower the number of springs, the higher divergence from theoretical value we observe. The average number of springs connected to one node for the cubic lattice MSM is , and it seems that in our experiment all the curves reach plateau around this point. While the effects of tuning are positive for MSM with mid to high , for values lower than 14 other issues related to low network connectivity seem to dominate and the tuning can no longer compensate for them. For we observe a rapid decrease of rigidity of the network. This result is consistent with [29], where the loss of rigidity caused by reduced network connectivity is studied. Authors show, that weakened FCC networks with around 8–10 suffer from the loss of rigidity and become floppy for lower values of (exact numbers depend on applied strain).
7. Conclusions
In this article, we have demonstrated possible accuracy problems one may face when using disordered MSMs. We have proposed two tuning procedures which aim to improve the accuracy of such MSMs. The first one, kL-tuning, eliminates unbalanced forces on MSM nodes which allows for better estimates of K (and E) of the whole network. The second, ikL-tuning aims to additionally reduce local stress variations. In both cases, the implementation details are of a lesser importance, than the effects each tuning procedure has on the MSM quality (as mentioned one might simply use linear solvers).
The presented analysis gives an overview of what should be expected of randomised models and what are their limitations. The proposed techniques can be used to reduce both global and local discrepancies and inhomogeneities present in the material, however one should keep in mind that such tuning may not always be necessary or even desirable. As mentioned in the introduction, real materials are not perfect, and the presence of inhomogeneities may be advantageous for certain applications and purposes. Overaggressive tuning may simply destroy the desired properties of our models (For the same reason, we did not even consider annealing-like approaches which modify position of nodes—such procedures may very well lead to node reorganisation into crystalline structures).
In the view of this, one may decide to abandon the tuning altogether and use for the whole network, with k scaled to match the desired K, not based on Equation (14), but rather on experiments. Typically a given network characteristics ( and ) lead to discrepancies of the same order, independent on the specific specimen of the MSM, therefore once we establish, that e.g., k should be increased by relative to the original estimate, we can simply apply the increase for all models generated with these parameters and get plausible results. The stress and strain figures in Section 5 should give a good intuition as to what to expect.
In our reference single threaded implementations, for the model with 55,000 springs, kL-tuning took 1s to complete, while ikL-tuning about 10s. The achieved reduction of stress variations is about 60% for the stress measured with resolution comparable to internode distances. However if such localised measurements are not needed, the kL-tune alone may be sufficient as it is considerably faster and much easier to implement.
Finally, we should remember, that problems discussed here concern disordered MSMs. If for a given application, a crystal-like structure is appropriate, then cubic lattice MSMs offer very high accuracy for typical deformation scenarios [7,30], and if we consider simple compression or shearing, the errors in local stresses and deformations are of an order of numerical precision of floating point numbers.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declare no conflict of interest.
References
- Klapetek, P.; Charvátová Campbell, A.; Buršíková, V. Fast mechanical model for probe–sample elastic deformation estimation in scanning probe microscopy. Ultramicroscopy 2019, 201, 18–27. [Google Scholar] [CrossRef] [PubMed]
- Cristoforetti, A.; Masè, M.; Bonmassari, R.; Dallago, M.; Nollo, G.; Ravelli, F. A patient-specific mass-spring model for biomechanical simulation of aortic root tissue during transcatheter aortic valve implantation. Phys. Med. Biol. 2019, 64, 085014. [Google Scholar] [CrossRef] [PubMed]
- Quillen, A.C.; Martini, L.; Nakajima, M. Near/far side asymmetry in the tidally heated Moon. Icarus 2019, 329, 182–196. [Google Scholar] [CrossRef] [PubMed]
- Quillen, A.C.; Zhao, Y.; Chen, Y.; Sánchez, P.; Nelson, R.C.; Schwartz, S.R. Impact excitation of a seismic pulse and vibrational normal modes on asteroid Bennu and associated slumping of regolith. Icarus 2019, 319, 312–333. [Google Scholar] [CrossRef] [PubMed]
- Sahputra, I.; Alexiadis, A.; Adams, M. A Coarse Grained Model for Viscoelastic Solids in Discrete Multiphysics Simulations. ChemEngineering 2020, 4, 30. [Google Scholar] [CrossRef]
- Vicente, G.S.; Buchart, C.; Borro, D.; Celigüeta, J.T. Maxillofacial surgery simulation using a mass-spring model derived from continuum and the scaled displacement method. Int. J. Comput. Assist. Radiol. Surg. 2009, 4, 89–98. [Google Scholar] [CrossRef]
- Kot, M.; Nagahashi, H.; Szymczak, P. Elastic moduli of simple mass spring models. Vis. Comput. 2015, 31, 1339–1350. [Google Scholar] [CrossRef]
- Chen, H.; Lin, E.; Jiao, Y.; Liu, Y. A generalized 2D non-local lattice spring model for fracture simulation. Comput. Mech. 2014, 54, 1541–1558. [Google Scholar] [CrossRef]
- Goehring, L.; Mahadevan, L.; Morris, S.W. Nonequilibrium scale selection mechanism for columnar jointing. Proc. Natl. Acad. Sci. USA 2009, 106, 387–392. [Google Scholar] [CrossRef]
- Aydin, A.; Degraff, J. Evoluton of Polygonal Fracture Patterns in Lava Flows. Science 1988, 239, 471–476. [Google Scholar] [CrossRef]
- Hofmann, M.; Anderssohn, R.; Bahr, H.A.; Weiß, H.J.; Nellesen, J. Why Hexagonal Basalt Columns? Phys. Rev. Lett. 2015, 115, 154301. [Google Scholar] [CrossRef] [PubMed]
- Maurini, C.; Bourdin, B.; Gauthier, G.; Lazarus, V. Crack patterns obtained by unidirectional drying of a colloidal suspension in a capillary tube: Experiments and numerical simulations using a two-dimensional variational approach. Int. J. Fract. 2013, 184. [Google Scholar] [CrossRef]
- Gauthier, G.; Lazarus, V.; Pauchard, L. Shrinkage star-shaped cracks: Explaining the transition from 90 degrees to 120 degrees. EPL 2010, 89, 26002. [Google Scholar] [CrossRef][Green Version]
- Goehring, L. Evolving fracture patterns: Columnar joints, mud cracks and polygonal terrain. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2013, 371, 20120353. [Google Scholar] [CrossRef] [PubMed]
- Frouard, J.; Quillen, A.; Efroimsky, M.; Giannella, D. Numerical Simulation of Tidal Evolution of a Viscoelastic Body Modelled with a Mass-Spring Network. Mon. Not. R. Astron. Soc. 2016, 458, stw491. [Google Scholar] [CrossRef]
- Kot, M.; Nagahashi, H. Mass Spring Models with Adjustable Poisson’s Ratio. Vis. Comput. 2017, 33, 283–291. [Google Scholar] [CrossRef]
- Golec, K.; Palierne, J.F.; Zara, F.; Nicolle, S.; Damiand, G. Hybrid 3D mass-spring system for simulation of isotropic materials with any Poisson’s ratio. Vis. Comput. 2019. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Liu, T.; Bargteil, A.W.; O’Brien, J.F.; Kavan, L. Fast Simulation of Mass-Spring Systems. ACM Trans. Graph. 2013, 32. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 1906. [Google Scholar]
- Baudet, V.; Beuve, M.; Jaillet, F.; Shariat, B.; Zara, F. Integrating Tensile Parameters in 3D Mass-Spring System; Technical Report RR-LIRIS-2007-004, LIRIS UMR 5205 CNRS/INSA de Lyon/Université Claude Bernard Lyon 1/Université Lumiére Lyon 2/École Centrale de Lyon; 2007; Available online: https://link.springer.com/article/10.1007/s11548-008-0271-0 (accessed on 1 December 2020).
- Lloyd, B.A.; Szekely, G.; Harders, M. Identification of Spring Parameters for Deformable Object Simulation. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1081–1094. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Lattice models in micromechanics. Appl. Mech. Rev. 2002, 55, 35–60. [Google Scholar] [CrossRef]
- Chen, H.; Lin, E.; Liu, Y. A novel Volume-Compensated Particle method for 2D elasticity and plasticity analysis. Int. J. Solids Struct. 2014, 51, 1819–1833. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Y. A Nonlocal Lattice Particle Framework for Modeling of Solids. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2016; p. V001T03A001. [Google Scholar] [CrossRef]
- Golec, K. Hybrid 3D Mass Spring System for Soft Tissue Simulation. Ph.D. Theses, Université de Lyon, Lyon, France, 2018. [Google Scholar]
- Hardy, R.J. Formulas for determining local properties in molecular-dynamics simulations—Shock waves. J. Chem. Phys. 1982, 76, 622–628. [Google Scholar] [CrossRef]
- Zimmerman, J.A.; WebbIII, E.B.; Hoyt, J.J.; Jones, R.E.; Klein, P.A.; Bammann, D.J. Calculation of stress in atomistic simulation. Model. Simul. Mater. Sci. Eng. 2004, 12, S319. [Google Scholar] [CrossRef]
- Sheinman, M.; Broedersz, C.P.; MacKintosh, F.C. Nonlinear effective-medium theory of disordered spring networks. Phys. Rev. E 2012, 85, 021801. [Google Scholar] [CrossRef] [PubMed]
- Banks, M.K.; Hazel, A.L.; Riley, G.D. Quantitative Validation of Physically Based Deformable Models in Computer Graphics. In Workshop on Virtual Reality Interaction and Physical Simulation; Andrews, S., Erleben, K., Jaillet, F., Zachmann, G., Eds.; The Eurographics Association: Genoa, Italy, 2018. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).