A Coarse Grained Model for Viscoelastic Solids in Discrete Multiphysics Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Background
2.1.1. Hertz Theory for Elastic Normal Contact Force
2.1.2. Viscoelastic Normal Contact Force
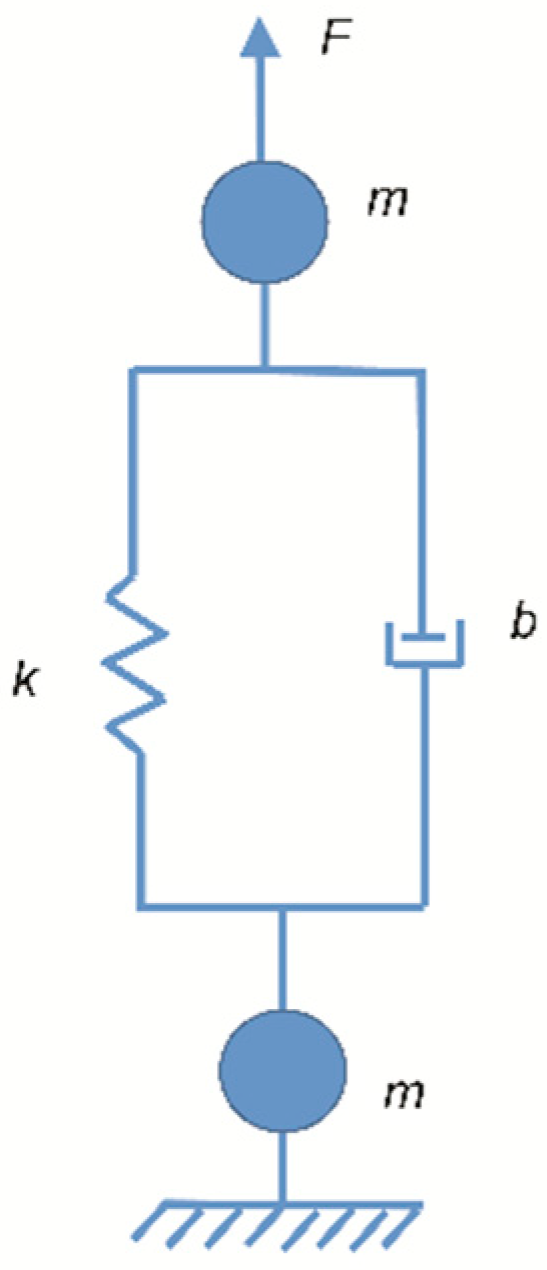
2.1.3. Mass-Spring-Dashpot Models
2.2. Model and Simulation
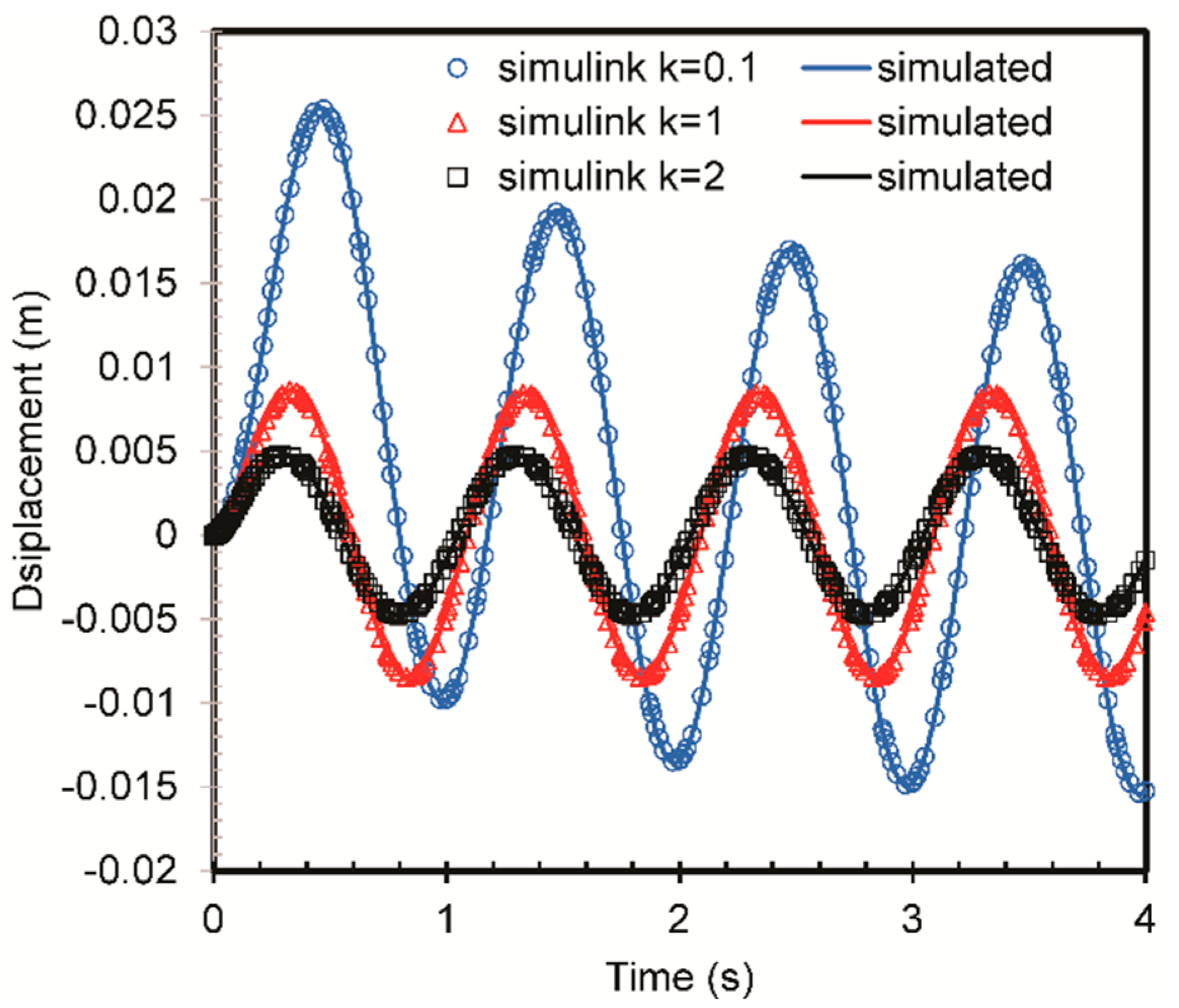
2.2.1. Validation of a Single KV Bond
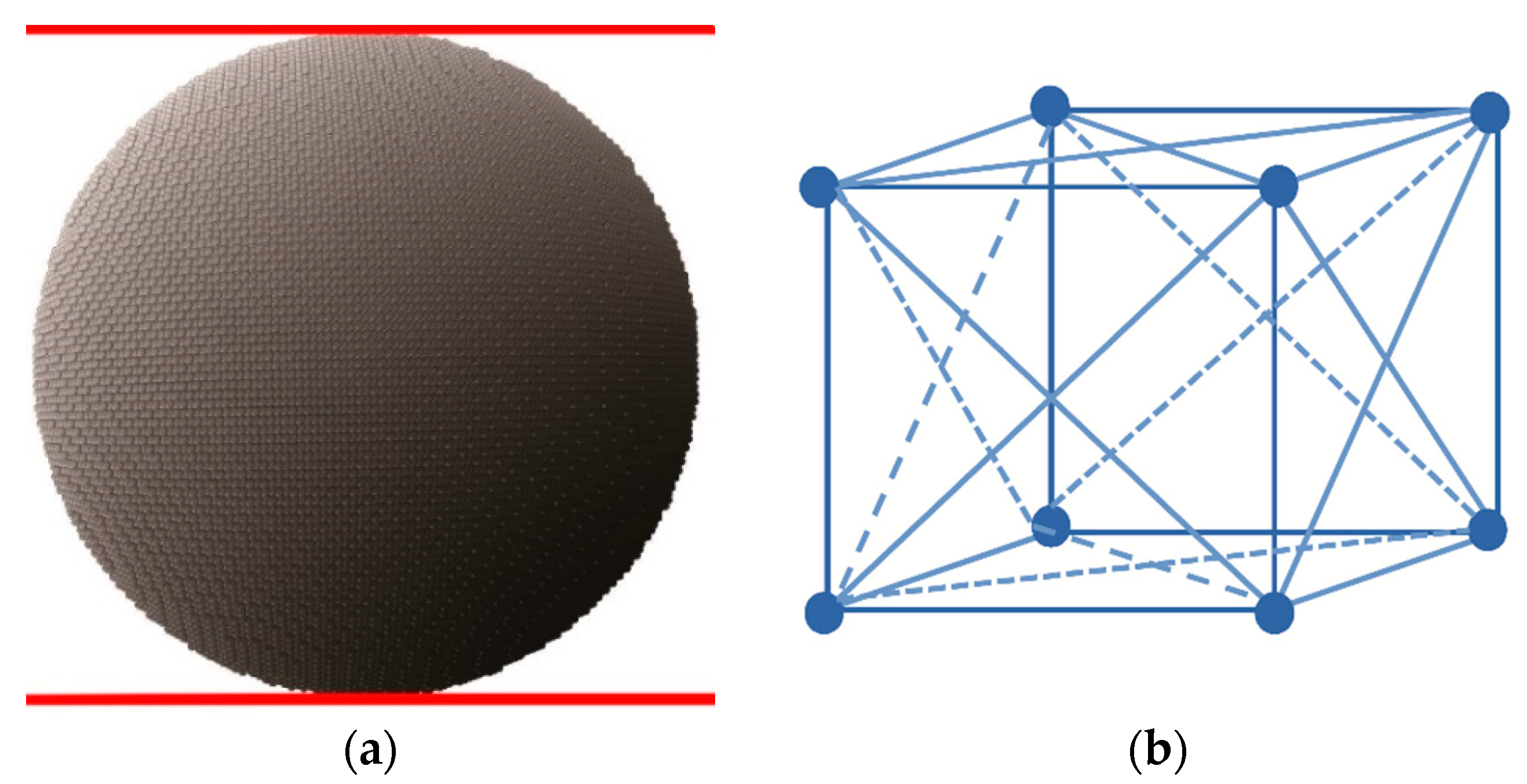
2.2.2. Modelling the Diametric Compression of a Spherical Particle
3. Result and Discussion
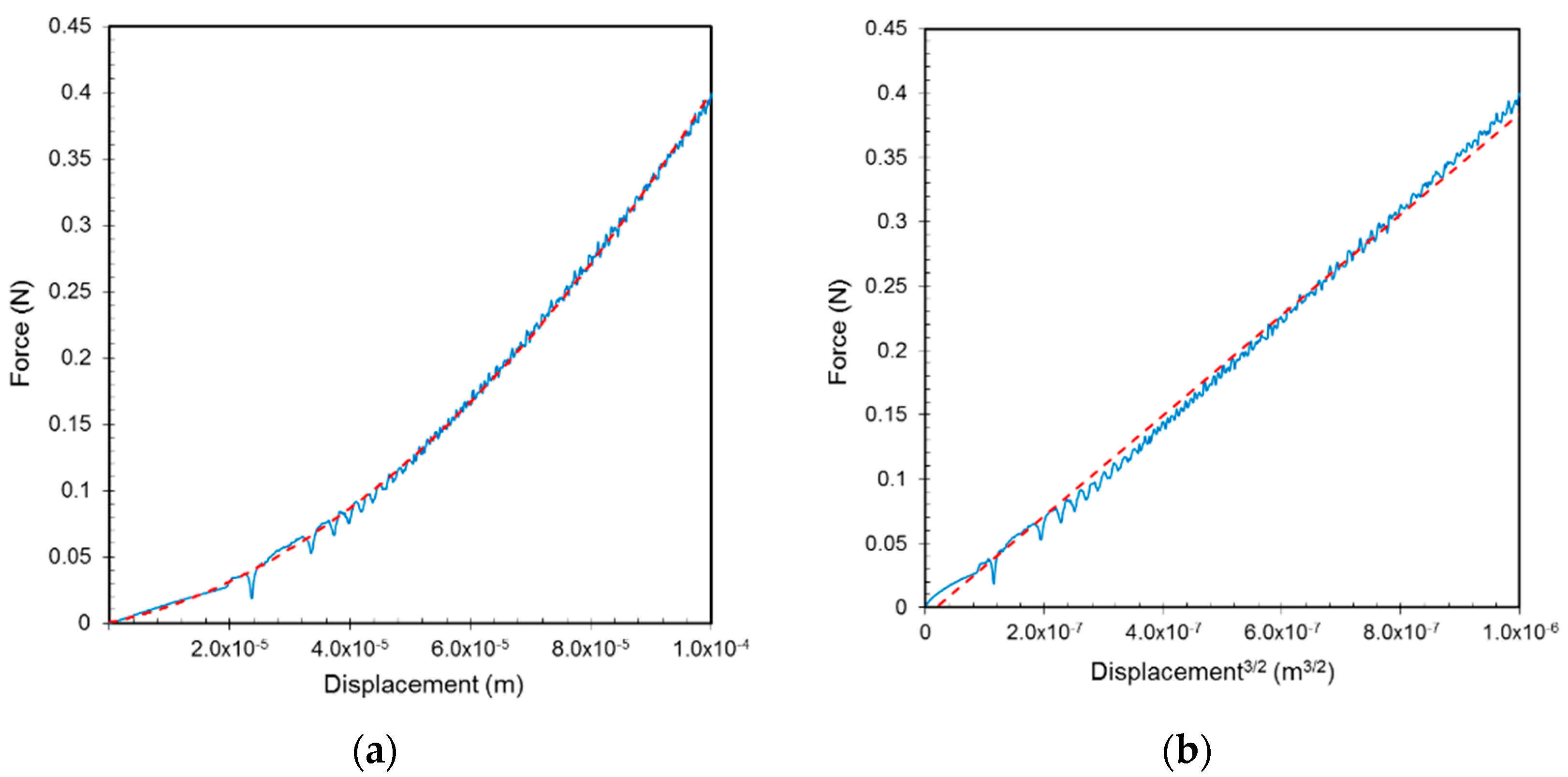
3.1. Perfectly Elastic Spherical Particles
3.1.1. Cubic Lattice Cell Model
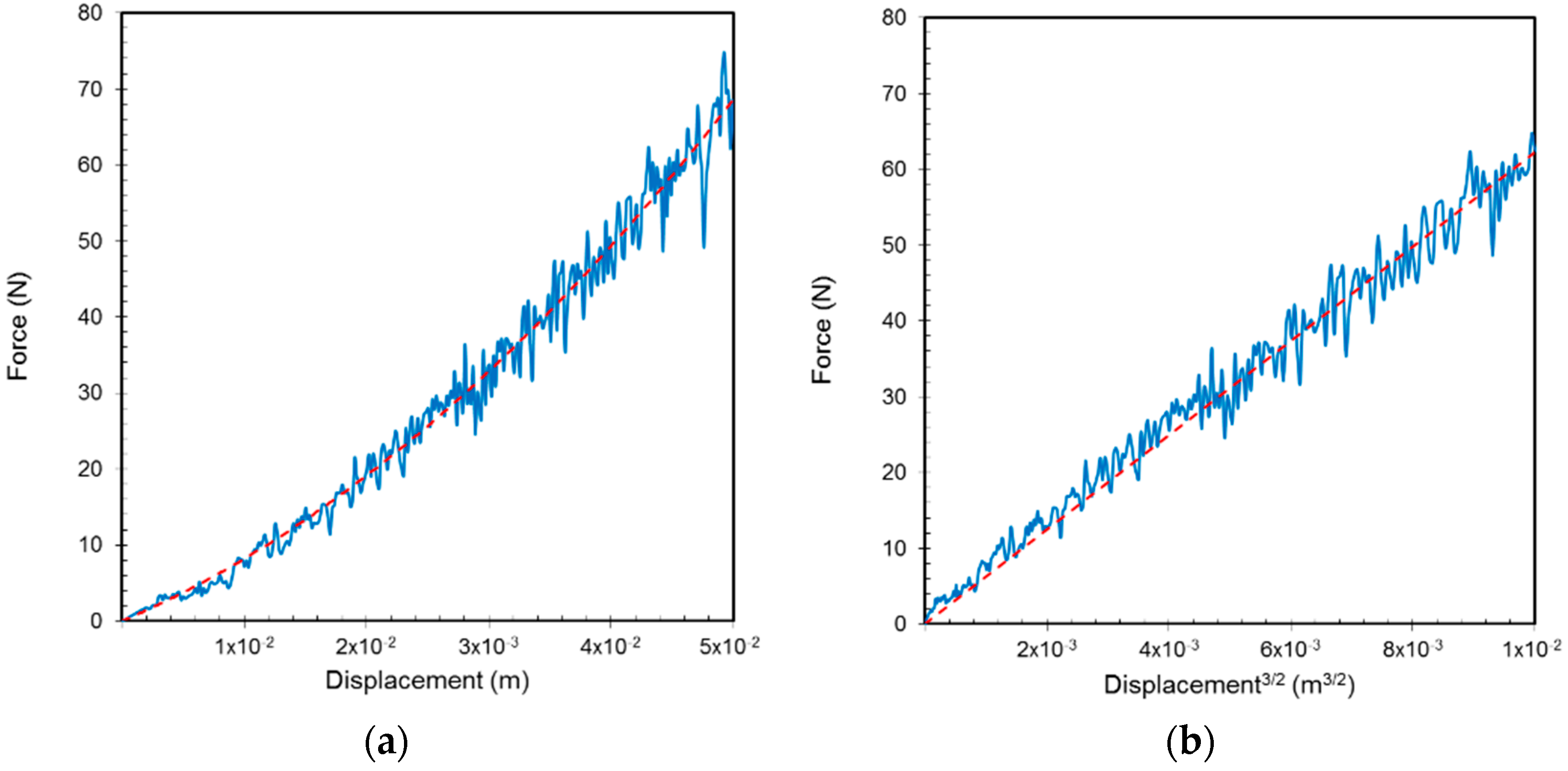
3.1.2. Disorder Model
3.2. Viscoelastic Spherical Particles
3.2.1. Cubic Lattice Cell Model
3.2.2. Disorder Model
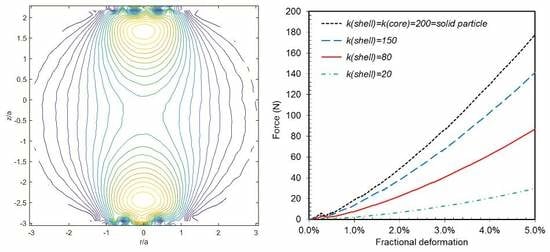
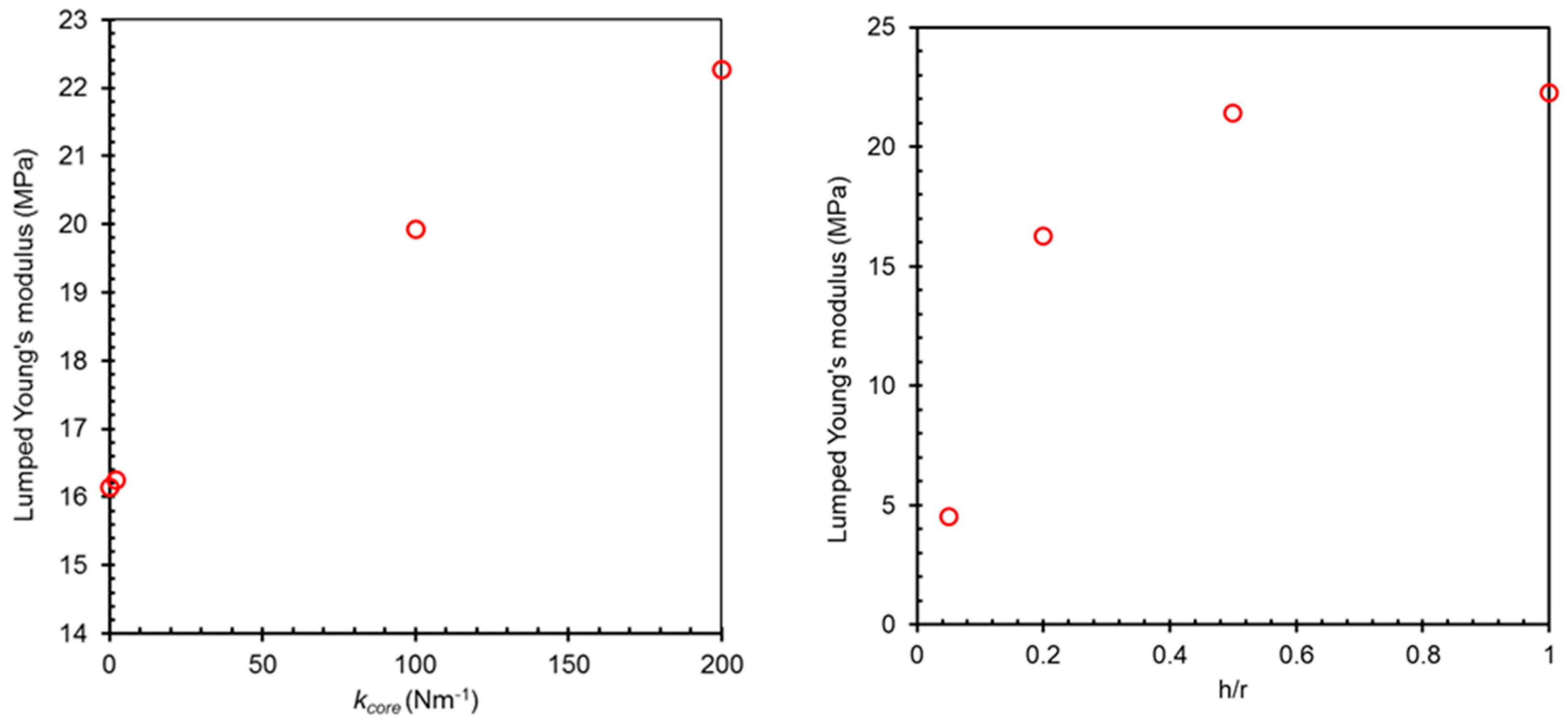
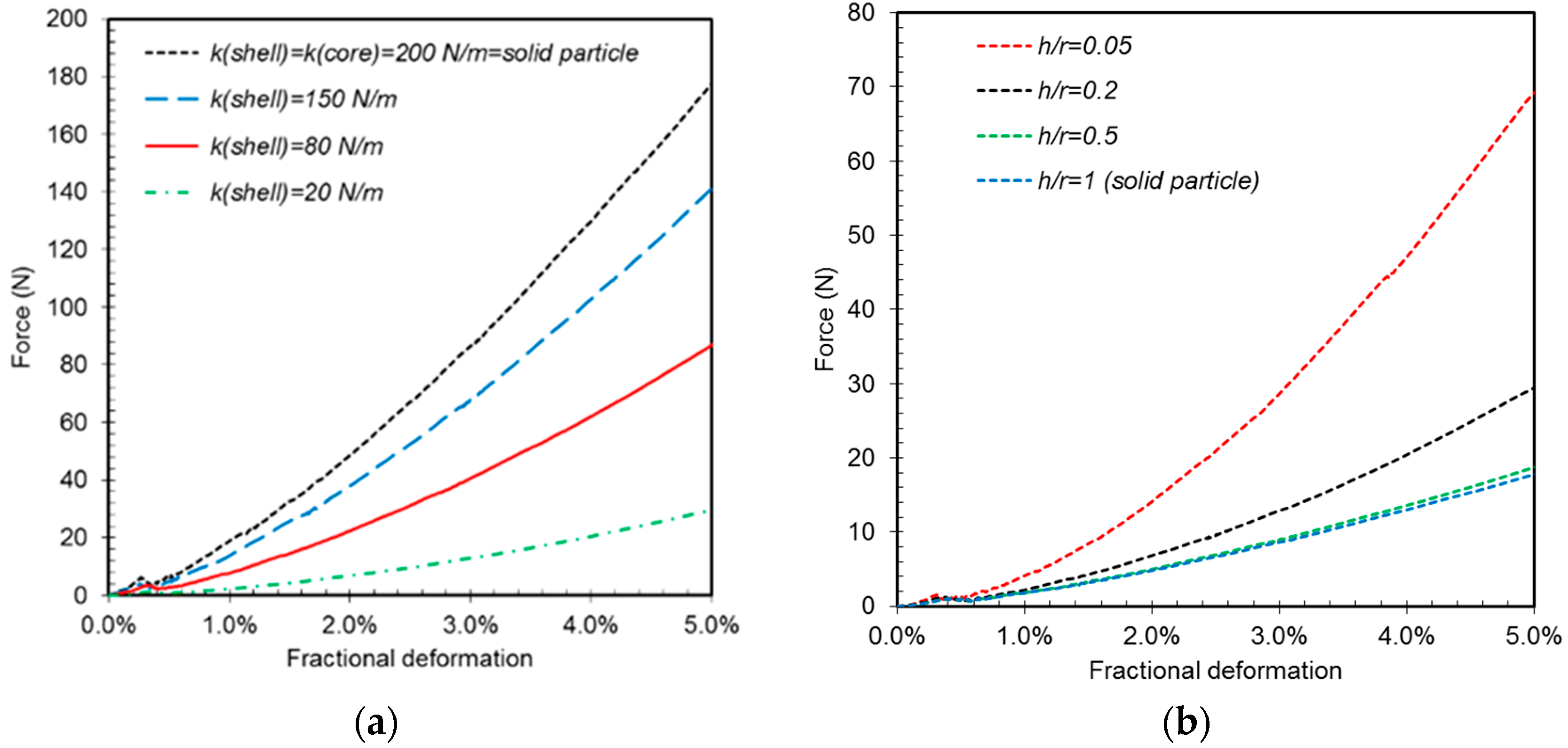
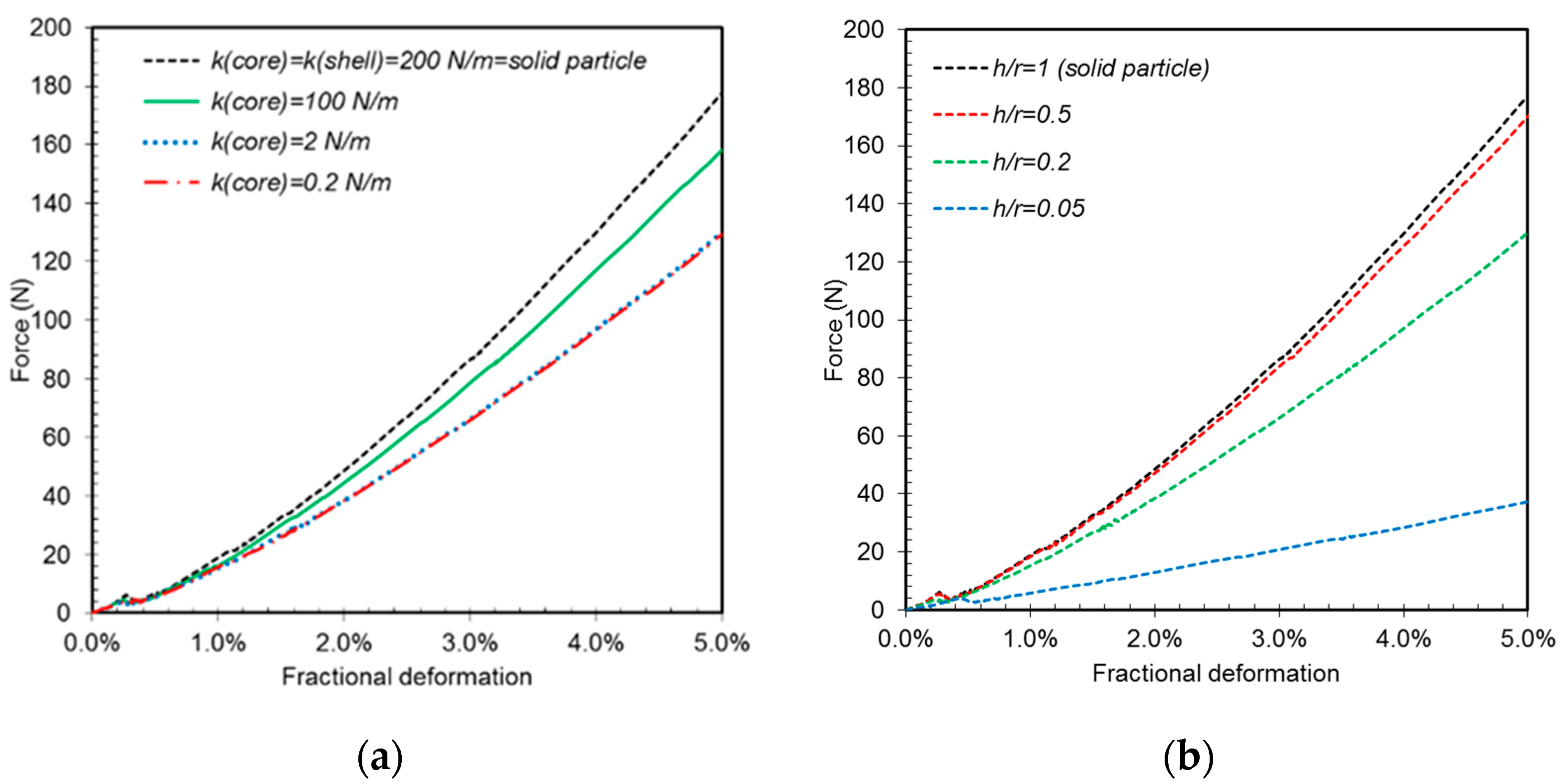
3.3. Application of the Elastic Disorder Model: Hard Core-Soft Shell and Soft Core-Hard Shell Spherical Particles under Compression
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a | contact radius |
| API | Active Pharmaceutical Ingredients |
| b | dashpot constant |
| δ | relative displacement |
| rate of displacement | |
| DEM | Discrete Element Method |
| DMP | Discrete Multiphysics |
| E | Young’s modulus |
| F | force |
| F(r) | force (diametric compression) |
| FE | viscoelastic normal contact force |
| FH | force (Hertz theory) |
| FKV | force (Kelvin–Voigt model) |
| h | shell thickness |
| HC-SS | hard core-softer shell |
| k | spring constant |
| KV | Kelvin–Voigt |
| l | length of an edge of the cell |
| LSM | Lattice Spring Model |
| m | mass |
| r | radius |
| rb-Ri | distance from the bead to the compression plane |
| Ri | position of the compression plane |
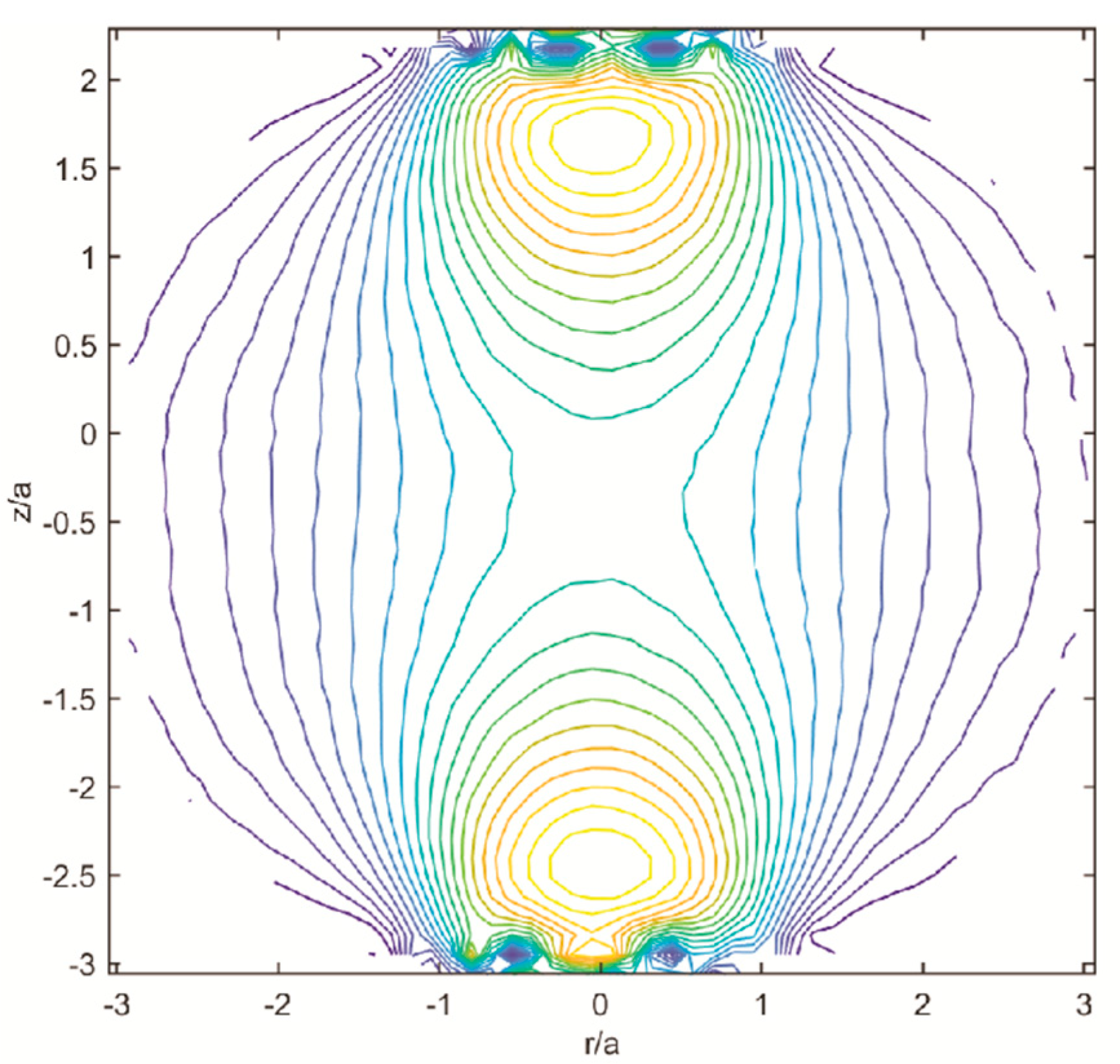
| σ1, σ3 | principal stresses |
| S | specified force constant |
| SC-HS | soft core-harder shell |
| υ | Poisson’s ratio |
| X | distance from equilibrium position |
References
- Alian, M.; Ein-Mozaffari, F.; Upreti, S.R. Analysis of the mixing of solid particles in a plowshare mixer via discrete element method (DEM). Powder Technol. 2015, 274, 77–87. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; am Ende, M.T.; Hancock, B.C. Process modeling in the pharmaceutical industry using the discrete element method. J. Pharm. Sci. 2009, 98, 442–470. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wu, C.-Y.; Adams, M. DEM analysis of the effect of particle–wall impact on the dispersion performance in carrier-based dry powder inhalers. Int. J. Pharm. 2015, 487, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.; Third, J.; Müller, C. Discrete element models for non-spherical particle systems: From theoretical developments to applications. Chem. Eng. Sci. 2015, 127, 425–465. [Google Scholar] [CrossRef]
- Garg, S.; Pant, M. Meshfree methods: A comprehensive review of applications. Int. J. Comput. Methods 2018, 15, 1830001. [Google Scholar] [CrossRef]
- Alexiadis, A. A smoothed particle hydrodynamics and coarse-grained molecular dynamics hybrid technique for modelling elastic particles and breakable capsules under various flow conditions. Int. J. Numer. Methods Eng. 2014, 100, 713–719. [Google Scholar] [CrossRef]
- Alexiadis, A. The discrete multi-hybrid system for the simulation of solid-liquid flows. PLoS ONE 2015, 10, e0124678. [Google Scholar] [CrossRef]
- Ariane, M.; Allouche, M.H.; Bussone, M.; Giacosa, F.; Bernard, F.; Barigou, M.; Alexiadis, A. Discrete multi-physics: A mesh-free model of blood flow in flexible biological valve including solid aggregate formation. PLoS ONE 2017, 12, e0174795. [Google Scholar] [CrossRef]
- Ariane, M.; Allouche, M.H.; Bussone, M.; Giacosa, F.; Bernard, F.; Barigou, M.; Alexiadis, A. Modelling and simulation of flow and agglomeration in deep veins valves using discrete multi physics. Comput. Biol. Med. 2017, 89, 96–103. [Google Scholar] [CrossRef]
- Ariane, M.; Vigolo, D.; Brill, A.; Nash, F.G.B.; Barigou, M.; Alexiadis, A. Using Discrete Multi-Physics for studying the dynamics of emboli in flexible venous valves. Comput. Fluids 2018, 166, 57–63. [Google Scholar] [CrossRef]
- Alexiadis, A.; Ghraybeh, S.; Qiao, G. Natural convection and solidification of phase-change materials in circular pipes: A SPH approach. Comput. Mater. Sci. 2018, 150, 475–483. [Google Scholar] [CrossRef]
- Alexiadis, A. A new framework for modelling the dynamics and the breakage of capsules, vesicles and cells in fluid flow. Procedia IUTAM 2015, 16, 80–88. [Google Scholar] [CrossRef]
- Rahmat, A.; Barigou, M.; Alexiadis, A. Deformation and rupture of compound cells under shear: A discrete multiphysics study. Phys. Fluids 2019, 31, 051903. [Google Scholar] [CrossRef]
- Rahmat, A.; Barigou, M.; Alexiadis, A. Numerical simulation of dissolution of solid particles in fluid flow using the SPH method. Int. J. Numer. Methods Heath Fluid Flow 2019. [Google Scholar] [CrossRef]
- O’Brien, G.S. Discrete visco-elastic lattice methods for seismic wave propagation. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Paul, J.; Romeis, S.; Tomas, J.; Peukert, W. A review of models for single particle compression and their application to silica microspheres. Adv. Powder Technol. 2014, 25, 136–153. [Google Scholar] [CrossRef]
- Kuo-Kang, L. Deformation behaviour of soft particles: A review. J. Phys. D Appl. Phys. 2006, 39, R189. [Google Scholar]
- Bakhshian, S.; Sahimi, M. Computer simulation of the effect of deformation on the morphology and flow properties of porous media. Phys. Rev. E 2016, 94, 042903. [Google Scholar]
- Hertz, H. Ueber die Berührung fester elastischer Körper. J. Reine Angew. Math. 1882, 1882, 156–171. [Google Scholar]
- Mook, W.M.; Nowak, J.D.; Perrey, C.R.; Carter, C.B.; Mukherjee, R.; Girshick, S.L.; Gerberich, W.W. Compressive stress effects on nanoparticle modulus and fracture. Phys. Rev. B 2007, 75, 214112. [Google Scholar] [CrossRef]
- Brilliantov, N.V.; Spahn, F.; Hertzsch, J.M.; Pöschel, T. Model for collisions in granular gases. Phys. Rev. E 1996, 53, 5382–5392. [Google Scholar] [CrossRef] [PubMed]
- Schwager, T.; Pöschel, T. Coefficient of restitution for viscoelastic spheres: The effect of delayed recovery. Phys. Rev. E 2008, 78, 051304. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.J.; Zhu, H.P.; Yu, A.B. Finite element analysis of the contact forces between a viscoelastic sphere and rigid plane. Powder Technol. 2012, 26, 130–142. [Google Scholar] [CrossRef]
- Kuwabara, G.; Kono, K. Restitution Coefficient in a Collision between Two Spheres. Jpn. J. Appl. Phys. 1987, 26, 1230–1233. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Ladd, A.J.; Kinney, J.H.; Breunig, T.M. Deformation and failure in cellular materials. Phys. Rev. E 1997, 55, 3271. [Google Scholar] [CrossRef]
- Kot, M.; Nagahashi, H.; Szymczak, P. Elastic moduli of simple mass spring models. Vis. Comput. 2015, 31, 1339–1350. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.; Hamilton, J. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085. [Google Scholar] [CrossRef]
- Nguyen, S. Generalized Kelvin model for micro-cracked viscoelastic materials. Eng. Fract. Mech. 2014, 127, 226–234. [Google Scholar] [CrossRef]
- Chen, H.; Lin, E.; Liu, Y. A novel Volume-Compensated Particle method for 2D elasticity and plasticity analysis. Int. J. Solids Struct. 2014, 51, 1819–1833. [Google Scholar] [CrossRef]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Lee, S.C.; Ren, N. The Subsurface Stress Field Created by Three-Dimensionally Rough Bodies in Contact with Traction. Tribol. Trans. 1994, 37, 615–621. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Z.; Stokes, J.R.; Zhou, Q.Z.; Ma, G.H.; Adams, M.J. Mechanical characterization of agarose micro-particles with a narrow size distribution. Powder Technol. 2009, 192, 122–130. [Google Scholar] [CrossRef]
- Butt, H.-J.; Cappella, B.; Kappl, M. Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahputra, I.H.; Alexiadis, A.; Adams, M.J. A Coarse Grained Model for Viscoelastic Solids in Discrete Multiphysics Simulations. ChemEngineering 2020, 4, 30. https://doi.org/10.3390/chemengineering4020030
Sahputra IH, Alexiadis A, Adams MJ. A Coarse Grained Model for Viscoelastic Solids in Discrete Multiphysics Simulations. ChemEngineering. 2020; 4(2):30. https://doi.org/10.3390/chemengineering4020030
Chicago/Turabian StyleSahputra, Iwan H., Alessio Alexiadis, and Michael J. Adams. 2020. "A Coarse Grained Model for Viscoelastic Solids in Discrete Multiphysics Simulations" ChemEngineering 4, no. 2: 30. https://doi.org/10.3390/chemengineering4020030
APA StyleSahputra, I. H., Alexiadis, A., & Adams, M. J. (2020). A Coarse Grained Model for Viscoelastic Solids in Discrete Multiphysics Simulations. ChemEngineering, 4(2), 30. https://doi.org/10.3390/chemengineering4020030