Using the Cahn–Hilliard Theory in Metastable Binary Solutions
Abstract
:1. Introduction
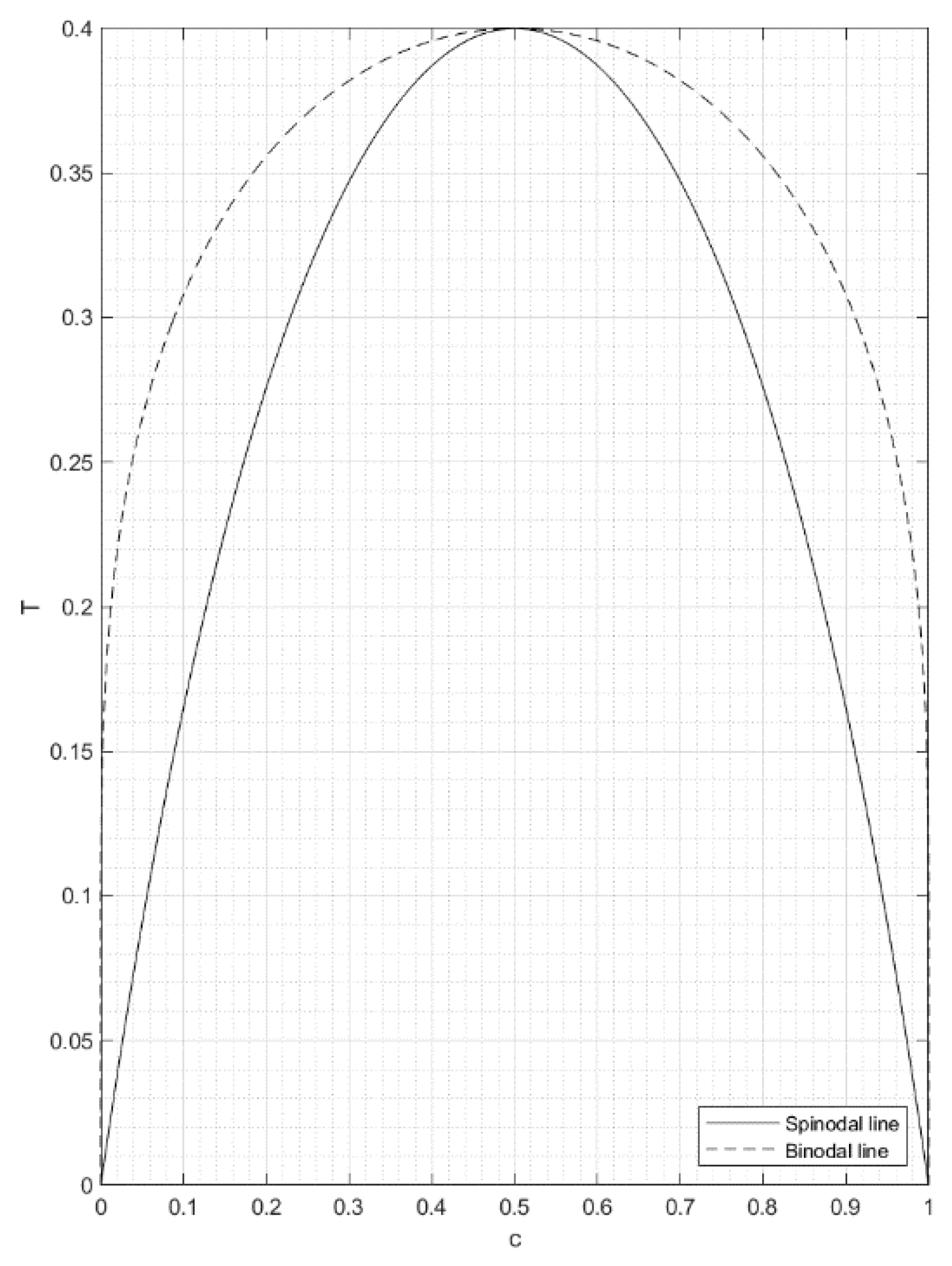
2. Model Development
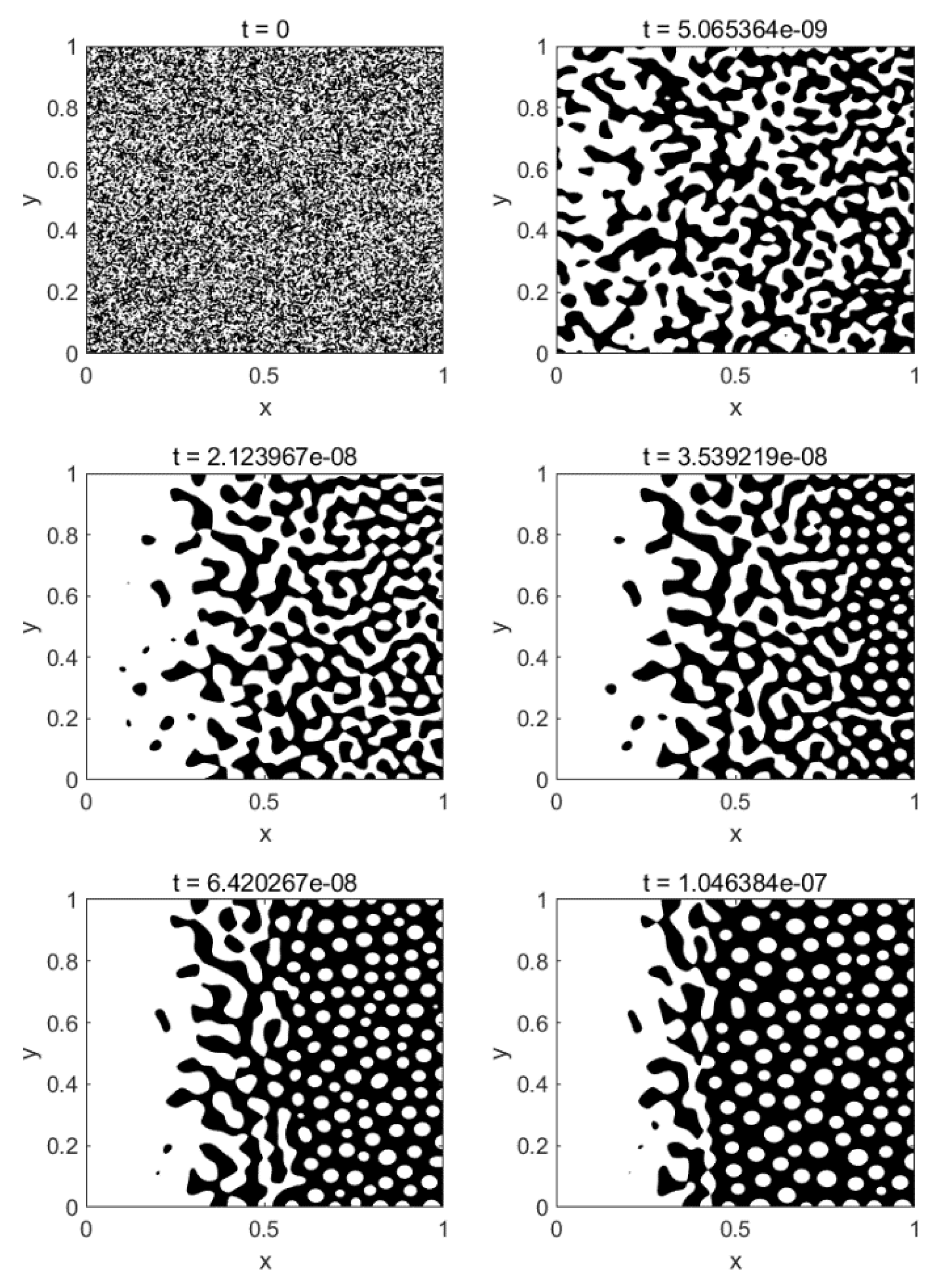
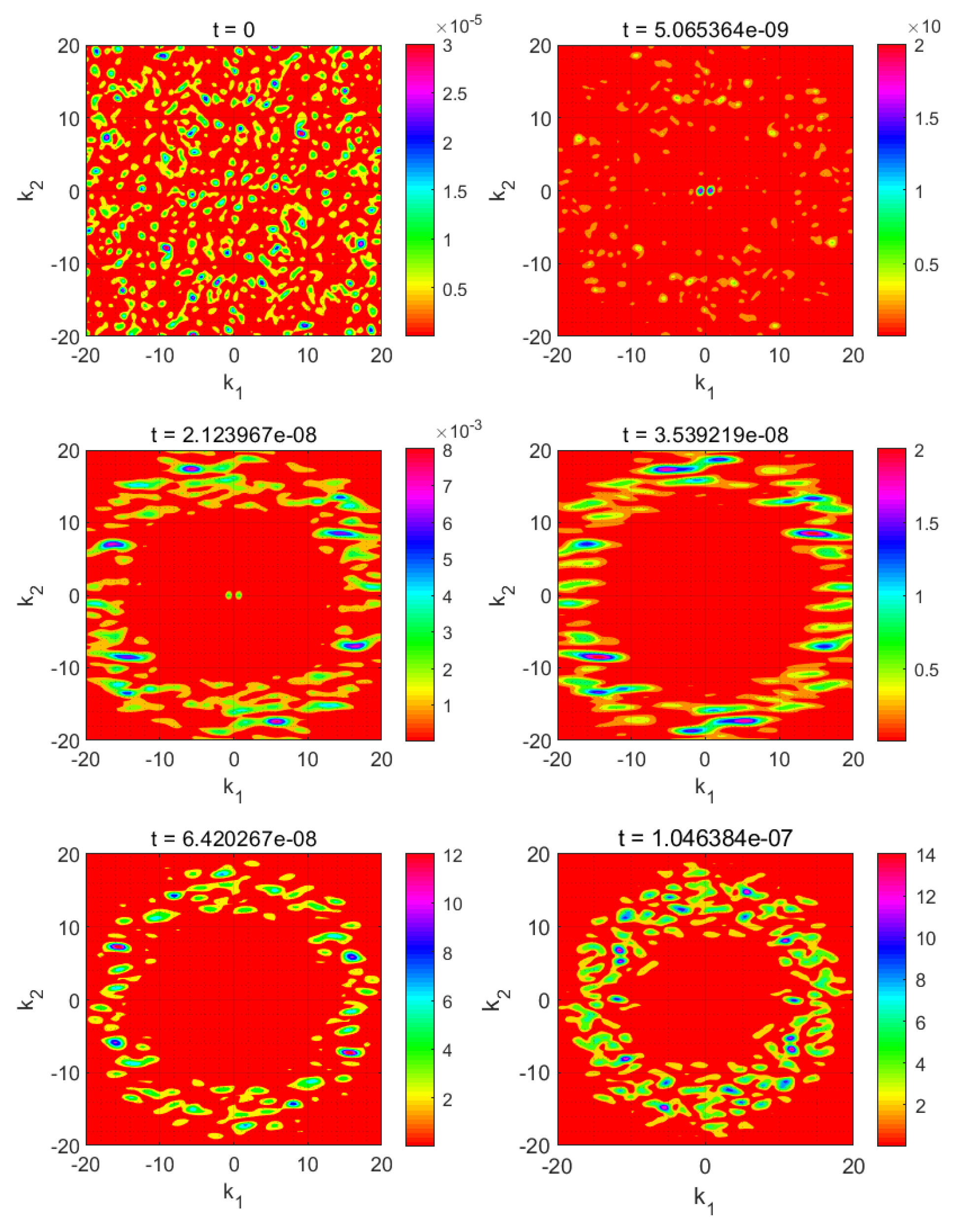
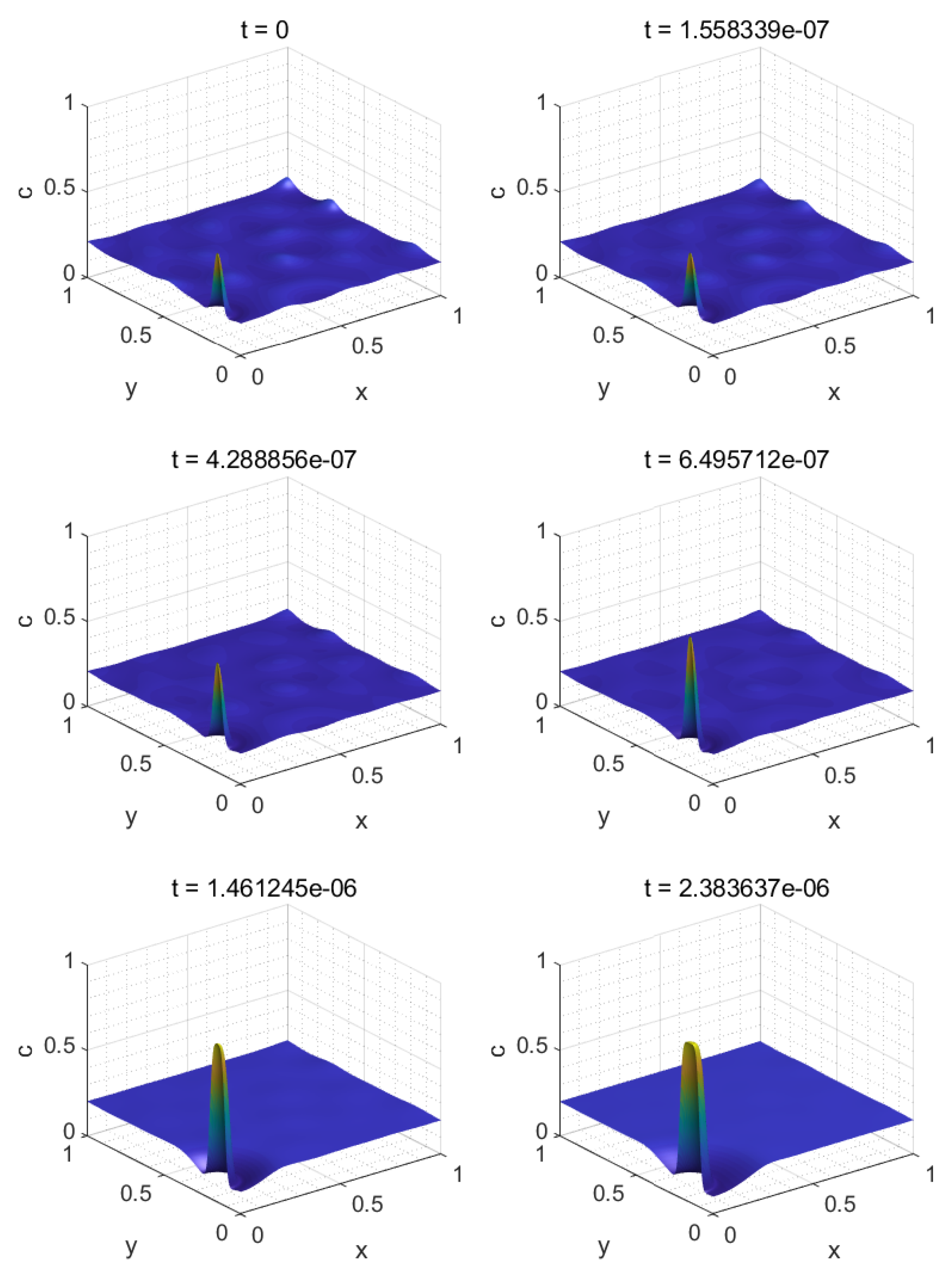
3. Results and Discussion
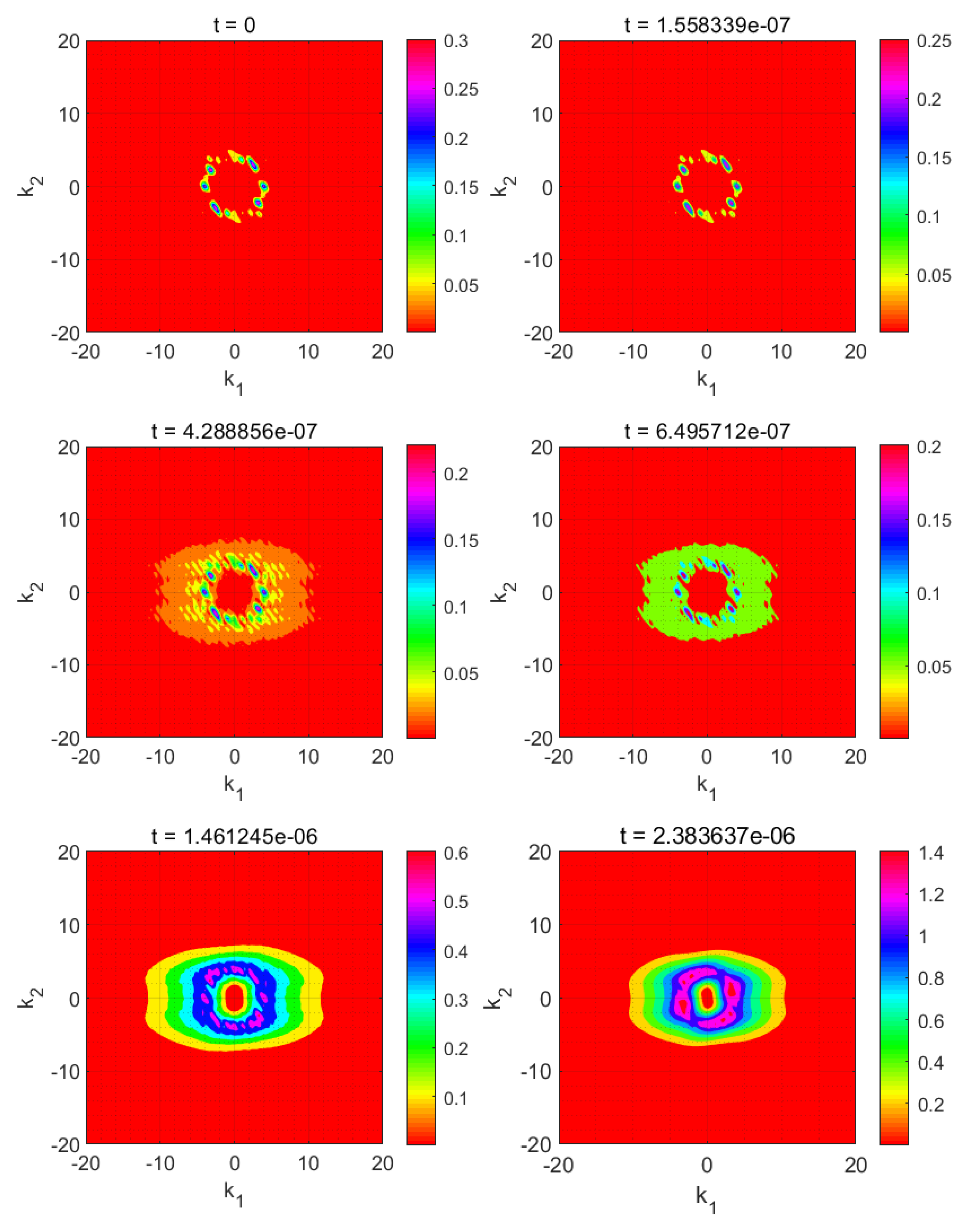
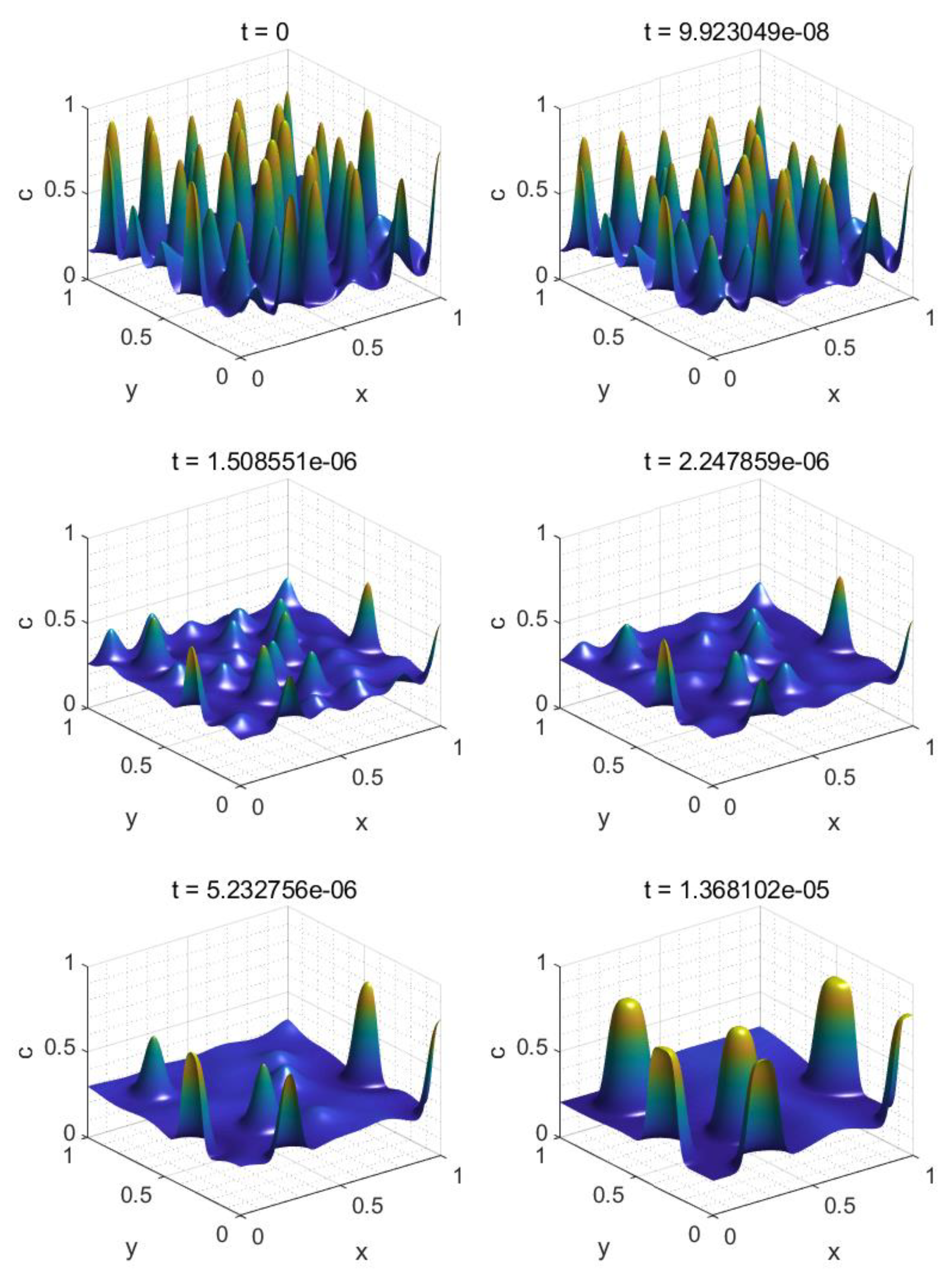
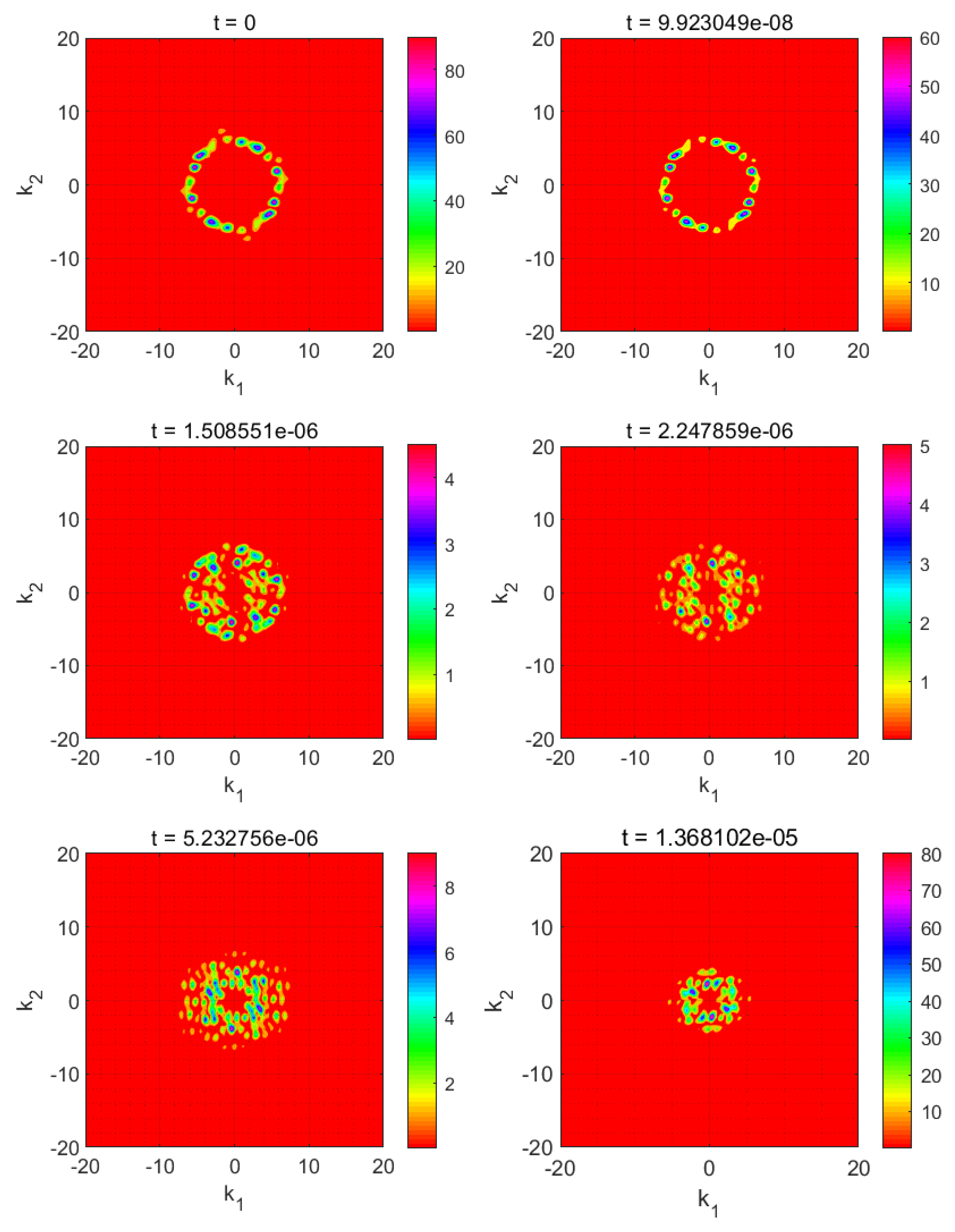
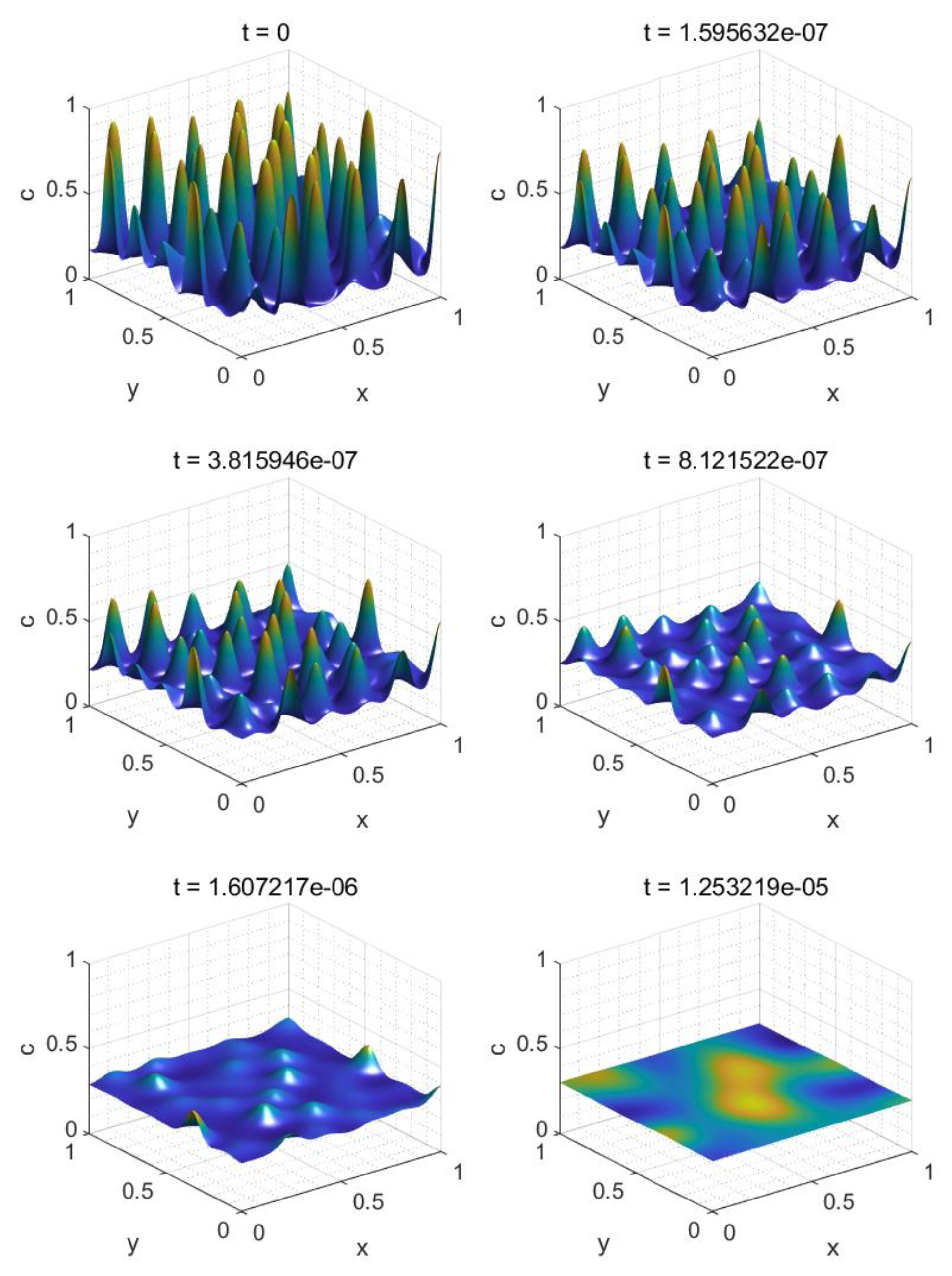
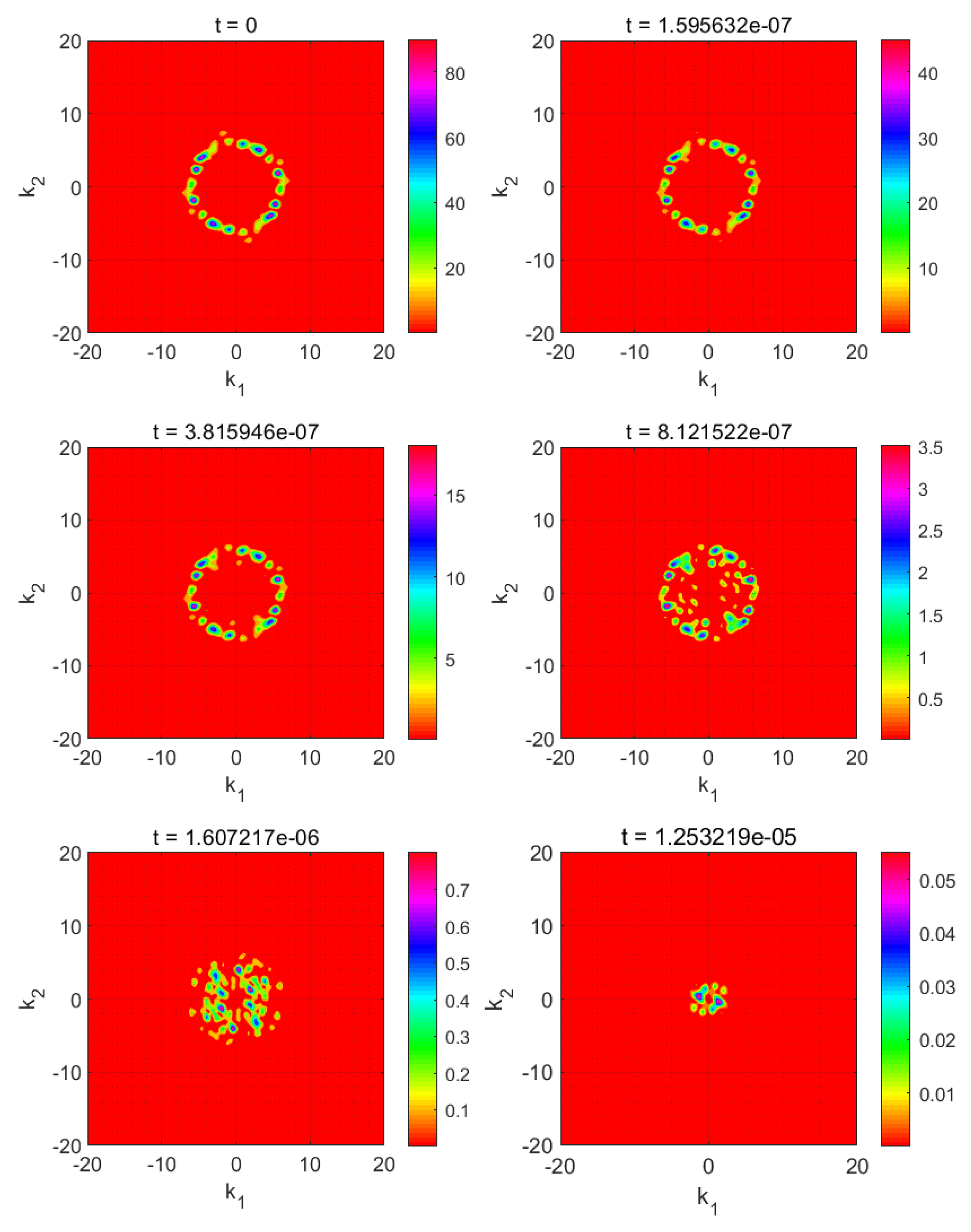
3.1. Anisotropic Quenching
3.2. Double Quenching
3.2.1. Narrow Metastable Region
3.2.2. Wide Metastable Region
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doane, J.W. Polymer dispersed liquid crystal displays. In Liquid Crystals: Applications and Uses; Bahadur, B., Ed.; World Scientific: Singapore, 1990; Volume 1. [Google Scholar]
- Higgins, D.A. Probing the mesoscopic chemical and physical properties of polymer-dispersed liquid crystals. Adv. Mater. 2000, 12, 251–264. [Google Scholar] [CrossRef]
- Barton, B.F.; McHugh, A.J. Modeling the dynamics of membrane structure formation in quenched polymer solutions. J. Membr. Sci. 2000, 166, 119–125. [Google Scholar] [CrossRef]
- Matsuyama, H.; Yuasa, M.; Kitamura, Y.; Teramoto, M.; Lloyd, D.R. Structure control of anisotropic and asymmetric polypropylene membrane prepared by thermally induced phase separation. J. Membr. Sci. 2000, 179, 91–100. [Google Scholar] [CrossRef]
- Dalmoro, A.; Barba, A.A.; Lamberti, G.; Grassi, M.; d’Amore, M. Pharmaceutical applications of biocompatible polymer blends containing sodium alginate. Adv. Polym. Technol. 2012, 31, 219–230. [Google Scholar] [CrossRef]
- Evans, D.F.; Wennerstrom, H. The Colloidal Domain: Where Physics, Chemistry, Biology and Technology Meet, 2nd ed.; Wiley-VCH: New York, NY, USA, 1999. [Google Scholar]
- Norde, W. Colloids and Interfaces in Life Sciences; Marcel Dekker: New York, NY, USA, 2003. [Google Scholar]
- Yaseen, M.; Salacinski, H.J.; Seifalian, A.M.; Lu, J.R. Dynamic protein adsorption at the polyurethane copolymer/water interface. Biomed. Mater. 2008, 3, 034123. [Google Scholar] [CrossRef] [PubMed]
- Mishra, K.; Hashmi, S.A.; Rai, D.K. Nanocomposite blend gel polymer electrolyte for proton battery application. J. Solid State Electrochem. 2013, 17, 785–793. [Google Scholar] [CrossRef]
- Zeng, J.H.; Wang, Y.F.; Gou, S.Q.; Zhang, L.P.; Chen, Y.; Jiang, J.X.; Shi, F. Sulfur in hyper-cross-linked porous polymer as cathode in lithium-sulfur batteries with enhanced electrochemical properties. ACS Appl. Mater. Interfaces 2017, 9, 34783. [Google Scholar] [CrossRef]
- Nyholm, L.; Nystrom, G.; Mihranyan, A.; Stromme, M. Toward flexible polymer and paper-based storage devices. Adv. Mater. 2011, 23, 3751–3769. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Miyata, F.; Nakao, S. Polymer electrolyte membranes with a pore-filling structure for a direct methanol fuel cell. Adv. Mater. 2003, 15, 1198–1201. [Google Scholar] [CrossRef]
- Kimmins, S.D.; Cameron, N.R. Functional porous polymers by emulsion templating: Recentadvances. Adv. Funct. Mater. 2011, 21, 211–225. [Google Scholar] [CrossRef]
- Van Driessche, A.E.S.; Van Gerven, N.; Bomans, P.H.H.; Joosten, R.R.M.; Friedrich, D.G.-C.; Sommerdijk, N.A.J.M.; Sleutel, M. Molecular nucleation mechanisms and control strategies for crystal polymorph selection. Nature 2018, 556, 89–94. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sleutel, M.; Van Driessche, A.E.S. Nucleation of protein crystals—A nanoscopic perspective. Nanoscale 2018, 26, 12256–12267. [Google Scholar] [CrossRef] [PubMed]
- Cahn, J.W. Phase separation by spinodal decomposition in isotropic systems. J. Chem. Phys. 1965, 42, 93–99. [Google Scholar] [CrossRef]
- Caneba, G.T.; Soong, D.S. Polymer membrane formation through the thermal-inversion process. 2. Mathematical modeling of membrane structure formation. Macromolecules 1985, 18, 2545–2555. [Google Scholar] [CrossRef]
- Chan, P.K.; Rey, A.D. Computational analysis of spinodal decomposition dynamics in polymer solutions. Macromol. Theory Simul. 1995, 4, 873–899. [Google Scholar] [CrossRef]
- Tran, T.L.; Chan, P.K.; Rousseau, D. Morphology control in symmetric polymer blends using spinodal decomposition. Chem. Eng. Sci. 2005, 60, 7153–7159. [Google Scholar] [CrossRef]
- Clarke, N. Target morphologies via a two-step dissolution-quench process in polymer blends. Phys. Rev. Lett. 2002, 89, 215506. [Google Scholar] [CrossRef]
- Lee, K.-W.; Chan, P.K.; Feng, X. Morphology development and characterization of the phase-separated structure resulting from the thermal-induced phase separation phenomenon in polymer solutions under a temperature gradient. Chem. Eng. Sci. 2004, 59, 1491–1504. [Google Scholar] [CrossRef]
- Hong, S.; Chan, P.K. Simultaneous use of temperature and concentration gradients to control polymer solution morphology development during thermal-induced phase separation. Model. Simul. Mater. Sci. Eng. 2010, 18, 025013. [Google Scholar] [CrossRef]
- Tabatabaieyazdi, M.; Chan, P.K.; Wu, J. A computational study of short-range surface-directed phase separation in polymer blends under a linear temperature gradient. Chem. Eng. Sci. 2015, 137, 884–895. [Google Scholar] [CrossRef]
- Henderson, I.C.; Clarke, N. Two-phase separation in polymer blends. Macromolecules 2004, 37, 1952–1959. [Google Scholar] [CrossRef]
- Tran, T.L.; Chan, P.K.; Rousseau, D. Morphology control in symmetric polymer blends using two-step phase separation. Comput. Mater. Sci. 2006, 37, 328–335. [Google Scholar] [CrossRef]
- Kwak, K.D.; Okada, M.; Chiba, T.; Nose, T. Growth rate of microdomains during phase separation by a two-step temperature jump. Macromolecules 1993, 26, 4047–4049. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. III. Nucleation in a two-component incompressible fluid. J. Chem. Phys. 1959, 31, 688–699. [Google Scholar] [CrossRef]
- Bates, P.W.; Fife, P.C. The dynamics of nucleation for the Cahn-Hilliard equation. SIAM J. Appl. Math. 1993, 53, 990–1008. [Google Scholar] [CrossRef]
- Kyu, T.; Lee, J.-H. Nucleation initiated spinodal decomposition in a polymerizing system. Phys. Rev. Lett. 1996, 76, 3746–3749. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Lapidus, L.; Pinder, G.F. Numerical Solution of Partial Differential Equations in Science and Engineering; John Wiley: New York, NY, USA, 1999. [Google Scholar]
- MATLAB for Artificial Intelligence. Available online: http://www.mathworks.com.




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran Duc, V.-N.; Chan, P.K. Using the Cahn–Hilliard Theory in Metastable Binary Solutions. ChemEngineering 2019, 3, 75. https://doi.org/10.3390/chemengineering3030075
Tran Duc V-N, Chan PK. Using the Cahn–Hilliard Theory in Metastable Binary Solutions. ChemEngineering. 2019; 3(3):75. https://doi.org/10.3390/chemengineering3030075
Chicago/Turabian StyleTran Duc, Viet-Nhien, and Philip K. Chan. 2019. "Using the Cahn–Hilliard Theory in Metastable Binary Solutions" ChemEngineering 3, no. 3: 75. https://doi.org/10.3390/chemengineering3030075



