An Efficient Computational Scheme for Two-Phase Steam Condensation in the Presence of CO2 for Wellbore and Long-Distance Flow
Abstract
1. Introduction
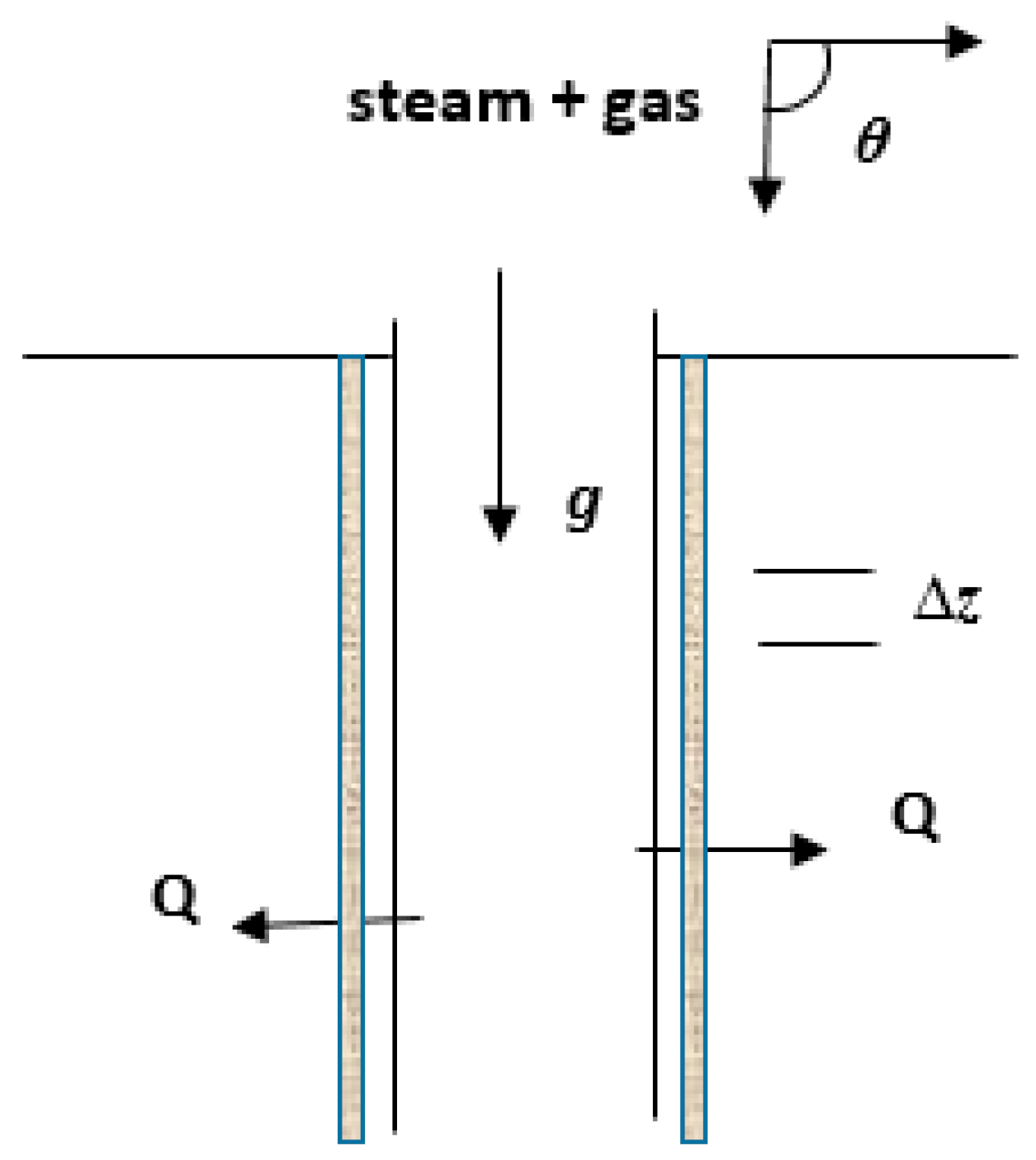
2. Model Equations
- (a)
- The state of the multicomponent mixture is described by the pertinent equation-of-state combined with the mixing rule used, while the partitioning details between species are ignored.
- (b)
- Heat is transferred only in the transverse direction.
- (c)
- Heat transfer is characterized by an overall heat transfer coefficient and the temperature differential between fluids and ambient formations.
- (d)
- The liquid and gas phases exist in thermodynamic equilibrium.
- (e)
- The interfacial geometry, effect of wall shear stress, and shear stresses between phases are neglected.
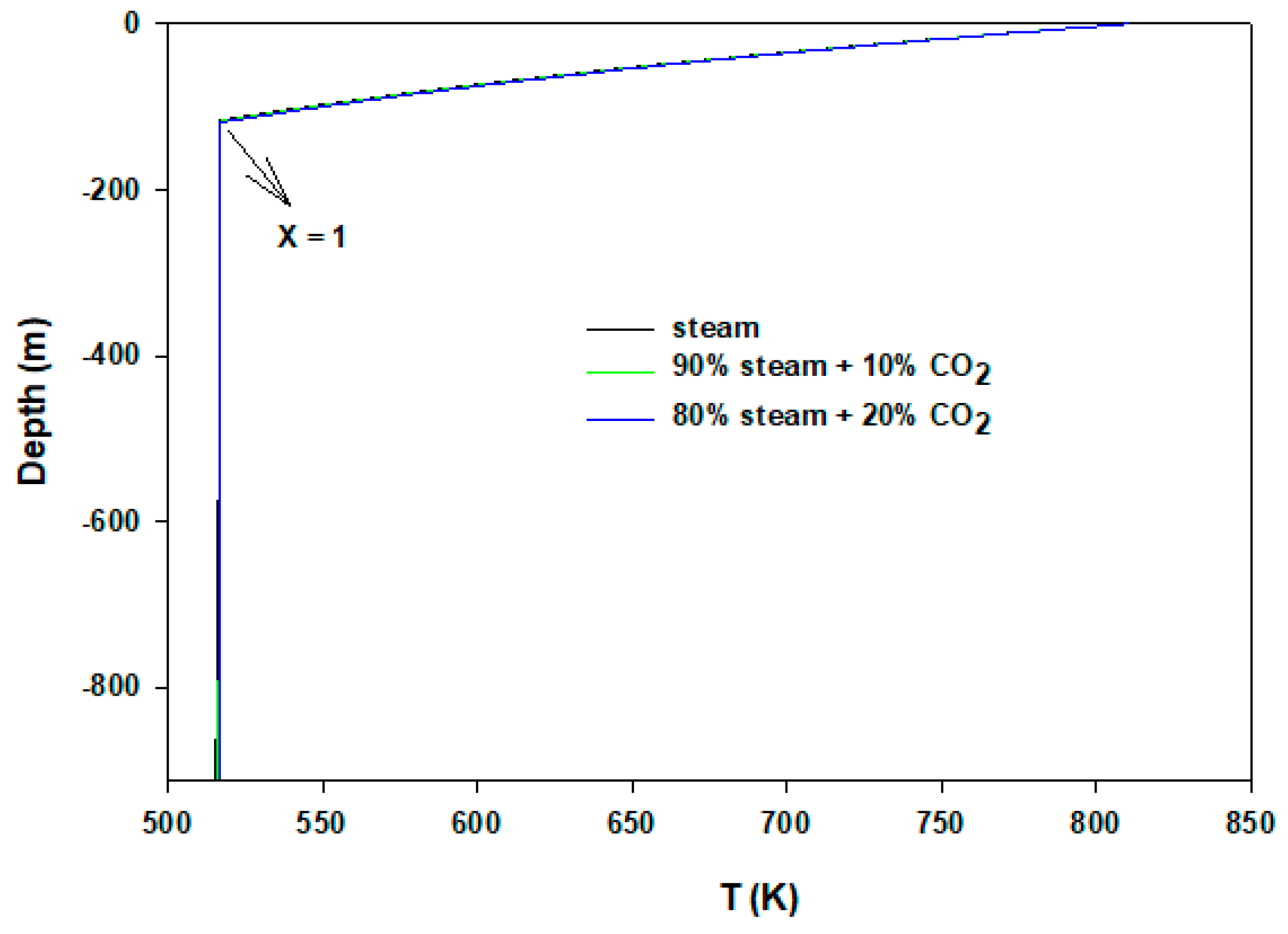
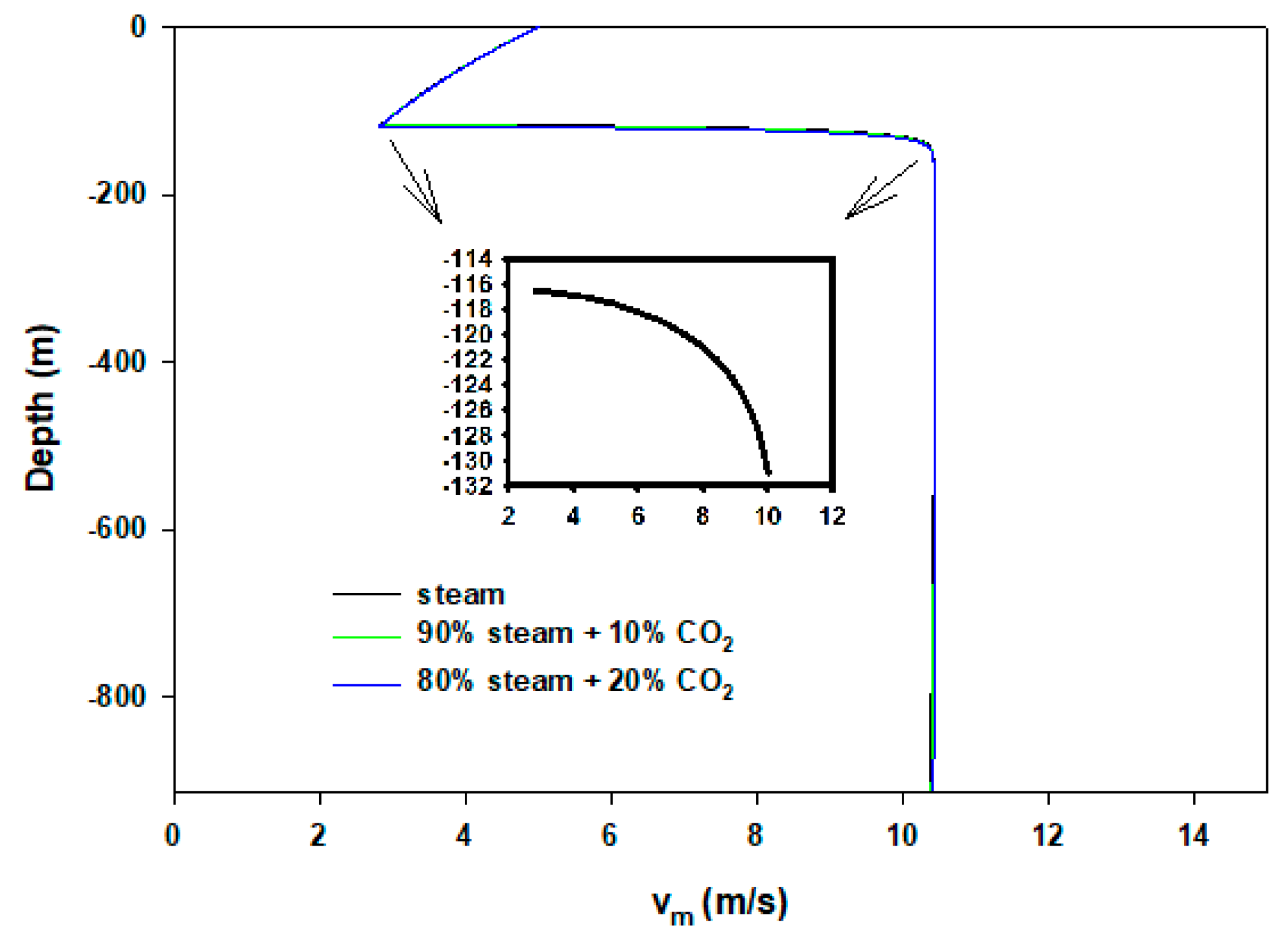
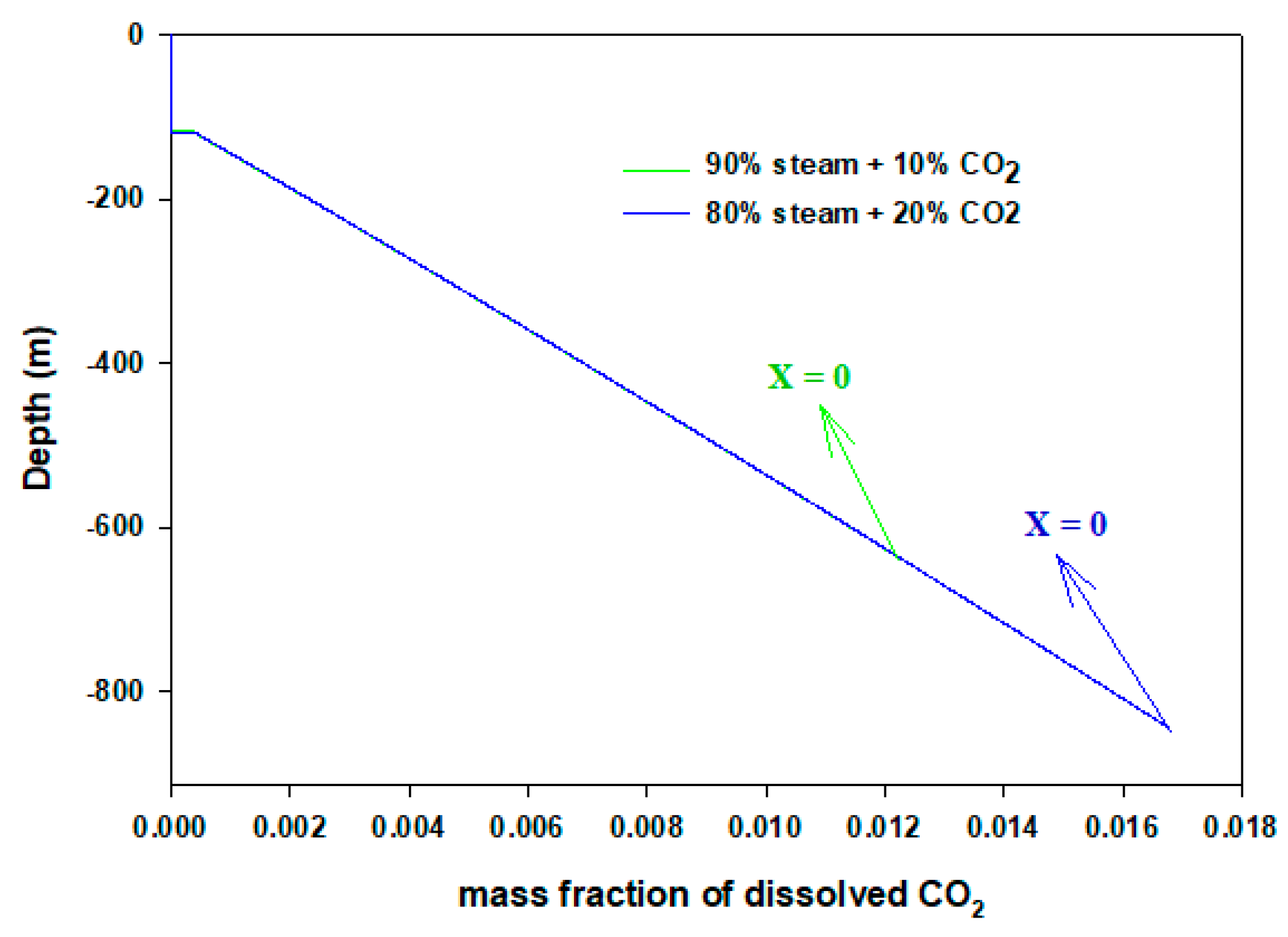
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Notations
| A | cross sectional area (m2) |
| C | specific heat (kJ/kg/K) |
| d | diameter (m) |
| f | volume fraction (-) |
| τ | friction factor (-) |
| g | gravity (m/s2) |
| H | enthalpy (kJ/kg) |
| L | length (m) |
| µ | viscosity (Pa·s) |
| n | number of components |
| p | pressure (Pa) |
| q | volumetric flux (m3/m2) |
| r | radius (m) |
| R | universal gas constant (kJ/kg/K) |
| ρ | density (kg/m3) |
| T | temperature (K) |
| ν | velocity (m/s) |
| U | overall heat transfer coefficient (J/s/m2/K) |
| V | volume (m3/kg) |
| x | component mass fraction in liquid phase (-) |
| y | component mass fraction in in gas phase (-) |
| z | vertical/horizontal distance (m) |
| Re | Reynolds number (= ) |
| θ | inclination angle (°) |
| Superscript | |
| 0 | saturated condition |
| Subscripts | |
| ii | grid cell no. |
| g | gas phase |
| l | liquid phase |
| m | mixture |
| p | pressure |
| in | in-situ |
| Acronyms | |
| fm | fluid mixture |
| nf | neighboring formation |
| swv | saturated water vapor |
| wv | water vapor |
| wh | well head |
Appendix A
Appendix B
References
- Shi, H.; Holmes, J.A.; Durlofsky, L.J.; Aziz, K.; Diaz, L.R.; Alkaya, B.; Oddie, G. Drift-Flux modeling of two-phase flow in wellbores. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003. [Google Scholar] [CrossRef]
- Pan, L.; Webb, S.; Oldenburg, C. Analytical solution for two-phase flow in a wellbore using the drift-flux model. Adv. Water Res. 2011, 34, 1656–1665. [Google Scholar] [CrossRef]
- Gunaltun, Y.; Larrey, D. Water-condensation rate critical in predicting, preventing TLC in wet-gas lines. Oil Gas J. 2000, 98, 58. [Google Scholar]
- Levy, S. Forced Convection Subcooled Boiling—Prediction of Vapor Volumetric Fraction; General Electric Company: Boston, MA, USA, 1966. [Google Scholar]
- Boldizsar, T. The distribution of temperature in flowing wells. Am. J. Sci. 1958, 256, 294–298. [Google Scholar] [CrossRef]
- Hasan, R.; Kabir, C. Two-phase flow in vertical and inclined annuli. Int. J. Multiphase Flow 1992, 18, 279–293. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. One dimensional drift-flux model and constituitive equations for relative motion between phases in various two-phase flow regimes. Int. J. Multiphase Flow 2003, 46, 4935–4948. [Google Scholar] [CrossRef]
- Ishii, M. One Dimensional Drift Flux Model and Constituitive Equations for Relative Motion between Phases in Various Two-Phase Flow Regimes; Argonne National Laboratory: Lemont, IL, USA, 1977. [Google Scholar]
- Nassos, G.; Bankoff, S. Slip velocity ratios in air-water system under steady-state and transient conditions. Chem. Eng. Sci. 1967, 22, 661–668. [Google Scholar] [CrossRef]
- Shi, H.; Holmes, J.; Durlofsky, L.; Aziz, K.; Diaz, L.; Alkaya, B.; Oddie, G. Drift-flux modeling of two phase flow in wellbores. SPEJ 2005, 24–33. [Google Scholar] [CrossRef]
- Wallis, G. One Dimensional Two Phase Flow; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Zuber, N.; Findlay, J. Average volumetric concentration in two-phase flow systems. J. Heat Transf. 1965, 87, 453–468. [Google Scholar] [CrossRef]
- Bian, H.; Sun, Z.; Zhang, N.; Meng, Z.; Ding, M. Numerical investigation on steam condensation in the presence of air on external surfaces of 3 × 3 tube bundles. Prog. Nuclear Energy 2019, 111, 42–50. [Google Scholar] [CrossRef]
- Bian, H.; Sun, Z.; Ding, M.; Zhang, N.; Yang, Y.; Tian, W. A Fluid film CFD model for steam Condensation in presence of Air. In Proceedings of the 24th International Conference on Nuclear Engineering, Charlotte, NC, USA, 26–30 June 2016. [Google Scholar] [CrossRef]
- Punetha, M.; Khandekar, S. A CFD based modeling approach for predicting steam condensation in the presence of non-condensable gases. Nuclear Eng. Des. 2017, 324, 280–296. [Google Scholar] [CrossRef]
- Lindeberg, E. Modeling pressure and temperature profile in a CO2 injection well. Energy Procedia 2011, 4, 3935–3941. [Google Scholar] [CrossRef]
- Paterson, L.; Lu, M.; Luke, D.; Ennis-King, J. Numerical modeling of pressure and temperature profiles including phase transitions in Carbon dioxide wells. In SPE ATCE; Society of Petroleum Engineers: Denver, CO, USA, 2008. [Google Scholar] [CrossRef]
- Prausnitz, J.; Lichtenthaler, R.; Azevedo, E. Molecular Thermodynamics of Fluid-Phase Equilibria; Pearson Education: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Satter, M. Heat loses during flow of steam down a wellbore. J. Pet. Technol. 1965, 17, 845–851. [Google Scholar] [CrossRef]
- Hasan, R.; Kabir, C. Fluid Flow and Heat Transfer in Wellbores; SPE Richrdson: Richardson, TX, USA, 2002. [Google Scholar]
- Lu, M.; Connell, L. Non-isothermal flow of carbon dioxide in injection wells during geological storage. Int. J. Greenhouse Gas Control 2008, 2, 248–258. [Google Scholar] [CrossRef]
- Peng, D.; Robinson, D. A new two-constant equation of state. Ind. Eng. Chem. Fund. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Ramey, H., Jr. Wellbore heat transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Islam, A.; Sun, A. Corrosion model of CO2 injection based on non-isothermal wellbore hydraulics. Int. J. Greenhouse Gas Control 2016, 54, 219–227. [Google Scholar] [CrossRef]
- Islam, A.; Sun, A. Detecting CO2 leakage around the wellbore by monitoring temperature profiles: A scoping analysis. Int. J. Therm. Sci. 2017, 118, 367–373. [Google Scholar] [CrossRef]
- Xu, B.; Kabir, C.; Hasan, A. Nonisothermal reservoir/wellbore flow modeling in gas reservoirs. J. Natural Gas Sci. Eng. 2018, 57, 89–99. [Google Scholar] [CrossRef]
- Han, W.; Stillman, G.; Lu, M.; Lu, C.; McPherson, B.; Park, E. Evaluation of potential nonisothermal processes and heat transport during CO2 sequestration. J. Geophys. Res. 2010, 115, B07209. [Google Scholar] [CrossRef]
- Islam, A.; Carlson, E. Application of SAFT equation for CO2+H2O phase equilibrium calculations over a wide pressure and temperature range. Fluid Phase Equilib. 2012, 321, 17–24. [Google Scholar] [CrossRef]
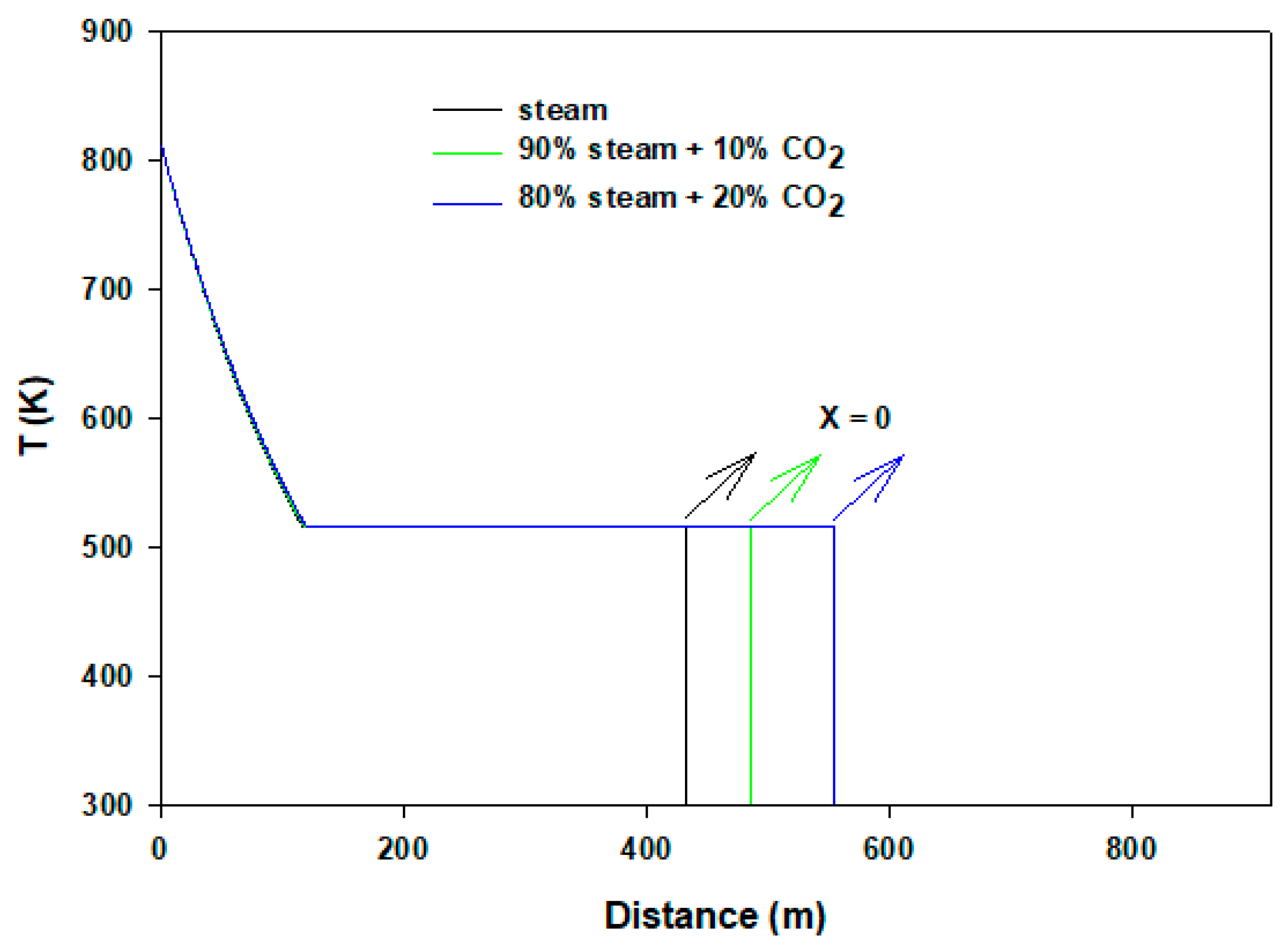
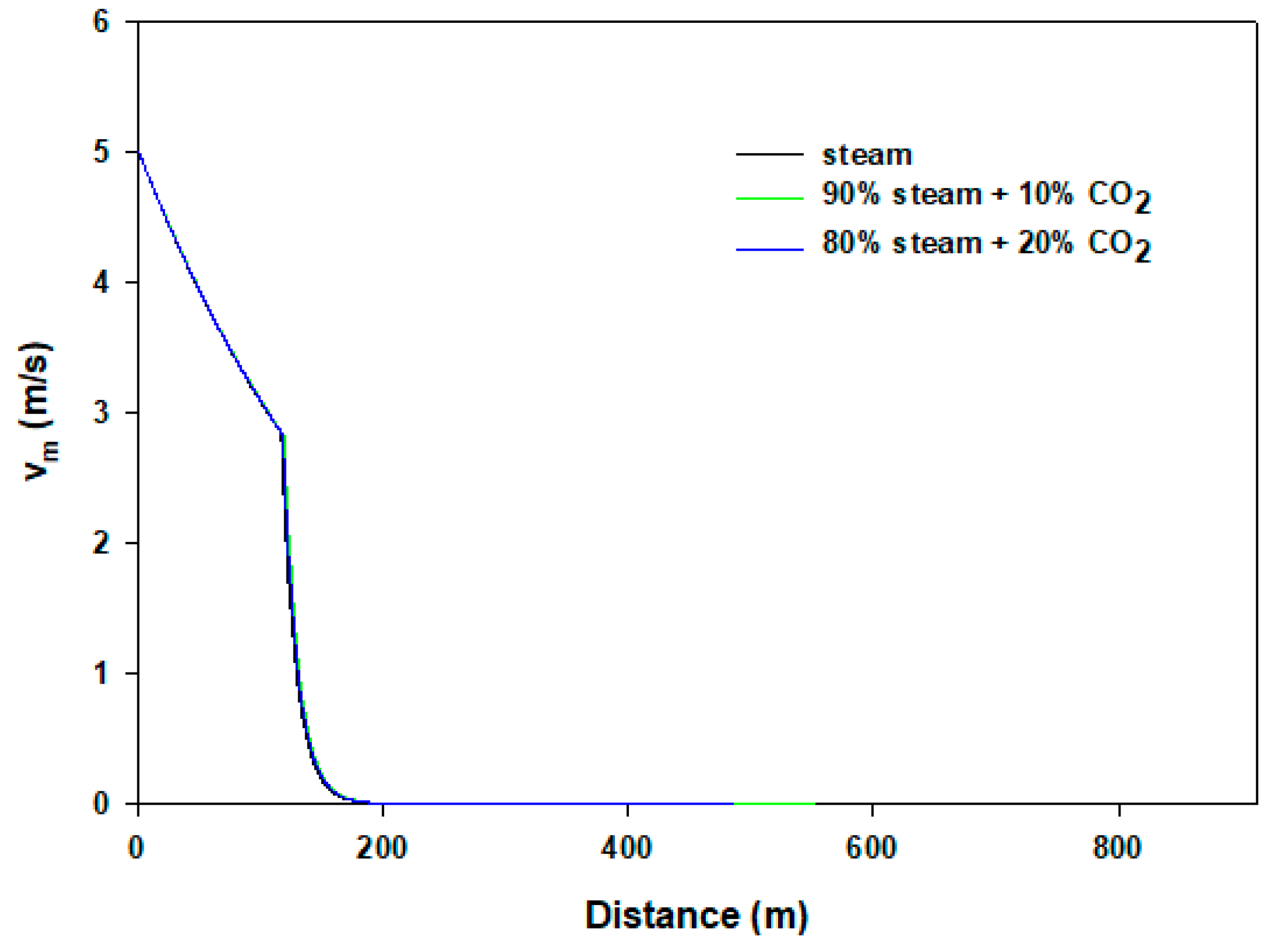
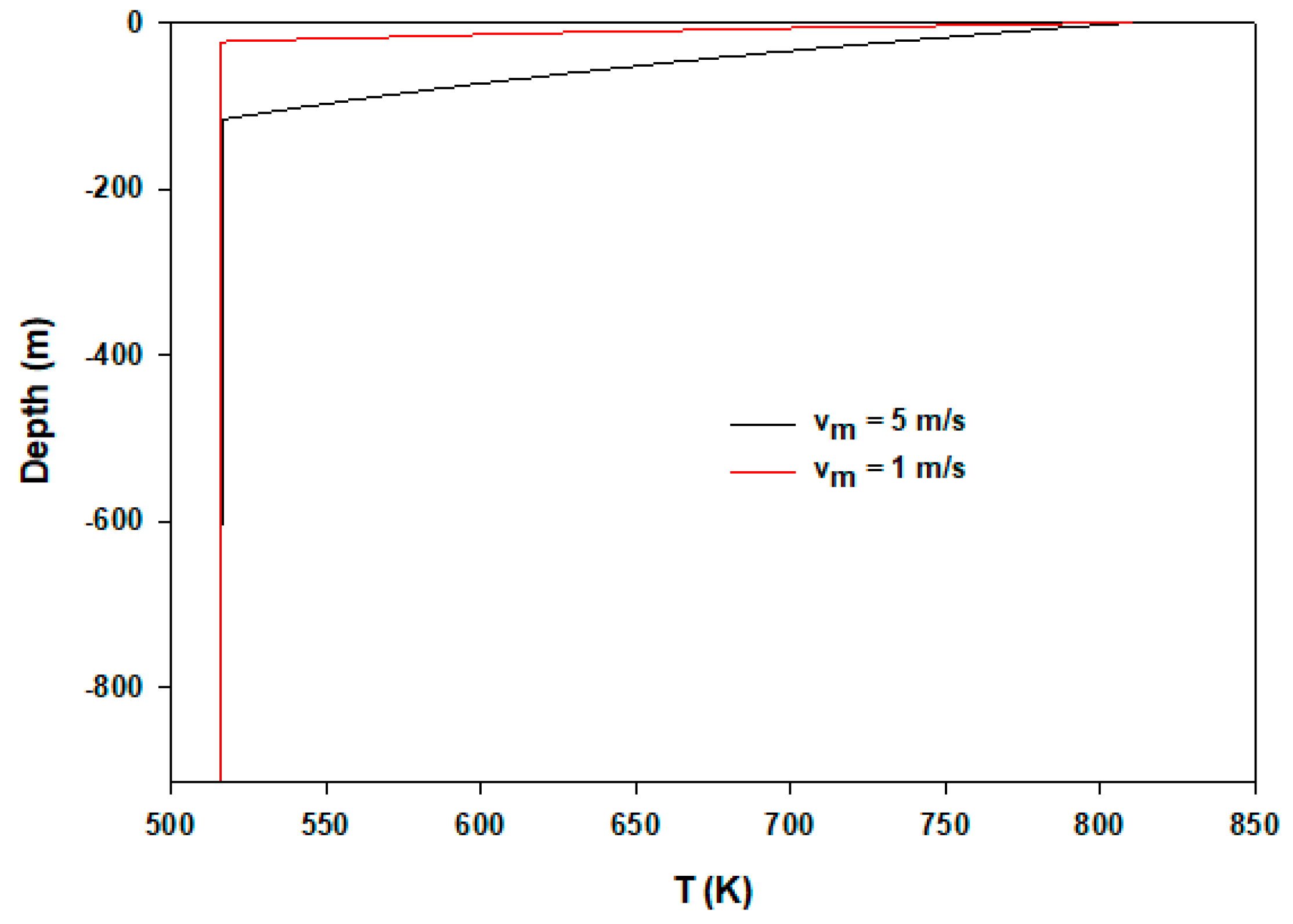
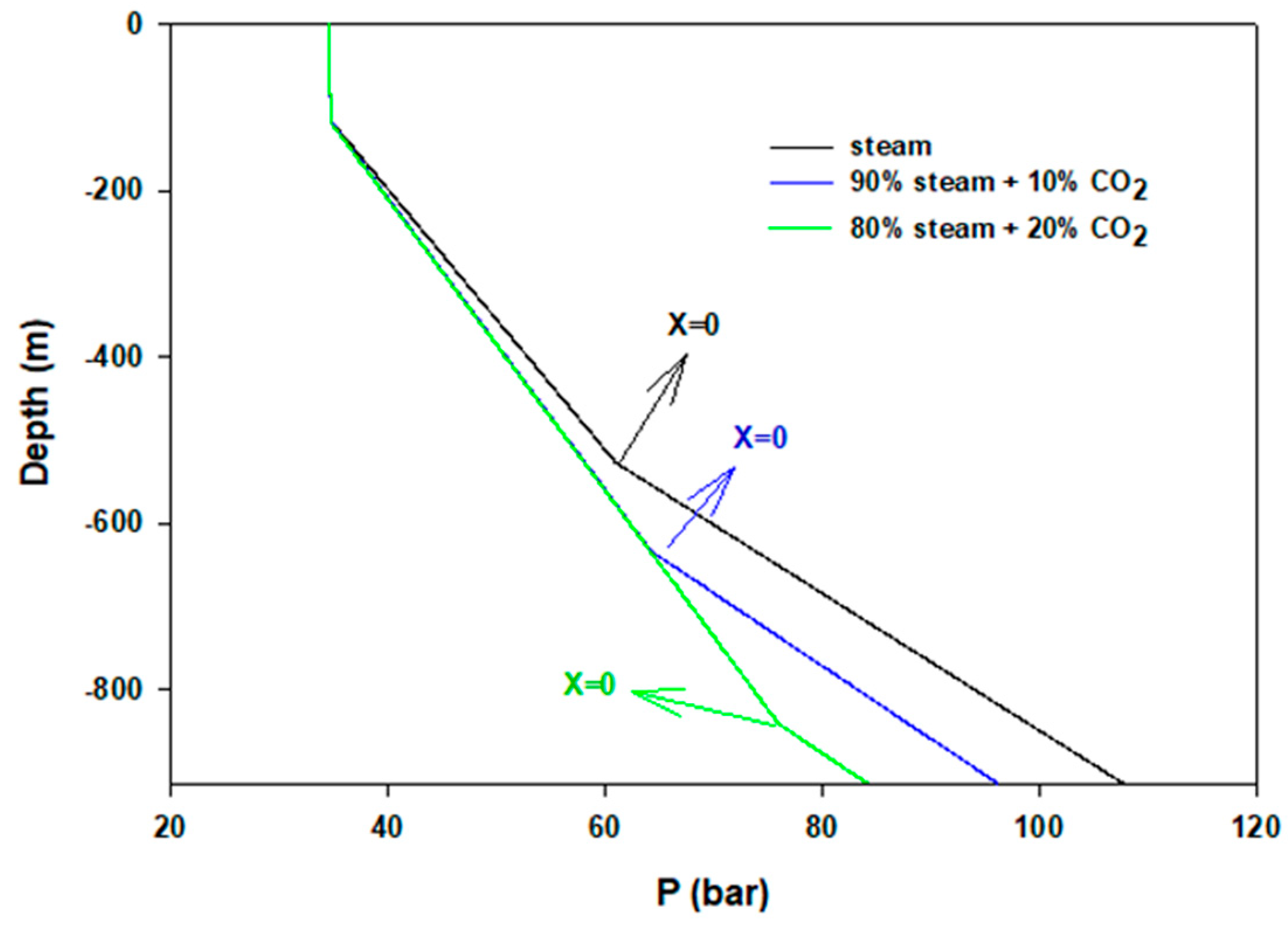
| Model Parameter | Values |
|---|---|
| L | 924 m |
| θ | 90° |
| d | 0.12 m |
| U | 11.0 J/s/m2/K |
| Surface temperature | 297 K |
| Geothermal gradient | 0.02 K/m |
| Twh | 810 K |
| Pwh | 34 bar |
| Injecting velocity | 5.0 m/s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, A.; Sun, A.; Sepehrnoori, K. An Efficient Computational Scheme for Two-Phase Steam Condensation in the Presence of CO2 for Wellbore and Long-Distance Flow. ChemEngineering 2019, 3, 4. https://doi.org/10.3390/chemengineering3010004
Islam A, Sun A, Sepehrnoori K. An Efficient Computational Scheme for Two-Phase Steam Condensation in the Presence of CO2 for Wellbore and Long-Distance Flow. ChemEngineering. 2019; 3(1):4. https://doi.org/10.3390/chemengineering3010004
Chicago/Turabian StyleIslam, Akand, Alexander Sun, and Kamy Sepehrnoori. 2019. "An Efficient Computational Scheme for Two-Phase Steam Condensation in the Presence of CO2 for Wellbore and Long-Distance Flow" ChemEngineering 3, no. 1: 4. https://doi.org/10.3390/chemengineering3010004
APA StyleIslam, A., Sun, A., & Sepehrnoori, K. (2019). An Efficient Computational Scheme for Two-Phase Steam Condensation in the Presence of CO2 for Wellbore and Long-Distance Flow. ChemEngineering, 3(1), 4. https://doi.org/10.3390/chemengineering3010004






