Abstract
Here we present an efficient and robust calculation scheme for two-phase, one-dimensional (1D) steady state steam condensation in the presence of CO2, based on conservation rules and thermodynamic phase relations. The mixing of fluids and phases is assumed to be homogeneous. Heat transfer is considered between the fluids and the ambient formations. For convenience, state equations are presented in terms of the entropy changes of individual phases, and the simple additive rule for the mixture. To monitor phase changes, the phase rule is checked. This investigation has practical significance for steam injection operation and long-distance pipe flow applications in the geothermal and mid- and up-stream oil and gas industries.
Keywords:
two-phase flow; condensation; phase rule; steam injection; CO2 injection; 1D flow; wellbore flow 1. Introduction
Two-phase flow effects in wellbores and pipes have a strong impact on the performance of reservoirs and surface facilities. In the case of horizontal or vertical wells, for instance, pressure losses in the well can result in underestimated production at the toe, or overestimated at the heel [1]. The characterization of discrete pathways through geologic formations, boreholes, and wells is critical to the success of many water, energy, and environmental management operations (e.g., geologic carbon sequestration, oil and gas production, geothermal energy production, compressed air energy storage, and subsurface environmental remediation). Simulating two-phase flow in wellbores is an important yet challenging task in the design and performance of fluid production, injection, and transport systems [2]. Moreover, steam condensation adds complexities in determining flow quality. Condensation can affect production performance (e.g., geothermal energy) significantly. In the case of CO2 injection for geologic sequestration or steam injection for enhanced oil recovery operations, vapor–liquid equilibrium properties (the saturation pressure relationship) between the fluids need to be accurately calculated, because bottom-hole pressure is sensitive to the positions where phase transition occurs within the wellbore. To this end, integration of the calculations of steam condensation and the phase equilibria in the flow model would be a useful development.
It is important to predict phase changes in pipeline transportation. Transportation faces no significant technological barriers, and is usually in a liquid or supercritical state to avoid two-phase flow regimes. The transported fluid (e.g., CO2, natural gas) should be moisture or condensate free. Moisture-laden CO2 or gas mixtures are prone to high corrosion, increasing operation costs several times over. Wet gas pipelines face water condensation, often leading to localized corrosion [3].
The proposed scheme aims to model steam condensation during flow either as a pure component or with gas (e.g., CO2). No other inert gases are considered. In the case of gas mixtures, the variance in equilibrium quantities of the phases along the well/pipe is accounted for. For state equations, entropy changes are incorporated in the individual phases and enthalpy is calculated as a mixing property. To capture condensation, instead of using the classical “profile fit” [4] or iterative procedure [5], saturated water vapor pressure is calculated, followed by a phase rule check. As in the drift–flux model [6,7,8,9,10,11,12], we solve one momentum equation in terms of the average mixing properties of the components, offering kinematic constitutive equations that specify the relative motion of the phases. This approach offers convenient solutions compared with the two-fluid model. In recent studies, Bian et al. [13,14] and Punetha and Khandekar [15] have performed numerical investigations of steam condensation in the presence of air using commercial CFD (Computational Fluid Dynamics) code. Although these studies considered relatively complex three-dimensional geometries, the thermodynamic properties of non-condensing air are very different from those of CO2. Unlike air, the phase behavior of CO2 changes with respect to temperature and pressure. Moreover, CO2 dissolves in water condensate. In the present work, phase change and dissolution of CO2 is assumed during flow. The detailed calculation process is also discussed.
2. Model Equations
It is assumed that steam combined with some other gases (e.g., CO2, CH4, air) is injected into the well, as shown in Figure 1. Wellbore flow can be time dependent, whereby fluid properties change rapidly, or in the quasi-steady state. Unsteady flow is particularly associated with times soon after injection, or immediately after a change in the operational conditions of the flow [16,17]. Heat transfer between the fluids and ambient formations governs this early stage flow transitions into a quasi-steady state, where transients and flow properties are relatively unchanged. Assuming a cylindrical flow conduit with inner radius r, cross sectional area A (= ), horizontal inclination angle , and length (from injection to exit) L, the following considerations are emphasized in this model:
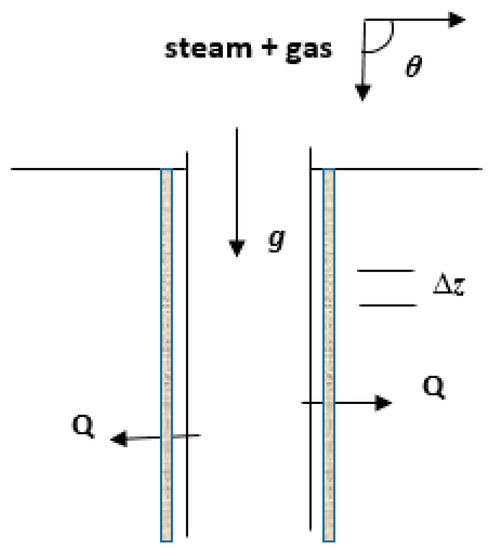
Figure 1.
Schematic diagram of 1D flow.
- (a)
- The state of the multicomponent mixture is described by the pertinent equation-of-state combined with the mixing rule used, while the partitioning details between species are ignored.
- (b)
- Heat is transferred only in the transverse direction.
- (c)
- Heat transfer is characterized by an overall heat transfer coefficient and the temperature differential between fluids and ambient formations.
- (d)
- The liquid and gas phases exist in thermodynamic equilibrium.
- (e)
- The interfacial geometry, effect of wall shear stress, and shear stresses between phases are neglected.
The three conservation equations of the mixture are
Mass Conservation
Momentum Conservation
Energy Conservation
Here Q quantifies heat exchange between the flowing fluids and neighboring formations. It is calculated by . The mass and energy balances between the two phases, respectively, are
The state equations of the two phases considering are
The phase equilibrium condition of the two phases can be presented as shown in Equation (8) [18]. Concentrations of species in each phase are quantified as average properties, hence right terms of Equations (9) and (10) disappear. For equilibrium condition, entropy changes are computed by Equations (9) and (10) below.
The Equations (1)–(10) are solved simultaneously to obtain where . The following mixing rule constraints shown by Equations (11)–(19) of the two phases and species of each phase must be fulfilled.
Constraints
Here the slip ratio is . In our model, homogeneous flow is assumed and, hence, slip ratio is 1. The components concentrations (x, y) in each phase can be calculated by the vapor–liquid equilibrium scheme [18]. According to the phase rule, steam condensation is captured by checking two simultaneous conditions (). In Appendix A and Appendix B, calculation method and pseudo-code for steam/CO2 mixture are discussed.
3. Results and Discussion
To validate our model, a sanity test is performed by comparing with the experimental results (field data) of Satter [19]. In later years, Hasan and Kabir [20] and Lu and Connel [21] also benchmarked their model results with the above reference. The same well and steam injection data were used. We have reproduced results within 3% quantitative tolerance. The first dew point we obtained was 507 K, whereas the literature value was 491 K. This discrepancy can be attributed to using different equation-of-states. We have used the Peng–Robinson method [22] and the author used Ramey’s [23] method. We present calculations based on synthetic input values reported in Table 1. In the case of the wellbore flow, the heat transfer coefficient can vary significantly based on fluids, wellbore materials (tubing, casing, cementing), geothermal gradient, and surrounding rock (earth) formations. The heat transfer coefficient of condensing steam is significantly different than superheated steam. However, because we were mainly interested in capturing the condensing point (the distance at which condensation begins), we have kept the value the same throughout our calculations. Figure 2 displays the temperature profiles of flowing steam/CO2 mixture in the wellbore. Here, X = 1 shows the end point of 100% gas phase or from where steam (superheated) begins to condense. Conversely, X = 0 indicates full condensation. While flowing down from the wellhead towards the reservoir, fluids lose heat to the surrounding cold formations. On the other hand, they become more pressurized as depth is increased (0.1 bar/m). It is noteworthy that the hydrostatic gradient (ρg) changes along the well depth due to the density change. For more accurate calculations this can be determined from the liquid holdup, after each discretization, j, iteratively. Density, ρ, can be predicted from Equation 14. Because our main objective is to present the calculation scheme, for simplicity we have used the mentioned gradient throughout the flowing length. Though in articles by Islam and Sun [24,25], Lu and Connell [21], Xu et al. [26], and Han et al. [27] the U is reported from 0.5–4.0 J/s/m2/K, we used 11.0 J/s/m2/K. Pressure loss from friction is neglected. The ambient temperature increases by 0.02 K/m from surface. In the case of pure steam injection, condensation commences at 117 m depth. It is discernible that after condensation begins until steam fully liquefies, the temperature remains the same. At this time, saturated steam gradually loses latent heat of vaporization and condenses further. Due to the gravity effect after condensation occurs, the flowing velocity increases rapidly; however, with increased hydrostatic pressure, the flow rate remains the same. Figure 3 shows velocity results of injected fluids. The inset presents rapid rise of velocity until it becomes constant. Interestingly, in the cases of 10% and 20% CO2 mixtures, the gas phases travel almost the same depth without condensation. The 10% and 20% CO2 mixtures condense at 119 and 121 m depths, respectively. It turns out that by adding another gas component the distance of unwanted condensation differs by very little. On the other hand, 10% and 20% gas mixtures, themselves, almost show no difference in the flow properties. The additional gas stream does not play any significant role because gravity effect and thermodynamics properties remain the same. In all cases, after condensation, the flowing velocities of heavy fluid mixtures are the same (~10 m/s). When the two phases (vapor–liquid) appear, CO2 also dissolves in the condensate. Figure 4 exhibits dissolved CO2 concentrations in the flowing two-phase mixtures. In this case, as expected, the hydrostatic pressure is added. The CO2–H2O phase equilibrium calculation is taken from Islam and Carlson [28].

Table 1.
Steam–CO2 injection data.
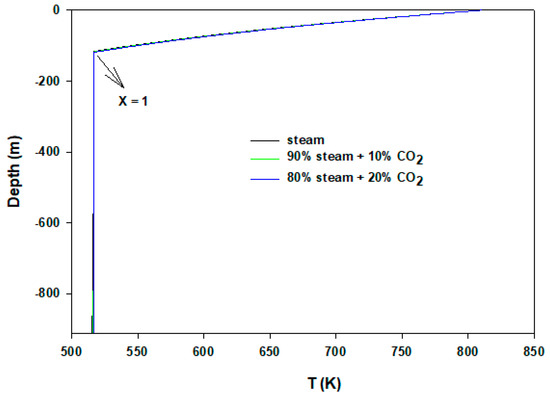
Figure 2.
Temperature profiles of steam–CO2 injections.
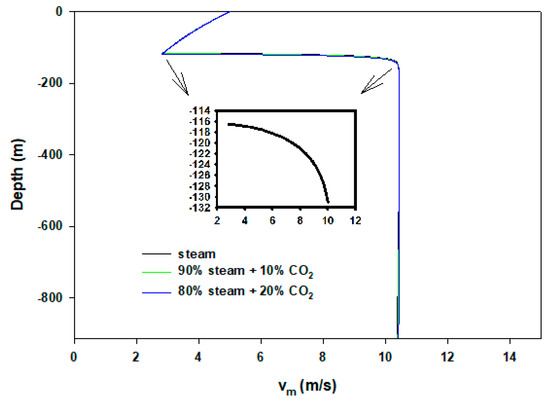
Figure 3.
Velocity profiles of steam–CO2 injections. Inset shows rapid rise of velocity right after condensation incepts.
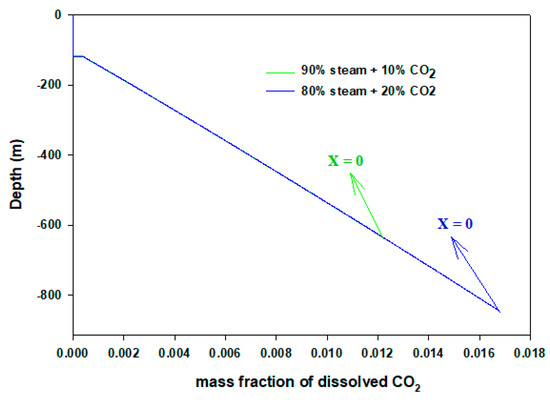
Figure 4.
Dissolved CO2 concentrations in condensates.
To understand the flow behaviors of horizontal pipe flow ( = 0°), Figure 5 shows temperature distributions of the mixture. In this case the flowing fluids lose heat almost monotonically to the neighboring surface (20 °C) before condensation occurs. The flowing pure steam converts into two phases after traveling 118 m distance, and then the temperature remains the same as observed previously. After complete condensation, the velocity falls rapidly because of heavy pressure loss and becomes almost stagnant. However, the results are different in steam–CO2 mixtures, whereby in 10% and 20% CO2 streams the dew points experienced are after about 320 and 370 m, respectively. CO2 continues to be dissolved in condensate during the flows. Unlike the case of vertical wellbore flow, steam condensation can be manipulated by CO2 addition or by other impurities. In our calculations, the presence of no other inert gases except CO2 is assumed. Figure 6 renders velocity profiles of the flows. It is expected that velocity drops almost linearly as gases flow until the dew point of steam is reached. After condensation begins, velocity reduces abruptly because of the presence of liquid. In the case of pure steam, or with mixing of 10% or 20% CO2, velocity profiles do not show traceable differences. For horizontal flow, the presence of CO2 has negligible impact due to the absence of gravity effect. Furthermore, there is no additional friction loss for CO2.
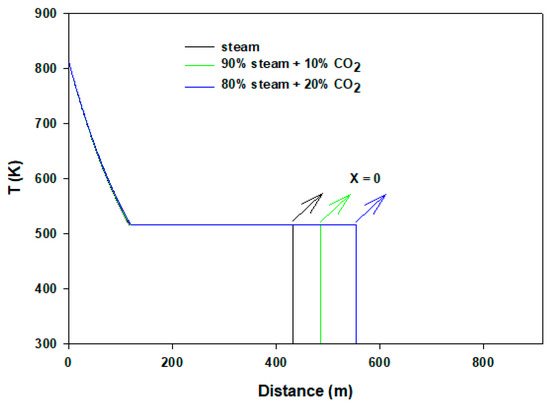
Figure 5.
Temperature profiles of horizontal flows.
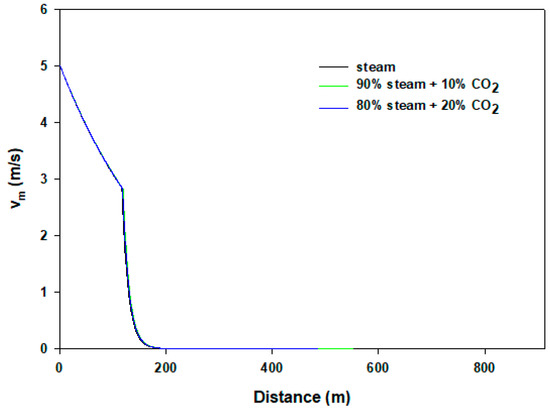
Figure 6.
Velocity results of horizontal flows.
Figure 7 shows flow temperatures at the two different injecting velocities. At the lower flow rate, because of higher residence time, steam loses heat quickly. Hence, in 1 m/s injecting velocity condensation appears only in 40 m depth, compared to 117 m in the case of the higher initial velocity of 5 m/s. In all calculations, the same U is applied. To understand the pressure distribution during flows, Figure 8 shows pressure profiles of three cases. Until condensation begins, pressure change is very low. Pressure rises gradually during condensation and then after completion it increases sharply.
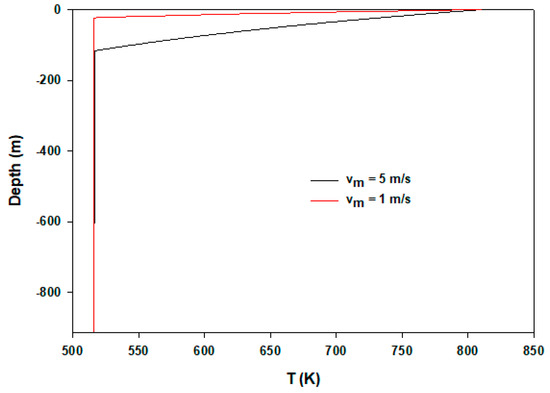
Figure 7.
Temperature distributions of two different injecting velocities.
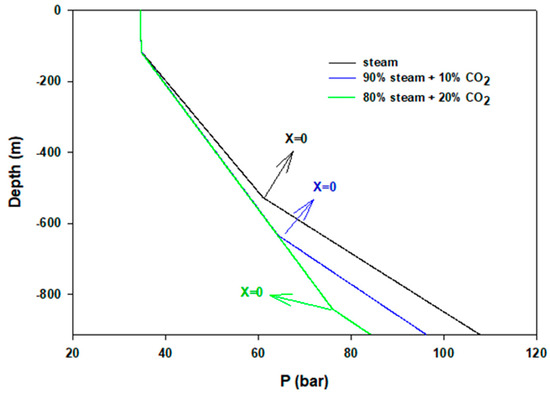
Figure 8.
Pressure distributions of steam injections.
4. Concluding Remarks
A two-phase steam condensation model is presented for subsurface injection and long-distance pipe flows. In addition to mass, momentum, and energy conservations, the set of equations are based on thermodynamics phase equilibrium phenomena. This model can be introduced as an in-between of drift-flux and two-fluid flow approaches. The calculated results, based on synthetic inputs, are discussed considering different flow scenarios. Though this model is shown for steam condensation, it can be applied to any other vapor condensation. The model can be applied to simulate flow behaviors of fluid mixture where phase transitions can occur from gas to liquid phase, or vice versa. By changing the slip ratio this model can be implemented for other flow patterns (e.g., slug, churn, and bubbly). Applying the phase rule captures the phase transition. In the case of steam injection, addition of a CO2 stream, even up to 20%, affects condensation very minimally in the vertical wellbore flow. However, in horizontal flow the effect can be important.
Author Contributions
A.I. designed the research and performed the simulations. A.S. and K.S. contributed to the interpretation of the results and to the writing.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interests.
Notations
| A | cross sectional area (m2) |
| C | specific heat (kJ/kg/K) |
| d | diameter (m) |
| f | volume fraction (-) |
| τ | friction factor (-) |
| g | gravity (m/s2) |
| H | enthalpy (kJ/kg) |
| L | length (m) |
| µ | viscosity (Pa·s) |
| n | number of components |
| p | pressure (Pa) |
| q | volumetric flux (m3/m2) |
| r | radius (m) |
| R | universal gas constant (kJ/kg/K) |
| ρ | density (kg/m3) |
| T | temperature (K) |
| ν | velocity (m/s) |
| U | overall heat transfer coefficient (J/s/m2/K) |
| V | volume (m3/kg) |
| x | component mass fraction in liquid phase (-) |
| y | component mass fraction in in gas phase (-) |
| z | vertical/horizontal distance (m) |
| Re | Reynolds number (= ) |
| θ | inclination angle (°) |
| Superscript | |
| 0 | saturated condition |
| Subscripts | |
| ii | grid cell no. |
| g | gas phase |
| l | liquid phase |
| m | mixture |
| p | pressure |
| in | in-situ |
| Acronyms | |
| fm | fluid mixture |
| nf | neighboring formation |
| swv | saturated water vapor |
| wv | water vapor |
| wh | well head |
Appendix A
Here the calculation procedure of steam–CO2 mixture is shown. After applying pertinent constraint relations, shown by Equations (1), (4), and (5), the equations of two components are as follows:
Adding these three equations with Equations (2), (3), and (6)–(10), the set of unknowns are
The coefficient matrix of ,
The coefficients are
The right-hand side constants matrix appears as
Finally, the unknowns can be computed by solving .
Appendix B
Here pseudo code of calculations for the steam–CO2 mixture is demonstrated. At injection conditions of T= 810 K and P = 34 bar, the mixture initially is in gas phase. Hence, we solve the flow properties only for gas phase (Equations (1)–(3), (6), (8), and (9)) until condensation conditions () are met. If each phase is considered as a single fluid (quasi component), the phase rule can define the state of the fluid. At given P, can be calculated from the Antoine equation. can also be computed by predicting the condition of . Thereafter we solve the set of Equations (1)–(10) until full condensation of steam occurs (). It is noteworthy that, for the case of gas mixture with close boiling points (e.g., steam/oil vapors), all fluids may condense completely during the flow. In that case, the equations should be solved for liquid phase only (Equations (1)–(3), (7), (8), and (10)).
References
- Shi, H.; Holmes, J.A.; Durlofsky, L.J.; Aziz, K.; Diaz, L.R.; Alkaya, B.; Oddie, G. Drift-Flux modeling of two-phase flow in wellbores. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003. [Google Scholar] [CrossRef]
- Pan, L.; Webb, S.; Oldenburg, C. Analytical solution for two-phase flow in a wellbore using the drift-flux model. Adv. Water Res. 2011, 34, 1656–1665. [Google Scholar] [CrossRef]
- Gunaltun, Y.; Larrey, D. Water-condensation rate critical in predicting, preventing TLC in wet-gas lines. Oil Gas J. 2000, 98, 58. [Google Scholar]
- Levy, S. Forced Convection Subcooled Boiling—Prediction of Vapor Volumetric Fraction; General Electric Company: Boston, MA, USA, 1966. [Google Scholar]
- Boldizsar, T. The distribution of temperature in flowing wells. Am. J. Sci. 1958, 256, 294–298. [Google Scholar] [CrossRef]
- Hasan, R.; Kabir, C. Two-phase flow in vertical and inclined annuli. Int. J. Multiphase Flow 1992, 18, 279–293. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. One dimensional drift-flux model and constituitive equations for relative motion between phases in various two-phase flow regimes. Int. J. Multiphase Flow 2003, 46, 4935–4948. [Google Scholar] [CrossRef]
- Ishii, M. One Dimensional Drift Flux Model and Constituitive Equations for Relative Motion between Phases in Various Two-Phase Flow Regimes; Argonne National Laboratory: Lemont, IL, USA, 1977. [Google Scholar]
- Nassos, G.; Bankoff, S. Slip velocity ratios in air-water system under steady-state and transient conditions. Chem. Eng. Sci. 1967, 22, 661–668. [Google Scholar] [CrossRef]
- Shi, H.; Holmes, J.; Durlofsky, L.; Aziz, K.; Diaz, L.; Alkaya, B.; Oddie, G. Drift-flux modeling of two phase flow in wellbores. SPEJ 2005, 24–33. [Google Scholar] [CrossRef]
- Wallis, G. One Dimensional Two Phase Flow; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Zuber, N.; Findlay, J. Average volumetric concentration in two-phase flow systems. J. Heat Transf. 1965, 87, 453–468. [Google Scholar] [CrossRef]
- Bian, H.; Sun, Z.; Zhang, N.; Meng, Z.; Ding, M. Numerical investigation on steam condensation in the presence of air on external surfaces of 3 × 3 tube bundles. Prog. Nuclear Energy 2019, 111, 42–50. [Google Scholar] [CrossRef]
- Bian, H.; Sun, Z.; Ding, M.; Zhang, N.; Yang, Y.; Tian, W. A Fluid film CFD model for steam Condensation in presence of Air. In Proceedings of the 24th International Conference on Nuclear Engineering, Charlotte, NC, USA, 26–30 June 2016. [Google Scholar] [CrossRef]
- Punetha, M.; Khandekar, S. A CFD based modeling approach for predicting steam condensation in the presence of non-condensable gases. Nuclear Eng. Des. 2017, 324, 280–296. [Google Scholar] [CrossRef]
- Lindeberg, E. Modeling pressure and temperature profile in a CO2 injection well. Energy Procedia 2011, 4, 3935–3941. [Google Scholar] [CrossRef]
- Paterson, L.; Lu, M.; Luke, D.; Ennis-King, J. Numerical modeling of pressure and temperature profiles including phase transitions in Carbon dioxide wells. In SPE ATCE; Society of Petroleum Engineers: Denver, CO, USA, 2008. [Google Scholar] [CrossRef]
- Prausnitz, J.; Lichtenthaler, R.; Azevedo, E. Molecular Thermodynamics of Fluid-Phase Equilibria; Pearson Education: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Satter, M. Heat loses during flow of steam down a wellbore. J. Pet. Technol. 1965, 17, 845–851. [Google Scholar] [CrossRef]
- Hasan, R.; Kabir, C. Fluid Flow and Heat Transfer in Wellbores; SPE Richrdson: Richardson, TX, USA, 2002. [Google Scholar]
- Lu, M.; Connell, L. Non-isothermal flow of carbon dioxide in injection wells during geological storage. Int. J. Greenhouse Gas Control 2008, 2, 248–258. [Google Scholar] [CrossRef]
- Peng, D.; Robinson, D. A new two-constant equation of state. Ind. Eng. Chem. Fund. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Ramey, H., Jr. Wellbore heat transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Islam, A.; Sun, A. Corrosion model of CO2 injection based on non-isothermal wellbore hydraulics. Int. J. Greenhouse Gas Control 2016, 54, 219–227. [Google Scholar] [CrossRef]
- Islam, A.; Sun, A. Detecting CO2 leakage around the wellbore by monitoring temperature profiles: A scoping analysis. Int. J. Therm. Sci. 2017, 118, 367–373. [Google Scholar] [CrossRef]
- Xu, B.; Kabir, C.; Hasan, A. Nonisothermal reservoir/wellbore flow modeling in gas reservoirs. J. Natural Gas Sci. Eng. 2018, 57, 89–99. [Google Scholar] [CrossRef]
- Han, W.; Stillman, G.; Lu, M.; Lu, C.; McPherson, B.; Park, E. Evaluation of potential nonisothermal processes and heat transport during CO2 sequestration. J. Geophys. Res. 2010, 115, B07209. [Google Scholar] [CrossRef]
- Islam, A.; Carlson, E. Application of SAFT equation for CO2+H2O phase equilibrium calculations over a wide pressure and temperature range. Fluid Phase Equilib. 2012, 321, 17–24. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).