Hydrodynamics of Bubble Columns: Turbulence and Population Balance Model
Abstract
1. Introduction
2. Physical Model
3. Governing Equations
3.1. Population Balance Model (PBM)
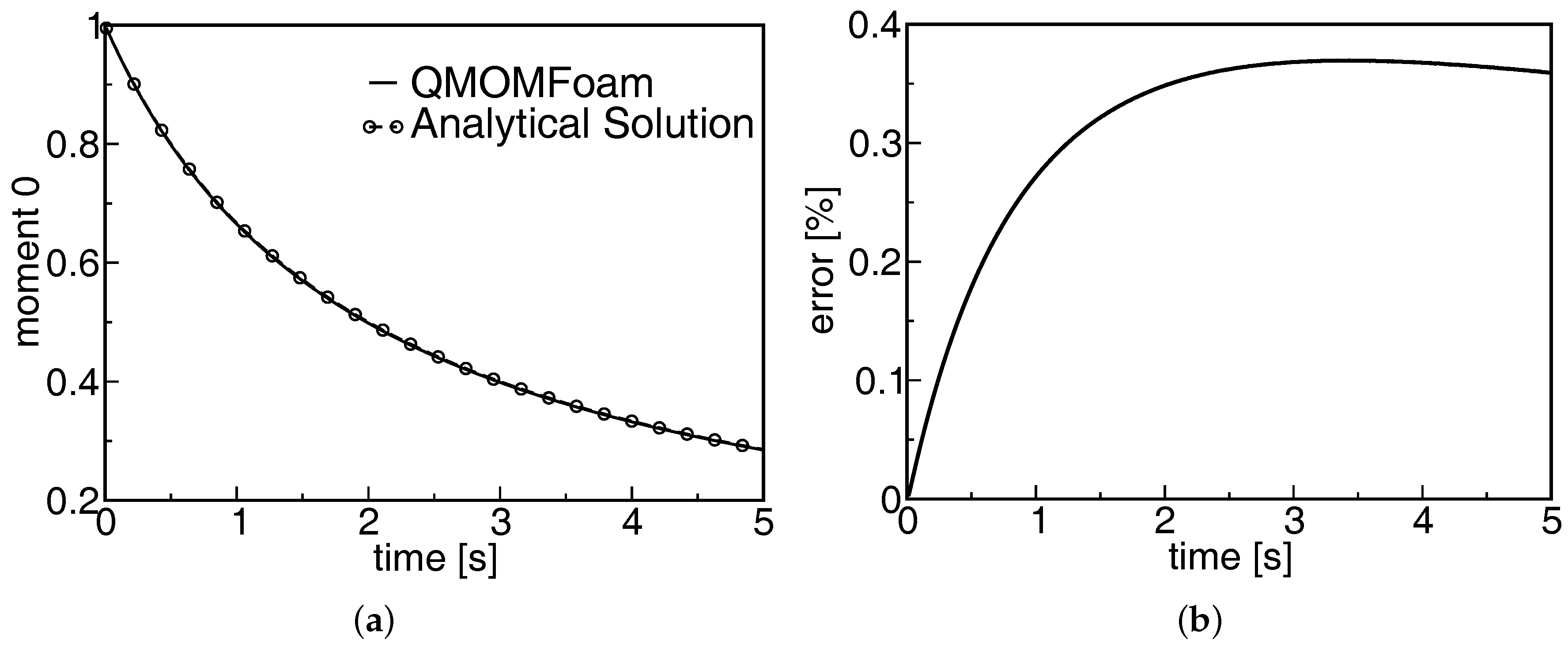
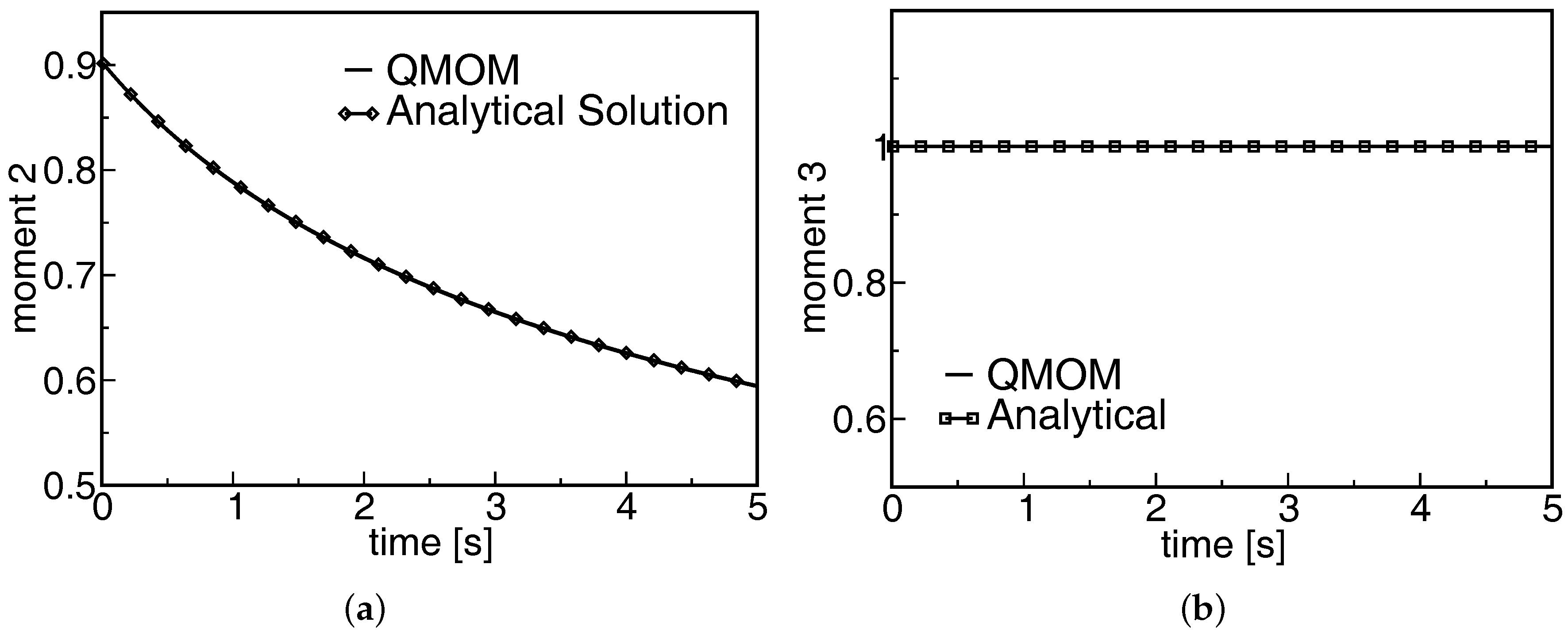
3.2. Validation and Verification
3.3. Boundary Conditions
3.4. Numerical Methods
4. Results and Discussion
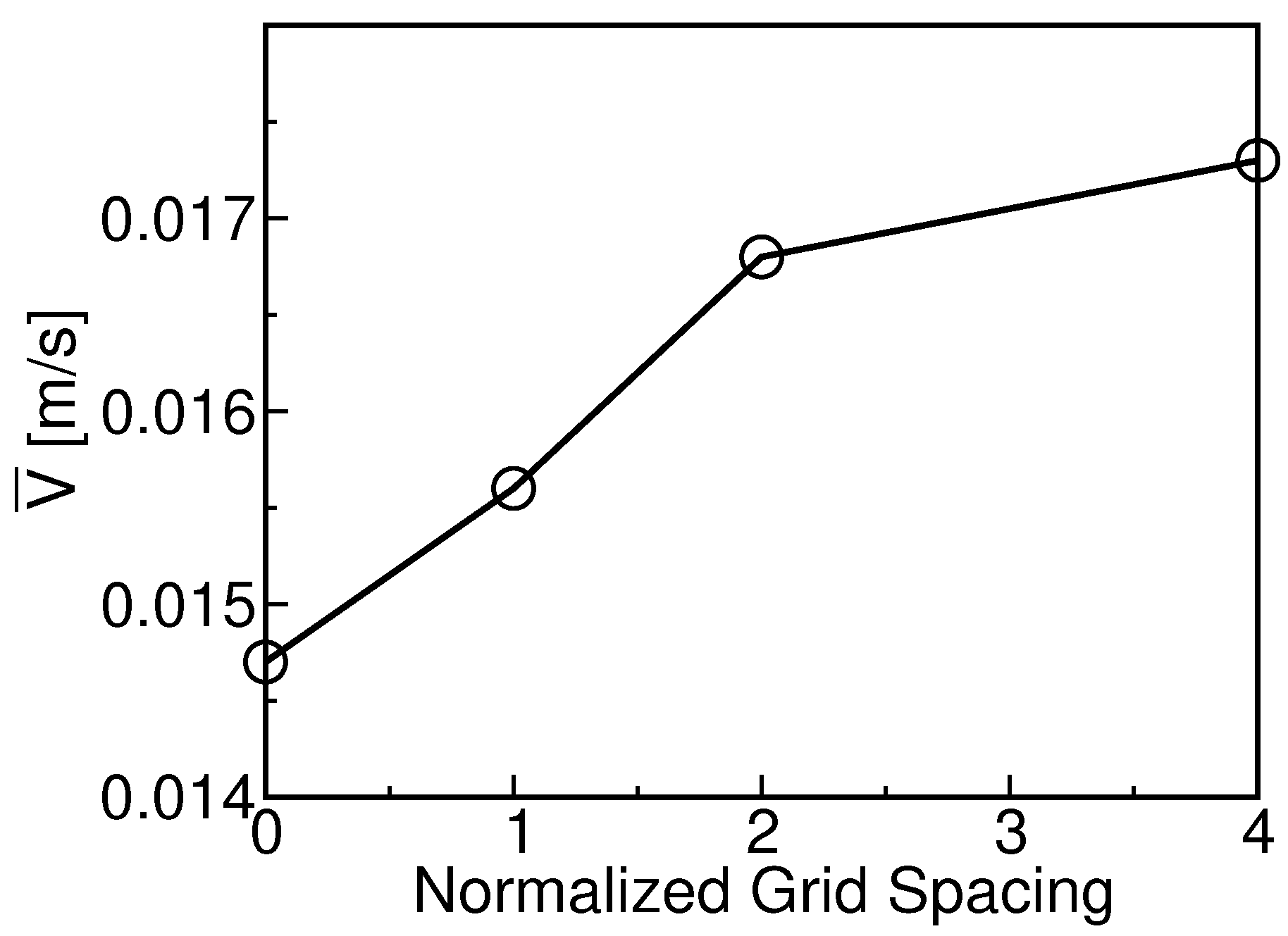
4.1. Mesh Sensitivity Study
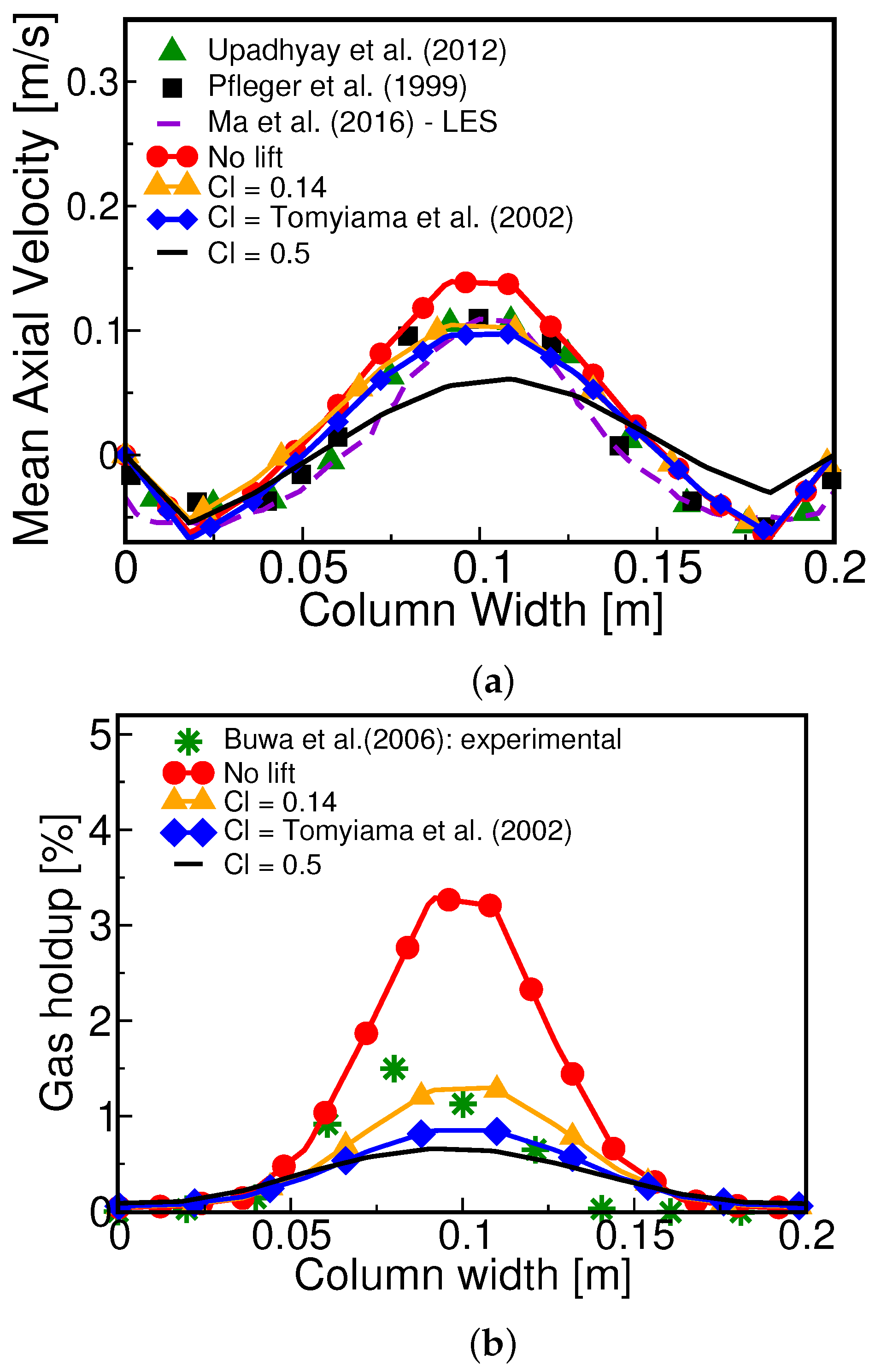
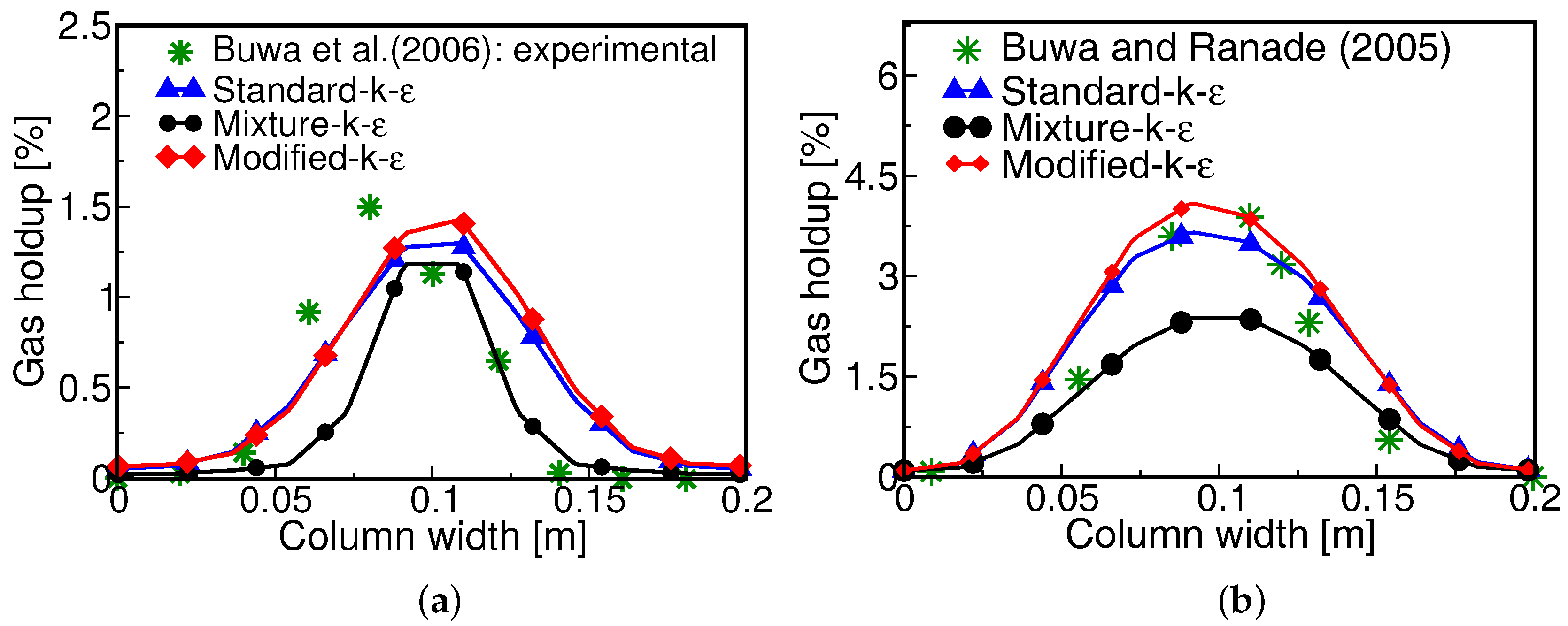
4.2. Influence of the Interfacial Forces on the Fluid Dynamics
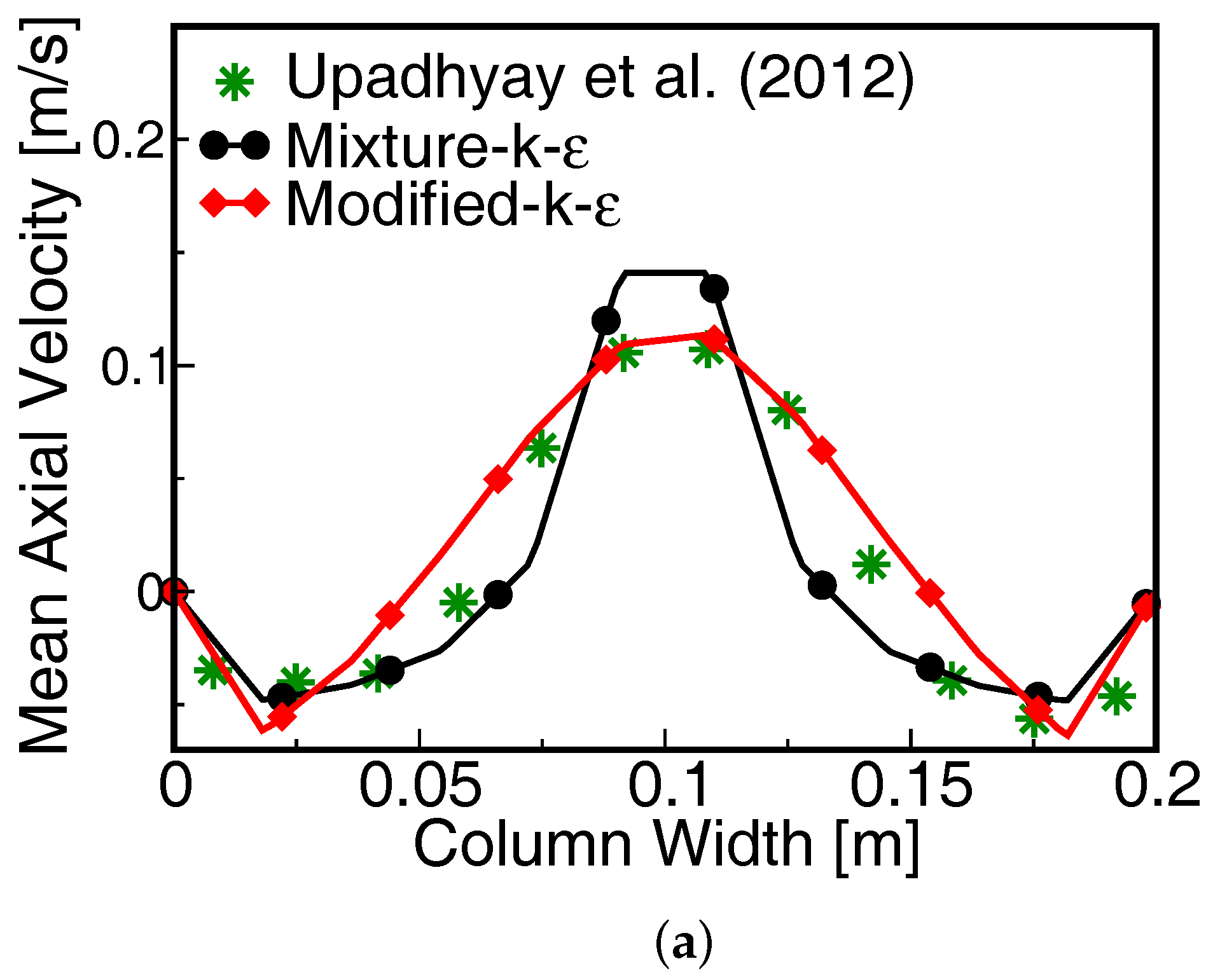
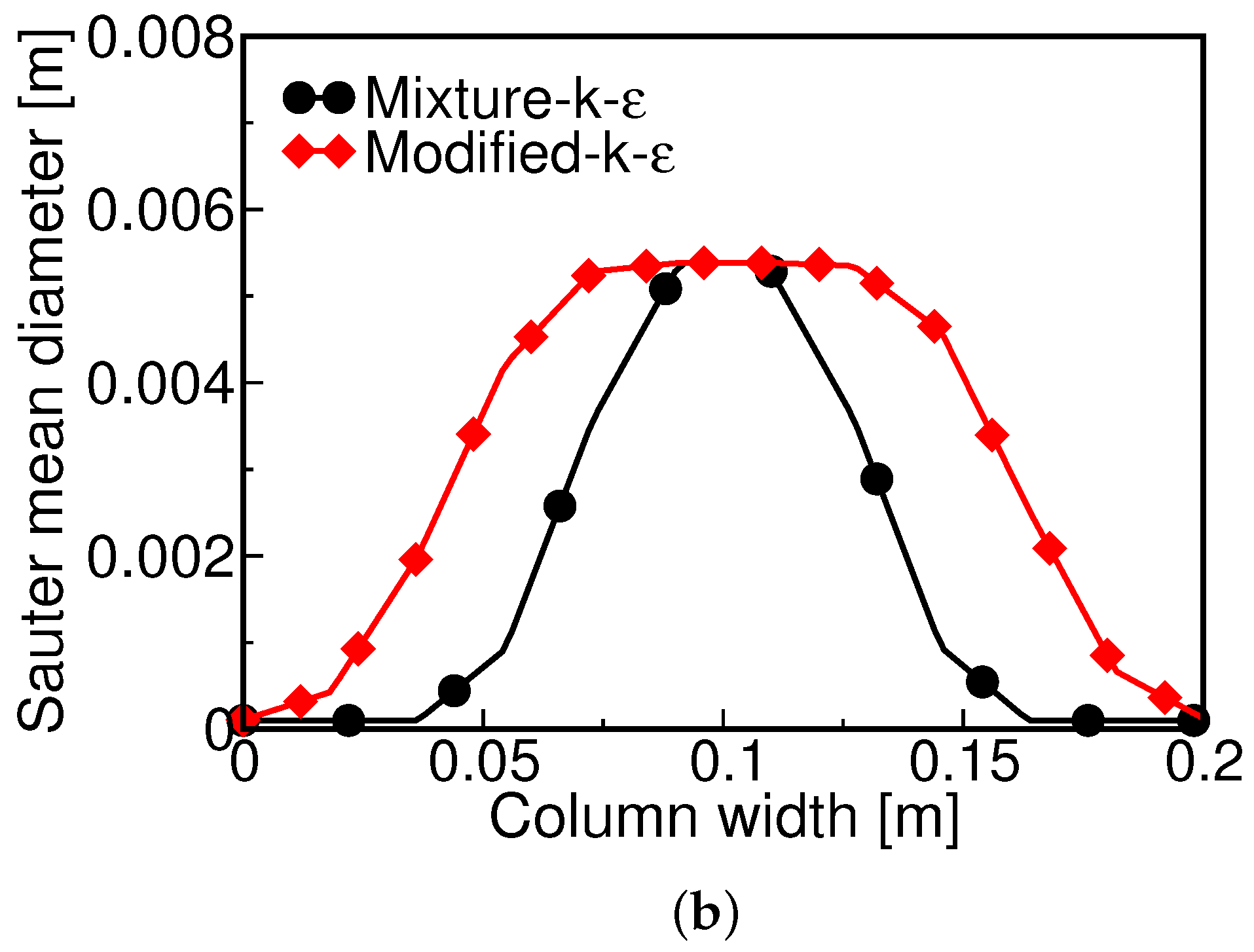
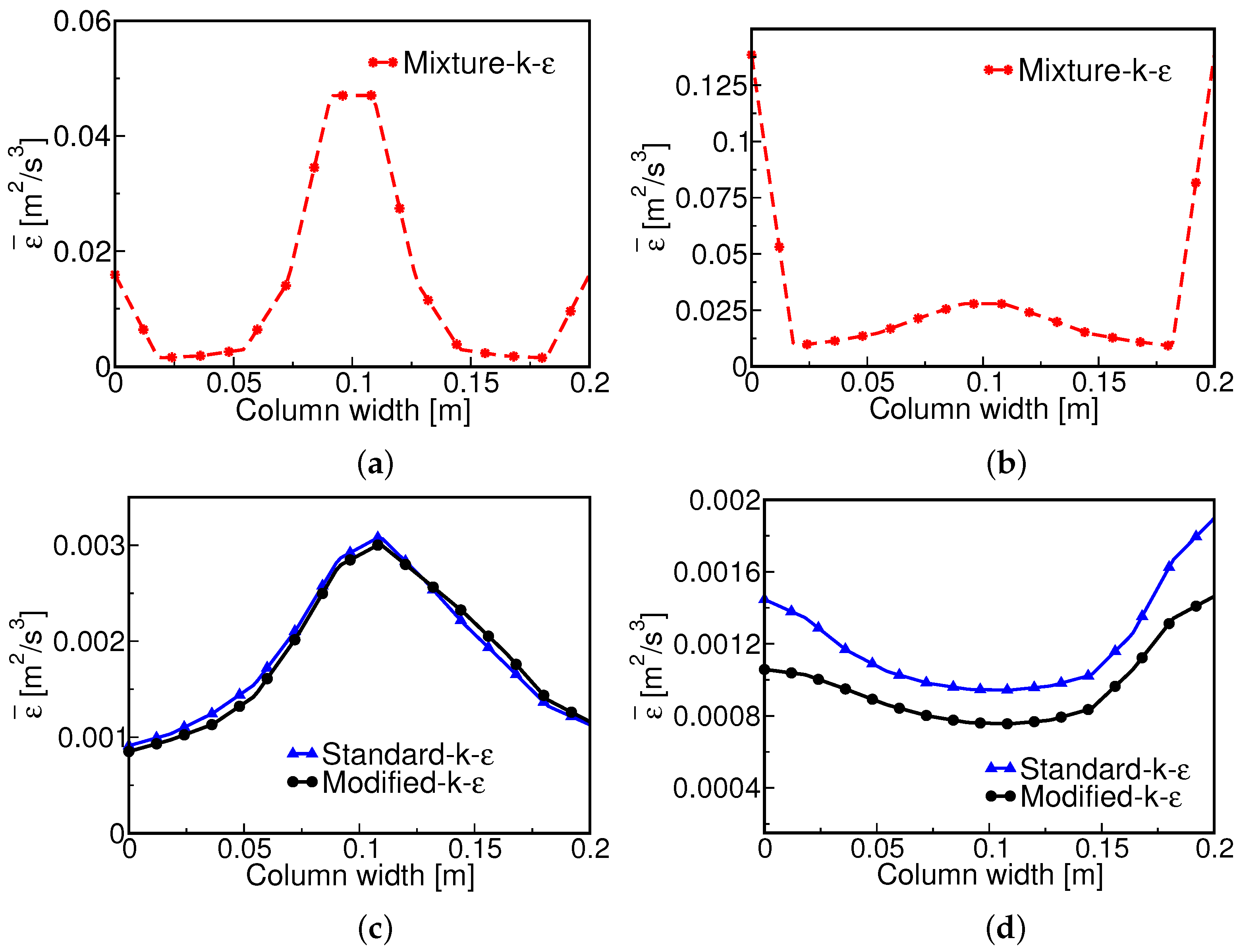
4.3. Influence of the Turbulence Model on the Hydrodynamics
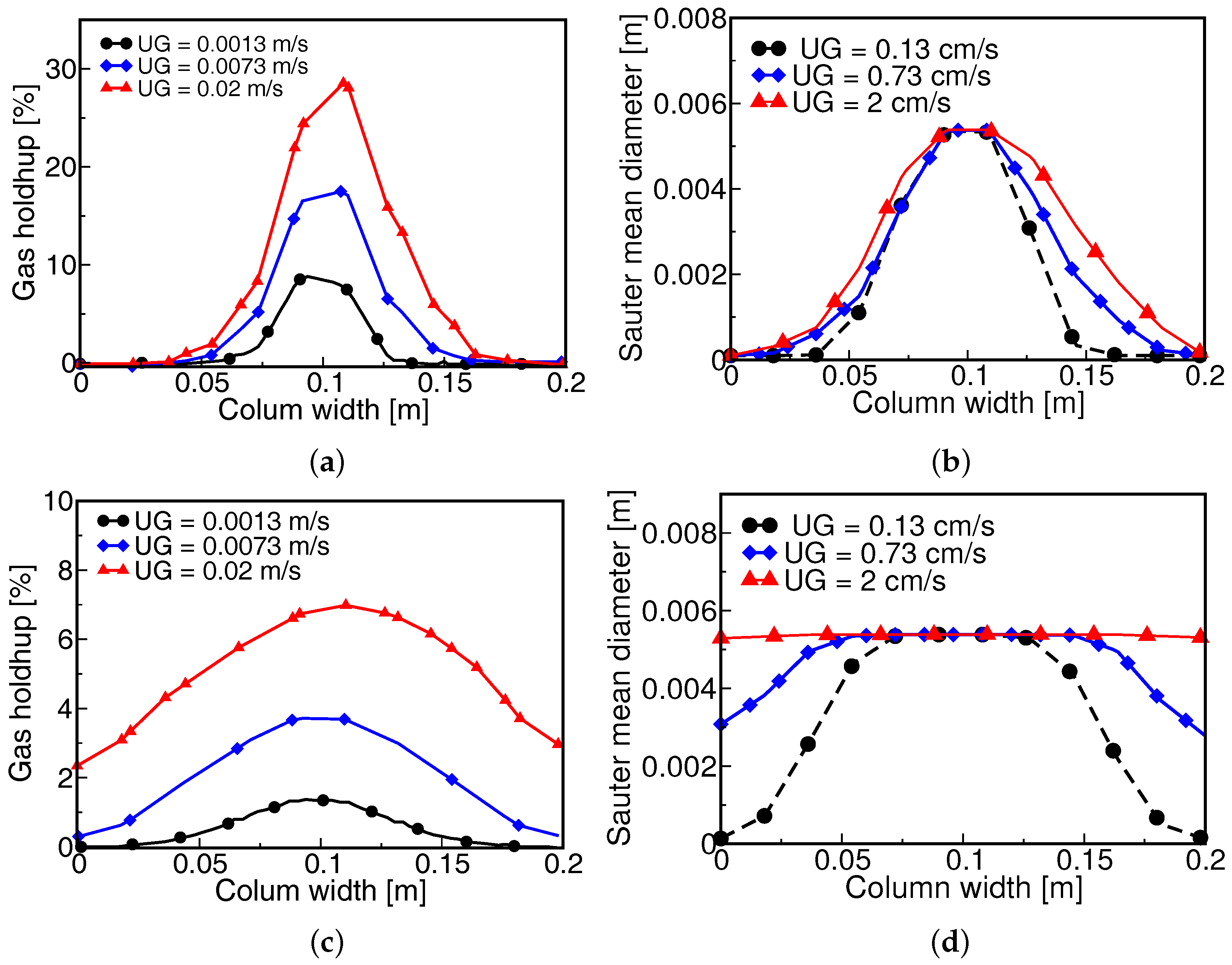
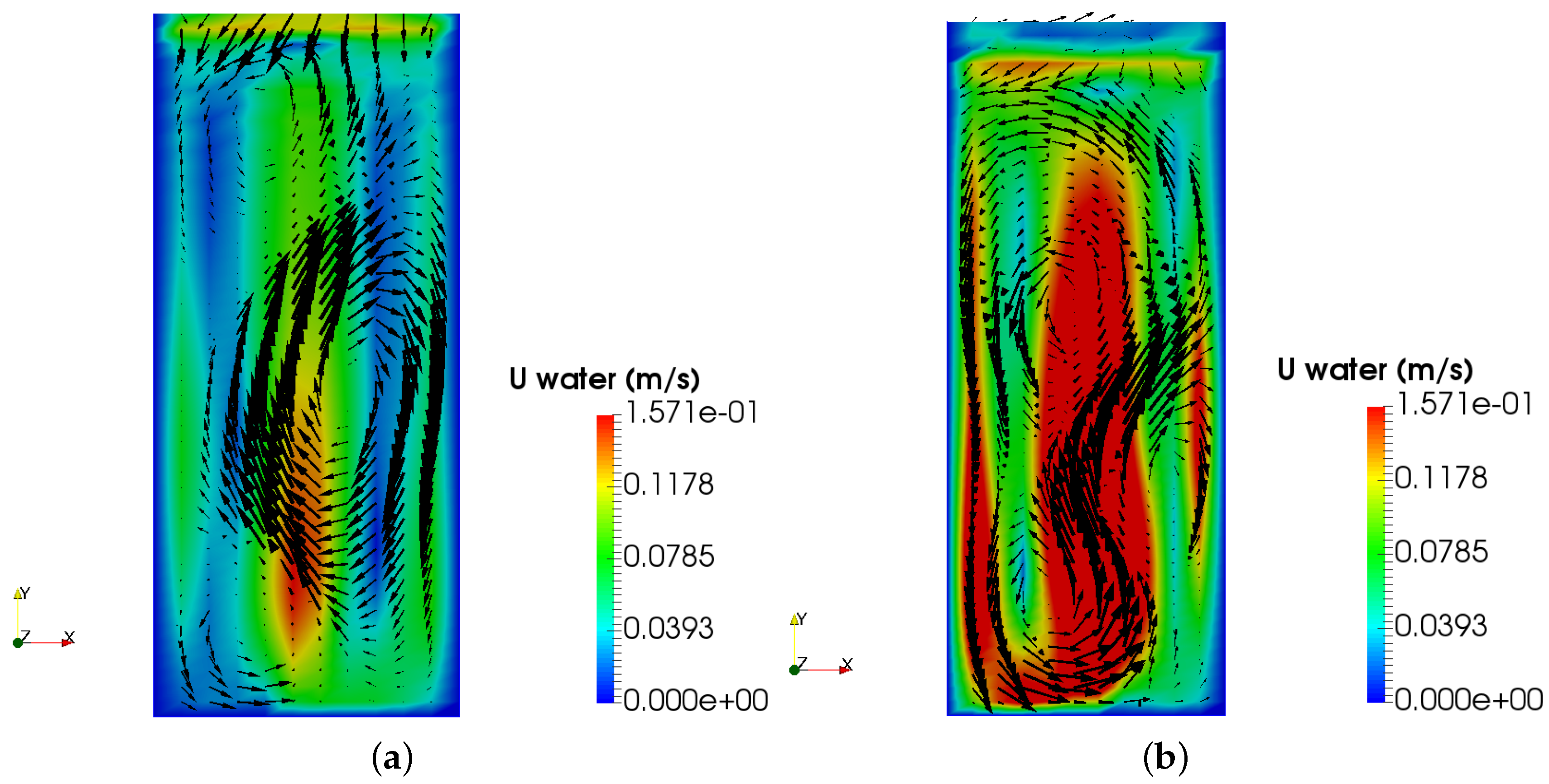
4.4. Influence of the Air Superficial Gas Velocity at Inlet on the Fluid Behavior
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Sauter mean diameter [m] | |
| G | gas |
| H | height of the cavity [m] |
| I | turbulence intensity |
| k | turbulent kinetic energy [m/s] |
| l | laminar |
| eddy size [m] | |
| L | liquid |
| characteristic length [m] | |
| friction velocity: | |
| mean velocity vector [m/s] | |
| W | column width [m] |
| w | water phase |
| dimensionless wall distance: | |
| Greek symbols | |
| phase volume fraction | |
| dissipation rate of turbulent kinetic energy [m/s] | |
| molecular kinematic viscosity [m/s] | |
| turbulent kinematic viscosity [m/s] | |
| specific mass [kg/m] | |
| surface tension [N/m] | |
| shear stress [kg/(m·s)] | |
| Acronyms | |
| CFL | Courant–Friedrichs–Lewy condition |
| LES | Large Eddy Simulation |
| PBM | Population Balance Model |
| PIMPLE | merged Piso-sIMPLE algorithm |
| QMOM | Quadrature Method of Moments |
| RSM | Reynolds Stress Model |
References
- Degaleesan, S.; Dudukovic, M.; Pan, Y. Experimental study of gas-induced liquid-flow structures in bubble columns. AIChE J. 2001, 47, 1913–1931. [Google Scholar] [CrossRef]
- Becker, S.; De Bie, H.; Sweeney, J. Dynamic flow behaviour in bubble columns. Chem. Eng. Sci. 1999, 54, 4929–4935. [Google Scholar] [CrossRef]
- Lain, S.; Broder, D.; Sommerfeld, M. Experimental and numerical studies of the hydrodynamics in a bubble column. Chem. Eng. Sci. 1999, 54, 4913–4920. [Google Scholar] [CrossRef]
- Kantarci, N.; Borak, F.; Ulgen, K. Bubble column reactors. Process Biochem. 2005, 40, 2263–2283. [Google Scholar] [CrossRef]
- Guédon, G.; Besagni, G.; Inzoli, F. Prediction of gas-liquid flow in an annular gap bubble column using a bi-dispersed Eulerian model. Chem. Eng. Sci. 2017, 161, 138–150. [Google Scholar] [CrossRef]
- Shnip, A.; Kolhatkar, R.; Swamy, D.; Joshi, J. Criteria for the transition from the homogenous to the heterogeneous regime in two-dimensional bubble column reactors. Int. J. Multiph. Flow 1992, 18, 705–726. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J. Mass transfer in bubble columns. Catal. Today 2003, 79–80, 67–75. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenheim, T.; Lucas, D. Computational fluid-dynamics modeling of the pseudo-homogeneous flow regime in large-scale bubble columns. Chem. Eng. Sci. 2016, 160, 144–160. [Google Scholar] [CrossRef]
- Vijayan, M.; Schlaberg, H.; Wang, S. Effects of sparger geometry on the mechanism of flow pattern transition in a bubble column. Chem. Eng. J. 2007, 130, 171–178. [Google Scholar] [CrossRef]
- Upadhyay, R.; Roy, S.; Pant, H. Benchmarking radioactive particle tracking (RPT) with Laser Doppler Anemometry (LDA). Int. J. Chem. React. Eng. 2012, 10. [Google Scholar] [CrossRef]
- Upadhyay, R.; Pant, H.; Roy, S. Liquid flow patterns in rectangular ait-water bubble column investigated with radioactive particle tracking. Chem. Eng. Sci. 2013, 96, 152–164. [Google Scholar] [CrossRef]
- Liu, Y.; Hinrichsen, O. Study on CFD-PBM turbulence closures based on k-ε and Reynolds stress models for heterogeneous bubble column flows. Comput. Fluids 2014, 105, 91–100. [Google Scholar] [CrossRef]
- Gupta, A.; Roy, S. Euler-euler simulation of bubbly flow in a rectangular bubble column: Experimental validation with radioactive particle tracking. Chem. Eng. J. 2013, 225, 818–836. [Google Scholar] [CrossRef]
- Marchisio, D.; Vigil, R.; Fox, R. Quadrature method of moments for aggregation-breakage processes. J. Colloid Interface Sci. 2003, 258, 322–334. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization ii—A moving pivot technique. Chem. Eng. Sci. 1996, 51, 1333–1342. [Google Scholar] [CrossRef]
- Smith, M.; Matsoukas, T. Constant number Monte Carlo simulation of population balances. Chem. Eng. Sci. 1998, 53, 1777–1786. [Google Scholar] [CrossRef]
- McGrow, R. Description of Aerosol Dynamics by the Quadrature Method Moments. Aerosol Sci. Technol. 1997, 27, 255–265. [Google Scholar] [CrossRef]
- Rong, F.; Marchisio, D.; Fox, R. Application of direct quadrature method of moments to polydisperse gas solid fluidized beds. Powder Technol. 2004, 139, 7–20. [Google Scholar]
- Aboulhasanzadeh, B.; Thomas, S.; Taeibi-Rahni, M.; Tryggvason, G. Multiscale computations of mass transfer from buoyant bubbles. Chem. Eng. Sci. 2012, 75, 456–467. [Google Scholar] [CrossRef]
- Tryggvason, G.; Dabiri, S.; Aboulhasanzadeh, B.; Lu, J. Multiscale considerations in direct numerical simulations of multiphase flows. Phys. Fluids 2013, 25, 031302. [Google Scholar] [CrossRef]
- Pfleger, D.; Gomes, S.; Gilbert, N.; Wagner, H.G. Hydrodynamic simulations of laboratory scale bubble columns fundamental studies of the Eulerian-Eulerian modeling approach. Chem. Eng. Sci. 1999, 54, 5091–5099. [Google Scholar] [CrossRef]
- Bannari, R.; Kerdouss, F.; Selma, B.; Bannari, A.; Proulx, P. Three-dimensional mathematical modeling of dispersed two-phase flow using class method of population balance in bubble columns. Comput. Chem. Eng. 2008, 32, 3224–3237. [Google Scholar] [CrossRef]
- Ekambara, K.; Dhotre, M. CFD simulation of bubble column. Nucl. Eng. Des. 2010, 240, 963–969. [Google Scholar] [CrossRef]
- Buwa, V.; Ranade, V. Characterization of gas-liquid flows in rectangular bubble columns using conductivity probes. Chem. Eng. Commun. 2005, 192, 1129–1150. [Google Scholar] [CrossRef]
- Murgan, I.; Bunea, F.; Ciocan, G.D. Experimental PIV and LIF characterization of a bubble column flow. Flow Meas. Instrum. 2017, 54, 224–235. [Google Scholar] [CrossRef]
- Borchers, O.; Busch, C.; Sokolichin, A.; Eigenberger, G. Applicability of the standard k-ε turbulence model to the dynamic simulation of bubble columns. Part II: Comparison of detailed experiments and flow simulations. Chem. Eng. Sci. 1999, 54, 5927–5935. [Google Scholar] [CrossRef]
- Mudde, R.F.; Simonin, O. Two- and three-dimensional simulations of a bubble plume using a two-fluid model. Chem. Eng. Sci. 1999, 54, 5061–5069. [Google Scholar] [CrossRef]
- Becker, S.; Sokolichin, A.; Eigenberger, G. Gas liquid flow in bubble columns and loop reactors: Part ii. Comparison of detailed experiments and flow simulations. Chem. Eng. Sci. 1994, 49, 5747–5762. [Google Scholar] [CrossRef]
- Van Thai, D.; Minier, J.; Simonin, O.; Freydier, P.; Olive, J. Multidimensional two-fluid model computation of turbulent dispersed two-phase flows. In Numerical Methods in Multiphase Flows; ASME: New York, NY, USA, 1994; Volume FED 185, pp. 277–291. [Google Scholar]
- Li, G.; Yang, X.; Dai, G. CFD simulation of effects of the configuration of gas distributors on gas-liquid flow and mixing in a bubble column. Chem. Eng. Sci. 2009, 64, 5104–5116. [Google Scholar] [CrossRef]
- Chen, J.; Li, F.; Degaleesan, S.; Gupta, P.; Al-Dahhan, M.; Dudukovic, M.; Toseland, B. Fluid dynamic parameters in bubble columns with internals. Chem. Eng. Sci. 1999, 54, 2187–2197. [Google Scholar] [CrossRef]
- Sato, Y.; Sadatomi, M.; Sekoguchi, K. Momentum and heat transfer in two-phase bubble flow theory. Int. J. Multiph. Flow 1975, 7, 167–177. [Google Scholar] [CrossRef]
- Kulkarni, A.; Ekambara, K.; Joshi, J. On the development of flow pattern in a bubble column reactor: Experiments and CFD. Chem. Eng. Sci. 2007, 62, 1049–1072. [Google Scholar] [CrossRef]
- Buwa, V.; Deo, D.; Ranade, V. Eulerian-lagrangian simulations of unsteady gas-liquid flows in bubble columns. Int. J. Multiph. Flow 2006, 32, 864–885. [Google Scholar] [CrossRef]
- Rampure, M.; Kulkarni, A.; Ranade, V. Hydrodynamics of bubble column reactors at high gas velocity: Experiments and computational fluid dynamics (CFD) simulations. Ind. Eng. Chem. Res. 2007, 46, 8431–8447. [Google Scholar] [CrossRef]
- Zhang, D.; Deen, N.; Kuipers, J. Numerical simulation of the dynamic flow behavior in a bubble column: A study of closures for turbulence and interface forces. Chem. Eng. Sci. 2006, 61, 7593–7608. [Google Scholar] [CrossRef]
- Deen, N. An Experimental and Computational Study of Fluid Dynamics in Gas-Liquid Chemical Reactor. Ph.D. Thesis, Aalborg University, Esbjerg, Denmark, 2001. [Google Scholar]
- Ma, T.; Ziegehein, T.; Lucas, D.; Frohlich, J. Large eddy simulation of the gas-liquid flow in a rectangular bubble column. Nucl. Eng. Des. 2016, 299, 146–153. [Google Scholar] [CrossRef]
- Luo, H.; Svendsen, H. Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Luo, H. Coalescence, Breakup and Liquid Circulation in Bubble Column Reactor. Ph.D. Thesis, The Norwegian Institute of Technology, Trondheim, Norway, 1993. [Google Scholar]
- Saffman, P.; Turner, J. On the collision of drops in turbulent clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
- Hagesather, L.; Jakobsen, H.; Hjarbo, K.; Svendsen, H. A coalescence and breakup module for implementation in CFD codes. Comput. Aided Chem. Eng. 2000, 8, 367–372. [Google Scholar]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics; Longman Scientific and Technical: Harlow, UK, 2011. [Google Scholar]
- Sato, Y.; Sekoguchi, K. Liquid velocity distribution in two-phase bubble flow. Int. J. Multiph. Flow 1975, 2, 79–95. [Google Scholar] [CrossRef]
- Tabib, M.V.; Roy, S.A.; Joshi, J.B. CFD simulation of bubble column—An analysis of interphase forces and turbulence models. Chem. Eng. J. 2008, 139, 589–614. [Google Scholar] [CrossRef]
- Pourtousi, M.; Sahu, J.; Ganesan, P. Effect of interfacial forces and turbulence models on predicting flow pattern inside the bubble column. Chem. Eng. Process. 2014, 75, 38–47. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, Z. A drag coefficient correlation. Z. Vereins Deutsch. Ing. 1935, 77, 318–320. [Google Scholar]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse migration of single bubbles in simple shear flows. Chem. Eng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Wellek, R.; Agrawal, A.; Skelland, A. Shape of liquid drops moving in liquid media. AIChE J. 1966, 12, 854–862. [Google Scholar] [CrossRef]
- Odar, F.; Hamilton, W. Forces on a sphere accelerating in a viscous fluid. J. Fluid Mech. 1964, 18, 302–314. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College of Science, Technology and Medicine, London, UK, 2002. [Google Scholar]
- Behzadi, A.; Issa, R.; Rusche, H. Modelling of dispersed bubble and droplet flow at high phase fractions. Chem. Eng. Sci. 2004, 59, 759–770. [Google Scholar] [CrossRef]
- Gordon, R. Error bounds in equilibrium statistical mechanics. J. Math. Phys. 1968, 9, 655–663. [Google Scholar] [CrossRef]
- Sack, R.; Doovan, A. An algorithm for Gaussian quadrature given modified moments. Numer. Math. 1971, 18, 465–478. [Google Scholar]
- Marchisio, D.; Fox, R. Computational Models for Polydisperse Particulate and Multiphase Systems; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Su, J.; Gu, Z.; Li, Y.; Feng, S.; Xu, Y. Solution of population balance equation quadrature method of moments with an adjustable factor. Chem. Eng. Sci. 2007, 62, 5897–5911. [Google Scholar] [CrossRef]
- Hinze, J. Turbulence; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Deju, L.; Cheung, S.; Yeoh, G.; Qi, F.; Tu, J. Comparative analysis of coalescence and breakage kernels in vertical gas-liquid flow. Can. J. Chem. Eng. 2015, 93, 1295–1309. [Google Scholar] [CrossRef]
- Sanya, J.; Marchisio, D.; Fox, R.; Kumar, D. On the comparison between population balance models for CFD simulation of bubble columns. Ind. Eng. Chem. Res. 2005, 44, 5063–5072. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Y.; Jin, Y. Population balance model gas-liquid flows: influence of bubble coalescence and breakup models. Ind. Eng. Chem. 2005, 44, 7540–7549. [Google Scholar] [CrossRef]
- AIAA. AIAA Guide for the Verification and Validation of Computational Fluid Dynamics Simulations; AIAA Report G-077-1988; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1998. [Google Scholar]
- Roache, P. Verification and Validation in Computational Science and Engineering; Hermosa Publishers: Socorro, NM, USA, 1998; pp. 358–359. [Google Scholar]
- Wilcox, D. Turbulence Modeling for CFD; DCW Industries Inc.: La Cañada Flintridge, CA, USA, 1993. [Google Scholar]
- Schetz, J.A.; Fuhs, A. Fundamentals of Fluid Mechanics; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- User Guide; OpenFOAM-User Guide Version 4.0; OpenFOAM Foundation: London, UK, 2016; pp. 140–141.
- Chieng, C.; Launder, B. On the calculation of turbulent heat transport downstream from an abrupt pipe expansion. J. Numer. Heat Transf. 1980, 3, 189–207. [Google Scholar]
- Craft, T.; Launder, B.; Suga, K. Development and application of a cubic eddy-viscosity model of turbulence. Int. J. Heat Fluid Flow 1996, 17, 108–115. [Google Scholar] [CrossRef]
- Issa, R. Solution of implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; Series in Computational Methods in Mechanics and Thermal Sciences; Taylor and Francis: Milton Park, Didcot, UK, 1980. [Google Scholar]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM(R), 4th ed.; Holzmann CFD: Leoben, Austria, 2016; pp. 108–128. [Google Scholar]
- OpenFOAM. OpenFOAM Guide The PIMPLE Algorithm in OpenFOAM; OpenFOAM: London, UK, 2016. [Google Scholar]
- Ziegenhein, T.; Rzehak, R.; Lucas, D. Transient simulation for large scale flow in bubble columns. Chem. Eng. Sci. 2015, 122, 1–13. [Google Scholar] [CrossRef]
- Milelli, M. A Numerical Analysis of Confined Turbulent Bubble Plume. Diss. ETH No. 14799. Ph.D. Thesis, Swiss Federal Institute of Technology Zurich, Zurich, Switzerland, 2002; pp. 4146–4157. [Google Scholar]
- Richardson, L. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with application to the stresses in a masonry dam. Philos. Trans. R. Soc. Lond. 1911, 210, 307–357. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar]
- Slater, J. Examining Spatial (Grid) Convergence. Available online: http://www.grc.nasa.gov/WWW/wind/valid/tutorial/spatconv.html (accessed on 5 January 2018).
- Lucas, D.; Prasser, H.M.; Manera, A. Influence of the lift force on the stability of a bubble column. Chem. Eng. Sci. 2005, 60, 3609–3619. [Google Scholar]
- Lucas, D.; Krepper, E.; Prasser, H.M.; Manera, A. Investigations on the stability of the flow characteristics in a bubble column. Chem. Eng. Technol. 2006, 29, 1066–1072. [Google Scholar] [CrossRef]
- Lucas, D.; Krepper, E.; Prasser, H.M. Use of models for lift, wall and turbulent dispersion forces acting on bubbles for poly-disperse flows. Chem. Eng. Sci. 2007, 62, 4146–4157. [Google Scholar] [CrossRef]
- Kulkarni, A. Lift force on bubbles in a bubble column reactor: Experimental analysis. Chem. Eng. Sci. 2008, 63, 1710–1723. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Bubble size distributions and shapes in annular gap bubble column. Exp. Therm. Fluid Sci. 2016, 74, 27–48. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T.; Dirk, L. The pseudo-homogeneous flow regime in large-scale bubble columns: Experimental benchmark and computational fluid dynamics modeling. Petroleum 2017. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. The effect of liquid phase properties on bubble column fluid dynamics: Gas holdup, flow regime transition, bubble size distributions and shapes, interfacial areas and foaming phenomena. Chem. Eng. Sci. 2017, 170, 270–296. [Google Scholar] [CrossRef]
- Prince, M.; Blanch, H. Bubble coalescence and break-up in air-sparged bubble columns. AIChE J. 1990, 36, 1485–1499. [Google Scholar] [CrossRef]
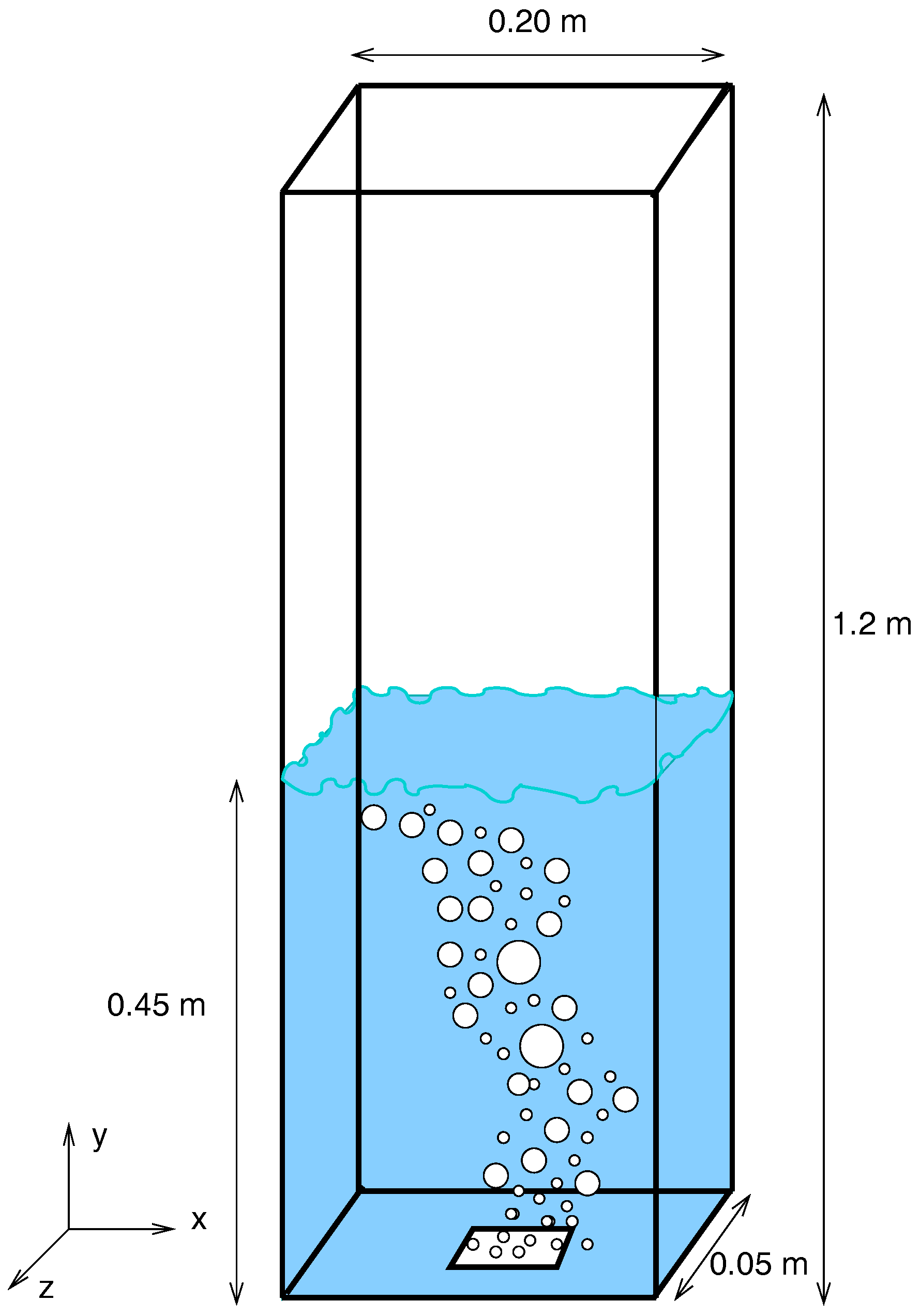
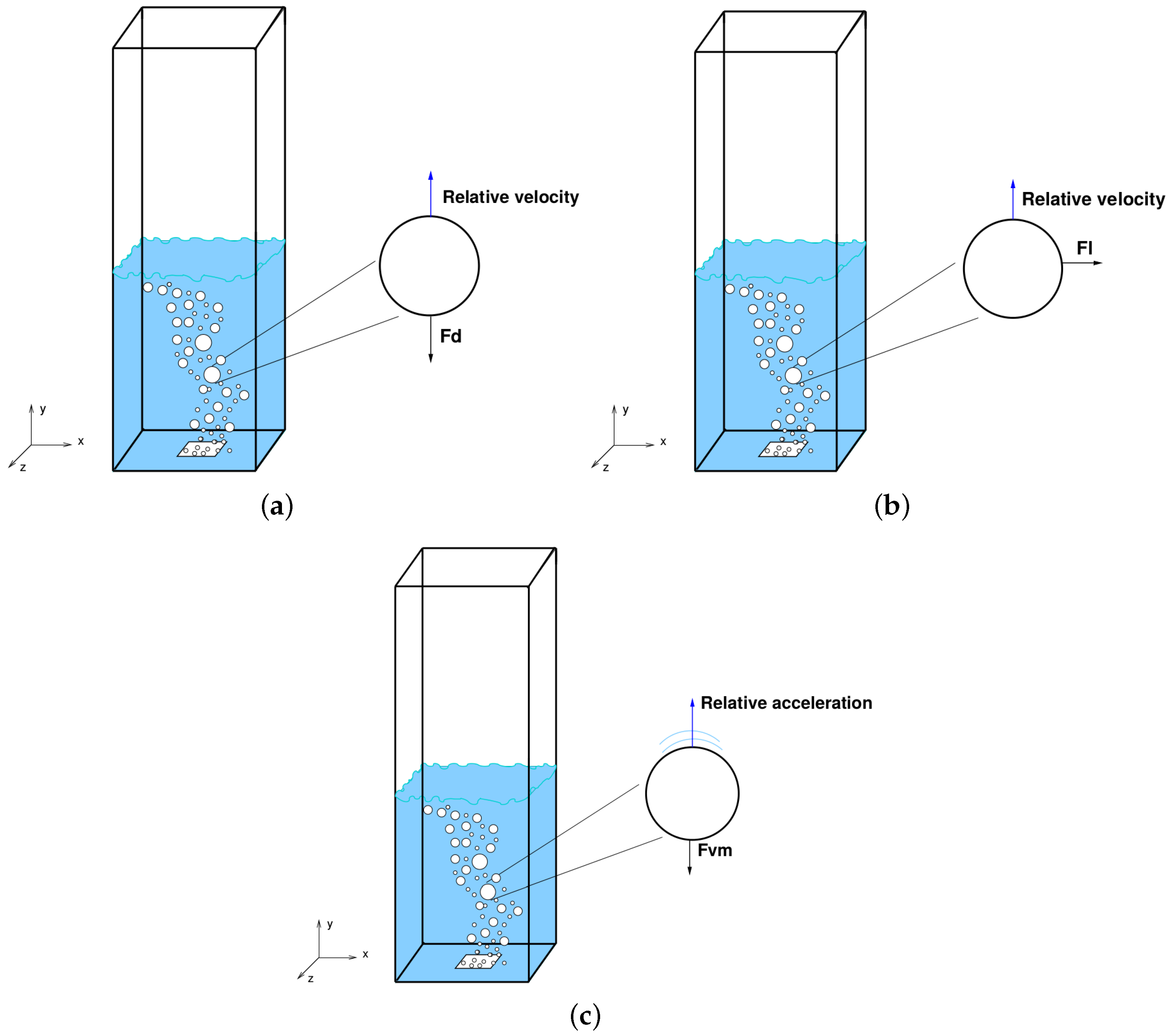


| Author | Geometry (in m) | Air Inlet | Main Data Provided |
|---|---|---|---|
| Pfleger et al. [22] | Rectangular (H = 1.20, FH = 0.45, W = 0.20, D = 0.05) | 0.0013 m/s | Turbulent kinetic energy × Column depth; Vertical fluid velocity × Column width |
| Buwa and Ranade [25] | Rectangular with same dimensions of [22] | 0.0016–0.12 m/s | Time-averaged gas hold-up × Column width |
| Upadhyay et al. [10] | Rectangular with same dimensions of Pfleger et al. [22] | 0.0013 m/s | Mean axial velocity × Column width; Total kinetic energy × Column width |
| Upadhyay et al. [11] | Rectangular with same dimensions of Pfleger et al. [22] | 0.0013, 0.00833, 0.0125 m/s | Mean z-component velocity × Column width; Turbulent kinetic energy × Column width |
| Becker et al. [2] | Rectangular (FH = 0.45, W = 0.20, D = 0.04), cylindrical (FH = 2.5, Di = 0.295) | 0.0017 m/s (rectangular column), 0.0015–0.01 m/s (cylindrical) | Axial velocity × Time, at different locations. |
| Murgan et al. [26] | Rectangular (H = 1.10, W = 0.30, D = 0.30) | 0.000133 m/s | Water and bubble velocity fields; Bubble ascension velocity; diameter and interfacial area of bubbles. |
| Borchers et al. [27] | Rectangular (H = 2.0, W = 0.50, D = 0.08) | 0.0000167 m/s, 0.000033 m/s | Time series of the vertical velocity component at different locations. |
| Author | Geometry | Interfacial Forces | Bubble Diameter | PBM Kernels | Turbulence Models | Remarks |
|---|---|---|---|---|---|---|
| Mude and Simonin [28] | Rectangular column [29]; = 0.20 m/s | D-Vm | 0.003 m | - | k- [30] and low-k- | No significant discrepancy on the results were found between the turbulence models investigated. |
| Li et al. [31] | Cylindrical column [32]; = 0.10 m/s; | D-L-Vm-WL-TD | Class method | Break: L-S; Coal: P-B | Modified-k- [33] | The configuration and location of gas distributor affects the overall gas hold-up and bubble sizes. |
| Ekambara and Dhotre [24] | Cylindrical column [34]; = 0.02 m/s | D-L-Vm | 0.006 m | - | k-, standard k-, RSM, RNG-k-, LES | RSM and LES provided a better prediction near the sparger, where the flow is more anisotropic. |
| Buwa et al. [35] | Rectangular column [22]; = 0.0016 m/s–0.12 m/s | D-L | 0.005 m | - | Standard k- | Satisfactory performance of Euler-Euler, with lift force, was found. |
| Liu and Hinrichsen [12] | Cylindrical column [36]; = 0.10 m/s–0.12 m/s | D-L | Class Method | Break: L-S; Coal: L | Modified-k- [33] and RSM | Tomyiana lift provided better agreement with experimental data, for both k- and RSM. |
| Zhang et al. [37] | Rectangular column [38]; = 0.0049 m/s | D-L-Vm | 0.004 m | - | Sub-grid scale model and different k- | The lift force strongly influences the bubble plume dynamics, and Tomiyana lift coefficient provided better results. |
| Bannari et al. [23] | Rectangular column [22]; = 0.0014 m/s and 0.0073 m/s | D-L-Vm | Class Method | Break: L-S; Coal: S-T and H | k- [28] | Good agreement with experimental data was found when using PBM for the bubble size. |
| Ma et al. [39] | Rectangular column [22]; = 0.0013 m/s | D-L-Vm | 0.002 m | - | LES | Good agreement with experimental data. |
| Interfacial Force | Model |
|---|---|
| Drag () | Schiller and Naumann [48] |
| Lift () | Tomiyama et al. [49] and Constant (0.14 and 0.5) |
| Virtual mass () | Constant (0.5) |
| Variable | Inlet | Outlet | Walls |
|---|---|---|---|
| k | Equation (36) | ||
| Equation (37) | |||
| p | |||
| UG (m/s) | Parameters Studied | Results |
|---|---|---|
| 0.0013 | Interfacial forces (Section 4.2) | Mean axial velocity (validation) |
| gas hold-up (validation) | ||
| 0.0013 and 0.0073 | Turbulence model (Section 4.3) | Mean axial velocity (UG = 0.0013 m/s) |
| profiles (UG = 0.0013 m/s) | ||
| profiles (UG = 0.0013 m/s) | ||
| gas hold-up (both UGs) | ||
| 0.0013, 0.0073 and 0.02 | Inlet gas velocity (Section 4.4) | gas hold-up profiles |
| profiles and fields | ||
| Water velocity fields |
| Mesh Index (i) | Number of Cells | ( m) | (m/s) | Normalized Grid Space |
|---|---|---|---|---|
| 1 | 11,800 | 108 | 0.0173 | 4 |
| 2 | 21,120 | 54 | 0.0168 | 2 |
| 3 | 42,240 | 27 | 0.0156 | 1 |
| r | p | ca | ||
|---|---|---|---|---|
| 2 | 1.26 | 2.6 | 6.4 | 1.028 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braga Vieira, C.; Litrico, G.; Askari, E.; Lemieux, G.; Proulx, P. Hydrodynamics of Bubble Columns: Turbulence and Population Balance Model. ChemEngineering 2018, 2, 12. https://doi.org/10.3390/chemengineering2010012
Braga Vieira C, Litrico G, Askari E, Lemieux G, Proulx P. Hydrodynamics of Bubble Columns: Turbulence and Population Balance Model. ChemEngineering. 2018; 2(1):12. https://doi.org/10.3390/chemengineering2010012
Chicago/Turabian StyleBraga Vieira, Camila, Giuliana Litrico, Ehsan Askari, Gabriel Lemieux, and Pierre Proulx. 2018. "Hydrodynamics of Bubble Columns: Turbulence and Population Balance Model" ChemEngineering 2, no. 1: 12. https://doi.org/10.3390/chemengineering2010012
APA StyleBraga Vieira, C., Litrico, G., Askari, E., Lemieux, G., & Proulx, P. (2018). Hydrodynamics of Bubble Columns: Turbulence and Population Balance Model. ChemEngineering, 2(1), 12. https://doi.org/10.3390/chemengineering2010012





