Are Stakeholders’ Opinions Redundant? †
Abstract
1. Introduction
2. Methodology
2.1. Random Generation of Weight Regimes
2.2. Data
2.3. Partial Ordering
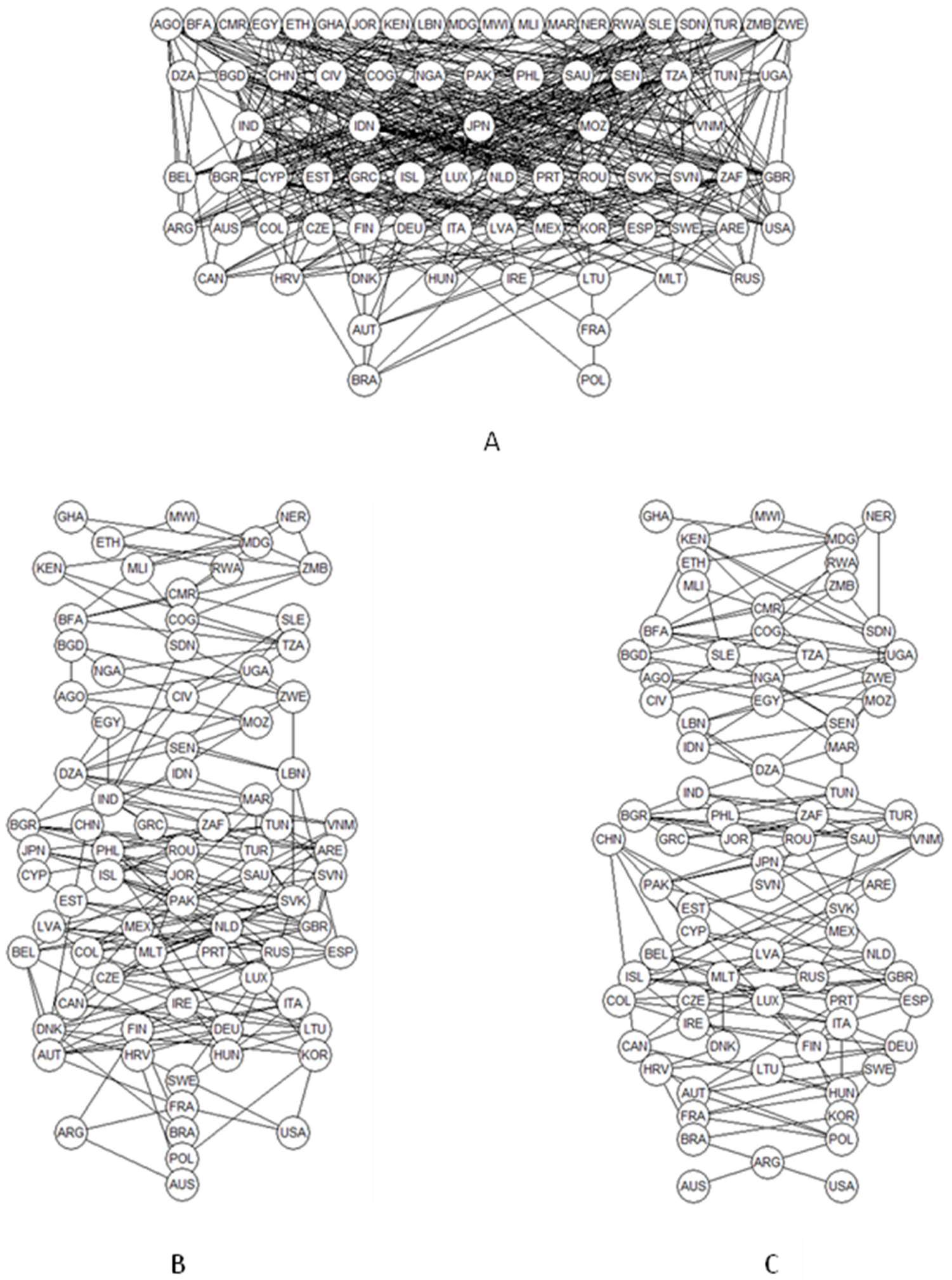
The Hasse Diagram
2.4. Generalized Linear Aggregation (GLA)
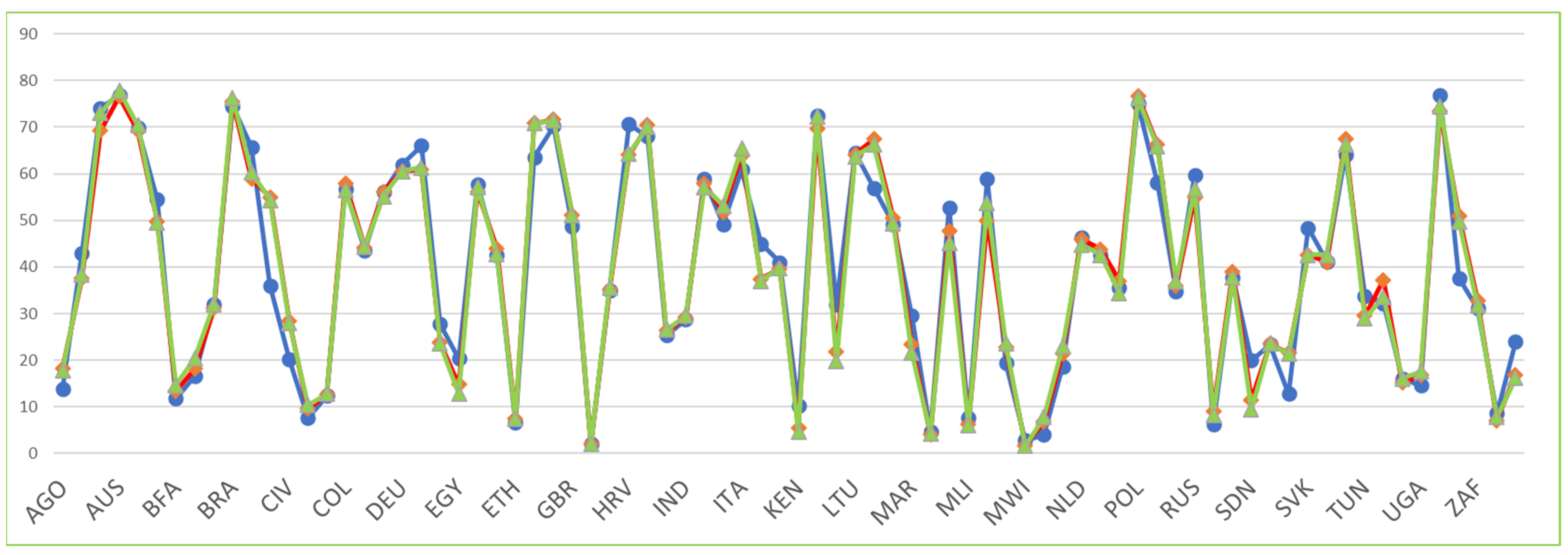
2.5. Average Ranks
2.6. Software
3. Results and Discussion
4. Conclusions and Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Munda, G. Social Multi-Criteria Evaluation for a Sustainable Economy; Springer: Berlin/Heidelberg, Germany, 2008; Available online: https://www.springer.com/la/book/9783540737025 (accessed on 12 September 2023).
- Bruggemann, R.; Patil, G.P. Ranking and Prioritization for Multi-Indicator Systems—Introduction to Partial Order Applications; Springer: New York, NY, USA, 2011; Available online: https://www.springer.com/gp/book/9781441984760 (accessed on 12 September 2023).
- Smith, L.W. Stakeholder Analysis: A Pivotal Practice of Successful Projects. In Proceedings of the Project Management Institute Annual Seminars & Symposium, Houston, TX, USA, 7–16 September 2000; Project Management Institute: Newtown Square, PA, USA, 2000. Available online: https://www.pmi.org/learning/library/stakeholder-analysis-pivotal-practice-projects-8905 (accessed on 12 December 2023).
- Stakeholder Influence. Available online: https://www.stakeholdermap.com/stakeholder-influence.html (accessed on 1 December 2023).
- Lienert, J. Stakeholder Importance and Influence. 2020. Available online: https://sswm.info/es/humanitarian-crises/prolonged-encampments/planning-process-tools/exploring-tools/stakeholder-importance-and-influence (accessed on 1 December 2023).
- Greany, K. 4 Fresh Strategies to Transform Your Stakeholder Relationships and Influence Change. eLearning Industry. 2021. Available online: https://elearningindustry.com/fresh-strategies-transform-stakeholder-relationships-and-influence-change (accessed on 1 December 2023).
- Carlsen, L.; Bruggemann, R. Partial Order as Decision Support Between Statistics and Multicriteria Decision Analyses. Standards 2022, 2, 306–328. [Google Scholar] [CrossRef]
- Carlsen, L.; Bruggemann, R. Combining different stakeholders’ opinions in multi-criteria decision analyses applying partial order methodology. Standards 2022, 2, 503–521. [Google Scholar] [CrossRef]
- Food Sustainability Index. See also the Associated Workbook: Food_Sustainability_Index_2021.xlsm. 2021. Available online: https://impact.economist.com/projects/foodsustainability/ (accessed on 12 September 2023).
- Nardo, M.; Saisana, M.; Saltelli, A.; Tarantola, S.; Hoffman, A.; Giovannini, E. Handbook on Constructing Composite Indicators: Methodology and User Guide; OECD: Ispra, Italy, 2008; Available online: https://www.oecd.org/sdd/42495745.pdf (accessed on 12 September 2023).
- Brüggemann, R.; Carlsen, L. Introduction to partial order theory exemplified by the Evaluation of Sampling Sites. In Partial Order in Environmental Sciences and Chemistry; Bruggemann, R., Carlsen, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 61–110. [Google Scholar] [CrossRef]
- Brüggemann, R.; Carlsen, L. An Improved Estimation of Averaged Ranks of Partial Orders. MATCH Commun. Math. Comput. Chem. 2011, 65, 383–414. [Google Scholar]
- Bruggemann, R.; Annoni, P. Average Heights in Partially Ordered Sets. MATCH Commun. Math. Comput. Chem. 2014, 71, 117–142. [Google Scholar]
- Bruggemann, R.; Carlsen, L.; Voigt, K.; Wieland, R. PyHasse Software for Partial Order Analysis. In Multi-Indicator Systems and Modelling in Partial Order; Bruggemann, R., Carlsen, L., Wittmann, J., Eds.; Springer: New York, NY, USA, 2014; pp. 389–423. [Google Scholar] [CrossRef]
| Indicator | ||
|---|---|---|
| r1 | Pct. Of sugar in diets | Percent sugar in the diet |
| r2 | Meat consumption levels | The difference in meat consumption (g/capita(day) from the daily recommended intake (90 g/capita/day) |
| r3 | Saturated fat consumption | g/capita/day |
| r4 | Salt consumption | Average g/day sodium consumption |
| ID | r1 | r2 | r3 | r4 | |
|---|---|---|---|---|---|
| Algeria | DZA | 47.3 | 86.9 | 91 | 24.9 |
| Angola | AGO | 65.8 | 91.2 | 57.3 | 72.9 |
| Argentina | ARG | 12.2 | 7.4 | 14.9 | 59.2 |
| Australia | AUS | 13.3 | 11.4 | 6 | 48 |
| Austria | AUT | 22.4 | 41.1 | 28.3 | 33.8 |
| Bangladesh | BGD | 84.2 | 69.4 | 88.6 | 44.8 |
| Belgium | BEL | 15.7 | 76.9 | 31.9 | 47.2 |
| Brazil | BRA | 21.7 | 26.8 | 26.2 | 29.5 |
| Bulgaria | BGR | 40.9 | 70.8 | 69.4 | 42.6 |
| Burkina Faso | BFA | 78.2 | 79.4 | 80.8 | 62.5 |
| Cameroon | CMR | 74.9 | 78.2 | 79.8 | 83.6 |
| Canada | CAN | 19.6 | 35.3 | 48.8 | 40.2 |
| China | CHN | 84.6 | 68.2 | 15 | 10.2 |
| Colombia | COL | 27.5 | 69.4 | 30.5 | 30 |
| Cote d’Ivoire | CIV | 77.2 | 76.1 | 48 | 64.6 |
| Croatia | HRV | 4.1 | 48.7 | 40.2 | 40.2 |
| Cyprus | CYP | 46.8 | 52.2 | 58.1 | 30.8 |
| Czech Republic | CZE | 33.9 | 44.3 | 43.7 | 33 |
| Dem. Rep. of Congo | COG | 69.4 | 80.1 | 79.8 | 74.8 |
| Denmark | DNK | 7.5 | 49.2 | 29.8 | 52 |
| Egypt | EGY | 43.8 | 99.1 | 90.8 | 41 |
| Estonia | EST | 46.9 | 60.7 | 48 | 33.8 |
| Ethiopia | ETH | 77.5 | 72.5 | 94.3 | 78.8 |
| Finland | FIN | 40.7 | 50.6 | 0 | 36.5 |
| France | FRA | 25.4 | 49.6 | 8.3 | 38.6 |
| Germany | DEU | 22.6 | 49.9 | 26.1 | 44.8 |
| Ghana | GHA | 78 | 81.7 | 95.6 | 76.7 |
| Greece | GRC | 45.9 | 56.1 | 71.2 | 38.6 |
| Hungary | HUN | 31.2 | 44.1 | 25.8 | 26.3 |
| India | IND | 45.5 | 69.2 | 83.4 | 39.9 |
| Indonesia | IDN | 56.8 | 78.5 | 73.1 | 49.6 |
| Ireland | IRE | 25.4 | 50.8 | 33.9 | 39.4 |
| Israel | ISL | 53.8 | 28.2 | 43.9 | 38.1 |
| Italy | ITA | 42.3 | 46.6 | 31.4 | 21.2 |
| Japan | JPN | 41.9 | 82.1 | 77 | 8.6 |
| Jordan | JOR | 15.8 | 99.8 | 64.8 | 29 |
| Kenya | KEN | 49.6 | 82.1 | 90.1 | 100 |
| Latvia | LVA | 40.8 | 58.3 | 50.9 | 27.3 |
| Lebanon | LBN | 7.3 | 98.3 | 88.6 | 55.8 |
| Lithuania | LTU | 28 | 44.3 | 33.9 | 30.6 |
| Luxembourg | LUX | 49.1 | 46.6 | 11.1 | 30.6 |
| Madagascar | MDG | 74.2 | 79.5 | 94.1 | 80.7 |
| Malawi | MWI | 68.6 | 78.8 | 95.5 | 95.2 |
| Mali | MLI | 77.2 | 88 | 97.6 | 55.2 |
| Malta | MLT | 16.9 | 50.9 | 63.6 | 29.8 |
| Mexico | MEX | 10.2 | 60.6 | 35.2 | 65.7 |
| Morocco | MAR | 35.9 | 100 | 88.1 | 24.1 |
| Mozambique | MOZ | 60.2 | 75.4 | 60.5 | 79.6 |
| Netherlands | NLD | 32.3 | 60.7 | 34.7 | 50.7 |
| Niger | NER | 100 | 74.3 | 92.4 | 61.4 |
| Nigeria | NGA | 74 | 73 | 69.4 | 64.1 |
| Pakistan | PAK | 37.8 | 82.8 | 41.1 | 34.9 |
| Philippines | PHL | 43.7 | 96.8 | 48.2 | 24.7 |
| Poland | POL | 18.7 | 39 | 7.2 | 36.7 |
| Portugal | PRT | 52.3 | 32 | 30.4 | 26 |
| Romania | ROU | 50.4 | 65.5 | 63.8 | 29.2 |
| Russia | RUS | 19.8 | 53.4 | 57.9 | 27.9 |
| Rwanda | RWA | 70.4 | 73.3 | 80.4 | 96.8 |
| Saudi Arabia | SAU | 42.4 | 87.3 | 22.3 | 53.9 |
| Senegal | SEN | 54.2 | 81.4 | 74.8 | 55.2 |
| Sierra Leone | SLE | 84.9 | 74.4 | 52 | 72.4 |
| Slovakia | SVK | 29.1 | 73.9 | 65.1 | 26.3 |
| Slovenia | SVN | 45.3 | 60.2 | 64.1 | 26.3 |
| South Africa | ZAF | 30.4 | 66.4 | 57 | 73.2 |
| South Korea | KOR | 31.3 | 58.5 | 33.1 | 0 |
| Spain | ESP | 39 | 27.4 | 54.9 | 31.9 |
| Sudan | SDN | 23.8 | 88.3 | 95.5 | 76.1 |
| Sweden | SWE | 27.8 | 56.2 | 4.1 | 41.8 |
| Tanzania | TZA | 70 | 76.6 | 82.1 | 66 |
| Tunisia | TUN | 36 | 96.5 | 80.5 | 20.9 |
| Turkey | TUR | 46.9 | 94.1 | 43.4 | 29.8 |
| United Arab Emirates | ARE | 29.3 | 61.8 | 68.1 | 41.3 |
| Uganda | UGA | 62.7 | 78 | 69.2 | 83.1 |
| United Kingdom | GBR | 40.9 | 51.6 | 31.7 | 42.9 |
| United States | USA | 0 | 0 | 41.5 | 43.2 |
| Vietnam | VNM | 75.6 | 65.2 | 24.6 | 16.6 |
| Zambia | ZMB | 66 | 85.7 | 87.1 | 78.8 |
| Zimbabwe | ZWE | 27.9 | 85.3 | 100 | 56.6 |
| Indicators | Expert | Political | Outcome | Uniform |
|---|---|---|---|---|
| i1: Percentage of sugar in diets | 0.375 | 0.143 | 0.400 | 0.250 |
| i2: Meat consumption levels | 0.250 | 0.286 | 0.200 | 0.250 |
| i3: Saturated fat consumption | 0.163 | 0.286 | 0.200 | 0.250 |
| i4: Salt consumption | 0.213 | 0.286 | 0.200 | 0.250 |
| ID | Rank_a | Rank_b | Rank_c | Rank_d | Rank_e | Average | Std |
|---|---|---|---|---|---|---|---|
| AGO | 19 | 16 | 16 | 17 | 13.5 | 16.3 | 1.987 |
| ARE | 42 | 45 | 40 | 38 | 42 | 41.4 | 2.608 |
| ARG | 75 | 76 | 75 | 72 | 76 | 74.8 | 1.643 |
| AUS | 78 | 78 | 78 | 76 | 77.5 | 77.5 | 0.866 |
| AUT | 69 | 71 | 72 | 70 | 73 | 71 | 1.581 |
| BEL | 56.5 | 51 | 50 | 43 | 51 | 50.3 | 4.817 |
| BFA | 11 | 9 | 11 | 13 | 12 | 11.2 | 1.483 |
| BGD | 13 | 12 | 13 | 20 | 21 | 15.8 | 4.324 |
| BGR | 29 | 32 | 32 | 29 | 32 | 30.8 | 1.643 |
| BRA | 74 | 74 | 74 | 75 | 74 | 74.2 | 0.447 |
| CAN | 61 | 66 | 68 | 60 | 64.5 | 63.9 | 3.362 |
| CHN | 43 | 36 | 46 | 55 | 44 | 44.8 | 6.834 |
| CIV | 23 | 27.5 | 25 | 21 | 23 | 23.9 | 2.460 |
| CMR | 9 | 8 | 8 | 7 | 10 | 8.4 | 1.140 |
| COG | 12 | 13 | 12 | 11 | 11 | 11.8 | 0.837 |
| COL | 60 | 55 | 52 | 57 | 53 | 55.4 | 3.209 |
| CYP | 37 | 46.5 | 47 | 45 | 47 | 44.5 | 4.272 |
| CZE | 54 | 54 | 58 | 58 | 56 | 56 | 2.000 |
| DEU | 64 | 65 | 59 | 53 | 59 | 60 | 4.796 |
| DNK | 66 | 72 | 67 | 56 | 66 | 65.4 | 5.814 |
| DZA | 26 | 21 | 24 | 30 | 28 | 25.8 | 3.493 |
| EGY | 21 | 11 | 15 | 24 | 17 | 17.6 | 5.079 |
| ESP | 52 | 60 | 62 | 61 | 61 | 59.2 | 4.087 |
| EST | 45 | 46.5 | 44 | 44 | 46 | 45.1 | 1.140 |
| ETH | 5 | 6 | 7 | 5.5 | 9 | 6.5 | 1.581 |
| FIN | 68 | 67 | 64 | 63 | 67 | 65.8 | 2.168 |
| FRA | 72 | 73 | 73 | 68 | 71 | 71.4 | 2.074 |
| GBR | 51 | 52 | 51 | 47 | 52 | 50.6 | 2.074 |
| GHA | 1.5 | 2 | 1 | 5.5 | 2 | 2.4 | 1.782 |
| GRC | 31 | 38 | 37 | 33 | 36 | 35 | 2.915 |
| HRV | 71 | 70 | 70 | 67 | 69 | 69.4 | 1.517 |
| HUN | 67 | 68 | 71 | 73 | 72 | 70.2 | 2.588 |
| IDN | 25 | 25 | 27 | 27 | 26 | 26 | 1.000 |
| IND | 27 | 29 | 30 | 28 | 30 | 28.8 | 1.304 |
| IRE | 59 | 62 | 57 | 54 | 58 | 58 | 2.915 |
| ISL | 44 | 50 | 53 | 48 | 54 | 49.8 | 4.025 |
| ITA | 62 | 57 | 60 | 71 | 60 | 62 | 5.339 |
| JOR | 48 | 43 | 38 | 40 | 39 | 41.6 | 4.037 |
| JPN | 36 | 33 | 34 | 51 | 38 | 38.4 | 7.301 |
| KEN | 10 | 14 | 9 | 4 | 5 | 8.4 | 4.037 |
| KOR | 73 | 63 | 69 | 77 | 70 | 70.4 | 5.177 |
| LBN | 33 | 30 | 28 | 26 | 25 | 28.4 | 3.209 |
| LTU | 65 | 64 | 65 | 66 | 64.5 | 64.9 | 0.742 |
| LUX | 63 | 61 | 61 | 64 | 62 | 62.2 | 1.304 |
| LVA | 49 | 48 | 49 | 52 | 49 | 49.4 | 1.517 |
| MAR | 28 | 18 | 22 | 32 | 27 | 25.4 | 5.459 |
| MDG | 4 | 4.5 | 3 | 3 | 3 | 3.5 | 0.707 |
| MEX | 53 | 58 | 54 | 37 | 50 | 50.4 | 8.019 |
| MLI | 7 | 3 | 4.5 | 12 | 6 | 6.5 | 3.428 |
| MLT | 56.5 | 56 | 55 | 59 | 55 | 56.3 | 1.643 |
| MOZ | 20 | 27.5 | 26 | 18 | 20 | 22.3 | 4.177 |
| MWI | 1.5 | 4.5 | 2 | 1 | 1 | 2 | 1.458 |
| NER | 3 | 1 | 4.5 | 9 | 8 | 5.1 | 3.362 |
| NGA | 18 | 19.5 | 19 | 19 | 19 | 18.9 | 0.548 |
| NLD | 50 | 49 | 48 | 41 | 48 | 47.2 | 3.564 |
| PAK | 46 | 42 | 41 | 42 | 40 | 42.2 | 2.280 |
| PHL | 38 | 34 | 31 | 39 | 34 | 35.2 | 3.271 |
| POL | 76 | 75 | 76 | 74 | 75 | 75.2 | 0.837 |
| PRT | 55 | 59 | 66 | 69 | 68 | 63.4 | 6.107 |
| ROU | 34 | 35 | 36 | 35 | 35 | 35 | 0.707 |
| RUS | 58 | 53 | 56 | 65 | 57 | 57.8 | 4.438 |
| RWA | 6 | 10 | 10 | 2 | 7 | 7 | 3.317 |
| SAU | 39 | 39 | 39 | 31 | 37 | 37 | 3.464 |
| SDN | 17 | 24 | 18 | 15 | 16 | 18 | 3.536 |
| SEN | 24 | 22 | 23 | 23 | 22 | 22.8 | 0.837 |
| SLE | 15 | 17 | 20 | 14 | 18 | 16.8 | 2.387 |
| SVK | 47 | 44 | 43 | 50 | 45 | 45.8 | 2.775 |
| SVN | 41 | 41 | 42 | 46 | 41 | 42.2 | 2.168 |
| SWE | 70 | 69 | 63 | 62 | 63 | 65.4 | 3.782 |
| TUN | 32 | 26 | 29 | 36 | 29 | 30.4 | 3.782 |
| TUR | 35 | 31 | 33 | 34 | 33 | 33.2 | 1.483 |
| TZA | 14 | 15 | 14 | 16 | 15 | 14.8 | 0.837 |
| UGA | 16 | 19.5 | 17 | 10 | 13.5 | 15.2 | 3.616 |
| USA | 77 | 77 | 77 | 78 | 77.5 | 77.3 | 0.447 |
| VNM | 40 | 40 | 45 | 49 | 43 | 43.4 | 3.782 |
| ZAF | 30 | 37 | 35 | 25 | 31 | 31.6 | 4.669 |
| ZMB | 8 | 7 | 6 | 8 | 4 | 6.6 | 1.673 |
| ZWE | 22 | 23 | 21 | 22 | 24 | 22.4 | 1.140 |
| Indicators: | R1 | R2 | R3 | R4 |
|---|---|---|---|---|
| i1: Percentage of sugar in diets | 0.193 | 0.165 | 0.352 | 0.29 |
| i2: Meat consumption levels | 0.494 | 0.044 | 0.167 | 0.294 |
| i3: Saturated fat consumption | 0.265 | 0.258 | 0.29 | 0.186 |
| i4: Salt consumption | 0.445 | 0.087 | 0.229 | 0.24 |
| Objects | Average | Std | [8] |
|---|---|---|---|
| Top 10 | |||
| MWI | 2 | 1.458 | MWI |
| GHA | 2.4 | 1.782 | GHA |
| MDG | 3.5 | 0.707 | MDG |
| NER | 5.1 | 3.362 | NER |
| ETH | 6.5 | 1.581 | ETH |
| MLI | 6.5 | 3.428 | RWA |
| ZMB | 6.6 | 1.673 | KEN |
| RWA | 7 | 3.317 | MLI |
| CMR | 8.4 | 1.140 | ZMB |
| KEN | 8.4 | 4.037 | CMR |
| Bottom 10 | |||
| HRV | 69.4 | 1.517 | HUN |
| HUN | 70.2 | 2.588 | HRV |
| KOR | 70.4 | 5.177 | AUT |
| AUT | 71 | 1.581 | FRA |
| FRA | 71.4 | 2.074 | KOR |
| BRA | 74.2 | 0.447 | BRA |
| ARG | 74.8 | 1.643 | POL |
| POL | 75.2 | 0.837 | ARG |
| USA | 77.3 | 0.447 | AUS |
| AUS | 77.5 | 0.866 | USA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carlsen, L. Are Stakeholders’ Opinions Redundant? Standards 2024, 4, 39-51. https://doi.org/10.3390/standards4020003
Carlsen L. Are Stakeholders’ Opinions Redundant? Standards. 2024; 4(2):39-51. https://doi.org/10.3390/standards4020003
Chicago/Turabian StyleCarlsen, Lars. 2024. "Are Stakeholders’ Opinions Redundant?" Standards 4, no. 2: 39-51. https://doi.org/10.3390/standards4020003
APA StyleCarlsen, L. (2024). Are Stakeholders’ Opinions Redundant? Standards, 4(2), 39-51. https://doi.org/10.3390/standards4020003






