Genetic Algorithms for Interior Comparative Optimization of Standard BCS Parameters in Selected Superconductors and High-Temperature Superconductors
Abstract
1. Introduction
- K: Constant parameter. Range specific for every element.
- Mi: Atomic mass (AMU) of any element isotope of (n) isotopes.
- α: Constant parameter. Range specific for every element.
- TC: Critical temperature (K (usually) or C). Range specific for every element isotopes.
- i: Corresponding isotope for every element.
- Jα (u): Functions with regularization parameter alpha.
- R: Real space.
- u: Searched parameter solution.
- A: Model matrix vector data.
- K: Constant parameter matrix. Range specific for every element.
- α: Constant parameter. Range specific for every element.
- α1: Constant parameter. Tikhonov regularization parameter.
- ‖ • ‖2: L2 Norm (at algorithm power 2).
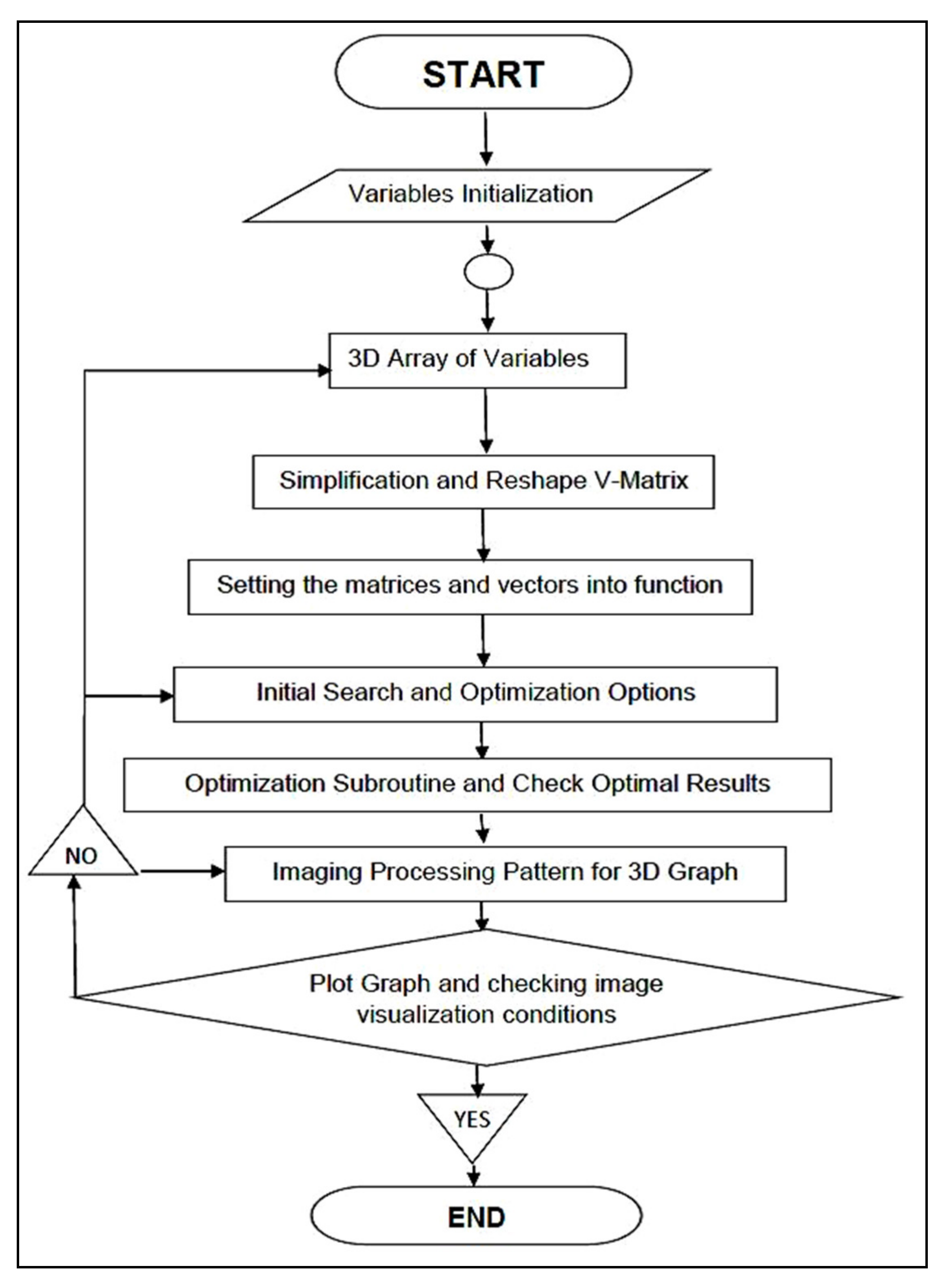
2. Mathematical and Computational Methods
2.1. Numerical Data for Chrome and HTSC Hg-Cuprates
2.2. Mathematical Techniques and Inverse Least Squares Algorithms for Optimization Methods
- K: Constant parameter. Range specific for every element.
- Mi: Atomic mass (AMU) of any element isotope of (n) isotopes.
- α: Constant parameter. Range specific for every element.
- TC: Critical temperature (K (usually) or C). Range specific for every element.
- i: Corresponding isotope for every element.
- MO: MO is the molecular mass of every compound in the HTSC group selected.
- i: N degree of polynomial parameter power. Range [0, N].
- ai: Polynomial coefficient. Range [0, N].
- TC: Critical temperature (K (usually) or C) for each class of compound.
- Jα (u): Function with regularization parameter alpha.
- R: Real space.
- u: Searched parameter solution.
- A: Model matrix vector data.
- K: Constant parameter matrix. Range specific for every element.
- α: Constant parameter. Range specific for every element.
- α1: Constant parameter. Tikhonov regularization parameter selected null.
- | • |1: L1 Chevshev norm (at an algorithm power of 1).
- a, a1: Constraint range specified in Table 1.
- b, b1: Constraint range specified in Table 1.
- c, c1: K optimization parameter range for the program, approximately [20.0, 50.0].
- d, d1: α constant range for the program, approximately [0.0001, 0.8].
- Jα (u): Function with regularization parameter alpha.
- R: Real space.
- u: Searched parameter solution.
- A: Model matrix vector data.
- K: Constant parameter matrix. Range specific for every element.
- α: Constant parameter. Range specific for every element.
- α1: Constant parameter. Tikhonov regularization parameter selected null.
- ‖ • ‖2: L2 norm (at an algorithm power of 2).
- a, a1: Constraint range specified in Table 1.
- b, b1: Constraint range specified in Table 1.
- c, c1: K optimization parameter range for the program, approximately [20.0, 50.0].
- d, d1: α constant range for the program, approximately [0.0001, 0.8].
2.3. Hypothesis and Algorithms for Molecular Effect Model
- Jα (u): Function with regularization parameter alpha.
- R: Real space.
- u: Searched parameter solution.
- MOi: Molecular mass for the HTSC cuprates from Table 1.
- P(MOi): Polynomial optimization parameter matrix of HTSC cuprates range in Table 1.
- α1: Constant parameter. Tikhonov regularization parameter, selected null.
- ‖ • ‖2: L2 Norm (at an algorithm power of 2).
- a, a1: Constraint range specified in Table 1 for the HTSC cuprates.
- b, b1: Constraint range specified in Table 1 for the HTSC cuprates.
2.4. Genetic Algorithm (GA) Methods
2.5. GA and Inverse Least Squares Computational Software
3. Results
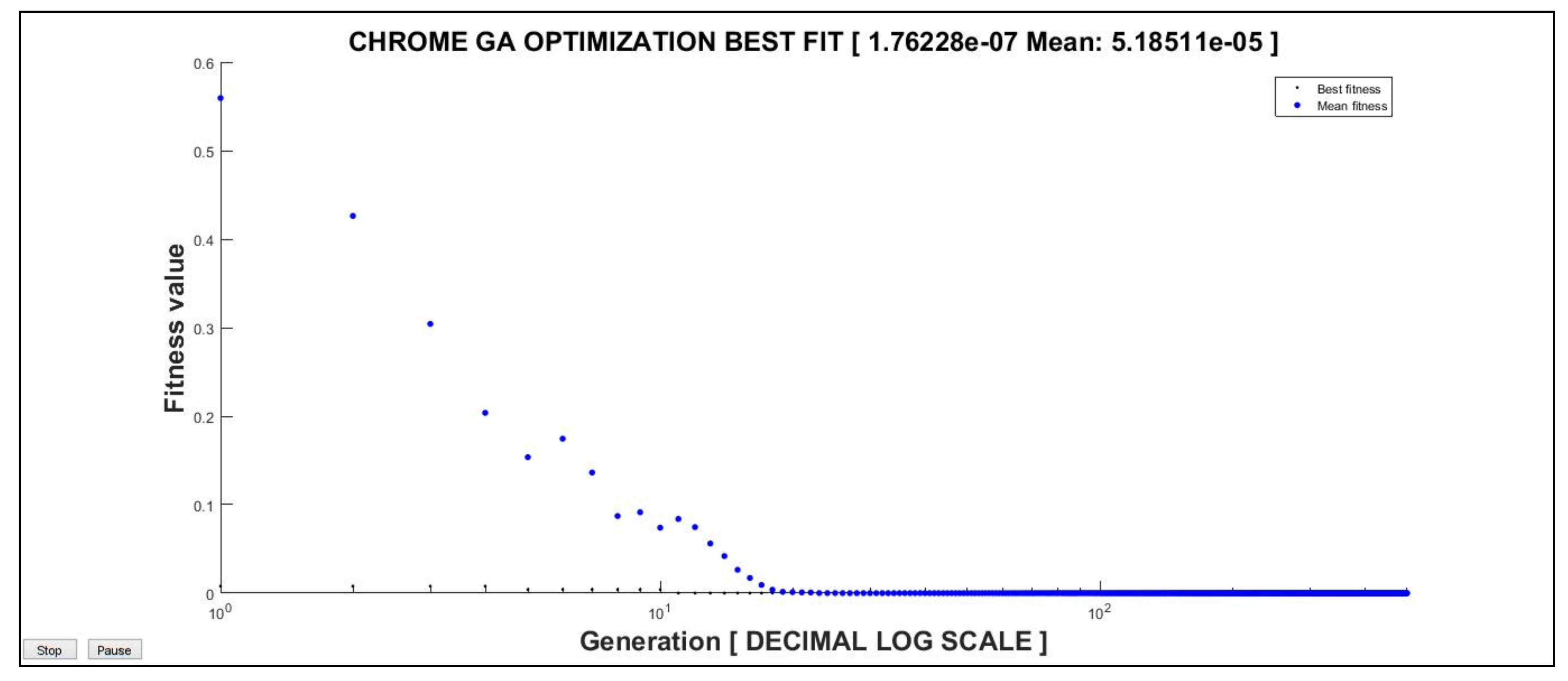
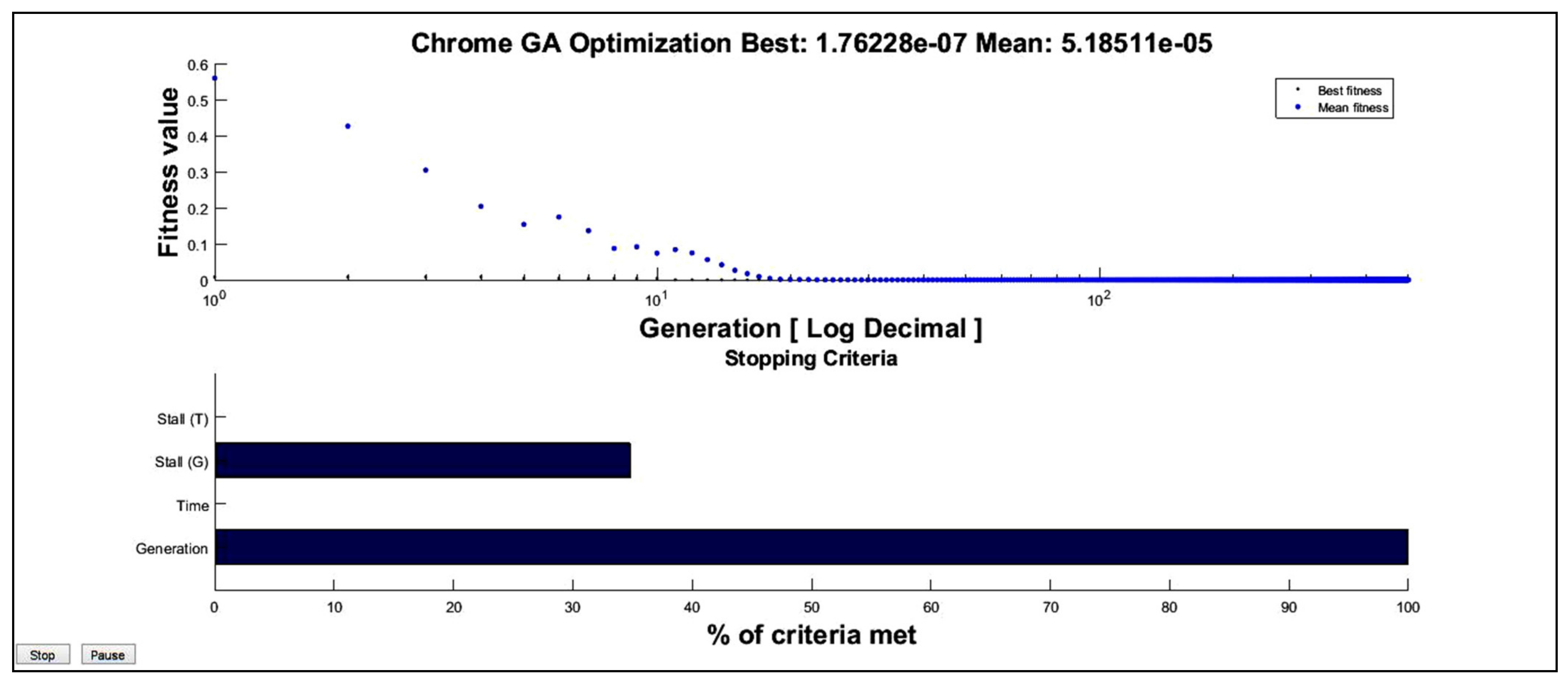
3.1. GA Numerical Results for Chrome
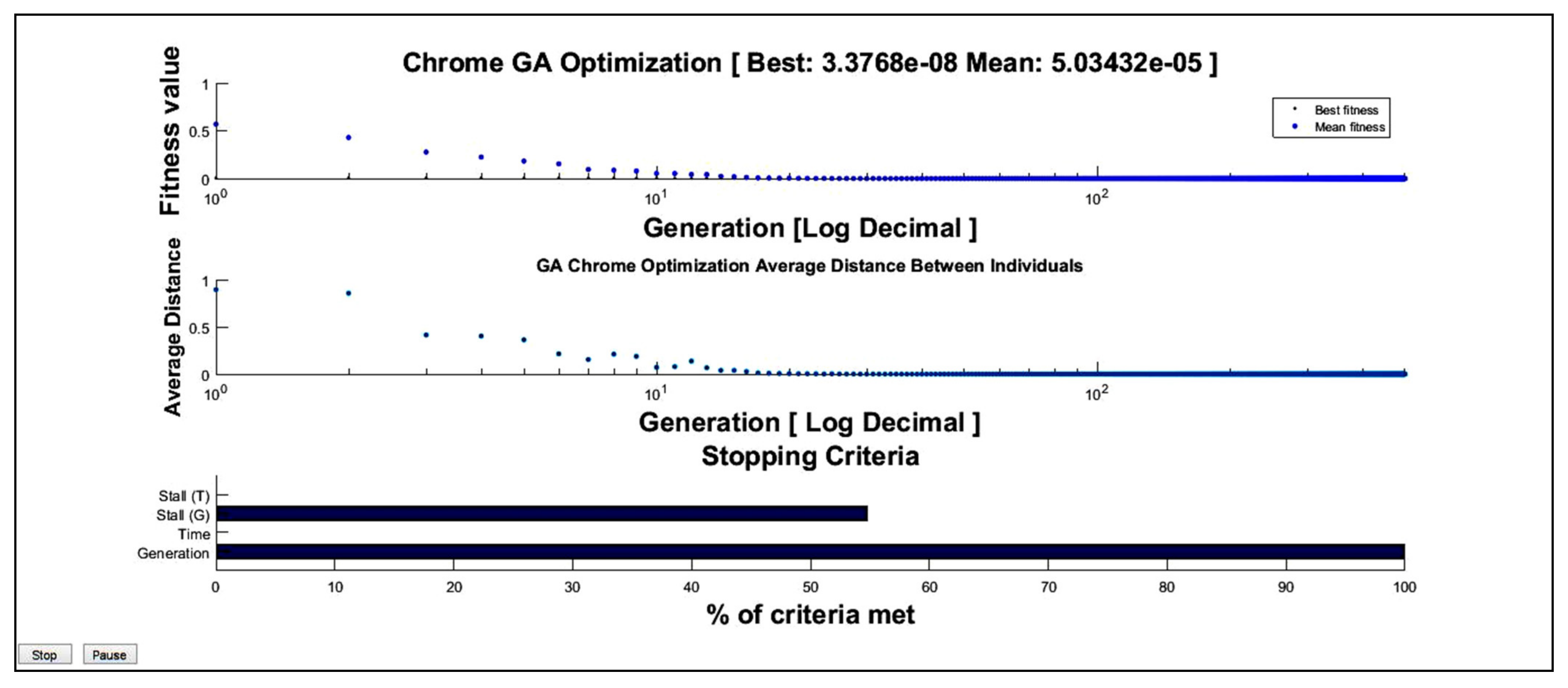
3.2. Interior Tikhonov Optimization Numerical Results for Chrome
3.3. GA Interior Optimization 2D Graphical Results for Chrome
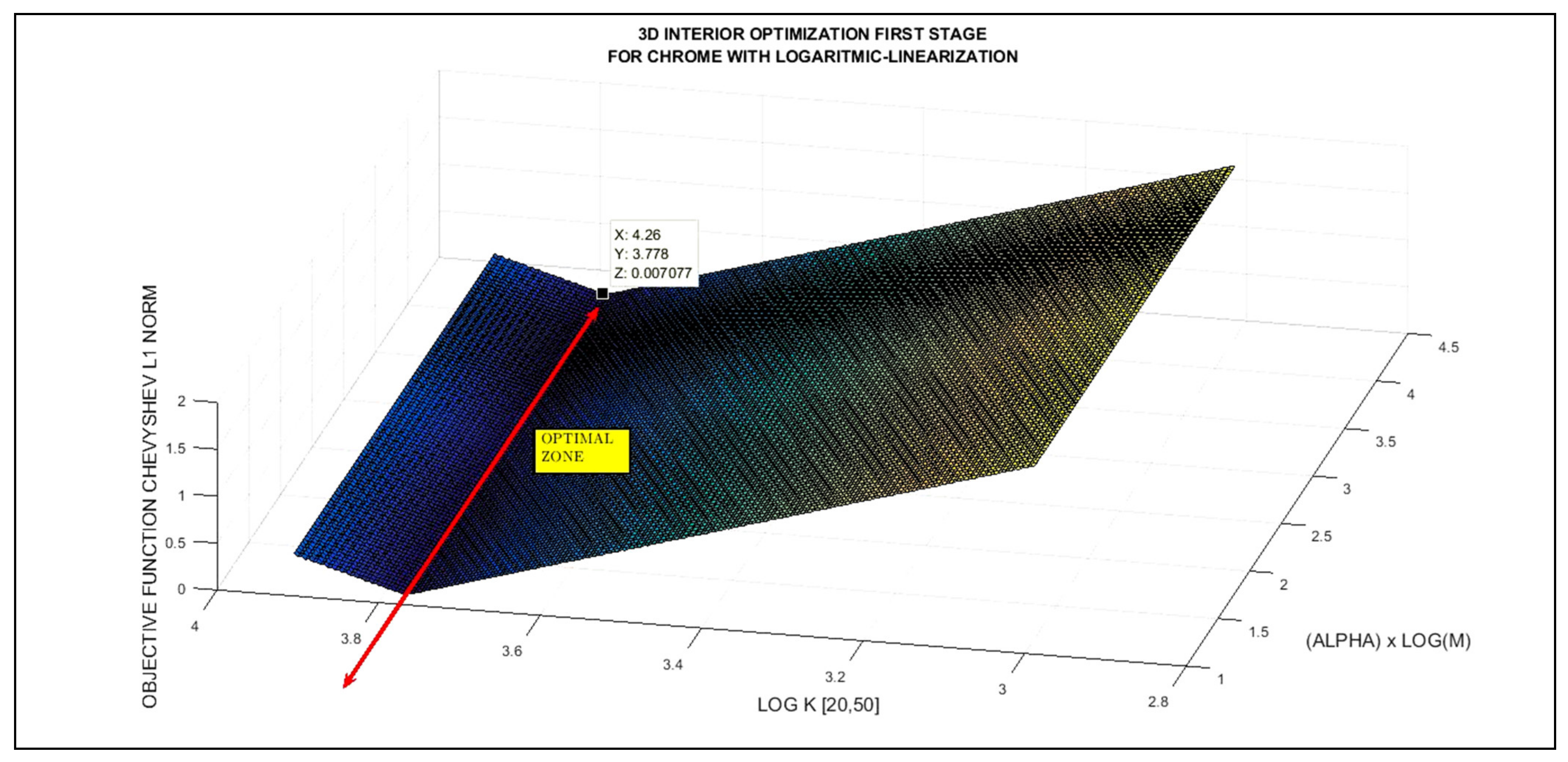
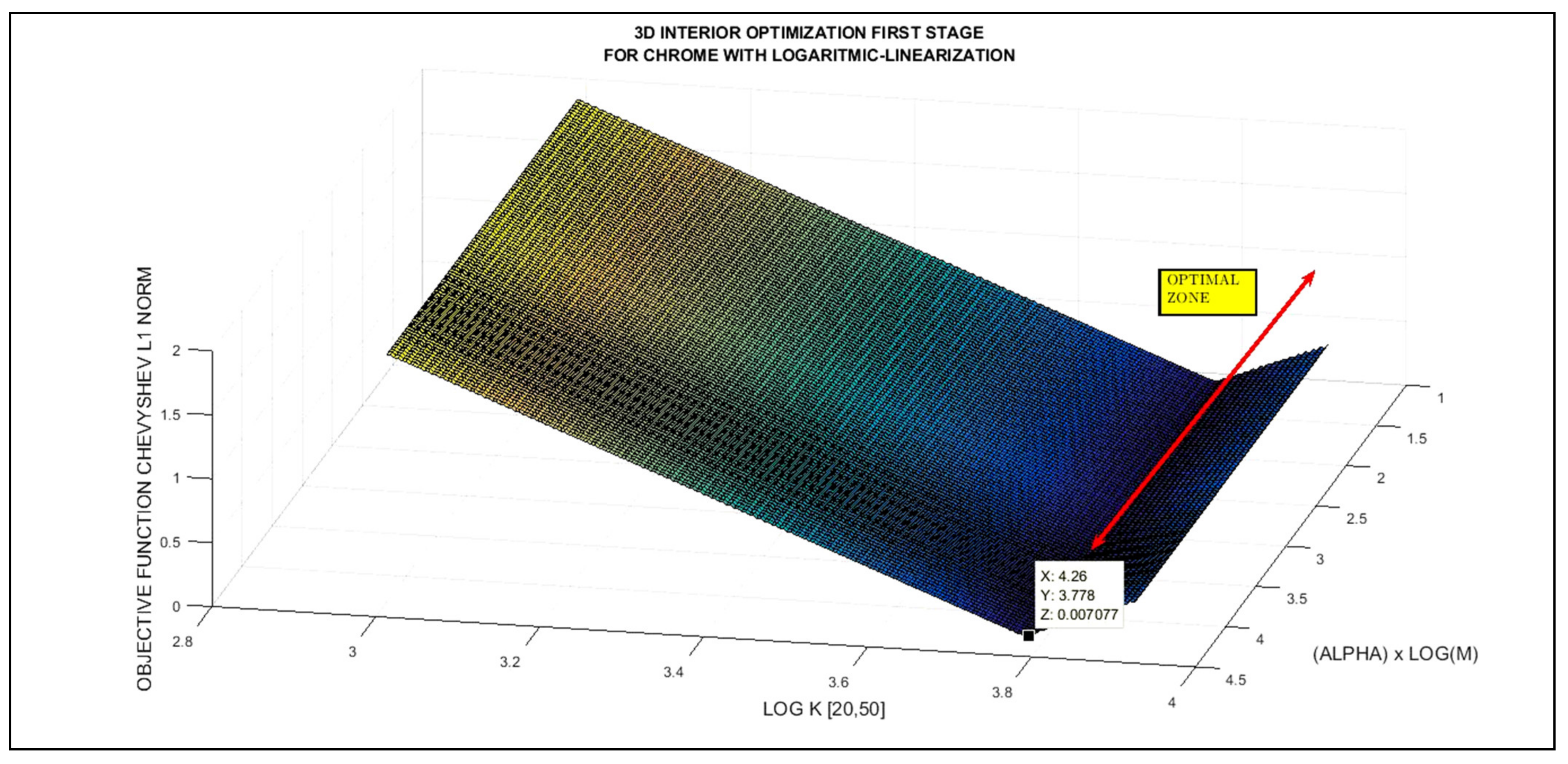
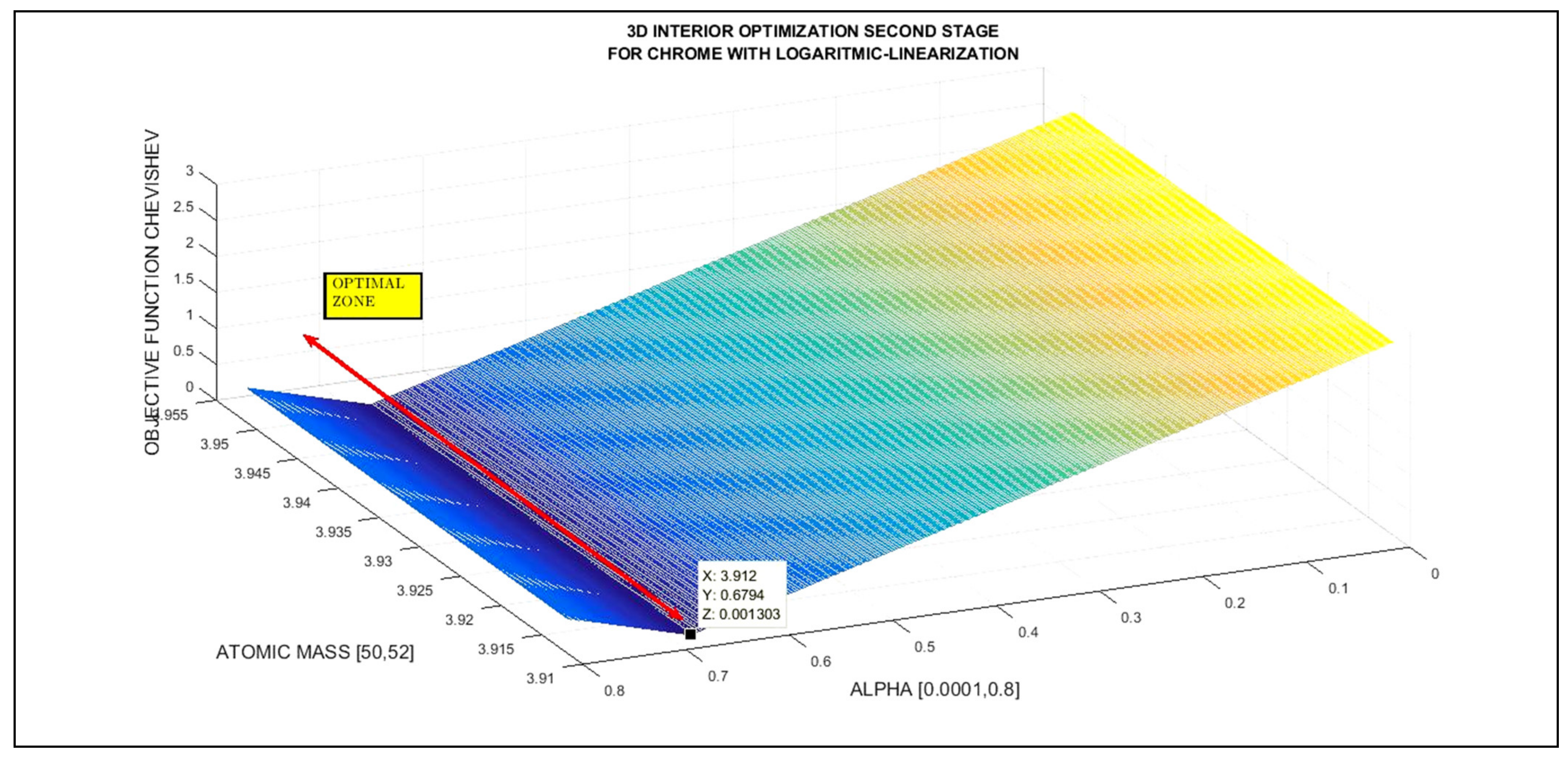
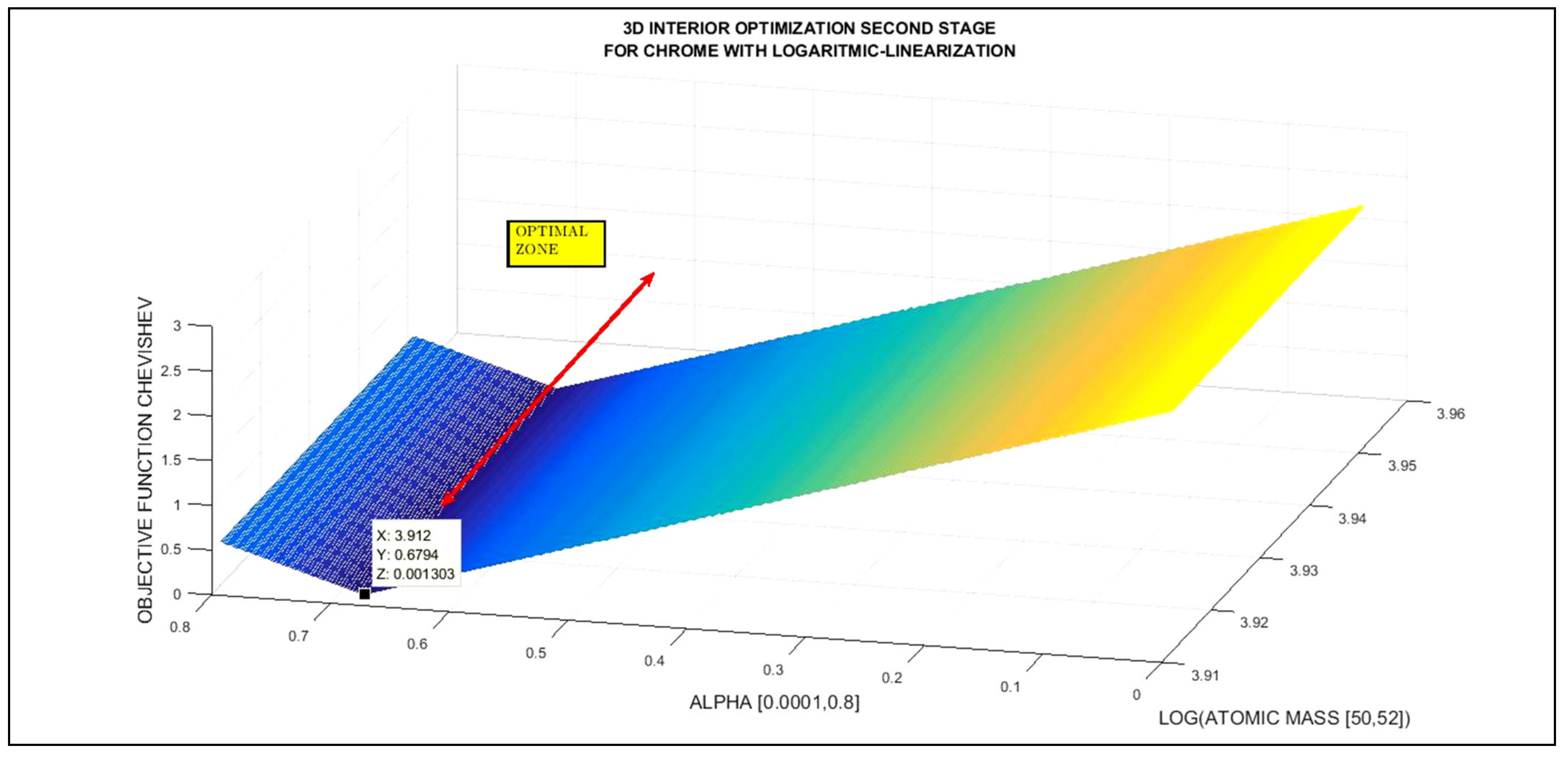
3.4. Inverse 3D Interior Tikhonov Optimization Graphical Results for Chrome
3.5. Inverse Least Squares Numerical Results for HTSC Hg-Cuprates with Molecular Effect Model
3.6. Numerical Results and Predictive Model Use Verification
4. Electronics Physics and Engineering Applications
5. Discussion and Conclusions
6. Scientific Ethics Standards
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Vora, A.M. Modified Transition Temperature Equation for Superconductors. Chin. Phys. Lett. 2008, 25, 2162. [Google Scholar] [CrossRef]
- Casesnoves, F. Interior Optimization Methods with Electronics Applications. Int. J. Sci. Res. Sci. Eng. Technol. 2020, 7, 428–436. [Google Scholar] [CrossRef]
- Casesnoves, F. Advanced Interior Optimization Methods with Electronics Applications. Int. J. Sci. Res. Sci. Eng. Technol. 2020, 7, 97–110. [Google Scholar] [CrossRef]
- Casesnoves, F. Multiobjective Interior Optimization Computational Methods for Electronics BCS Superconductivity. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2020, 6, 280–293. [Google Scholar] [CrossRef]
- Plakida, N. High-Temperature Cuprate Superconductors Experiment, Theory, and Applications. In Springer Series in Sol-id-State Sciences; Springer: Berlin/Heidelberg, Germany, 2010; ISSN 01711873. [Google Scholar]
- Alexandrev, A.S. Theory of Superconductivity, from Weak to Strong Coupling. Series in Condensed Matter Physics; Institute of Physics Publishing: Philadelphia, PA, USA, 2003. [Google Scholar]
- Khare, N. Handbook of High-Temperature Superconductor; Marcel Dekker: New York, NY, USA, 2003; ISBN 0824708237. [Google Scholar]
- Buschow, K. Magnetic & Superconducting Materials, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Seidel, P. Applied Superconductivity; Wiley-VCH: Hoboken, NJ, USA, 2015; Volumes 1 and 2. [Google Scholar]
- Drechsler, S.; Mishonov, T. High-T C Superconductors and Related Materials Material Science, Fundamental Properties, and Some Future Electronic Applications; Springer Science Media: Berlin/Heidenberg, Germany, 1998. [Google Scholar]
- Kazufumi, I.; Bangti, J. Inverse Problems, Tikhonov Theory and Algorithms; Series on Applied Mathematics; World Scientific: Singapore, 2015; Volume 22. [Google Scholar]
- Casesnoves, F. Mathematical Models and Optimization of Erosion and Corrosion. Ph.D. Thesis, Taltech University, Tallinn, Estonia, 14 December 2018. ISSN 25856898. [Google Scholar]
- Casesnoves, F. Die Numerische Reuleaux-Methode Rechnerische und Dynamische Grundlagen mit Anwendungen (Erster Teil); Sci-encia Scripts: Chisinau, Moldova, 2019; ISBN 139786200895608/106200895600. [Google Scholar]
- Casesnoves, F. Primary Modelling for Electromagnetic Waves Transmission in Extreme Weather Conditions. Int. J. Innov. Res. Sci. Eng. Technol. 2018, 7, 10294–10300. [Google Scholar] [CrossRef]
- Casesnoves, F. The Numerical Reuleaux Method, a Computational and Dynamical Base with Applications. First Part; Lambert Academic Publishing: Saarland, Germany, 2019; ISBN 103659917478. [Google Scholar]
- Darwin, C. The Origin of Species; Barnes & Noble Classics: New York, NY, USA, 2004. [Google Scholar]
- Haupt, R.; Haupt, S. Practical Genetic Algorithms, 2nd ed.; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; U.S. Government Printing Office: Champaign, IL, USA, 1964; Volume 55.
- Casesnoves, F.; Suzenkov, A. Mathematical Models in Biotribology with 2D-3D Erosion Integral-Differential Model and Computational-Optimization/Simulation Programming. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2017, 2, 329–356, ISSN 24563307. [Google Scholar]
- Casesnoves, F.; Antonov, M.; Kulu, P. Mathematical models for erosion and corrosion in power plants. A review of appli-cable modelling optimization techniques. IEEE Xplore database and will be cross referred in SCOPUS. In Proceedings of the RUTCON2016 Power Engineering Conference, Riga, Latvia, 13 October 2016. [Google Scholar]
- Casesnoves, F. 2D computational-numerical hardness comparison between Fe-based hardfaces with WC-Co reinforcements for Integral-Differential modelling. Key Eng. Mater. J. 2018, 762, 330–338, ISSN 16629795. [Google Scholar] [CrossRef]
- Casesnoves, F.; Surzhenkov, A. Inverse methods for computational simulations and optimization of erosion models in power plants. In Proceedings of the RUTCON2017 Power Engineering Conference, Riga, Latvia, 5 December 2017. [Google Scholar] [CrossRef]
- Casesnoves, F. Computational Simulations of Vertebral Body for Optimal Instrumentation Design. J. Med. Devices 2012, 6, 021014. [Google Scholar] [CrossRef]
- Casesnoves, F. Large-Scale Matlab Optimization Toolbox (MOT) Computing Methods in Radiotherapy Inverse reatment Planning. In High Performance Computing Meeting; Nottingham University: Nottingham, UK, 2007. [Google Scholar]
- Casesnoves, F. A Monte-Carlo Optimization method for the movement analysis of pseudo-rigid bodies. In Proceedings of the 10th SIAM Conference in Geometric Design and Computing, San Antonio, TX, USA, 4–8 November 2007. Contributed Talk. [Google Scholar]
- Casesnoves, F. Applied Inverse Methods for Deformable Solid Dynamics/Kinematics in Numerical Reuleaux Method (NRM). Int. J. Numer. Methods Appl. 2013, 9, 109–131. [Google Scholar]
- Casesnoves, F. Nonlinear comparative optimization for biomaterials wear in artificial implants technology. In Proceedings of the Applied Chemistry and Materials Science RTU2018 Conference Proceedings, Rajasthan Technical University, Kota, India, 17–18 March 2018. [Google Scholar]
- Allison, J.; Amako, K.; Apotolakis, J.; Araujo, H.; Dubois, P.A.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 Developments and Applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Batič, M.; Hoff, G.; Pia, M.G.; Saracco, P.; Weidenspointner, G. The Geant4 Simulation Toolkit. IEEE Nucl. Sci. Symp. Med. Imaging Conf. Seoul 2013, 60, 2934–2957. [Google Scholar]
- Luenberger, G.D. Linear and Nonlinear Programming, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Huang, X. Does the isotope effect of mercury support the BCS theory? arXiv 2011, arXiv:1102.1467. [Google Scholar]
- Hummel, R.E. Electronic Properties of Materials; Springer: New York, NY, USA, 2011. [Google Scholar]
- Kasap, F.; Capper, P. (Eds.) Springer Handbook of Electronic and Photonic Materials, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Kessel, W. On a General Formula for the Transition Temperature of Superconductors. Naturforschung 1974, 29a, 445–451. [Google Scholar] [CrossRef]
- Kulu, P.; Casesnoves, F.; Simson, T.; Tarbe, R. Prediction of abrasive impact wear of composite hardfacings. Solid State Phenomena. In Proceedings of 26th International Baltic Conference on Materials Engineering; Trans Tech Publications: Bäch, Swit-zerland, 2017; Volume 267, pp. 201–206. [Google Scholar] [CrossRef]
- Luiz, A. Superconductivity—Theory and Applications; InTechOpen: London, UK, 2010; ISBN 9789533071510. [Google Scholar]
- Reynolds, C.A.; Serin, B.; Nesbitt, L.B. The Isotope Effect in Superconductivity. I. Mercury. Phys. Rev. 1951, 84, 691. [Google Scholar] [CrossRef]
- Seri, B.; Reynolds, C.A.; Nesbitt, L.B. Mass Dependence of the Superconducting Transition Temperature of Mercury. Letters to Editor. Phys. Rev. 1950, 80, 761. [Google Scholar] [CrossRef]
- Todinov, M. Reliability and Risk Models; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Vidyasagar, M. Nonlinear Systems Analysis, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Wesche, R. Chapter 50. High-Temperature Superconductors. In Springer Handbook of Electronic and Photonic Materials; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Parinov, I.A. Microstructure and Properties of High-Temperature Superconductors, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Fossheim, K.; Sudbø, A. Superconductivity Physics and Applications; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Wang, Y.F. Fundamental Elements of Applied Superconductivity in Electrical Engineering; Wiley: New York, NY, USA, 2013. [Google Scholar]
- European Textbook on Ethics in Research. European Commission, Directorate-General for Research. Unit L3. Governance and Ethics. European Research Area. Science and Society. EUR 24452 EN. Available online: https://op.europa.eu/en/publication-detail/-/publication/12567a07-6beb-4998-95cd-8bca103fcf43 (accessed on 28 June 2021).
- ALLEA. The European Code of Conduct for Research Integrit, Revised ed.; ALLEA: Bern, Switzerland, 2017. [Google Scholar]
- Swedish Research Council. Good Research Practice; Swedish Research Council: Stockholm, Sweden, 2017; ISBN 978-91-7307-354-7. [Google Scholar]
| NUMERICAL OPTIMIZATION DATA CHROME [SUPERCONDUCTOR, ISOTOPE EFFECT] | ||
|---|---|---|
| Cr ISOTOPE TYPE BY ATOMIC MASS, (AMU) | PERCENTAGE | APPROXIMATE TC (Kelvin) |
| 52 (NATURAL) | 83.789% | 3 |
| 53 | 9.501% | 3 |
| 54 | 2.365% | 3 |
| 50 | 4.345% | 3 |
| NUMERICAL OPTIMIZATION DATA FOR Hg-CUPRATES [HT-SUPERCONDUCTOR, MOLECULAR EFFECT HYPOTHESIS] | ||
| FORMULATION | MOLECULAR WEIGHT (UAM) | APPROXIMATE TC (Kelvin) |
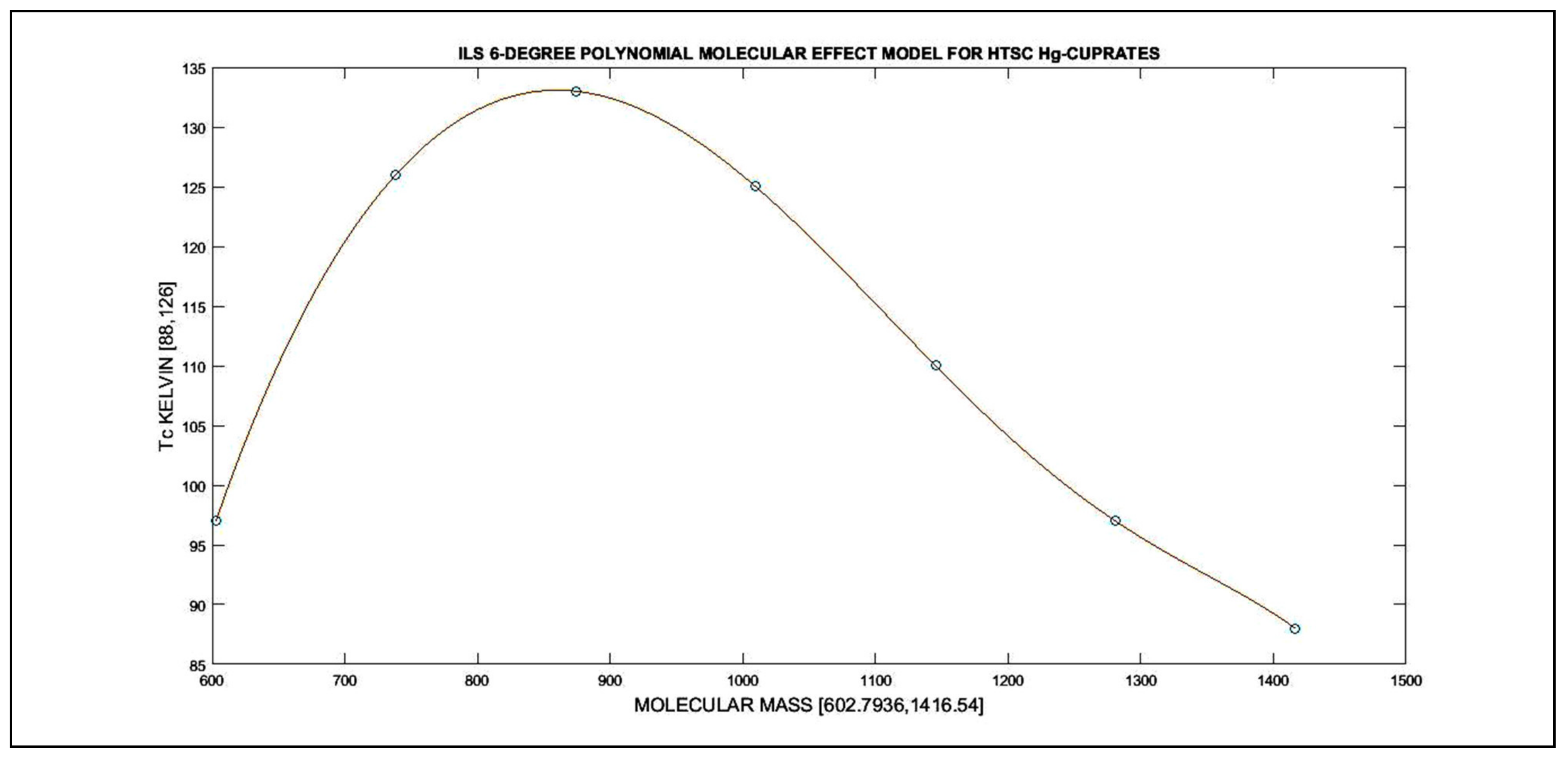
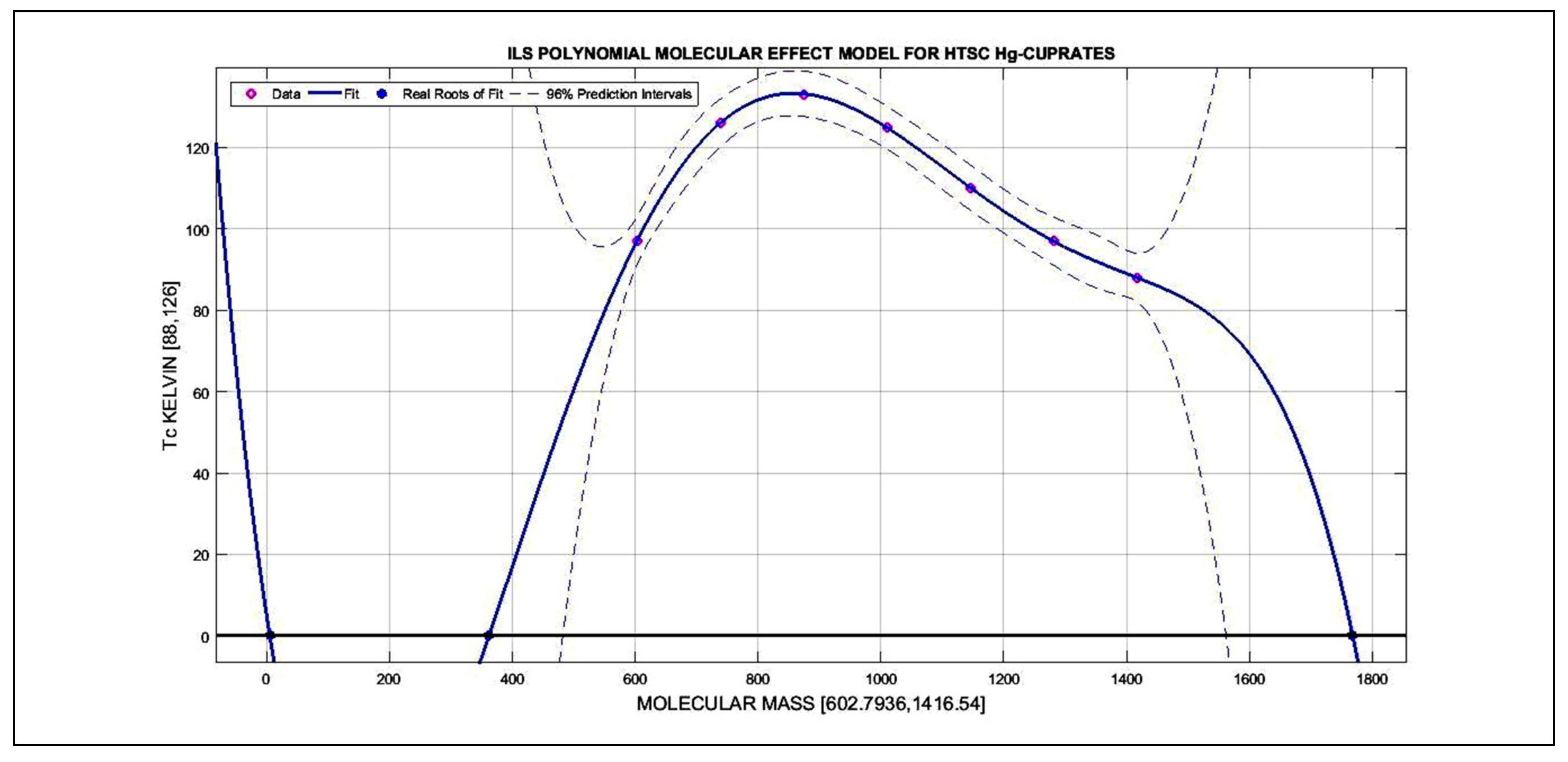
| HgBa2CuO4 | 602.7936 | 97 |
| HgBa2CaCu2O6 | 738.42 | 126 |
| HgBa2Ca2Cu3O8 | 874.0432 | 133 |
| HgBa2Ca3Cu4O10 | 1009.7 | 125 |
| HgBa2Ca4Cu5O12 | 1145.3 | 110 |
| HgBa2Ca5Cu6O14 | 1280.9 | 97 |
| HgBa2Ca6Cu7O16 | 1416.54 | 88 |
| NUMERICAL GA OPTIMIZATION RESULTS FOR CHROME FIRST STAGE | ||
|---|---|---|
| Cr ISOTOPE TYPE RANGE (BY ATOMIC MASS, AMU) | K OPTIMAL | OBJECTIVE FUNCTION RESIDUAL (L1 Chebyshev Optimization Norm) |
| [49, 55] | 41.378132 | 176.23 × 10−9 |
| NUMERICAL GA OPTIMIZATION RESULTS FOR CHROME SECOND STAGE | ||
| Cr ISOTOPE TYPE RANGE (BY ATOMIC MASS, AMU) | OPTIMAL ALPHA | OBJECTIVE FUNCTION RESIDUAL (L1 Chebyshev Optimization Norm) |
| [49, 55] | 0.6661 | 13.51 × 10−9 |
| NUMERICAL 3D/4D INTERIOR OPTIMIZATION RESULTS FOR CHROME FIRST STAGE | ||
|---|---|---|
| Cr ISOTOPE TYPE RANGE (BY ATOMIC MASS, AMU) | K OPTIMAL | OBJECTIVE FUNCTION RESIDUAL (L1 Chebyshev Optimization Norm) |
| [49, 55] | 43.336596 | 7 × 10−3 |
| NUMERICAL 3D/4D INTERIOR OPTIMIZATION RESULTS FOR CHROME SECOND STAGE | ||
| Cr ISOTOPE TYPE RANGE (BY ATOMIC MASS, AMU) | OPTIMAL ALPHA | OBJECTIVE FUNCTION RESIDUAL (L1 Chebyshev Optimization Norm) |
| [49, 55] | 0.6794 | 1 × 10−3 |
| NUMERICAL ILS RESULTS FOR MOLECULAR EFFECT MODEL FOR Hg-CUPRATES FIRST STAGE | ||
|---|---|---|
| Hg-CUPRATES MOLECULE TYPE RANGE (BY MOLECULAR MASS, AMU) | OPTIMAL ALPHA | OBJECTIVE FUNCTION RESIDUAL (L1 Chebyshev Optimization Norm, 3000 functions) |
| [738.42, 1416.54] | 5.35 × 10−3 | 9.704343 |
| PROGRAMMING FIRST-STAGE DATA | ||
| K | ALPHA | Tc |
| LOG [80, 150] | [0.0001, 1] | [88, 126] |
| NUMERICAL ILS RESULTS FOR MOLECULAR EFFECT MODEL FOR Hg-CUPRATES FIRST STAGE | ||
| Hg-CUPRATES MOLECULE TYPE RANGE (BY MOLECULAR MASS, AMU) | OPTIMAL K | OBJECTIVE FUNCTION RESIDUAL (L1 Chebyshev Optimization Norm, 3000 functions) |
| [738.42, 1416.54] | 109.2585 | 10.45268 |
| PROGRAMMING SECOND-STAGE DATA | ||
| K | FIXED ALPHA | Tc |
| LOG [80, 150] | 5.35 × 10−3 | [88, 126] |
| ILS MOLECULAR EFFECT MODEL 2 (6-DEGREE) | |||
|---|---|---|---|
| COEFFICIENT | VARIABLE X | COEFFICIENT APPROX | VARIABLE X SELECTED |
| −1.4683 × 103 | CONSTANT | [−1.468] | CONSTANT |
| 8.5713 | X | [8.571] | X |
| −20.8471 × 10−3 | X2 | [−20.847 × 10−3] | X2 |
| 29.0052 × 10−6 | X3 | [29.005 × 10−6] | X3 |
| −23.4857 × 10−9 | X4 | 0 | X4 |
| 10.1448 × 10−12 | X5 | 0 | - |
| −1.7944 × 10−15 | X6 | 0 | - |
| RESIDUAL = 32.703892 × 10−12 | |||
| APPROXIMATE POLYNOMIAL | |||
| Tc = [−1.468] + [8.571] MO + [−20.847 × 10−3] MO2 + [29.005 × 10−6] MO3 + [−23 × 10−9] MO4 | |||
| ILS MOLECULAR EFFECT MODEL 2 (5-DEGREE) | |||
|---|---|---|---|
| COEFFICIENT | VARIABLE X | COEFFICIENT APPROX | VARIABLE X SELECTED |
| 4.8106 | CONSTANT | [4.811] | CONSTANT |
| −982.4692 × 10−3 | X | [−982.469 × 10−3] | X |
| 4.4871 × 10−3 | X2 | [4.487 × 10−3] | X2 |
| −6.1759 × 10−6 | X3 | [−6176 × 10−6] | X3 |
| 3.5178 × 10−9 | X4 | 0 | - |
| −725.5851 × 10−15 | X5 | 0 | - |
| RESIDUAL = 264.499782 × 10−3 | |||
| APPROXIMATE POLYNOMIAL | |||
| Tc = [4.811] + [−982.469 × 10−3] MO + [4.487 × 10−3] MO2 + [−6176 × 10−6] MO3 | |||
| CHROME GA NUMERICAL VALIDATION | ||
|---|---|---|
| ISOTOPE [UAM] | K PREDICTED | K OPTIMAL BY GA |
| 50 | 40.6261 | 41.3781 |
| 51 | 41.1655 | |
| 52 | 41.7014 | |
| 53 | 42.2339 | |
| CHROME 3D/4D ILS INTERIOR OPTIMIZATION NUMERICAL VALIDATION | ||
|---|---|---|
| ISOTOPE [UAM] | K PREDICTED | K OPTIMAL BY ILS- INTERIOR OPTIMIZATION |
| 50 | 42.7958 | 43.3365 |
| 51 | 43.3755 | |
| 52 | 41.9512 | |
| 53 | 42.5240 | |
| PROGRAMMING RESULTS FOR ILS MOLECULAR EFFECT MODEL 2 (6-DEGREE) | |||
|---|---|---|---|
| MOLECULAR WEIGHT (AMU) | Tc EXPERIMENTAL [K] | Tc PROGRAM PREDICTED [MO] | ERROR |
| 602.7936 | 97 | 97.0000 | 9.3223 × 10−12 |
| 738.42 | 126 | 126.0000 | 1.8190 × 10−12 |
| 874.0432 | 133 | 133.0000 | 3.8654 × 10−12 |
| 1009.7 | 125 | 125.0000 | 5.9117 × 10−12 |
| 1145.3 | 110 | 110.0000 | 3.6380 × 10−12 |
| 1280.9 | 97 | 97.0000 | 6.8212 × 10−13 |
| 1416.54 | 88 | 88.0000 | −2.6375 × 10−11 |
| NUMERICAL PROGRAM VALIDATION | |||
| MO SIMULATED | Tc PROGRAM PREDICTED | ||
| 602.7936 | 97.0000 | ||
| 750.42 | 127.3895 | ||
| 890.0432 | 132.7059 | ||
| 1029.7 | 123.0025 | ||
| 1180.3 | 106.1526 | ||
| 1295.9 | 95.9194 | ||
| 1480.54 | 80.5684 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casesnoves, F. Genetic Algorithms for Interior Comparative Optimization of Standard BCS Parameters in Selected Superconductors and High-Temperature Superconductors. Standards 2022, 2, 430-448. https://doi.org/10.3390/standards2030029
Casesnoves F. Genetic Algorithms for Interior Comparative Optimization of Standard BCS Parameters in Selected Superconductors and High-Temperature Superconductors. Standards. 2022; 2(3):430-448. https://doi.org/10.3390/standards2030029
Chicago/Turabian StyleCasesnoves, Francisco. 2022. "Genetic Algorithms for Interior Comparative Optimization of Standard BCS Parameters in Selected Superconductors and High-Temperature Superconductors" Standards 2, no. 3: 430-448. https://doi.org/10.3390/standards2030029
APA StyleCasesnoves, F. (2022). Genetic Algorithms for Interior Comparative Optimization of Standard BCS Parameters in Selected Superconductors and High-Temperature Superconductors. Standards, 2(3), 430-448. https://doi.org/10.3390/standards2030029




