Mathematical Standard-Parameters Dual Optimization for Metal Hip Arthroplasty Wear Modelling with Medical Physics Applications
Abstract
:1. Introduction
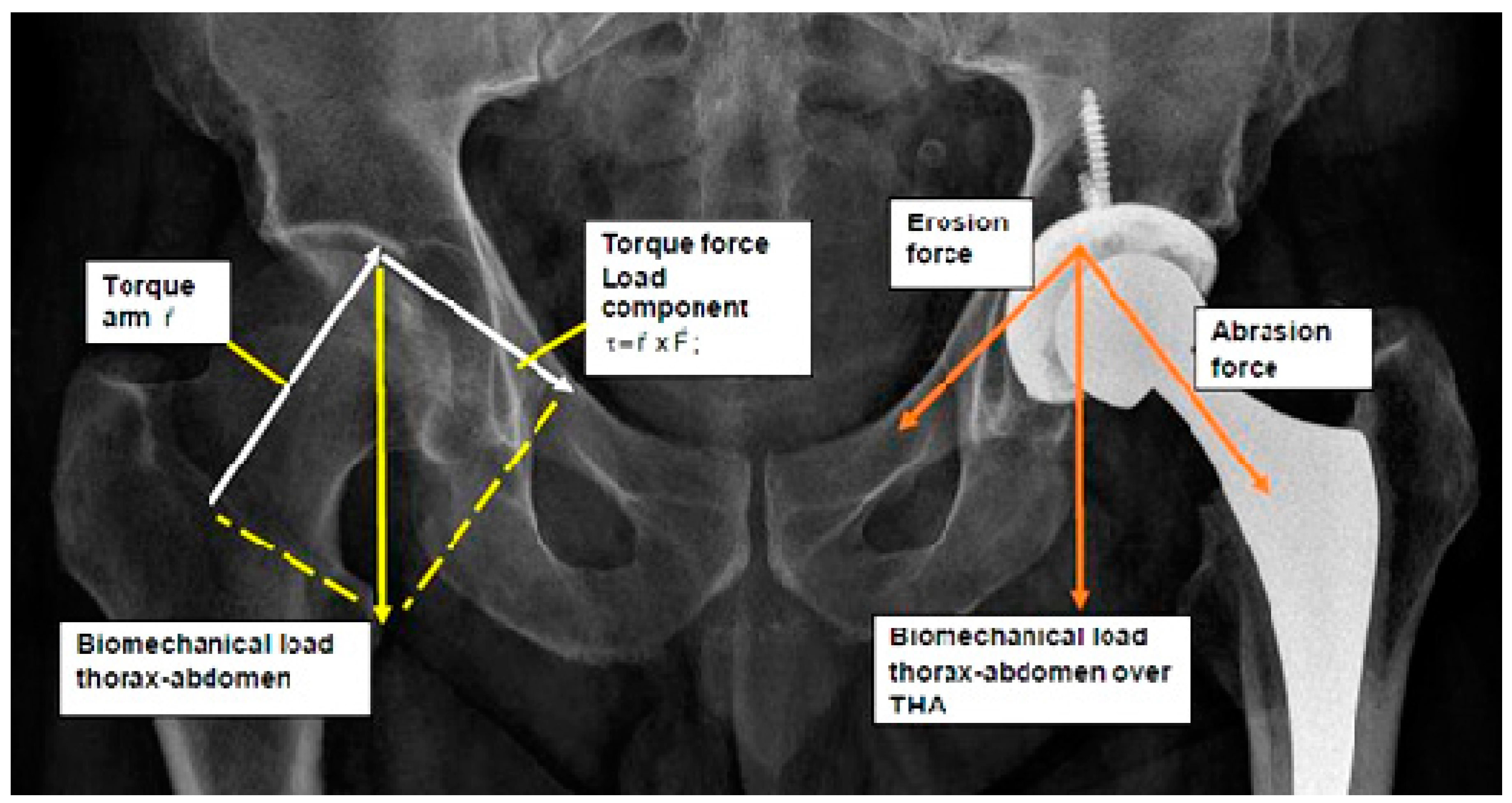
Theoretical and Clinical Biomechanics THA Modelling Pathogenesis with Physics Fundamentals
2. Materials and Methods
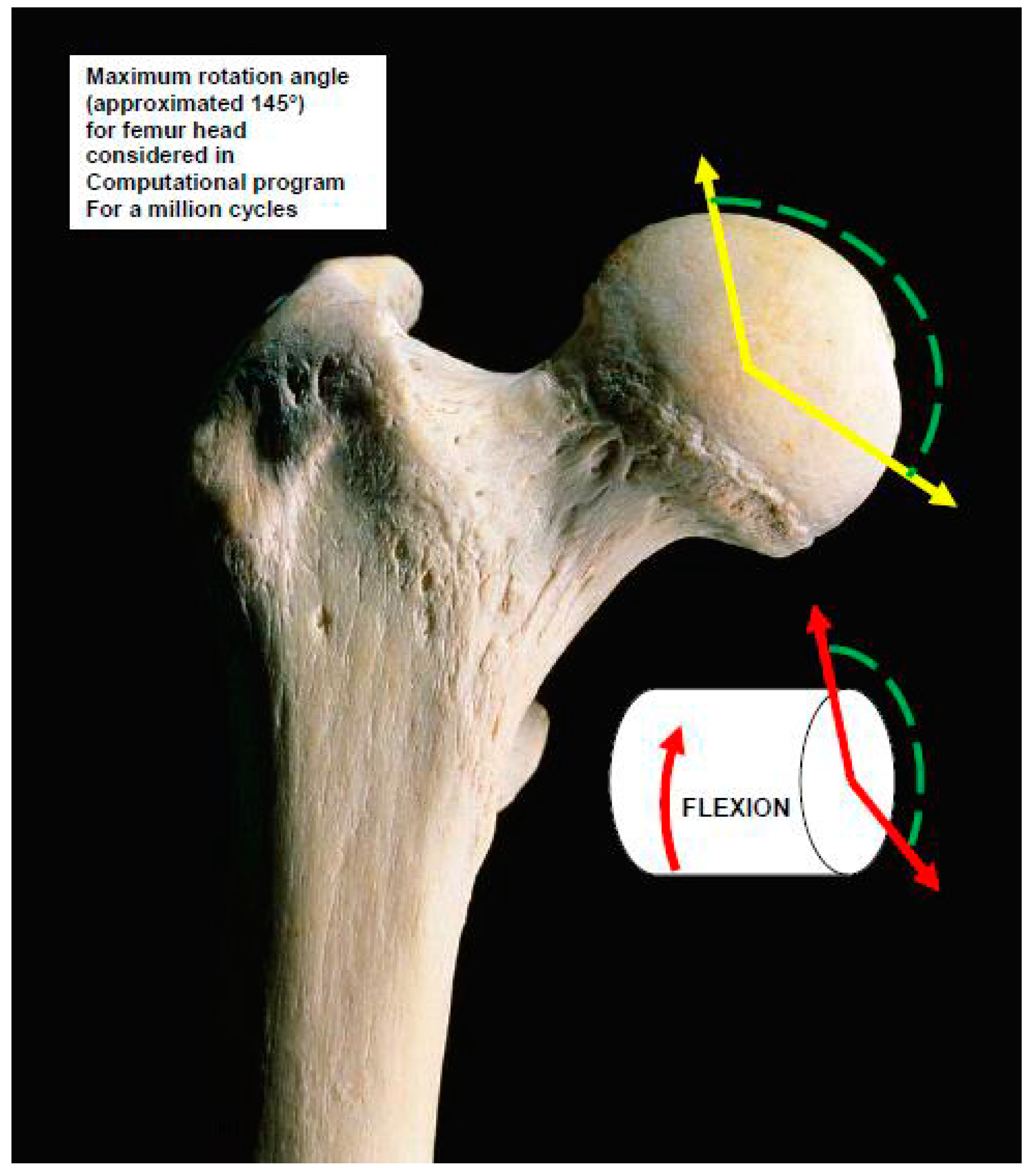
2.1. Material and Computational Data
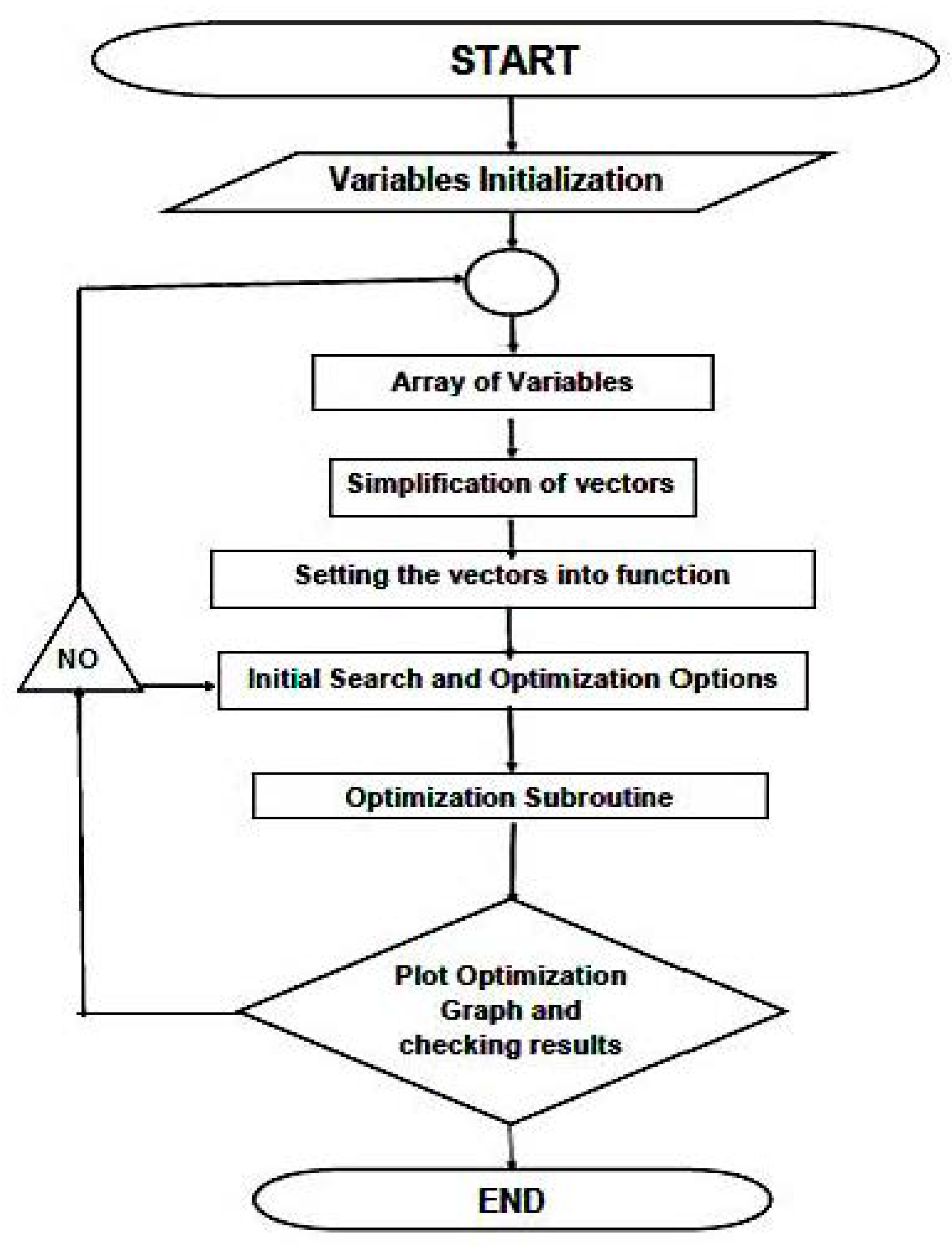
2.2. Optimization Algorithms and Programming-Software Design
3. Results
3.1. Optimization Numerical Results
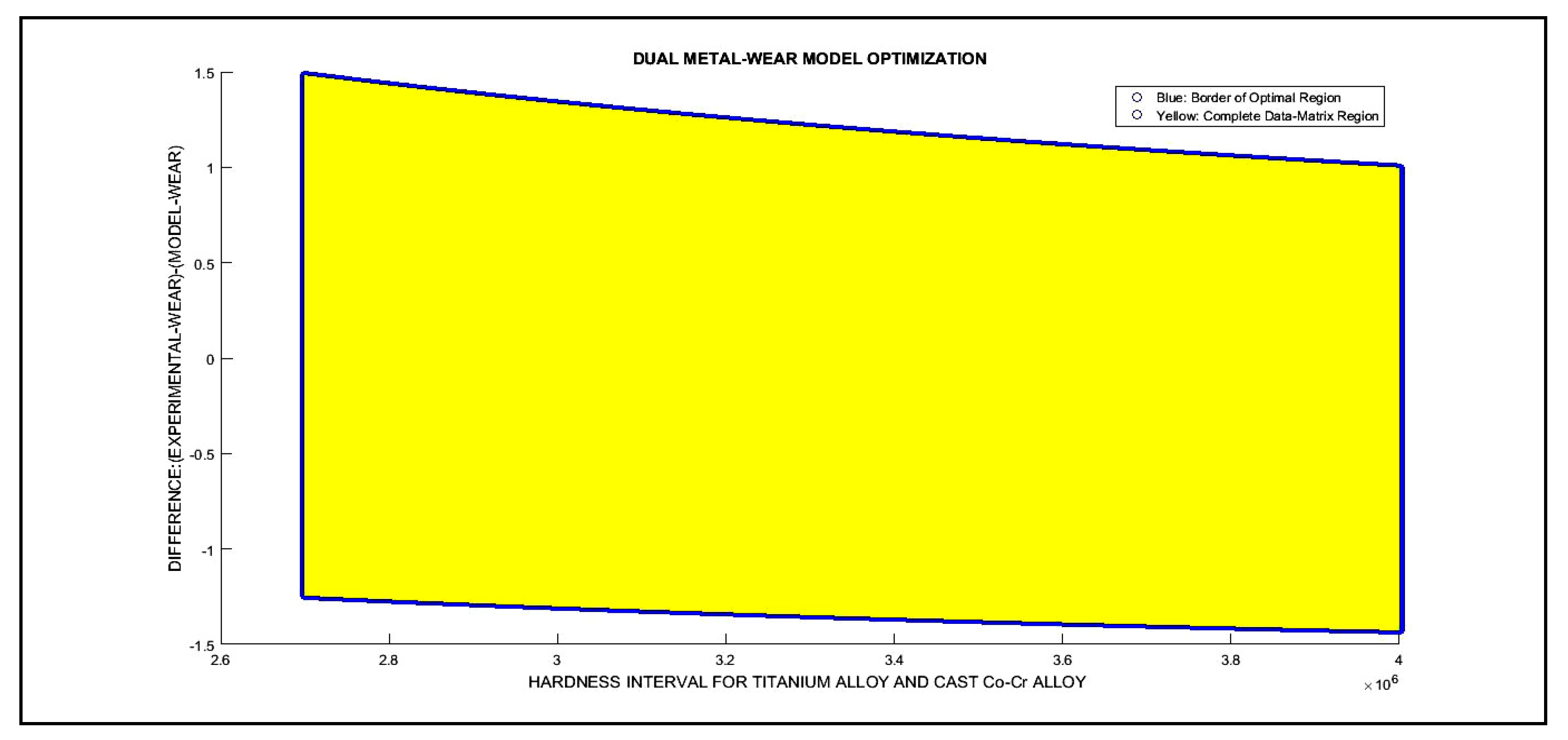
3.2. 2D Optimization Results
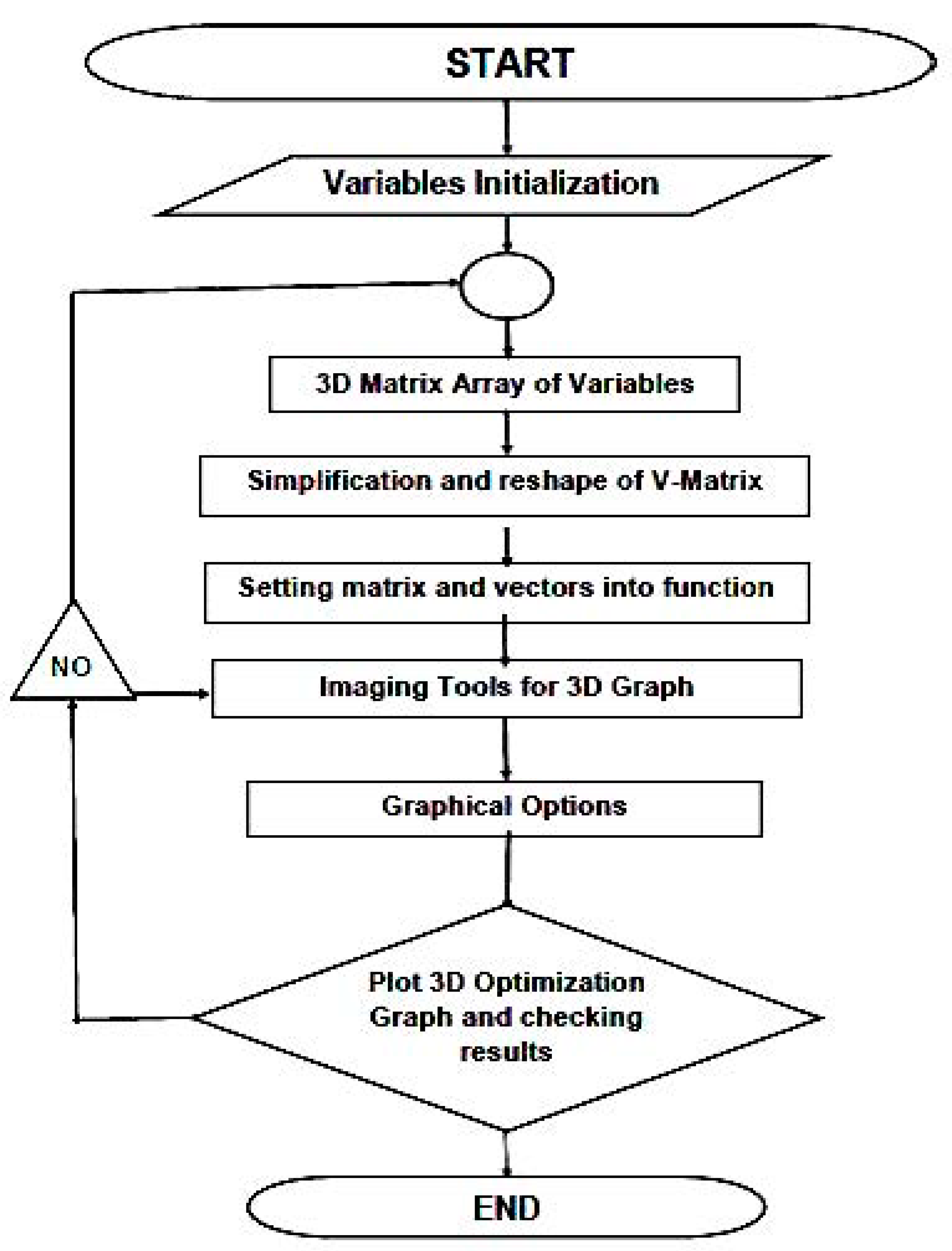
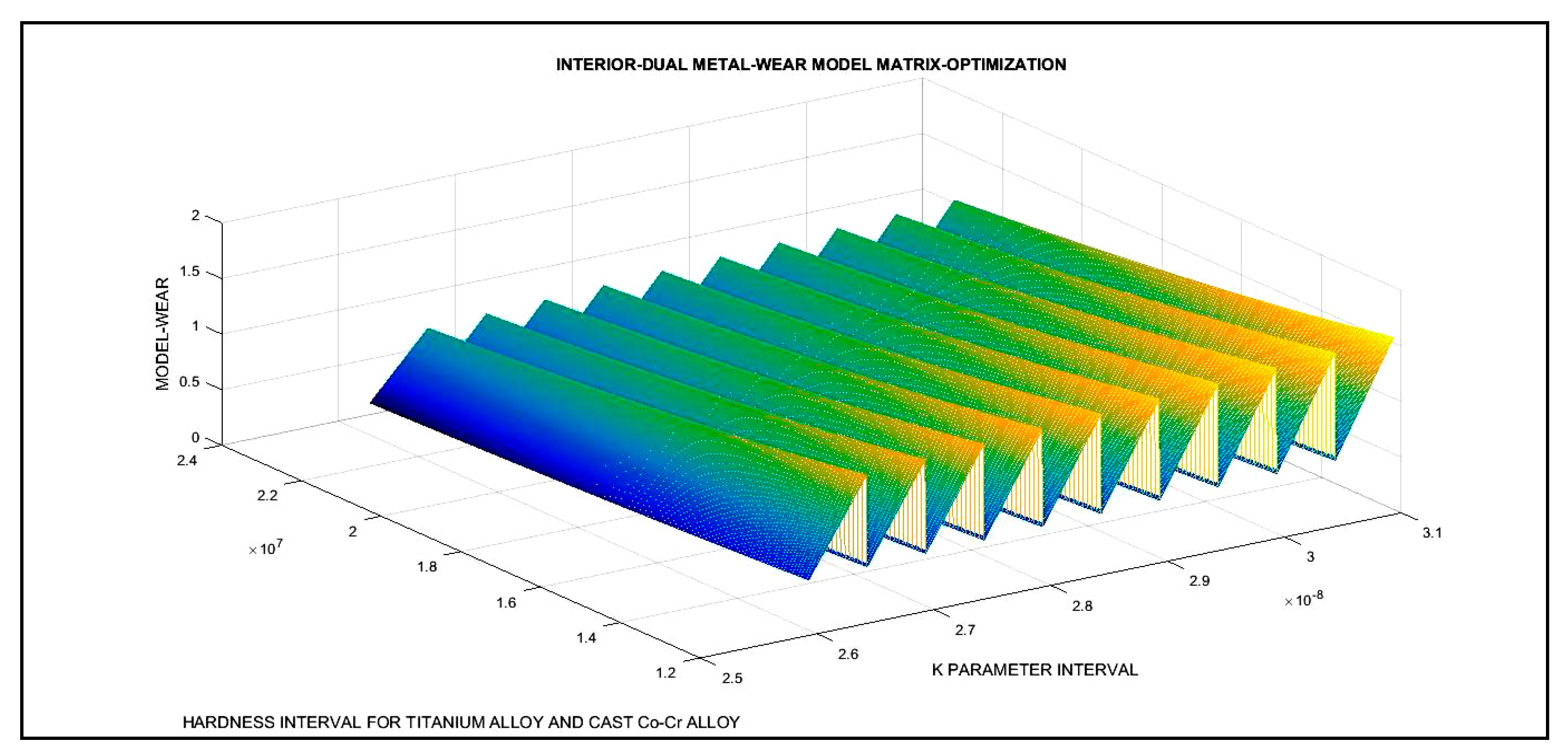
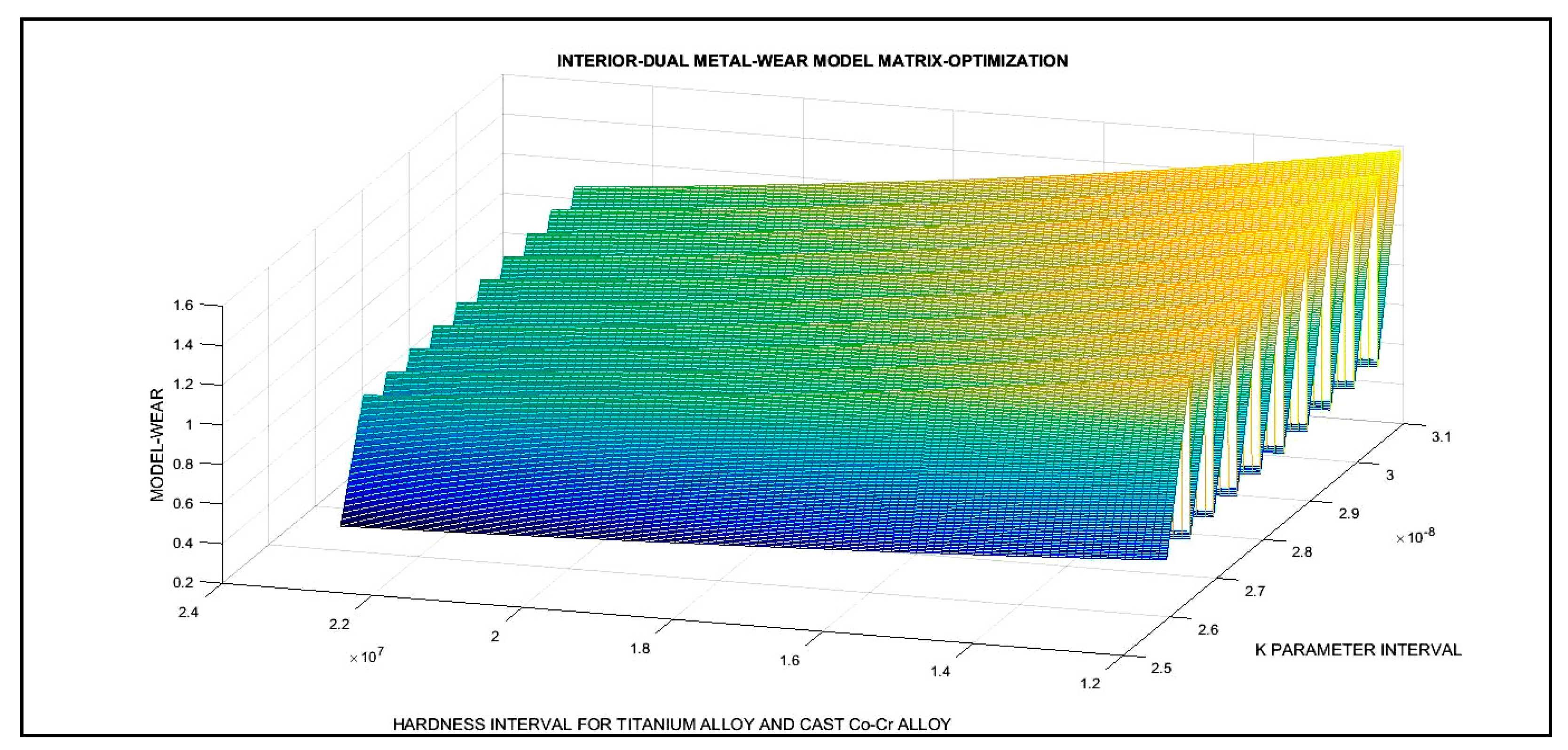
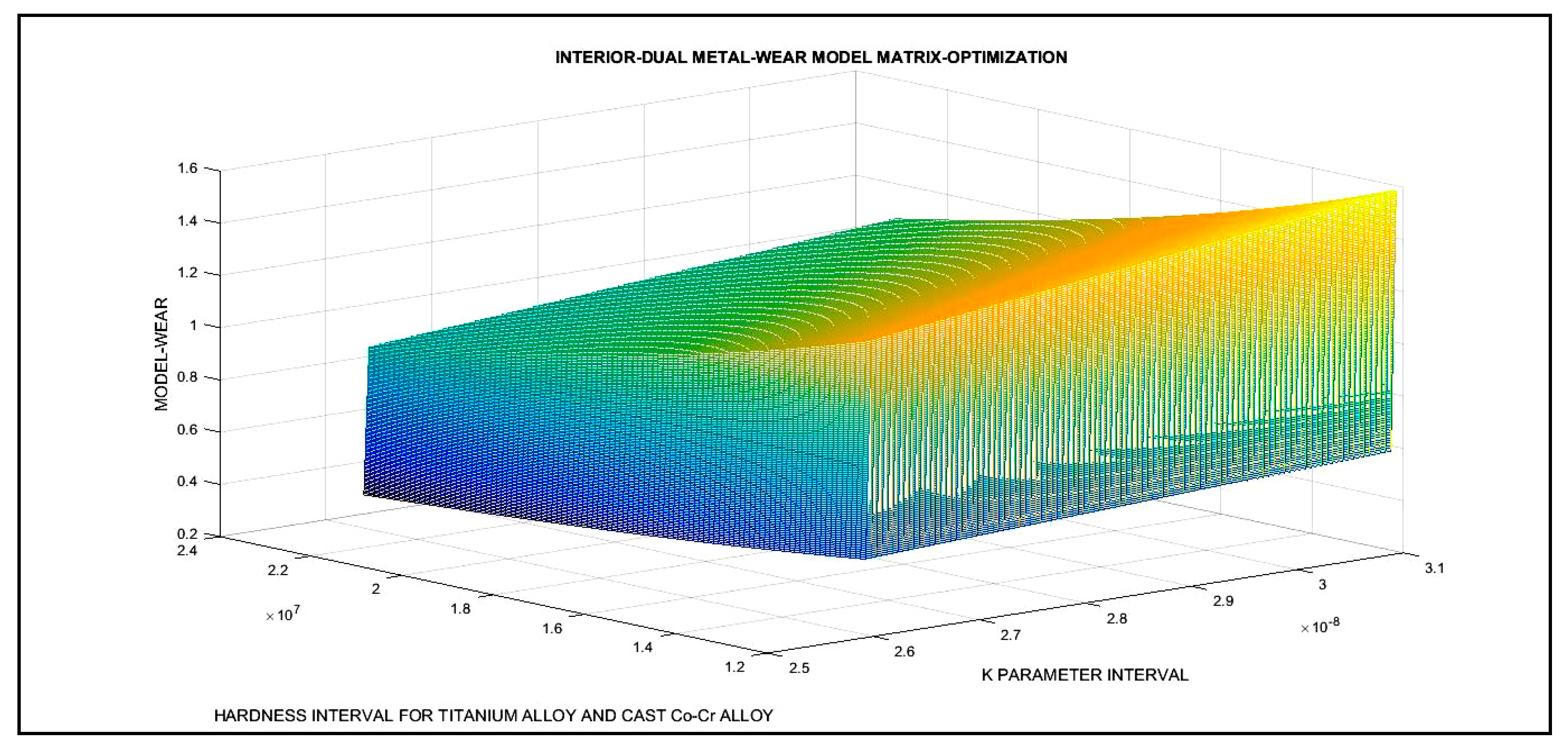
3.3. 3D Optimization Results
3.4. Optimization Numerical Results Verification
4. Discussion and Conclusions
5. Scientific Ethics Standards
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Casesnoves, F. Multiobjective Optimization for Ceramic Hip Arthroplasty with Medical Physics Applications. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2021, 7, 582–598. [Google Scholar] [CrossRef]
- Casesnoves, F. Nonlinear comparative optimization for biomaterials wear in artificial implants technology. In Proceedings of the Applied Chemistry and Materials Science RTU2018 Conference Proceedings, Riga, Latvia, 26 October 2018. [Google Scholar]
- Merola, M.; Affatato, S. Materials for Hip Prostheses: A Review of Wear and Loading Considerations. Materials 2019, 12, 495. [Google Scholar] [CrossRef] [Green Version]
- Navarro, N. Biomaterials in orthopaedics. J. R. Soc. Interface 2008, 5, 1137–1158. [Google Scholar] [CrossRef] [Green Version]
- Kurtz, S. Advances in Zirconia Toughened Alumina Biomaterials for Total Joint Replacement. J. Mech. Behav. Biomed. Mater. 2014, 31, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Sachin, G.; Mankar, A.; Bhalerao, Y. Biomaterials in Hip Joint Replacement. Int. J. Mater. Sci. Eng. 2016, 4, 113–125. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.; Zhao, H.; Qu, S.; Li, X.; Li, Y. New Developments of Ti-Based Alloys for Biomedical Applications. Materials 2014, 7, 1709–1800. [Google Scholar] [CrossRef] [Green Version]
- Kolli, R.; Devaraj, A. A Review of Metastable Beta Titanium Alloys. Metals 2018, 8, 506. [Google Scholar] [CrossRef] [Green Version]
- Holzwarth, U.; Cotogno, G. Total Hip Arthroplasty. JRC Scientific and Policy Reports; European Commission: Brussels, Belgium, 2012. [Google Scholar]
- Delimar, D. Femoral head wear and metallosis caused by damaged titanium porous coating after primary metal-on-polyethylene total hip arthroplasty: A case report. Croat. Med. J. 2018, 59, 253–257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, M.; Fan, Y. Computational Biomechanics of the Musculoskeletal System; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Dreinhöfer, K.; Dieppe, P.; Günther, K.; Puhl, W. Eurohip. Health Technology Assessment of Hip Arthroplasty in Europe; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Casesnoves, F. 2D computational-numerical hardness comparison between Fe-based hardfaces with WC-Co reinforcements for Integral-Differential modelling. Trans. Tech. 2018, 762, 330–338. [Google Scholar] [CrossRef]
- Hutchings, I.; Shipway, P. Tribology Friction and Wear of Engineering Materials, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Shen, X.; Lei, C.; Li, R. Numerical Simulation of Sliding Wear Based on Archard Model. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010. [Google Scholar] [CrossRef]
- Affatato, S.; Brando, D. Introduction to Wear Phenomena of Orthopaedic Implants; Woodhead Publishing: Sawston, UK, 2012. [Google Scholar]
- Matsoukas, G.; Kim, Y. Design Optimization of a Total Hip Prosthesis for Wear Reduction. J. Biomech. Eng. 2009, 131, 051003. [Google Scholar] [CrossRef] [PubMed]
- Casesnoves, F.; Antonov, M.; Kulu, P. Mathematical models for erosion and corrosion in power plants. A review of applicable modelling optimization techniques. In Proceedings of RUTCON2016 Power Engineering Conference, Riga, Latvia, 13 October 2016. [Google Scholar]
- Galante, J.; Rostoker, W. Wear in Total Hip Prostheses. Acta Orthop. Scand. 2014, 43, 1–46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mattei, L.; DiPuccio, F.; Piccigallo, B.; Ciulli, E. Lubrication and wear modelling of artificial hip joints: A review. Tribol. Int. 2011, 44, 532–549. [Google Scholar] [CrossRef]
- Jennings, L. Enhancing the safety and reliability of joint replacement implants. Orthop. Trauma 2012, 26, 246–252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Casesnoves, F. Die Numerische Reuleaux-Methode Rechnerische und Dynamische Grundlagen mit Anwendungen (Erster Teil); Sciencia Scripts, 2019; ISBN-13: 978-620-0-89560-8. [Google Scholar]
- Kulu, P.; Casesnoves, F.; Simson, T.; Tarbe, R. Prediction of abrasive impact wear of composite hardfacings. Solid State Phenomena. In Proceedings of the 26th International Baltic Conference on Materials Engineering, Vilnius, Lithuania, 26–27 October 2017; Trans Tech Publications: Bäch, Switzerland, 2017; Volume 267, pp. 201–206. [Google Scholar] [CrossRef]
- Casesnoves, F. Mathematical Models and Optimization of Erosion and Corrosion. Ph.D. Thesis, Taltech University, Tallinn, Estonia, 14 December 2018. [Google Scholar]
- Saifuddin, A.; Blease, S.; Macsweeney, E. Axial loaded MRI of the lumbar spine. Clin. Radiol. 2003, 58, 661–671. [Google Scholar] [CrossRef]
- Damm, P. Loading of Total Hip Joint Replacements. Ph.D. Thesis, Technischen Universität, Berlin, Germany, 2014. [Google Scholar]
- Casesnoves, F. The Numerical Reuleaux Method, a Computational and Dynamical Base with Applications. First Part; Lambert Academic Publishing: Republic of Moldava, 2019; ISBN-10 3659917478. [Google Scholar]
- Casesnoves, F. Large-Scale Matlab Optimization Toolbox (MOT) Computing Methods in Radiotherapy Inverse Treatment Planning. High Performance Computing Meeting; Nottingham University: Nottingham, UK, 2007. [Google Scholar]
- Casesnoves, F. A Monte-Carlo Optimization method for the movement analysis of pseudo-rigid bodies. In Proceedings of the 10th SIAM Conference in Geometric Design and Computing, San Antonio, TX, USA, 4–8 November 2007. Contributed Talk. [Google Scholar]
- Casesnoves, F. ‘Theory and Primary Computational Simulations of the Numerical Reuleaux Method (NRM)’, Casesnoves, Francisco. Int. J. Math. Computation 2011, 13, 89–111. Available online: http://www.ceser.in/ceserp/index.php/ijmc/issue/view/119 (accessed on 28 June 2021).
- Casesnoves, F. Applied Inverse Methods for Optimal Geometrical-Mechanical Deformation of Lumbar artificial Disks/Implants with Numerical Reuleaux Method. 2D Comparative Simulations and Formulation. Comput. Sci. Appl. 2015, 2, 1–10. Available online: www.ethanpublishing.com (accessed on 28 June 2021).
- Casesnoves, F. Inverse methods and Integral-Differential model demonstration for optimal mechanical operation of power plants–numerical graphical optimization for second generation of tribology models. Electr. Control Commun. Eng. 2018, 14, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Casesnoves, F.; Surzhenkov, A. Inverse methods for computational simulations and optimization of erosion models in power plants. In Proceedings of the IEEE Proceedings of RUTCON2017 Power Engineering Conference, Riga, Latvia, 5 December 2017. [Google Scholar] [CrossRef]
- Abramobitz, S. Handbook of Mathematical Functions. Appl. Math. Ser. 1972, 55. [Google Scholar]
- Luenberger, G.D. Linear and Nonlinear Programming, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Casesnoves, F. Exact Integral Equation Determination with 3D Wedge Filter Convolution Factor Solution in Radiotherapy. Series of Computational-Programming 2D-3D Dosimetry Simulations. Int. J. Sci. Res. Sci. Eng. Technol. 2016, 2, 699–715. [Google Scholar]
- Panjabi, M.; White, A. Clinical Biomechanics of the Spine. Lippincott 1980, 42, S3. [Google Scholar]
- Casesnoves, F. Software Programming with Lumbar Spine Cadaveric Specimens for Computational Biomedical Applications. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2021, 7, 7–13. [Google Scholar]
- Surzhenkov, A.; Viljus, M.; Simson, T.; Tarbe, R.; Saarna, M.; Casesnoves, F. Wear resistance and mechanisms of composite hardfacings atabrasive impact erosion wear. J. Phys. 2017, 843, 012060. [Google Scholar] [CrossRef]
- Casesnoves, F. Computational Simulations of Vertebral Body for Optimal Instrumentation Design. ASME J. Med. Devices 2012, 6, 021014. [Google Scholar] [CrossRef]
- Barker, P. The effect of applying tension to the lumbar fasciae on segmental flexion and extension. In Proceedings of the 5th International Congress of Low Back and Pelvic Pain, Melbourne, Australia, 10–13 November 2014; pp. 50–52. [Google Scholar]
- European Textbook on Ethics in Research. European Commission, Directorate-General for Research. Unit L3. Governance and Ethics. European Research Area. Science and Society. EUR 24452 EN. Available online: https://op.europa.eu/en/publication-detail/-/publication/12567a07-6beb-4998-95cd-8bca103fcf43 (accessed on 28 June 2021).
- ALLEA. The European Code of Conduct for Research Integrity, Revised ed.; ALLEA: Berlin, Germany, 2017. [Google Scholar]

| Programming Numerical Data | ||
|---|---|---|
| Material | Hardness (Hv) and Histocompatibility | Head Diameter (mm) |
| Cast Co-Cr alloy | 300 Average/good | 28 [22, 28] |
| Titanium alloy | 362 (approx) /excellent | 28 [22, 28] |
| Optimization Data Intervals | ||
| Hardness (GPa) | [2.7, 4.0] | |
| Experimental Erosion (mm3/Mc) | [0.01, 1.8] | |
| Complementary Data | ElasticityModulus and Fracture Thoughness are useful for other type of calculations. The standard femoral head used diameter is 28mm. Cast Co-Cr alloy hardness varies in literature. There are a large number of Titanium alloys available with closely hardness. | |
| Dual 2D Optimization Results and 3D Interior Optimization Results | ||
|---|---|---|
| Material | Optimal K Adimensional | Optimal Hardness (kg, mm) |
| Cast Co-Cr alloy | 28.93 × 10−9 (truncated) | 3.05 × 106 (truncated) |
| Titanium | ||
| Residual for Optimal K | 660.44 × 103 (truncated) | |
| 3D Interior Optimization Results | ||
| 3D matrix Program | Validation of K optimal adimensional parameter. In chart. Validation of erosion rises when Hardness decreases | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casesnoves, F. Mathematical Standard-Parameters Dual Optimization for Metal Hip Arthroplasty Wear Modelling with Medical Physics Applications. Standards 2021, 1, 53-66. https://doi.org/10.3390/standards1010006
Casesnoves F. Mathematical Standard-Parameters Dual Optimization for Metal Hip Arthroplasty Wear Modelling with Medical Physics Applications. Standards. 2021; 1(1):53-66. https://doi.org/10.3390/standards1010006
Chicago/Turabian StyleCasesnoves, Francisco. 2021. "Mathematical Standard-Parameters Dual Optimization for Metal Hip Arthroplasty Wear Modelling with Medical Physics Applications" Standards 1, no. 1: 53-66. https://doi.org/10.3390/standards1010006
APA StyleCasesnoves, F. (2021). Mathematical Standard-Parameters Dual Optimization for Metal Hip Arthroplasty Wear Modelling with Medical Physics Applications. Standards, 1(1), 53-66. https://doi.org/10.3390/standards1010006




