Abstract
The International System of Quantities has to be used by scientific and engineering journals as well as by authors of their articles, conference papers, and corresponding books, especially textbooks. This paper describes the historical development and the state of the art of international communications in science, engineering, technology, production, and sustainable development. The International System of Quantities (ISQ) which systematically elaborated on the standards of the International Organization for Standardization and International Electrotechnical Commission on quantities and units (ISO/IEC 80000) still needs to be generally accepted and used. The list of standardized base and derived quantities with their symbols, and rules for terminology of other quantities are presented. In addition, names and symbols of base, derived, and “compound” units for these quantities are given. The most frequent mistakes and some recommendations about the use of quantities, units, prefixes, quantity value expressions, numbers, and symbols of chemical elements are shown, too. The standards shall be available in open access. The lack of standardized quantities regarding science, engineering, and economics is drawn to attention. Further development of the international systems of quantities and units could bring substantial synergies worldwide.
1. Introduction
Alphabetic writing started three millennia ago in the Sinai peninsula, and continued in ancient Phoenicia, Israel, Greece, and Italy. The Latin alphabet was developed in the Roman Empire and its symbols and letters have been changing over the last millennium but they have become the main global script today. They are used not only in Western and Central Europe, North and South America, and Australasia but also in Central and South Africa, and in some countries of Asia. Today, Greek letters are still used in Greece, and in science and engineering.
World languages evolved mostly with empires; ancient Greek and Latin languages are most known but also Chinese, Persian, Arabic languages became widespread. In modern ages Spanish, English, French, and Russian languages became internationally used. Today, about 1.2 G (billion) people speak native Chinese, 1.1 G English, 0.8 G Indo-Aryan, and 0.5 G Arab languages. Latin and Arab languages are still used worldwide for religious purposes but in the 19th century French and in the 20th century English has overtaken world communications in international relations, business, commerce, science, and education.
A similar development occurred with numbers and their symbols—numerals. The Egyptians had been the first to use the ciphered numeral system, followed by Greeks’ numbers and the Roman numeral system which had combined several letters of the Roman alphabet (I, V, X, L, C, D, and M) into numbers which were used in Europe until the end of the 14th century when the Hindu-Arabic numeral system started to substitute them; it spread out to the whole world at the present. However, Roman numerals are still used, e.g., in denoting centuries, months, and the 21 cards (trumps) in the tarot game.
Weights and measures were the next groups that evolved with human development. A unit of measurement was agreed upon, most often imposed by a national sovereign or international emperor. In the beginning, the measures were based on the human body, e.g., inch, foot, or natural phenomena, e.g., day, year. Various definitions existed in different countries, e.g., for a pound—it originated from the Roman libra (abbreviated as lb); an international agreement about the value of a pound was accepted as late as 1959 (1 lb = 0.453 592 37 kg, exactly). The multiplier was most often the number 12, e.g., 1 ft = 12 inches, 1 foot is equal to 12 inches, as it was easily divided by 2, 3, and 4.
1.1. The International System of Units
The French revolution brought up the metric, decimal system. It was initiated in 1792 and the first prototypes of metre and kilogram were standardized in 1799. In 1861 coherent measurement units were introduced with the units of length (centimetre), mass (gram), and time (second). In 1875 the Metre Convention (Convention du Mètre, also known as Treaty of the Metre) was signed by 17 member states. The following international organization and its two bodies were formed:
- The General Conference on Weights and Measures (Conférence Générale des Poids et Mesures, CGPM),
- The International Committee for Weights and Measures (Comité International des Poids et Mesures, CIPM) and,
- The International Bureau for Weights and Measures (Bureau International des Poids et Mesures, BIPM).
In 1901 the CGPM declared a kilogram as a unit of mass, not of weight. In 1960, the CGPM accepted the International System of Units (Système International d’Unités, SI [1]) with four additional “base units” to metre and kilogram: second for a time duration, ampere for electric current, kelvin for thermodynamic temperature, and candela for luminous intensity; 16 “derived units” with special names were accepted, too. The seventh base unit, mole for amount of substance was accepted by the CGPM in 1971. Six additional derived units with special names have been gradually adopted, bringing their number to 22. The SI base units have been redefined several times and the last time took place in 2018 following Feller’s proposal [2] of using “exact numerical values for seven defining constants expressed in terms of their SI units” (1, pp. 127–135); e.g., “the metre was redefined in terms of the speed of light, and the second was redefined based on the microwave frequency of a caesium atomic clock”. In the European Union (EU), the SI acceptance and adaptations are being led by the European Commission, and its directives are realized by member states.
Today, SI is prevailing in the world, only Myanmar (Burma) and Hong Kong are not using it. The UK and USA are still predominantly using the old English system with the UK imperial units and US customary units, respectively, besides the SI (the so-called hybrid system); they are used in general public but not in science, engineering, medicine, and many industrial companies—especially not in multinational ones. Besides, they have been defined exactly by the SI units. The United States National Institute of Standards and Technology, NIST, has adopted and published the SI [3].
Symbols of base units and derived units with special names have been developed in parallel with the metric units and are now well established. The SI system also provides twenty prefixes to the unit names and unit symbols that may be used when specifying power-of-ten (i.e., decimal) multiples or submultiples of SI units.
1.2. The International System of Quantities—ISQ
The system of quantities was the last to be developed and standardized globally. Quantity is a property of a phenomenon, body, or substance, where the property has a magnitude that can be expressed by means of a number and a reference (unit). The first international organizations trying to adopt chemical and physical quantities were the International Union of Pure and Applied Physics, IUPAP (established in 1922) and the International Union of Pure and Applied Chemistry, IUPAC (formed in 1919). IUPAP prepared its first edition of Symbols, Units and Nomenclature in Physics in 1961—for official use only [4]; its 1987 revision is available online [5]. IUPAC published the first edition of the Manual of Symbols and Terminology for Physicochemical Quantities and Units in 1969 [6]. After the 3rd edition they changed the title of the manual and published it as the Green Book, again with three editions [7]. The Green Book is available on Internet, too.
In 1988, the International Organization for Standardization, ISO, in cooperation with the International Electrotechnical Commission, IEC, published the first edition of the international standard ISO 31 Quantities and units in 14 parts [8], and ISO 1 000 SI units and recommendations for use [9]. In 1992 both standards were substituted by ISO 80000 Quantities and units containing 13 somewhat reorganized parts; the last edition was published in 2019 with the exception of the parts mentioned in parentheses [10]:
- General (2009)
- Mathematics
- Space and time
- Mechanics
- Thermodynamics
- Electromagnetism (2008)
- Light and radiation
- Acoustics (2020)
- Physical chemistry and molecular physics
- Atomic and nuclear physics
- Characteristic numbers
- Condensed matter physics
- Information science and technology (2008)
The general part contains information about quantities and units, printing rules, rules for terms in names for physical quantities, rounding of numbers, logarithmic quantities, and international organizations in the field. In parts 3–13, the quantities of each subset are listed including: item number, quantity name, symbol and definition, unit symbol, and eventual remarks. Each part has an alphabetical index of quantities at the end to enable searching the items. Most of the parts have been updated in 2019 and 2020 with the exception of parts 1 (2009), 6 (2008), 13 (2008), and 14 (2008, withdrawn); the first two of them are planned to be updated in the year 2021.
In 1984 the first edition of the International vocabulary of basic and general terms in metrology was published by the ISO [11]. The Joint Committee for Guides in Metrology (JCGM) was formed in 1997 by seven International Organizations: BIPM, IEC, the International Federation of Clinical Chemistry and Laboratory Medicine (IFCC), ISO, IUPAC, IUPAP, and the International Organization of Legal Metrology (OIML); in 2005, the International Laboratory Accreditation Cooperation (ILAC) officially joined the seven founding international organizations. JCMG prepared the International vocabulary of basic and general terms in metrology (VIM)—its third edition (2008) with small corrections (2012) is available on the Internet [12]. It includes English and French terms of quantities and units, measurements, devices for measurement, properties of measurement devices, and measurements standards (Etalons).
After having worldwide acceptable letters, numerals, and measurement units we have already had for some decades the International System of Quantities (ISQ), which was legally accepted by members from 165 countries (including the UK and USA). The authors of scientific journals and journal lectors shall use the International System of Units (SI) for all dimensional quantities, and respect the ISO 80000 standard rules on the names and symbols of quantities and units. ISQ is still developing—we are urgently missing rules for quantities in some additional fields, e.g., in chemical engineering and economics.
Many mistakes exist that authors of scientific papers and articles do not pay attention to in the SI and ISQ systems. Even most international journals do not require the authors to use ISQ rules; the author’s corrections which are respecting the ISO rules may even be changed during the final corrections into wrong printing. All scientists and engineers (mechanical, chemical, electrical, civil, textile, metallurgical, etc.) need to talk the same language (terminology) and use the same symbols for quantities and units to understand each other and avoid crucial mistakes. That is why the international standard on quantities and units is essential; every one shall respect it and its principles, not use “field languages”. Universities are expected to respect the rules of ISO 80000, teach and apply the legal nomenclature thus making the students’ knowledge acquisition easier. It is difficult for students if the lecturers of different courses, e.g., in physics or chemistry and engineering are using different names, symbols, and units for the same physical or chemical quantity—often they miss the synergy of using the same name, symbol, and unit. The same is true for the terminology used in scientific and professional journals, conference proceedings, books, and manuals. Besides that the SI and ISO standards:
- Ensure that products and services are safe, reliable and of good quality;
- For business, they are strategic tools that reduce costs by minimizing waste, losses, and errors and increase productivity; they help companies to access new markets, level the playing field for developing countries, and facilitate free and fair global trade.
In the following sections, the most important rules from the SI Brochure [1] and ISO 80000-1 [10], and the most common mistakes regarding quantities, dimensions, measurement units, numbers, and printing rules will be explained. The article brings practical advice on how to use agreed upon names and symbols of quantities, and reduce the mistakes and time losses that arise when using different names and symbols for the same quantity.
2. Quantities
2.1. Quantity Names and Definitions
ISQ contains 7 base quantities and 22 derived quantities with special names of their units. Derived quantities are defined in terms of base quantities. The parts of ISO 80000 cite 715 quantities and 238 mathematical items. This is far from the number of quantities used today. As mentioned before, some engineering and economic fields are completely missing. Therefore, we have to respect the nearly 1 000 of those agreed upon. Besides that, the ISO 80000-1 presents some norms to names of physical quantities (Table 1). The most often occurring mistakes are misuse of terms coefficient and factor, (amount of substance) concentration and mass concentration, molarity and concentration, mass and weight, (mass, volume, amount of substance, and number) ratios and fractions. Ordinal properties, such as Rockwell hardness, and nominal properties, such as the colour of light, are not a part of the ISQ.

Table 1.
Terms in names for physical quantities.
Here are more elaborate explanations of the quantities in Table 1:
- The term “coefficient” should be used when two quantities A and B have different dimensions, e.g., linear expansion coefficient αl, dl/l = αl dT—its unit is not equal to 1; sometimes, the term “modulus” is used instead of the term “coefficient”, e.g., modulus of elasticity E, σ = Eε.
- The term “factor” should be used when the two quantities A and B have the same dimension, e.g., friction factor, μ, F = μFn; its unit is 1.
- The adjective “specific” is added to the name of a quantity to indicate the quotient of that quantity by mass, e.g., specific heat capacity c, c = C/m; specific volume v, v = V/m
- Combination of quantities which occur in equations are often considered to constitute a new quantity called “parameter”, e.g., Grüneisen parameter γ, γ = αV/(kcVρ).
- The quotient of two quantities of the same dimension is often called “ratio”, e.g., ratio of specific heat capacities γ, γ = cp/cV; its unit is 1;
- ○
- The term “index” is sometimes used instead of ratio, e.g., refractive index n, n = c0/c
- ○
- The term “fraction” is used for ratios smaller than one, e.g., mass fraction of a substance X, wX, wX = mX/m; amount of substance fraction xX, yX, xX = nX/n; volume fraction φX, φX = xXVm,X/(Σi xXVm,i) (Vm,X being molar volume); their unit is 1;
- The term “percentage” shall not be used in a quantity name, because it is misleading; if a mass fraction is 0.78 (w = 78%), is the percentage than 78 or 78% = 0.78? Instead, the unambiguous term (volume, number, time, or amount of substance) “fraction” shall be used; the terms “mole fraction” and “share in %” are deprecated, too.
- The noun “density” is added to the name of a quantity to indicate the quotient of that quantity by the volume, e.g., mass density ρ, ρ = m/V; energy density e, e = E/V
- ○
- The noun “density” is also used to express a flux or current to indicate the quotient of such a quantity by the surface area, e.g., density of heat flow rate q, q = Φ/A
- ○
- The term “surface … density” is added to the name of a quantity to indicate the quotient of that quantity by the area, e.g., surface mass density ρA, ρA = dm/dA
- ○
- The term “linear … density” or the adjective “linear” is added to the name of a quantity to indicate the quotient of that quantity by the length, e.g., linear mass density or linear density ρl, ρl = dm/dl
- ○
- The term “linear” is also added to the name of a quantity, solely to distinguish between similar quantities, e.g., linear expansion coefficient αl, αl = (1/l)(dl/dT), and cubic expansion coefficient αV, αV = (1/V)(dV/dT)
- The adjective “molar” is added to the name of a quantity to indicate the quotient of that quantity by the amount of substance, e.g., molar volume Vm, Vm = V/n; molar mass M, M = m/n.
- The term “concentration” is added to the name of a quantity to indicate the quotient of that quantity by the total volume, e.g., amount of substance (B) concentration cB, cB = nB/V; mass concentration ρB, ρB = mB/V; number (particle or molecular) concentration CB, CB = NB/V; in chemistry, the name “amount of substance concentration” can be abbreviated to “concentration” or replaced by specifying the substance, e.g., concentration of benzene, but the adjective “mass” should never be omitted from the name “mass concentration”. “Molarity” with a symbol M and the unit mol/L shall be avoided—use (amount of substance) concentration and the symbol c.
Ordinal properties are defined by a conventional procedure, for which a total ordering relation can be established, according to magnitude, but no algebraic operations among these properties exist. They have neither measurement units nor quantity dimensions. Ordinal properties are arranged according to ordinal scales. Some examples are: Rockwell C hardness, octane number for petroleum fuel, earthquake strength on the Richter scale.
The nominal property of a phenomenon, body, or substance has no magnitude but it has a value, which can be expressed in words, by alpha-numerical codes, or by other means. Some examples include: sex of a human being, the colour of a paint sample, ISO two-letter country code, the sequence of amino acids in a polypeptide.
2.2. Symbols for Quantities
Symbols for quantities are generally single letters from the Latin or Greek alphabet, sometimes with subscripts or explanations in parentheses. Symbols for characteristic numbers are written with two letters, the initial of which is always a capital, e.g., Ma for Mach number.
The quantity symbols are always printed in italic (sloping) type irrespective of the type used in the rest of the text—italics are used automatically with the Equation Editor. On the other side, the symbols of units are printed in roman type. Therefore, m means metre while m stands for mass. A subscript that represents a physical quantity or a mathematical variable, such as running number, is printed in italic (sloping) style, e.g., Cp (p: pressure), ci (i: running number), but μr (r: relative), Sm (m: molar). The e or exp as a base of natural logarithms is printed in roman. The same is true for the constant π (Ludolf number), and for mathematical symbols in expressions lg x, ln x, min(a, b), max f(x), lim f(x), sin x, sinh x, erf x, etc.
When symbols for quantities are combined in a product of two or more quantities, this combination is indicated in one of the following ways: ab, a b, a · b, e.g., –r = kcAcB2. Division of one quantity by another is indicated in one of the following ways: , a/b, a b−1, a · b−1; the solidus (/) can be substituted by a horizontal bar. Do not write ab−1, without a thin space between a and b−1, as ab−1 could be misinterpreted as (ab)−1. Parentheses shall be used in more complex expressions, e.g., a/(b · c), (a · b)(c + d).
Authors often do not distinguish between symbols of quantities and acronyms. Acronyms are abbreviations, usually formed from the initial letters of a group of words, e.g., BTC for the “blow-down treatment cost”. They are printed in roman type and they shall not be used in equations. Symbols and abbreviations shall be explained when used for the first time if further usage is planned. Also, a list of quantity symbols (with names and units) and acronyms shall be presented.
ISO 80000 does not cover fields of economics, operational research, or statistics. Economists often use acronyms instead of single-letter symbols for economic quantities, even in equations, e.g., NPV for net present value, IRR for internal rate of return. In accordance with ISO 80000-1 rules, we suggest using the following symbols for economic quantities: C for cost, D for depreciation, E for expenses, FC for cash flow, i for interest rate, IFC for fixed capital investment, N for number, RIR for internal return rate, S for sales, tpb for payback time, VB for book value, VNP for net present value (or worth), etc.
2.3. Frequent Mistakes
Frequent mistakes connected with names of quantities are:
Quantities shall be clearly defined, e.g., mass fraction of sodium, w(Na) or wNa, or its amount fraction, x(Na) or xNa.
- Specification of quantities, e.g., chemical oxygen demand is a part of the name of a quantity, it is not a part of the unit (mass concentration of O2 in mg/l, not mg O2 per litre).
- “Amount (of substance)” is a chemical quantity expressed in moles; therefore, the word is not to be used for values in general (e.g., amount of heat)—be specific (use e.g., volume, mass, amount of substance, number, heat) or use magnitude, value, or contents as a general term.
- Velocity is a vector (rate of change of a position vector); speed is the magnitude of a velocity.
Differentiate between:
- Mass, m in kg, and weight Fg in N;
- Mass density or density, ρ or ρm in kg/m3, surface (mass) density, ρA in kg/m2, linear (mass) density, ρl in kg/m, and density of heat flow rate, q or ϕ in W/m2;
- Mass flow rate, qm in kg/s, and mass flow, jm in kg/(m2 s);
- Work, W in J, energy, E in J, heat, Q in J, enthalpy H in J, and pressure, p in Pa;
- Power, P in W, heat flow rate, Φ in W, and enthalpy flow rate, I in W;
- Heat capacity, C in J/K, specific heat capacity, c in J/(kg K), specific heat capacity at constant pressure, cp in J/(kg K), and specific heat capacity at constant volume, cV in J/(kg K);
- Depreciation (decrease in value of a property over an estimated period of time, e.g., per year), and amortization (decrease in value when the period of time is definitely known).
Regarding quantity symbols, mind the following mistakes and recommendations:
- Find the right symbol by examining each Index of ISO 80000 parts 3–13 (hopefully, a new edition of ISO Standards Handbook [13] with a joint index will be published soon);
- Any attachment to a unit symbol as a means of giving information about the special nature of the quantity or context of measurement under consideration is not permitted, e.g., Pe = 700 kW, not P = 700 kWe; Umax = 500 V, not U = 500 Vmax;
- Do not use different symbols for the same quantity; when, for one quantity, different applications or different values are of interest, a distinction can be made by the use of subscripts, e.g., FF for an amount flow rate of feed to the distillation column, FB for bottom product one, FD for distillate flow rate;
- Do not use two different symbols for the same quantity, e.g., A and S for area;
- Do not use the same symbol for two different quantities instead of two different symbols, e.g., γ for mass concentration (g/L), w for mass fraction, and ζ for mass ratio (e.g., in g/kg);
- Use N for number of entities (not n, which is used for the amount of substance in moles);
- Use qV for volume flow rate (in m3/s), but qm for the mass flow rate (in kg/s).
3. Units
3.1. SI Base Units
The International System of Units (SI) is a set of base units, together with their names and symbols, multiples and submultiples, defined in accordance with given rules. The SI is based on seven base quantities (Table 2). In each coherent system, there is only one base unit for each base quantity, e.g., in the SI, the metre is the base unit of length. Symbols representing the dimensions of the abase quantities in the ISQ are also presented; they are printed in single upper case letters in roman, sans serif type, e.g., Calibri, Helvetica, but not Times New Roman.

Table 2.
Seven International System of Quantities (ISQ) base quantities, their International System of Units (SI) base units, and quantity dimensions.
3.2. SI Derived Units
A derived unit is a measurement unit for a derived quantity; for example, the metre per second, symbol m/s, and the centimetre per second, cm/s, are derived units of speed in SI. Coherent derived unit is a product of powers of base units with no other proportionality factor than one; e.g., metre per second is the coherent derived unit for velocity when velocity is defined by the quantity equation v = dr/dt. The kilometre per hour is not a coherent derived unit in SI. Centimetre per second is also not a coherent derived unit in SI but it is a coherent derived unit in the CGS (centimetre, gram, second) system.
Dimension expresses a derived quantity with the base quantity dimensions as a product of powers of factors corresponding to the base quantities, dim Q = LαMβTγIδΘεNζJη, omitting any numerical factor, e.g., the dimension of force is denoted by dim F = LMT−2. In ISQ, dim ρB = ML−3 is the quantity dimension of mass concentration of component B, ρB, and also the dimension of mass density, ρ. Quantities with the same dimension are named quantities of the same kind. When all exponents of the factors corresponding to a base quantity in its quantity dimension are zero, a quantity of dimension number (“dimensionless quantity”) is obtained.
The derived unit for force is kg m/s2, which is rather inconvenient. Therefore, special names and symbols have been approved for the 22 most common SI-derived units (Table 3)—the last four of them are admitted for reasons of safeguarding human health. Symbols for units consist of one or two letters from the Latin or Greek alphabet. These letters are lower case, except that the initial letter is a capital when the unit is derived from a proper name of a person, e.g., V for volt, A for ampere.

Table 3.
SI derived units with special names and symbols.
There are some non-SI, non-coherent units that are allowed to be used with the SI (Table 4); the year (symbol a, 1 a = 365.242 20 d = 31 556 926 s) is not included. Atomic and CGS units, imperial and US customary units (foot, pound, and second) as well as the units carat, tex, atmosphere (atm, and at), torr, mmH2O, calories (cal) are deprecated.

Table 4.
Units used with SI.
Finally, “compound units” can be formed by multiplication and/or division of different base and/or derived units. The SI Brochure lists some examples of SI coherent derived units, dividing them into two groups:
- Those expressed in terms of base units, e.g., m3 for volume, m/s for velocity or speed, kg/m3 for (mass) density or mass concentration, A/m for magnetic field strength, mol/m3 for the amount of substance concentration, cd/m2 for luminance, etc.
- Those whose names and symbols include SI coherent derived units with special names and symbols, e.g., Pa s for dynamic viscosity, N m for the moment of force, rad/s for angular acceleration, W/m2 for heat flux density or irradiance, J/(kg K) for specific heat capacity, J/m3 for energy density, J/mol for molar energy, J/(mol K) for molar entropy or molar heat capacity, Gy/s for absorbed dose rate, kat/m3 for catalytic activity concentration.
Measurement units of quantities with the same dimension may be designated by the same name and symbol even when they are not of the same kind. The measurement unit of quantities of dimension number is the number one, symbol 1. In some cases, they are expressed by quotients such as millimole per mole, equal to 10−3, and microgram per kilogram, equal to 10−9.
“Compound units”, formed by multiplication of two or more units shall be printed in one of the two forms: N m or N · m, kW h, or kW · h. “Compound units” formed by dividing one unit by another one can be written in one of the following ways: , m/s, m s−1, m · s−1. Exponentiation has priority over multiplication and division. A solidus (/) shall not be followed by a multiplication sign or a division sign on the same line unless parentheses are inserted to avoid any ambiguity, e.g., J/ (mol K).
3.3. SI Prefixes
In order to avoid large or small numerical values, decimal multiples and submultiples of the coherent SI units are formed with the SI prefixes listed in Table 5. These SI multiple units and SI submultiple units are not coherent with respect to ISQ.

Table 5.
SI prefixes.
The symbol of a prefix shall be combined with the single unit symbol to which it is directly attached, without a space between the symbol for the prefix and the symbol for the unit, forming a new symbol for a decimal multiple or submultiple. They can be raised to a positive or negative power or be combined with other unit symbols to form symbols for compound units, e.g., 1 cm3 = (10−2 m)3 = 10−6 m3.
Compound prefixes shall not be used, e.g., write nm (nanometre) for 10−9 m, not mμm. For historical reasons, the name of the base unit of mass, the kilogram, contains the SI prefix “kilo”. The names of its multiples are formed by adding the prefixes to the gram with the symbol g, e.g., milligram, symbol mg instead of microkilogram (μkg). The SI prefixes shall not be used to denote binary multiples, e.g., 1 kbit = 1 000 bit, but 1 Kibit = 1 024 bit (other prefixes for binary multiples are presented in ISO 80000-1, p. 8).
The SI prefixes are also used together with the ISO currency codes, e.g., 1 kEUR = 1 000 European euros (€); 1 MUSD = 106 US dollars ($), 1 GSEK = 109 Swedish crowns.
The unit one, symbol 1 is generally not written out explicitly when such a quantity is expressed numerically, e.g., the number of turns in a winding N = 25 × 1 = 25. In the case of certain quantities, the unit one has a special name and symbol, e.g., plane angle α = 0.52 rad = 0.52; level of power quantity LF = 12 Np = 12. Such special names and symbols may be used in expressions for derived units, e.g., angular velocity ω = 17 rad/s; attenuation coefficient α = 0.83 Np/m.
Often per cent, symbol %, or per mil, symbol ‰, are used as a submultiple of the unit one. They are not quantities, therefore the “percentage” as a quantity name is not allowed. Additional information, such as % (m/m) or % (V/V) shall not be attached to the unit symbol %. The preferred way of expressing, e.g., the mass fraction of B, is wB = 78%. Abbreviations such as ppm, ppb, and ppt are ambiguous and shall not be used; instead of them, alternative mass or volume or amount of substance fractions can be expressed in units such as μg/g = 10−6, ml/m3 = 10−9, or pmol/mol = 10−12.
3.4. Frequent Mistakes and Some Recommendations
Some of the most often observed mistakes and recommendations regarding units are:
- When using an Arabic symbol for a number, the symbol of a unit shall be used, not the spelt-out name, e.g., 20% (not 20 per cent), 15 min (not 15 min). Spelt out numbers and names (e.g., fifteen minutes) are not familiar in science and engineering.
- The unit symbol rpm is not an SI unit symbol for rotational frequency (its symbol is n)—use min−1;
- The symbol for the unit degree Celsius is °C (Insert/Symbol/°), do not use the superscript 0, °C, or superscript o, °C;
- The symbol for the unit year is a, e.g., kt/a, not kt/yr or kt per year;
- A submultiple of 10−6 metre is micrometre, symbol μm, not micron;
- The SI multiple of the unit for mass can be kt (1000 kg), or Gg (109 g) but not million kg, Mkg;
- The SI unit for volume fraction is mL/m3 or μL/L (not ppm), μL/m3 or nL/L (not ppb);
- The SI unit for amount fraction is μmol/mol (not ppm), and nmol/mol (not ppb);
- The SI unit of concentration is mol/L or its submultiple mmol/L (not milli-equivalent).
4. Quantity Values and Numbers
4.1. Quantity Values
To express values of physical quantities, Arabic numerals followed by the international symbol for the unit shall be used, e.g., the wavelength of one of the sodium spectral lines is λ = 5.896 × 10−7 m = 589.6 nm. If the point is used as the decimal sign, the cross and not the half-high dot shall be used as the multiplication sign between two numbers. If the comma is used as the decimal sign, as practised by the ISO standards [14], both the cross and the half-high dot may be used as the multiplication sign between numbers. In some cases multiplication signs may be omitted, e.g., 4c – 5d, 6ab, 7(a + b), 3 ln 2.
The symbol for the unit shall be placed after the numerical value in the expression for a quantity, with a thin space between them, e.g., 12 m, 45 kg, 20 °C. This rule applies also to the units per cent, %, and per mil, ‰, e.g., 78%. The only exception to this rule applies for the units degree, minute, and second for plane angle where there is no space between the numerical value and the unit symbol, e.g., 90°, 50′, 32″.
If the quantity is expressed as a sum or a difference of quantities, then either parenthesis shall be used to combine numerical values, placing the common unit symbol after the complete numerical value, e.g., l = (12 – 7) m, or the expression shall be written as the sum or difference of expressions for quantities, e.g., l = 12 m – 7 m, but not l = 12 – 7 m; t = 23.6 °C, not t = 23.6 °C.
There shall be a thin space on both sides of a sign for dyadic operators such as mathematical signs –, <, ≤, =, >, ≥, +, –, ±, ×, e.g., a ≥ b, but not with monadic operators, e.g., +2.5, –r, ≥72. Other mathematical signs and symbols are given in ISO 80000-2.
Descriptive terms or names of quantities shall not be arranged in the form of a quantity names equation but rather expressed with the quantity symbols, e.g., density, ρ = m/V where m is mass and V is volume, not density = mass/volume.
In expressing the value of a quantity as the product of a numerical value and a unit, both of them may be treated by ordinary rules of algebra. For example, the equation p = 48 kPa may equally be written p/kPa = 48. The quotient of a quantity and a unit shall be used in a column heading of a table so that the entries in the table are simply numbers. For example, a table of velocity squared versus pressure may be formatted as shown in Table 6.

Table 6.
Expressing values of quantities using recommended column headings [1].
The axes of a graph may also be labelled in this way so that the tick marks are only numbers (Figure 1).
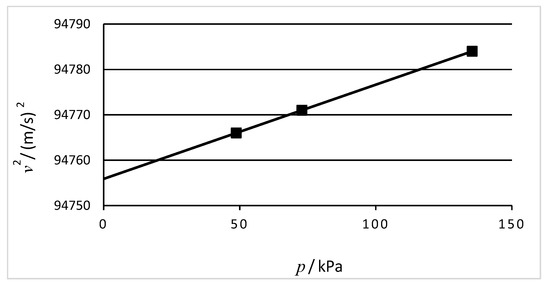
Figure 1.
Labelling of axes in a graph [1].
4.2. Numbers
Numbers shall be printed in roman type, irrespective of the type used in the rest of the text. Numbers shall be ordered in groups of three digits, counting from the decimal sign towards the left and the right, and the groups shall be separated by a small space and not by a point or a comma or by other means, e.g., 7 172.656 03. The separation into groups of three should not be used for ordinal numbers used as reference numbers, e.g., ISO 80000-1. The year shall always be written without a space, e.g., 2021. If the magnitude (absolute value) of the number is less than 1, the decimal sign shall be preceded by a zero, e.g., 0.657 89.
The sign for multiplication of numbers is a cross (×, not x) or a half-high dot (·). There shall be a thin space on both sides of the cross or the dot. They shall be used to indicate the multiplication of numbers and numerical values, e.g., l = 2.5 × 103 m; A = 80 mm × 25 mm, also in vector products and Cartesian products. The half-high dot shall be used to indicate a scalar product of vectors and is preferred for the multiplication of letter symbols. If the point is used as a decimal sign, the cross and not the half-high dot shall be used as a multiplication sign between numbers, e.g., 4 711.32 × 0.351 2. Division of one number by another is indicated in one of the following ways: , 1/2, 1 2−1, 1 · 2−1.
Digits of a number are called significant digits if the corresponding number is considered to lie within the error limit of the last digit(s); e.g., the number 401 000 can have from three to six significant digits what is differentiated by writing from 401 × 103 to 401.000 × 103. A standard uncertainty can be expressed in terms of the least significant digits in parentheses, e.g., l = 23.478 2(32) has the numerical value 23.478 2 and the standard uncertainty 32. The mathematical format 23.478 2 ± 0.003 2 shall be avoided as it does not contain all values between 23.481 4 and 23.475 0. Engineering tolerances 23.478 2 ± 0.003 2 contain the (upper and lower) limits and also all the values between them, symmetrically dispersed around the numerical value 23.478 2.
The rounding of numbers is explained in Annex B of the ISO 80000-1 standard.
4.3. Chemical Elements and Nuclides
Symbols of chemical elements shall be printed in roman type. The initial letter is a capital and the following letter, if any, is a lower case one. The nucleon (mass) number of a nuclide is shown in the left superscript position, e.g., 14N. The number of atoms of a nuclide in a molecule is shown in the right subscript position, e.g., 14N2; the number of atoms is equal to 1, if it is not indicated, e.g., H2O. The proton (atomic) number of a nuclide is shown in the left subscript position, e.g., 64Gd. The state of ionization and the state of electrical excitation are shown in the right superscript position, e.g., Na+, (PO4)3–. The state of nuclear excitation is shown with the symbol * in the left superscript position, e.g., 127*Xe.
5. Some Other Frequent Mistakes
There are some mistakes in printing that most authors are not aware of. The most frequent one is the use of a hyphen instead of the dash or minus. There are two slightly different conventions for using a dash. The more modern one is to put white spaces at both ends of a dash, while the older style uses no white spaces at all. Using the first one—you simply print a hyphen with a space before and after it (–), and the computer turns it into a dash after you finish the next word and add a space after it. This dash is called an en-dash as it takes approximately the width of the letter “N” or “n” (–) while an em-dash takes approximately the same width as the letter “M” or “m” (–). In addition:
- A hyphen (-) shall not be used instead of minus (–), or dash (–) in cases like Cl−, m−1; pH = 6–9, γ(Fe2+) = 3–4 mg/L, July 8–12.
- The dash (not the hyphen), used with number range has no spaces before and after it, e.g., 80–97%, 1.5–1.8 USD/m3, pp. 23–29. Spaces before and after each of them change their meanings from number range to minus.
- A range of values can be expressed by units at both bounds, e.g., from 20 MW to 35 MW, or a dash must be used, 20–35 MW.
The references shall be printed after carefully reading the Journal’s Instructions for Authors. Besides using the dash, not the hyphen with the above-mentioned number ranges of pages (the same is true for a number range of journal’s volumes), the following is observed:
- Journal names should be abbreviated according to the List of Title Word Abbreviations, e.g., [15].
- The www-references have to contain the date of access—according to ISO 8601 standard the calendar date is represented by the form YYYY-MM-DD, e.g., 2021-02-08.
- Initials of author names shall be separated by a space, e.g., Akal Solmaz, S. K., etc.
In the tables, numbers shall be vertically aligned according to the decimal sign. Acronyms shall not be used either in the article title or its abstract. The abstract shall be written in a single paragraph, including one sentence about: (a) the background/context, (b) findings, (c) discussion, (d) conclusions. Underscore the scientific value added by your paper in your abstract. Use the third person singular, instead of the first person singular or plural. Further observations include:
- Differentiate I/we will and I/we shall (future time).
- Make sure the pages are numbered.
- Several of your sentences are not properly referenced. Please make sure you attribute or reference them.
- Please avoid reference overkill/run-on, i.e., do not use more than three references per sentence. If you need to use more, make sure you state the key relevant idea of each reference.
- Make sure your conclusions section underscores the scientific value added by your paper, and/or the applicability of your findings/results.
- Mark that there is no spacing between the announcing sentence before the bulleted lines and the first bulleted line.
6. Conclusions and Outlook
This paper presents a need to join the efforts of the International Organization for Standardization and spread out the International System of Quantities, ISQ. After adopting the Latin and Greek letters, Arabic numerals, and International System of Units (SI), it is time to accept the ISQ in science and engineering by using it in articles, papers, and books from all fields. The ISQ covers nearly 1 000 physical quantities and mathematical items that are most frequently used in schools, in research and development, in industry and professional associations. The hesitation of many authors, scientists, and engineers as well as many scientific and professional journal editors to decide to use it is difficult to understand. How to explain to a pupil or a student that the same quantity has two or three different names, often even more symbols and units, preventing them to easily understand the connection of terms used in schools at different courses, e.g., physics, chemistry, electrical or mechanical engineering. What a loss of time and effort, synergy, and understanding!
The great disadvantage of ISO 80000 is that in contrast to the SI Brochure [1] it is not available in open access. Only some small parts of the standard can be reached on the Internet. Even of the general one, ISO 80000-1, only 12 pages out of 45 are open to the public. The member states of ISO and IEC shall agree to open the standards to all the interested in order to enable its wide usage. The costs for it are negligible in comparison to the potential public benefit. This is true also for national translations of the ISO 80000 standard series.
The present ISO 80000 part covers physics, physical chemistry, mechanical, electrical, and nuclear engineering. ISQ shall be extended to other fields of science and engineering. Life sciences (biology, ecology, medicine, etc.) are not covered so far although their importance is increasing. Chemical and process engineering and technology which covers chemicals and pharmaceuticals production, fuels extraction and refining, food and beverages value chain, production of materials (metals and alloys, ceramics and glass, pulp, paper and cardboard, cement and lime, plastics, leather, textiles and rubber, and corrosion protection) are not included in ISO 80000. ISO 80000-9 and the IUPAC Green Book [6] only cover physical chemistry and molecular physics. Unit operations, physicochemical separation and reaction processes, process design, optimization, and control as well as sustainable development urgently need standards of quantities, symbols, and units.
Multidisciplinary environmental engineering is of the utmost importance for biodiversity existence and for the sustainable development of the human race on Earth—it covers climate change, resource reduction, and efficiency, waste minimization towards zero waste, water, air and soil pollution, cleaning and reuse, energy and waste management with recycling, life cycle assessment, and circular economy, critical raw materials, dangerous substances, and human health. The need for ISO 80000 extension is urgent for civil engineering, too.
Social aspects with population growth and ageing, health and safety, social responsibility, quality management, and responsible care are also very important but the most urgent field is economics which is important during the process and product design, optimization, operations research, production, and evaluation of business results. The problem of applying economics is that there is no international standard available, the literature uses different definitions of terms, and acronyms are used instead of symbols for quantities.
Funding
This research was funded by the author.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bureau International des Poids et Mesures, BIPM. The International System of Units (SI), 9th ed.; SI Brochure: Sèvres, France, 2019; pp. 115–216. [Google Scholar]
- Feller, U. The International System of Units—A case for reconsideration. Accredit. Qual. Assur. 2011, 16, 143–153. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. The International System of Units (SI); Special Publication 330; Newell, D.B., Tiesinga, Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019. [Google Scholar] [CrossRef]
- Commission for Symbols, Units, Nomenclature, Atomic Masses and Fundamental Constants (SUN/AMCO Commission). Symbols, Units and Nomenclature in Physics; UIP-9, [SUN 61-44]; International Union of Pure and Applied Physics: Oak Ridge, TN, USA, 1961. [Google Scholar]
- Cohen, E.R.; Giacomo, P. Symbols, Units, Nomenclature and Fundamental Constants; 1987 Revision (2010 Reprint). Available online: https://iupap.org/wp-content/uploads/2014/05/A4.pdf (accessed on 10 January 2021).
- McGlashan, M.L. Manual of Symbols and Terminology for Physicochemical Quantities and Units, 1st ed. Pure Appl. Chem. 1970, 21, 1–38. [Google Scholar] [CrossRef]
- Cohen, E.R. Quantities, Units and Symbols in Physical Chemistry, 3rd ed.; Greenbook; IUPAC & RSC Publishing: Cambridge, UK, 2008. [Google Scholar]
- International Organization for Standardization. ISO 31-0–31-13, Quantities and Units; ISO: Genève, Switzerland, 1988. [Google Scholar]
- International Organization for Standardization. ISO 1000, SI Units and Recommendations for the Use of Their Multiples and of Certain other Units; ISO: Genève, Switzerland, 1992. [Google Scholar]
- International Organization for Standardization. ISO, International Electrotechnical Commission, IEC, ISO 800000 Quantities and Units; ISO: Geneve, Switzerland, 2020; Parts 1–13. [Google Scholar]
- International Organization for Standardization. International Vocabulary of Basic and General Terms in Metrology; ISO: Geneve, Switzerland, 1984; ISBN 10: 9267010328. [Google Scholar]
- International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM), 3rd ed. 2012. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf (accessed on 8 February 2021).
- International Organization for Standardization. Quantities and units. In ISO Standards Handbook, 3rd ed.; ISO: Genève, Switzerland, 1993. [Google Scholar]
- ISO/IEC Directives, Part 2. In Principles and Rules for the Structure and Drafting of ISO and IEC Documents, 8th ed.; ISO: Geneva, Switzerland, 2018.
- Journal Title Abbreviations, Caltech Library. Available online: https://www.library.caltech.edu/journal-title-abbreviations (accessed on 10 February 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).