Additivity and Interactions in Ecotoxicity of Pollutant Mixtures: Some Patterns, Conclusions, and Open Questions
Abstract
:1. Introduction and Aims
2. Additivity and Deviations from Additivity
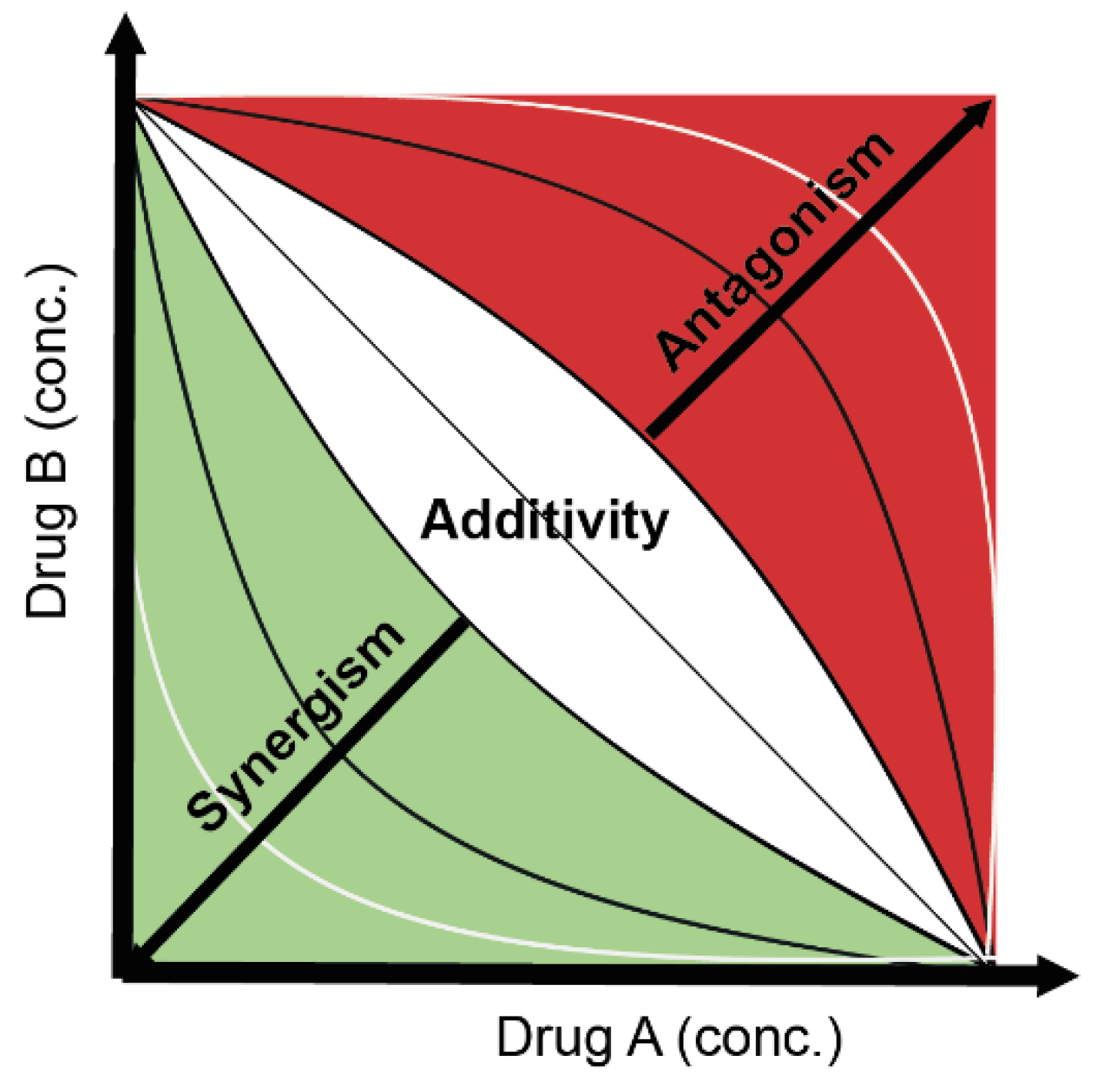

3. Concentration Addition and Independent Action in Ecotoxicology
4. Combination Index in Ecotoxicology
5. Is It Possible to Predict Synergism?
5.1. Prediction of Synergism (or Antagonism) among Pairs of Chemicals
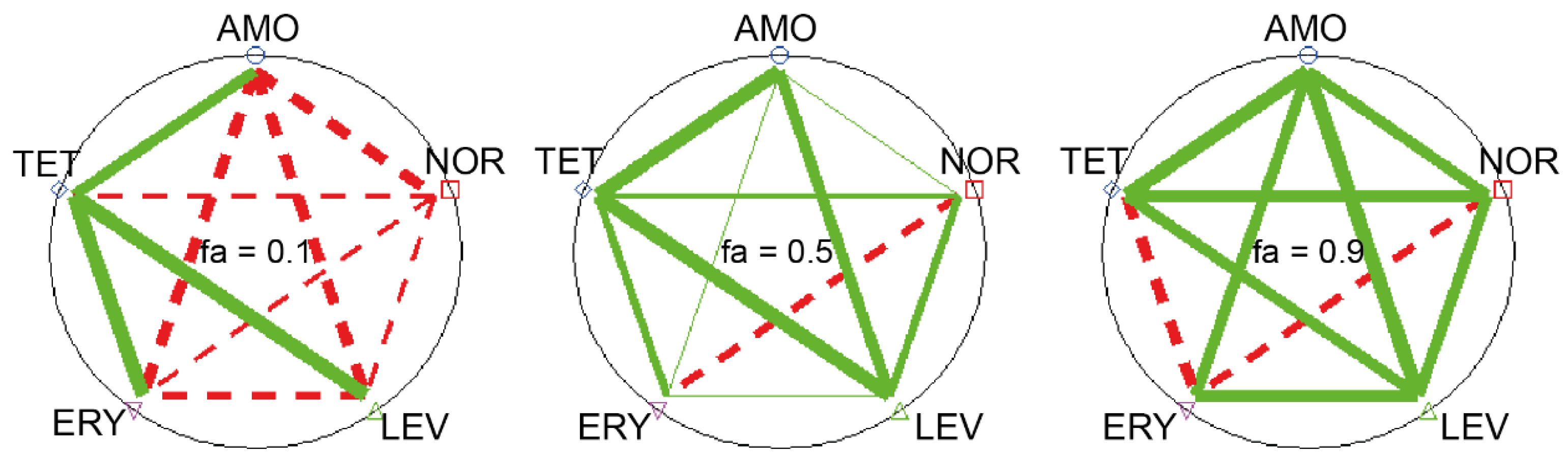
5.2. The Prediction of Multicomponent Interactions Based on Previous Knowledge on Component-Component Interactions
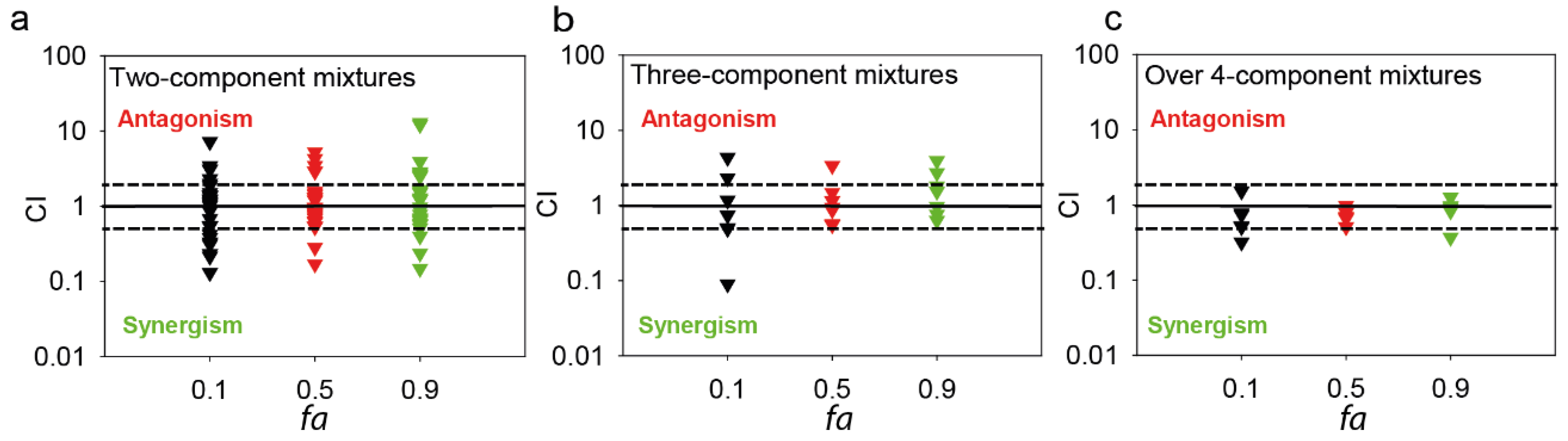
6. Fractional Approaches in Real World Conditions: Are They a Suitable Way Forward?
6.1. Chemical Concentrations at or Near the Toxicological Thresholds of Observable Effects
6.2. Mixtures of Individually “Active” Chemicals Only
6.3. Mixtures at Limited and Very Specific Component Ratios
6.4. Considering the Mixture and Its Potential Toxicity as a Static Entity
6.5. Mixtures Evaluated on Apical End-Points and Not Considering Interactions with Other Toxicologically Relevant Non-Chemical Factors
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Altenburger, R.; Backhaus, T.; Boedeker, W.; Faust, M.; Scholze, M. Simplifying complexity: Mixture toxicity assessment in the last 20 years. Environ. Toxicol. Chem. 2013, 32, 1685–1687. [Google Scholar] [CrossRef] [PubMed]
- Artigas, J.; Arts, G.; Babut, M.; Caracciolo, A.B.; Charles, S.; Chaumot, A.; Combourieu, B.; Dahllöf, I.; Despréaux, D.; Ferrari, B.; et al. Towards a renewed research agenda in ecotoxicology. Environ. Pollut. 2012, 160, 201–206. [Google Scholar] [CrossRef] [PubMed]
- Beketov, M.A.; Liess, M. Ecotoxicology and macroecology—Time for integration. Environ. Pollut. 2012, 162, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Brack, W.; Altenburger, R.; Schüürmann, G.; Krauss, M.; Herráez, D.L.; van Gils, J.; Slobodnik, J.; Munthe, J.; Gawlik, B.M.; van Wezel, A.; et al. The solutions project: Challenges and responses for present and future emerging pollutants in land and water resources management. Sci. Total Environ. 2015, 503–504, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Chou, T.C. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in drug combination studies. Pharmacol. Rev. 2006, 58, 621–681. [Google Scholar] [CrossRef] [PubMed]
- Kortenkamp, A.; Backhaus, T.; Faust, M. State of the Art Report on Mixture Toxicity; European Commission: Brussels, Belgium, 2009. [Google Scholar]
- European Commission. Scher, Sccs, Scenihr, Opinion on the Toxicity and Assessment of Chemical Mixtures; European Commission, DG SANCO: Brussels, Belgium, 2012. [Google Scholar]
- Goldin, A.; Mantel, N. The employment of combinations of drugs in the chemotherapy of neoplasia: A review. Cancer Res. 1957, 17, 635–654. [Google Scholar] [PubMed]
- US Environmental Protection Agency (EPA). Technical Support Document on Health Risk Assessment of Chemical Mixtures; US Environmental Protection Agency: Washington, DC, USA, 1990. [Google Scholar]
- Mumtaz, M.M.; Hertzberg, R. The status of interactions data in risk assessment of chemical mixtures. In Hazard Assessment of Chemicals; Saxena, J., Ed.; Taylor & Francis: Washington, DC, USA, 1993; Volume 8, pp. 47–79. [Google Scholar]
- Hertzberg, R.; Rice, G.; Teuchler, L.K. Methods for health risk assessment of combustion mixtures. In Hazardous Waste Incineration: Evaluating the Human Health and Environmental Risks; Roberts, S., Teaf, C., Bean, J., Eds.; CRC Press LLC: Boca Raton, FL, USA, 1999; pp. 105–148. [Google Scholar]
- US Environmental Protection Agency (EPA). Supplementary Guidance for Conducting Health Risk Assessment of Chemical Mixtures. US Environmental Protection Agency: Washington, DC, USA, 2000. [Google Scholar]
- U.S. Department of Health and Human Services, Public Health Service Agency for Toxic Substances and Disease Registry, Division of Toxicology (ATSDR). Guidance Manual for the Assessment of Joint Toxic Action of Chemical Mixtures; U.S. Department of Health and Human Services, Public Health Service Agency for Toxic Substances and Disease Registry, Division of Toxicology: Atlanta, GA, USA, 2004.
- Berenbaum, M.C. Criteria for analyzing interactions between biologically active agents. Adv. Cancer Res. 1981, 35, 269–335. [Google Scholar] [PubMed]
- Tallarida, R.J. Quantitative methods for assessing drug synergism. Genes Cancer 2011, 2, 1003–1008. [Google Scholar] [CrossRef] [PubMed]
- Bliss, C.I. The toxicity of poisons applied jointly. Ann. Appl. Biol. 1939, 26, 585–615. [Google Scholar] [CrossRef]
- Finney, D.J. The analysis of toxicity tests on mixtures of poisons. Ann. Appl. Biol. 1942, 29, 82–94. [Google Scholar] [CrossRef]
- Greco, W.R.; Bravo, G.; Parsons, J.C. The search for synergy: A critical review from a response surface perspective. Pharmacol. Rev. 1995, 47, 331–385. [Google Scholar] [PubMed]
- Loewe, S.; Muischnek, H. Über kombinationswirkungen. Arch. Exp. Pathol. Pharmakol. 1926, 114, 313–326. [Google Scholar] [CrossRef]
- Backhaus, T. Medicines, Shaken and Stirred: A Critical Review on the Ecotoxicology of Pharmaceutical Mixtures. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014. [Google Scholar] [CrossRef] [PubMed]
- Junghans, M.; Backhaus, T.; Faust, M.; Scholze, M.; Grimme, L.H. Application and validation of approaches for the predictive hazard assessment of realistic pesticide mixtures. Aquat. Toxicol. 2006, 76, 93–110. [Google Scholar] [CrossRef] [PubMed]
- Fraser, T.R. Lecture on the antagonism between the actions of active substances. Br. Med. J. 1872, 2, 485–487. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Loewe, S. Die quantitativen probleme der pharmakologie. Ergeb. Physiol. 1928, 27, 47–187. [Google Scholar] [CrossRef]
- Loewe, S. The problem of synergism and antagonism of combined drugs. Arzneim. Forsch. 1953, 3, 285–290. [Google Scholar]
- Cokol, M.; Chua, H.N.; Tasan, M.; Mutlu, B.; Weinstein, Z.B.; Suzuki, Y.; Nergiz, M.E.; Costanzo, M.; Baryshnikova, A.; Giaever, G.; et al. Systematic Exploration of Synergistic Drug Pairs. Mol. Syst. Biol. 2011. [Google Scholar] [CrossRef] [PubMed]
- Syberg, K.; Elleby, A.; Pedersen, H.; Cedergreen, N.; Forbes, V.E. Mixture toxicity of three toxicants with similar and dissimilar modes of action to daphnia magna. Ecotoxicol. Environ. Saf. 2008, 69, 428–436. [Google Scholar] [CrossRef] [PubMed]
- Carter, W.H., Jr.; Gennings, C. Analysis of chemical combinations: Relating isobolograms to response surfaces. In Toxicology of Chemical Mixtures; Yang, R.S.H., Ed.; Academic Press: San Diego, CA, USA, 1994; pp. 643–663. [Google Scholar]
- Chou, T.C.; Talalay, P. Generalized equations for the analysis of inhibitions of michaelis-menten and higher-order kinetic systems with two or more mutually exclusive and nonexclusive inhibitors. Eur. J. Biochem. 1981, 115, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Chou, T.C.; Talalay, P. Quantitative analysis of dose-effect relationships: The combined effects of multiple drugs or enzyme inhibitors. Adv. Enzym. Regul. 1984, 22, 27–55. [Google Scholar] [CrossRef]
- Chou, T.C.; Talaly, P. A simple generalized equation for the analysis of multiple inhibitions of michaelis-menten kinetic systems. J. Biol. Chem. 1977, 252, 6438–6442. [Google Scholar] [PubMed]
- Chou, T.C.; Martin, N. Compusyn for Drug Combinations: PC Software and User’s Guide: A Computer Program for Quantification of Synergism and Antagonism in Drug Combinations and the Determination of ic50 and ed50 and ld50 Values. ComboSyn, Inc.: Paramus, NJ, USA, 2005. [Google Scholar]
- Chou, T.C.; Talalay, P. Analysis of combined drug effects: A new look at a very old problem. Trends Pharmacol. Sci. 1983, 4, 450–454. [Google Scholar] [CrossRef]
- Rodea-Palomares, I.; Leganes, F.; Rosal, R.; Fernandez-Pinas, F. Toxicological interactions of perfluorooctane sulfonic acid (PFOS) and perfluorooctanoic acid (PFOA) with selected pollutants. J. Hazard. Mater. 2012, 201–202, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Rodea-Palomares, I.; Petre, A.L.; Boltes, K.; Leganes, F.; Perdigon-Melon, J.A.; Rosal, R.; Fernandez-Pinas, F. Application of the combination index (CI)-isobologram equation to study the toxicological interactions of lipid regulators in two aquatic bioluminescent organisms. Water Res. 2010, 44, 427–438. [Google Scholar] [CrossRef] [PubMed]
- Rosal, R.; Rodea-Palomares, I.; Boltes, K.; Fernandez-Pinas, F.; Leganes, F.; Petre, A. Ecotoxicological assessment of surfactants in the aquatic environment: Combined toxicity of docusate sodium with chlorinated pollutants. Chemosphere 2010, 81, 288–293. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chen, C.; Qian, Y.; Zhao, X.; Wang, Q. Ternary toxicological interactions of insecticides, herbicides, and a heavy metal on the earthworm eisenia fetida. J. Hazard. Mater. 2015, 284, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chen, C.; Qian, Y.; Zhao, X.; Wang, Q.; Kong, X. Toxicity of mixtures of λ-cyhalothrin, imidacloprid and cadmium on the earthworm eisenia fetida by combination index (CI)-isobologram method. Ecotoxicol. Environ. Saf. 2015, 111, 242–247. [Google Scholar]
- Gonzalez-Pleiter, M.; Gonzalo, S.; Rodea-Palomares, I.; Leganes, F.; Rosal, R.; Boltes, K.; Marco, E.; Fernandez-Pinas, F. Toxicity of five antibiotics and their mixtures towards photosynthetic aquatic organisms: Implications for environmental risk assessment. Water Res. 2013, 47, 2050–2064. [Google Scholar]
- Hermens, J.; Leeuwangh, P.; Musch, A. Joint toxicity of mixtures of groups of organic aquatic pollutants to the guppy (Poecilia reticulata). Ecotoxicol. Environ. Saf. 1985, 9, 321–326. [Google Scholar]
- Altenburger, R.; Backhaus, T.; Boedeker, W.; Faust, M.; Scholze, M.; Grimme, L.H. Predictability of the toxicity of multiple chemical mixtures to vibrio fischeri: Mixtures composed of similarly acting chemicals. Environ. Toxicol. Chem. 2000, 19, 2341–2347. [Google Scholar] [CrossRef]
- Backhaus, T.; Scholze, M.; Grimme, L.H. The single substance and mixture toxicity of quinolones to the bioluminescent bacterium vibrio fischeri. Aquat. Toxicol. 2000, 49, 49–61. [Google Scholar] [CrossRef]
- Faust, M.; Altenburger, R.; Backhaus, T.; Blanck, H.; Boedeker, W.; Gramatica, P.; Hamer, V.; Scholze, M.; Vighi, M.; Grimme, L.H. Predicting the joint algal toxicity of multi-component s-triazine mixtures at low-effect concentrations of individual toxicants. Aquat. Toxicol. 2001, 56, 13–32. [Google Scholar] [CrossRef]
- Faust, M.; Altenburger, R.; Backhaus, T.; Blanck, H.; Boedeker, W.; Gramatica, P.; Hamer, V.; Scholze, M.; Vighi, M.; Grimme, L.H. Joint algal toxicity of 16 dissimilarly acting chemicals is predictable by the concept of independent action. Aquat. Toxicol. 2003, 63, 43–63. [Google Scholar] [CrossRef]
- Faust, M.; Altenburger, R.; Backhaus, T.; Bödeker, W.; Scholze, M.; Grimme, L.H. Predictive assessment of the aquatic toxicity of multiple chemical mixtures. J. Environ. Qual. 2000, 29, 1063–1068. [Google Scholar] [CrossRef]
- Faust, M.; Altenburger, R.; Boedeker, W.; Grimme, L.H. Additive effects of herbicide combinations on aquatic non-target organisms. Sci. Total Environ. 1993, 134, 941–952. [Google Scholar] [CrossRef]
- Walter, H.; Consolaro, F.; Gramatica, P.; Scholze, M.; Altenburger, R. Mixture toxicity of priority pollutants at no observed effect concentrations (NOECS). Ecotoxicology 2002, 11, 299–310. [Google Scholar] [CrossRef] [PubMed]
- Teuschler, L.K. Deciding which chemical mixtures risk assessment methods work best for what mixtures. Toxicol. Appl. Pharmacol. 2007, 223, 139–147. [Google Scholar] [CrossRef] [PubMed]
- Rohr, J.R.; Schotthoefer, A.M.; Raffel, T.R.; Carrick, H.J.; Halstead, N.; Hoverman, J.T.; Johnson, C.M.; Johnson, L.B.; Lieske, C.; Piwoni, M.D.; et al. Agrochemicals increase trematode infections in a declining amphibian species. Nature 2008, 455, 1235–1239. [Google Scholar] [CrossRef] [PubMed]
- The Council of the European Union. Combination Effects of Chemicals; Council of the European Union: Brussels, Belgium, 2009. [Google Scholar]
- Meek, M.E.; Boobis, A.R.; Crofton, K.M.; Heinemeyer, G.; Raaij, M.V.; Vickers, C. Risk assessment of combined exposure to multiple chemicals: A who/ipcs framework. Regul. Toxicol. Pharmacol. 2011, 60, 1–14. [Google Scholar]
- Rodea-Palomares, I.; Fernandez-Piñas, F.; González-García, C.; Leganes, F. Use of lux-marked cyanobacterial bioreporters for assessment of individual and combined toxicities of metals in aqueous samples. In Handbook on Cyanobacteria: Biochemistry, Biotechnology and Applications; Nova Science Publishers, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Boltes, K.; Rosal, R.; Garcia-Calvo, E. Toxicity of mixtures of perfluorooctane sulphonic acid with chlorinated chemicals and lipid regulators. Chemosphere 2012, 86, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, R.N.; Arukwe, A.; Ait-Aissa, S.; Bado-Nilles, A.; Balzamo, S.; Baun, A.; Belkin, S.; Blaha, L.; Brion, F.; Conti, D.; et al. Mixtures of chemical pollutants at european legislation safety concentrations: How safe are they? Toxicol. Sci. 2014, 141, 218–233. [Google Scholar] [PubMed]
- Chen, C.; Wang, Y.; Qian, Y.; Zhao, X.; Wang, Q. The synergistic toxicity of the multiple chemical mixtures: Implications for risk assessment in the terrestrial environment. Environ. Int. 2015, 77, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Wang, Y.; Zhao, X.; Wang, Q.; Qian, Y. Comparative and combined acute toxicity of butachlor, imidacloprid and chlorpyrifos on earthworm, eisenia fetida. Chemosphere 2014, 100, 111–115. [Google Scholar] [CrossRef] [PubMed]
- Marx, C.; Muhlbauer, V.; Krebs, P.; Kuehn, V. Environmental risk assessment of antibiotics including synergistic and antagonistic combination effects. Sci. Total Environ. 2015, 524–525, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Backhaus, T.; Faust, M. Predictive environmental risk assessment of chemical mixtures: A conceptual framework. Environ. Sci. Technol. 2012, 46, 2564–2573. [Google Scholar] [CrossRef] [PubMed]
- Cedergreen, N. Quantifying synergy: A systematic review of mixture toxicity studies within environmental toxicology. PLoS ONE 2014, 9, e96580. [Google Scholar] [CrossRef] [PubMed]
- Bansal, M.; Yang, J.; Karan, C.; Menden, M.P.; Costello, J.C.; Tang, H.; Xiao, G.; Li, Y.; Allen, J.; Zhong, R.; et al. A community computational challenge to predict the activity of pairs of compounds. Nat. Biotech. 2014, 32, 1213–1222. [Google Scholar] [CrossRef] [PubMed]
- Spurgeon, D.J.; Jones, O.A.H.; Dorne, J.L.C.M.; Svendsen, C.; Swain, S.; Stürzenbaum, S.R. Systems toxicology approaches for understanding the joint effects of environmental chemical mixtures. Sci. Total Environ. 2010, 408, 3725–3734. [Google Scholar] [CrossRef] [PubMed]
- DREAM7-NCI-DREAM, Drug Sensitivity and Drug Synergy Challenges. Available online: https://www.synapse.org/#!Synapse:syn2785778/wiki/70254 (accessed on 25 June 2015).
- Warne, M.S.; Hawker, D.W. The number of components in a mixture determines whether synergistic and antagonistic or additive toxicity predominate: The funnel hypothesis. Ecotoxicol. Environ. Saf. 1995, 31, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Laetz, C.A.; Baldwin, D.H.; Collier, T.K.; Hebert, V.; Stark, J.D.; Scholz, N.L. The synergistic toxicity of pesticide mixtures: Implications for risk assessment and the conservation of endangered pacific salmon. Environ. Health Perspect. 2009, 117, 348–353. [Google Scholar] [CrossRef] [PubMed]
- Laetz, C.A.; Baldwin, D.H.; Hebert, V.; Stark, J.D.; Scholz, N.L. Interactive neurobehavioral toxicity of diazinon, malathion, and ethoprop to juvenile coho salmon. Environ. Sci. Technol. 2013, 47, 2925–2931. [Google Scholar] [CrossRef] [PubMed]
- Barran-Berdon, A.L.; Rodea-Palomares, I.; Leganes, F.; Fernandez-Pinas, F. Free Ca2+ as an early intracellular biomarker of exposure of cyanobacteria to environmental pollution. Anal. Bioanal. Chem. 2011, 400, 1015–1029. [Google Scholar] [CrossRef] [PubMed]
- Cedergreen, N.; Sorensen, H.; Svendsen, C. Can the joint effect of ternary mixtures be predicted from binary mixture toxicity results? Sci. Total Environ. 2012, 427–428, 229–237. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.; Lin, Z.; Yu, J.; Yin, D. Influence factors of multicomponent mixtures containing reactive chemicals and their joint effects. Chemosphere 2012, 88, 994–1000. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.; Lin, Z.; Ding, J.; Yin, D.; Zhang, Y. Application of the similarity parameter (λ) to prediction of the joint effects of nonequitoxic mixtures. Arch. Environ. Contam. Toxicol. 2012, 62, 195–209. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.; Lin, Z.; Zhou, X.; Yin, D. The underlying toxicological mechanism of chemical mixtures: A case study on mixture toxicity of cyanogenic toxicants and aldehydes to photobacterium phosphoreum. Toxicol. Appl. Pharmacol. 2013, 272, 551–558. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Tian, D.; Lin, Z.; Wang, D.; Yu, H. Study on the variation rules of the joint effects for multicomponent mixtures containing cyanogenic toxicants and aldehydes based on the transition state theory. J. Hazard. Mater. 2014, 267, 98–108. [Google Scholar] [CrossRef] [PubMed]
- Mumtaz, M.M.; Durkin, P.R. A weight-of-evidence approach for assessing interactions in chemical mixtures. Toxicol. Ind. Health 1992, 8, 377–406. [Google Scholar] [PubMed]
- Mason, A.M.; Borgert, C.J.; Bus, J.S.; Mumtaz, M.M.; Simmons, J.E.; Sipes, I.G. Improving the scientific foundation for mixtures joint toxicity and risk assessment: Contributions from the sot mixtures project—Introduction. Toxicol. Appl. Pharmacol. 2007, 223, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, E.J. Hormesis and mixtures. Toxicol. Appl. Pharmacol. 2008, 229, 262–263. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, E.J. Hormesis: Why it is important to toxicology and toxicologists. Environ. Toxicol. Chem. 2008, 27, 1451–1474. [Google Scholar] [CrossRef] [PubMed]
- Quinn, B.; Gagne, F.; Blaise, C. Evaluation of the acute, chronic and teratogenic effects of a mixture of eleven pharmaceuticals on the cnidarian, hydra attenuata. Sci. Total Environ. 2009, 407, 1072–1079. [Google Scholar] [CrossRef] [PubMed]
- McMahon, T.A.; Romansic, J.M.; Rohr, J.R. Nonmonotonic and monotonic effects of pesticides on the pathogenic fungus batrachochytrium dendrobatidis in culture and on tadpoles. Environ. Sci. Technol. 2013, 47, 7958–7964. [Google Scholar] [CrossRef] [PubMed]
- McMahon, T.A.; Halstead, N.T.; Johnson, S.; Raffel, T.R.; Romansic, J.M.; Crumrine, P.W.; Boughton, R.K.; Martin, L.B.; Rohr, J.R. The fungicide chlorothalonil is nonlinearly associated with corticosterone levels, immunity, and mortality in amphibians. Environ. Health Perspect. 2011, 119, 1098–1103. [Google Scholar] [CrossRef] [PubMed]
- Backhaus, T.; Faust, M.; Kortenkamp, A. Cumulative risk assessment: A european perspective on the state of the art and the necessary next steps forward. Integr. Environ. Assess. Manag. 2013, 9, 547–548. [Google Scholar] [CrossRef] [PubMed]
- Escher, B.I.; van Daele, C.; Dutt, M.; Tang, J.Y.M.; Altenburger, R. Most oxidative stress response in water samples comes from unknown chemicals: The need for effect-based water quality trigger values. Environ. Sci. Technol. 2013, 47, 7002–7011. [Google Scholar] [CrossRef] [PubMed]
- Fischer, B.B.; Pomati, F.; Eggen, R.I.L. The toxicity of chemical pollutants in dynamic natural systems: The challenge of integrating environmental factors and biological complexity. Sci. Total Environ. 2013, 449, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Frische, T.; Faust, M.; Meyer, W.; Backhaus, T. Toxic masking and synergistic modulation of the estrogenic activity of chemical mixtures in a yeast estrogen screen (YES). Environ. Sci. Pollut. Res. Int. 2009, 16, 593–603. [Google Scholar] [CrossRef] [PubMed]
- Chung, E.; Genco, M.C.; Megrelis, L.; Ruderman, J.V. Effects of bisphenol a and triclocarban on brain-specific expression of aromatase in early zebrafish embryos. Proc. Natl. Acad. Sci. USA 2011, 108, 17732–17737. [Google Scholar] [CrossRef] [PubMed]
- Jernbro, S.; Rocha, P.S.; Keiter, S.; Skutlarek, D.; Farber, H.; Jones, P.D.; Giesy, J.P.; Hollert, H.; Engwall, M. Perfluorooctane sulfonate increases the genotoxicity of cyclophosphamide in the micronucleus assay with v79 cells. Further proof of alterations in cell membrane properties caused by pfos. Environ. Sci. Pollut. Res. Int. 2007, 14, 85–87. [Google Scholar] [PubMed]
- Adam, O.; Badot, P.M.; Degiorgi, F.; Crini, G. Mixture toxicity assessment of wood preservative pesticides in the freshwater amphipod Gammarus pulex (L.). Ecotoxicol. Environ. Saf. 2009, 72, 441–449. [Google Scholar] [CrossRef]
- Dondero, F.; Banni, M.; Negri, A.; Boatti, L.; Dagnino, A.; Viarengo, A. Interactions of a pesticide/heavy metal mixture in marine bivalves: A transcriptomic assessment. BMC Genom. 2011. [Google Scholar] [CrossRef] [PubMed]
- Backhaus, T.; Karlsson, M. Screening level mixture risk assessment of pharmaceuticals in stp effluents. Water Res. 2014, 49, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Cedergreen, N.; Christensen, A.M.; Kamper, A.; Kudsk, P.; Mathiassen, S.K.; Streibig, J.C.; Sørensen, H. A review of independent action compared to concentration addition as reference models for mixtures of compounds with different molecular target sites. Environ. Toxicol. Chem. 2008, 27, 1621–1632. [Google Scholar] [CrossRef] [PubMed]
- Charles, J.; Crini, G.; Degiorgi, F.; Sancey, B.; Morin-Crini, N.; Badot, P.M. Unexpected toxic interactions in the freshwater amphipod Gammarus pulex (L.) exposed to binary copper and nickel mixtures. Environ. Sci. Pollut. Res. Int. 2014, 21, 1099–1111. [Google Scholar] [CrossRef] [PubMed]
- Segner, H.; Schmitt-Jansen, M.; Sabater, S. Assessing the impact of multiple stressors on aquatic biota: The receptor’s side matters. Environ. Sci. Technol. 2014, 48, 7690–7696. [Google Scholar] [CrossRef] [PubMed]
- Blanck, H.; Wängberg, S.A. Pollution-induced community tolerance. A new ecotoxicological tool. In Functional Testing of Aquatic Biota for Estimating Hazards of Chemicals; Cairns, J., Pratt, J.R., Eds.; American Society for Testing Materials: Philadelphia, PA, USA, 1988. [Google Scholar]
- McClellan, K.; Altenburger, R.; Schmitt-Jansen, M. Pollution-induced community tolerance as a measure of species interaction in toxicity assessment. J. Appl. Ecol. 2008, 45, 1514–1522. [Google Scholar] [CrossRef]
- Brack, W.; Klamer, H.J.; de Alda, M.L.; Barcelo, D. Effect-directed analysis of key toxicants in european river basins a review. Environ. Sci. Pollut. Res. Int. 2007, 14, 30–38. [Google Scholar] [PubMed]
- Baas, J.; Jager, T.; Kooijman, B. Understanding toxicity as processes in time. Sci. Total Environ. 2010, 408, 3735–3739. [Google Scholar] [CrossRef] [PubMed]
- Altenburger, R.; Scholz, S.; Schmitt-Jansen, M.; Busch, W.; Escher, B.I. Mixture toxicity revisited from a toxicogenomic perspective. Environ. Sci. Technol. 2012, 46, 2508–2522. [Google Scholar] [CrossRef]
- Vandenbrouck, T.; Soetaert, A.; van der Ven, K.; Blust, R.; de Coen, W. Nickel and binary metal mixture responses in daphnia magna: Molecular fingerprints and (sub)organismal effects. Aquat. Toxicol. 2009, 92, 18–29. [Google Scholar] [CrossRef]
- Scholze, M.; Silva, E.; Kortenkamp, A. Extending the applicability of the dose addition model to the assessment of chemical mixtures of partial agonists by using a novel toxic unit extrapolation method. PLoS ONE 2014. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, K.D.; Kriya, L.D.; Anna, R.G. Bias, complexity, and uncertainty in ecosystem risk assessment: Pharmaceuticals, a new challenge in scale and perspective. Environ. Res. Lett. 2014. [Google Scholar] [CrossRef]
- Klaminder, J.; Jonsson, M.; Fick, J.; Sundelin, A.; Brodin, T. The conceptual imperfection of aquatic risk assessment tests: Highlighting the need for tests designed to detect therapeutic effects of pharmaceutical contaminants. Environ. Res. Lett. 2014. [Google Scholar] [CrossRef]
- De Zwart, D.; Posthuma, L. Complex mixture toxicity for single and multiple species: Proposed methodologies. Environ. Toxicol. Chem. 2005, 24, 2665–2676. [Google Scholar] [CrossRef] [PubMed]
- Liess, M.; Foit, K.; Becker, A.; Hassold, E.; Dolciotti, I.; Kattwinkel, M.; Duquesne, S. Culmination of low-dose pesticide effects. Environ. Sci. Technol. 2013, 47, 8862–8868. [Google Scholar] [CrossRef] [PubMed]
- Beketov, M.A.; Kefford, B.J.; Schäfer, R.B.; Liess, M. Pesticides reduce regional biodiversity of stream invertebrates. Proc. Natl. Acad. Sci. USA 2013, 110, 11039–11043. [Google Scholar] [CrossRef] [PubMed]
- Pilière, A.; Schipper, A.M.; Breure, T.M.; Posthuma, L.; Zwart, D.D.; Dyer, S.D.; Huijbregts, M.A.J. Unraveling the relationships between freshwater invertebrate assemblages and interacting environmental factors. Freshw. Sci. 2014, 33, 1148–1158. [Google Scholar] [CrossRef]
- Smetanová, S.; Bláha, L.; Liess, M.; Schäfer, R.B.; Beketov, M.A. Do predictions from species sensitivity distributions match with field data? Environ. Pollut. 2014, 189, 126–133. [Google Scholar] [CrossRef] [PubMed]
- Schipper, A.M.; Posthuma, L.; de Zwart, D.; Huijbregts, M.A. Deriving field-based species sensitivity distributions (f-SSDs) from stacked species distribution models (S-SDMs). Environ. Sci. Technol. 2014, 48, 14464–14471. [Google Scholar] [CrossRef] [PubMed]
- Laskowski, R.; Bednarska, A.J.; Kramarz, P.E.; Loureiro, S.; Scheil, V.; Kudłek, J.; Holmstrup, M. Interactions between toxic chemicals and natural environmental factors—A meta-analysis and case studies. Sci. Total Environ. 2010, 408, 3763–3774. [Google Scholar] [CrossRef] [PubMed]
- Holmstrup, M.; Bindesbøl, A.M.; Oostingh, G.J.; Duschl, A.; Scheil, V.; Köhler, H.R.; Loureiro, S.; Soares, A.M.V.M.; Ferreira, A.L.G.; Kienle, C.; et al. Interactions between effects of environmental chemicals and natural stressors: A review. Sci. Total Environ. 2010, 408, 3746–3762. [Google Scholar] [CrossRef] [PubMed]
- Menezes-Oliveira, V.B.; Scott-Fordsmand, J.J.; Soares, A.M.V.M.; Amorim, M.J.B. Development of ecosystems to climate change and the interaction with pollution—Unpredictable changes in community structures. Appl. Soil Ecol. 2014, 75, 24–32. [Google Scholar] [CrossRef]
- Landis, W.G.; Rohr, J.R.; Moe, S.J.; Balbus, J.M.; Clements, W.; Fritz, A.; Helm, R.; Hickey, C.; Hooper, M.; Stahl, R.G.; et al. Global climate change and contaminants, a call to arms not yet heard? Integr. Environ. Assess. Manag. 2014, 10, 483–484. [Google Scholar] [CrossRef] [PubMed]
- Stahl, R.G., Jr.; Hooper, M.J.; Balbus, J.M.; Clements, W.; Fritz, A.; Gouin, T.; Helm, R.; Hickey, C.; Landis, W.; Moe, S.J. The influence of global climate change on the scientific foundations and applications of environmental toxicology and chemistry: Introduction to a setac international workshop. Environ. Toxicol. Chem. SETAC 2013, 32, 13–19. [Google Scholar] [CrossRef] [PubMed]
- De Laender, F.; Janssen, C.R. Brief communication: The ecosystem perspective in ecotoxicology as a way forward for the ecological risk assessment of chemicals. Integr. Environ. Assess. Manag. 2013, 9, E34–E38. [Google Scholar] [CrossRef] [PubMed]
- Schmitt-Jansen, M.; Veit, U.; Dudel, G.; Altenburger, R. An ecological perspective in aquatic ecotoxicology: Approaches and challenges. Basic Appl. Ecol. 2008, 9, 337–345. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodea-Palomares, I.; González-Pleiter, M.; Martín-Betancor, K.; Rosal, R.; Fernández-Piñas, F. Additivity and Interactions in Ecotoxicity of Pollutant Mixtures: Some Patterns, Conclusions, and Open Questions. Toxics 2015, 3, 342-369. https://doi.org/10.3390/toxics3040342
Rodea-Palomares I, González-Pleiter M, Martín-Betancor K, Rosal R, Fernández-Piñas F. Additivity and Interactions in Ecotoxicity of Pollutant Mixtures: Some Patterns, Conclusions, and Open Questions. Toxics. 2015; 3(4):342-369. https://doi.org/10.3390/toxics3040342
Chicago/Turabian StyleRodea-Palomares, Ismael, Miguel González-Pleiter, Keila Martín-Betancor, Roberto Rosal, and Francisca Fernández-Piñas. 2015. "Additivity and Interactions in Ecotoxicity of Pollutant Mixtures: Some Patterns, Conclusions, and Open Questions" Toxics 3, no. 4: 342-369. https://doi.org/10.3390/toxics3040342
APA StyleRodea-Palomares, I., González-Pleiter, M., Martín-Betancor, K., Rosal, R., & Fernández-Piñas, F. (2015). Additivity and Interactions in Ecotoxicity of Pollutant Mixtures: Some Patterns, Conclusions, and Open Questions. Toxics, 3(4), 342-369. https://doi.org/10.3390/toxics3040342







