Investigating the Spectral Characteristics of High-Temperature Gases in Low-Carbon Chemical Pool Fires and Developing a Spectral Model
Abstract
1. Introduction
2. Materials and Methods
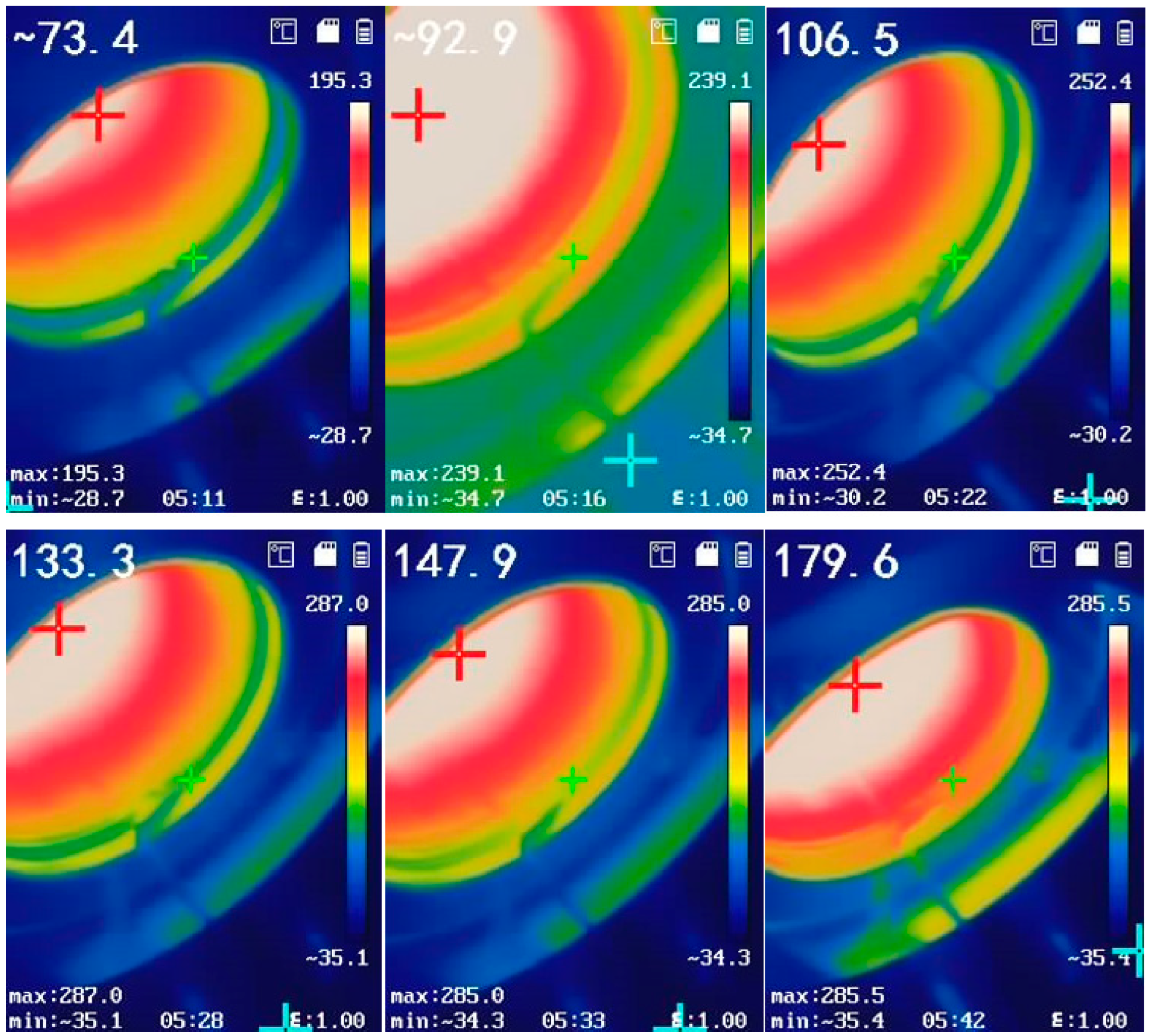
2.1. High-Temperature Gas Spectral Testing Platform
- (1)
- Measurement process of E1: Turn on the blackbody furnace and slowly heat it up at a temperature gradient of 100 °C. When the temperature reaches the target temperature of 800 °C, keep it constant. Then, open the valve at the air inlet and then open the valve at the air outlet of the gas distribution system to introduce inert gas and exhaust the air inside cavity 2. Nitrogen is selected as the background gas in this experiment. Move the rotating chassis to position the heating chamber in front of the blackbody and Fourier transform infrared (FT-IR) spectrometer. By adjusting the angle of the rotating chassis and its position on the slide rail, ensure that the radiation from the blackbody can pass through the chamber and fully enter the field of view of the FT-IR spectrometer. After completing the above operations, turn on the FT-IR spectrometer to scan and obtain E1.
- (2)
- Measurement process of E2: Maintain the position of each part on the platform during the measurement process of E1. Gently pull the handle to open the lens heating chamber, place the lens to be tested inside, adjust the sliding block, and press the lens firmly against the high-temperature heating plate to ensure uniform heating. Then, open the valve at the air inlet, and then open the valve at the air outlet of the gas distribution system to introduce inert gas or nitrogen to exhaust the air inside the cavity. Turn on the lens heating temperature control box to raise the lens to the target temperature. After completing the above operations, use an FT-IR spectrometer to scan and obtain E2.
- (3)
- Measurement process of E3: Move the blackbody furnace to the other side of the slide rail to ensure that it is not within the field of view of the FT-IR spectrometer, and there is no light source within the field of view. Rotate the rotating chassis by 180°, placing the lens end within the field of view of the FT-IR spectrometer. After completing the above operations, use the FT-IR spectrometer to scan and obtain E3.
2.2. Spectral Denoising and Smoothing Processing
2.3. Single- and Mixed-Gas High-Temperature Spectral Testing
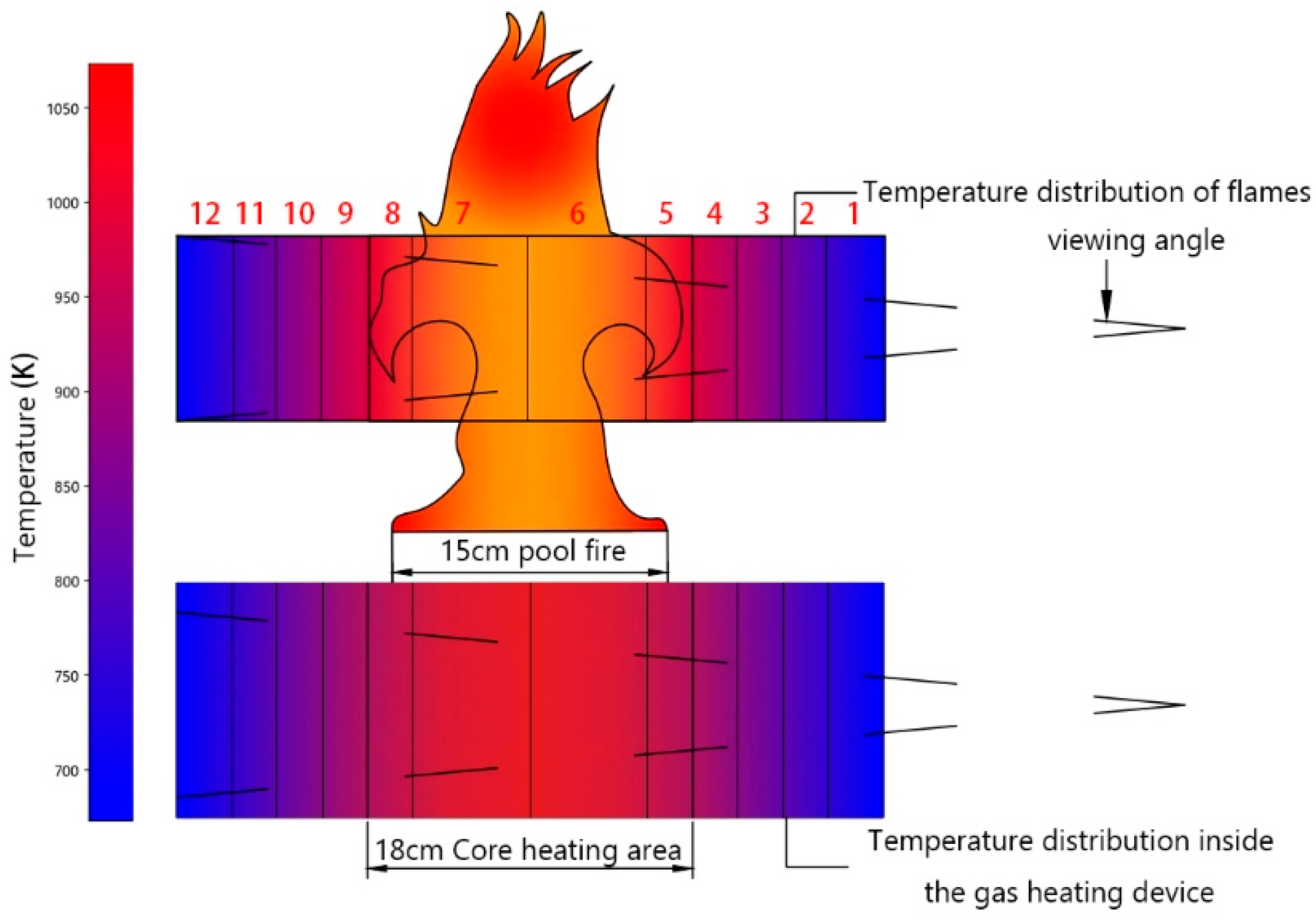
2.4. Simulated Combustion Spectral Testing
2.5. Developing a Spectral Radiation Model for High-Temperature Gases
3. Results and Discussion
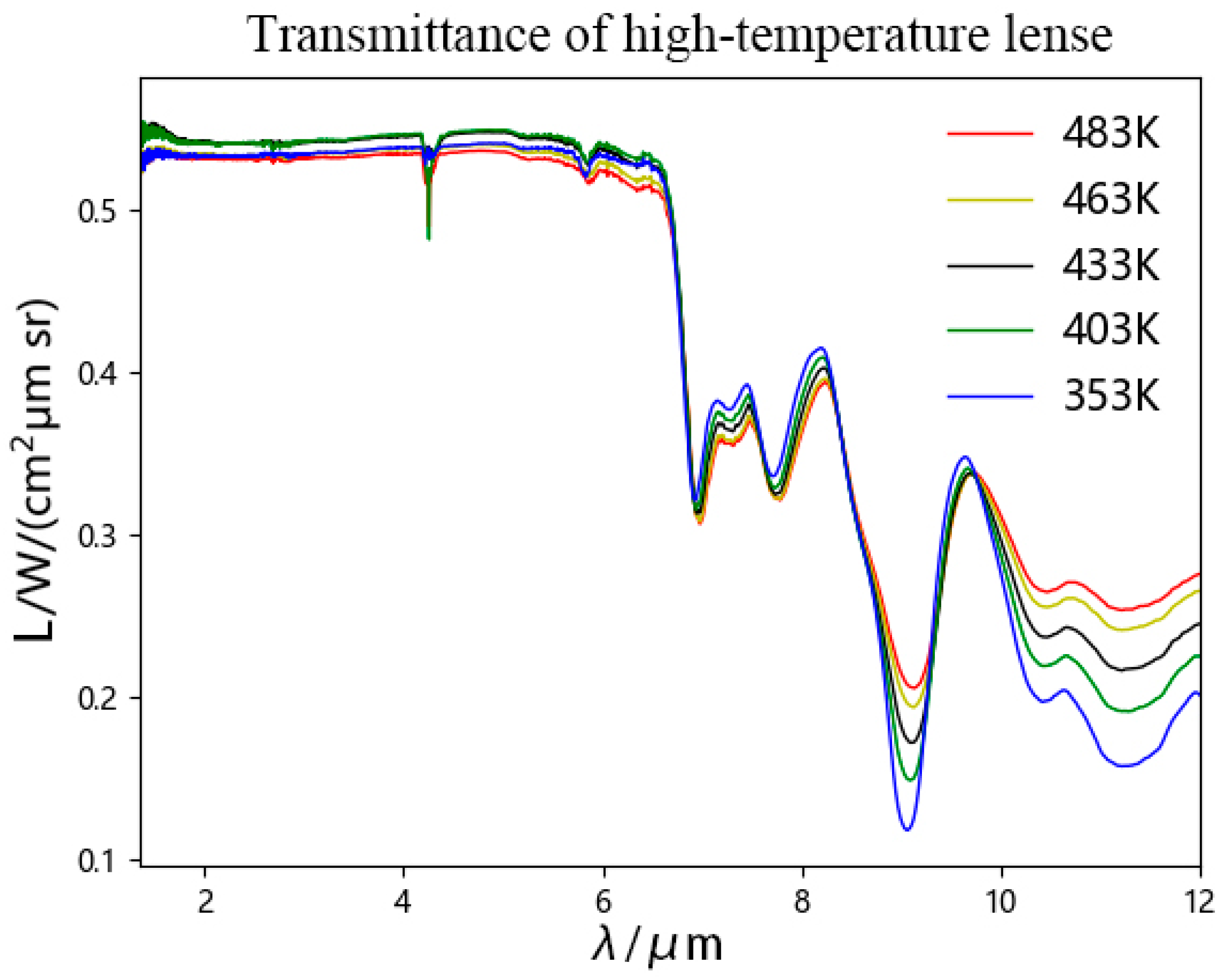
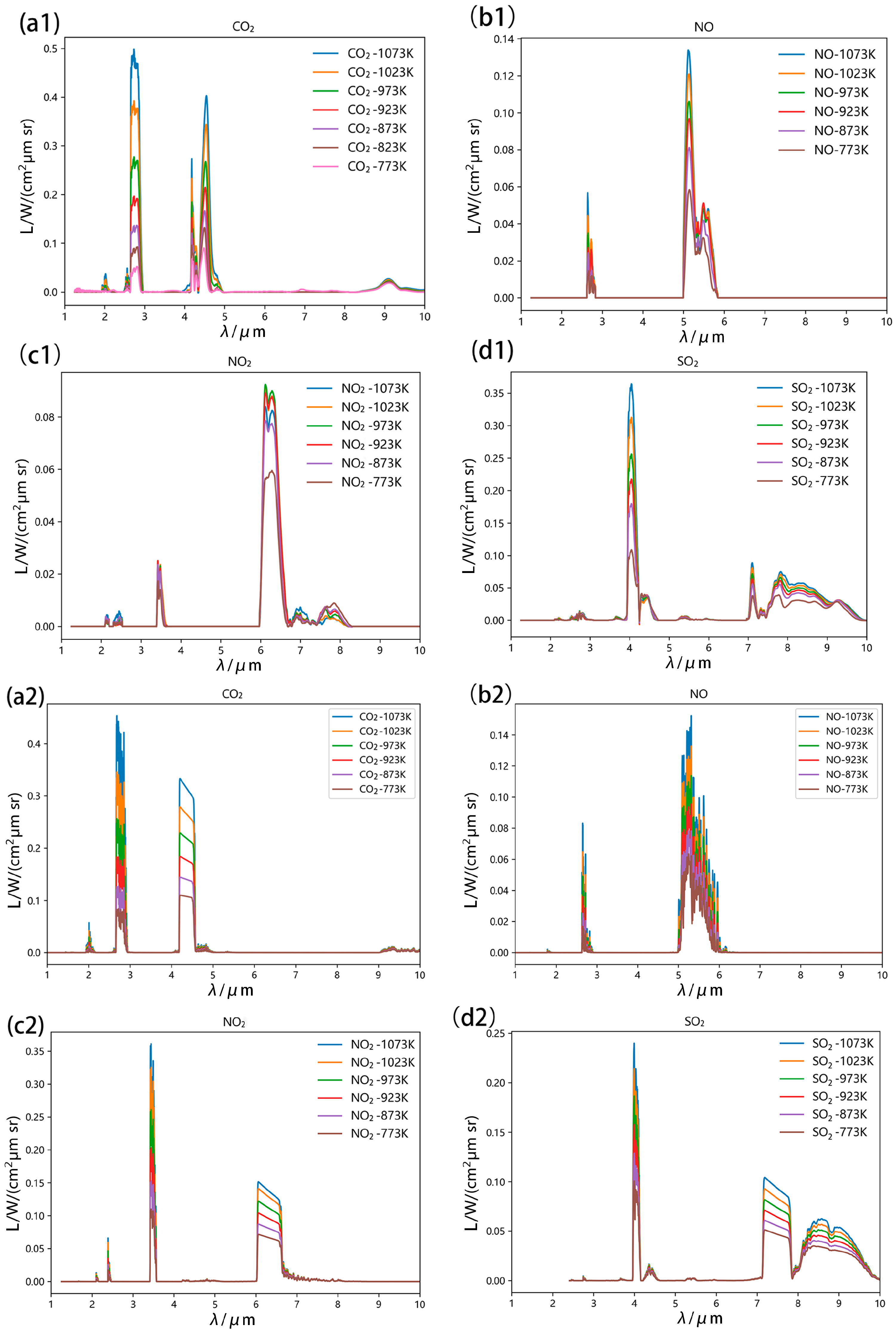
3.1. High-Temperature Single-Gas Spectral Analysis
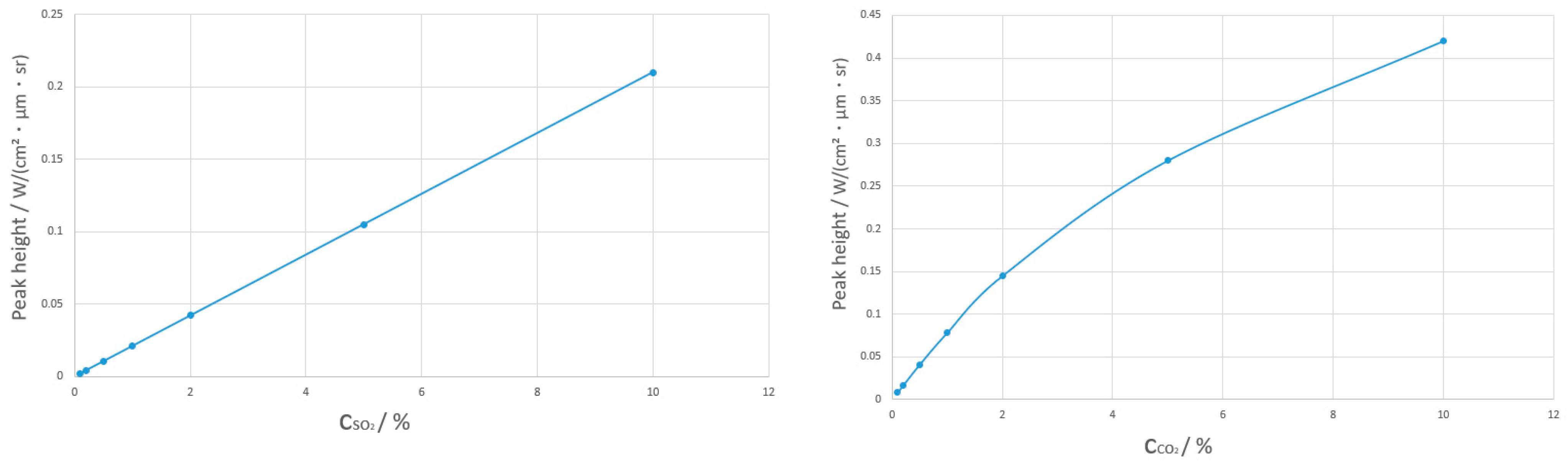
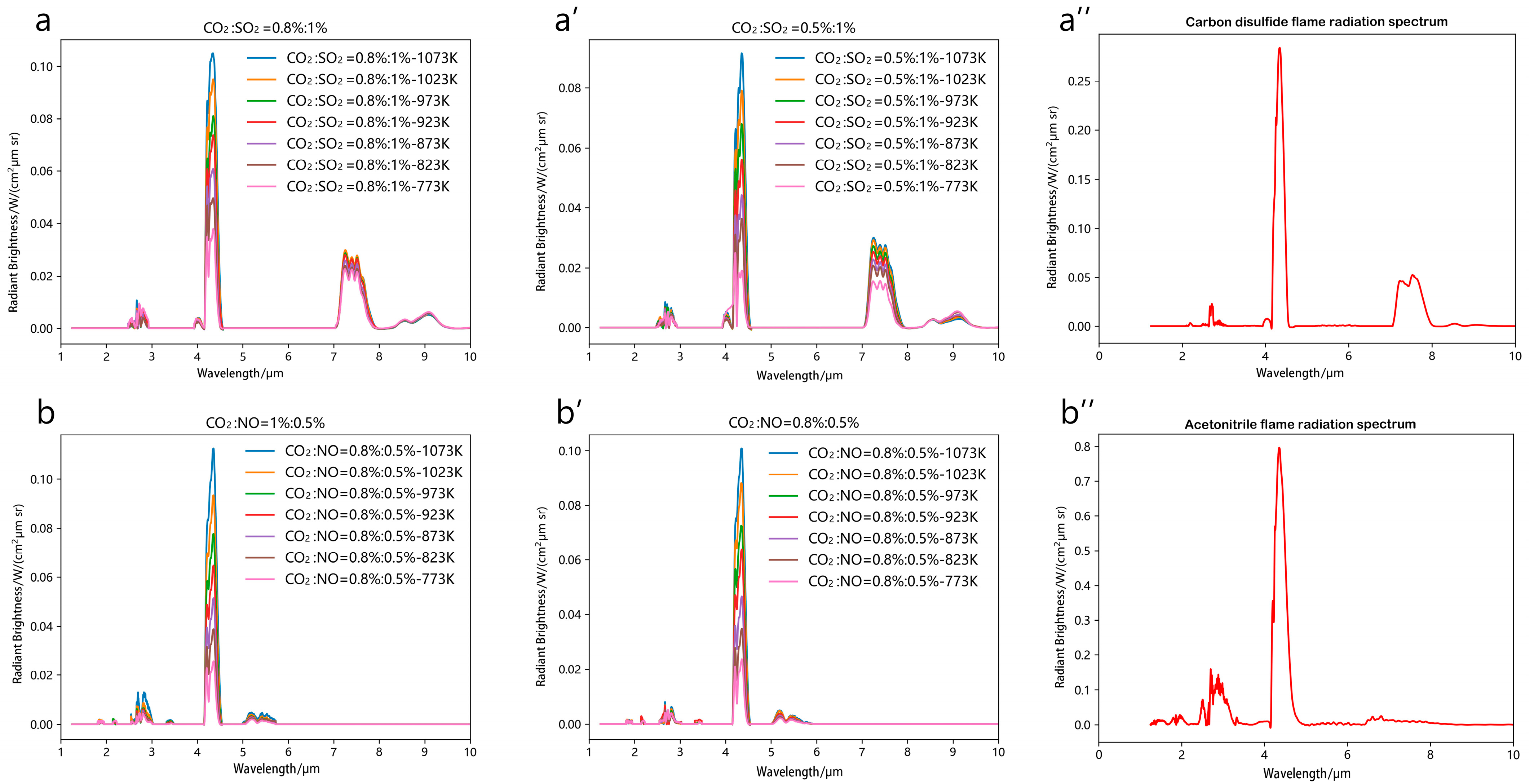
3.2. High-Temperature Gas Mixture Spectral Analysis
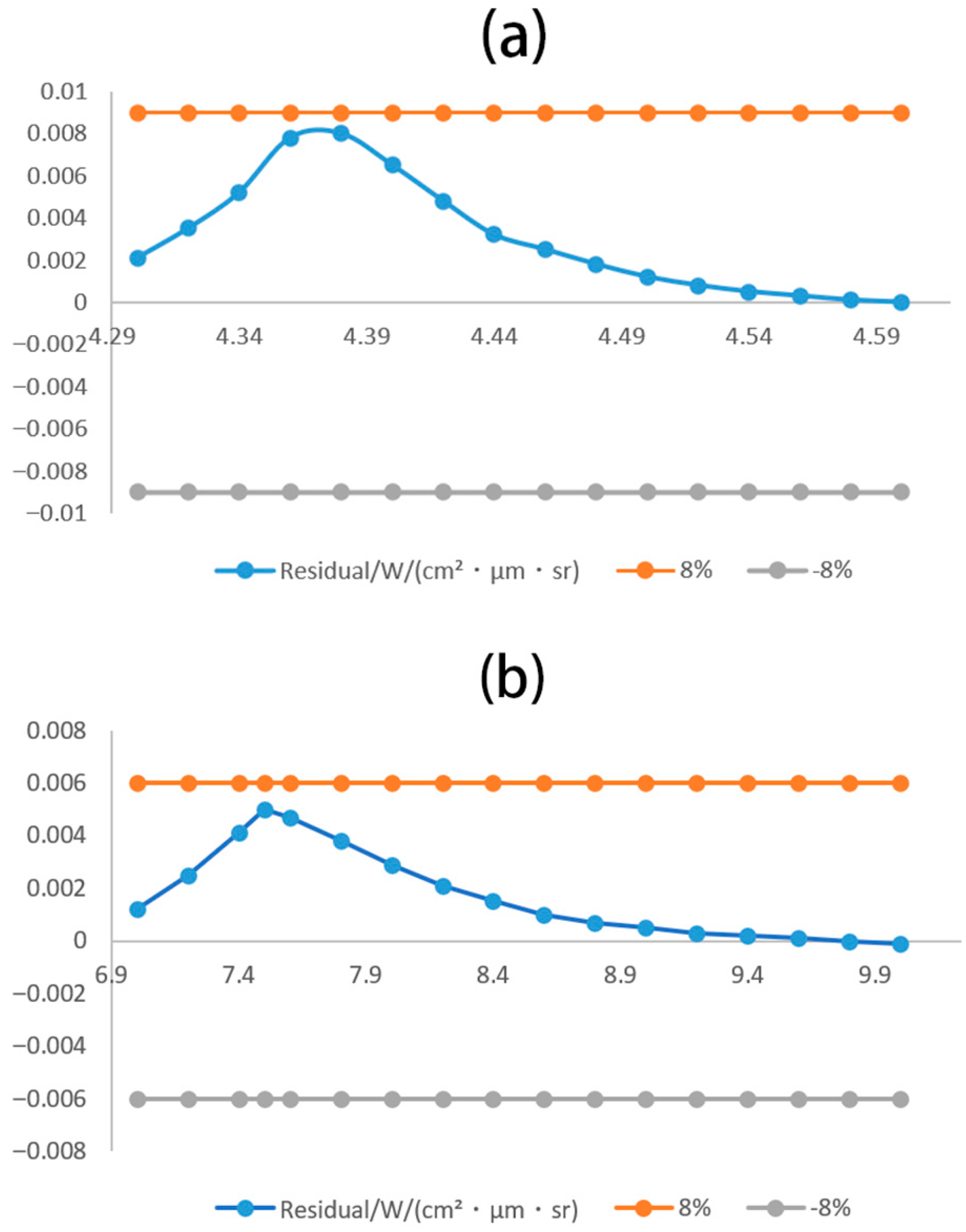
3.3. High-Temperature Gas Spectral Validation
3.4. Analog Computation and Validation of High-Temperature Spectral Radiation Model
3.4.1. Gas Spectral Interference
3.4.2. Parameter Acquisition
3.5. Model Validation
4. Conclusions
5. Strengths and Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Santana, J.A.D.; Arana, Y.C.; Gómez, O.G.; Furka, D.; Furka, S.; Orozco, J.L.; Di Benedetto, A.; Russo, D.; Portarapillo, M.; Febles, J.S. Fire and Explosion Economic Losses (FEEL) Index: A new approach for quantifying economic damages due to accidents in hydrocarbon storage sites. Process. Saf. Environ. Prot. 2022, 165, 77–92. [Google Scholar] [CrossRef]
- Shao, R.; Pan, H.; Huang, J. Safety risk assessment of chemical production process based on local and global objectives. J. Loss Prev. Process. Ind. 2022, 79, 104827. [Google Scholar] [CrossRef]
- Cui, W.; Wei, Y.; Ji, N. Global trends of waste-to-energy (WtE) technologies in carbon neutral perspective: Bibliometric analysis. Ecotoxicol. Environ. Saf. 2024, 270, 115913. [Google Scholar] [CrossRef]
- Gupta, P.; Shukla, A.K.; Shukla, D.P. Sentinel 2 based burn severity mapping and assessing post-fire impacts on forests and buildings in the Mizoram, a north-eastern Himalayan region. Remote. Sens. Appl. Soc. Environ. 2024, 36, 101279. [Google Scholar] [CrossRef]
- Raj, P.K. Large hydrocarbon fuel pool fires: Physical characteristics and thermal emission variations with height. J. Hazard. Mater. 2006, 140, 280–292, Erratum in J. Hazard. Mater. 2007, 149, 246. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. The NIST Chemistry WebBook: A Chemical Data Resource on the Internet. J. Chem. Eng. Data 2001, 46, 1059–1063. [Google Scholar] [CrossRef]
- Saito, T.H.K.; Yanagisawa, M. Spectral Database for Organic Compounds (SDBS). 2006. Available online: https://sdbs.db.aist.go.jp/ (accessed on 8 October 2025).
- Stolarczyk, N.; Thibault, F.; Cybulski, H.; Jóźwiak, H.; Kowzan, G.; Vispoel, B.; Gordon, I.; Rothman, L.; Gamache, R.; Wcisło, P. Evaluation of different parameterizations of temperature dependences of the line-shape parameters based on ab initio calculations: Case study for the HITRAN database. J. Quant. Spectrosc. Radiat. Transf. 2019, 240, 106676. [Google Scholar] [CrossRef]
- Zhu, M.; Zhang, F.; Li, W.; Wu, Y.; Xu, N. The impact of various HITRAN molecular spectroscopic databases on infrared radiative transfer simulation. J. Quant. Spectrosc. Radiat. Transf. 2019, 234, 55–63. [Google Scholar] [CrossRef]
- Hashemi, R.; Gordon, I.E.; Tran, H.; Kochanov, R.V.; Karlovets, E.V.; Tan, Y.; Lamouroux, J.; Ngo, N.H.; Rothman, L.S. Revising the line-shape parameters for air- and self-broadened CO2 lines toward a sub-percent accuracy level. J. Quant. Spectrosc. Radiat. Transf. 2020, 256, 107283. [Google Scholar] [CrossRef]
- Karlovets, E.; Gordon, I.; Hashemi, R.; Kochanov, R.; Hargreaves, R.; Rothman, L. Addition of the line list for carbon disulfide to the HITRAN database: Line positions, intensities, and half-widths of the 12C32S2, 32S12C34S, 32S12C33S, and 13C32S2 isotopologues. J. Quant. Spectrosc. Radiat. Transf. 2020, 258, 107275. [Google Scholar] [CrossRef]
- Delahaye, T.; Armante, R.; Scott, N.; Jacquinet-Husson, N.; Chédin, A.; Crépeau, L.; Crevoisier, C.; Douet, V.; Perrin, A.; Barbe, A.; et al. The 2020 edition of the GEISA spectroscopic database. J. Mol. Spectrosc. 2021, 380, 111510. [Google Scholar] [CrossRef]
- Gordon, I.; Rothman, L.; Hargreaves, R.; Hashemi, R.; Karlovets, E.; Skinner, F.; Conway, E.; Hill, C.; Kochanov, R.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2021, 277, 107949. [Google Scholar] [CrossRef]
- Mellau, G.C.; Makhnev, V.Y.; Gordon, I.E.; Zobov, N.F.; Tennyson, J.; Polyansky, O.L. An experimentally-accurate and complete room-temperature infrared HCN line-list for the HITRAN database. J. Quant. Spectrosc. Radiat. Transf. 2021, 270, 107666. [Google Scholar] [CrossRef]
- Perrin, A.; Manceron, L.; Flaud, J.-M.; Kwabia-Tchana, F.; Armante, R.; Roy, P.; Doizi, D. The new nitrogen dioxide (NO2) linelist in the GEISA database and first identification of the ν1+2ν3-ν3 band of 14N16O2. J. Mol. Spectrosc. 2021, 376, 111394. [Google Scholar] [CrossRef]
- Alberti, M.; Weber, R.; Mancini, M.; Fateev, A.; Clausen, S. Validation of HITEMP-2010 for carbon dioxide and water vapour at high temperatures and atmospheric pressures in 450–7600 cm−1 spectral range. J. Quant. Spectrosc. Radiat. Transf. 2015, 157, 14–33. [Google Scholar] [CrossRef]
- Hargreaves, R.J.; Gordon, I.E.; Rothman, L.S.; Tashkun, S.A.; Perevalov, V.I.; Lukashevskaya, A.A.; Yurchenko, S.N.; Tennyson, J.; Müller, H.S. Spectroscopic line parameters of NO, NO2, and N2O for the HITEMP database. J. Quant. Spectrosc. Radiat. Transf. 2019, 232, 35–53. [Google Scholar] [CrossRef]
- Huang, X.; Freedman, R.S.; Tashkun, S.; Schwenke, D.W.; Lee, T.J. AI-3000K Infrared line list for hot CO2. J. Mol. Spectrosc. 2023, 392, 111748. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, Z.; Zheng, D.; Zhang, M.; Ding, Y.; Du, Y. High-temperature line strength and line shape parameters measurements of Ar- and N2-perturbed CO2 lines near 4.18 µm in a shock tube. J. Mol. Spectrosc. 2024, 400, 111890. [Google Scholar] [CrossRef]
- Phillips, W.J.; Plemmons, D.H.; Galyen, N.A. HITRAN/HITEMP Spectral Databases and Uncertainty Propagation by Means of Monte Carlo Simulation with Ap-Plication to Tunable Diode Laser Absorption Diagnostics. 2011. Available online: https://itea.org/images/pdf/conferences/2011-Test-Instrumentation-presentations/ITEA%20Monte%20Carlo-TDLAS.pdf? (accessed on 8 October 2025).
- Wakatsuki, K.; Jackson, G.; Hamins, A.; Nyden, M. Effects of fuel absorption on radiative heat transfer in methanol pool fires. Proc. Combust. Inst. 2007, 31, 2573–2580. [Google Scholar] [CrossRef]
- Zhang, B.; Laboureur, D.M.; Liu, Y.; Gopalaswami, N.; Mannan, M.S. Experimental Study of a Liquefied Natural Gas Pool Fire on Land in the Field. Ind. Eng. Chem. Res. 2018, 57, 14297–14306. [Google Scholar] [CrossRef]
- Qian, Z.; Xiao-Jun, L.; Lei, H. Video Image Fire Recognition Based on Color Space and Moving Object Detection. In Proceedings of the 2020 International Conference on Artificial Intelligence and Computer Engineering (ICAICE), Beijing, China, 23–25 October 2020. [Google Scholar]
- Baek, J.; Alhindi, T.J.; Jeong, Y.-S.; Jeong, M.K.; Seo, S.; Kang, J.; Shim, W.; Heo, Y. Real-time fire detection system based on dynamic time warping of multichannel sensor networks. Fire Saf. J. 2021, 123, 103364. [Google Scholar] [CrossRef]
- Buffington, T.; Bilyaz, S.; Ezekoye, O.A. Brain-STORM: A deep learning model for computationally fast transient high-rise fire simulations. Fire Saf. J. 2021, 125, 103443. [Google Scholar] [CrossRef]
- Stoellinger, M.; Roekaerts, D. Using a flamelet generated manifold method in transported probability density function modeling of soot formation and thermal radiation. Comput. Fluids 2022, 245, 105567. [Google Scholar] [CrossRef]
- Tsai, K.-C.; Cheng, L.-H.; Yeh, C.-F.; Tseng, T.-P.; Huang, L.-J.; Yeh, S.-H.; Hsu, H.-T.; Lin, C.-H.; Lai, C.-H.; Brimblecombe, P.; et al. Fire dynamics, fire generated pollutants, and acute health implications: A scaling law analysis of heavy-fuel-oil pool fires. Fuel 2025, 381, 133210. [Google Scholar] [CrossRef]
- Wang, L.; Ding, P.; Yan, S.; Li, J.; Zhang, J.; Wang, C.; Cao, Z.; Zhou, Q.; Mu, J.; Meng, G.; et al. Soot volume fraction measurements in aero-engine model combustor outlet using two-color laser-induced incandescence. Chin. J. Aeronaut. 2025, 38, 103247. [Google Scholar] [CrossRef]
- Liu, H.-T.; Chen, Z.-L.; Yang, Y.; Yin, W.-Q.; Liu, Q. Research on Heat Transfer Characteristics in Oil Pool Fire Based on Spectral Analysis. Guang Pu Xue Yu Guang Pu Fen Xi 2016, 36, 3297–3302. [Google Scholar]
- Jiang, B.; Ji, Q.; Teng, G. Using GOCI to detect the diffusion of pollution after the TianJin harbour explosion. Int. J. Remote. Sens. 2017, 39, 1744–1753. [Google Scholar] [CrossRef]
- Hadjipanayis, M.; Beyrau, F.; Lindstedt, R.; Atkinson, G.; Cusco, L. Thermal radiation from vapour cloud explosions. Process. Saf. Environ. Prot. 2015, 94, 517–527. [Google Scholar] [CrossRef]
- Paul, C.; Roy, S.; Sailer, J.; Brännström, F.; Ahmed, M.M.; Trouvé, A.; Bordbar, H.; Hostikka, S.; McDermott, R. Detailed radiation modeling of two flames relevant to fire simulation using Photon Monte Carlo—Line by Line radiation model. J. Quant. Spectrosc. Radiat. Transf. 2024, 329, 109177. [Google Scholar] [CrossRef]
- Yang, C.S.-C.; Jin, F.; Trivedi, S.; Hommerich, U.; Nemes, L.; Samuels, A.C. Long-wave infrared laser-induced breakdown spectroscopy of complex gas molecules in the vicinity of a laser-induced plasma. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 294, 122536. [Google Scholar] [CrossRef]
- Zhang, K.; Ren, D.; Han, Y.; Zhu, C. Experimental and numerical study on the combustion and infrared radiation characteristics of Mg/PTFE/Viton pyrotechnic compositions. Infrared Phys. Technol. 2023, 133, 104841. [Google Scholar] [CrossRef]
- Parent, G.; Erez, G.; Collin, A.; Suzanne, M.; Thiry-Muller, A.; Weber, M.; Faure, E.; Boulet, P. Spectral radiation emitted by kerosene pool fires. Fire Saf. J. 2019, 108, 102847. [Google Scholar] [CrossRef]
- Bordbar, H.; Alinejad, F.; Conley, K.; Ala-Nissila, T.; Hostikka, S. Flame detection by heat from the infrared spectrum: Optimization and sensitivity analysis. Fire Saf. J. 2022, 133, 103673. [Google Scholar] [CrossRef]
- Raj, P.K. LNG fires: A review of experimental results, models and hazard prediction challenges. J. Hazard. Mater. 2006, 140, 444–464, Corrigendum in J. Hazard. Mater. 2007, 143, 603. [Google Scholar] [CrossRef] [PubMed]
- Vinnem, J.E. Risk analysis and risk acceptance criteria in the planning processes of hazardous facilities—A case of an LNG plant in an urban area. Reliab. Eng. Syst. Saf. 2010, 95, 662–670. [Google Scholar] [CrossRef]
- Qi, R.; Raj, P.K.; Mannan, M.S. Underwater LNG release test findings: Experimental data and model results. J. Loss Prev. Process. Ind. 2011, 24, 440–448. [Google Scholar] [CrossRef]
- Niu, Q.; He, Z.; Dong, S. IR radiation characteristics of rocket exhaust plumes under varying motor operating conditions. Chin. J. Aeronaut. 2017, 30, 1101–1114. [Google Scholar] [CrossRef]
- Qiao, Y.; Nie, W.S.; Wu, G.Y.; Feng, S.J. Study on Radiation Characteristics of Multi-Nozzle Liquid Rocket Engine Plumes. Missiles Space Veh. 2017, 4, 53–58. (In Chinese) [Google Scholar]
- Yang, B.; Li, W.; Xie, J.; Zhu, X.; Wang, F.; Yang, Y.; Li, Z. Hydrogen sulfide measurement of combustion gaseous product using ultraviolet absorption spectroscopy. Measurement 2023, 214, 112766. [Google Scholar] [CrossRef]
- Huang, W.; Gao, G.; Zhang, M.; Ruan, S.; Cai, T. Simultaneous measurement of temperature and C2H4 concentration in hydrocarbon flames using interference-immune differential absorption spectroscopy at 3.3 μm. Infrared Phys. Technol. 2024, 142, 105556. [Google Scholar] [CrossRef]
- Chang, K.; Liu, M.; He, Z.; Luo, Z.; Cheng, Q. Radiative characteristics detection and generation mechanism analysis of soot and PAHs during the combustion process of raw coal and tar coal. Fuel 2025, 382, 133767. [Google Scholar] [CrossRef]
- Ruan, S.; Gao, G.; Yang, Y.; Yang, H.; Cai, T. Measurement and validation of high-temperature CO spectral line parameters near 2.3 μm using TDLAS for combustion diagnostics. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2025, 329, 125577. [Google Scholar] [CrossRef]
- JJG 856-2015; Radiation Thermometers. General Administration of Quality Supervision, Inspection and Quarantine (AQSIQ): Beijing, China, 2015.
- Karman, T.; Gordon, I.E.; van der Avoird, A.; Baranov, Y.I.; Boulet, C.; Drouin, B.J.; Groenenboom, G.C.; Gustafsson, M.; Hartmann, J.-M.; Kurucz, R.L.; et al. Update of the HITRAN collision-induced absorption section. Icarus 2019, 328, 160–175. [Google Scholar] [CrossRef]
- Parra-Verde, E.R.; Gutiérrez-Vega, J.C. Steady-state solutions of the Whittaker–Hill equation of fractional order. Commun. Nonlinear Sci. Numer. Simul. 2024, 131, 107812. [Google Scholar] [CrossRef]
- Mishra, S.; Vishwakarma, P.K.; Sharma, A.; Mishra, K.B. Experimental investigation of small-scale CS2 (carbon disulphide) pool fires. Process. Saf. Environ. Prot. 2021, 145, 203–210. [Google Scholar] [CrossRef]
- Alzueta, M.U.; Guerrero, M.; Millera, Á.; Marshall, P.; Glarborg, P. Experimental and kinetic modeling study of oxidation of acetonitrile. Proc. Combust. Inst. 2021, 38, 575–583. [Google Scholar] [CrossRef]
- Salem, S.I.; Higa, H.; Ishizaka, J.; Pahlevan, N.; Oki, K. Spectral band-shifting of multispectral remote-sensing reflectance products: Insights for matchup and cross-mission consistency assessments. Remote. Sens. Environ. 2023, 299, 113846. [Google Scholar] [CrossRef]
- Peng, H.; Ning, J.; Chen, Z.; Tang, J.; Liu, L.; Chen, L. Construction of CS2 Combustion Flame Spectral Radiation Model and Inversion of Characteristic Pollution Product Concentration. Spectrosc. Spectr. Anal. 2022, 42, 672–677. [Google Scholar]


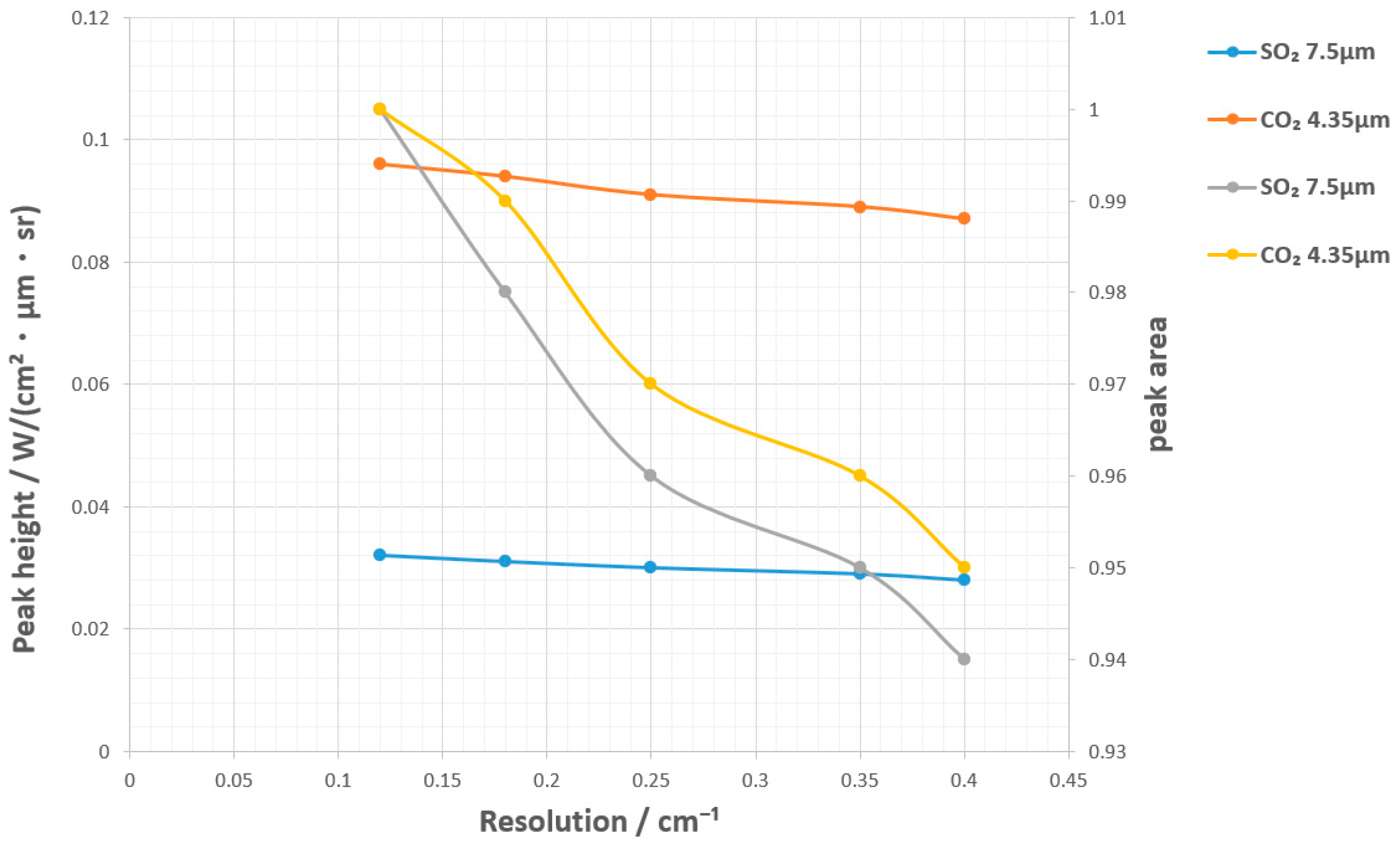
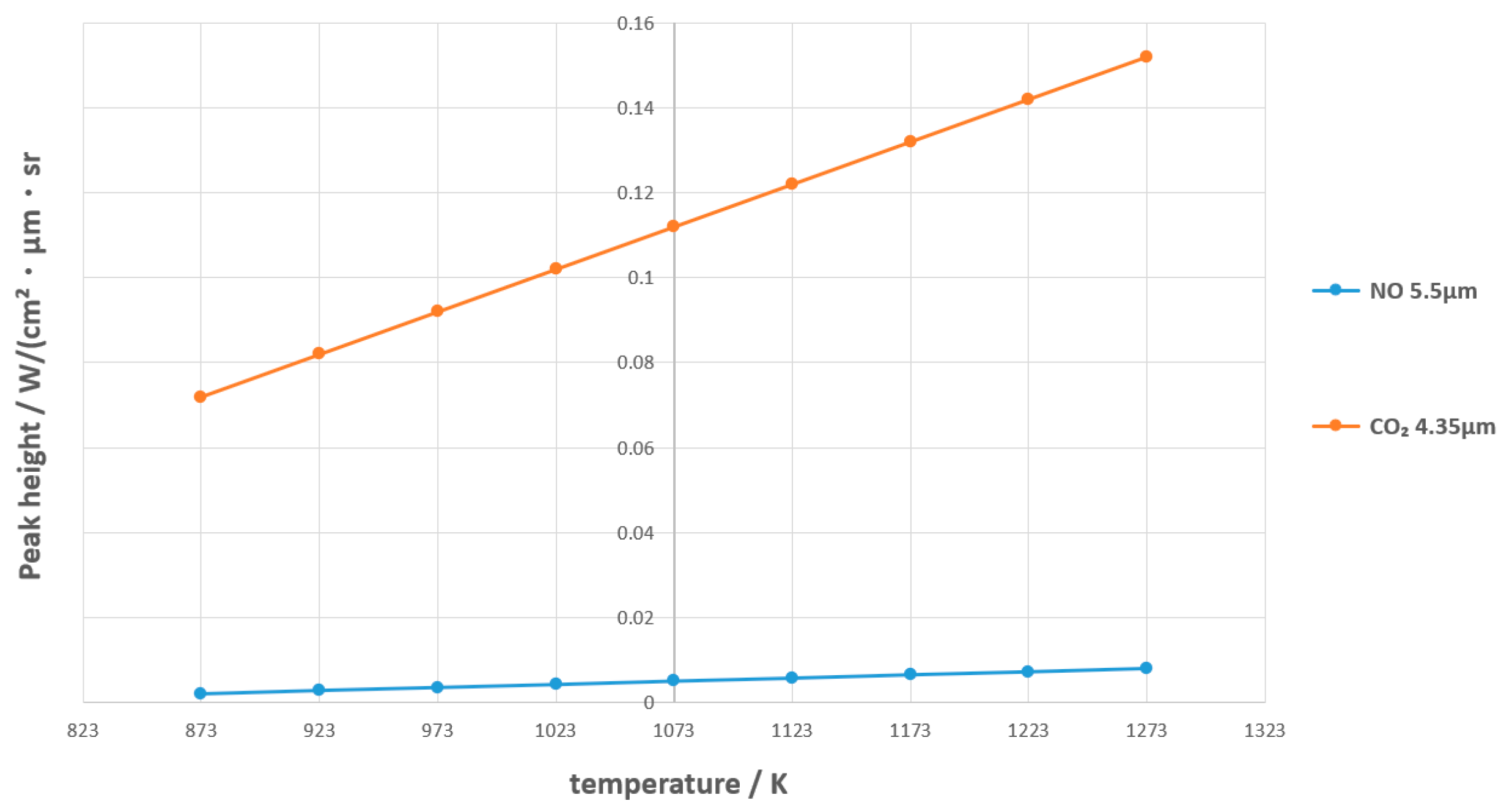
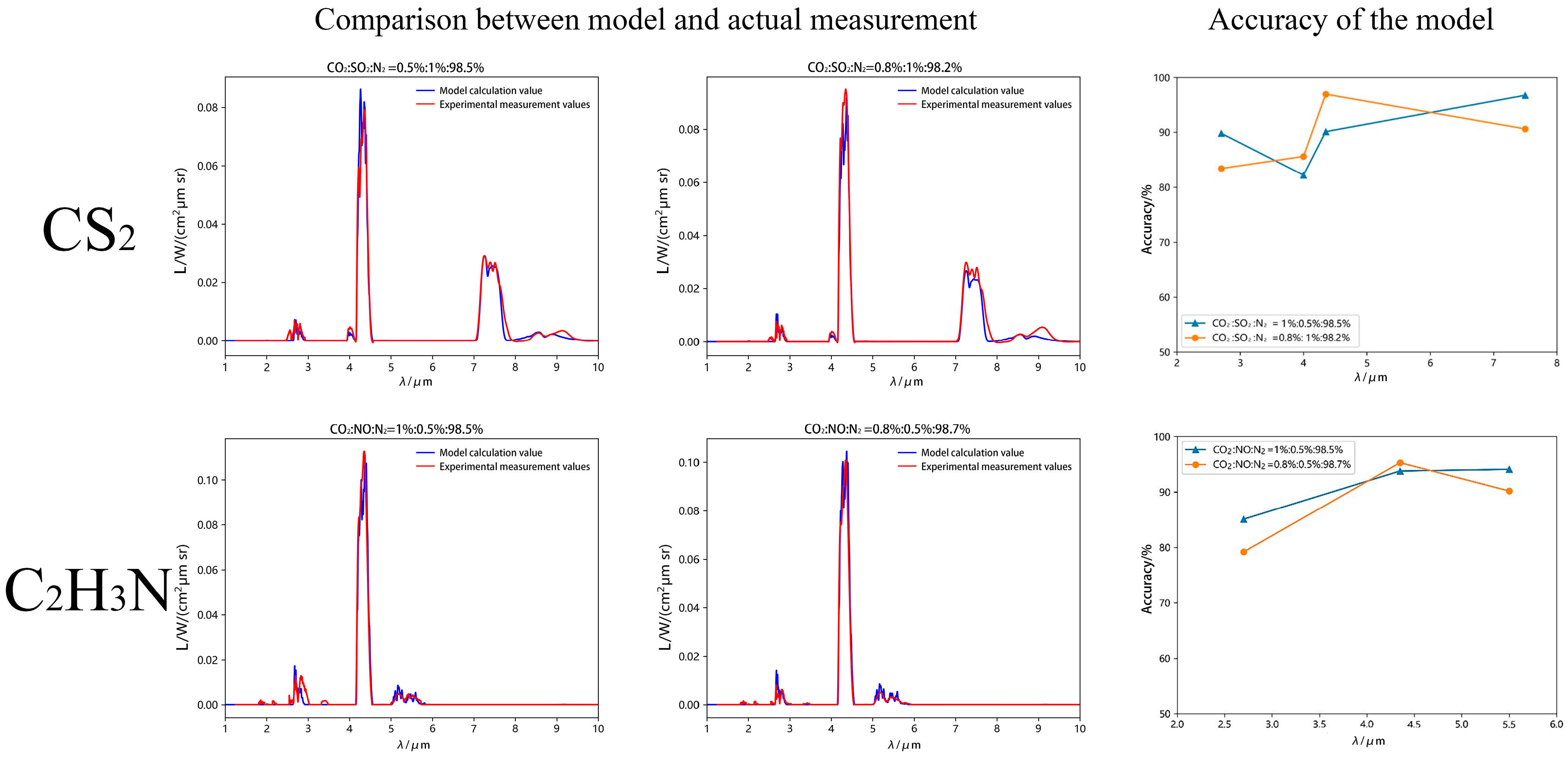
| Parameter Name | Parameter Value |
|---|---|
| Spectral Range | 350–8300 cm−1 |
| Spectral Resolution | 0.5, 1, 2, 4, 8, 16, 32 cm−1 |
| Number of Scans | 2, 4, 8, 16 times |
| Field of View | 10–15 mrads |
| Detector | DTGs detector, liquid nitrogen cooled MCT detector |
| Measurement Speed | 1–25 spectra per second |
| Scan Type | Background, interferogram, sample, single-beam |
| Error Source | 1.3–6.6 μm | 8.6–12 μm |
|---|---|---|
| Lens Transmittance Measurement Error | ±0.012 | ±0.042 |
| E3 Measurement Error | ±5% | ±5% |
| Final Radiance Uncertainty | ±7.3% | ±9.8% |
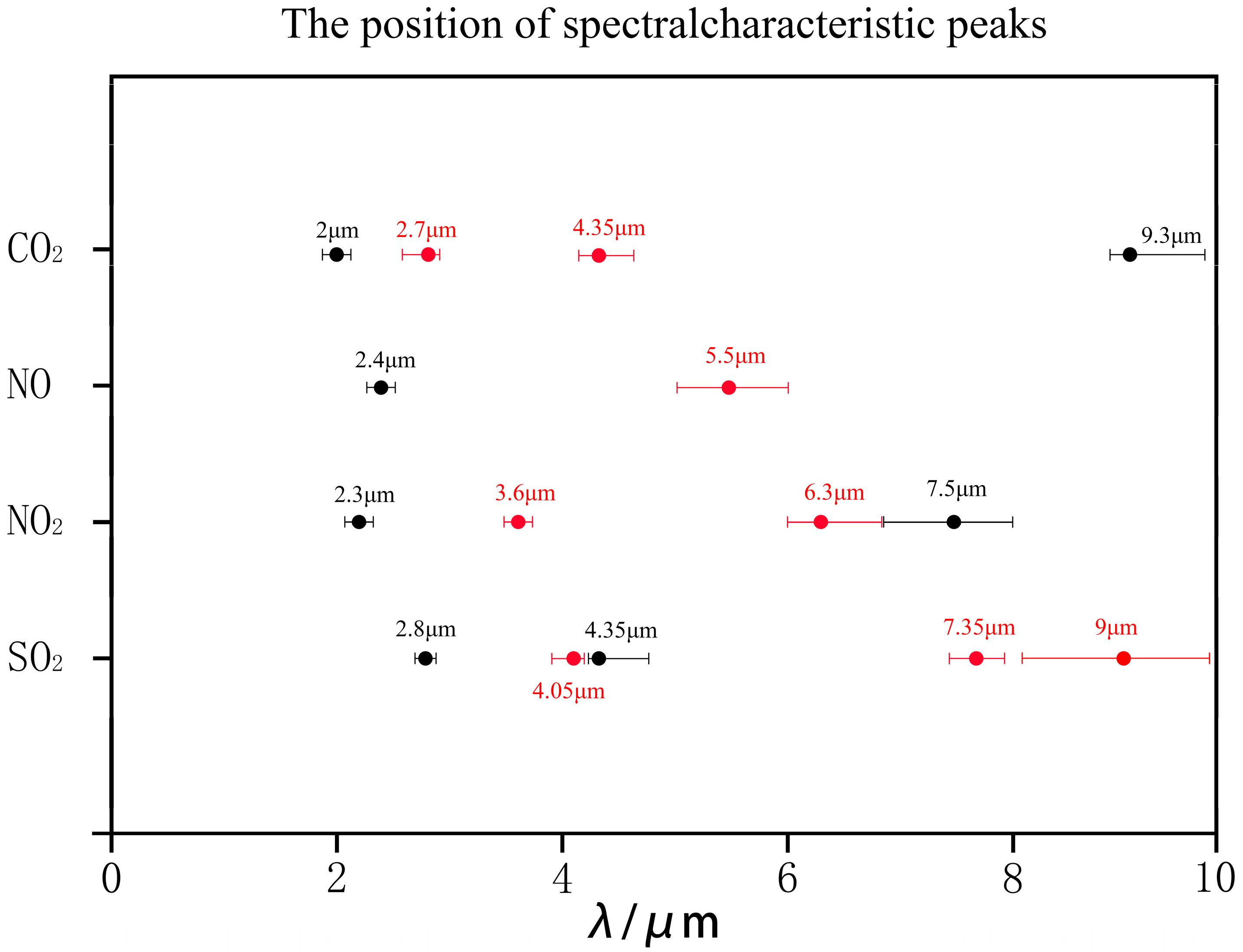
| Gas | Characteristic Band | RMSE | MAE | Pearson r | Peak Center Error Δλ (μm) | Peak Height Error (%) |
|---|---|---|---|---|---|---|
| CO2 | 2.7 | 0.008 | 0.006 | 0.987 | ±0.02 | ±3.2 |
| CO2 | 4.35 | 0.012 | 0.009 | 0.982 | ±0.03 | ±4.5 |
| SO2 | 7.5 | 0.005 | 0.004 | 0.991 | ±0.01 | ±2.8 |
| NO | 5.5 | 0.003 | 0.002 | 0.995 | ±0.01 | ±1.9 |
| NO2 | 3.6 | 0.015 | 0.011 | 0.973 | ±0.04 | ±6.7 |
| Source of Uncertainty | Value |
|---|---|
| Radiometric calibration | ±7.3% |
| Baseline calibration (AirPLS) | ±3.5% |
| Lens transmittance | ±4.2% |
| HITRAN parameters | ±5.1% |
| Total | ±10.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Chen, Z.; Liang, Y.; Li, P.; Liu, Q.; Zhou, L. Investigating the Spectral Characteristics of High-Temperature Gases in Low-Carbon Chemical Pool Fires and Developing a Spectral Model. Toxics 2025, 13, 877. https://doi.org/10.3390/toxics13100877
Jiang G, Chen Z, Liang Y, Li P, Liu Q, Zhou L. Investigating the Spectral Characteristics of High-Temperature Gases in Low-Carbon Chemical Pool Fires and Developing a Spectral Model. Toxics. 2025; 13(10):877. https://doi.org/10.3390/toxics13100877
Chicago/Turabian StyleJiang, Gengfeng, Zhili Chen, Yaquan Liang, Peng Li, Qiang Liu, and Lv Zhou. 2025. "Investigating the Spectral Characteristics of High-Temperature Gases in Low-Carbon Chemical Pool Fires and Developing a Spectral Model" Toxics 13, no. 10: 877. https://doi.org/10.3390/toxics13100877
APA StyleJiang, G., Chen, Z., Liang, Y., Li, P., Liu, Q., & Zhou, L. (2025). Investigating the Spectral Characteristics of High-Temperature Gases in Low-Carbon Chemical Pool Fires and Developing a Spectral Model. Toxics, 13(10), 877. https://doi.org/10.3390/toxics13100877







