Three-Dimensional Mass Transfer Modeling of Hydroquinone Adsorption on Phragmites australis Biochar
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation
2.3. Characterization
2.4. Adsorption Experiment
3. Mathematical Modeling
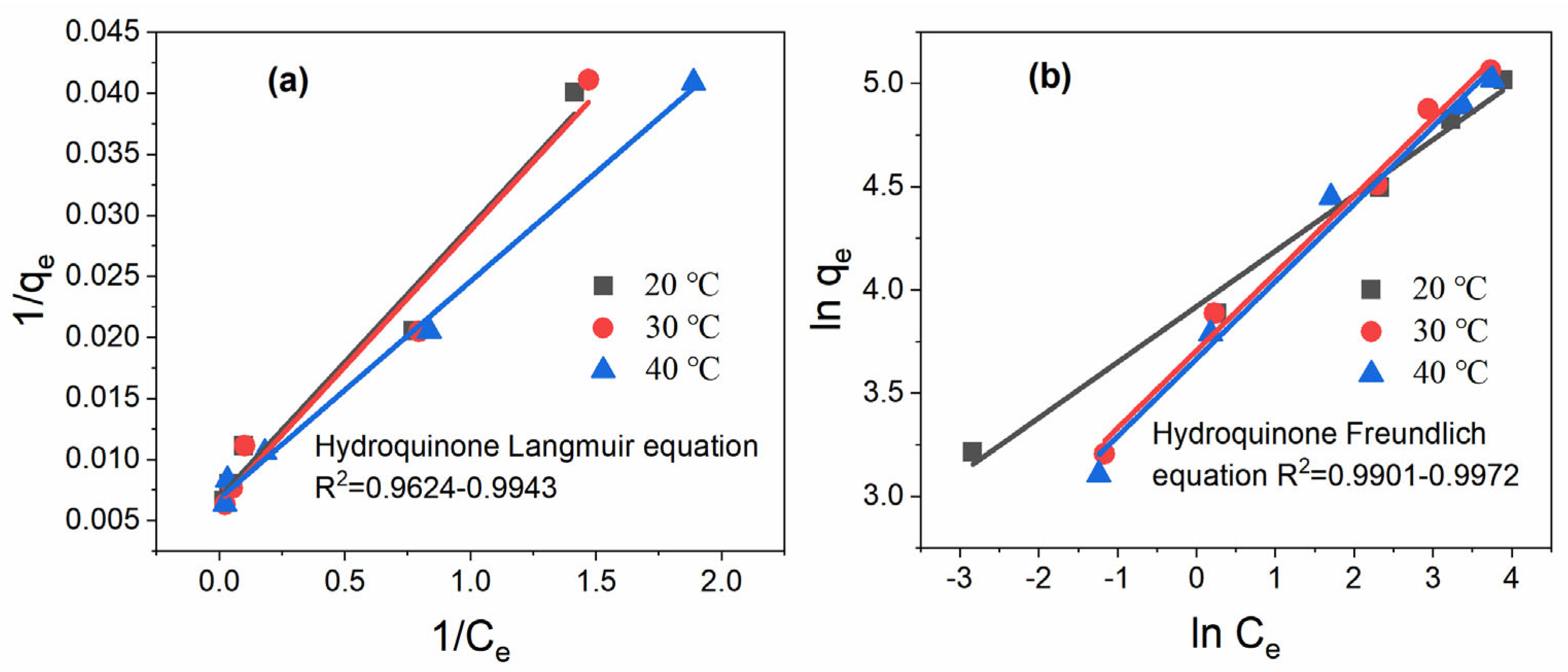
3.1. Isotherm Models
3.2. 3D Mass Transfer Model
4. Results and Discussion
4.1. Characterisation of Solid Density
4.2. Adsorption Isotherm
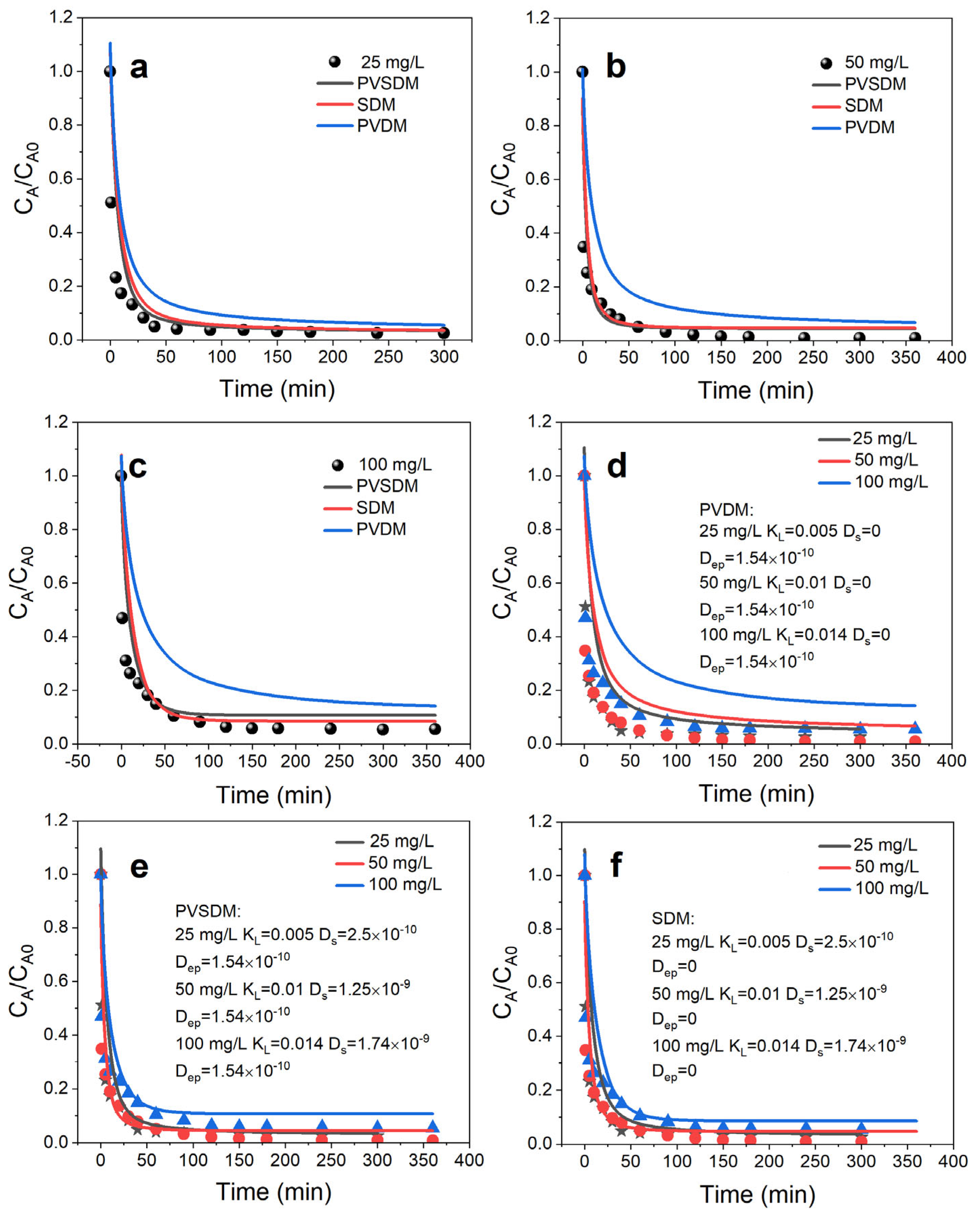
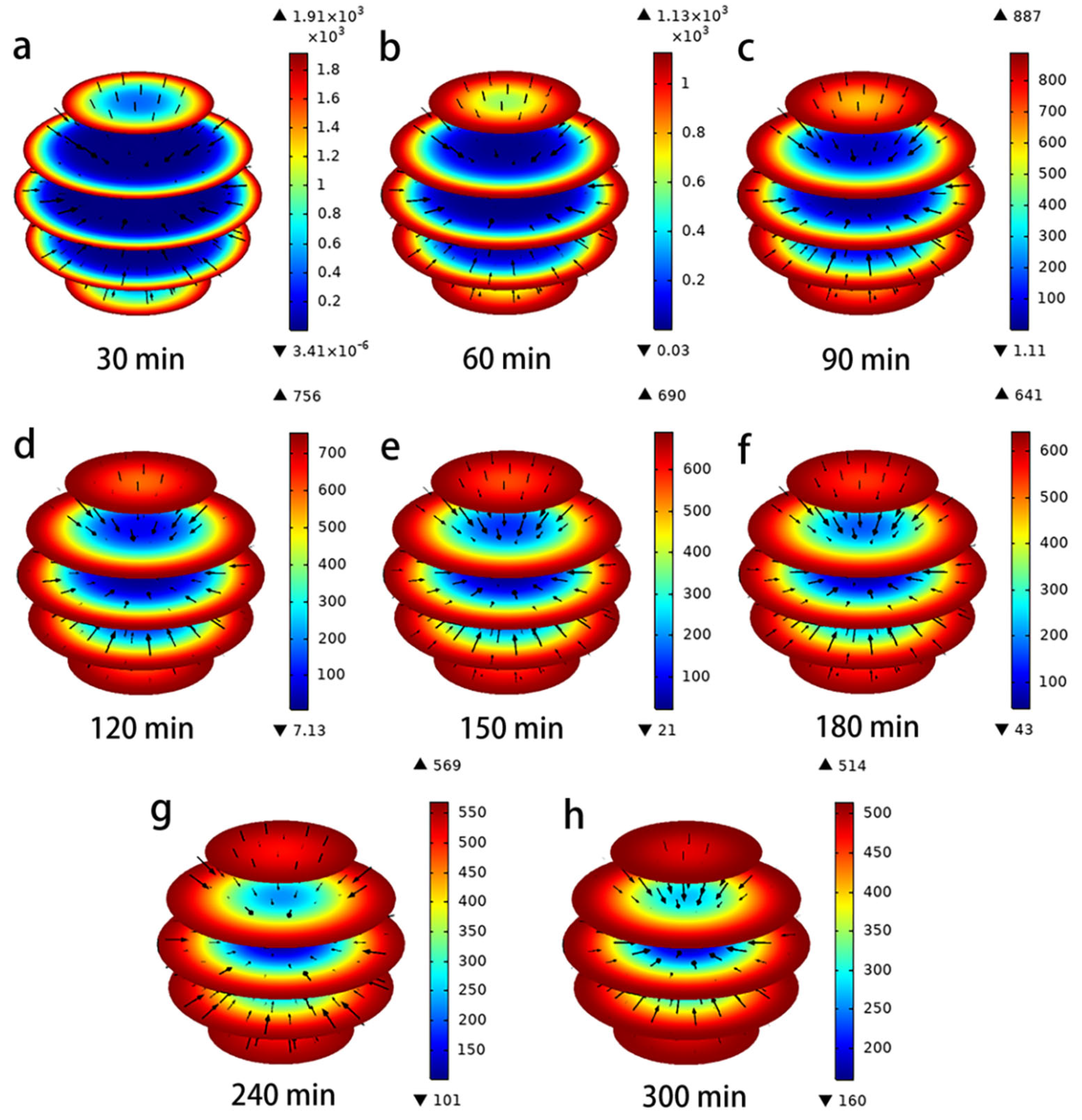
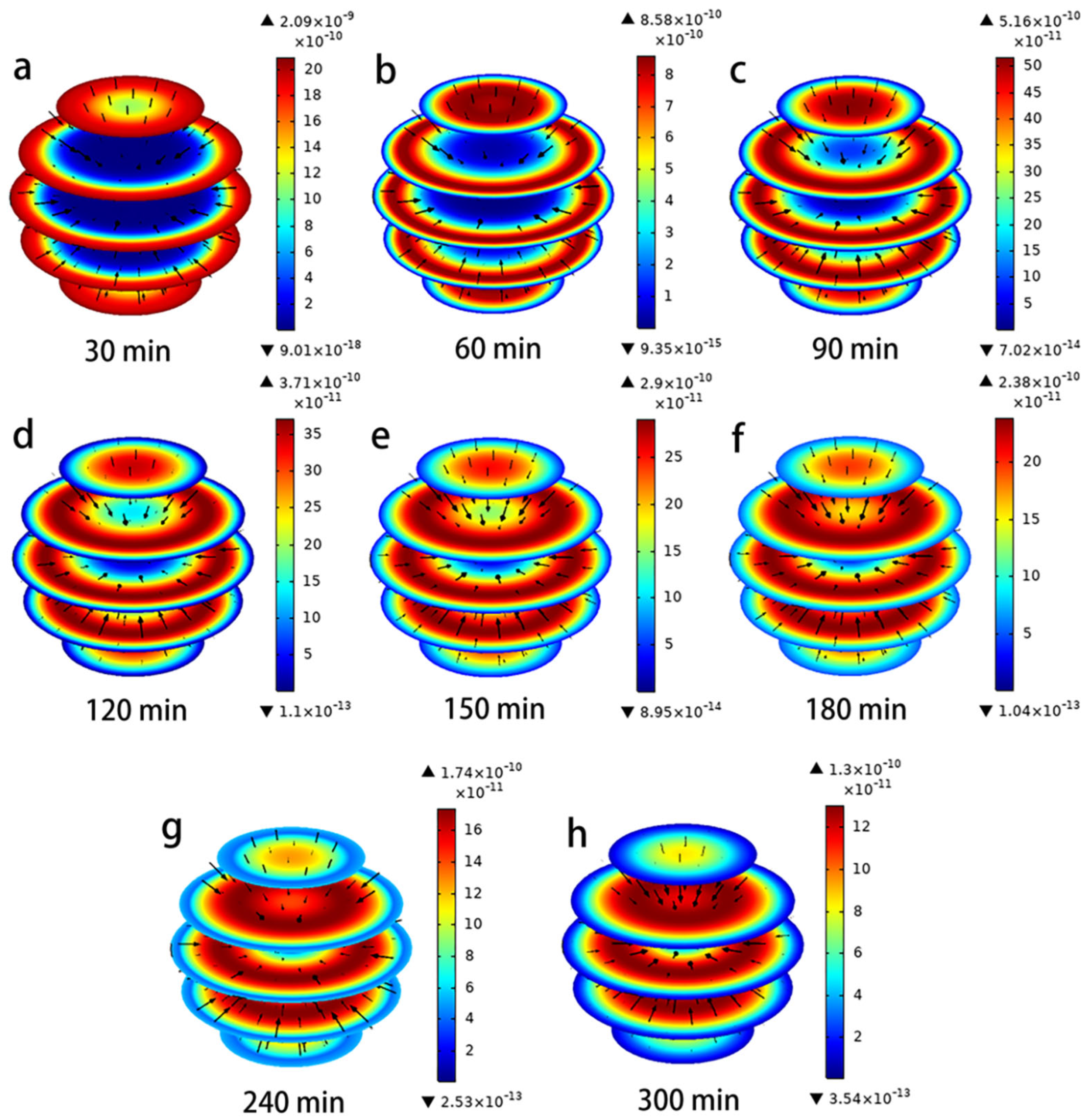
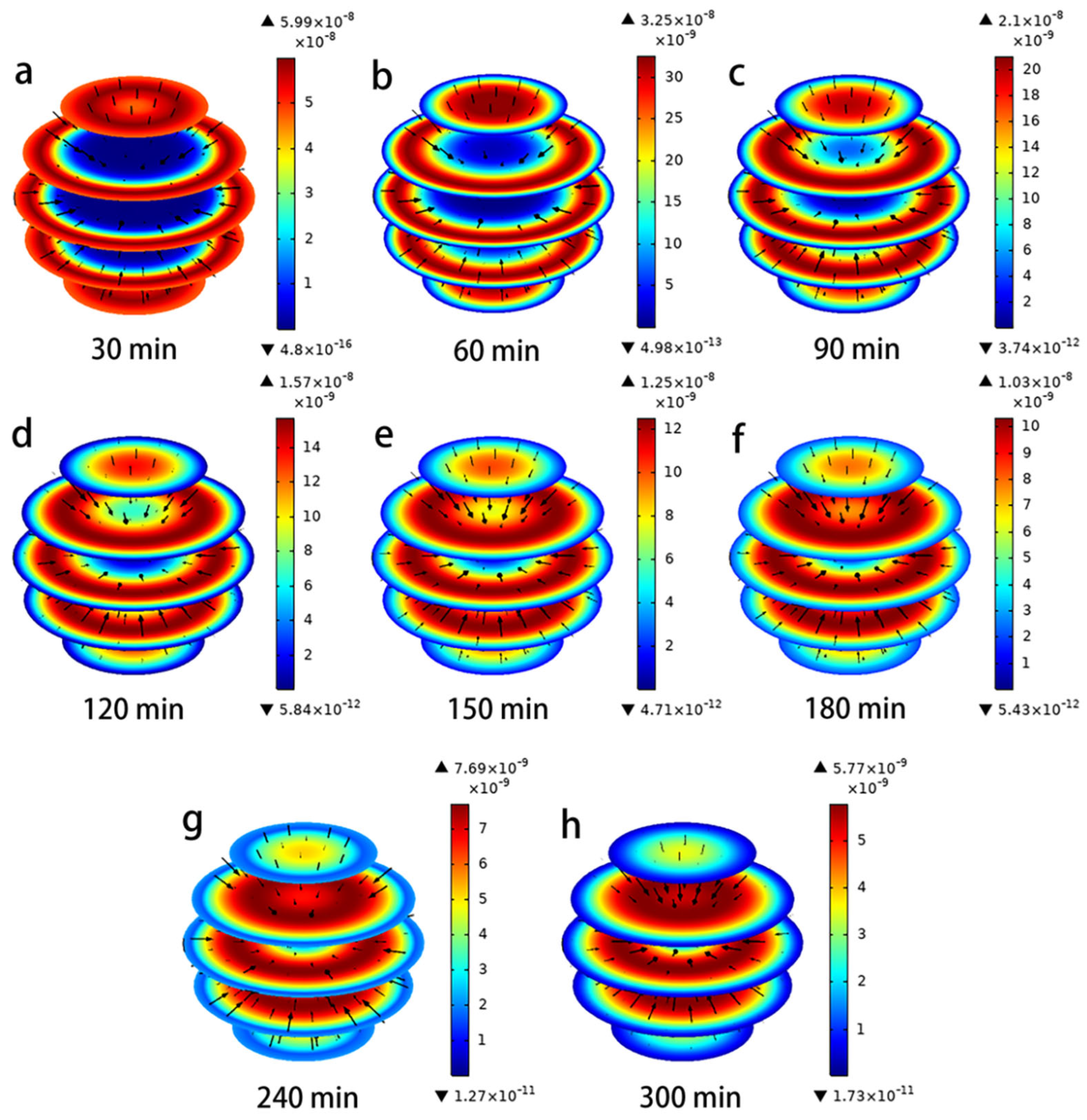
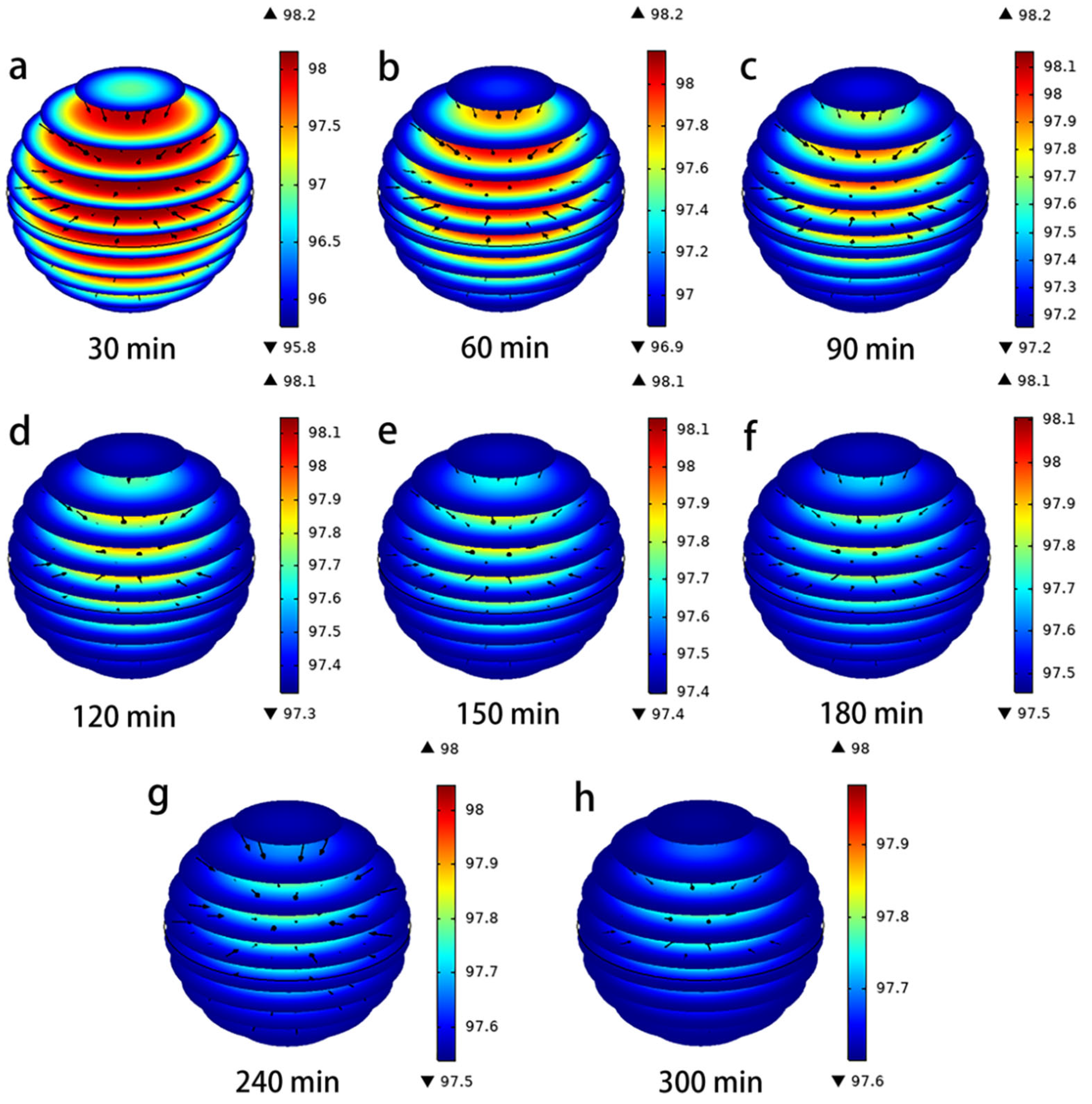
4.3. Simulation of Intraparticle Adsorption and Mass Transfer Processes
4.3.1. Concentration Decay Curve for Hydroquinone
4.3.2. Concentration Decay Curve for Hydroquinone
4.3.3. Simulation Applications of Pore Volume and Surface Diffusion Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Y. Anodic Enhancement by Advanced Oxidation and Coupled Biological Treatment of Refractory Organic Wastewater. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2020. [Google Scholar]
- Shi, S.; Lv, J.; Liu, Q.; Nan, F.; Feng, J.; Xie, S. Optimized preparation of Phragmites australis activated carbon using the Box–Behnken method and desirability function to remove hydroquinone. Ecotoxicol. Environ. Saf. 2018, 165, 411–422. [Google Scholar]
- Li, G.; Pang, S.; Wu, Y.; Ouyang, J. Enhanced removal of hydroquinone by graphene aerogel-Zr-MOF with immobilized laccase. Chem. Eng. Commun. 2018, 205, 698–705. [Google Scholar] [CrossRef]
- Shi, S. Removal Potential and Mechanism of Phenolic Pollutants by Phragmites australis Biomass Functionalised Materials. Ph.D. Thesis, Shanxi University, Taiyuan, China, 2021. [Google Scholar]
- Díaz-Blancas, V.; Ocampo-Pérez, R.; Leyva-Ramos, R.; Alonso-Dávila, P.A.; Moral-Rodríguez, A.I. 3D Modeling of the overall adsorption rate of metronidazole on granular activated carbon at low and high concentrations in aqueous solution. Chem. Eng. J. 2018, 349, 82–91. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving methods. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef]
- Souza, P.R.; Dotto, G.L.; Salau, N.P.G. Detailed numerical solution of pore volume and surface diffusion model in adsorption systems. Chem. Eng. Res. Des. 2017, 122, 298–307. [Google Scholar] [CrossRef]
- Ocampo-Pérez, R.; Rivera-Utrilla, J.; Gómez-Pacheco, C.; Sánchez-Polo, M.; López-Peñalver, J.J. Kinetic study of tetracycline adsorption on sludge–derived adsorbents in aqueous phase. Chem. Eng. J. 2012, 213, 88–96. [Google Scholar] [CrossRef]
- Ocampo-Pérez, R.; Daiem, M.M.A.; Rivera-Utrilla, J.; Méndez-Díaz, J.D.; Sánchez-Polo, M. Modeling adsorption rate of organic micropollutants present in landfill leachates onto granular activated carbon. J. Colloid Interface Sci. 2012, 385, 174–182. [Google Scholar] [CrossRef]
- Largitte, L.; Pasquier, R. A review of the kinetics adsorption models and their application to the adsorption of lead by an activated carbon. Chem. Eng. Res. Des. 2016, 109, 495–504. [Google Scholar] [CrossRef]
- Qiu, H.; Lv, L.; Pan, B.-C.; Zhang, Q.-J.; Zhang, W.-M.; Zhang, Q.-X. Critical review in adsorption kinetic models. J. Zhejiang Univ.–Sci. A 2009, 10, 716–724. [Google Scholar] [CrossRef]
- Knust, K.N.; Foley, M.P.; Mubarak, M.S.; Skljarevski, S.; Raghavachari, K.; Peters, D.G. Electrochemical reduction of 5–chloro–2–(2,4–dichlorophenoxy) phenol (triclosan) in dimethylformamide. J. Electroanal. Chem. 2010, 638, 100–108. [Google Scholar] [CrossRef]
- Xu, R.; Xie, Y.; Tian, J.; Chen, L. Adsorbable organic halogens in contaminated water environment: A review of sources and removal technologies. J. Clean. Prod. 2021, 283, 124645. [Google Scholar] [CrossRef]
- De Gisi, S.; Lofrano, G.; Grassi, M.; Notarnicola, M. Characteristics and adsorption capacities of low-cost sorbents for wastewater treatment: A review. Sustain. Mater. Technol. 2016, 9, 10–40. [Google Scholar] [CrossRef]
- Ocampo-Perez, R.; Leyva-Ramos, R.; Alonso-Davila, P.; Rivera-Utrilla, J.; Sanchez-Polo, M. Modeling adsorption rate of pyridine onto granular activated carbon. Chem. Eng. J. 2010, 165, 133–141. [Google Scholar] [CrossRef]
- Leyva-Ramos, R.; Geankoplis, C.J. Model simulation and analysis of surface diffusion of liquids in porous solids. Chem. Eng. Sci. 1985, 40, 799–807. [Google Scholar] [CrossRef]
- Comerton, A.M.; Andrews, R.C.; Bagley, D.M.; Yang, P. Membrane adsorption of endocrine disrupting compounds and pharmaceutically active compounds. J. Membr. Sci. 2007, 303, 267–277. [Google Scholar] [CrossRef]
- Yüksel, S.; Kabay, N.; Yüksel, M. Removal of bisphenol A (BPA) from water by various nanofiltration (NF) and reverse osmosis (RO) membranes. J. Hazard. Mater. 2013, 263, 307–310. [Google Scholar] [CrossRef]
- Sun, Y.Y. Preparation, Characterization and Adsorption Performance of Reed Bamboo Activated Carbon. Ph.D. Thesis, Shandong University, Jinan, China, 2014. [Google Scholar]
- Wu, J.; Yu, H. Biosorption of 2,4–dichlorophenol from aqueous solution by Phanerochaete chrysosporium biomass: Isotherms, kinetics and thermodynamics. J. Hazard. Mater. 2006, 137, 498–508. [Google Scholar] [CrossRef]
- Hu, X.; Jia, L.; Cheng, J.; Sun, Z. Magnetic ordered mesoporous carbon materials for adsorption of minocycline from aqueous solution: Preparation, characterization and adsorption mechanism. J. Hazard. Mater. 2019, 362, 1–8. [Google Scholar] [CrossRef]
- Fu, J.; Zhu, J.; Wang, Z.; Wang, Y.; Wang, S.; Yan, R.; Xu, Q. Highly–efficient and selective adsorption of anionic dyes onto hollow polymer microcapsules having a high surface–density of amino groups: Isotherms, kinetics, thermodynamics and mechanism. J. Colloid Interface Sci. 2019, 542, 123–135. [Google Scholar] [CrossRef]
- Freundlich, H.M.F. Uber die adsorption in lusungen. J. Phys. Chem. 1985, 57, 387–470. [Google Scholar]
- Freundlich, H.M.F. Over the adsorption in solution. J. Phys. Chem. 1906, 57, 385–471. [Google Scholar]
- Arshadi, M.; Mousavinia, F.; Amiri, M.J.; Faraji, A.R. Adsorption of methyl orange and salicylic acid on a nano–transition metal composite: Kinetics, thermodynamic and electrochemical studies. J. Colloid Interface Sci. 2016, 483, 118–131. [Google Scholar] [CrossRef]
- Qu, J.; Akindolie, M.S.; Feng, Y.; Jiang, Z.; Zhang, G.; Jiang, Q.; Deng, F.; Cao, B.; Zhang, Y. One–pot hydrothermal synthesis of NaLa(CO3)2 decorated magnetic biochar for efficient phosphate removal from water: Kinetics, isotherms, thermodynamics, mechanisms and reusability exploration. Chem. Eng. J. 2020, 394, 124915. [Google Scholar] [CrossRef]
- Xu, P.; Zeng, G.M.; Huang, D.L.; Lai, C.; Zhao, M.H.; Wei, Z.; Li, N.J.; Huang, C.; Xie, G.X. Adsorption of Pb(II) by iron oxide nanoparticles immobilized Phanerochaete chrysosporium: Equilibrium, kinetic, thermodynamic and mechanisms analysis. Chem. Eng. J. 2012, 203, 423–431. [Google Scholar] [CrossRef]
- Frhlich, A.C.; Ocampo-Pérez, R.; Diaz-Blancas, V.; Salau NP, G.; Dotto, G.L. Three–dimensional mass transfer modeling of ibuprofen adsorption on activated carbon prepared by sonication. Chem. Eng. J. 2018, 341, 65–74. [Google Scholar] [CrossRef]
- Ocampo-Perez, R.; Aguilar-Madera, C.G.; Díaz-Blancas, V. 3D modeling of overall adsorption rate of acetaminophen on activated carbon pellets. Chem. Eng. J. 2017, 321, 510–520. [Google Scholar] [CrossRef]
- Furusawa, T.; Smith, J.M. Fluid-particle and intraparticle mass transport rates in slurries. Ind. Eng. Chem. Fundam. 1973, 12, 197–203. [Google Scholar] [CrossRef]
- Wilke, C.R.; Chang, P. Correlation of diffusion coefficients in dilute solutions. AIChE J. 1955, 1, 264–270. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids; McGraw–Hill: New York, NY, USA, 1977; pp. 401–452. [Google Scholar]
| Project | Value |
|---|---|
| ρs (kg/m3) | 1.63 |
| ρp (kg/m3) | 0.52 |
| εp | 0.68 |
| Isotherm Models | Hydroquinone | |||
|---|---|---|---|---|
| 20 °C | 30 °C | 40 °C | ||
| Langmuir | qm (mg/g) | 147.06 | 156.25 | 158.73 |
| kL (L/mg) | 0.3063 | 0.3170 | 0.3535 | |
| Adj R2 | 0.9647 | 0.9624 | 0.9943 | |
| Freundlich | kF (mg/g(L/mg)1/n) | 50.32 | 40.65 | 39.05 |
| n | 3.71 | 2.68 | 2.67 | |
| Adj R2 | 0.9972 | 0.9969 | 0.9901 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, S.; Luo, A.; Hao, J.; Xie, S.; Feng, J. Three-Dimensional Mass Transfer Modeling of Hydroquinone Adsorption on Phragmites australis Biochar. Toxics 2023, 11, 639. https://doi.org/10.3390/toxics11070639
Shi S, Luo A, Hao J, Xie S, Feng J. Three-Dimensional Mass Transfer Modeling of Hydroquinone Adsorption on Phragmites australis Biochar. Toxics. 2023; 11(7):639. https://doi.org/10.3390/toxics11070639
Chicago/Turabian StyleShi, Shengli, Aiguo Luo, Jianwei Hao, Shulian Xie, and Jia Feng. 2023. "Three-Dimensional Mass Transfer Modeling of Hydroquinone Adsorption on Phragmites australis Biochar" Toxics 11, no. 7: 639. https://doi.org/10.3390/toxics11070639
APA StyleShi, S., Luo, A., Hao, J., Xie, S., & Feng, J. (2023). Three-Dimensional Mass Transfer Modeling of Hydroquinone Adsorption on Phragmites australis Biochar. Toxics, 11(7), 639. https://doi.org/10.3390/toxics11070639







