Proposal of a Methodology for Prediction of Indoor PM2.5 Concentration Using Sensor-Based Residential Environments Monitoring Data and Time-Divided Multiple Linear Regression Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement Method
2.2. Data Analysis
2.2.1. Statistics Analysis
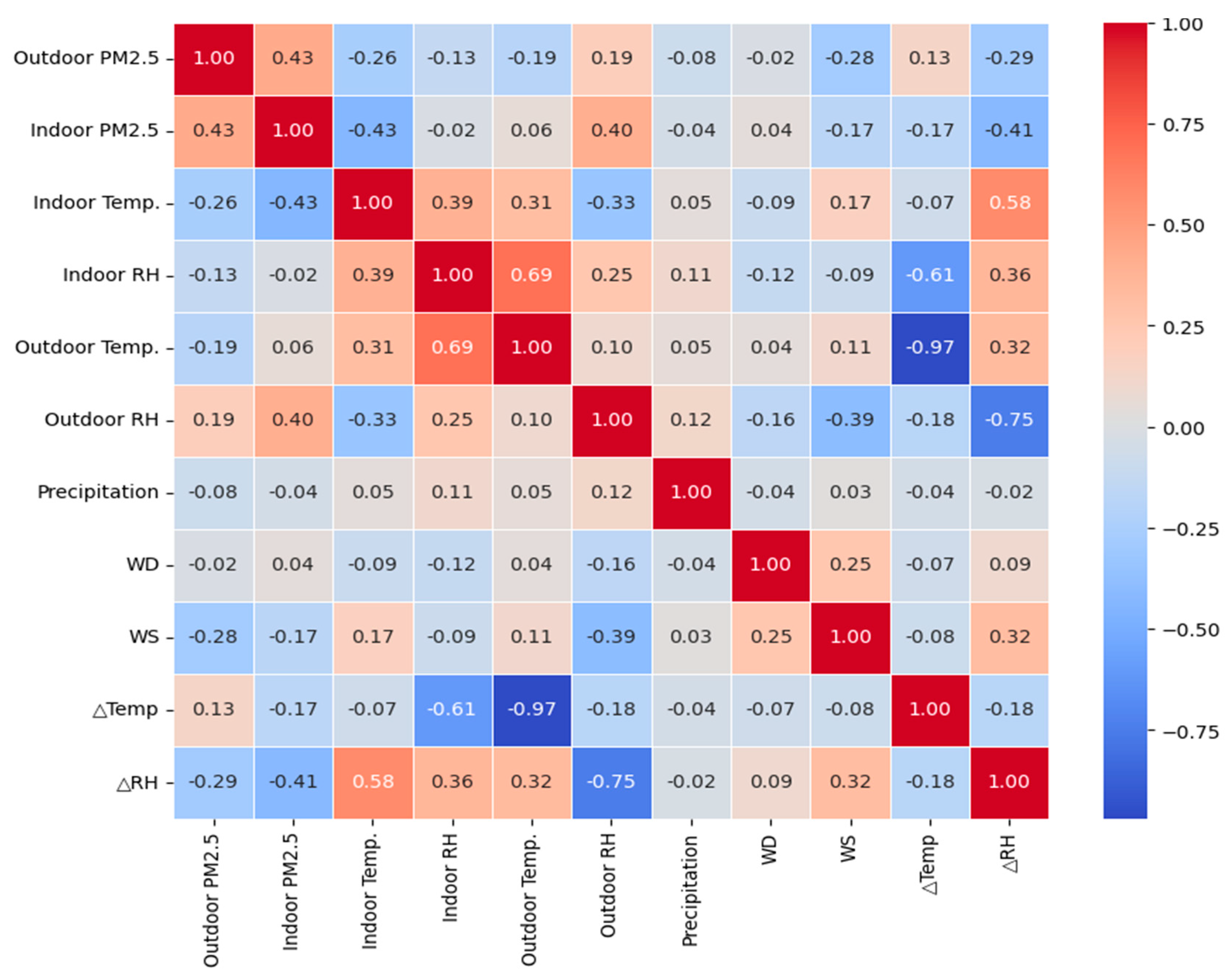
2.2.2. Selection of Input Variables
2.3. Data Preprocessing before Training
2.4. Multiple Linear Regression Model
2.5. Performance Indicators
3. Results
3.1. Distribution Characteristics of Indoor and Outdoor Measurement Data
3.2. Selection of Input Variables
3.3. Model Training Result
3.3.1. MLR Model
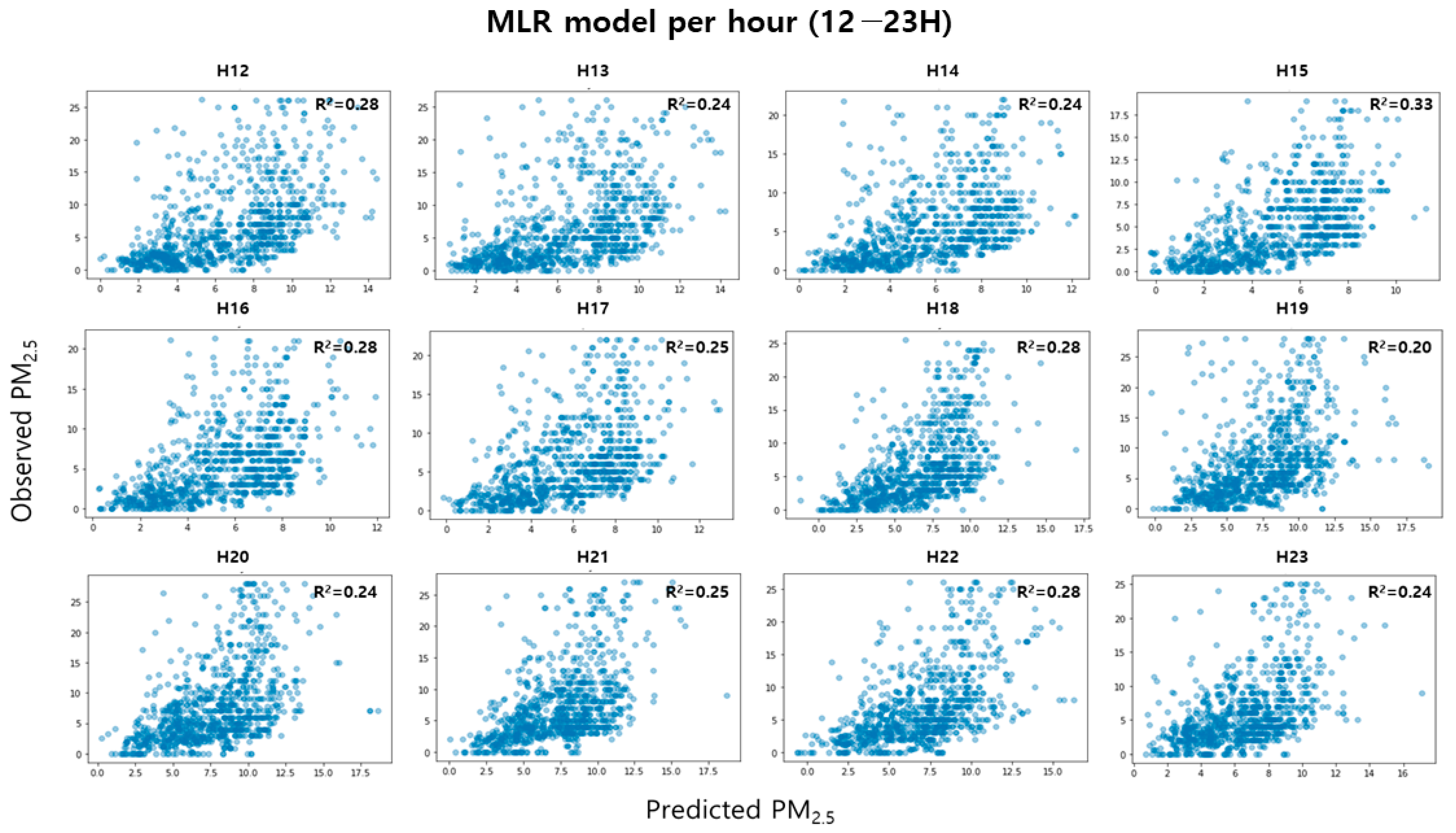
3.3.2. MLR Model Divided by Hour
4. Discussion
4.1. Indoor PM2.5 Concentration and Outdoor Variables
4.2. Previous Studies about Indoor PM2.5 Concentration Prediction Model
| Indoor Type | Variable | Time Division (O/X) (1) | Data | RMSE | R2 | Ref. | |
|---|---|---|---|---|---|---|---|
| Indoor | Outdoor | ||||||
| Dwelling | Survey result | PM2.5 | X | (1) Country: America (2) Sampling period: 48 h samping (3) Sampling the indoor and outdoor data simultaneously, nearby | - | 0.35 | [36] |
| Apartment | Survey results, building characteristics | PM2.5 concentration, temperature, wind speed | X | (1) Country: Mongolia (2) Sampling period: 7 days, during 24 h (3) Indoor data: The direct measurement of indoor air (4) Outdoor data: The national monitoring network | 0.48, 0.50 (val) (2) | 0.52, 0.49 (val) | [46] |
| Dwelling | PM10_2.5, survey result, VOCs, building characteristics | PM10_2.5, RH, PM2.5 | X | (1) Country: Japan (2) Sampling period: 7 days, during 24 h (3) Sampling the indoor and outdoor data simultaneously, nearby | 15.70 (val) | 0.42 (val) | [47] |
| School | Relative humidity, temperature, Ventilation | PM2.5, CO2, wind speed, PM10 | O | (1) Country: Israel (2) Sampling period: 7 days, 7:00–12:00 in winter and spring, 12:00–17:00 in fall (3) Indoor and outdoor measurements alternately at 15 min intervals | 0.17 (Fall), 0.13 (Winter), 0.14 (Spring), 0.08 (Annual) | 0.58 (Fall), 0.69 (Winter), 0.69 (Spring), 0.88 (Annual) | [50] |
| Laboratory building | Temperature, Relative humidity, PM10, NO2 | Temperature, Relative humidity, PM10, NO2, PM2.5 | X | (1) Country: America (2) Sampling period: May-September 2020 during 24 h (3) Sampling the indoor and outdoor data simultaneously, nearby (4) Reflection of time delay effect (TSR model) | 0.09 | 0.99 | [51] |
4.3. MLR Model
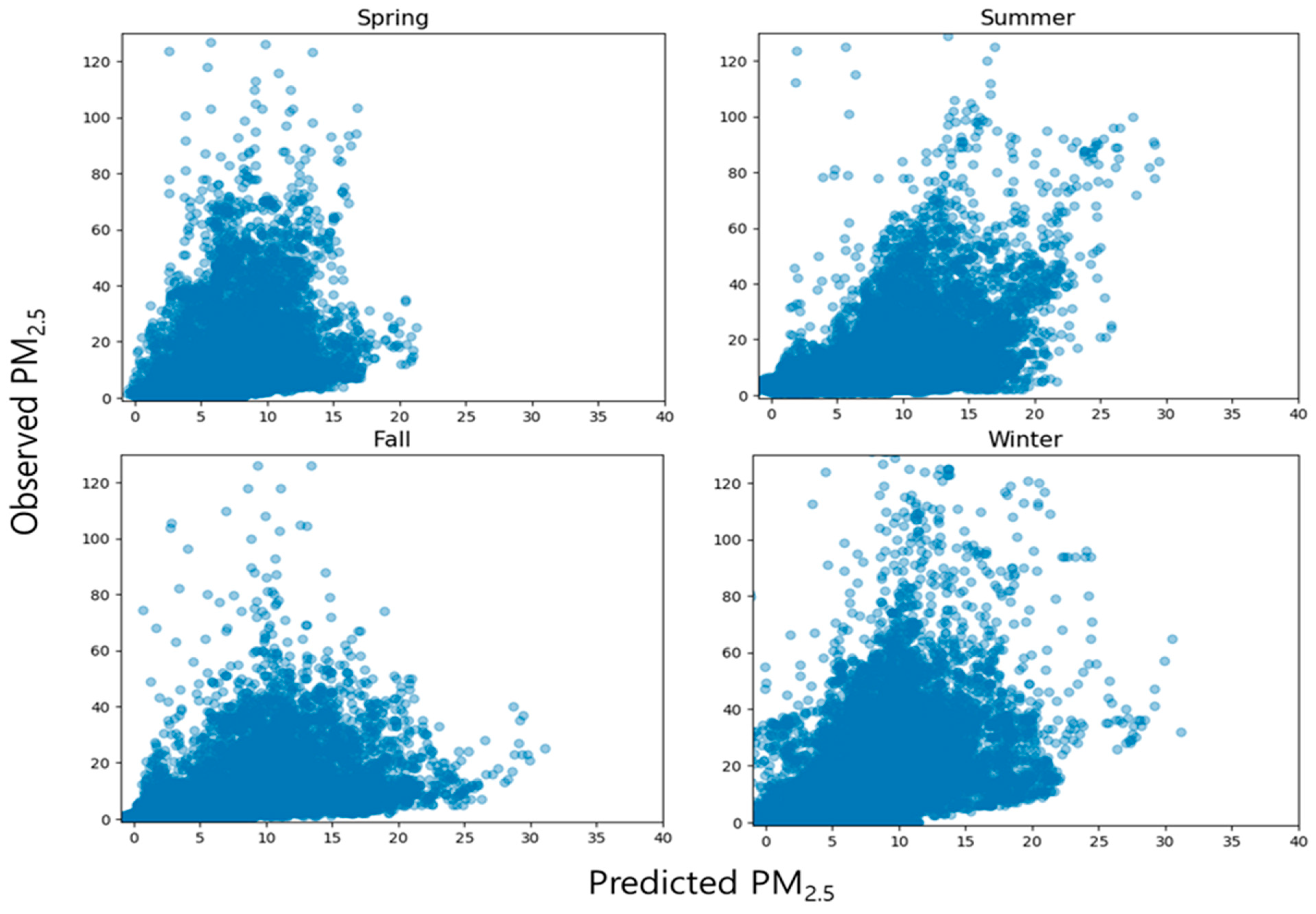
4.4. Influence of Seasonal Characteristics on Prediction Results of PM2.5 Cocentration
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anonymous. Korean Exposure Factors Handbook; Risk Assessment Division; National Institute of Environmental Research: Incheon, Republic of Korea, 2019.
- F KSOSTAT. Kindicator. 2022. Available online: http://www.index.go.kr/unify/idx-info.do?idxCd=4275#:~:text=%EA%B5%AD%EC%A0%9C%EC%A0%81%EC%9C%BC%EB%A1%9C%20%ED%95%9C%EA%B5%AD%EC%9D%98%20%EB%AF%B8%EC%84%B8,2%EB%B0%B0%20%EC%A0%95%EB%8F%84%20%EC%8B%AC%ED%95%9C%20%EA%B2%83%EC%9D%B4%EB%8B%A4 (accessed on 27 March 2023).
- Wang, X.; Xu, Z.; Su, H.; Ho, H.C.; Song, Y.; Zheng, H.; Hossain, M.Z.; Khan, M.A.; Bogale, D.; Zhang, H.; et al. Ambient Particulate Matter (PM1, PM2.5, PM10) and Childhood Pneumonia: The Smaller Particle, the Greater Short-Term Impact? Sci. Total Environ. 2021, 772, 145509. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, J. Harvesting and Long Term Exposure Effects in the Relation between Air Pollution and Mortality. Am. J. Epidemiol. 2000, 151, 440–448. [Google Scholar] [CrossRef]
- Franklin, M.; Koutrakis, P.; Schwartz, J. The Role of Particle Composition on the Association between PM2.5 and Mortality. Epidemiology 2008, 19, 680. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.Y.; Tsay, Y.S.; Jung, C.C. Machine Learning Models for Indoor PM2.5 Concentrations in Residential Architecture in Taiwan. In Proceedings of the CLIMA 2022 Conference, UT Austin, Austin, TX, USA, 23–26 May 2022. [Google Scholar]
- Jung, J.; Ahn, J. Intelligent User Pattern Recognition Based on Vision, Audio and Activity for Abnormal Event Detections of Single Households. J. Korea Soc. Comput. Inf. 2019, 24, 59–66. [Google Scholar]
- Lee, S.H.; Yoon, Y.A.; Jung, J.H.; Chang, T.W.; Kim, Y.S. A Machine Learning Model for Predicting Silica Concentrations through Time Series Analysis of Mining Data. J. Korean Soc. Qual. Manag. 2020, 48, 511–520. [Google Scholar]
- Wei, W.; Ramalho, O.; Malingre, L.; Sivanantham, S.; Little, J.C.; Mandin, C. Machine Learning and Statistical Models for Predicting Indoor Air Quality. Indoor Air 2019, 29, 704–726. [Google Scholar] [CrossRef]
- Choi, Y.J.; Choi, E.J.; Cho, H.U.; Moon, J.W. Development of an Indoor Particulate Matter (PM2.5) Prediction Model for Improving School Indoor Air Quality Environment. KIEAE J. 2021, 21, 35–40. [Google Scholar] [CrossRef]
- Lagesse, B.; Wang, S.; Larson, T.V.; Kim, A.A. Predicting PM2.5 in Well-Mixed Indoor Air for a Large Office Building Using Regression and Artificial Neural Network Models. Environ. Sci. Technol. 2020, 54, 15320–15328. [Google Scholar] [CrossRef]
- Choi, Y.; Choi, E.; Cho, H.; Moon, J. Development of a Prediction Model for Indoor Fine Dust (PM2.5) to Improve Indoor Air Quality in School Facilities. KIEAE J. 2021, 21, 35–40. [Google Scholar] [CrossRef]
- Phillips, J.L.; Field, R.; Goldstone, M.; Reynolds, G.L.; Lester, J.N.; Perry, R. Relationships between indoor and outdoor air quality in four naturally ventilated offices in the United Kingdom. Atmos. Environ. Part A Gen. Top 1993, 27, 1743–1753. [Google Scholar] [CrossRef]
- Ji, W.; Zhao, B. Contribution of Outdoor-Originating Particles, Indoor-Emitted Particles and Indoor Secondary Organic Aerosol (SOA) to Residential Indoor PM2.5 Concentration: A Model-Based Estimation. Build. Environ. 2015, 90, 196–205. [Google Scholar] [CrossRef]
- Liu, D.L.; Nazaroff, W.W. Modeling Pollutant Penetration Across Building Envelopes. Atmos. Environ. 2001, 35, 4451–4462. [Google Scholar] [CrossRef]
- Bakht, A.; Han, S.; Khan, M.S.; Jang, K.; Kim, K.H. Deep Learning-Based Indoor Air Quality Forecasting Framework for Indoor Subway Station Platforms. Toxics 2022, 10, 557. [Google Scholar] [CrossRef] [PubMed]
- Marzouk, M.; Atef, M. Assessment of Indoor Air Quality in Academic Buildings Using IoT and Deep Learning. Sustainability 2022, 14, 7015. [Google Scholar] [CrossRef]
- AirKorea. Available online: https://www.airkorea.or.kr/index (accessed on 27 March 2023).
- Chen, C.; Zhao, B. Review of Relationship between Indoor and Outdoor Particles: I/O Ratio, Infiltration Factor and Penetration Factor. Atmos. Environ. 2011, 45, 275–288. [Google Scholar] [CrossRef]
- Kang, J.-W.; An, C.-J.; Choi, W. Surrounding environment and indoor fine dust concentration distribution characteristics based on indoor/outdoor concentration ratio (I/O ratio): Focusing on previous research reviews and measurement results in Busan and Pyeongtaek elementary schools in summer. J. Korean Soc. Remote Sens. 2020, 36, 1691–1710. [Google Scholar]
- Abdipour, M.; Ramazani, S.H.R.; Younessi-Hmazekhanlu, M.; Niazian, M. Modeling Oil Content of Sesame (Sesamum indicum L.) Using Artificial Neural Network and Multiple Linear Regression Approaches. J. Am. Oil Chem. Soc. 2018, 95, 283–297. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Parsaeian, M.; Baradaran, M. Seed Yield Prediction of Sesame Using Artificial Neural Network. Eur. J. Agron. 2015, 68, 89–96. [Google Scholar] [CrossRef]
- May, R.J.; Dandy, G.C.; Maier, H.R. Review of Input Variable Selection Methods for Artificial Neural Networks. In Artificial Neural Networks—Methodological Advances and Biomedical Applications; InTech: Rijeka, Croatia, 2011; pp. 215–241. [Google Scholar]
- Czernecki, B.; Półrolniczak, M.; Kolendowicz, L.; Marosz, M.; Kendzierski, S.; Pilguj, N. Influence of the Atmospheric Conditions on PM10 Concentrations in Poznań, Poland. J. Atmos. Chem. 2017, 74, 115–139. [Google Scholar] [CrossRef]
- Xu, C.; Xu, D.; Liu, Z.; Li, Y.; Li, N.; Chartier, R.; Li, N. Estimating Hourly Average Indoor PM2.5 Using the Random Forest Approach in Two Megacities, China. Build. Environ. 2020, 180, 107025. [Google Scholar] [CrossRef]
- Yeom, M.-S.; Cho, G.-Y. Natural Ventilation of a High-Rise Residential Building Using a Double Skin System. Archit 2007, 51, 57–62. [Google Scholar]
- Isixsigma. Variance Inflation Factor (VIF). Available online: https://www.isixsigma.com/dictionary/variance-inflation-factor-vif/ (accessed on 27 March 2023).
- Jeon, Y.T.; Yu, S.H.; Kwon, H.Y. Improvement of PM Forecasting Performance by Outlier Data Removing. J. Korea Multimed. Soc. 2020, 23, 747–755. [Google Scholar]
- Kashi, H.; Emamgholizadeh, S.; Ghorbani, H. Estimation of Soil Infiltration and Cation Exchange Capacity Based on Multiple Regression, ANN (RBF, MLP), and ANFIS Models. Commun. Soil Sci. Plant Anal. 2014, 45, 1195–1213. [Google Scholar] [CrossRef]
- Masood, A.; Ahmad, K. A Model for Particulate Matter (PM2.5) Prediction for Delhi Based on Machine Learning Approaches. Procedia Comput. Sci. 2020, 167, 2101–2110. [Google Scholar] [CrossRef]
- Scikit-Learn. Sklearn.linear_model.SGDRegressor. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.SGDRegressor.html (accessed on 27 March 2023).
- Kang, M.J. Comparison of Gradient Descent for Deep Learning. J. Korea Acad. Ind. Coop. Soc. 2020, 21, 189–194. [Google Scholar]
- Konečný, J.; Liu, J.; Richtárik, P.; Takáč, M. Mini-Batch Semi-Stochastic Gradient Descent in the Proximal Setting. IEEE J. Sel. Top. Signal Process. 2015, 10, 242–255. [Google Scholar] [CrossRef]
- Taşan, S.; Demir, Y. Comparative analysis of MLR, ANN, and ANFIS models for prediction of field capacity and permanent wilting point for Bafra plain soils. Commun. Soil Sci. Plant Anal. 2020, 51, 604–621. [Google Scholar] [CrossRef]
- Nishihama, Y.; Ishikuro, M.; Miyashita, C.; Yamamoto-Hanada, K.; Sato, M.; Kato, N.; Minami, Y.; Hori, T.; Doi, H.; Araki, A.; et al. Indoor Air Quality of 5000 Households and Its Determinants. Part A: Particulate Matter (PM2.5 and PM10–2.5) Concentrations in the Japan Environment and Children’s Study. Environ. Res. 2021, 198, 111196. [Google Scholar] [CrossRef]
- National Institute of Environmental Research. Annual Report of Air Quality in Korea 2021. Available online: https://www.niehs.nih.gov/research/programs/geh/partnerships/network/centres/south_korea/index.cf (accessed on 27 March 2023).
- Ministry of Environment. Implementation Regulations of Indoor Air Quality Management Act. Year. Available online: https://www.law.go.kr/%EB%B2%95%EB%A0%B9/%EC%8B%A4%EB%82%B4%EA%B3%B5%EA%B8%B0%EC%A7%88%EA%B4%80%EB%A6%AC%EB%B2%95%EC%8B%9C%ED%96%89%EA%B7%9C%EC%B9%99 (accessed on 23 April 2023).
- Park, B.R.; Choi, D.H.; Kang, D.H. Seasonal Contribution of Indoor Generated and Outdoor Originating PM2.5 to Indoor Concentration Depending on Airtightness of Apartment Units. J. Archit. Inst. Korea Struct. Constr. 2020, 36, 155–163. [Google Scholar]
- Park, J.; Kim, E.; Choe, Y.; Ryu, H.; Kim, S.; Woo, B.L.; Cho, M.; Yang, W. Indoor to Outdoor Ratio of Fine Particulate Matter by Time of the Day in House According to Time-activity Patterns. J. Environ. Health Sci. 2020, 45, 504–512. [Google Scholar]
- Park, S.; Yoon, D.; Kong, H.; Kang, S.; Lee, C. A Case Study on Distribution Characteristics of Indoor and Outdoor Particulate Matters (PM10, PM2.5) and Black Carbon (BC) by Season and Time of the Day in Apartment. J. Environ. Health Sci. 2021, 47, 339–355. [Google Scholar]
- Han, Y.; Qi, M.; Chen, Y.; Shen, H.; Liu, J.; Huang, Y.; Chen, H.; Liu, W.; Wang, X.; Liu, J. Influences of Ambient Air PM2.5 Concentration and Meteorological Condition on the Indoor PM2.5 Concentrations in a Residential Apartment in Beijing Using a New Approach. Environ. Pollut. 2015, 205, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Chen, C.; Wang, P.; Chen, Z.; Cao, S.; Wang, Q.; Xie, G.; Wan, Y.; Wang, Y.; Lu, B. Influence of Atmospheric Fine Particulate Matter (PM2.5) Pollution on Indoor Environment during Winter in Beijing. Build. Environ. 2015, 87, 283–291. [Google Scholar] [CrossRef]
- Qi, M.; Zhu, X.; Du, W.; Chen, Y.; Chen, Y.; Huang, T.; Pan, X.; Zhong, Q.; Sun, X.; Zeng, E.Y. Exposure and Health Impact Evaluation Based on Simultaneous Measurement of Indoor and Ambient PM2.5 in Haidian, Beijing. Environ. Pollut. 2017, 220, 704–712. [Google Scholar] [CrossRef]
- Kearney, J.; Wallace, L.; MacNeill, M.; Heroux, M.-E.; Kindzierski, W.; Wheeler, A. Residential Infiltration of Fine and Ultrafine Particles in Edmonton. Atmos. Environ. 2014, 94, 793–805. [Google Scholar] [CrossRef]
- Yang, S.; Mahecha, S.D.; Moreno, S.A.; Licina, D. Integration of Indoor Air Quality Prediction into Healthy Building Design. Sustainability 2022, 14, 7890. [Google Scholar] [CrossRef]
- Yuchi, W.; Gao, J.; Xie, W.; Wang, L.; Zhang, Z.; Lai, A.C.K. Evaluation of Random Forest Regression and Multiple Linear Regression for Predicting Indoor Fine Particulate Matter Concentrations in a Highly Polluted City. Environ. Pollut. 2019, 245, 746–753. [Google Scholar] [CrossRef]
- Elbayoumi, M.; Ramli, N.A.; Yusof, N.F.F.M.; Yahaya, A.S.B.; Al Madhoun, W.; Ul-Saufie, A.Z. Multivariate Methods for Indoor PM10 and PM2.5 Modelling in Naturally Ventilated Schools Buildings. Atmosphere 2014, 94, 11–21. [Google Scholar] [CrossRef]
- Zhang, H.; Srinivasan, R.; Yang, X. Simulation and Analysis of Indoor Air Quality in Florida Using Time Series Regression (TSR) and Artificial Neural Networks (ANN) Models. Symmetry 2021, 13, 952. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Yang, X.; Wang, J.; Xie, M.; Wei, X.; Liu, H.; Yuan, Y. Factors Influencing Indoor Air Pollution in Buildings Using PCA-LMBP Neural Network: A Case Study of a University Campus. Build. Environ. 2022, 225, 109643. [Google Scholar] [CrossRef]
- Zhong, J.; Ding, J.; Su, Y.; Shen, G.; Yang, Y.; Wang, C.; Tao, S. Carbonaceous Particulate Matter Air Pollution and Human Exposure from Indoor Biomass Burning Practices. Environ. Eng. Sci. 2012, 29, 1038–1045. [Google Scholar] [CrossRef]
- Abt, E.; Suh, H.H.; Catalano, P.; Koutrakis, P. Relative Contribution of Outdoor and Indoor Particle Sources to Indoor Concentrations. Environ. Sci. Technol. 2000, 34, 3579–3587. [Google Scholar] [CrossRef]
- Pagel, É.; Costa Reis, N.; de Alvarez, C.E.; Santos, J.M.; Conti, M.M.; Boldrini, R.S.; Kerr, A.S. Characterization of the Indoor Particles and Their Sources in an Antarctic Research Station. Environ. Monit. Assess. 2016, 188, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Shrubsole, C.; Ridley, I.; Biddulph, P.; Milner, J.; Vardoulakis, S.; Ucci, M.; Oreszczyn, T.; Wilkinson, P.; Marmot, A.; Davies, M. Indoor PM2.5 Exposure in London’s Domestic Stock: Modelling Current and Future Exposures Following Energy Efficient Refurbishment. Atmosphere 2012, 3, 623–646. [Google Scholar] [CrossRef]
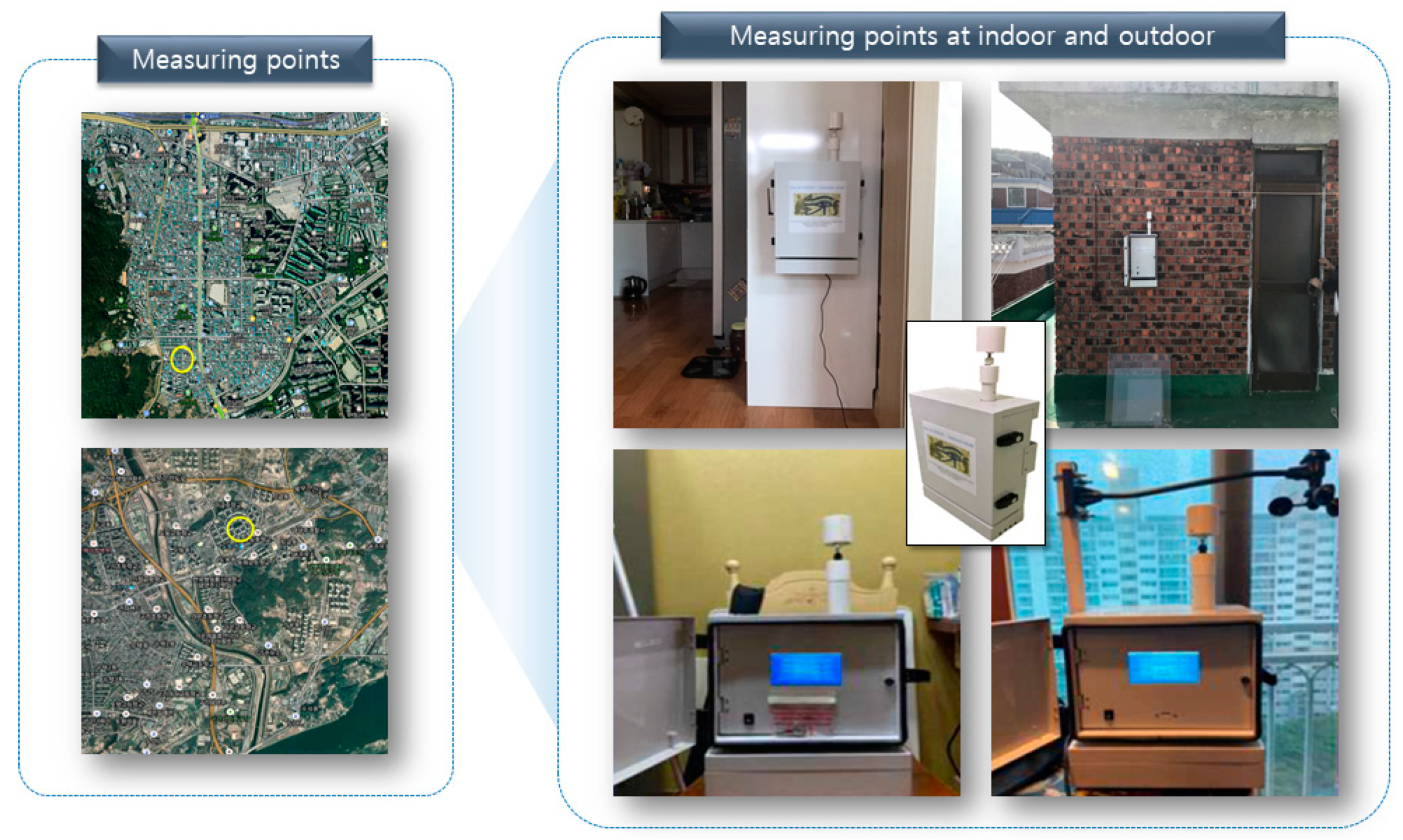





| Specification | Dust Mon (Sentry Co. Ltd., Seoul, Republic of Korea) | |
|---|---|---|
| Appearance |  | |
| 300 (W) × 150 (D) × 430 (H) MM, 9 kg | ||
| Metrics | Particulate matter | PM2.5 |
| Other | Temperature, Relative humidity | |
| Measurement Range | Particulate matter | 0–100,000 µg/m3 |
| Flux | 0.5 L/min | |
| Operating range | −30 °C~60 °C, 0~99% relative humidity (RH) | |
| Working power | 220 VAC/60 Hz | |
| Power | 144 kW/month | |
| Communications | LTE Cat M1 | |
| Data storage | SD CARD | |
| Variable | Units | I/O | N | Mean ± S.D. | Median | Max | I/O Ratio | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | |||||||||
| PM2.5 | µg/m3 | Indoor | 80,572 | 10.31 ± 13.70 | 6.00 | 460.56 | 0.39 | 0.29 | 4.44 | 50.27 |
| Outdoor | 80,572 | 26.28 ± 20.69 | 21.00 | 227.00 | 1.76 | 5.38 | ||||
| Temperature | °C | Indoor | 80,572 | 27.01 ± 2.61 | 27.00 | 33.30 | 2.15 | 2.16 | 0.28 | −0.36 |
| Outdoor | 80,572 | 12.55 ± 10.65 | 12.50 | 40.00 | −0.06 | −0.80 | ||||
| Relative humidity | % | Indoor | 80,572 | 46.29 ± 18.61 | 41.06 | 94.25 | 0.61 | 0.48 | 1.39 | 1.18 |
| Outdoor | 80,572 | 75.37 ± 22.89 | 86.19 | 99.90 | −0.91 | −0.42 | ||||
| Model | N (Train/Test) | Coefficients | Intercept. | RMSE | MAE | R2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e | f | ||||||
| Previous method | 72,300 (50,610/ 21,690) | 16.44 | −9.44 | 4.46 | −0.71 | −4.57 | 0.69 | 9.62 | 4.86594 | 3.66157 | 0.25 |
| Model | N (Train/Test) | RMSE | MAE | R2 | Model | N (Train/Test) | RMSE | MAE | R2 |
|---|---|---|---|---|---|---|---|---|---|
| H0 | 2113/906 | 4.41158 | 3.36610 | 0.25 | H12 | 2097/899 | 5.12931 | 3.72021 | 0.28 |
| H1 | 2153/923 | 4.57719 | 3.54399 | 0.31 | H13 | 2116/907 | 5.16333 | 3.78103 | 0.24 |
| H2 | 2204/945 | 4.49406 | 3.41214 | 0.31 | H14 | 2109/905 | 4.23131 | 3.13249 | 0.24 |
| H3 | 2223/953 | 4.65165 | 3.53079 | 0.29 | H15 | 2073/889 | 3.34157 | 2.55109 | 0.33 |
| H4 | 2199/942 | 4.75141 | 3.60395 | 0.34 | H16 | 2072/889 | 3.94571 | 2.91574 | 0.28 |
| H5 | 2199/943 | 4.61411 | 3.57164 | 0.30 | H17 | 2064/885 | 4.39213 | 3.26841 | 0.25 |
| H6 | 2137/916 | 4.80890 | 3.69874 | 0.31 | H18 | 2093/897 | 4.70427 | 3.61987 | 0.28 |
| H7 | 2132/914 | 6.50780 | 5.01471 | 0.25 | H19 | 2143/919 | 5.65613 | 4.12237 | 0.20 |
| H8 | 2140/918 | 7.17099 | 5.37863 | 0.22 | H20 | 2133/915 | 5.59225 | 4.18854 | 0.24 |
| H9 | 2136/916 | 6.87636 | 5.08694 | 0.33 | H21 | 2089/896 | 5.10041 | 3.79425 | 0.25 |
| H10 | 2150/922 | 6.57170 | 4.95590 | 0.31 | H22 | 2074/889 | 4.89382 | 3.64940 | 0.28 |
| H11 | 2141/918 | 5.64699 | 4.10089 | 0.25 | H23 | 2077/891 | 4.54320 | 3.38853 | 0.24 |
| Model | Coefficients | Intercept. | Model | Coefficients | Intercept. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e | f | a | b | c | d | e | f | ||||
| H0 | 14.00 | −6.45 | 5.83 | −0.29 | −0.16 | −0.19 | 4.47 | H12 | 8.22 | −5.21 | 5.64 | −1.97 | −3.61 | 0.22 | 6.17 |
| H1 | 13.62 | −6.41 | 6.76 | −0.56 | 0.07 | −0.73 | 3.50 | H13 | 9.78 | −3.63 | 4.67 | −2.27 | −4.25 | −0.84 | 6.56 |
| H2 | 9.86 | −6.92 | 5.83 | 0.27 | −0.38 | 0.03 | 4.05 | H14 | 6.76 | −3.86 | 4.69 | −1.45 | −4.53 | −0.33 | 6.20 |
| H3 | 8.92 | −8.17 | 5.63 | 1.40 | −0.86 | 0.84 | 4.04 | H15 | 4.98 | −3.22 | 3.35 | −1.72 | −5.28 | −0.87 | 6.75 |
| H4 | 10.06 | −8.50 | 5.27 | 0.19 | −0.03 | 0.17 | 4.70 | H16 | 5.72 | −2.66 | 3.61 | −1.53 | −4.41 | −0.56 | 5.77 |
| H5 | 9.60 | −9.36 | 4.81 | 3.31 | −0.40 | 0.95 | 5.15 | H17 | 6.86 | −2.87 | 3.17 | −0.82 | −6.02 | −1.26 | 6.91 |
| H6 | 8.70 | −8.01 | 5.12 | 2.45 | 0.65 | 0.3 | 3.84 | H18 | 9.11 | −3.61 | 3.09 | −2.23 | −6.92 | −0.58 | 8.55 |
| H7 | 14.73 | −7.58 | 5.27 | 0.34 | 2.45 | −0.86 | 5.19 | H19 | 10.91 | −4.63 | 4.37 | −2.61 | −3.76 | −0.06 | 6.74 |
| H8 | 15.70 | −15.77 | 9.09 | −0.56 | −2.23 | 3.74 | 9.27 | H20 | 9.51 | −4.59 | 5.90 | −2.81 | −3.04 | 0.40 | 5.86 |
| H9 | 12.15 | −17.11 | 9.56 | 0.59 | −3.58 | 5.12 | 9.85 | H21 | 10.07 | −5.07 | 4.99 | −3.10 | −1.95 | 0.16 | 6.02 |
| H10 | 12.12 | −13.90 | 7.43 | 0.03 | −4.47 | 1.67 | 11.85 | H22 | 10.26 | −4.39 | 5.82 | −2.87 | −0.76 | −1.06 | 4.30 |
| H11 | 8.84 | −9.03 | 5.49 | −1.72 | −4.51 | 0.79 | 10.18 | H23 | 10.68 | −4.83 | 5.35 | −1.40 | −1.64 | −0.43 | 4.42 |
| Model | Year | Spring | Summer | Fall | Winter |
|---|---|---|---|---|---|
| H0 | 4.41158 | 12.34248 | 6.96156 | 6.56937 | 15.74986 |
| H1 | 4.57719 | 11.13504 | 7.01424 | 6.83583 | 15.80936 |
| H2 | 4.49406 | 8.10813 | 8.29448 | 7.56207 | 13.25280 |
| H3 | 4.65165 | 11.32884 | 10.50381 | 6.68133 | 11.75929 |
| H4 | 4.75141 | 9.55735 | 13.42097 | 7.39000 | 9.87304 |
| H5 | 4.61411 | 9.58722 | 14.30802 | 6.70083 | 9.71402 |
| H6 | 4.80890 | 14.22191 | 13.67163 | 9.14738 | 12.81491 |
| H7 | 6.50780 | 14.79353 | 18.09313 | 11.90778 | 17.34678 |
| H8 | 7.17099 | 17.38503 | 13.09771 | 8.77013 | 20.58378 |
| H9 | 6.87636 | 18.37358 | 15.05030 | 12.30992 | 21.72775 |
| H10 | 6.57170 | 13.15244 | 13.09226 | 8.31716 | 19.67714 |
| H11 | 5.64699 | 11.99965 | 11.74966 | 7.32458 | 17.13957 |
| H12 | 5.12931 | 12.72795 | 12.71104 | 6.55808 | 15.19633 |
| H13 | 5.16333 | 12.26430 | 14.66854 | 8.40014 | 13.69871 |
| H14 | 4.23131 | 9.99186 | 13.51807 | 8.57123 | 12.54090 |
| H15 | 3.34157 | 14.57501 | 15.19851 | 6.61890 | 16.26682 |
| H16 | 3.94571 | 14.08520 | 14.94630 | 5.25771 | 13.67740 |
| H17 | 4.39213 | 10.96050 | 13.81440 | 20.00288 | 12.47072 |
| H18 | 4.70427 | 11.03774 | 12.46243 | 11.41809 | 14.39600 |
| H19 | 5.65613 | 9.94045 | 8.85166 | 17.84064 | 15.55853 |
| H20 | 5.59225 | 14.90723 | 11.33855 | 13.60358 | 21.36625 |
| H21 | 5.10041 | 11.61009 | 8.888941 | 7.98565 | 16.00126 |
| H22 | 4.89382 | 13.85268 | 9.27154 | 7.68929 | 17.13908 |
| H23 | 4.54320 | 13.696636 | 9.81764 | 7.23575 | 16.53751 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-Y.; Yoon, D.-K.; Park, S.-H.; Jeon, J.-I.; Lee, J.-M.; Yang, W.-H.; Cho, Y.-S.; Kwon, J.; Lee, C.-M. Proposal of a Methodology for Prediction of Indoor PM2.5 Concentration Using Sensor-Based Residential Environments Monitoring Data and Time-Divided Multiple Linear Regression Model. Toxics 2023, 11, 526. https://doi.org/10.3390/toxics11060526
Park S-Y, Yoon D-K, Park S-H, Jeon J-I, Lee J-M, Yang W-H, Cho Y-S, Kwon J, Lee C-M. Proposal of a Methodology for Prediction of Indoor PM2.5 Concentration Using Sensor-Based Residential Environments Monitoring Data and Time-Divided Multiple Linear Regression Model. Toxics. 2023; 11(6):526. https://doi.org/10.3390/toxics11060526
Chicago/Turabian StylePark, Shin-Young, Dan-Ki Yoon, Si-Hyun Park, Jung-In Jeon, Jung-Mi Lee, Won-Ho Yang, Yong-Sung Cho, Jaymin Kwon, and Cheol-Min Lee. 2023. "Proposal of a Methodology for Prediction of Indoor PM2.5 Concentration Using Sensor-Based Residential Environments Monitoring Data and Time-Divided Multiple Linear Regression Model" Toxics 11, no. 6: 526. https://doi.org/10.3390/toxics11060526
APA StylePark, S.-Y., Yoon, D.-K., Park, S.-H., Jeon, J.-I., Lee, J.-M., Yang, W.-H., Cho, Y.-S., Kwon, J., & Lee, C.-M. (2023). Proposal of a Methodology for Prediction of Indoor PM2.5 Concentration Using Sensor-Based Residential Environments Monitoring Data and Time-Divided Multiple Linear Regression Model. Toxics, 11(6), 526. https://doi.org/10.3390/toxics11060526









