Optimization of Engineering Vehicle Scheduling in Shipbuilding and Repair Yards Based on the Dual-Cycle Strategy

Abstract

Background: As a labor-, capital-, and technology-intensive sector, shipbuilding supports water transportation, international trade, and marine development, driving economic growth and employment. Yet rising raw material/labor costs now bottleneck enterprise performance, making cost reduction and efficiency improvement urgent for shipbuilding and repair firms. It is an effective way to improve logistics transportation efficiency for reducing the cost of shipbuilding and repair firms. However, there are still few methods specifically designed for logistics transportation scheduling in shipbuilding and repair firms. Methods: In this paper, a “dual-cycle” strategy is proposed to optimize material transportation and cut logistics vehicles’ empty-load rate in the shipbuilding and repair process. A mixed-integer programming model is built to minimize total empty travel time, considering task priorities and time windows. A genetic algorithm-based scheduling method is proposed to solve this complex scheduling model. Results: Simulation with real shipyard logistics data shows the proposed model and algorithm can effectively address the shipbuilding logistics vehicle scheduling problem. In addition, the proposed algorithm performs better than two other compared algorithms in handling the studied problem. Conclusions: This study aids shipbuilding and repair logistics managers in making scheduling plans and determining optimal vehicle numbers, supporting cost-efficiency improvement.

1. Introduction

During ship repair and construction, material transportation is a critical link that guarantees the smooth execution of production plans [1]. Thus, developing an efficient vehicle scheduling plan remains a critical research issue. Extensive studies have been devoted to logistics scheduling problems in shipyards.

Jiang et al. [2] investigated a shipyard vehicle scheduling problem under the “multiple trucks to one cargo” mode and established a synchronization-constrained optimization model that minimizes non-value-added travel time and CO₂ emissions. Guo et al. [3] took into account time windows and payload limitations during the transportation of ship components and proposed a model that minimizes empty travel time and energy consumption. In addition to transportation efficiency, on-time delivery is another major concern. Tao et al. [4] incorporated task-priority relations and hard time windows into the component transportation problem.

From the above investigations, the shipyard logistics vehicle scheduling problem can be regarded as an extension of the vehicle routing problem (VRP) [5].

For the classical VRP, Sang et al. [6] developed a shop-floor scheduling model for automated guided vehicles (AGV) that simultaneously considers total travel distance, total tardiness, and machine depreciation cost. Lee et al. [7] addressed a cold-chain routing problem for refrigerated trucks by introducing time windows that respect product storage requirements and shelf lives, and formulated a mixed-integer linear programming (MILP) model to maximize profit. Amir et al. [8] studied a single-depot electric-vehicle scheduling problem in which battery charging and multi-day consecutive operations were explicitly modeled.

The aforementioned studies all address a single-depot scheduling scenario, namely, vehicles depart from and finally return to the same parking location. This restriction inevitably reduces operational flexibility, motivating researchers to investigate the multi-depot VRP (MDVRP). Xiao et al. [9] proposed a semi-open multi-depot model that minimizes total travel distance. Azuero et al. [10] minimized the number of allocated vehicles as well as emission cost under multi-depot and multi-product settings. Arias et al. [11] optimized both total distance and the standard deviation of route lengths in a multi-depot scenario. Lopes et al. [12] integrated the MDVRP with crew scheduling in a unified model.

The VRP family is NP-hard [13]; consequently, a variety of solution approaches have been developed. Ananda et al. [14] hybridized the whale optimization algorithm with a variable neighborhood search (VNS) for tourist trip design. Jiang et al. [15] combined simulated annealing and VNS to solve a drone routing problem. Fan et al. [16] embedded a neural network into a heuristic framework and reported superior performance compared with either pure neural or pure heuristic methods. Maichel et al. [17] developed a multi-start local-search heuristic for the split-delivery VRP. In summary, meta-heuristics are the most common solution paradigm for VRP and its variants.

Although the aforementioned studies provide valuable insights, none of the existing models can be directly adapted to the operating mode of shipyard transportation vehicles. Therefore, this paper introduces a “dual-cycle” transportation strategy [18] into the shipyard vehicle scheduling context and proposes a multi-vehicle, multi-depot MILP model that simultaneously considers task priorities, hard time windows, and inter-vehicle synchronization requirements. A bi-level genetic algorithm (GA) is designed to solve the model. Compared with the traditional single-cycle mode, the proposed strategy significantly reduces the empty-load ratio and improves transport efficiency. Parameter sensitivity analysis is conducted to determine the optimal fleet size under a given task volume.

The rest of the paper is structured as follows: Section 2 presents the vehicle scheduling problem in shipyard outdoor logistics under the dual-cycle mode. Section 3 presents the logistics vehicle scheduling model. Section 4 introduces the scheduling optimization method based on the genetic algorithm. Section 5 validates the method through experimental tests. Section 6 concludes the study.

2. Vehicle Scheduling Problem in Shipyard Outdoor Logistics Under the Dual-Cycle Mode

2.1. Characteristics of Outdoor Logistics Scheduling

Based on the shipyard layout and its production operations, the scheduling of engineering vehicles exhibits the following characteristics:

(1) Multiple parking depots: Several parking depots with varying capacities are distributed within the yard.

(2) Fixed routes: The roadway network is simple, limiting vehicles to a fixed set of paths.

(3) Task priorities: Different transportation tasks have varying impacts on the overall project schedule, necessitating a priority hierarchy.

(4) Time windows: Designated personnel are required for loading/unloading, mandating that vehicles arrive within stipulated time intervals.

(5) Multi-vehicle cooperation: A single task may require coordinated execution by multiple vehicles.

2.2. Task-Point Construction and the Dual-Cycle Strategy

Based on the above characteristics of outdoor logistics scheduling in ship repair and construction, each transport task is abstracted as a loaded node to simplify modeling. The construction of a loaded node is as follows:

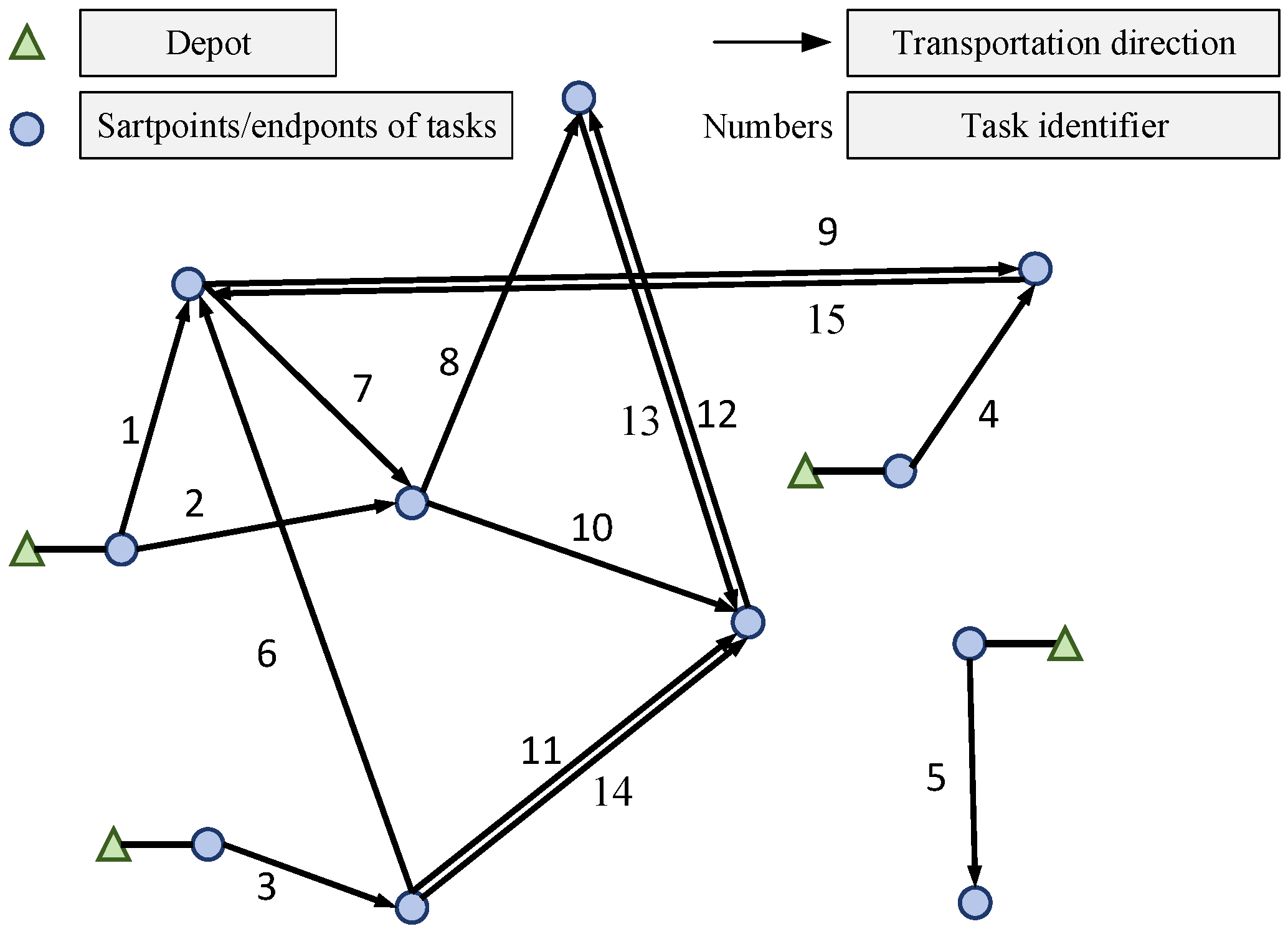
As illustrated in Figure 1, every directed line segment represents a specific transportation task, where the endpoints correspond to the pickup and delivery locations, and the associated number indicates the task identifier. During model formulation, each segment is treated as a loaded node. Only the origin and destination of each node are considered functionally relevant, while the actual transit path is disregarded. Additionally, a virtual task point is introduced adjacent to each depot to facilitate decoupling between depot and task node within the model, under the assumption that the physical distance between them is negligible.

Certain node pairs are interconnected by two distinct directed segments: segments oriented in the same direction denote tasks occurring at different times but sharing the same origin and destination, whereas segments with opposing directions represent tasks with reversed origin–destination pairs.

The dual-cycle strategy dictates that a vehicle can be assigned a new task immediately upon completion of the current one, thereby establishing a continuous back-and-forth operational pattern. In contrast to the single-cycle approach, which requires a vehicle to return to its original depot after each task, the dual-cycle strategy permits a vehicle that has departed from any depot and serviced a loaded node to proceed directly to another loaded node or return to any depot of choice.

3. Logistics Vehicle Scheduling Model in Shipyard

Based on the above operational process description, a model is constructed for in-plant logistics vehicle scheduling. Prior to modeling, the following assumptions are made for the problem:

(1) The locations of all vehicle depots, pickup points, and delivery points are known.

(2) Information regarding all transportation tasks within a certain time period (e.g., one day) is known, including cargo volume, time windows, etc.

(3) All available delivery vehicles in the plant area are of the same model, and their maximum loading capacity is known.

(4) Tasks are considered divisible, meaning multiple vehicles can be assigned to collaboratively complete tasks whose cargo volume exceeds the maximum loading capacity of a single vehicle.

(5) Vehicle failures and traffic congestion are not considered, and vehicles travel at constant speed.

Before modeling, relevant variables and parameters are first defined as shown in

Table 1. Definitions of parameters and variables.

Symbol	Description
Sets
M	Task set, where N1 represents the total number of tasks within a certain time period, M = {1, …, N1}
N	Vehicle depot set, where N2 represents the total number of vehicle depots, N = {N1 + 1, …, N1 + N2}
K	Delivery vehicle set, K = {1, …, Nk}
Parameters
${\mathrm{G}}_i$	Cargo volume of the ith task
$K_m$	Minimum number of vehicles required to complete all tasks
$q_i$	Number of vehicles required to complete task i
Q	Loading capacity of delivery vehicles
$a_{M+i}$	Number of empty vehicles available at depot i, i = 1, 2, 3, …, N2
$C_{ij}$	Empty travel time from point i to point j (i, j are depots or loaded points), i, j = 1, 2, 3, …, N1 + N2
$S{T}_{ikj}$	Departure time of vehicle k from i to j
$A{T}_{ikj}$	Arrival time of vehicle k from i to j
$\left[E{T}_i,L{T}_i\right]$	Earliest and latest start time constraints for task i, respectively
$W{T}_m$	Total time to complete task m
$T_i$	Maximum dwell time of vehicles after completing task i
V	Average vehicle speed
$d_{ij}$	Distance from loaded point i to j
H	A sufficiently large positive number
Decision Variables
$x_{ij}$	Number of empty vehicles dispatched from point i to point j (i, j are depots or loaded points)
$x_{ikj}$	Binary variable: 1 if vehicle k travels from i to j, 0 otherwise

.

The optimization objective of the plant vehicle scheduling is to minimize the total empty travel time of vehicles required to complete all tasks, as shown in Equation (1).

$$\min Z={\displaystyle \sum _{i=1}^{N_1}{\displaystyle \sum _{j=1}^{N_1+N_2}{x}_{ij}{C}_{ij}}}$$

(1)

The constraints are as follows:

$${\displaystyle \sum _{j=1}^{N_1+N_2}{x}_{ij}=q_i},\forall i\in M$$

(2)

$${\displaystyle \sum _{i=1}^{N_1+N_2}{x}_{ij}=q_i},\forall j\in M$$

(3)

$${\displaystyle \sum _{i=1}^{N_1+N_2}{\displaystyle \sum _{j=1}^{N_1}{x}_{ikj}=1,\forall k\in K}}$$

(4)

$${\displaystyle \sum _{i=N_1+1}^{N_1+N_2}{\displaystyle \sum _{j=N_1+1}^{N_1+N_2}{x}_{ikj}=0,\forall k\in K}}$$

(5)

$${\displaystyle \sum _{i=1}^{N_1}{\displaystyle \sum _{j=N_1+1}^{N_1+N_2}{x}_{ikj}=1,\forall k\in K}}$$

(6)

$${\displaystyle \sum _{j=1}^{N_1+N_2}{x}_{ij}\le a_i},\forall i\in N$$

(7)

$${\displaystyle \sum _{i=1}^{N_1+N_2}{x}_{ij}\le a_i},\forall j\in N$$

(8)

$$x_{ij}={\displaystyle \sum _{k=1}^{N_k}{x}_{ikj}},\forall k\in K$$

(9)

$$S{T}_{ikj}+C_{ij}=A{T}_{ikj}$$

(10)

$$\begin{array}{c}S{T}_{jkp}-(A{T}_{ikj}+W{T}_j+T_j)+H(1-x_{jkp})\le 0\\ \forall j,p\in M\end{array}$$

(11)

$${\displaystyle \sum _{i=N_1+1}^{N_1+N_2}{\displaystyle \sum _{j=1}^{N_1+N_2}{x}_{ij}}}={\displaystyle \sum _{j=N_1+1}^{N_1+N_2}{\displaystyle \sum _{i=1}^{N_1+N_2}{x}_{ij}}}=K_m$$

(12)

$$x_{ij}\ge 0,x_{ikj}\in \{0,1\}$$

(13)

Among these, Equations (2) and (3) ensure that tasks can be completed and that the number of vehicles arriving at a task point equals the number of vehicles departing from that point, i.e., task points can only serve as temporary parking locations. Equations (4)–(6) ensure that each vehicle can only depart from one depot and return to one depot, and cannot depart from a depot and return directly to the same depot. Equations (7) and (8) represent the depot capacity constraints. Equation (9) describes the relationship between the two variables x_ikj and x_ij. Equation (10) ensures the continuity of vehicle operation time. Equation (11) specifies that the temporary parking time at loaded points cannot exceed the given time limit. Equation (12) calculates the total number of vehicles used. Equation (13) represents the constraints on decision variables.

4. Scheduling Optimization Method Based on Genetic Algorithm

It is evident from the model that this vehicle scheduling problem constitutes a nonlinear mixed-integer programming problem. Such problems have been demonstrated to be NP-hard, and as the problem size increases, NP-hard problems become computationally intractable for verifying solution correctness within polynomial time. Genetic algorithm, being a well-established intelligent optimization technique, has found extensive application in solving problems of this nature. Consequently, this study employs the genetic algorithm for model optimization and solution.

4.1. Encoding and Decoding

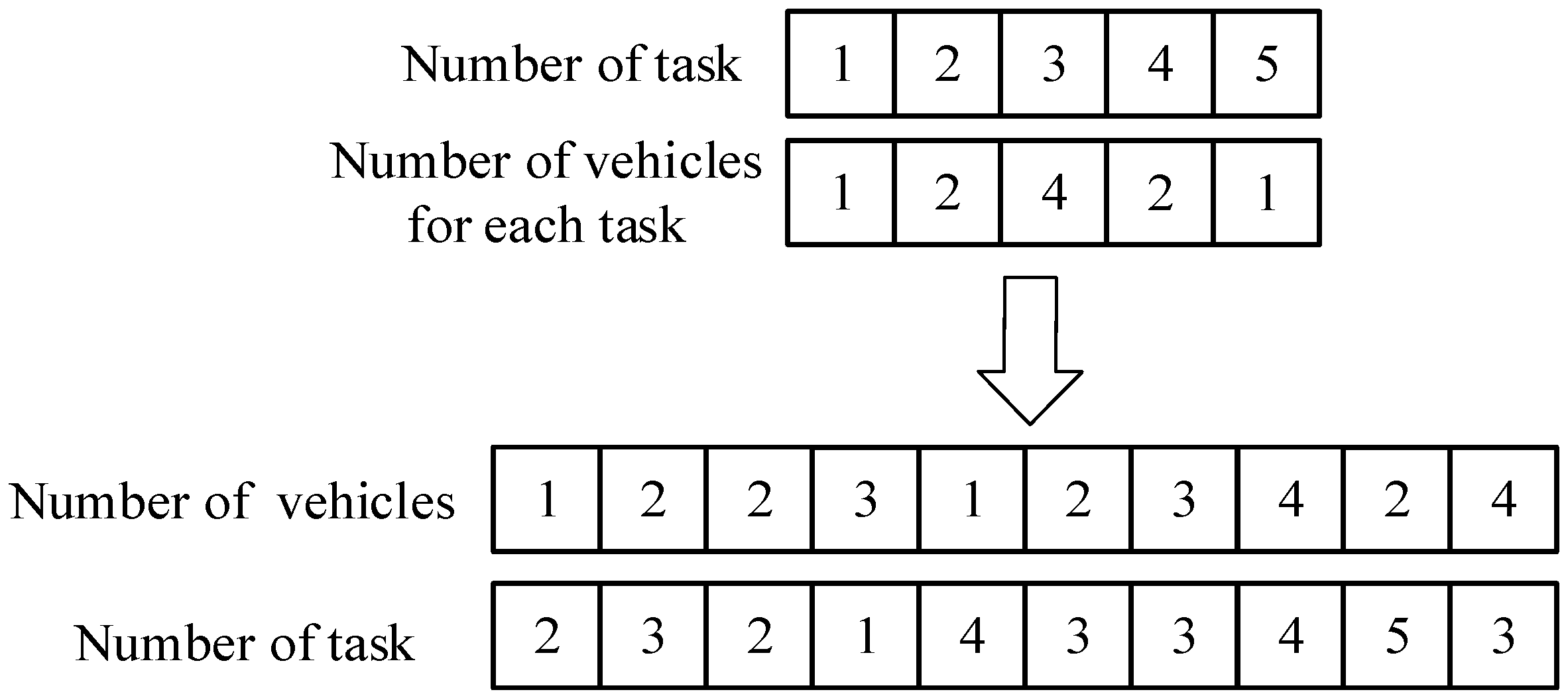
The scheduling solution in this paper represents an individual chromosome in the genetic algorithm, employing a two-layer integer encoding scheme. The first layer represents vehicle numbers, while the second layer represents task numbers. If a task requires multiple vehicles for completion, the task number appears multiple times according to the number of vehicles required for that task. The sum of occurrences of all task numbers equals the chromosome length.

The upper part of Figure 2 shows the number of vehicles required for each of the 5 tasks. In the example shown in the lower part, it can be observed from the first layer encoding that there are four vehicles in total. The entire chromosome encoding indicates that the transportation route for vehicle 1 is: 2→4; the transportation route for vehicle 2 is: 3→2→3→5; the transportation route for vehicle 3 is: 1→3; and the transportation route for vehicle 4 is: 4→3.

4.2. Population Initialization

First, the chromosome length is determined. Given that the total number of tasks within a certain time period is M, the sum of vehicles required for each task is M’, and the number of depots is N, the chromosome length is M’ + N. Both the vehicle numbers in the first layer and the task numbers in the second layer are randomly generated. Subsequently, decoding is performed to obtain the transportation route for each vehicle, and depot numbers are added at the beginning and end of the task sequence in the transportation route. The depot numbers are random integers within the range [M, M + N]. The above operations are repeated to generate all individuals.

4.3. Fitness Calculation and Selection Strategy

The objective function of the plant vehicle scheduling optimization model based on the “dual-cycle” approach is to minimize the total empty travel time of vehicles required to complete all tasks. This objective function value can intuitively reflect the quality of chromosomes, where smaller objective function values indicate better chromosome quality. Therefore, for solving this scheduling problem, the reciprocal of the objective function value is used as the individual fitness value, as shown in Equation (14), where z(i) represents the objective function value of individual i. Meanwhile, the roulette wheel selection strategy is adopted, which determines the probability of being selected for the offspring population based on individual fitness values. The selection probability p(i) for individual i is shown in Equation (15), where N represents the total number of individuals.

$$f(i)={\displaystyle \frac{1}{z(i)}}$$

(14)

$$p(i)={\displaystyle \frac{f(i)}{{\displaystyle \sum _{i=1}^{N}f(i)}}}$$

(15)

4.4. Crossover

This paper adopts a position-based mapping crossover method. Using the chromosome encoding example from Figure 2, the specific operations are as follows:

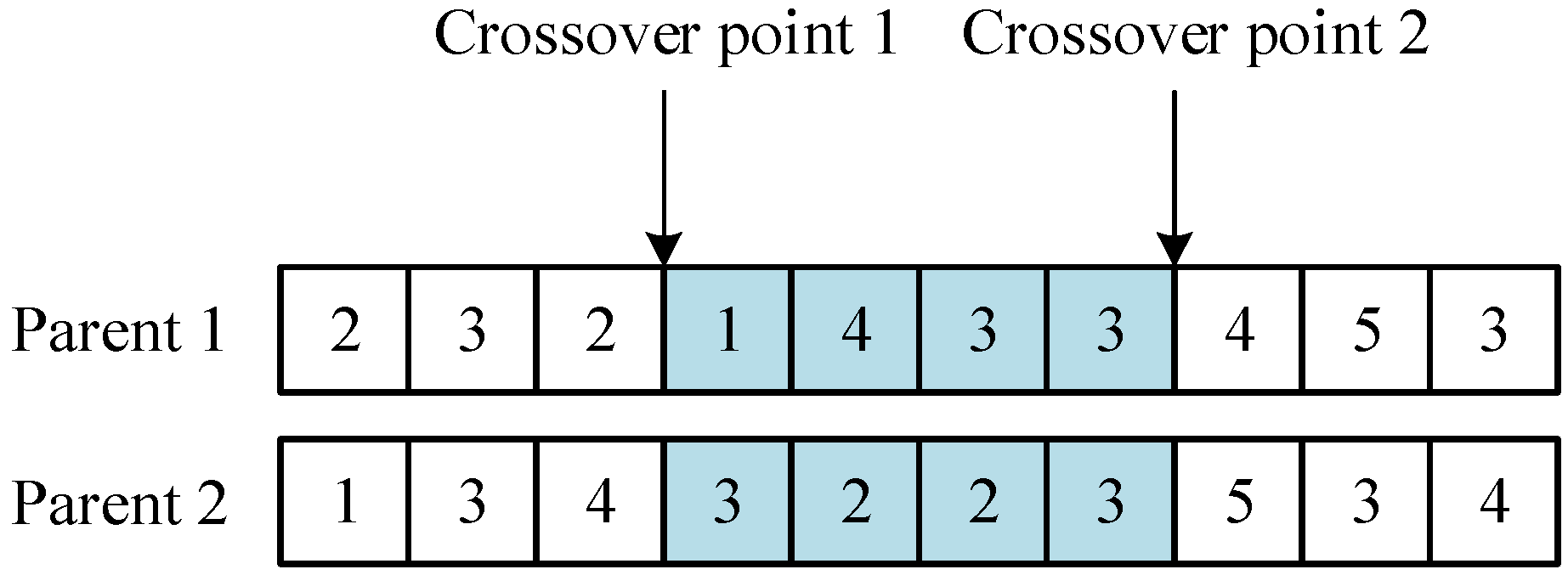
(1) Two chromosomes are selected from the population as parent 1 and parent 2 for crossover operation. Based on the chromosome string length, two unequal crossover points are randomly generated on each chromosome, dividing the two parent chromosomes into three parts. The specific operation is shown in Figure 3, where the arrows are the positions of two crossover points and the blue part is the gene segment between the two crossover points.

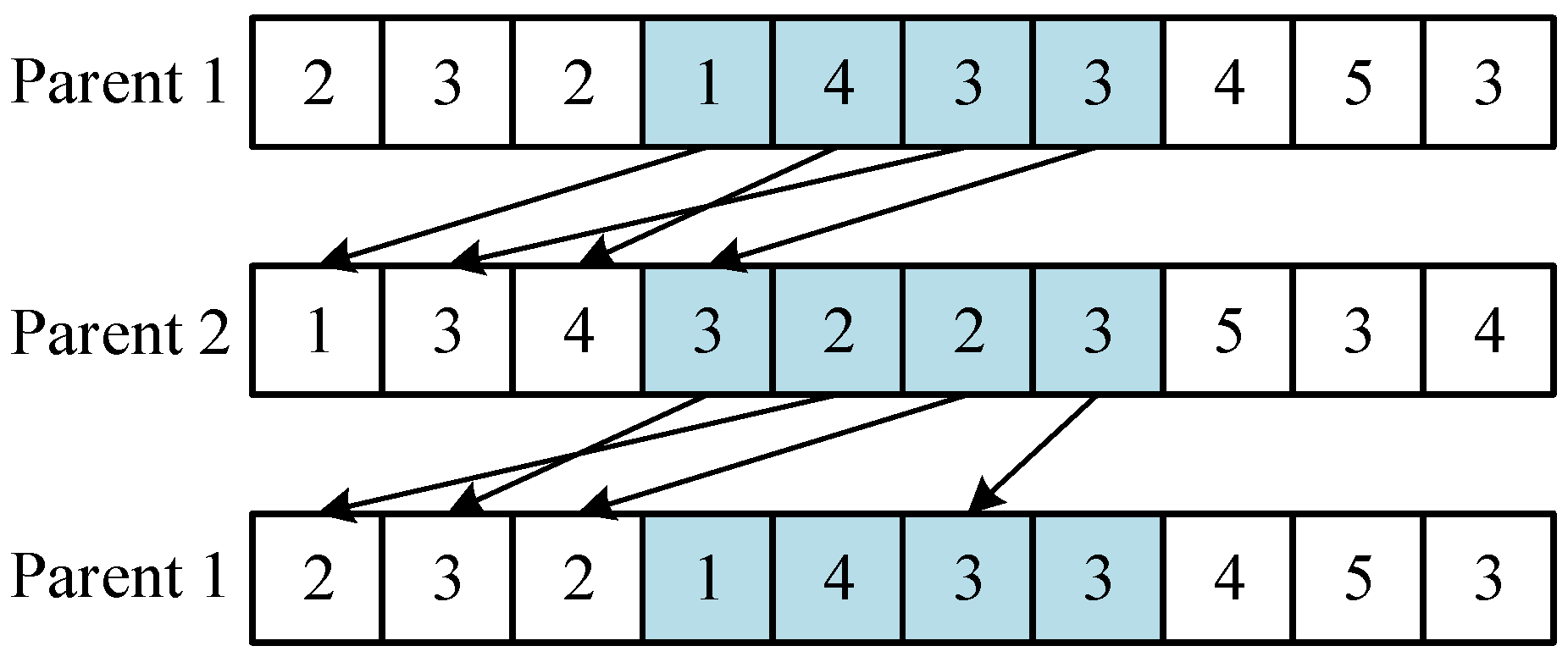
(2) Find the sequential order of genes in the crossover segment of parent 1 that are mapped onto parent 2, then rearrange the genes according to the order of these genes in parent 2 to obtain the new gene segment of parent 1. If there are identical genes, the first occurrence of the gene is selected as the mapped gene when searching from front to back. Similarly, the crossover segment of parent 2 can also obtain a new gene segment through mapping with parent 1. The specific operation is shown in Figure 4, where the arrows indicate the locations of gene mapping and the blue part is also the gene segment between the two crossover points.

(3) Replace the original crossover segments with the new gene segments to obtain the offspring chromosomes, as shown in Figure 5, where the blue part is the genes obtained after performing the crossover operation.

4.5. Mutation

To ensure that the mutated chromosome still represents a feasible scheduling solution, this paper employs a swap mutation operator. For each chromosome in the population, a random number in the range [0,1] is first generated. When the random number is less than the mutation probability, the mutation operation is performed; otherwise, no mutation operation is conducted. After determining that a mutation operation is needed, two different genes are randomly selected on the chromosome, and their positions are swapped to generate a new chromosome. The operation is shown in Figure 6, where the arrows are the positions of swap mutation points and the blue part is the genes that performs swap mutation.

5. Experimental Analysis and Discussion

In order to verify the effectiveness and feasibility of the vehicle scheduling model and proposed algorithm based on a “dual-cycle” strategy, an example is designed based on the actual survey data, and then the effectiveness of the proposed model and algorithm is verified. Finally, the sensitivity analysis of the model is conducted. All codes were solved based on MATLAB 2022a.

5.1. Experimental Parameter Setting

In this paper, the model is verified and solved based on the actual data of a shipyard in Zhoushan, and the specific data are as follows:

(1) There is one parking lot for workshop 1, dock 2, dock 3, and berth, and the total number of vehicles available for use is ten.

(2) The maximum number of parking lots in workshop 1 is five, and the maximum number of parking lots in other parking lots is four.

(3) The driving speed of vehicles in the factory is 0–60 m/min, and the average driving speed of vehicles can be considered to be 30 m/min.

(4)

Table 2. Node name and number.

Node Name	Node Number
Dock 1	1
Dock 2	2
Dock 3	3
Workshop 1	4
Workshop 2	5
Assembly and distribution center	6
Slipway	7
Set up storage and preassembly space	8
Section drying space	9
Painting shop	10

shows the number of important nodes in the factory.

(5) The distance of each node in the ship repair plant is shown in

Table 3. Node distance table (m).

Number	1	2	3	4	5	6	7	8	9	10
1	0	30	160	300	800	810	1100	580	630	670
2	30	0	130	270	770	780	1070	550	600	640
3	160	130	0	140	640	650	940	420	470	510
4	300	270	140	0	500	510	800	280	330	370
5	800	770	640	500	0	20	300	220	170	230
6	810	780	650	510	20	0	290	230	180	140
7	1100	1070	940	800	300	290	0	520	470	430
8	580	550	420	280	220	230	520	0	50	90
9	630	600	470	330	170	180	470	50	0	40
10	670	640	510	370	230	140	430	90	40	0

. For the node with parking lot, the default distance from the parking lot to the corresponding node is 5 m.

(6) The task information in a certain period of time is shown in

Table 4. Task information.

Task Route	Time Window/min	Number of Vehicles Required	Number of Tasks	Task Number
4/5→6	[0,56]/[50,85]/[166,200]/[180,220]/[240,300]	1	15	1~15
6→4/5	[30,100]/[15,65]/[0,30]/[0,40]/[20,80]/[10,55]	1	15	16~30
4/5→8	[14,56]/[9,30]/[0,14]/[0,19]/[11,40]/[6,25]	1/2	10	31~40
8→10	[20,46]/[60,95]/[185,210]	1/2	4	41~44
10→9	[14,56]/[50,85]/[175,200]/[180,220]	1/2	6	45~50
9→1/2/3	[20,252]/[33,188]/[0,102]/[0,90]/[38,170]	1/2/3	15	51~65
9→7	[14,56]/[50,85]/[175,200]/[180,220]	1/2/3	5	66~70
6→1/2/3	[0,56]/[50,85]/[166,200]/[180,220]/[240,300]	1/2	15	71~85
6→7	[15,60]/[50,85]/[175,200]/[189,240]	1/2	5	86~90
6→8	[14,56]/[50,85]/[175,200]/[180,220]/[230,280]	1/2	10	91~100

, where the time window is the approximate time window, and the specific time window of each task follows the normal distribution with the approximate time window given as the mean and five as the standard deviation.

Algorithm parameter settings: The parameters in the genetic algorithm are designed as follows: population size NIND = 100; the maximum number of iterations G_max = 500; crossover probability Pc = 0.9; and mutation probability Pm = 0.1.

5.2. Comparison with Other Methods

To validate the effectiveness of our proposed scheduling optimization method based on GA, we compare it with the particle swarm optimization (PSO) [19] and whale optimization algorithm with variable neighborhood search strategy (WOA-VNS) [14]. We run the experiment instance 20 times, and achieve the mean results.

Table 5. Comparison of total cost and average no-load rate reduction.

Algorithms	Total Cost/min	Average Reduction in No-Load Rate
GA	6850.5	82.2222%
PSO	7722.4	70.5050%
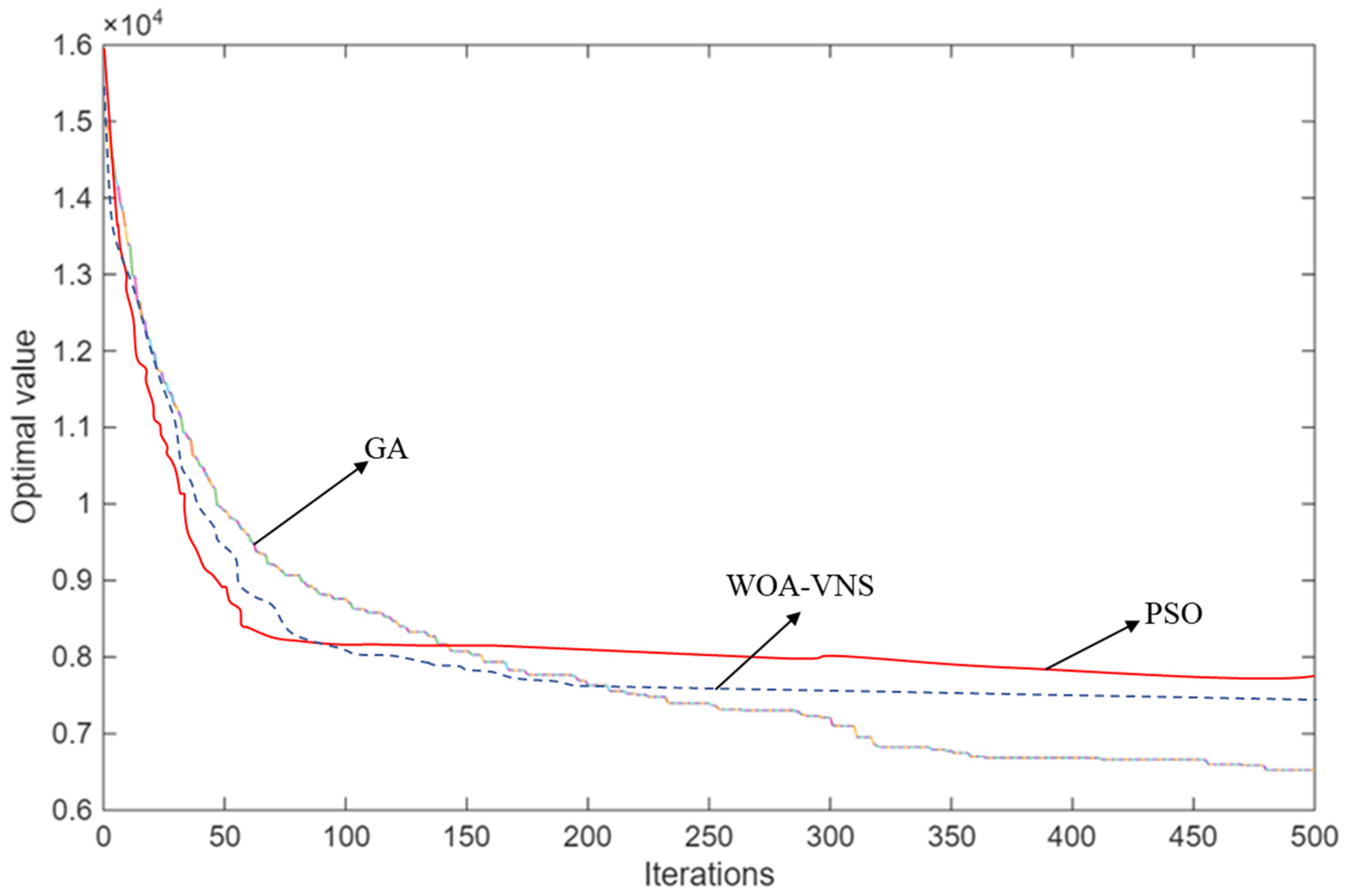
WOA-VNS	7546.3	75.4235%

presents the total cost and average reduction in no-load rate of the three methods, where the best result is marked in bold. We find that our proposed scheduling optimization method based on GA obtains the better result than the PSO and WOA-VNS in terms of the total cost (i.e., total empty travel time) and average reduction in no-load rate. This implies the superiority of the proposed algorithm in solving the studied problem.

Figure 7 shows the curve changes in the optimal value of the objective function of the three scheduling algorithms. It can be seen from the figure that the curve of our proposed algorithm changed smoothly and maintained a better evolution trend. At the end of the evolution process, our proposed algorithm converges to the smallest objective function value.

5.3. Effect of Dual-Cycle Strategy

To validate the effectiveness of the dual-cycle strategy, we obtain the specific scheduling schemes with the dual-cycle strategy. We set the total number of vehicles as 10. In this case, the algorithm gives four different scheduling schemes according to the number of vehicles used, as shown in

Table 6. Scheduling scheme 1.

Number of Vehicles Used: 7, Total Cost: 7071.3 min, Average Reduction in No-Load Rate: 81.8456%
Route of vehicle 1	102→74→38→94→80→80→103→17→65→25→24→16→50→99→79→28→38→31→78→40→92→13→27→51→26→71→ 89→34→51→4→90→102, Reduction in no-load rate: 90.625%
Route of vehicle 2	101→42→101→42→32→103→63→104→19→4→103→89→31→40→22→59→48→73→23→1→30→9→36→77→101, Reduction in no-load rate: 76%
Route of vehicle 3	104→67→57→104→35→86→14→25→65→79→4→2→47→66→82→84→100→11→59→33→103, Reduction in no-load rate: 85.7143%
Route of vehicle 4	102→61→101→31→94→81→102→97→46→101→39→48→16→45→97→85→44→77→48→49→22→60→15→83→102, Reduction in no-load rate: 80%
Route of vehicle 5	103→5→30→83→41→84→74→17→8→26→76→45→69→93→102, Reduction in no-load rate: 86.6667%
Route of vehicle 6	104→86→103→87→102→18→102→20→23→68→33→26→58→10→89→104→52→74→91→54→29→37→102, Reduction in no-load rate: 73.913%
Route of vehicle 7	104→67→55→95→104→62→21→72→21→72→21→72→12→37→53→44→101, Reduction in no-load rate: 80%

,

Table 7. Scheduling scheme 2.

Number of Vehicles Used: 8, Total Cost: 6831.7 min, Average Reduction in No-Load Rate: 82.4254%
Route of vehicle 1	103→74→96→59→26→77→103→59→4→12→51→45→74→103→5→8→102→60→103→102→97→72→89→26→47→72→ 25→31→86→102, Reduction in no-load rate: 77.4194%
Route of vehicle 2	104→24→101→41→57→8→19→40→35→93→90→57→4→97→48→79→20→42→11→73→15→102, Reduction in no-load rate: 86.3636%
Route of vehicle 3	103→98→101→33→20→104→55→82→38→77→62→88→23→4→42→49→22→34→66→10→103, Reduction in no-load rate: 80.9524%
Route of vehicle 4	102→67→54→87→51→23→3→83→48→99→50→100→89→54→104, Reduction in no-load rate: 86.6667%
Route of vehicle 5	101→75→65→25→33→31→16→61→84→91→85→58→21→75→38→6→76→103, Reduction in no-load rate: 88.8889%
Route of vehicle 6	104→37→78→45→94→14→89→2→80→30→93→30→47→29→9→17→103, Reduction in no-load rate: 88.2353%
Route of vehicle 7	104→86→104→32→103→71→44→13→56→59→81→103, Reduction in no-load rate: 66.6667%
Route of vehicle 8	103→5→43→40→53→101→31→77→17→27→95→23→21→79→84→52→39→10→101, Reduction in no-load rate: 84.2105%

,

Table 8. Scheduling scheme 3.

Number of Vehicles Used: 9, Total Cost: 6933.8 min, Average Reduction in No-Load Rate: 81.2455%
Route of vehicle 1	103→95→97→50→79→31→56→102, Reduction in no-load rate: 75%
Route of vehicle 2	102→92→19→60→104→30→40→4→47→4→103, Reduction in no-load rate: 72.7273%
Route of vehicle 3	104→42→44→28→102→72→61→57→40→103→94→66→49→48→91→54→70→104, Reduction in no-load rate: 77.7778%
Route of vehicle 4	104→30→95→44→29→101→67→11→58→26→45→5→59→69→38→100→93→31→75→81→103, Reduction in no-load rate: 85.7143%
Route of vehicle 5	104→67→8→33→103→65→97→93→63→16→27→74→86→6→89→102→101, Reduction in no-load rate: 76.4706%
Route of vehicle 6	103→42→10→65→25→38→102→48→73→99→64→83→15→23→80→59→26→1→48→20→23→17→104, Reduction in no-load rate: 86.9565%
Route of vehicle 7	104→20→74→77→36→62→33→94→3→84→52→39→22→12→51→4→85→92→40→104, Reduction in no-load rate: 90%
Route of vehicle 8	103→86→103→27→77→43→54→26→51→9→21→68→23→21→45→96→16→41→101, Reduction in no-load rate: 84.2105%
Route of vehicle 9	102→5→101→18→77→78→71→90→82→37→89→2→59→34→47→37→102, Reduction in no-load rate: 82.3529%

and

Table 9. Scheduling scheme 4.

Number of Vehicles Used: 10, Total Cost: 5894.9 min, Average Reduction in No-Load Rate: 79.4596%
Route of vehicle 1	102→94→24→101→83→99→26→26→103, Reduction in no-load rate: 66.6667%
Route of vehicle 2	104→7→93→44→102→80→52→34→36→104, Reduction in no-load rate: 70%
Route of vehicle 3	102→87→81→89→65→58→9→62→88→79→23→92→104, Reduction in no-load rate: 84.6154%
Route of vehicle 4	103→78→20→59→82→38→100→56→46→77→57→4→57→21→11→29→9→103, Reduction in no-load rate: 88.8889%
Route of vehicle 5	102→86→17→104→41→61→15→25→74→77→64→51→23→77→68→53→30→102, Reduction in no-load rate: 83.3333%
Route of vehicle 6	101→87→102→90→86→33→20→74→39→40→26→51→23→1→54→103, Reduction in no-load rate: 81.25%
Route of vehicle 7	101→76→103→63→33→38→38→104→79→95→37→89→2→97→102→45→71→101, Reduction in no-load rate: 72.2222%
Route of vehicle 8	103→95→8→74→40→66→84→84→89→75→16→5→14→30→104, Reduction in no-load rate: 86.6667%
Route of vehicle 9	104→42→40→27→10→101→55→93→31→12→69→4→45→85→104, Reduction in no-load rate: 80%
Route of vehicle 10	104→65→102→37→37→65→25→70→102→4→35→83→48→50→59→48→47→47→91→21→98→102, Reduction in no-load rate: 80.9524%

. As for Table 6, Table 7, Table 8 and Table 9, it should be noted that numbers less than 100 represent the number of transportation tasks, while numbers greater than 100 represent the number of nodes (as defined in Table 2) plus the total number of tasks.

The pairs of four schemes are shown in

Table 10. Comparison of four schemes.

Options	Number of Vehicles Used	Total Cost/min	Average Reduction in No-Load Rate
1	7	7071.3	81.8456%
2	8	6831.7	82.4254%
3	9	6933.8	81.2455%
4	10	5894.9	79.4596%

. The results show that after applying the “dual-cycle” strategy, the average reduction rate of the four schemes is about 80%, indicating that the strategy has a significant effect on reducing the vehicle empty rate.

As in Table 10, the average reduction rate of the four schemes is relatively close, and the total cost of the first three schemes is also relatively close, but the total cost of the fourth scheme is significantly reduced compared with the first three schemes. Therefore, the first scheme can be selected from the perspective of using the least number of vehicles. If the enterprise management decision-maker considers cost issues, the fourth scheme should be a preferable choice.

5.4. Effect of Task Priorities and Time Window

This section discusses the impact of task priorities and time window on scheduling performance. We make modifications to our proposed scheduling model (referred to as Model 1) in Section 3 and proposed two variant models. The first variant model (referred to as Model 2) is a model obtained based on Model 1, excluding the task priorities. The second variant model (referred to as Model 3) is the model obtained by removing the time window from Model 1. Each model is optimized by our proposed algorithm for 20 times. The mean optimal objective function values under different models are compared in

Table 11. Result comparison of three different models.

Model	Total Cost/min	Average Reduction in No-Load Rate
1	5950	80.0056%
2	6600	75.2345%
3	6238	78.5362%

. For Table 11, the total costs of Model 2 and Model 3 are both larger than that of Model 1, while the average reductions in no-load rate of Model 2 and Model 3 are both smaller than that of Model 1. This means that both task priorities and time window have an impact on scheduling performance. In particular, for the two influencing factors, the task priorities have a greater impact on scheduling performance.

5.5. Sensitivity Analysis

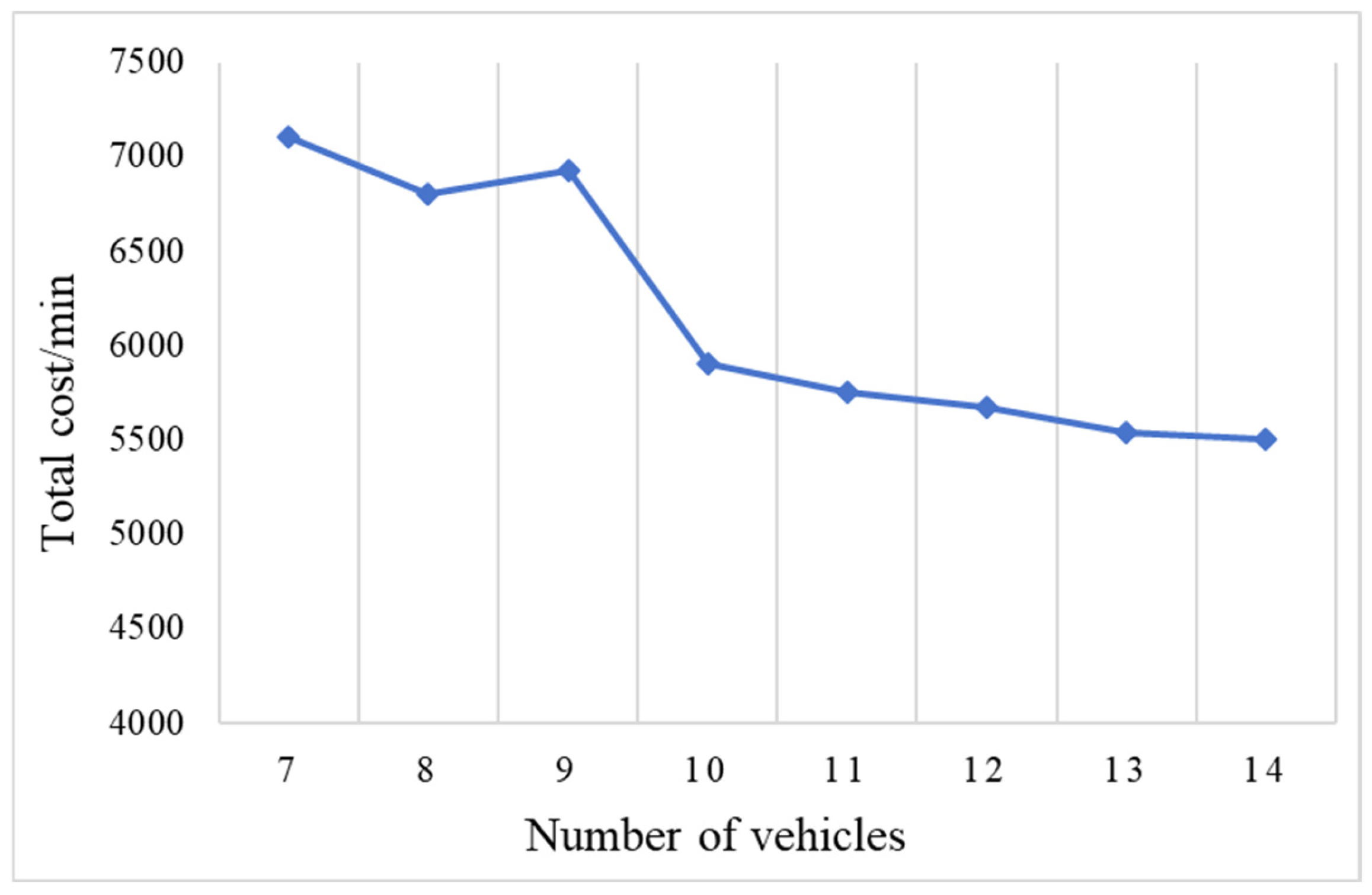
Based on the case in the previous section, when the number of available vehicles is increased from 10 to 15, the changes in the total cost and the average reduction ratio of empty vehicles are analyzed. Figure 8 shows the change in the total cost when the number of available vehicles is increased. Obviously, the total cost shows a decreasing trend with the increase in the number of vehicles used, and the total cost is significantly reduced when the number of vehicles is increased from 9 to 10. However, when the number of vehicles used exceeds 10, the total cost only decreases slightly. This indicates that the optimal number of vehicles used is 10 in the current actual task situation.

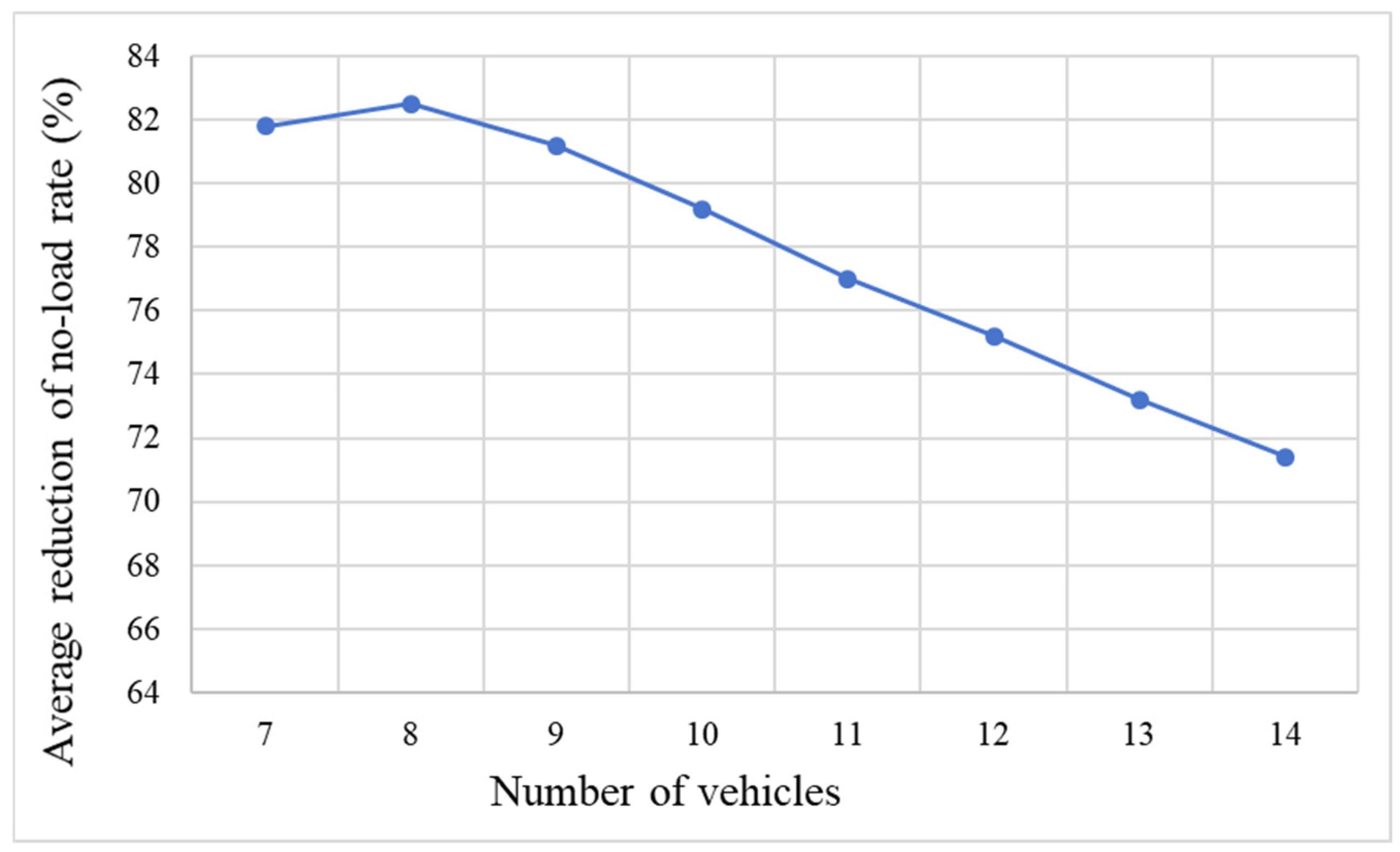
Figure 9 shows the change in the average reduction in no-load ratio for different numbers of vehicles used. As the number of vehicles used increases, the average reduction empty rate gradually decreases. This is because with the same number of tasks assigned to more vehicles, each vehicle completes fewer tasks individually and returns to the parking lot earlier, therefore the average reduction rate decreases.

6. Conclusions

This paper introduces the dual-cycle operation mode into the scheduling of logistics vehicles in the factory, and analyzes the significant effect of the “dual-cycle” scheduling strategy on reducing the vehicle empty rate and improving the transportation efficiency. By constraining the continuous variables of vehicles and factory tasks, the vehicle scheduling scheme is determined. Aiming to reduce the vehicle empty rate, a multi-depot vehicle scheduling model based on the concept of “dual-cycle” is established, and a vehicle scheduling method based on the genetic algorithm is designed to solve the model. It is proved that under the same resource allocation, the application of the “dual-cycle” strategy and the proposed algorithm can significantly reduce the vehicle no-load rate.