Fuzzy–Monte Carlo-Based Assessment for Enhanced Urban Transport Planning in Amman, Jordan

Abstract

Background: Cities worldwide face continuous challenges in sustainable development, particularly in transportation systems where decisions have long-lasting impacts on urban infrastructure and quality of life. The evaluation of sustainable transportation alternatives requires careful consideration of multiple indicators, making it a complex multi-criteria decision-making process. Existing multi-criteria decision-making (MCDM) frameworks often overlook the dual uncertainties introduced by both fuzzy expert judgments and probabilistic performance measures, hindering robust evaluation of transportation alternatives in developing countries. Methods: In response, this study introduces a novel hybrid methodology combining fuzzy set theory and Monte Carlo simulation to evaluate transportation alternatives through 14 comprehensive sustainability indicators. Addressing the critical need for sustainable public transportation assessment in rapidly urbanizing developing countries, where existing assessment frameworks frequently prove inadequate, we present a case study from Amman, Jordan. Results: The results reveal that a Bus Rapid Transit (BRT) system outperforms both conventional automobiles and small buses in 87.06% of simulation scenarios, underscoring its robust sustainability profile. The sensitivity analysis highlights that a BRT system is highly robust, with minimal sensitivity to changes in most criteria and strong responsiveness to critical factors such as land usage. Conclusions: This research provides decision-makers with a comprehensive, evidence-based tool for evaluating public transport investment under uncertainty. The methodology’s ability to account for multiple stakeholder perspectives while handling uncertainty makes it particularly valuable for urban planners and policymakers facing complex transportation infrastructure decisions in rapidly evolving urban environments.

1. Introduction

Cities are developing continuously due to rapid population growth, urbanization, expansion of human activities, and technological advancements [1]. The United Nations (UN) projects that over 6.4 billion people will reside in urban centers by 2050 [2], intensifying the need for the implementation of sustainable solutions to address urban challenges. The ability to effectively adopt sustainability will heavily depend on the ability of decision-makers and authorities to dedicate an effective long-term framework and embrace policies accompanied by appropriate measures that might increase sustainability inside cities, considering the complex interactions between society, decision-makers, technology, the environment, and economic aspects.

While the transport system provides adequate economic development for the citizens inside cities [3], there is increasing recognition and concern about its negative impacts on environmental and human well-being, such as greenhouse gas emissions, pollution, and noise, as highlighted by [4,5,6]. As these difficulties become increasingly pressing, there is an urgent need to reconsider urban mobility systems to limit their negative consequences. The severity of these impacts has intensified with urban growth, compelling decision-makers and governments to focus on implementing policies that can balance mobility needs with environmental preservation under the principles of sustainable development, with an overarching aim to balance the three main dimensions: environmental, social, and economic [7,8].

Public transportation plays an important role in advancing sustainable urban development, offering energy-efficient mobility alternatives that reduce dependence on private vehicles and decrease greenhouse gas emissions [9,10,11]. Its role is particularly significant in developing countries, where rapid urbanization and limited resources exacerbate energy and environmental challenges [12]. These countries face the dual challenge of meeting increasing mobility demand while responding to ecological problems and energy resource limitations. Therefore, in recent years, there has been a conscious push to build inclusive public transport infrastructure that is attractive and resource-efficient, while acknowledging that emerging transport modes are also reshaping mobility patterns [13].

The evaluation of sustainability in the public transportation system presents several challenges that current research has yet to fully address. The evaluation process involves various stakeholders with divergent perspectives and priorities, making consensus difficult to establish, as noted in [14]. Furthermore, accurately quantifying the relative importance of these indicators is compounded by profound uncertainty, especially when integrating qualitative expert judgments into a robust analytical framework [15,16]. While existing multi-criteria decision-making tools typically address either fuzziness in expert judgments or probabilistic risk, they rarely integrate both simultaneously to provide a truly comprehensive and uncertainty-aware assessment. This limitation is particularly critical in the rapidly evolving urban landscapes of developing countries. For instance, cities like Amman, Jordan, are experiencing an unprecedented urbanization rate. Jordan’s urbanization rate rose from 87.17% to 91.63% between 2011 and 2021 [17,18], intensifying sustainability concerns and introducing unique complexities in transport system functionality. Traditional evaluation frameworks often fall short in providing reliable decision support within such dynamic and data-challenged environments.

To overcome these challenges and address the need for robust decision support in contexts such as Amman, this study introduces a novel hybrid methodological framework for public transportation alternatives. Our approach integrates fuzzy logic to model qualitative expert judgments, providing a robust input for Monte Carlo simulation. Monte Carlo simulation generates comprehensive probability distributions of sustainability performance. This unique integration enables more informed and resilient decision-making. Our framework provides a practical and novel integrated framework for complex sustainability assessment, particularly in dynamic and data-challenged urban environments.

The article is organized as follows: Section 2 presents the literature review. Section 3 describes the methodological procedure. A case study is presented in Section 4. In Section 5, we present the comparative analysis. Section 6 illustrates the sensitivity analysis. Section 7 summarizes the main conclusions of the study and outlines directions for future research.

2. Literature Review

The concept of sustainable development was established in the aftermath of the Brundtland Report, published by the World Commission on Environment and Development. It has since become widely recognized as “development that meets the needs of the present without compromising the ability of future generations to meet their own needs” [19]. Efforts have been made to apply the concept of sustainable development to the transport sector, where the definition of sustainable transport must align with the sustainable development definition and principles. Numerous definitions have been introduced by researchers. According to Black [20] and Booth et al. [21], for a transport system to be defined as sustainable, it must meet individuals’ needs in a safe environment, ensure intergenerational equity, be affordable, support a vibrant economy, and minimize emissions, waste, and the use of non-renewable resources.

Public transport has been highlighted in research and strategies as an essential tool for attaining sustainable development [22], particularly in developing nations, where rapid urbanization coincides with growing environmental concerns and resource scarcity. As a result, there has been a concerted effort in recent years to build attractive, resource-efficient, and inclusive public transport infrastructure. Makarova et al. [23] proposed a decision support system designed to enhance the sustainability of urban public transportation, including a conceptual model and interaction scheme tailored for the city of Naberezhnye Chelny. Lukic Vujadinovic et al. [24] highlighted the potential for AI-driven optimization to improve the resilience and efficiency of public transport systems. Abdelwahed et al. [25] introduced a dynamic transit bus system that combines the convenience of on-demand services with the sustainability of public transport, aiming to attract more passengers by reducing walk-to-station distances and total travel time compared with fixed-route systems.

Multi-criteria decision-making (MCDM) techniques provide structured frameworks for ranking alternatives and supporting policy decisions in transportation systems. Kalifa et al. [26] employed multi-criteria decision-making (MCDM) methods, specifically the Analytic Network Process (ANP) and Elimination Et Choice Translating Reality (ELECTRE III), to evaluate and identify the most suitable public transport mode in Kampala, Uganda, from a transportation operator’s perspective. Broniewicz and Ogrodnik [27] conducted a comparative evaluation of sustainable transport using a hybrid approach combining DEMATEL, REMBRANDT, and VIKOR methods.

To overcome the limitations of crisp data assumptions in classical MCDM, fuzzy logic has been widely integrated in transportation systems. Kundu et al. [28] proposed a multi-criteria group decision-making (MCGDM) framework integrating fuzzy Best-Worst Method (BWM) and fuzzy Multi-Attribute Ideal-Real Comparative Analysis (MAIRCIA) techniques to evaluate six urban transport systems based on 11 selection criteria identified through expert consultations. Additionally, Awasthi et al. [29] proposed a multi-criteria decision-making approach based on fuzzy set theory to assess and select sustainable urban transportation systems. The complexity of urban sustainability and transport has led to the development of various hybrid evaluation frameworks in recent years. For instance, [30] examined the diverse connections between urban densification and several aspects of urban resilience, highlighting the need for multi-dimensional evaluation frameworks that can holistically address the multifaceted nature of urban systems. Furthermore, other hybrid fuzzy-based methods have been successfully applied to urban planning challenges, such as selecting optimal locations for multi-story parking [31]. However, a notable gap in such frameworks is their limited capacity to comprehensively address the uncertainty throughout the entire decision model.

Several research studies employed Monte Carlo models to investigate transportation systems. Guimarães et al. [32] evaluated the performance of transportation alternatives using Monte Carlo simulation, considering social, economic, and environmental indicators for the route between Rio de Janeiro and Niterói. They found that cost is the most influential indicator for individual transportation alternatives, while trip time is the most relevant for collective alternatives. Oszczypała et al. [33] developed a simulation model based on Monte Carlo methods for the analysis, evaluation, and prediction of the efficiency and reliability of vehicle operating processes in transport systems. Wang et al. [34] investigated on-demand vehicle deployment for night bus routes in a realistic scenario using the Monte Carlo Method, considering some key performance measures, including the average waiting time per passenger, the maximum waiting time of a single passenger, and the average in-vehicle time per passenger. The authors of [35] conducted a Monte Carlo simulation to estimate the effects of disinformation-induced disruptions on commuter time and cost in a complicated urban transit network. While their research focuses on network resilience and the use of AI/NLP to predict disruption scenarios, it also highlights the importance of Monte Carlo simulation as a useful tool for assessing the effects of highly uncertain events on system performance.

Assessing the sustainability of public transport systems, particularly in the dynamic and frequently data-limited contexts of rapidly urbanizing cities such as Amman, requires robust approaches capable of handling complex uncertainties. Conventional deterministic multi-criteria decision-making (MCDM) methods rely on fixed weighting values, inherently ignoring uncertainty [36], while fuzzy approaches are excellent at capturing subjective expert judgments but fall short in quantifying probabilistic consequences [37], whereas Monte Carlo simulations typically assume precise input weights—an unrealistic constraint given the inherent ambiguities in sustainability assessments [38,39]. To address this critical analytical gap in sustainable public transit assessment, we propose a novel integrated framework. This framework combines fuzzy set theory to effectively model the subjectivity of expert judgments, with Monte Carlo simulation to holistically account for uncertainty and quantify the probabilistic outcomes of alternative performances. The need for this integrated framework is particularly critical in rapidly urbanizing developing countries such as Jordan. Here, the unique complexities within their transportation networks and significant data limitations pose substantial challenges that traditional evaluation approaches often fail to reliably overcome. This novel integration provides a tailored conceptual and analytical framework for a more realistic and reliable evaluation of public transport sustainability. This approach offers significant advancement in the field by delivering robust, evidence-based insights for strategic urban mobility planning.

3. Methodological Procedure

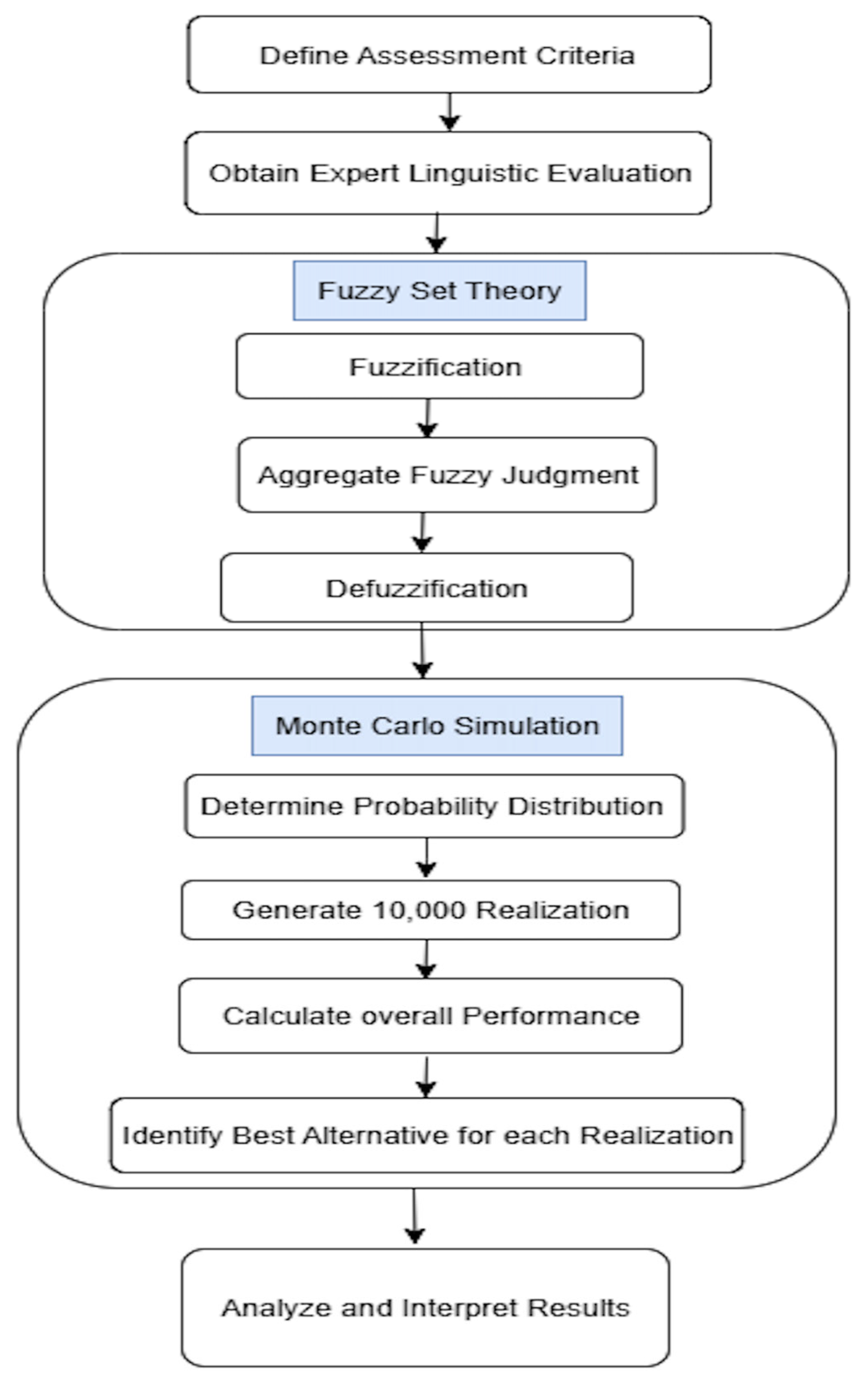
In this study, a hybrid methodological approach integrating fuzzy set theory and Monte Carlo simulation is employed to systematically analyze and evaluate the criteria for assessing public transport systems. This combined methodology is specifically designed to address the complexities of urban mobility assessment, which often involves both qualitative, subjective judgments and quantitative data subject to significant uncertainty [40,41]. The overall methodological process is visually illustrated in Figure 1. The process begins by defining the assessment criteria and obtaining linguistic evaluations from experts. Fuzzification transforms these qualitative judgments into quantitative values, which are then aggregated across experts and defuzzified to produce crisp scores. In the first stage, the qualitative judgment of experts is handled using fuzzy set theory. Monte Carlo simulation is then applied by specifying probability distributions, generating 10,000 realizations, and calculating overall performance measures for each run. For every realization, the best-performing alternative is identified, allowing the analysis to capture the variability of outcomes under uncertainty. Finally, the combined findings are analyzed and evaluated to establish the most robust alternative.

3.1. Defining Assessment Criteria

A comprehensive evaluation of significant academic literature on sustainable urban transport, public transport planning, and multi-criteria decision analysis (MCDA) was performed. In this stage, we identified well-established performance, environmental, social, and economic variables relevant to the evaluation of public transport systems.

3.2. Data Collection and Sources

Data collection in this study relied exclusively on expert judgments, which provided the primary input for the fuzzy set theory component. These evaluations were specifically associated with the analysis of public transport options in Amman, Jordan. Experts were selected using a purposive sampling approach, ensuring a diverse and relevant representation of transportation planning. The panel included specialists from local government authorities, public transport operators, and academia in Jordan. Selection criteria for experts included several years of practical or research experience, specifically in public policy, urban transport planning, and sustainability assessment. A structured questionnaire was used to collect expert opinions on the importance of each criterion (including digital transformation) and the performance of certain public transit alternatives under examination for Amman. The questionnaire used Likert scales, which were immediately converted to the fuzzy linguistic variables shown in

Table 1. Linguistic variable for weighting the importance of each criterion.

Very Low (VL)	(0, 0, 0.1)
Low (L)	(0, 0.1, 0.3)
Medium Low (ML)	(0.1, 0.3, 0.5)
Medium (M)	(0.3, 0.5, 0.7)
Medium High (MH)	(0.5, 0.7, 0.9)
High (H)	(0.7, 0.9, 1)
Very High (VH)	(0.9, 1, 1)

and

Table 2. Linguistic variable for weighting the importance of alternatives.

Very Poor (VP)	(0, 0, 1)
Poor (P)	(0, 1, 3)
Medium Poor (MP)	(1, 3, 5)
Medium (M)	(3, 5, 7)
Medium Good (MG)	(5, 7, 9)
Good (H)	(7, 9, 10)
Very Good (VG)	(9, 10, 10)

. The questionnaire comprised two primary sections: one to assess the relative importance of each sustainability criterion, and another to evaluate the performance of each public transport alternative with respect to the criteria.

3.3. Fuzzy Logic

Fuzzy set theory is utilized to address the inherent uncertainties and ambiguities associated with qualitative and subjective judgments in the evaluation process [40]. Using fuzzy logic allowed for the effective handling of linguistic variables, enabling a more realistic representation of decision-making scenarios.

3.3.1. Fuzzification and Linguistic Variables

The fuzzification process transforms crisp sets with normal values into fuzzy membership functions. For a fuzzy set A, the membership function is defined by µA(x) ∈ [0, 1] and represents the degree of membership of x to the fuzzy set A. The triangular membership function feature is one of the most widely accepted and used membership functions. It is specified by three parameters {a, b, c}, where a and c represent the base of the triangle and b defines the mode of the triangle. The membership function µA(x) for each value x is represented below [42,43]:

$${\mu }_{A\left(x;a,b,c\right)}=\left\{\begin{array}{c}0 if \mathrm{x} < \mathrm{a} \\ {\displaystyle \frac{\mathrm{x}-\mathrm{a}}{\mathrm{b}-\mathrm{a}}} if \mathrm{a} \le \mathrm{x} \le \mathrm{b}\\ {\displaystyle \frac{\mathrm{c}-\mathrm{x}}{\mathrm{c}-\mathrm{b}}} if \mathrm{b} \le \mathrm{x} \le \mathrm{c} \\ 0 if \mathrm{x} > \mathrm{c}\end{array}\right.$$

(1)

In addition, the fuzzy set theory can handle both quantitative and qualitative data, which may apply to sustainability indicators in the transport sector. Table 1 and Table 2 present the linguistic variables used for criteria and alternatives, respectively.

3.3.2. Fuzzy Decision Matrix Construction

The first step in the fuzzy evaluation process involved constructing the fuzzy decision matrix. Let A = {A₁, A₂, …, A_m} be all possible alternatives, against n criteria C = {C₁, C₂, …, C_n}, ${\mathrm{X}}_{\mathrm{i}\mathrm{j}}$ represents the rating of alternatives Ai with respect to criterion ${\mathrm{C}}_j$ (Figure 2).

The weight of each criterion is represented by a fuzzy vector W = [w1, w2, …, w_n]. To compute the aggregate weight of each criterion, the following equation is used, where k refers to the decision makers:

$$W_j= {\displaystyle \frac{1}{\mathrm{K}}}{\sum }_{k=1}^K{w}_{jk}$$

(2)

This equation is a standard fuzzy aggregation method for computing the aggregate weight of each criterion across multiple decision-makers [44], and has been widely utilized in multi-criteria decision-making to ensure consistency and resilience in managing uncertain linguistic assessments.

3.3.3. Normalization of the Fuzzy Decision Matrix

Normalize the fuzzy decision matrix: The quantitative data are identified in measurable units, which need to be converted into normalized values between 0 and 1 so that the different indicators can be compared easily. The indicators can be divided into two main categories—benefit and cost indicators—depending on their effects on the transport system. The benefit indicators should be maximized, while the cost indicators should be minimized [45]. For benefit and cost indicator normalization, the following equations are used, respectively, where ${{\mathrm{C}}_j}^{+}$ refers to the maximum score for specific criteria, and ${{\mathrm{C}}_j}^{-}$ refers to the minimum score for specific criteria:

$${\mathrm{x}}_{\mathrm{i}\mathrm{j}}=\left({\displaystyle \frac{{\mathrm{a}}_{ij}}{{{\mathrm{C}}_j}^{+}}},{\displaystyle \frac{{\mathrm{b}}_{ij}}{{{\mathrm{C}}_j}^{+}}},{\displaystyle \frac{{\mathrm{c}}_{ij}}{{{\mathrm{C}}_j}^{+}}}\right)$$

(3)

$${\mathrm{x}}_{\mathrm{i}\mathrm{j}}=\left({\displaystyle \frac{{{\mathrm{C}}_j}^{-}}{{\mathrm{C}}_{ij}}},{\displaystyle \frac{{{\mathrm{C}}_j}^{-}}{{\mathrm{b}}_{ij}}},{\displaystyle \frac{{{\mathrm{C}}_j}^{-}}{{\mathrm{a}}_{ij}}}\right)$$

(4)

Construct the weighted normalized matrix: In this step, the weighted fuzzy values (${\mathrm{w}}_{\mathrm{n}}$) and the normalized fuzzy decision matrices are multiplied to obtain the weighted normalized matrix ῦ:

$$\mathsf{ῦ}={\mathrm{x}}_{\mathrm{i}\mathrm{j}}\times W_j$$

(5)

3.4. Monte Carlo Simulation

The next step is to apply a Monte Carlo Simulation to assess and rank the alternatives using the outcome of the weighted normalized matrix. The use of Monte Carlo Simulation could help overcome uncertainty in the final results, as the use of probability distributions could illustrate the uncertainty of the variables more realistically [46]. The weighted normalized matrix, represented by ῦ, consists of the three fuzzy numbers that serve as the inputs for the Monte Carlo simulation. A triangular probability distribution is used to generate a sufficiently large number of random realizations for each indicator. This stochastic analysis employed 10,000 Monte Carlo iterations to propagate uncertainty through the evaluation model. This iteration count aligns with convergence evidence from applied simulation studies [32,47], where 10,000 realizations were shown to produce stable distributions with negligible sampling error.

For each realization, the overall performance score of each alternative was computed by adding its weighted performance across all criteria. The alternative with the highest total performance score was chosen as the best option for that realization. After completing all realizations, we counted how many times each alternative was chosen as the best; then, the percentage of choosing each alternative as the most sustainable alternative was calculated. The alternatives were then ranked. All Monte Carlo simulation computations were performed using the Python 3.9 programming language.

4. Urban Mobility Evaluation in Amman, Jordan

To demonstrate the applicability of the presented methodology, a case study from the city of Amman, Jordan, is discussed. A comprehensive set of sustainability indicators is applied to evaluate the city’s public transport system. Amman, the capital of Jordan, is home to an estimated 4 million people, with a 5.8% population growth rate [48]. Existing public mobility services in the city are delivered through a multimodal system comprising rapid transit buses, standard buses, small buses, fixed-route service taxis, and conventional yellow taxis [49,50]. This study focused exclusively on bus services (rapid transit, buses, and small buses) to align with the city’s strategic priorities for mass transit optimization.

4.1. Description of the Alternatives

The Bus Rapid Transit (BRT) is a highly efficient transport mode that enhances the transportation system by offering high capacity and speed [51]. BRT features wide automatic doors that facilitate fast and efficient passenger boarding and alighting. Additionally, BRT reduces travel time for passengers through the use of segregated lanes, which minimize delays and improve trip efficiency [52]. Payment is managed via prepaid cards, which can be charged using various methods such as vending machines, electronic applications, and point-of-sale systems. However, BRT systems face challenges, including high travel costs compared with other transportation modes. Another limitation is the limited number of stops, which may require passengers, particularly those with disabilities, to walk longer distances to access stations rather than being picked up along the route.

Buses can transport a significant number of passengers along fixed routes that operate on a specific schedule. These routes share the road with other transportation modes, as they are integrated into the existing road network, which may increase passenger waiting and transit times. The payment method is prepaid boarding at the bus entrance. The largest proportion of bus users is in the lower- and middle-income groups, where the average travel cost is considered suitable. Bus stations are located relatively close to each other; thus, it takes a short time to walk between stations. Small buses are available for passengers along the entire route. They are more flexible and can stop for passengers regardless of the presence of station stops; they can also skip some stations, thus reducing passenger travel times. Their capacity is lower than that of the other transportation modes. The seats are also placed very close together, which may cause passengers discomfort. Their method of payment collection is cash only.

4.2. Definitions and Weights of Criteria

Many studies have explored sustainable indicators using different methodologies and frameworks across multiple dimensions, including transportation, economy, environment, and social aspects. Some studies have proposed comprehensive approaches for evaluating these indicators across different countries, while others have identified and categorized them based on their applicability in diverse contexts [40,53,54]. In this study, we present the widely used and most compatible with the presented case study, as shown in

Table 3. Sustainability indicators in the transport sector.

Sustainability Dimensions	Indicators (Criterion)	Description	Type	References	Unit
Economic	Operating costs (C1)	Cost (to the operator) of running and maintaining the transportation service.	C	[55]	Fuzzy Linguistic Scale
	Net present value (C2)	The investment cash flow over the entire life of an investment, discounted to the present.	B	[56]	Fuzzy Linguistic Scale
	Benefit to the economy (C3)	The benefits from the transportation mode that improve the quality of an individual’s life from an economic perspective, e.g., labor employment.	B	[1,57]	Fuzzy Linguistic Scale
	Investment attractiveness (C4)	The ability to attract assets for investors.	B	[58]	Fuzzy Linguistic Scale
Environmental	Noise (C5)	Intensity of noise generated by the transportation mode.	C	[59]	Fuzzy Linguistic Scale
	Air pollution (C6)	The amount of pollutants, such as gases and particles, that the transportation mode produces.	C	[56]	Fuzzy Linguistic Scale
	Land usage (C7)	The percentage of land used for transport system infrastructure.	C	[21]	Fuzzy Linguistic Scale
Social	Travel time (C8)	Number of fatal and severe injuries due to accidents.	C	[1,7]	Fuzzy Linguistic Scale
	Safety (C9)	Travelling time between given stations.	B	[60,61]	Fuzzy Linguistic Scale
	Accessibility (C10)	The density of stations.	B	[32,62]	Fuzzy Linguistic Scale
	Comfort (C11)	The cruise comfort provided by the transport mode during the total trip.	B	[38]	Fuzzy Linguistic Scale
	Expansion possibility (C12)	The possibility of expanding the presented services and contributing to the entire transportation network.	B	[29]	Fuzzy Linguistic Scale
	Convenient to use (C13)	Quality of suitability for use.	B	[29,63]	Fuzzy Linguistic Scale
	Digital transformation (C14)	Ability to integrate digital technology into the transport mode.	B	[64]	Fuzzy Linguistic Scale

.

Three decision-makers were selected to evaluate the alternatives based on their expertise in public transportation. Each decision-maker has a wealth of experience in transport operations, planning, and policy, which ensures a comprehensive evaluation of the criteria under consideration. This approach aligns with previous studies that have successfully utilized a similar number of evaluators in multi-criteria decision analysis [65,66]. The data collection process was conducted through structured surveys, where the decision-makers provided their evaluations based on their professional experience and domain knowledge using the linguistic variables in Table 1 and Table 2. The results are presented in

Table 4. Linguistic assessment of the criteria.

Criteria ID	Aggregate Using Fuzzy Numbers
C1	(0.567, 0.767, 0.93)
C2	(0.833, 0.967, 1.00)
C3	(0.9, 1.00, 1.00)
C4	(0.567, 0.767, 0.93)
C5	(0.63, 0.83, 0.967)
C6	(0.7, 0.867, 0.967)
C7	(0.63, 0.83, 0.967)
C8	(0.63, 0.83, 0.967)
C9	(0.767, 0.93, 1.00)
C10	(0.63, 0.83, 0.967)
C11	(0.63, 0.83, 0.967)
C12	(0.70, 0.90, 1.00)
C13	(0.567, 0.767, 0.93)
C14	(0.63, 0.83, 0.967)

.

The aggregate fuzzy matrix for the alternatives with respect to each criterion is calculated using the following equation:

$${{\mathrm{x}}_{\mathrm{i}\mathrm{j}}}^{\mathrm{K}}={\displaystyle \frac{1}{\mathrm{K}}}({{\mathrm{x}}_{\mathrm{i}\mathrm{j}}}^1+{{\mathrm{x}}_{\mathrm{i}\mathrm{j}}}^2+\dots +{{\mathrm{x}}_{\mathrm{i}\mathrm{j}}}^{\mathrm{k}})$$

(6)

The aggregate fuzzy decision matrix is presented in

Table 5. Fuzzy decision matrix.

Criteria	Alternatives
	A1	A2	A3
Operating costs (C1)	(6.30, 8.0, 9.30)	(5.67, 7.60, 9.30)	(6.30, 8.30, 9.67)
Net present value (C2)	(7.67, 9.30, 10.00)	(6.30, 8.30, 9.67)	(1.30, 3.00, 5.00)
Benefit to the economy (C3)	(8.3, 0 9.67, 10.00)	(5.67, 7.67, 9.00)	(1.00, 2.00, 3.67)
Investment attractiveness (C4)	(7.00, 8.67, 9.67)	(3.00, 5.00, 7.00)	(1.00, 2.00, 3.67)
Noise (C5)	(7.00, 9.00, 10.00)	(3.00, 5.00, 7.00)	(5.67, 7.67, 9.30)
Air pollution (C6)	(5.00, 7.00, 8.67)	(2.3,0 4.30, 6.30)	(3.67, 5.67, 7.30)
Land usage (C7)	(5.67, 7.30, 8.30)	(5.00, 7.00, 8.67)	(0.00, 0.67, 2.30)
Travel time (C8)	(9.00, 10.00, 10.00)	(1.67, 3.67, 6.30)	(2.67, 4.30, 6.30)
Safety (C9)	(6.30, 8.3, 0 9.67)	(2.30, 4.30, 6.30)	(0.00, 0.30, 1.67)
Accessibility (C10)	(4.33, 6.30, 8.30)	(3.67, 5.67, 7.30)	(2.67, 4.30, 6.30)
Comfort (C11)	(5.00, 7.00, 8.67)	(2.30, 4.30, 6.30)	(0.00, 0.67, 2.30)
Expansion possibility (C12)	(7.67, 9.30, 10.00)	(3.00, 5.00, 6.70)	(1.67, 2.67, 4.30)
Convenient to use (C13)	(6.30, 8.30, 9.67)	(3.00, 5.00, 7.00)	(0.00, 0.67, 2.30)
Digital transformation (C14)	(8.30, 9.60, 10.00)	(5.67, 7.67, 9.00)	(0.00, 0.30, 1.67)

.

The matrix is then converted into normalized values between 0 and 1 so that the different indicators can be compared easily. Equations (2) and (3) are used for the benefit and cost indicators, respectively.

Table 6. Normalized fuzzy decision matrix.

Criteria	Alternatives
	A1	A2	A3
Operating costs (C1)	(0.61, 0.80, 1.00)	(0.60, 0.75, 1.00)	(0.59, 0.69, 0.90)
Net present value (C2)	(0.77, 0.93, 1.00)	(0.60, 0.80, 0.97)	(0.13, 0.30, 0.50)
Benefit to the economy (C3)	(0.83, 0.967, 1.00)	(0.57, 0.77, 0.90)	(0.10, 0.20, 0.37)
Investment attractiveness (C4)	(0.70, 0.89, 1.00)	(0.3, 0.5, 0.7)	(0.10, 0.20, 0.38)
Noise (C5)	(0.30, 0.33, 0.40)	(0.40, 0.60,1.00)	(0.30, 0.40, 0.53)
Air pollution (C6)	(0.27, 0.33, 0.46)	(0.36, 0.50, 1.00)	(0.30, 0.40, 0.60)
Land usage (C7)	(0.01, 0.014, 0.018)	(0.01, 0.015, 0.02)	(0.04, 0.12, 1.00)
Travel time (C8)	(0.17, 0.17, 0.18)	(0.27, 0.46, 1.00)	(0.27, 0.38, 0.60)
Safety (C9)	(0.66, 0.86, 1.00)	(0.24, 0.40, 0.66)	(0.00, 0.03, 0.18)
Accessibility (C10)	(0.50, 0.76, 1.00)	(0.40, 0.69, 0.88)	(0.30, 0.50, 0.70)
Comfort (C11)	(0.58, 0.8, 1.00)	(0.27, 0.58, 0.73)	(0.00, 0.08, 0.27)
Expansion possibility (C12)	(0.77, 0.90, 1.00)	(0.30, 0.50, 0.67)	(0.17, 0.27, 0.43)
Convenient to use (C13)	(0.66, 0.86, 1.00)	(0.30, 0.50, 0.70)	(0.00, 0.07, 0.24)
Digital transformation (C14)	(0.83, 0.96, 1.00)	(0.567, 0.767, 0.90)	(0.00, 0.03, 0.17)

presents the normalized fuzzy decision matrix.

In the next step, the weighted normalized matrix is constructed using Equation (3). Both the weighted fuzzy numbers and the normalized scores are used to obtain the weighted normalized matrix, as shown in

Table 7. Weighted normalized fuzzy decision matrix.

Criteria	Alternatives
	A1	A2	A3
Operating costs (C1)	(0.35, 0.54, 0.84)	(0.35, 0.57, 0.93)	(0.33, 0.5, 0.84)
Net present value (C2)	(0.64, 0.89, 1.00)	(0.50, 0.80, 0.97)	(0.1,0 0.30, 0.5)
Benefit to the economy (C3)	(0.75, 0.97, 1.00)	(0.51, 0.77, 0.90)	(0.09, 0.20, 0.37)
Investments attractiveness (C4)	(0.41, 0.69, 0.93)	(0.18, 0.47, 0.67)	(0.06, 0.16, 0.35)
Noise (C5)	(0.19, 0.28, 0.41)	(0.30, 0.50, 0.97)	(0.20, 0.30, 0.50)
Air pollution (C6)	(0.19, 0.29, 0.44)	(0.26, 0.47, 0.97)	(0.22, 0.40, 0.60)
Land usage (C7)	(0.00, 0.01, 0.017)	(0.01, 0.012, 0.02)	(0.03, 0.12, 0.10)
Travel time (C8)	(0.11,0.14,0.18)	(0.17,0.40,0.97)	(0.17,0.30,0.60)
Safety (C9)	(0.50, 0.80, 1.00)	(0.18, 0.40, 0.65)	(0.00, 0.03, 0.18)
Accessibility (C10)	(0.33,0.63,0.97)	(0.28, 0.57, 0.85)	(0.20, 0.43, 0.70)
Comfort (C11)	(0.36, 0.673, 0.97)	(0.17, 0.40, 0.70)	(0.00, 0.06, 0.30)
Expansion possibility (C12)	(0.54, 0.84, 1.00)	(0.21, 0.45, 0.67)	(0.10, 0.25, 0.43)
Convenient to use (C13)	(0.37, 0.66, 0.93)	(0.18, 0.40, 0.70)	(0.00, 0.05, 0.20)
Digital transformation (C14)	(0.50, 0.80, 0.97)	(0.36, 0.64, 0.90)	(0.00, 0.03, 0.17)

.

To determine the most sustainable alternative of the three evaluated options, Monte Carlo Simulation was used to evaluate the values of the weighted normalized matrix ῦ. In this step, fuzzy triangular numbers were used as input in the Monte Carlo simulation model, and 10,000 random realizations of each indicator were generated to enhance the accuracy of the results by reducing estimation error [67]. For each realization, the overall performance score for each alternative was calculated by summing its weighted performance across all criteria. The alternative with the highest overall performance score was selected as the best for that realization.

After completing the realization, we counted how many times each alternative was chosen as the best. Finally, we divided the count by the total number of realizations and multiplied by 100 to obtain the percentage of times each alternative was selected as the best. The results clearly demonstrate the superiority of alternative A1, as in 87.06% of the realization cases, the BRT alternative outperforms buses and small buses; however, in approximately 12.94% of the cases, buses show higher performance than BRT and small buses, whereas small buses never outperform the other alternatives.

The finding supports previous theoretical research and global case studies that endorse high-capacity public transport systems, such as BRT, as fundamental components of sustainable urban mobility in increasingly urbanizing environments [68,69,70]. However, our study offers methodological validation by utilizing a sophisticated hybrid fuzzy set theory and Monte Carlo simulation technique in the setting of Amman, Jordan. Unlike many studies that rely on crisp data or single-point expert estimations, our methodology accounts for the inherent subjective uncertainties in expert judgments using fuzzy logic and probabilistic variability using Monte Carlo Simulation. This enables a more comprehensive evaluation of sustainability under uncertainty, significantly enhancing confidence in the BRT’s long-term viability as the preferred alternative for the city.

In addition, the results provide significant evidence for policymakers considering strategic investments in urban transport infrastructure in Amman. The clear preference for BRT (A1) in 87.06% of scenarios provides a strong, data-driven directive for prioritizing the development and expansion of the BRT system in Amman. These finding suggests that sustained investment in BRT and integrated BRT services will result in the highest sustainable outcomes regarding environmental impact, social equity, and economic efficiency for Amman. This study thus not only contributes to a robust methodology for assessing urban transport sustainability under uncertainty but also provides specific, context-relevant insights for strategic planning in Amman, identifying clear priorities while also establishing clear priorities for integrated policy formulation.

5. Comparative Analysis

To demonstrate the robustness of our methodology, we compared the results obtained using our approach with those derived using a conventional defuzzification method. The conventional method involves converting the fuzzified outputs into single crisp values, which are then used to rank the alternatives. For comparison, we employed the Centroid Method, a widely used defuzzification technique. In this method, the defuzzified value for each criterion is calculated as the weighted average of the fuzzy set:

$$\mathrm{x}={\displaystyle \frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{i}}\times {\mathrm{x}}_{\mathrm{i}}}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{i}}}}$$

(7)

where ${\mathrm{w}}_{\mathrm{i}}$, the weight of the i-th criterion, equals

$${\mathrm{w}}_{\mathrm{i}}={\displaystyle \frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{3}}$$

(8)

and ${\mathrm{x}}_{\mathrm{i}}$, the defuzzified value of the i-th criterion, equals

$${\mathrm{x}}_{\mathrm{i}}={\displaystyle \frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{3}}$$

(9)

Using this approach, the defuzzified values for the alternatives are 0.581 for A1, 0.494 for A2, and 0.248 for A3. These results indicate that the sustainability performances of A1 and A2 are relatively close. However, when applying Monte Carlo simulation to account for uncertainty, A1 demonstrated superior robustness and reliability, further solidifying its position as the preferred alternative. To enable a thorough comparison between our suggested methodology and the traditional defuzzification approach (Centroid Method),

Table 8. Comparative performance analysis (%) of alternatives across methodologies.

Alternatives	Centroid Method	Presented Approach
A1	0.44%	87.06%
A2	0.373%	12.94%
A3	0.187%	0%

presents the alternative selection frequencies as percentages to enable direct quantitative comparison of methodological performance.

Our methodology outperforms conventional approaches by providing more precise defuzzified values through the incorporation of Monte Carlo simulation, which effectively addresses uncertainty. This integration allows for a more robust and reliable evaluation of alternatives, especially in dynamic and uncertain decision-making contexts. The results indicate that our approach significantly enhances the accuracy of sustainability performance assessment.

6. Sensitivity Analysis

The sensitivity analysis in this study was conducted using a systematic weight variation to evaluate the robustness of the presented methodology under varying criteria weights. The weight of each criterion was varied over a wide range (−0.5 to 1.50) in 21 equally spaced intervals (i.e., −0.5, −0.4, …, 1.5), allowing for a comprehensive exploration of how changes in individual criterion weights affect the performance of the alternatives. The weight of the current criterion was adjusted while keeping the weight of the other criteria constant, to ensure that the analysis focused on the impact of each criterion. The adjusted weights were normalized to ensure that the sum of all weights equaled 1; then, the weighted normalized matrix was calculated. To account for the uncertainty of the other criteria, Monte Carlo simulation was applied after the weighted normalized matrix was prepared for each weight variation; the weights of the other criteria were randomly sampled based on triangular fuzzy distribution. The simulation was run for 10,000 iterations, and in each realization, the overall performance scores of the alternatives were calculated by summing their weighted performance across all criteria.

The results of the Monte Carlo simulation for all weight variations are summarized in

Table 9. Results of sensitivity analysis: range of scores of each criterion.

	Criterion Iteration	Alternative	Min Score	Max Score	Range
0	C1	A1	0.582	0.583	0.001
1	C1	A2	0.501	0.520	0.019
2	C1	A3	0.211	0.267	0.056
3	C2	A1	0.546	0.595	0.049
4	C2	A2	0.480	0.525	0.045
5	C2	A3	0.241	0.250	0.010
6	C3	A1	0.536	0.597	0.061
7	C3	A2	0.483	0.523	0.040
8	C3	A3	0.247	0.252	0.005
9	C4	A1	0.571	0.588	0.017
10	C4	A2	0.509	0.523	0.013
11	C4	A3	0.245	0.255	0.011
12	C5	A1	0.566	0.619	0.053
13	C5	A2	0.504	0.518	0.014
14	C5	A3	0.237	0.253	0.016
15	C6	A1	0.568	0.619	0.051
16	C6	A2	0.507	0.517	0.010
17	C6	A3	0.227	0.257	0.029
18	C7	A1	0.550	0.655	0.104
19	C7	A2	0.486	0.577	0.091
20	C7	A3	0.239	0.269	0.030
21	C8	A1	0.558	0.638	0.080
22	C8	A2	0.514	0.514	0.000
23	C8	A3	0.234	0.254	0.020
24	C9	A1	0.557	0.592	0.034
25	C9	A2	0.509	0.528	0.019
26	C9	A3	0.239	0.272	0.033
27	C10	A1	0.575	0.586	0.011
28	C10	A2	0.507	0.517	0.010
29	C10	A3	0.223	0.259	0.036
30	C11	A1	0.572	0.587	0.016
31	C11	A2	0.509	0.525	0.017
32	C11	A3	0.241	0.264	0.023
33	C12	A1	0.554	0.593	0.039
34	C12	A2	0.510	0.523	0.013
35	C12	A3	0.246	0.249	0.002
36	C13	A1	0.574	0.587	0.013
37	C13	A2	0.509	0.524	0.016
38	C13	A3	0.238	0.268	0.030
39	C14	A1	0.560	0.592	0.032
40	C14	A2	0.499	0.521	0.022
41	C14	A3	0.238	0.271	0.033

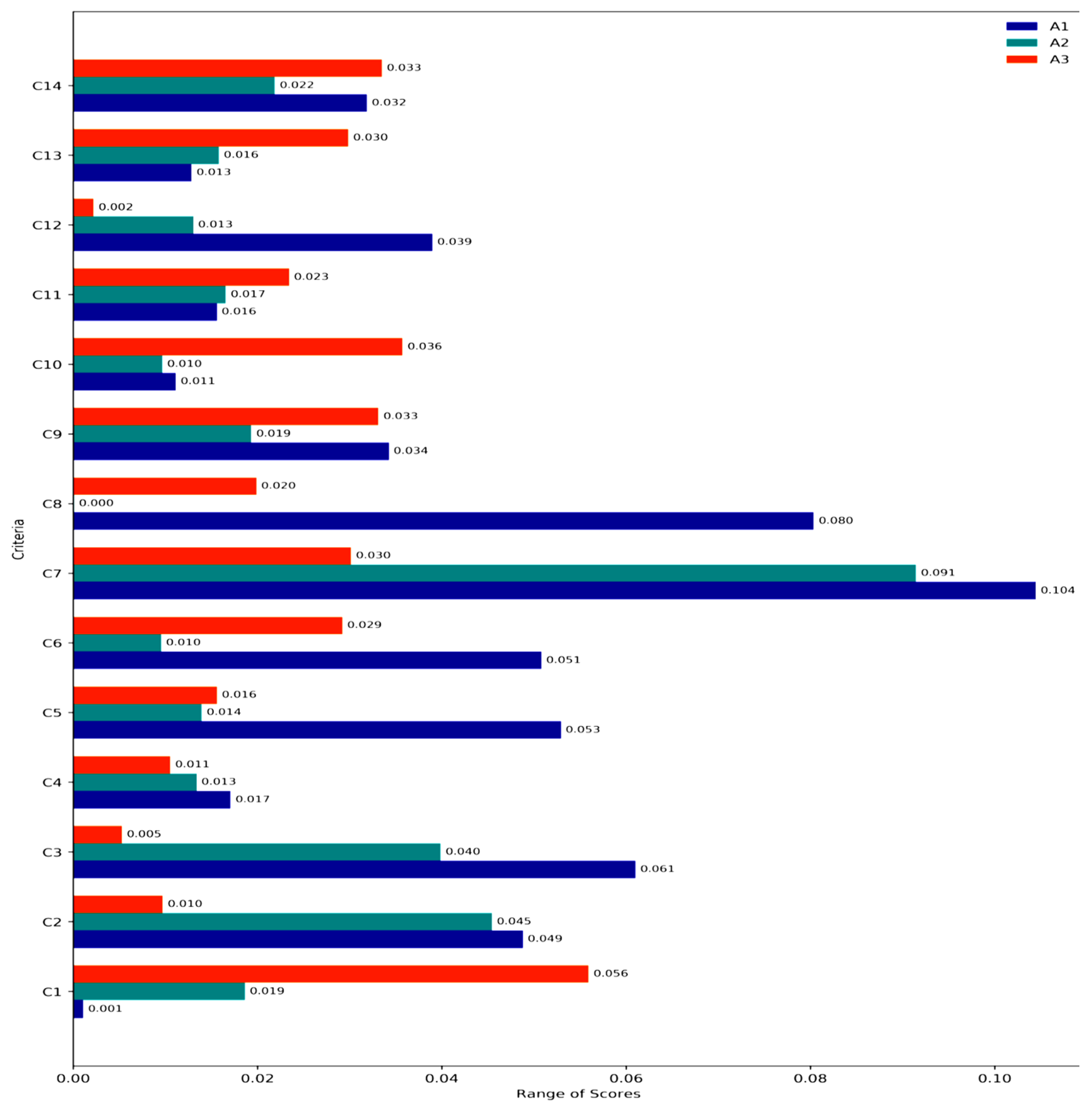
and visually represented in Figure 3 for clarity and ease of interpretation. Note that the minimum score and maximum score refer to the worst-case performance and best-case performance, respectively, while the range is the difference between the maximum and minimum scores. The importance of calculating the ranges lies in measuring the sensitivity of each alternative to the changes in the criterion’s weight. A large range indicates high sensitivity, while a small range indicates low sensitivity.

To clarify the sensitivity analysis results, operating costs (C1) are used as an illustrative example. As shown in Figure 3, A1 has a range of 0.001, indicating minimal variation in its performance due to fluctuations in the weight of C1. A2, on the other hand, shows a range of 0.0186, indicating a marginally higher sensitivity to variations in C1. A3 has a range of 0.056, indicating that changes in the weight of C1 have a significantly greater impact on its performance.

The alternatives are most significantly impacted by criteria with the largest ranges. Land usage (C7), for instance, has the largest range for A1 (0.104432) and A2 (0.091438), indicating that changes to C7’s weight have a major impact on the performance of these alternatives. However, C8 (Travel Time) has the smallest range for A2 (0.000090), which means that A2’s performance is essentially unaffected by changes in C8’s weight.

The high sensitivity of certain criteria, such as land usage, can be attributed to notable performance differences between alternatives, which increase the effect of weight adjustments. For instance, A1’s superior land usage efficiency (range: 0.104) contrasts markedly with A3’s limited responsiveness (range: 0.030), rendering rankings highly sensitive to changes in criterion weights.

In summary, A1 has the highest scores across all criteria, making it the most robust and preferred alternative. A2 is competitive in certain scenarios and can be considered moderately sensitive, making it a viable option in certain scenarios. A3 has the lowest scores and is generally less sensitive to changes in criteria weights.

7. Conclusions

Despite extensive research in sustainable transport assessment, current frameworks lack robust methodologies for quantifying and prioritizing these indicators under uncertainty, particularly when incorporating expert evaluations and regional variations in sustainability priorities, especially for applications in developing urban countries. To address these gaps, this study introduces a novel methodology for evaluating transportation alternatives by integrating fuzzy logic and Monte Carlo simulation. Our approach provides a comprehensive framework for handling uncertainty in expert evaluations and accounting for the complex interdependence between sustainability indicators.

Applied to the evaluation of BRT systems, buses, and small buses, the methodology yielded significant findings that advance both theoretical understanding and practical implementation of sustainable urban transportation. The superior performance of BRT systems, demonstrated in some 87% of simulation scenarios, provides strong empirical support for their adoption as a primary solution for sustainable urban transportation in Amman. This finding is significant given the comprehensive nature of our assessment, which considers 14 sustainability indicators across operational, economic, environmental, and social dimensions.

The sensitivity analysis highlights the robustness of BRT systems (A1), showing low sensitivity to changes in most criteria while demonstrating strong responsiveness to key factors such as land usage. This makes BRT systems the preferred choice for scenarios requiring flexibility and adaptability to shifting priorities. In contrast, buses (A2) remain a viable option in specific contexts, while small buses (A3) are less suitable due to their minimal sensitivity to changes in criteria weights. These findings, when combined with the results reported earlier and compared, demonstrate the effectiveness of our approach in providing practical insights for sustainable transportation planning.

In addition, the findings provide decision-makers with quantifiable levels of confidence for their investment decisions and help city planners and organizations optimize resource allocation across different aspects of the transportation system in Amman. The probabilistic nature of our results enables better risk assessment in transportation planning, while the fuzzy-based framework guarantees the systematic integration of both qualitative and quantitative sustainability indicators. While the empirical demonstration relies on a limited sample size, the combined use of fuzzy logic and Monte Carlo simulation enhances methodological rigor by mitigating bias from individual expert judgments and explicitly modeling uncertainty. Moreover, the framework is designed to be adaptable. By incorporating city-specific expert inputs and contextual indicators, it can be applied to other urban settings with differing resources, governance structures, or infrastructure challenges. These elements collectively enhance research by improving approaches for managing uncertainty in sustainability evaluation and support practice by offering a reliable, evidence-based tool for transportation planning amid uncertainty.

While this research provides valuable insights into sustainable transportation assessment, it has several limitations. Our dependence on expert evaluations, especially with a limited number of participants primarily from the Amman, Jordan, geographic area, could introduce biases and potentially skew the weight assignments. In future research, increasing the number and diversity of experts involved will be essential for reducing these professional and geographical biases, thus improving the data’s robustness and generalizability.

Although our method effectively addresses conflicting stakeholder priorities implicitly through its uncertainty-modeling approach, a potential area for future research is the integration of an explicit conflict resolution model, such as a negotiation-based approach.

Furthermore, a key limitation lies in the assumptions made within our modeling choices. The fuzzy logic assumptions in the criterion weights and the reliance on a triangular probability distribution in the Monte Carlo simulation are necessary simplifications of real-world variability. A more in-depth study might investigate the use of alternative distributions or collect empirical evidence to validate these assumptions.

In addition, the presented analysis excluded new sustainable alternatives, such as shared e-mobility, on-demand transit, and electric buses. Future research should extend the framework to capture these modes and evaluate their integration into Amman’s transport system. Such extensions would not only improve the comprehensiveness of the assessment but also provide policymakers with clearer guidance on transitioning toward low-carbon mobility options. The methodology could also be extended to a dynamic model to account for the evolution of transport systems over time. By providing a method for evaluating a key component of urban transport, our work offers a valuable tool for decision-making within the broader logistics context.

Overall, this study contributes to the field of transportation by presenting a robust framework for evaluating alternatives, while addressing uncertainty in expert evaluations and the complex interdependence of sustainability indicators.