Cost Modeling for Pickup and Delivery Outsourcing in CEP Operations: A Multidimensional Approach
Abstract
1. Introduction
2. Literature Review
2.1. Cost Modeling Approaches in CEP Outsourcing
2.2. Multidimensional and Sustainability-Oriented Models
2.3. Identified Gaps and Research Motivation
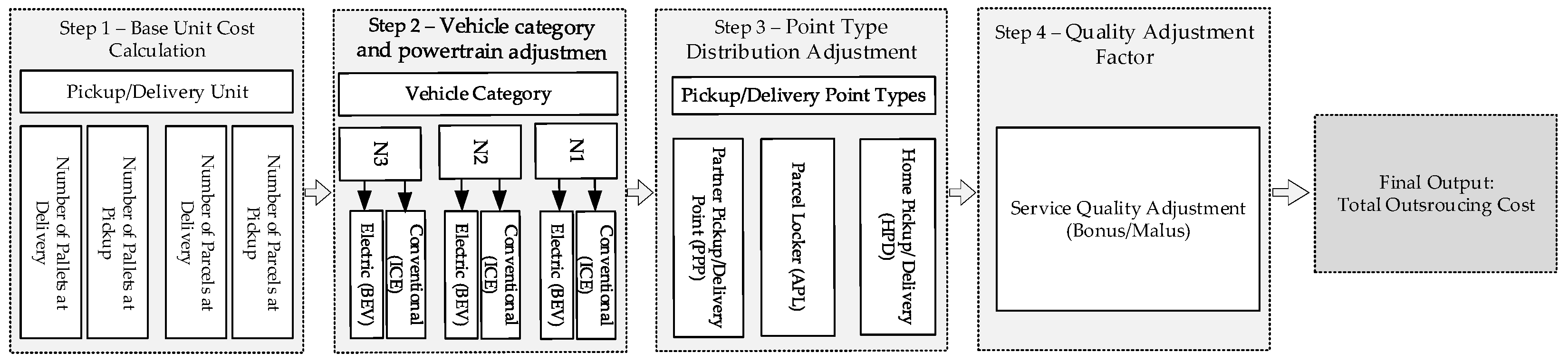
3. Methodology: Proposed Model
3.1. Problem Definition
3.2. Model Notation
3.3. Mathematical Formulation
3.3.1. Base Unit Cost Calculation
- and for parcels;
- and for pallets.
3.3.2. Vehicle Category and Powertrain Adjustments
- N1 ≤ 3.5 tons;
- N2 > 3.5 ≤ 12 tons;
- N3 > 12 tons.
3.3.3. Point Type Distribution Adjustment
- HPD—Home Pickup/Delivery;
- PL—Parcel Locker Pickup/Delivery;
- PPP—Partner Pickup Point (e.g., at retail stores or service stations).
- the need for physical delivery (HPD);
- the level of automation and accessibility (PL);
- the involvement of a third party (PPP).
3.3.4. Quality Adjustment Factor
- (a)
- Cost per parcel in the pickup phase:
- (b)
- Cost per parcel in the delivery phase:
- (c)
- Cost per pallet in the pickup phase:
- (d)
- Cost per pallet in the delivery phase:
3.3.5. Final Calculation of the Total Outsourcing Cost per Route and Vehicle
- —represents the final outsourcing compensation to be paid to the subcontractor for executing deliveries on route r, in period t, using a vehicle of category i and powertrain p.
- Each term on the right-hand side corresponds to the total cost component per shipment type and service phase, as adjusted by the vehicle, point type, and service quality.
- For CEP operators (principals), it supports fair pricing strategies and cost optimization.
- For subcontractors, it ensures compensation is aligned with service complexity and performance quality.
3.4. Algorithmic Implementation
| Algorithm 1 Practical application of the proposed multidimensional model |
| Input: R ← set of routes () T ← observation periods I ← vehicle categories (N1, N2, N3) P ← powertrain types (ICE, BEV) U ← unit types (PAR, PAL) S ← service stages (PCK, DEL) J ← point types (HPD, PL, PPP) Parameters: ← number of units by route, period, unit type, service stage, and point type ← base price per unit type and service stage ← vehicle-powertrain cost correction coefficient ← point-based cost adjustment coefficient ← service quality adjustment factor (bonus/malus) |
| Output: ← total outsourcing cost per route, period, vehicle, powertrain |
| Begin: 1. For each ∈ R: 2. For each ∈ T: 3. For each ∈ I: 4. For each ∈ P: 5. Set ← 0 6. For each ∈ U: 7. For each ∈ S: 8. Set base_cost ← 0 9. For each ∈ J 10. If u = PAL and j ≠ HPD continue 11. Retrieve units ← 12. Retrieve unit_cost ← 13. Retrieve k_factor ← 14. Retrieve alpha ← 15. Retrieve qf ← 16. Compute cost ← units×unit_cost×k_factor×alpha×qf 17. Update base_cost ← base_cost + cost 18. End for 19. Update ← + base_cost 20. End for 21. End for 22. End for 23. End for 24. End for 25. End for 26. Return all values |
| End |
3.5. Case Study
- To apply the proposed multidimensional model to real-world operational data;
- To obtain an accurate allocation of outsourcing costs based on input parameters such as service phase, shipment type, delivery point type, vehicle category, and powertrain;
- To compare the model results with invoice values calculated using fixed pricing;
- To demonstrate the advantages of the multidimensional approach in terms of transparency, accuracy, and decision-making support for both contractors and service providers.
3.5.1. Base Unit Cost Calculation
- For parcels in the pickup phase on route during period the cost is ;
- For parcels in the delivery phase on the same route and period, ;
- For pallets in the pickup phase, ;
- For pallets in the delivery phase, .
3.5.2. Cost Calculation by Vehicle Category and Powertrain Adjustment
3.5.3. Calculation of Cost Based on Point Type Distribution Adjustment
3.5.4. Calculation of the Quality Adjustment Factor
- (a)
- Costs of all parcels in pickup for route 1:
- (b)
- Cost per parcel in delivery for route 1:
- (c)
- Cost per pallet in pickup:
- (d)
- Cost per pallet in delivery:
4. Discussion and Conclusions
- Operational accuracy through detailed breakdowns by service phase and delivery type;
- Adaptability to different fleet compositions and internal cost structures;
- Compatibility with electric vehicle usage and alternative delivery points;
- A structured approach for integrating cost logic into route planning and contracting tools, enabling principals to transparently evaluate and compare outsourcing offers, while also allowing contractors to justify cost structures based on service complexity and performance parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEV | Battery Electric Vehicle |
| CEP | Courier, Express, and Parcel |
| PDP | Pickup and Delivery Problem |
| HPD | Home Pickup/Delivery |
| ICE | Internal Combustion Engine |
| KPI | Key Performance Indicator |
| PAL | Pallet |
| PAR | Parcel |
| PCK | Pickup |
| DEL | Delivery |
| PL | Parcel Locker |
| PPP | Partner Pickup Point |
| SLA | Service Level Agreement |
| TCO | Total Cost of Ownership |
References
- Ghazal, A.; Narayanan, S.; Adeniran, I.O.; Dörpinghaus, J.; Drees, L. Analysis of Logistics Measures of CEP Service Providers for the Last-Mile Delivery in Small- and Medium-Sized Cities: A Case Study for the Aachen City Region. Eur. Transp. Res. Rev. 2025, 17, 5. [Google Scholar] [CrossRef]
- Viu-Roig, M.; Alvarez-Palau, E.J. The Impact of E-Commerce-Related Last-Mile Logistics on Cities: A Systematic Literature Review. Sustainability 2020, 12, 6492. [Google Scholar] [CrossRef]
- Boysen, N.; Fedtke, S.; Schwerdfeger, S. Last-Mile Delivery Concepts: A Survey from an Operational Research Perspective. OR Spectr. 2021, 43, 1–58. [Google Scholar] [CrossRef]
- Bosona, T. Urban Freight Last Mile Logistics—Challenges and Opportunities to Improve Sustainability: A Literature Review. Sustain. 2020, 12, 8769. [Google Scholar] [CrossRef]
- Laseinde, O.T.; Mpofu, K. Providing Solution to Last Mile Challenges in Postal Operations. Int. J. Logist. Res. Appl. 2017, 20, 475–490. [Google Scholar] [CrossRef]
- Ducret, R. Parcel Deliveries and Urban Logistics: Changes and Challenges in the Courier Express and Parcel Sector in Europe—The French Case. Res. Transp. Bus. Manag. 2014, 11, 15–22. [Google Scholar] [CrossRef]
- Goigi. Retail E-Commerce. 2023. Available online: https://www.goigi.com/frontend/Retail_Ecommerce.pdf (accessed on 8 May 2025).
- Otto, A.; Boysen, N.; Scholl, A.; Walter, R. Ergonomic Workplace Design in the Fast Pick Area. OR Spectr. 2017, 39, 945–975. [Google Scholar] [CrossRef]
- Sawik, B. Optimizing Last-Mile Delivery: A Multi-Criteria Approach with Automated Smart Lockers, Capillary Distribution and Crowdshipping. Logistics 2024, 8, 52. [Google Scholar] [CrossRef]
- Latif, N.A.; Stephen, D.; Abu Mansor, S.; Adruce, S.A.Z. Fostering Economic Sustainability through the Pick-Up and Drop-Off (PUDO) Point Suitability Index: Optimising Last-Mile Delivery Efficiency. J. Sustain. Sci. Manag. 2025, 20, 101–121. [Google Scholar] [CrossRef]
- Ranjbari, A.; Diehl, C.; Dalla Chiara, G.; Goodchild, A. Do Parcel Lockers Reduce Delivery Times? Evidence from the Field. Transp. Res. Part E Logist. Transp. Rev. 2023, 172, 103070. [Google Scholar] [CrossRef]
- Mogire, E.; Kilbourn, P.; Luke, R. Electric Vehicles in Last-Mile Delivery: A Bibliometric Review. World Electr. Veh. J. 2025, 16, 52. [Google Scholar] [CrossRef]
- Oshri, I.; Kotlarsky, J.; Willcocks, L.P. The Handbook of Global Outsourcing and Offshoring; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Tsai, C.-A.; Ho, T.-H.; Lin, J.-S.; Tu, C.-C.; Chang, C.-W. Model for Evaluating Outsourcing Logistics Companies in the COVID-19 Pandemic. Logistics 2021, 5, 64. [Google Scholar] [CrossRef]
- Akhtar, M. Logistics Services Outsourcing Decision Making: A Literature Review and Research Agenda. Int. J. Prod. Manag. Eng. 2023, 11, 73–88. [Google Scholar] [CrossRef]
- Charles, M.; Ochieng, S.B. Strategic Outsourcing and Firm Performance: A Review of Literature. Int. J. Soc. Sci. Humanit. Res. 2023, 1, 20–29. [Google Scholar] [CrossRef]
- Zäpfel, G.; Bögl, M. Multi-Period Vehicle Routing and Crew Scheduling with Outsourcing Options. Int. J. Prod. Econ. 2008, 113, 980–996. [Google Scholar] [CrossRef]
- Ülkü, M.A.; Bookbinder, J.H. Optimal Quoting of Delivery Time by a Third Party Logistics Provider: The Impact of Shipment Consolidation and Temporal Pricing Schemes. Eur. J. Oper. Res. 2012, 221, 110–117. [Google Scholar] [CrossRef]
- Chaabouni, F.; Dhiaf, M.M. Logistics Outsourcing Relationships: Conceptual Model. In Proceedings of the 2013 International Conference on Advanced Logistics and Transport (ICALT), Sousse, Tunisia, 29–31 May 2013; pp. 458–463. [Google Scholar] [CrossRef]
- Gevaers, R.; Van de Voorde, E.; Vanelslander, T. Cost Modelling and Simulation of Last-Mile Characteristics in an Innovative B2C Supply Chain Environment with Implications on Urban Areas and Cities. Procedia Soc. Behav. Sci. 2014, 125, 398–411. [Google Scholar] [CrossRef]
- Ko, S.Y.; Cho, S.W.; Lee, C. Pricing and Collaboration in Last Mile Delivery Services. Sustainability 2018, 10, 4560. [Google Scholar] [CrossRef]
- Roy, J.; Pamučar, D.; Kar, S. Evaluation and Selection of Third Party Logistics Provider under Sustainability Perspectives: An Interval Valued Fuzzy-Rough Approach. Ann. Oper. Res. 2020, 293, 669–714. [Google Scholar] [CrossRef]
- Krstić, M.D.; Tadić, S.R.; Brnjac, N.; Zečević, S. Intermodal Terminal Handling Equipment Selection Using a Fuzzy Multi-Criteria Decision-Making Model. Promet–Traffic Transp. 2019, 31, 89–100. [Google Scholar] [CrossRef]
- Kosovac, A.; Muharemović, E. Pickup and Delivery Costs—A Proposed Outsourcing Model Based on the Number of Stops. J. Appl. Eng. Sci. 2021, 19, 270–274. [Google Scholar] [CrossRef]
- Kosovac, A.; Muharemović, E.; Trubint, N. A Cost Calculation Model for Outsourcing in Parcel Pick-up and Delivery by Commercial Postal Services Operators. TEM J. 2020, 9, 216–220. [Google Scholar] [CrossRef]
- Su, E.; Qin, H.; Li, J.; Pan, K. An Exact Algorithm for the Pickup and Delivery Problem with Crowdsourced Bids and Transshipment. Transp. Res. Part B Methodol. 2023, 177, 102831. [Google Scholar] [CrossRef]
- Alnaggar, A.; Gzara, F.; Bookbinder, J.H. Compensation Guarantees in Crowdsourced Delivery: Impact on Platform and Driver Welfare. Omega 2024, 122, 102965. [Google Scholar] [CrossRef]
- Schur, R.; Winheller, K. Optimizing Last-Mile Delivery: A Dynamic Compensation Strategy for Occasional Drivers. OR Spectr. 2024. [Google Scholar] [CrossRef]
- Dong, C.; Huang, Q.; Pan, Y.; Ng, C.T.; Liu, R. Logistics Outsourcing: Effects of Greenwashing and Blockchain Technology. Transp. Res. Part E Logist. Transp. Rev. 2023, 170, 103015. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, R.; Ding, J.Y.; Yang, Y.; You, K. Localized Package Shipment with Partial Outsourcing: An Exact Optimization Approach for Chinese Courier Companies. Transp. Res. Part E Logist. Transp. Rev. 2025, 194, 103901. [Google Scholar] [CrossRef]
- Taniguchi, E.; Thompson, R.G.; Qureshi, A.G. Modelling City Logistics Using Recent Innovative Technologies. Transp. Res. Procedia 2020, 46, 3–12. [Google Scholar] [CrossRef]
- Seghezzi, A.; Siragusa, C.; Mangiaracina, R. Parcel Lockers vs. Home Delivery: A Model to Compare Last-Mile Delivery Cost in Urban and Rural Areas. Int. J. Phys. Distrib. Logist. Manag. 2022, 52, 213–237. [Google Scholar] [CrossRef]
- Qi, F.; Zhou, G. An SLA-Based Performance Monitoring Mechanism for 3PL Business Process. J. Residuals Sci. Technol. 2016, 13, 51.1–51.6. [Google Scholar]
- Selviaridis, K.; Norrman, A. Performance-Based Contracting for Advanced Logistics Services. Int. J. Phys. Distrib. Logist. Manag. 2015, 45, 592–617. [Google Scholar] [CrossRef]
| Reference | Approach Type | Main Parameters Used | Limitations |
|---|---|---|---|
| [17] | Multi-period vehicle and driver scheduling with outsourcing option | Number of shipments, time windows, driver pool, tour duration, vehicle type, and outsourcing cost per route | No distinction by delivery point type or powertrain; focus on resource scheduling over multidimensional cost structure |
| [18] | Profit-maximizing model for delivery-time quoting and temporal pricing | Shipment arrival rate, consolidation cycle length, price- and time-sensitivity, and delivery-time guarantees | Focus on pricing dynamics; no cost breakdown by delivery phase or service-level dimensions (e.g., vehicle type, delivery point) |
| [19] | Conceptual framework for outsourcing relationships | Trust, commitment, communication, satisfaction, and reputation | No quantitative modeling; not operationalized for cost estimation |
| [20] | Last-mile cost simulation model based on time, distance, and urban delivery characteristics | Stops per route, distance, time windows, reverse logistics, delivery type, vehicle type, area density, ICT level, and packaging | No explicit outsourcing mechanism; cost drivers treated independently; lacks service quality and contractual dimensions |
| [21] | Multi-objective model combining pricing optimization and collaborative delivery planning | Delivery price, delivery demand (price-sensitive), market density, last-mile delivery time, profit, and region-based collaboration structure | Focus is on profit maximization and collaboration; lacks shipment-level granularity (e.g., parcel/pallet), vehicle/powertrain categorization, or service quality factor |
| [22] | Hybrid fuzzy–rough MCDM model for sustainable 3PL selection | Economic indicators (cost, delivery performance), environmental (emissions, energy), and social (flexibility, reputation) | Strategic-level model; not designed for detailed operational cost modeling or route-level outsourcing scenarios |
| [23] | Fuzzy MCDM model for selecting terminal handling equipment | Economic (purchase cost, operating cost), technical (lifting capacity, efficiency), and technological (automation level and energy source) criteria | Focused on infrastructure and equipment selection; not applicable to operational-level outsourcing or service-phase cost modeling |
| [24] | Stop-based cost model for pickup and delivery outsourcing | Number of stops by shipment type (parcel/pallet), vehicle category (N1–N3), and unit cost per stop | No integration of powertrain, delivery point type, or service quality; assumes uniform stop cost structure |
| [25] | Distance-based cost model for pickup and delivery outsourcing | Vehicle category (N1–N3), cost coefficient per km, route length (km), and number of routes | Does not include service phase distinction, delivery point type, or quality/performance criteria in the cost function |
| Reference | Approach Type | Main Parameters Used | Limitations |
|---|---|---|---|
| [26] | MILP model for the pickup and delivery problem with outsourcing and transshipment | Shipment demand, contractor bids, time windows, transshipment point locations, and routing constraints | Cost function is tightly coupled to assignment and bidding; lacks service-level granularity (e.g., quality, delivery point type) |
| [27] | Behavioral-economic model for evaluating guaranteed minimum compensation in crowdsourced delivery | Number of completed deliveries, idle time, compensation type (flat vs. guaranteed), and the platform revenue | Focus on driver incentives and platform economics; no modeling of delivery phases, routing, or cost transparency per service component |
| [28] | Real-time dynamic pricing and driver compensation model for last-mile delivery | Number of parcels, engagement duration, expected waiting time, delivery windows, and regional demand level | Focused on dynamic labor pricing; does not consider delivery point type, vehicle characteristics, or cost allocation across delivery phases |
| [29] | Behavioral and game-theoretic model integrating greenwashing and blockchain in logistics outsourcing | Sustainability effort level, service pricing, trust level, transparency (blockchain adoption), and logistics provider type | Strategic focus; lacks operational-level cost modeling or service-specific delivery parameters (e.g., vehicle, shipment type) |
| [30] | LPSPO (Localized Parcel Service with Partial Outsourcing) model for urban delivery | Delivery zones, vehicle type, parcel volume, partial outsourcing ratio, and routing constraints | Model is context-specific (urban Belgrade); not generalized for national CEP networks or cost transparency by delivery phase or quality factor |
| Symbol | Description | Typical Elements |
|---|---|---|
| Route/operation | ||
| Stage of service | PCK(Pick-up), DEL (Delivery), | |
| Unit type | PAR (Parcel), PAL (Pallet), | |
| Vehicle category | N1 ≤ 3.5 t, N2 > 3.5 ≤ 12 t, N3 > 12 t | |
| Powertrain | ||
| Pickup/Delivery point | ||
| Observation period | ||
| Combination of unit type and service stage |
| Parameter | Description |
|---|---|
| Number of units u, in phase s, on route r | |
| Number of units of type u, in phase s, at point type j, route r, time t | |
| (e.g., EUR per parcel pickup) | |
| , estimated via internal TCO or equivalent accounting models | |
| Cost correction coefficient for vehicle category i, powertrain p, unit type u, and service stage s; expressed as a ratio to the reference configuration (e.g., N1/ICE) | |
| ; values may be derived from operational workload data or route-specific effort levels | |
| Quality adjustment factor for unit type u and service phase s, reflecting SLA compliance (bonus/malus) | |
| Total adjusted cost per route, unit type, phase, vehicle type, and point |
| Parameter | ||||
|---|---|---|---|---|
| 230 | 218 | 194 | 166 | |
| 1452 | 1370 | 1504 | 1778 | |
| 8 | 5 | 16 | 3 | |
| 53 | 46 | 52 | 60 |
| Distribution of Parcels and Pallets by Point Type at Pickup | January |
| HPD PACK | 98.00% |
| HPD PAL | 100.00% |
| PL PACK | 1.00% |
| PPP PACK | 1.00% |
| Distribution of Parcels and Pallets by Point Type at Delivery | |
| HPD PACK | 82.0% |
| HPD PAL | 100.0% |
| PL PACK | 8.0% |
| PPP PACK | 10.0% |
| Pick/Delivery Point | Correction Coefficient for Parcels in Pickup and Delivery | Explanation |
|---|---|---|
| HPD | 1.00 | Reference point, most expensive due to home delivery. |
| PL | 0.8 | Parcel locker—automated, lower pickup and delivery cost [31,32]. |
| PPP | 0.9 | Partner Pickup Point—lower workload, but involves human factor. |
| Calculation Model | ||||
|---|---|---|---|---|
| Costs according to the multidimensional model (EUR) | 2006.85 | 1862.85 | 2052.17 | 2281.12 |
| Costs according to the current model (EUR) | 2154.67 | 2001.23 | 220.33 | 2452.70 |
| Difference (EUR) | 147.82 | 138.37 | 155.16 | 171.58 |
| Difference (%) | 6.86% | 6.91% | 7.03% | 7.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muharemović, E.; Kosovac, A.; Begović, M.; Tadić, S.; Krstić, M. Cost Modeling for Pickup and Delivery Outsourcing in CEP Operations: A Multidimensional Approach. Logistics 2025, 9, 96. https://doi.org/10.3390/logistics9030096
Muharemović E, Kosovac A, Begović M, Tadić S, Krstić M. Cost Modeling for Pickup and Delivery Outsourcing in CEP Operations: A Multidimensional Approach. Logistics. 2025; 9(3):96. https://doi.org/10.3390/logistics9030096
Chicago/Turabian StyleMuharemović, Ermin, Amel Kosovac, Muhamed Begović, Snežana Tadić, and Mladen Krstić. 2025. "Cost Modeling for Pickup and Delivery Outsourcing in CEP Operations: A Multidimensional Approach" Logistics 9, no. 3: 96. https://doi.org/10.3390/logistics9030096
APA StyleMuharemović, E., Kosovac, A., Begović, M., Tadić, S., & Krstić, M. (2025). Cost Modeling for Pickup and Delivery Outsourcing in CEP Operations: A Multidimensional Approach. Logistics, 9(3), 96. https://doi.org/10.3390/logistics9030096








