Managing Home Healthcare System Using Capacitated Vehicle Routing Problem with Time Windows: A Case Study in Chiang Mai, Thailand
Abstract
1. Introduction
2. Mathematical Formulation
- Indices:0 The starting node and the end node of all vehicles, here called the centerThe customerThe vehicle
- Parameters:The travel time from customer to customerThe available time for customerThe end time for customerThe service time for customerThe customer demandThe capacity of all vehiclesA sufficiently large numberThe maximum working hours of the caregiver.
- Variables:equal to 1 if the vehicle starts from the center to customer ; otherwise, 0equal to 1 if vehicle travels from customer to customer ; otherwise, 0equal to 1 if customer is the last customer visited in vehicle ; otherwise, 0Real variables for subtour eliminationThe starting time for customer which is equal to the available time if the vehicle arrives early at the node and is equal to the arrival time otherwiseThe completion time of the vehicleis the non-negative integer and is real
- Mathematical model
3. Algorithms
| Main algorithm: |
| , the . . Phase 1: Construct an initial solution , set the sequence set of customers in all vehicles to null . , and use earliest due date scheduling algorithms [41]). This problem is infeasible. End End Phase 2: Improve the solution . . . ). and set it to the new solution. Find the objective value of the new solution. Replace the best solution with the new solution, if the objective value of a new solution is better than the current best solution. . End |
3.1. Phase 1 (Initialization)
| Function: Construct a customer sequence |
| , the, ). ). and a customer is assigned to a vehicle . . Alternately choose between actions: in each iteration. . End , . . End |
3.2. Phase 2 (Improvement of the Solution)
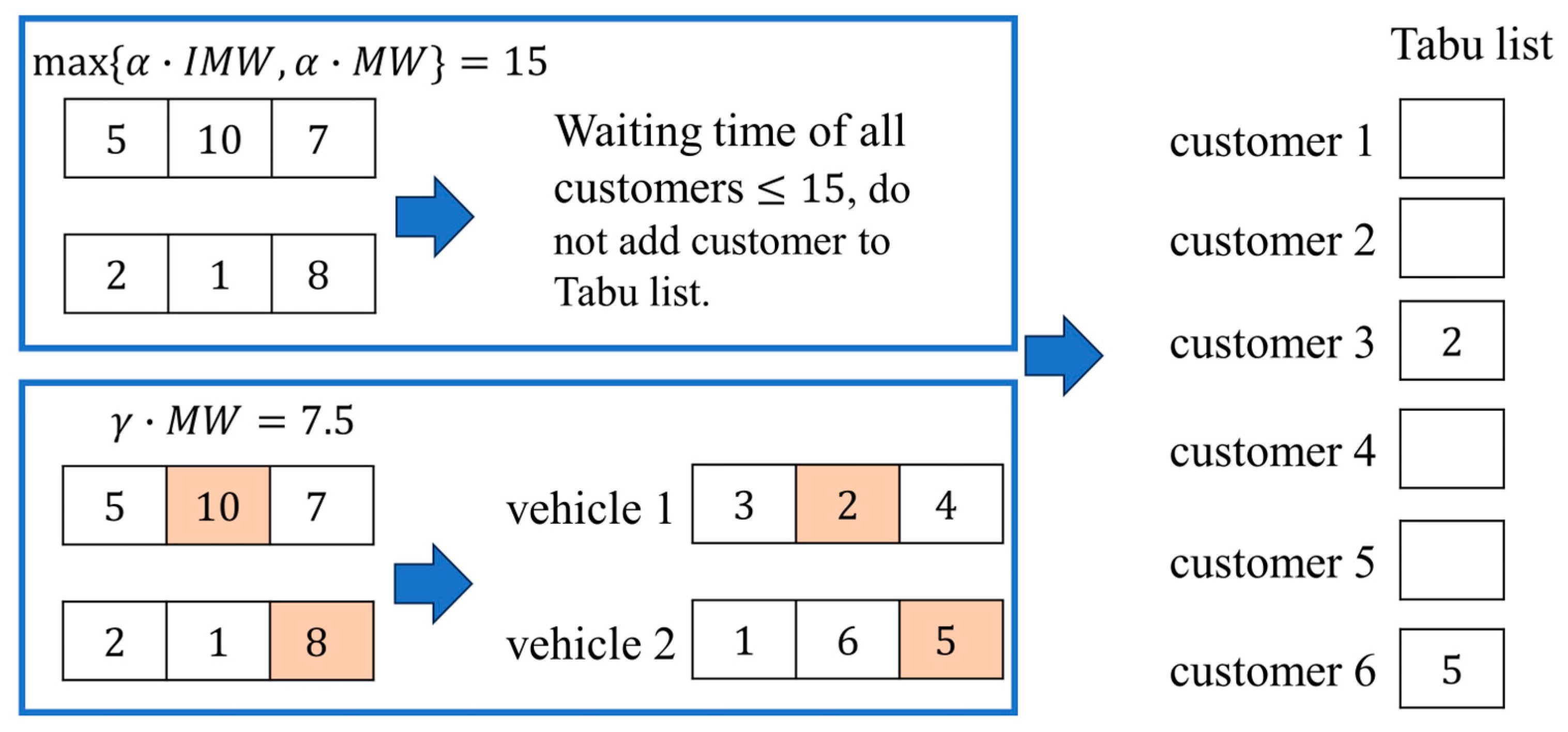
| Function: Tabu list |
| , and . . . End Check the waiting times of all customers. . End End |
| Function: Remove customers |
| ). ). . End . . . End . . . . End |
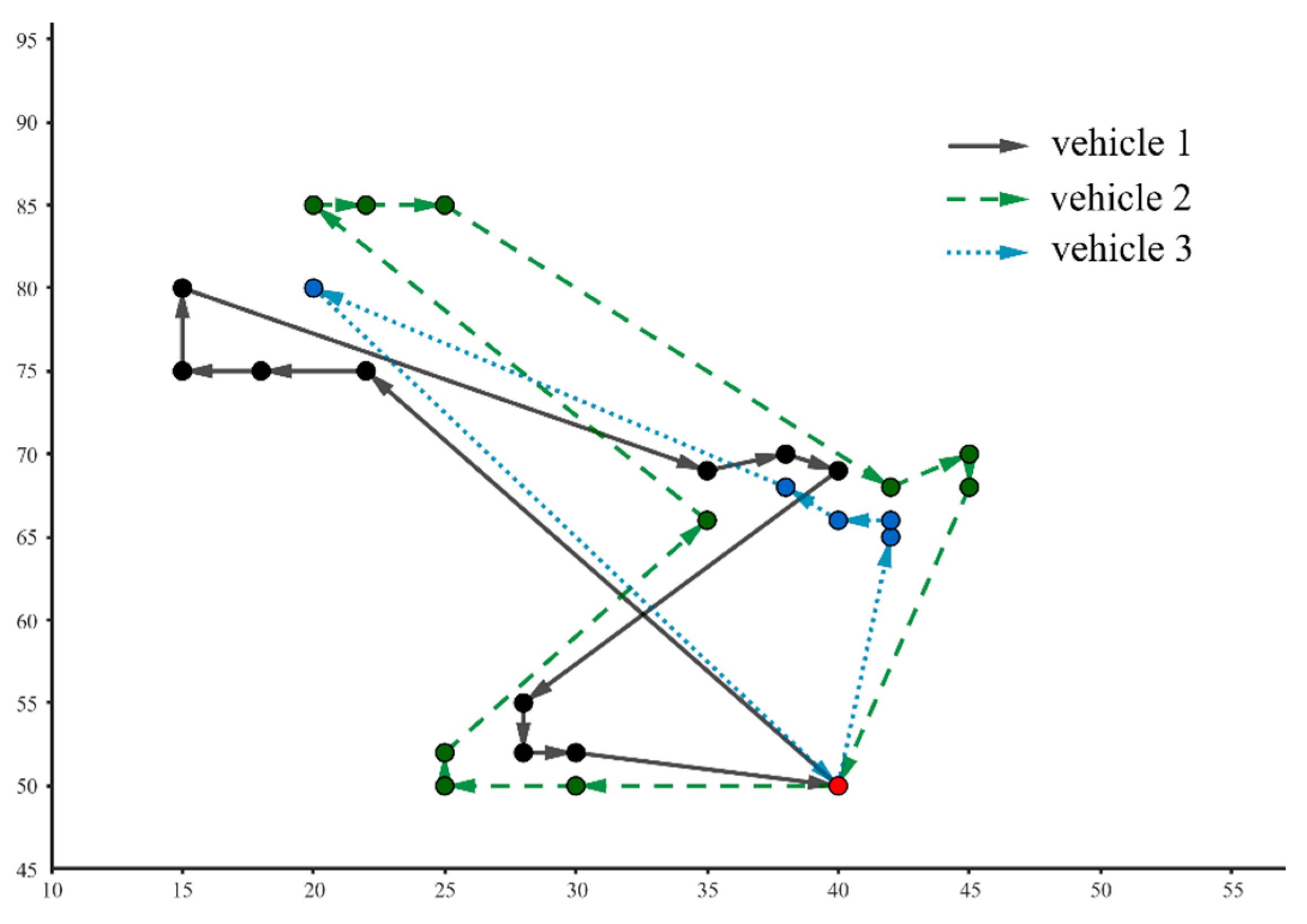
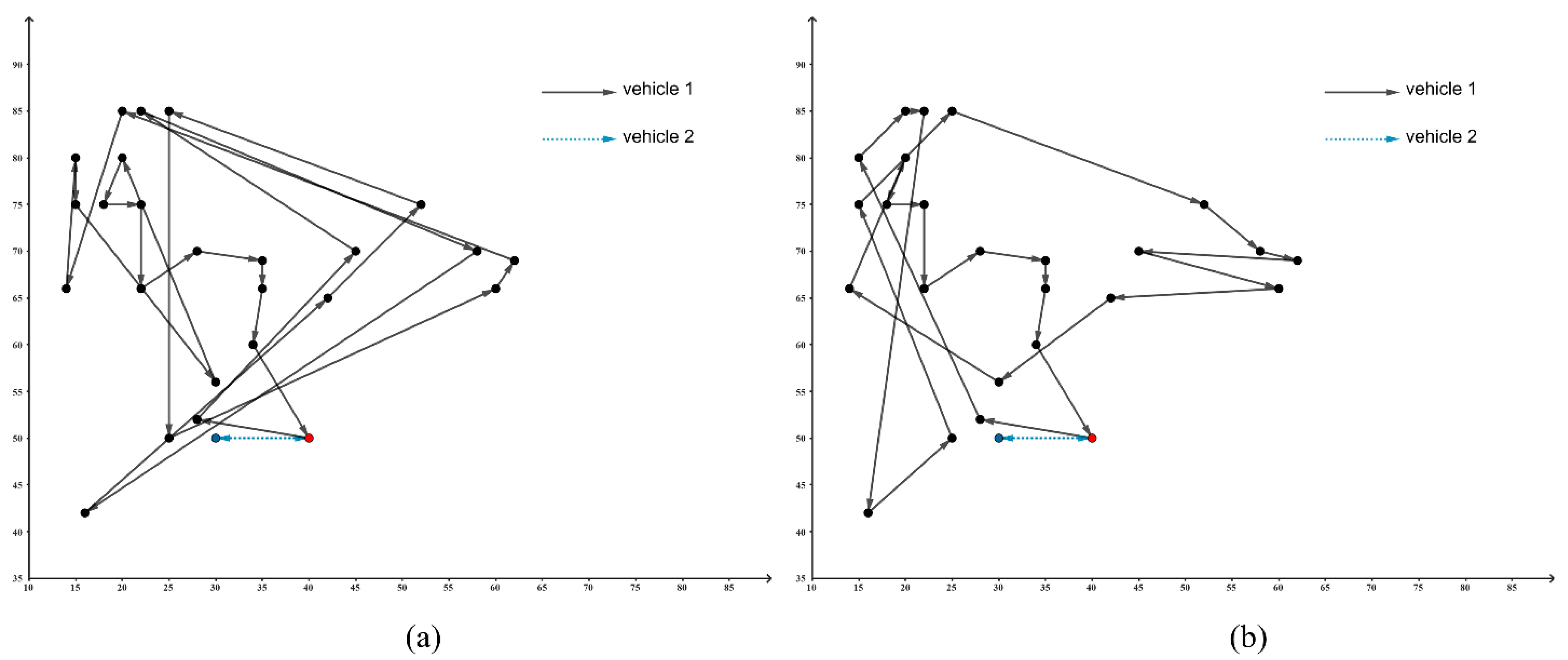
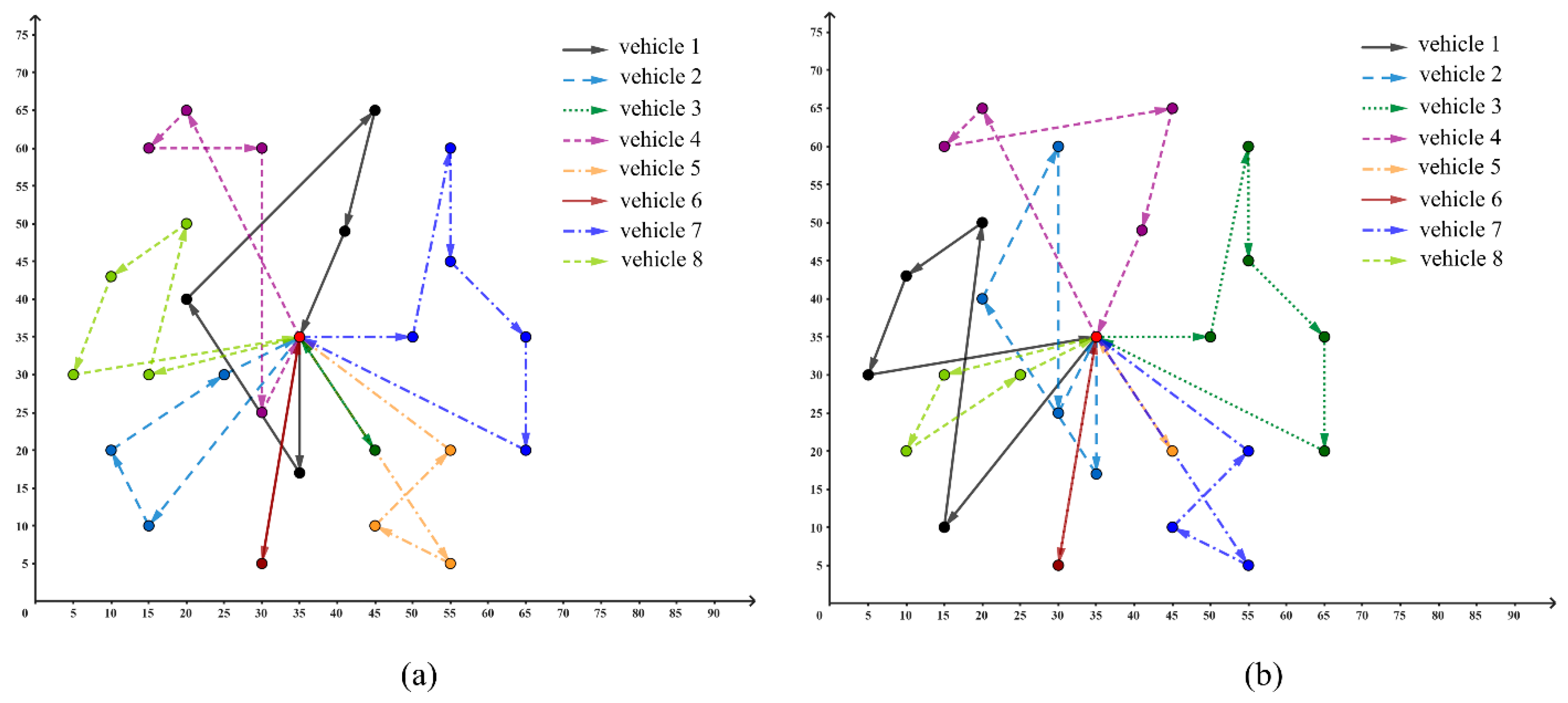
4. Simulation Results and Discussion
5. Real-World Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wy, J.; Kim, B.-I.; Kim, S. The rollon–rolloff waste collection vehicle routing problem with time windows. Eur. J. Oper. Res. 2013, 224, 466–476. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Ma, L.; Zhang, Z.; Liu, Y. A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows. Inform. Sci. 2019, 490, 166–190. [Google Scholar] [CrossRef]
- Huang, M.; Liu, M.; Kuang, H. Vehicle routing problem for fresh products distribution considering customer satisfaction through adaptive large neighborhood search. Comput. Ind. Eng. 2024, 190, 110022. [Google Scholar] [CrossRef]
- Gómez S., C.G.; Cruz-Reyes, L.; González B., J.J.; Fraire H., H.J.; Pazos R., R.A.; Martínez P., J.J. Ant colony system with characterization-based heuristics for a bottled-products distribution logistics system. J. Comput. Appl. Math. 2014, 259 Pt B, 965–977. [Google Scholar] [CrossRef]
- Mamoun, K.A.; Hammadi, L.; Ballouti, A.E.; Novaes, A.G.N.; De Cursi, E.S. Vehicle routing optimization algorithms for pharmaceutical supply chain: A systematic comparison. Transp. Telecommun. J. 2024, 25, 161–173. [Google Scholar] [CrossRef]
- Somar, S.; Urazel, B.; Sahin, Y.B. A modified metaheuristic algorithm for a home health care routing problem with health team skill levels. Appl. Soft Comput. 2023, 148, 110912. [Google Scholar] [CrossRef]
- United Nations Population Fund, Ageing. Available online: https://www.unfpa.org/ageing#readmore-expand (accessed on 29 November 2024).
- World Health Organization, Ageing and Health. Available online: https://www.who.int/news-room/fact-sheets/detail/ageing-and-health (accessed on 28 November 2024).
- Population Reference Bureau, 2024 World Population Data Sheet. Available online: https://2024-wpds.prb.org/wp-content/uploads/2024/09/2024-World-Population-Data-Sheet-Booklet.pdf (accessed on 12 December 2024).
- Eurostat, Population Structure and Ageing. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Population_structure_and_ageing (accessed on 10 December 2024).
- Economic and Social Commission for Asia and the Pacific (ESCAP), Demographic Changes Asia and the Pacific: Population Ageing Data. Available online: https://www.population-trends-asiapacific.org/data (accessed on 10 December 2024).
- United Nations, Thailand Economic Focus: Demographic Change in Thailand: How Planners Can Prepare for the Future. Available online: https://thailand.un.org/en/96303-thailand-economic-focus-demographic-change-thailand-how-planners-can-prepare-future (accessed on 29 November 2024).
- Liu, R.; Xie, X.; Augusto, V.; Rodriguez, C. Heuristic algorithms for a vehicle routing problem with simultaneous delivery and pickup and time windows in home health care. Eur. J. Oper. Res. 2013, 230, 475–486. [Google Scholar] [CrossRef]
- Haddadene, S.R.A.; Labadie, N.; Prodhon, C. A GRASP × ILS for the vehicle routing problem with time windows, synchronization and precedence constraints. Expert Syst. Appl. 2016, 66, 274–294. [Google Scholar] [CrossRef]
- Liu, R.; Yuan, B.; Jiang, Z. A branch and price algorithm for the home caregiver scheduling and routing problem with stochastic travel and service times. Flex. Serv. Manuf. J. 2019, 31, 989–1011. [Google Scholar] [CrossRef]
- Euchi, J.; Zidi, S.; Laouamer, L. A Hybrid Approach to Solve the Vehicle Routing Problem with Time Windows and Synchronized Visits In-Home Health Care. Arab. J. Sci. Eng. 2020, 45, 10637–10652. [Google Scholar] [CrossRef]
- Chaieb, M.; Sassi, D.B. Measuring and evaluating the Home Health Care Scheduling Problem. Appl. Soft Comput. 2021, 113, 107957. [Google Scholar] [CrossRef]
- Makboul, S.; Kharraja, S.; Abbassi, A.; Alaoui, A.E.H. A multiobjective approach for weekly Green Home Health Care routing and scheduling problem with care continuity and synchronized services. Oper. Res. Perspect. 2024, 12, 100302. [Google Scholar] [CrossRef]
- Baños, R.; Ortega, J.; Gil, C.; Fernández, A.; de Toro, F. A Simulated Annealing-based parallel multi-objective approach to vehicle routing problems with time windows. Expert Syst. Appl. 2013, 40, 1696–1707. [Google Scholar] [CrossRef]
- Hifi, M.; Wu, L. A hybrid metaheuristic for the Vehicle Routing Problem with Time Windows. In Proceedings of the International Conference on Control, Decision and Information Technologies (CoDIT), Metz, France, 3–5 November 2014. [Google Scholar] [CrossRef]
- François, V.; Arda, Y.; Crama, Y. Adaptive Large Neighborhood Search for Multitrip Vehicle Routing with Time Windows. Transp. Sci. 2019, 53, 1706–1730. [Google Scholar] [CrossRef]
- Ahmed, Z.H.; Maleki, F.; Yousefikhoshbakht, M.; Haron, H. Solving the vehicle routing problem with time windows using modified football game algorithm. Egypt. Inform. J. 2023, 24, 100403. [Google Scholar] [CrossRef]
- Saksuriya, P.; Likasiri, C. Vehicle Routing Problem with Time Windows to Minimize Total Completion Time in Home Healthcare Systems. Mathematics 2023, 11, 4846. [Google Scholar] [CrossRef]
- Yue, B.; Yang, J.; Ma, J.; Shi, J.; Shangguan, L. An improved sequential insertion algorithm and tabu search to vehicle routing problem with time windows. RAIRO Oper. Res. 2024, 58, 1979–1999. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Kallehauge, B.; Larsen, J.; Madsen, O.B.G.; Solomon, M.M. Vehicle Routing Problem with Time Windows. In Column Generation; Desaulniers, G., Desrosiers, J., Solomon, M.M., Eds.; Springer: Boston, MA, USA, 2005; pp. 67–98. [Google Scholar]
- Bräysy, O.; Gendreau, M. Vehicle Routing Problem with Time Windows, Part I: Route Construction and Local Search Algorithms. Transp. Sci. 2005, 39, 104–118. [Google Scholar] [CrossRef]
- Bräysy, O.; Gendreau, M. Vehicle Routing Problem with Time Windows, Part II: Metaheuristics. Transp. Sci. 2005, 39, 119–139. [Google Scholar] [CrossRef]
- Gehring, H.; Homberger, J. A Parallel Hybrid Evolutionary Metaheuristic for the Vehicle Routing Problem with Time Windows. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=e41b80d075429403f569980d278f6d4f91da2594 (accessed on 26 May 2025).
- Zong, Z.; Tong, X.; Zheng, M.; Li, Y. Reinforcement Learning for Solving Multiple Vehicle Routing Problem with Time Window. ACM Trans. Intell. Syst. Technol. 2024, 15, 32. [Google Scholar] [CrossRef]
- Bent, R.; Hentenryck, P.V. A two-stage hybrid algorithm for pickup and delivery vehicle routing problems with time windows. Comput. Oper. Res. 2006, 33, 875–893. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.G.; Gendreau, M.; Prins, C. A hybrid genetic algorithm with adaptive diversity management for a large class of vehicle routing problems with time-windows. Comput. Oper. Res. 2013, 40, 475–489. [Google Scholar] [CrossRef]
- Gmira, M.; Gendreau, M.; Lodi, A.; Potvin, J.-Y. Tabu search for the time-dependent vehicle routing problem with time windows on a road network. Eur. J. Oper. Res. 2021, 288, 129–140. [Google Scholar] [CrossRef]
- Wang, H.-F.; Chen, Y.-Y. A genetic algorithm for the simultaneous delivery and pickup problems with time window. Comput. Ind. Eng. 2012, 62, 84–95. [Google Scholar] [CrossRef]
- Srivastava, G.; Singh, A.; Mallipeddi, R. NSGA-II with objective-specific variation operators for multiobjective vehicle routing problem with time windows. Expert Syst. Appl. 2021, 176, 114779. [Google Scholar] [CrossRef]
- Melián-Batista, B.; Santiago, A.D.; AngelBello, F.; Alvarez, A. A bi-objective vehicle routing problem with time windows: A real case in Tenerife. Appl. Soft Comput. 2014, 17, 140–152. [Google Scholar] [CrossRef]
- Eydi, A.; Ghasemi-Nezhad, S.A. A bi-objective vehicle routing problem with time windows and multiple demands. Ain Shams Eng. J. 2021, 12, 2617–2630. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Erdelić, T.; Carić, T. Goods Delivery with Electric Vehicles: Electric Vehicle Routing Optimization with Time Windows and Partial or Full Recharge. Energies 2022, 15, 285. [Google Scholar] [CrossRef]
- Luo, T.; Heng, Y.; Xing, L.; Ren, T.; Li, Q.; Qin, H.; Hou, Y.; Wang, K. A Two-Stage Approach for Electric Vehicle Routing Problem with Time Windows and Heterogeneous Recharging Stations. Tsinghua Sci. Technol. 2024, 29, 1300–1322. [Google Scholar] [CrossRef]
- Smith, W.E. Various optimizers for single-stage production. Nav. Res. Logist. Q. 1956, 31, 59–66. [Google Scholar] [CrossRef]
- Department of Medical Services, Home Ward Standard and Guidelines. Available online: https://www.dms.go.th/backend//Content/Content_File/Publication/Attach/25650805113031AM_homeward.pdf (accessed on 26 May 2025). (In Thai).


| VRP on Distribution Problems | |||||
|---|---|---|---|---|---|
| Model | Objective | Algorithms | Benchmarks/Size | Applications/Size | Ref. |
| Roll-in–roll-off VRPTW | Minimize the number of vehicles and their total route time | Large neighborhood search | N/A | Waste collection in US/6-291 | [1] |
| VRPTW | Minimize the number of vehicles and their total route time | Ant colony | Solomon/100 | N/A | [4] |
| VRPTW | Minimize the total travel distance | Scatter search | Solomon/25–100 | Company in Tenerife, Spain/N/A | [36] |
| Multi-objective VRP with flexible time windows | Minimize the total travel cost and total fixed vehicle costs | Ant colony | Solomon/100 | Vegetable and food distribution in Beilin district, Xi’an, China/16 | [2] |
| VRPTW | Minimize the total travel cost and maximize the total quality of service | Hybrid genetic algorithm and simulated annealing | GHHC instances/4–75 | N/A | [6] |
| VRP for fresh products distribution considering customer satisfaction | Minimize the total travel cost and total fixed vehicle costs | Large neighborhood search | Solomon/25–50 | Fresh food distribution in Beijing/25 | [3] |
| VRPTW | Minimize the total travel distance | Exact algorithm and several heuristics | N/A | Pharmaceutical distribution in Morocco/12 | [5] |
| VRPTW | Minimize the total completion time | Modified k-means and local search | Solomon/100 | HHC in Chiang Mai/400 | [23] |
| VRPTW | Minimize the total travel distance | Reinforcement learning | Homberger/1000 | Online operation system of Hitachi in Guangzhou/500–700 | [30] |
| VRP on HHC problems | |||||
| Model | Objective | Algorithms | Benchmarks/Size | Applications/Size | Ref. |
| VRP with simultaneous delivery and pickup and time windows | Minimize the total travel cost | Genetic algorithm and tabu search | Solomon and Homberger/100–400 | N/A | [13] |
| VRPTW synchronization and precedence constraints | Minimize the total travel time and the sum of non-preferences | Hybrid greedy and local search | HHC instances/18–73 | N/A | [14] |
| Multiple depot VRP with stochastic travel and service time | Minimize the total travel cost | Branch-and-price algorithm | Instances generated by the authors/30–50 | N/A | [15] |
| VRPTW with synchronization visits | Minimize the total travel cost | Ant colony | Bredström and Rönnqvist’s instances/20–80 | N/A | [16] |
| VRP with simultaneous delivery and pickup and time windows | Minimize the total travel cost | K-means and tabu search | Solomon/25 | N/A | [17] |
| VRP/MILP | Minimize the total travel distance and CO2 emissions/maximize to ensure a fair workload | Genetic algorithm | TSPTW instances/200 | N/A | [18] |
| Works related to time windows | |||||
| Model | Objective | Algorithms | Benchmarks/Size | Applications/Size | Ref. |
| VRPTW | Minimize the total travel time or distance | Development of saving algorithm, nearest neighbor algorithm, insertion algorithm, and sweep algorithm | Solomon/100 | N/A | [25] |
| VRPTW | Minimize the number of vehicles and total travel distance | Hybrid evolutionary and tabu search | Solomon and Homberger/100–1000 | N/A | [29] |
| VRPTW | Minimize the total travel time or distance | Route construction and local search | Solomon/100 | N/A | [27] |
| VRPTW | Minimize the total travel time or distance | Tabu search and genetic algorithm | Solomon/100 | N/A | [28] |
| VRPTW | Minimize the number of vehicles and total travel distance | Branch-and-bound and column generation | Solomon/25–100 | N/A | [26] |
| PDPTW | Minimize the number of vehicles and total travel distance | Simulated annealing and large neighborhood search | PDPTW instances/100–600 | N/A | [31] |
| SDPPTW | Minimize the total travel cost | Genetic algorithm | SDPPTW instances (revised from Solomon)/25–100 | N/A | [34] |
| MOVRPTW | Minimize the total travel distance and distance imbalance among routes | Simulated annealing | Solomon/100 | N/A | [19] |
| VRPTW, PVRPTW, MDVRPTW, SDVRPTW | Minimize the total travel distance | Hybrid genetic search and adaptive diversity control algorithm | Solomon, Homberger, PVRPTW, MDVRPTW, and SDVRPTW instances/100–1000 | N/A | [32] |
| VRPTW | Minimize the number of vehicles and total travel distance | Hybrid ant colony and large neighborhood search | Solomon and Homberger/100–200 | N/A | [20] |
| Electric VRPTW | Minimize the total travel distance | Hybrid variable neighborhood search and tabu search | Extended Solomon/100 | N/A | [38] |
| Multi-trip VRPTW | Minimize the total duration and travel time | Adaptive large neighborhood search | Solomon/100 | N/A | [21] |
| MOVRPTW | Minimize the total travel cost and maximize customers’ demand satisfaction | Non-dominated sorting genetic algorithm | Solomon/25–100 | N/A | [37] |
| Time-dependent VRPTW | Minimize the total travel time | Tabu search heuristic | NEWLET/50–200 | N/A | [33] |
| MOVRPTW | Minimize the number of vehicles, total travel distance, total waiting time, and total delay time | Non-dominated sorting genetic algorithm | MOVRPTW instances/50–250 | N/A | [35] |
| Electric VRPTW | Minimize the total travel distance | Large neighborhood search | Extended Solomon/100 | N/A | [39] |
| VRPTW | Minimize the total travel distance | Modified football game | Solomon/100 | N/A | [22] |
| Electric VRPTW | Minimize the total travel distance and total recharging cost | Local search and dynamic programming | Solomon and Extended Solomon/100 | N/A | [40] |
| VRPTW | Minimize the total travel distance | Tabu search and variable neighborhood search | Solomon/25–100 | N/A | [24] |
| Problem | Solutions from the VRPTW-CT Model via Solver | Solutions from the Proposed Algorithm | %Gap | ||||
|---|---|---|---|---|---|---|---|
| Number of Vehicles | Total Travel Time | Total Completion Time | Number of Vehicles | Total Travel Time | Total Completion Time | ||
| C101 | 3 | 295.06 | 2624.01 * | 3 | 295.06 | 2624.01 | 0.00 |
| C102 | 3 | 239.50 | 2506.20 | 3 | 254.67 | 2521.30 | 0.60 |
| C103 | 3 | 271.20 | 2527.80 | 3 | 262.62 | 2518.73 | −0.36 |
| C104 | 3 | 293.50 | 2559.50 | 3 | 299.03 | 2556.95 | −0.10 |
| C105 | 3 | 275.10 | 2530.20 * | 3 | 286.02 | 2537.28 | 0.26 |
| C106 | 3 | 295.06 | 2630.01 * | 3 | 295.06 | 2630.01 | 0.00 |
| C107 | 3 | 236.90 | 2490.70 | 3 | 194.77 | 2444.80 | −1.84 |
| C108 | 3 | 239.30 | 2489.50 | 3 | 215.80 | 2465.80 | −0.95 |
| C109 | 3 | 224.90 | 2474.90 | 3 | 200.22 | 2450.20 | −1.00 |
| C201 | 2 | 356.14 | 3195.27 * | 2 | 328.90 | 3215.40 | 0.63 |
| C202 | 1 | 305.31 | 2989.41 * | 1 | 323.92 | 2989.41 | 0.00 |
| C203 | 2 | 516.12 | 3099.41 * | 2 | 362.45 | 3099.41 | 0.00 |
| C204 | 1 | 570.00 | 2988.60 * | 1 | 300.35 | 2988.60 | 0.00 |
| C205 | 1 | 326.90 | 3005.27 * | 1 | 336.80 | 3005.27 | 0.00 |
| C206 | 1 | 335.58 | 2989.68 * | 1 | 336.04 | 2989.68 | 0.00 |
| C207 | 1 | 299.20 | 2824.70 * | 1 | 294.65 | 2837.80 | 0.46 |
| C208 | 1 | 347.19 | 2845.27 * | 1 | 336.80 | 2845.27 | 0.00 |
| R101 | 8 | 685.95 | 1295.01 * | 8 | 708.07 | 1295.01 | 0.00 |
| R102 | 7 | 741.90 | 1188.70 | 7 | 786.04 | 1172.70 | −1.35 |
| R103 | 4 | 535.30 | 793.30 | 4 | 545.72 | 837.22 | 5.54 |
| R104 | 4 | 511.80 | 761.80 | 4 | 464.70 | 778.59 | 2.20 |
| R105 | 5 | 560.10 | 930.10 * | 5 | 582.46 | 957.33 | 2.93 |
| R106 | 5 | 627.40 | 877.40 | 5 | 578.48 | 888.46 | 1.26 |
| R107 | 4 | 539.70 | 789.70 | 4 | 504.73 | 764.17 | −3.23 |
| R108 | 4 | 447.40 | 697.70 | 4 | 475.89 | 758.78 | 8.80 |
| R109 | 4 | 469.10 | 762.30 | 4 | 479.48 | 780.93 | 2.44 |
| R110 | 5 | 498.10 | 766.70 | 5 | 514.71 | 783.06 | 2.13 |
| R111 | 5 | 511.80 | 794.50 | 5 | 564.85 | 841.87 | 5.96 |
| R112 | 4 | 426.40 | 691.20 | 4 | 448.78 | 713.65 | 3.25 |
| R201 | 2 | 772.80 | 1345.90 * | 2 | 821.74 | 1348.13 | 0.17 |
| R202 | 2 | 745.00 | 1322.20 | 2 | 726.81 | 1342.54 | 1.54 |
| R203 | 3 | 964.60 | 1341.10 | 1 | 660.82 | 1303.61 | −2.80 |
| R204 | 1 | 635.50 | 885.50 | 1 | 565.63 | 860.54 | −2.82 |
| R205 | 1 | 559.40 | 846.00 * | 1 | 579.24 | 848.02 | 0.24 |
| R206 | 1 | 582.10 | 832.10 | 1 | 533.14 | 830.00 | −0.25 |
| R207 | 1 | 570.10 | 820.10 | 1 | 535.76 | 805.36 | −1.80 |
| R208 | 1 | 525.20 | 775.20 | 1 | 411.98 | 782.54 | 0.95 |
| R209 | 1 | 488.20 | 756.00 | 1 | 484.46 | 738.65 | −2.29 |
| R210 | 2 | 634.40 | 909.50 * | 2 | 744.91 | 1119.00 | 23.03 |
| R211 | 2 | 481.10 | 734.30 | 1 | 466.65 | 724.01 | −1.40 |
| RC101 | 4 | 492.10 | 796.90 * | 4 | 488.48 | 801.65 | 0.60 |
| RC102 | 3 | 369.30 | 629.70 * | 3 | 358.83 | 631.67 | 0.31 |
| RC103 | 4 | 466.70 | 731.10 | 4 | 374.66 | 632.99 | −13.42 |
| RC104 | 4 | 455.70 | 705.70 | 3 | 366.67 | 619.87 | −12.16 |
| RC105 | 4 | 441.50 | 759.10 * | 4 | 495.92 | 811.54 | 6.91 |
| RC106 | 3 | 354.30 | 614.90 * | 3 | 361.62 | 625.37 | 1.70 |
| RC107 | 3 | 305.00 | 566.70 | 3 | 324.19 | 575.86 | 1.62 |
| RC108 | 7 | 580.30 | 831.00 | 3 | 321.86 | 571.86 | −31.18 |
| RC201 | 2 | 813.10 | 1295.30 * | 2 | 739.59 | 1396.00 | 7.77 |
| RC202 | 2 | 641.00 | 934.20 | 2 | 829.55 | 1264.50 | 35.36 |
| RC203 | 1 | 600.20 | 850.20 * | 1 | 570.72 | 878.42 | 3.32 |
| RC204 | 1 | 591.10 | 841.10 | 1 | 462.87 | 852.58 | 1.36 |
| RC205 | 2 | 767.30 | 1314.40 | 2 | 855.80 | 1596.30 | 21.45 |
| RC206 | 1 | 571.50 | 831.70 | 1 | 562.47 | 856.41 | 2.97 |
| RC207 | 2 | 604.00 | 883.90 | 2 | 674.63 | 1106.00 | 25.13 |
| RC208 | 1 | 394.40 | 659.80 | 1 | 394.08 | 673.01 | 2.00 |
| Problem | Number of Vehicle | Total Travel Time | Total Completion Time |
|---|---|---|---|
| C101 | 10 | 828.94 | 9828.94 |
| C102 | 10 | 1308.04 | 10,361.40 |
| C103 | 11 | 1556.45 | 10,629.86 |
| C104 | 10 | 1425.82 | 10,425.82 |
| C105 | 11 | 1598.83 | 10,671.81 |
| C106 | 10 | 932.80 | 9932.80 |
| C107 | 10 | 831.02 | 9831.02 |
| C108 | 11 | 941.44 | 9944.63 |
| C109 | 13 | 1321.20 | 10,337.65 |
| C201 | 3 | 591.56 | 9591.56 |
| C202 | 4 | 1404.67 | 10,614.11 |
| C203 | 4 | 1890.17 | 11,417.00 |
| C204 | 4 | 1783.91 | 10,799.84 |
| C205 | 3 | 608.33 | 9608.33 |
| C206 | 4 | 1235.55 | 10,237.43 |
| C207 | 5 | 1185.40 | 10,197.63 |
| C208 | 4 | 640.25 | 9640.25 |
| R101 | 19 | 1854.85 | 3407.07 |
| R102 | 19 | 2024.31 | 3266.04 |
| R103 | 17 | 1816.90 | 2889.36 |
| R104 | 13 | 1322.29 | 2393.69 |
| R105 | 15 | 1493.63 | 2732.52 |
| R106 | 13 | 1473.01 | 2523.85 |
| R107 | 13 | 1280.12 | 2426.15 |
| R108 | 10 | 1125.96 | 2127.89 |
| R109 | 13 | 1283.96 | 2414.51 |
| R110 | 12 | 1299.70 | 2339.74 |
| R111 | 12 | 1320.35 | 2340.58 |
| R112 | 11 | 1166.59 | 2170.96 |
| R201 | 4 | 1937.61 | 3065.54 |
| R202 | 5 | 1689.47 | 2940.95 |
| R203 | 5 | 1691.89 | 3022.30 |
| R204 | 4 | 1463.51 | 2512.12 |
| R205 | 5 | 1721.71 | 2751.49 |
| R206 | 5 | 1533.32 | 2550.57 |
| R207 | 5 | 1532.94 | 2537.42 |
| R208 | 5 | 1492.52 | 2492.52 |
| R209 | 4 | 1517.72 | 2531.41 |
| R210 | 4 | 1745.09 | 2793.51 |
| R211 | 4 | 1414.35 | 2416.48 |
| RC101 | 18 | 2060.39 | 3389.19 |
| RC102 | 16 | 1866.77 | 2965.84 |
| RC103 | 14 | 1737.67 | 2802.98 |
| RC104 | 14 | 1590.34 | 2591.88 |
| RC105 | 18 | 2060.39 | 3389.19 |
| RC106 | 15 | 1718.74 | 2826.07 |
| RC107 | 14 | 1618.48 | 2643.77 |
| RC108 | 13 | 1603.14 | 2608.84 |
| RC201 | 5 | 2312.12 | 3431.47 |
| RC202 | 5 | 2133.43 | 3214.11 |
| RC203 | 6 | 2004.32 | 3116.71 |
| RC204 | 6 | 1828.10 | 2936.37 |
| RC205 | 5 | 2243.16 | 3391.28 |
| RC206 | 6 | 1981.53 | 3089.99 |
| RC207 | 7 | 2606.09 | 3619.32 |
| RC208 | 4 | 1874.88 | 2891.81 |
| Solution | # Caregiver | Number of Customers per Caregiver | Completion Time Excluding Return Time per Caregiver (Hours) | Travel Time per Caregiver (Hours) | Total Completion time Excluding Return Time (Hours) | Total Completion Time Including Return Time (Hours) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Avg | Min | Max | Avg | Min | Max | Avg | ||||
| [23] | 34 | 8 | 18 | 11.7 | 1.5 | 6.9 | 4.4 | 1.3 | 2.2 | 1.5 | N/A | N/A |
| Obj. 1 | 14 | 12 | 60 | 28.6 | 6.9 | 7.9 | 7.6 | 1.7 | 4.0 | 2.4 | 107.1 | 110.8 |
| Obj. 2 | 14 | 8 | 60 | 28.6 | 7.4 | 7.9 | 7.7 | 1.8 | 4.3 | 2.4 | 107.4 | 110.6 |
| Obj. 3 | 14 | 13 | 60 | 28.6 | 7.4 | 7.8 | 7.6 | 1.7 | 4.0 | 2.3 | 106.6 | 110.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phonin, S.; Likasiri, C.; Pongvuthithum, R.; Chonsiripong, K. Managing Home Healthcare System Using Capacitated Vehicle Routing Problem with Time Windows: A Case Study in Chiang Mai, Thailand. Logistics 2025, 9, 85. https://doi.org/10.3390/logistics9030085
Phonin S, Likasiri C, Pongvuthithum R, Chonsiripong K. Managing Home Healthcare System Using Capacitated Vehicle Routing Problem with Time Windows: A Case Study in Chiang Mai, Thailand. Logistics. 2025; 9(3):85. https://doi.org/10.3390/logistics9030085
Chicago/Turabian StylePhonin, Sirilak, Chulin Likasiri, Radom Pongvuthithum, and Kornphong Chonsiripong. 2025. "Managing Home Healthcare System Using Capacitated Vehicle Routing Problem with Time Windows: A Case Study in Chiang Mai, Thailand" Logistics 9, no. 3: 85. https://doi.org/10.3390/logistics9030085
APA StylePhonin, S., Likasiri, C., Pongvuthithum, R., & Chonsiripong, K. (2025). Managing Home Healthcare System Using Capacitated Vehicle Routing Problem with Time Windows: A Case Study in Chiang Mai, Thailand. Logistics, 9(3), 85. https://doi.org/10.3390/logistics9030085






