Integrated Economic and Environmental Dimensions in the Strategic and Tactical Optimization of Perishable Food Supply Chain: Application to an Ethiopian Real Case
Abstract
1. Introduction
- Explores and optimizes multi-sourcing strategies, enabling supply chains to be more resilient and flexible. This approach helps to mitigate risks associated with supply disruptions and ensures continuous product availability by leveraging multiple suppliers.
- Provides actionable insights for decision makers looking to improve the efficiency and reliability of perishable food supply chains in various contexts. The model is tested and validated through a real case study conducted in Ethiopia, demonstrating its practical applicability.
- Combines strategic and tactical decisions to mitigate the adverse effects of uncertainties in decision-making processes and to assess the impact of incorporating environmental dimension within a multi-sourcing strategy supply chain.
- Offers valuable implications for policymakers, particularly in the areas of food security and supply chain resilience, by showing how advanced optimization techniques can be leveraged to support national and regional food distribution networks.
- Regarding the resolution method, we were obliged to develop an integrated ε-constraint and goal programming approach to address the complexity and large scale of the problem, which arises from its application to a country-level case study. This methodological advancement ensures effective handling of multiple objectives while maintaining computational tractability for large, real-world instances.
2. State of the Art
- We introduce a multi-echelon, multi-product, and multi-period model that emphasizes strategic and tactical levels that have been scarcely explored. This model integrates environmental dimension with previously unaddressed decision-making factors, such as storage across different echelons, capacity constraints, and supplier dependency constraints.
- We explore multi-objective multi-sourcing strategies and analyze their effects on strategic and tactical decisions with an aim to find an optimal solution. This analysis is further expanded by integrating environmental aspects.
3. Materials and Methods
3.1. Problem Statement
3.2. Model Formulation
3.3. Model Constraints
3.3.1. Production and Harvest Constraint
3.3.2. Multi-Sourcing Strategy
3.3.3. Capacity Constraints
3.3.4. Decision Variables for Allocation and Order Quantities
3.3.5. Constraints on the Discount Rate
3.3.6. Material Balance Constraints
3.3.7. Satisfaction of Demand Requirements
3.3.8. Constraint for Initialization
3.3.9. Constraints on Non-Negativity
3.4. Objective Function
4. Case Study
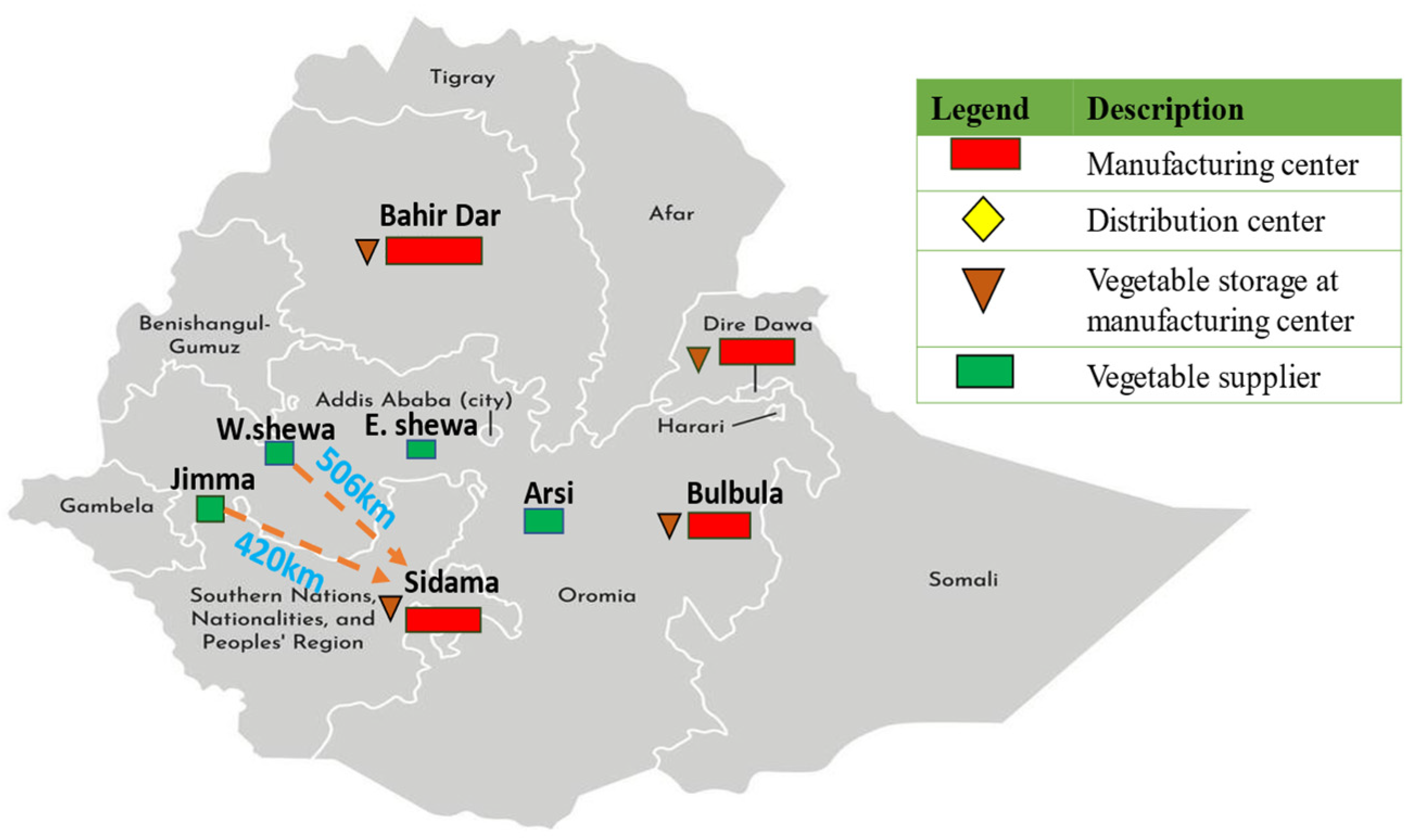
4.1. Candidate Location
4.2. Demand for Tomato
4.3. Data
5. Result and Discussion
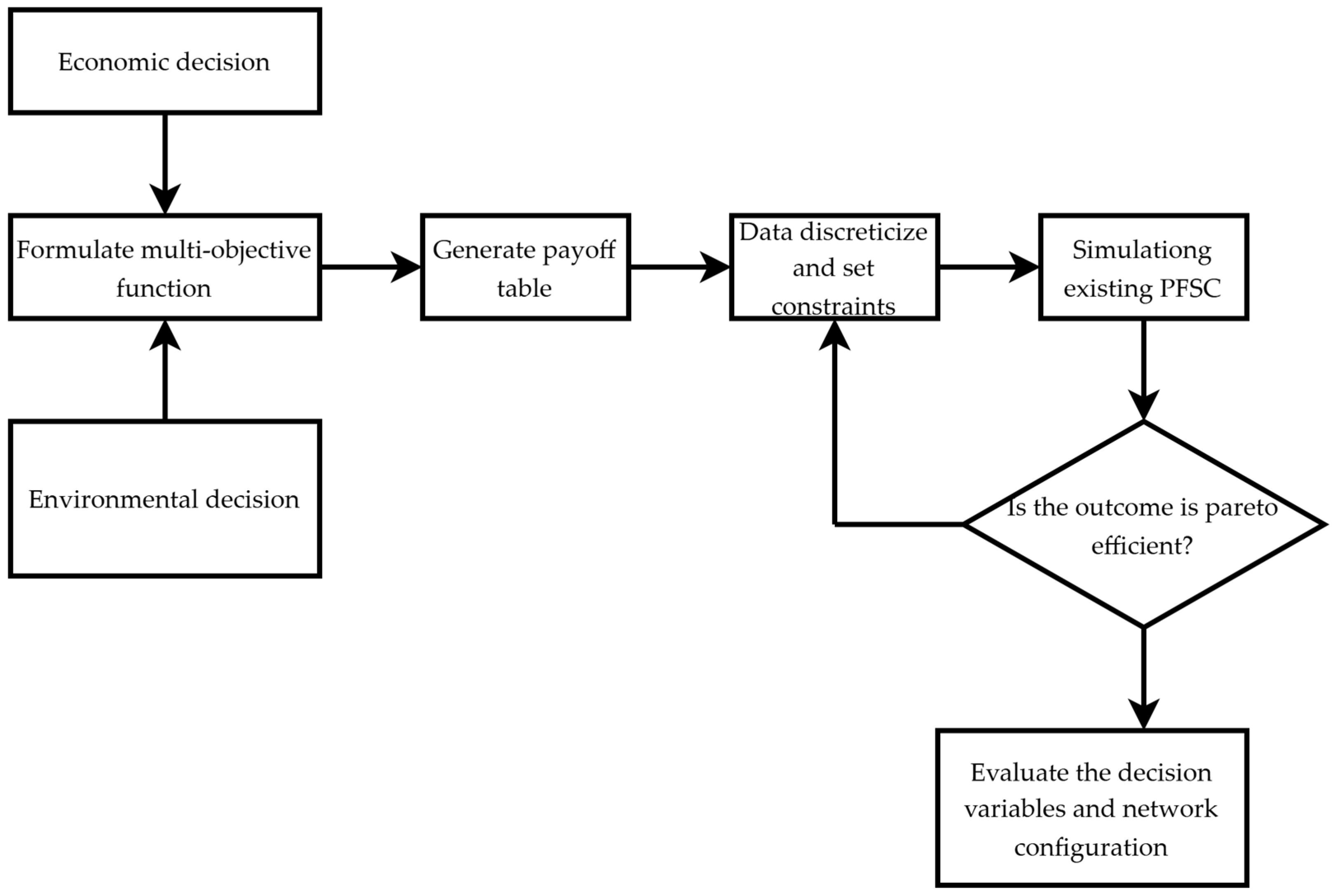
5.1. Multi-Objective Optimization Approach for Strategic and Tactical Decision Making
5.1.1. Case I
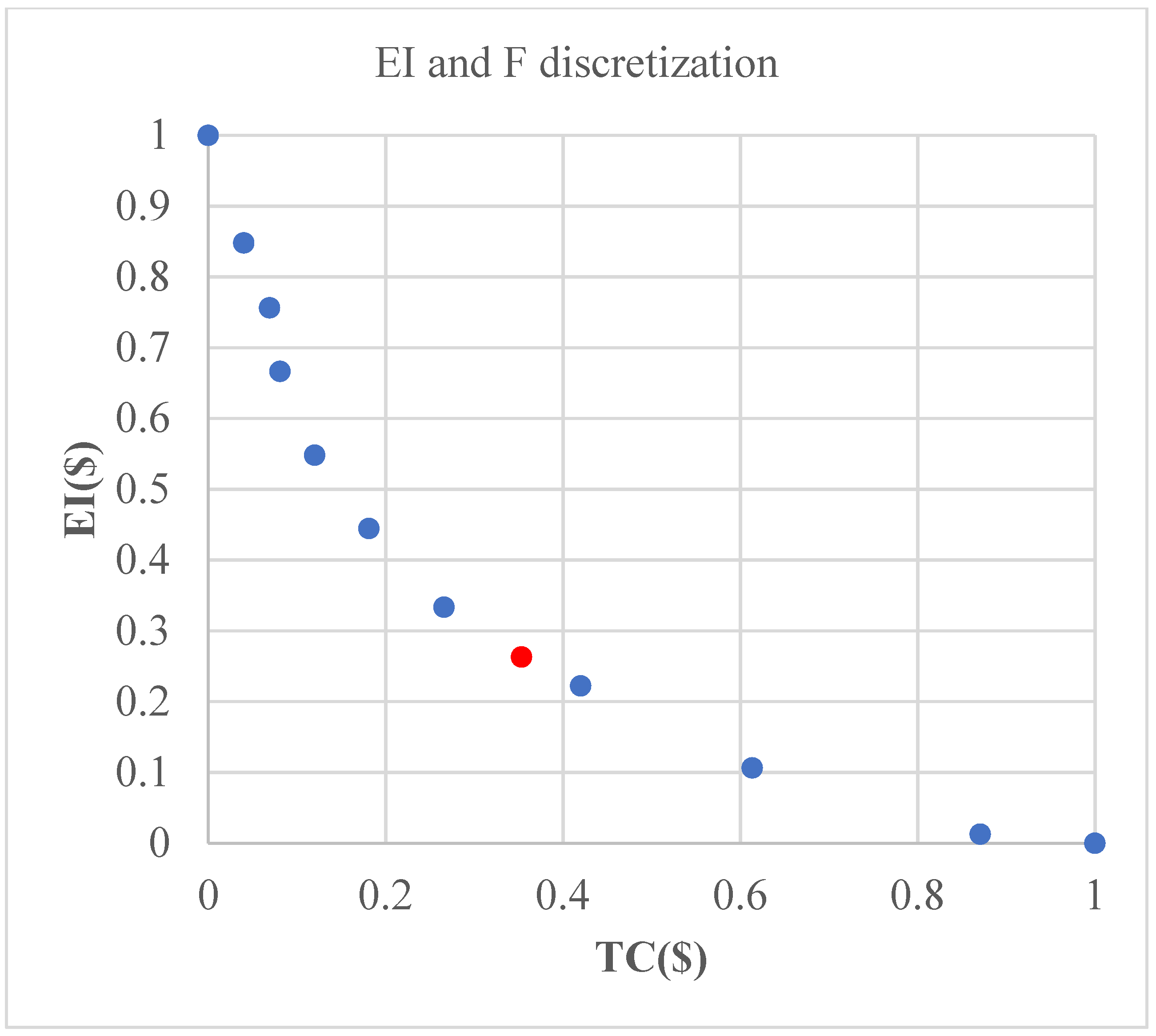
EI Discretization
5.1.2. Case II
EI and TC Discretization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reavis, M.; Ahlen, J.; Rudek, J.; Naithani, K. Evaluating Greenhouse Gas Emissions and Climate Mitigation Goals of the Global Food and Beverage Sector. Front. Sustain. Food Syst. 2022, 5, 789499. [Google Scholar] [CrossRef]
- Castillo-Díaz, F.J.; Belmonte-Ureña, L.J.; López-Serrano, M.J.; Camacho-Ferre, F. Assessment of the sustainability of the European agri-food sector in the context of the circular economy. Sustain. Prod. Consum. 2023, 40, 398–411. [Google Scholar] [CrossRef]
- MoA, Ministry of Agriculture. Transforming Ethiopian Agriculture, Briefing for Agricultural Scholars Consultative Forum. United Nations Conference Center. Addis Ababa (UNCC), April 2019. Available online: https://citizenengagement.nepad.org/pdf/20231005145754.pdf (accessed on 19 November 2022).
- Esteso, A. Conceptual framework for designing agri-food supply chains under uncertainty by mathematical program. Int. J. Prod. Res. 2018, 56, 4418–4446. [Google Scholar] [CrossRef]
- Soto-Silva, W.E.; Nadal-Roig, E.; Gonz´alez-Araya, M.C.; Pla-Aragones, L.M. Operational research models applied to the fresh fruit supply chain. Eur. J. Oper. Res. 2016, 251, 345–355. [Google Scholar] [CrossRef]
- Gustavsson, J.; Cederberg, C.; Sonesson, U. Global Food Losses and Food Waste: Extent, Causes, and Prevention; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2022. [Google Scholar]
- Osman, S.A.; Xu, C.; Akuful, M.; Paul, E.R. Perishable Food Supply Chain Management: Challenges and the Way Forward. Open J. Soc. Sci. 2023, 11, 349–364. [Google Scholar] [CrossRef]
- Hidayati, D.R. Enabling sustainable agrifood value chain transformation in developing countries. J. Clean. Prod. 2023, 395, 136300. [Google Scholar] [CrossRef]
- Rahbari, M.; Khamseh, A.A.; Mohammadi, M. Robust optimization and strategic analysis for agri-food supply chain under pandemic crisis: Case study from an emerging economy. Expert Syst. Appl. 2023, 225, 120081. [Google Scholar] [CrossRef]
- Yaghoubi, A.; Akrami, F. Proposing a new model for location—Routing problem of perishable raw material suppliers with using meta-heuristic algorithms. Heliyon 2019, 5, e03020. [Google Scholar] [CrossRef]
- Paredes-Rodríguez, A.M.; Osorio-Gómez, J.C.; Orejuela-Cabrera, J.P. Dynamic evaluation of distribution channels in a fresh food supply chain from a sustainability and resilience approach. Alex. Eng. J. 2024, 106, 42–51. [Google Scholar] [CrossRef]
- Pan, L.; Shan, M. Optimization of Sustainable Supply Chain Network for Perishable Products. Sustainability 2024, 16, 5003. [Google Scholar] [CrossRef]
- Nasiri, M.M.; Mousavi, H.; Nosrati-Abarghooee, S. A green location-inventory-routing optimization model with simultaneous pickup and delivery under disruption risks. Decis. Anal. J. 2023, 6, 100161. [Google Scholar] [CrossRef]
- Mousavi, R.; Bashiri, M.; Nikzad, E. Stochastic production routing problem for perishable products: Modeling and a solution algorithm. Comput. Oper. Res. 2022, 142, 105725. [Google Scholar] [CrossRef]
- Manouchehri, F.; Nookabadi, A.S.; Kadivar, M. Production routing in perishable and quality degradable supply chains. Heliyon 2020, 6, e03376. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhao, Q.; Santibanez Gonzalez, E.D.R.; Xi, X. Sourcing and production decisions for perishable items under quantity discounts and its impacts on environment. J. Clean. Prod. 2021, 317, 128455. [Google Scholar] [CrossRef]
- Komijani, M.; Sajadieh, M.S. An integrated planning approach for perishable goods with stochastic lifespan: Production, inventory, and routing. Clean. Logist. Supply Chain 2024, 12, 100163. [Google Scholar] [CrossRef]
- Huang, X.; Yang, S.; Wang, Z. Optimal pricing and replenishment policy for perishable food supply chain under inflation. Comput. Ind. Eng. 2021, 158, 107433. [Google Scholar] [CrossRef] [PubMed]
- Grillo, H.; Alemany, M.M.E.; Ortiz, A.; Fuertes-Miquel, V.S. Mathematical modelling of the order-promising process for fruit supply chains considering the perishability and subtypes of products. Appl. Math. Model. 2017, 49, 255–278. [Google Scholar] [CrossRef]
- Gioia, D.G.; Felizardo, L.K.; Brandimarte, P. Simulation-based inventory management of perishable products via linear discrete choice models. Comput. Oper. Res. 2023, 157, 106270. [Google Scholar] [CrossRef]
- Esteso, A.; Alemany, M.M.E.; Ortiz, Á. Impact of product perishability on agri-food supply chains design. Appl. Math. Model. 2021, 96, 20–38. [Google Scholar] [CrossRef]
- Ekanayake, C.; Bandara, Y.M.; Chipulu, M.; Chhetri, P. An order fulfilment location planning model for perishable goods supply chains using population density. Supply Chain Anal. 2023, 4, 100045. [Google Scholar] [CrossRef]
- Ge, H.; Goetz, S.J.; Cleary, R.; Yi, J.; Gómez, M.I. Facility locations in the fresh produce supply chain: An integration of optimization and empirical methods. Int. J. Prod. Econ. 2022, 249, 108534. [Google Scholar] [CrossRef]
- de Keizer, M.; Haijema, R.; Bloemhof, J.M.; van der Vorst, J.G.A.J. Hybrid optimization and simulation to design a logistics network for distributing perishable products. Comput. Ind. Eng. 2015, 88, 26–38. [Google Scholar] [CrossRef]
- Hiassat, A.; Diabat, A.; Rahwan, I. A genetic algorithm approach for location-inventory-routing problem with perishable products. J. Manuf. Syst. 2017, 42, 93–103. [Google Scholar] [CrossRef]
- Abbasian, M.; Sazvar, Z.; Mohammadisiahroudi, M. A hybrid optimization method to design a sustainable resilient supply chain in a perishable food industry. Environ. Sci. Pollut. Res. 2023, 30, 6080–6103. [Google Scholar] [CrossRef]
- Miao, X.; Pan, S.; Chen, L. Optimization of perishable agricultural products logistics distribution path based on IACO-time window constraint. Intell. Syst. Appl. 2023, 20, 200282. [Google Scholar] [CrossRef]
- Govindan, K.; Jafarian, A.; Khodaverdi, R.; Devika, K. Two-echelon multiple-vehicle location–routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ. 2014, 152, 9–28. [Google Scholar] [CrossRef]
- Soto-Silva, W.E.; González-Araya, M.C.; Oliva-Fernández, M.A.; Plà-Aragonés, L.M. Optimizing fresh food logistics for processing: Application for a large Chilean apple supply chain. Comput. Electron. Agric. 2017, 136, 42–57. [Google Scholar] [CrossRef]
- Jonkman, J.; Barbosa-Póvoa, A.P.; Bloemhof, J.M. Integrating harvesting decisions in the design of agro-food supply chains. Eur. J. Oper. Res. 2019, 276, 247–258. [Google Scholar] [CrossRef]
- Biza, A.; Montastruc, L.; Negny, S.; Admassu, S. Strategic and tactical planning model for the design of perishable product supply chain network in Ethiopia. Comput. Chem. Eng. 2024, 190, 108814. [Google Scholar] [CrossRef]
- Biuki, M.; Kazemi, A.; Alinezhad, A. An integrated location-routing-inventory model for sustainable design of a perishable products supply chain network. J. Clean. Prod. 2020, 260, 120842. [Google Scholar] [CrossRef]
- Rajabi, R.; Shadkam, E.; Khalili, S.M. Design and optimization of a pharmaceutical supply chain network under COVID-19 pandemic disruption. Sustain. Oper. Comput. 2024, 5, 102–111. [Google Scholar] [CrossRef]
- Klöpffer, W. (Ed.) Background and Future Prospects in Life Cycle Assessment; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Reyes, T.; Gouvinhas, R.P.; Laratte, B.; Chevalier, B. A method for choosing adapted life cycle assessment indicators as a driver of environmental learning: A French textile case study. Anal. Manuf. 2020, 34, 68–79. [Google Scholar] [CrossRef]
- Üçtuğ, F.G.; Tekin, Z.; Dayıoğlugil, Z.; Ulusoy, E.; Oktaylar Keyik, Ş. Life cycle assessment of tomato paste production: A case study. J. Eng. Sci. 2024, 30, 119–127. [Google Scholar] [CrossRef]
- Vogtländer, J.G.; Bijma, A. The ‘virtual pollution costs ‘99’, a single LCA-based indicator for emissions. Int. J. Life Cycl. Assess. 2000, 5, 13–124. [Google Scholar]
- Eslami, E.; Abdurrahman, E.; Pataro, G.; Ferrari, G. Increasing sustainability in the tomato processing industry: Environmental impact analysis and future development scenarios. Front. Sustain. Food Syst. 2024, 8, 1400274. [Google Scholar] [CrossRef]
- Teferra, T.F. The cost of postharvest losses in Ethiopia: Economic and food security implications. Heliyon 2022, 8, e09077. [Google Scholar] [CrossRef] [PubMed]
- Maroulis, Z.B.; Saravacos, G.D. Food Processing Design. Available online: https://books.tarbaweya.org/static/documents/uploads/pdf/Food%20Process%20Design%20by%20Zacharias%20B.%20Maroulis%2C%20George%20D.%20Saravacos%20(z-lib.org).pdf (accessed on 3 March 2021).
- Miret, C.; Chazara, P.; Montastruc, L.; Negny, S.; Domenech, S. Design of bioethanol green supply chain: Comparison between first and second-generation biomass concerning economic, environmental and social criteria. Comput. Chem. Eng. 2016, 85, 16–35. [Google Scholar] [CrossRef]
- Parin, M.A.; Zugarramurdi, A. Investment and production costs analysis in food processing plants. Int. J. Prod. Econ. 1994, 34, 83–89. [Google Scholar] [CrossRef]
- Abiso, E.; Satheesh, N.; Hailu, A. Effect of storage methods and ripening stages on postharvest quality of tomato (Lycopersicom esculentum Mill) CV. Chali. Ann. Food Sci. Technol. 2015, 16, 127–137. [Google Scholar]
- Kitinoja, L. Exploring the Potential for Cold Chain Development in Emerging and Rapidly Industrializing Countries. 2014. Available online: https://www.researchgate.net/publication/294259640_Exploring_the_potential_for_cold_chain_development_in_emerging_and_rapidly_industrializing_countries (accessed on 19 November 2022).
- Ramos, M.A.; Boix, M.; Montastruc, L.; Domenech, S. Multi objective Optimization Using Goal Programming for Industrial Water Network Design. Ind. Eng. Chem. Res. 2014, 53, 17722–17735. [Google Scholar] [CrossRef]
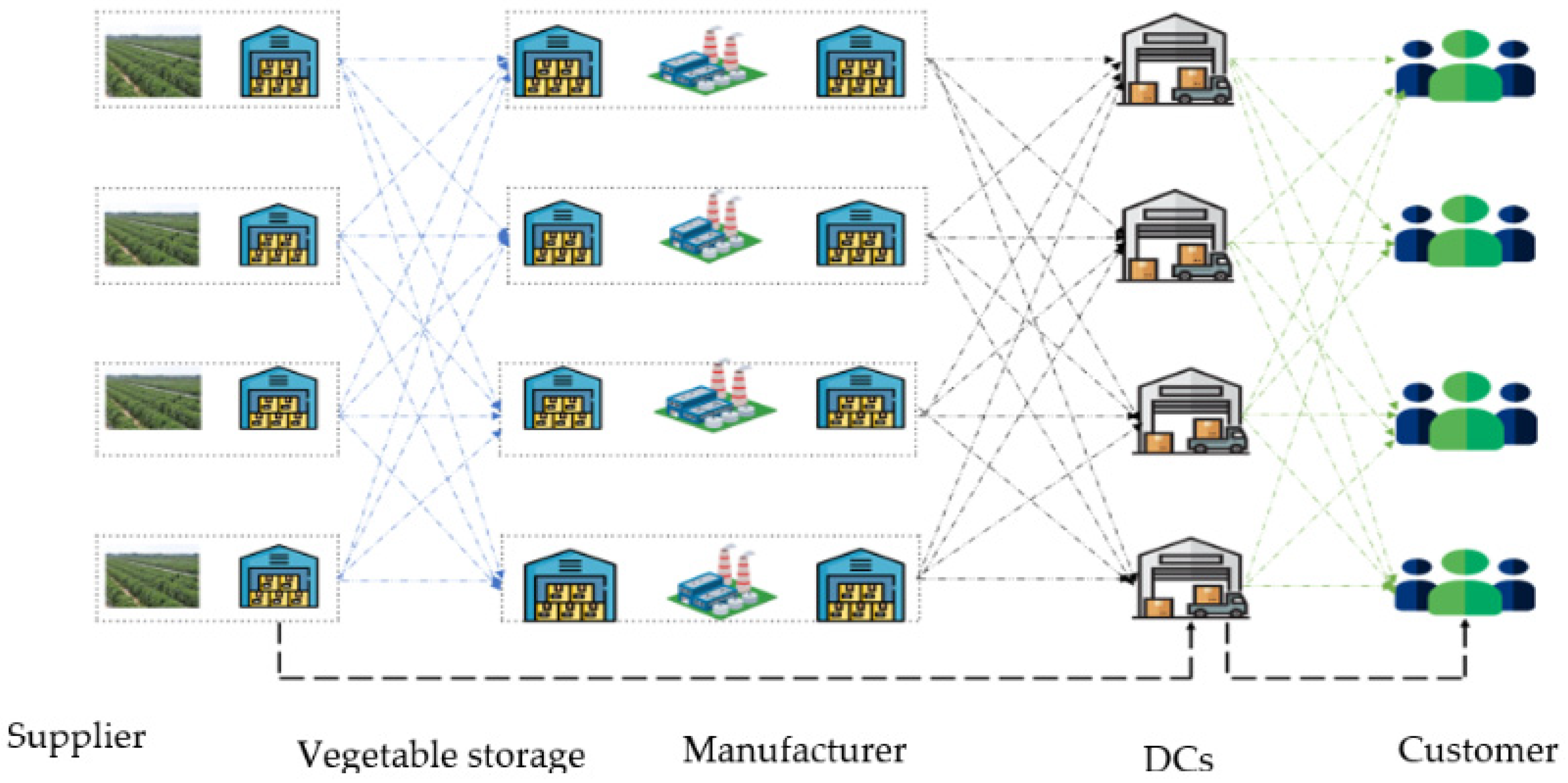
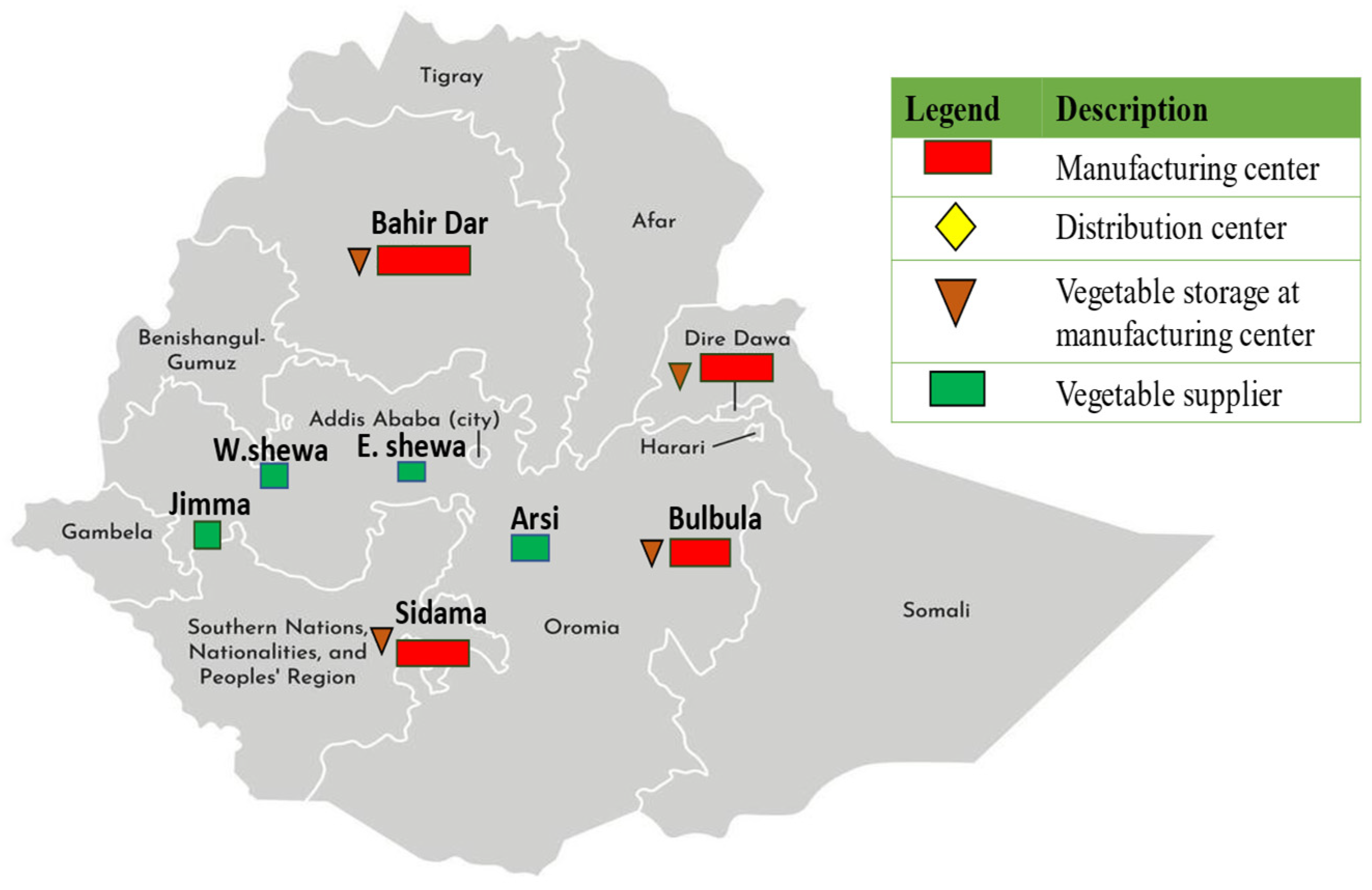
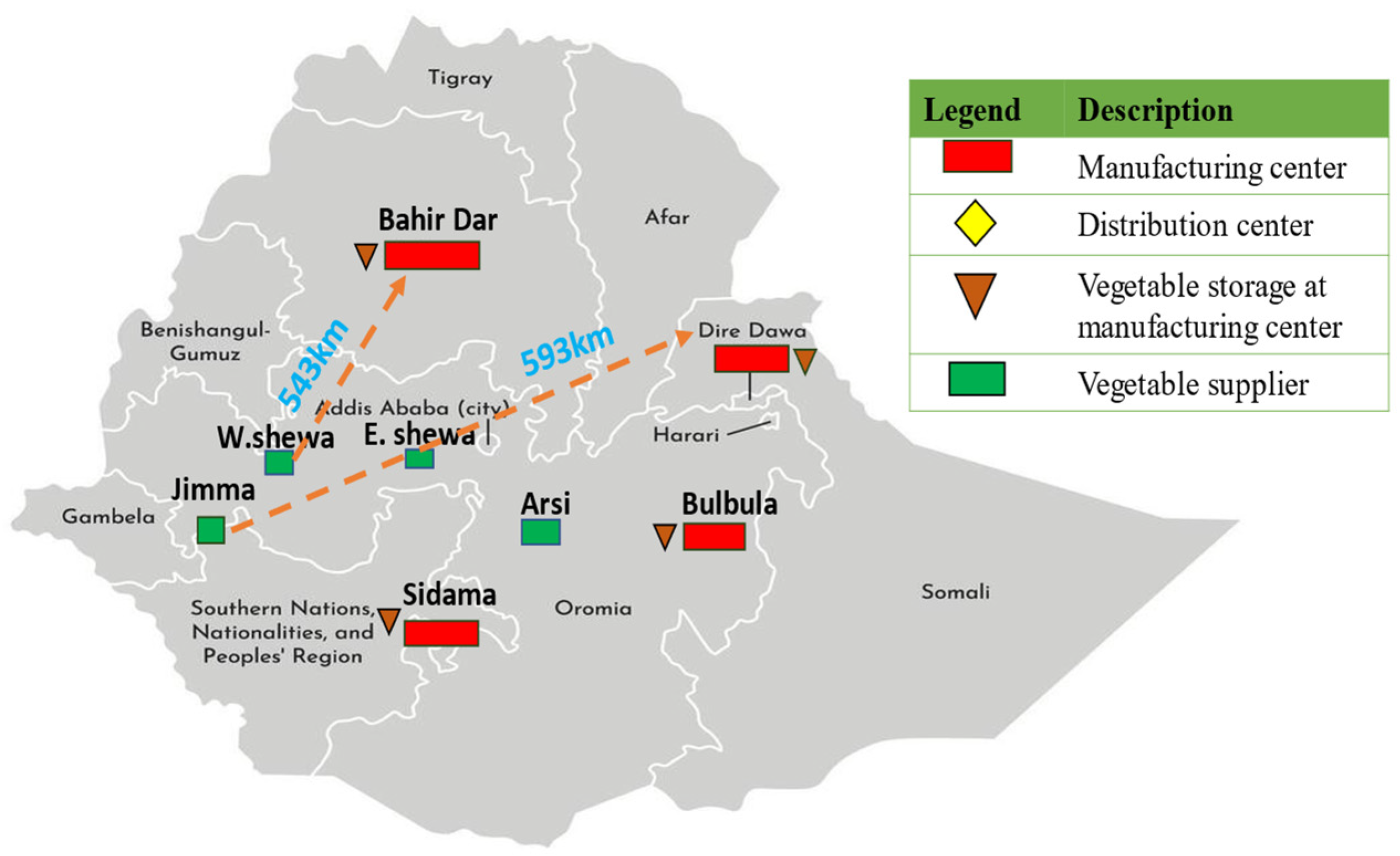
| Index Sets | |
| S | Suppliers; indexed by s Є S |
| M | Manufacturing centers; indexed by m Є M |
| D | Distribution centers; indexed by d Є D |
| K | Customers; indexed by k Є K |
| V | Vegetables; indexed by v Є V |
| P | Final products; indexed by |
| N | Intervals in the discount schedule; indexed by n Є N |
| A | Distribution center capacity; indexed by a Є A |
| E | Manufacturing center capacity; indexed by e Є E |
| T | Set time periods; index t Є T |
| Technical Parameters | |
| Deterioration rate of vegetable v, % | |
| Available amount of vegetable v at supplier s during period t, for processing, ton | |
| Available amount of vegetable v at supplier s during period t, for distribution, ton | |
| Conversion factor of vegetable v to product p, ton of product/ton of vegetable | |
| BC_LB1smv | Lower bound for the quantity of vegetable v shipped from supplier s to manufacturing center m to ensure business continuity in multi-sourcing strategy, ton |
| BC_UB1smv | Upper bound for the quantity of vegetable v shipped from supplier s to manufacturing center m to ensure business continuity in multi-sourcing strategy, ton |
| BC_LB2mdp | Lower bound for the quantity of product v shipped from manufacturing center m to distribution center d to ensure business continuity in multi-sourcing strategy, ton |
| BC_UB2mdp | Upper bound for the quantity of vegetable v shipped manufacturing center m to distribution center d to ensure business continuity in multi-sourcing strategy, ton |
| BC_LB3dkp | Lower bound for the quantity of product p shipped from distribution center d to customer k to ensure business continuity in multi-sourcing strategy, ton |
| BC_UB3dkp | Upper bound for the quantity of product p shipped from distribution center d to customer k to ensure business continuity in multi-sourcing strategy, ton |
| BC_LB4sdv | Lower bound for the quantity of vegetable v shipped from supplier s to distribution center m to ensure business continuity in multi-sourcing strategy, ton |
| BC_UB4sdv | Upper bound for the quantity of vegetable v shipped from supplier s to distribution center d to ensure business continuity in multi-sourcing strategy, ton |
| BC_LB5dkv | Lower bound for the quantity of vegetable v shipped from distribution center d to customer k to ensure business continuity in multi-sourcing strategy, ton |
| BC_UB5dkv | Upper bound for the quantity of vegetable v shipped from distribution center d to customer k to ensure business continuity in multi-sourcing strategy, ton |
| Product p demand at customer k during period t, ton | |
| Vegetable v demand by customer k during period t, ton | |
| Capacity of supplier s in supplying vegetable v per period t | |
| Capacity to process product p at manufacturing center m with capacity e, ton | |
| Storage capacity of product p at distribution center d with capacity a, ton | |
| Lower bound of interval n of discount schedule that is offered by supplier s for vegetable v, ton | |
| Lower bound for the safety stock for vegetable v at manufacturing center m, ton | |
| Upper bound of interval n of discount schedule that is offered by supplier s for vegetable v, ton | |
| M | Big M, a sufficiently large number |
| Weight of the long-term costs | |
| Weight of the mid-term costs | |
| Economic parameters | |
| Holding cost for vegetable v at supplier s for a period t, $/ton | |
| Holding cost for vegetable v at manufacturer m for a period t, $/ton | |
| Holding cost for product p at manufacturer m for a period t, $/ton | |
| Holding cost for product p at distribution center d for a period t, $/ton | |
| Holding cost for vegetable v at distribution center d for a period t, $/ton | |
| Unit manufacturing cost of product p in manufacturing center m, $/ton | |
| Periodic operating cost for distribution center d with capacity level a, $ | |
| Unit price of vegetable v within interval n of discount schedule that is offered by supplier s, $/ton | |
| Transportation distance for vegetable v from supplier s to manufacturer m, Km | |
| Transportation distance for product p from manufacturer m to distribution center d, Km | |
| Transportation distance for product p from distribution center d to customer k, Km | |
| Transportation distance for vegetable v from supplier s to distribution center d, Km | |
| Transportation distance for vegetable v from distribution center d to customer k, Km | |
| Sales price for product p in customer k, $/ton | |
| Unit transportation cost of product p, $/ton Km | |
| Unit transportation cost of vegetable v, $/ton Km | |
| Investment cost for opening manufacturing center m with capacity e, $ | |
| Investment cost for opening distribution center d with capacity a, $ | |
| Eco cost parameters | |
| Production eco-costs for manufacturing center m with capacity e | |
| Utilization eco-costs for distribution center d with capacity a | |
| Transport eco-costs for vegetable v from supplier s to manufacturing center m | |
| Transport eco-costs for product p from manufacturing center m to distribution center | |
| Transport eco-costs for product p from distribution center d to customer k | |
| Transport eco-costs for vegetable v from supplier s to distribution center d | |
| Transport eco-costs for vegetable v from distribution center d to customer k | |
| Decision variables | |
| Binary variable with value 1 when manufacturing center with capacity level e is established at location m; 0 otherwise | |
| Binary variable with value 1 when distribution center with capacity level a is established at location d; 0 otherwise | |
| Binary variable with value 1 when manufacturing center m is supplied by supplier s for vegetable v in period t; 0 otherwise | |
| Binary variable with value 1 when distribution center d is supplied by manufacturing center m for product p in period t; 0 otherwise | |
| Binary variable with value 1 when customer k is supplied by distribution center d for product p in period t; 0 otherwise | |
| Binary variable with value 1 when order quantity of manufacturing center m for vegetable v falls within interval n of the discount schedule of supplier s in time period t; 0 otherwise | |
| Amount of vegetable v obtained from supplier during period t, ton | |
| Amount of vegetable v transformed to product at manufacturing center m during time period t, ton | |
| Amount of product p produced from vegetable at manufacturing center m during time period t, ton | |
| Inventory level at supplier center s of vegetable v at the end of period t, ton | |
| Inventory level at manufacturing center m of vegetable v at the end of period t, ton | |
| Inventory level at manufacturing center m of product p at the end of period t, ton | |
| Inventory level at distribution center d of product p at the end of period t, ton | |
| Inventory level at distribution center d of vegetable v at the end of period t, ton | |
| Quantity of order for vegetable v that is released from manufacturing center m to supplier s within discount schedule n in the time period t, ton | |
| Quantity of order for vegetable v that is released from manufacturing center m to supplier s in the time period t, ton | |
| Quantity of order for product p that is released from distribution center d to manufacturing center m in the time period t, ton | |
| A fraction of order for product p by customer k that can be satisfied by distribution center d in the time period t, ton | |
| Quantity of vegetable v supplied from supplier s to distribution center d in the time period t, ton | |
| Quantity of vegetable v supplied from distribution center d customer k during the time period t, ton | |
| Mono Objective Optimization | Total Cost Value (Millions $) | Eco-Costs Value (Millions $) |
|---|---|---|
| Min TC | 52.634 | 122.5 |
| Min EI | 83.628 | 69.07 |
| Scenario | EImax ($) | EImin ($) | EI ($) | TC ($) | CPU Time (min), Intel 2.80-GHz |
|---|---|---|---|---|---|
| A | 112.25 | 107.45 | 112.25 | 52.634 | 0.68 |
| B | 107.45 | 102.65 | 105.69 | 52.789 | 46 |
| C | 102.65 | 97.856 | 101.72 | 52.902 | 75 |
| D | 97.85 | 93.08 | 97.85 | 53.09 | 27 |
| E | 93.055 | 88.266 | 92.73 | 53.098 | 244 |
| F | 88.266 | 83.466 | 88.261 | 53.334 | 155 |
| G | 83.466 | 78.666 | 83.466 | 53.663 | 17 |
| H | 78.666 | 73.666 | 78.666 | 54.259 | 148 |
| I | 73.666 | 69 | 73.666 | 55.006 | 1579 |
| K | 69.391 | 56.123 | 1141 |
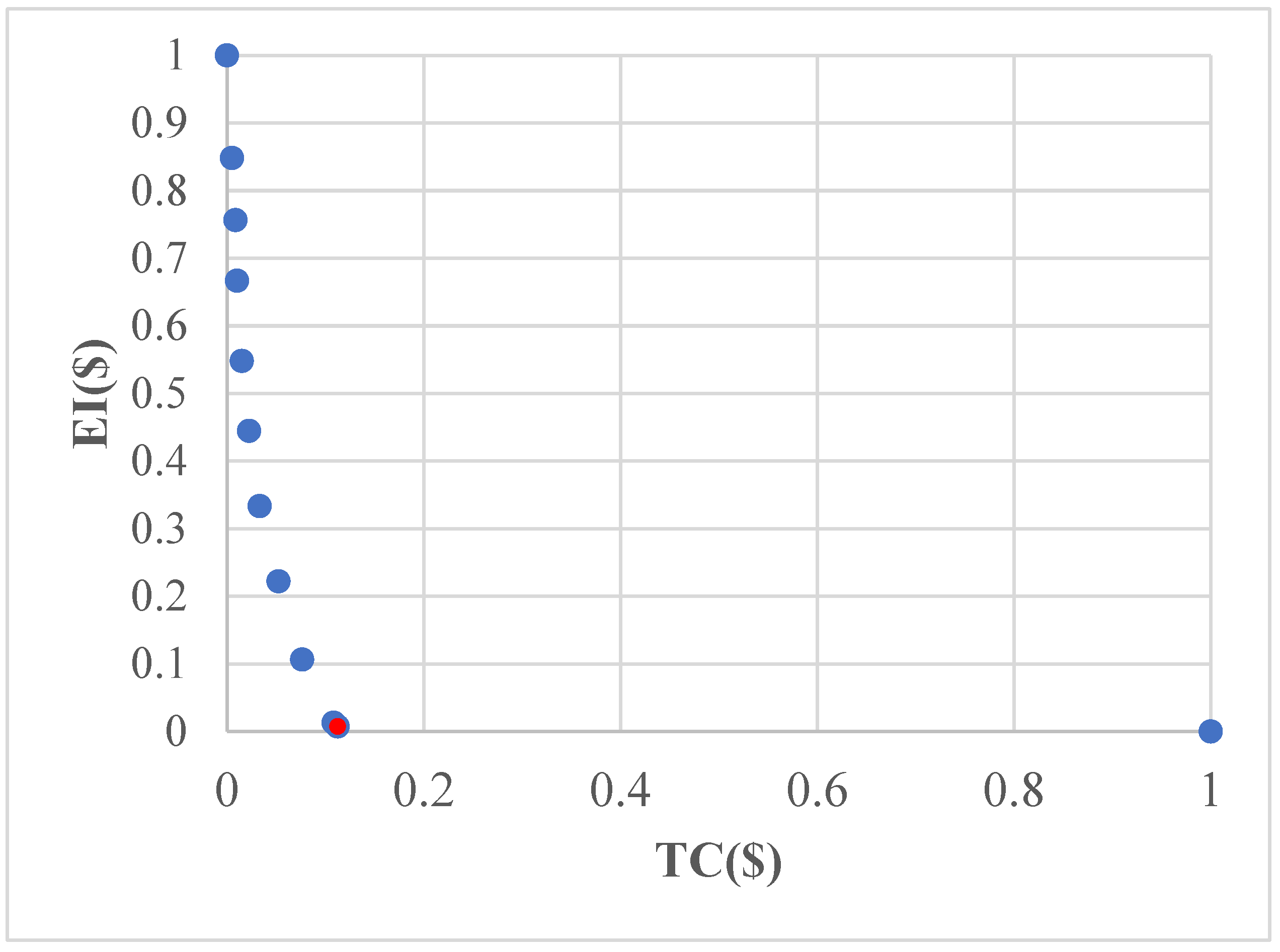
| Pareto Front Absolute | Pareto Front Relative | CPU Time (min), Intel 2.80-GHz | |||
|---|---|---|---|---|---|
| Scenario | TC ($) | EI ($) | TC | EI | |
| 52.634 | 112.25 | 0 | 1 | ||
| A | 52.634 | 112.25 | 0 | 1 | 0.68 |
| B | 52.789 | 105.69 | 0.04009312 | 0.84807781 | 46 |
| C | 52.901 | 101.72 | 0.06906363 | 0.7561371 | 75 |
| D | 52.947 | 97.85 | 0.08096223 | 0.66651227 | 27 |
| E | 53.098 | 92.737 | 0.12002069 | 0.54810097 | 244 |
| F | 53.334 | 88.26 | 0.1810657 | 0.44441871 | 155 |
| G | 53.662 | 83.466 | 0.26590792 | 0.33339509 | 17 |
| H | 54.258 | 78.666 | 0.42007243 | 0.22223252 | 148 |
| I | 55.006 | 73.666 | 0.61355406 | 0.10643817 | 1579 |
| J | 54 | 80.43 | 0.35333678 | 0.26308476 | 1836 |
| K | 56 | 69.625 | 0.87066736 | 0.01285317 | 1139 |
| 56.5 | 69.07 | 1 | 0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biza, A.; Montastruc, L.; Negny, S.; Emire, S.A. Integrated Economic and Environmental Dimensions in the Strategic and Tactical Optimization of Perishable Food Supply Chain: Application to an Ethiopian Real Case. Logistics 2025, 9, 80. https://doi.org/10.3390/logistics9030080
Biza A, Montastruc L, Negny S, Emire SA. Integrated Economic and Environmental Dimensions in the Strategic and Tactical Optimization of Perishable Food Supply Chain: Application to an Ethiopian Real Case. Logistics. 2025; 9(3):80. https://doi.org/10.3390/logistics9030080
Chicago/Turabian StyleBiza, Asnakech, Ludovic Montastruc, Stéphane Negny, and Shimelis Admassu Emire. 2025. "Integrated Economic and Environmental Dimensions in the Strategic and Tactical Optimization of Perishable Food Supply Chain: Application to an Ethiopian Real Case" Logistics 9, no. 3: 80. https://doi.org/10.3390/logistics9030080
APA StyleBiza, A., Montastruc, L., Negny, S., & Emire, S. A. (2025). Integrated Economic and Environmental Dimensions in the Strategic and Tactical Optimization of Perishable Food Supply Chain: Application to an Ethiopian Real Case. Logistics, 9(3), 80. https://doi.org/10.3390/logistics9030080





